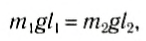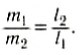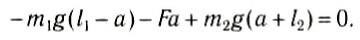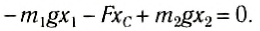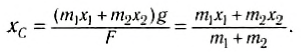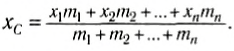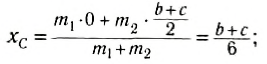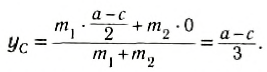Как найти центр тяжести двух шаров - Исправление недочетов и поиск решений вместе с Examum.ru

Два шара одинакового объема, цинковый и алюминиевый, скреплены в точке соприкосновения. Найдите положение центра тяжести системы двух шаров.

Спрятать решение

Решение.

Шары имеют одинаковый объем, плотность цинка больше плотности алюминия, следовательно, шар из цинка имеет большую массу. Масса шаров находится из формулы Тогда центр тяжести находится ближе к центру цинкового шара.

Запишем правило моментов

Находим расстояние от центра тяжести до центра цинкового шара

Ответ: на расстоянии 0,55R от центра цинкового шара.

Источник: Карпухина Е. А., Божинова Ф. Я. Сборник задач по физике для 10 класса, Х.: «Ранок», 2010 (№ 21.48)

Источник

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

Центр тяжести — геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.

На каждую точку тела в поле сил тяжести действует сила, а на все тело — равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.

Центр масс (центр инерции) — точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, — параллельными.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

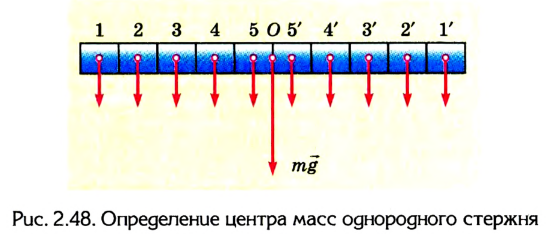
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О — середине стержня.

Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

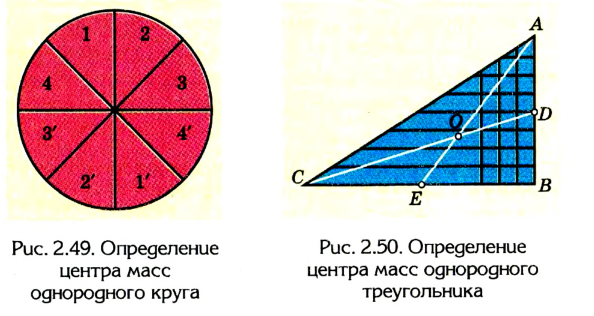
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

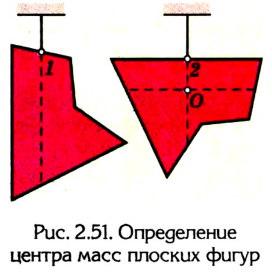
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

Заказать решение задач по физике

Центр тяжести тела и центр масс тела

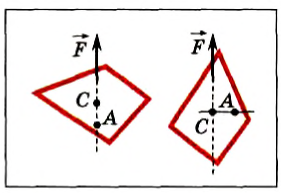
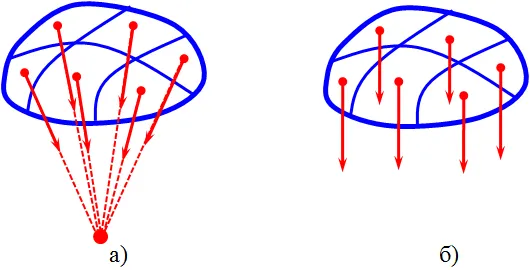
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

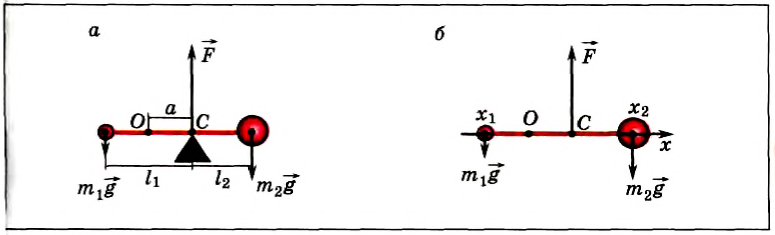
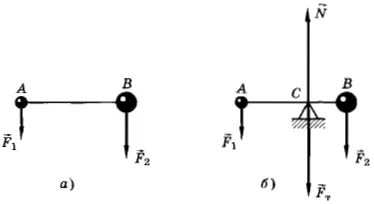
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

или

Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:

Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

Отсюда

При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

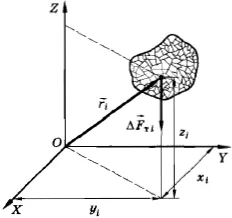
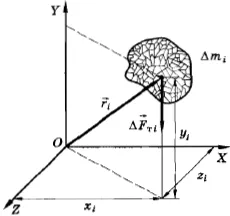
Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂…, m_n, и если известны координаты центров масс этих элементов x₁, x₂…, x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

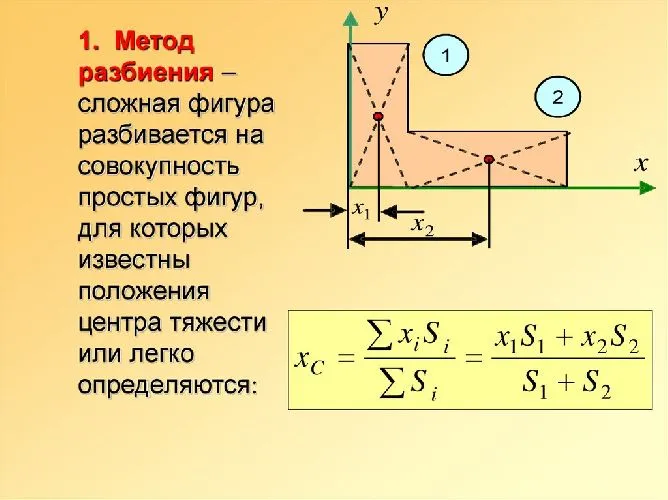
Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

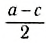
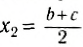
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х₁ = 0, y₁ =, а координаты центра масс линейки: , y₂ = 0 .
По формуле (3): .

Таким образом, центр масс угольника находится вне тела.

Главные выводы:

Центр тяжести — точка, в которой приложена сила тяжести.
Центр масс симметричных однородных тел находится в их геометрическом центре.
Координаты центра масс тела можно вычислить по формуле (3).

Импульс тела в физике
Замкнутая система в физике
Реактивное движение в физике
Освоение космоса — история, этапы и достижения с фотографиями
Международная система единиц СИ
Математика — язык физики
Законы Ньютона в физике
Гравитационные силы в физике

Источник

Тестирование онлайн

Центр тяжести

Центр тяжести тела — точка приложения силы тяжести (равнодействующей гравитационных сил).

Пусть тело состоит из двух шаров массами m₁ и m₂, насаженных на стержень, массой стержня можно пренебречь.

Система будет в равновесии, если опору разместить в центре тяжести, точке С. В этом случае векторная сумма моментов сил относительно точки С равна нулю, получим

Центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс.

Центр масс

Центр масс — точка пересечения прямых, вдоль которых действуют внешние силы, вызывающие поступательное движение тела. Это более общее понятие, чем понятие центра тяжести. Центр тяжести и центр масс часто совпадают. Центр масс симметричных тел находится в их геометрическом центре.

Определение центра масс*

Источник

Положение центра тяжести однородного тела зависит от формы опухоли, занимающей это тело, и называется центром тяжести этой опухоли.

§ 8.3. Центр тяжести

Импульс силы зависит от ее плеч, а значит, и от точки приложения силы. Положение точки приложения силы очевидно при воздействии силы на кабель, пружину или другое тело. Но что можно сказать о точке приложения силы тяжести?

Особенность гравитации в том, что она воздействует на тело не в какой-то один момент времени, а на весь объем тела. Строго говоря, они не параллельны, так как сила тяжести на отдельные элементы тела направлена к центру Земли. Однако размеры всех структур на Земле намного меньше их радиуса. Поэтому почти все эти силы можно рассматривать как параллельные.

Равновесной силой всех параллельных гравитационных сил, действующих на отдельные элементы тела (при любом данном положении тела в пространстве), является точка, называемая центром тяжести.

Определение центра тяжести тела простой формы

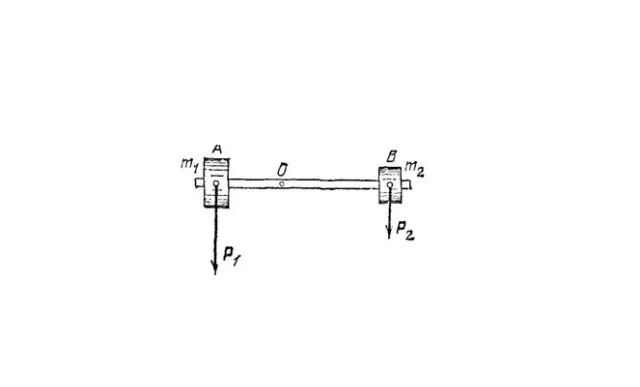
Сначала найдем положение центра тяжести в простейшем случае, когда тело состоит из двух шаров разной массы, соединенных со стержнем. Кроме того, длина стержня значительно превышает длину луча сферы. Тогда шары можно рассматривать как материальные точки (рис. 8.4, A).

Поэтому в материальных точках A и B, связанных с оголенным стержнем, силы тяжести₁ и₂в одно и то же время. Геометрическая сумма этих сил является результирующей гравитационной силой.

А также силы, направленные к центру Земли₁ и₂а его мера упругости равна сумме измерений добавленных сил.

Положение центра тяжести, т. е. точки приложения результирующей силы, можно определить, используя тот простой факт, что тело, закрепленное на оси, проходящей через центр тяжести С, должно находиться в равновесии. Ведь относительно этой оси моменты сил тяжести т и силы реакции опоры

С другой стороны, согласно равновесному состоянию (8.2.5), можно записать₁d₁ -f₂d₂ = 0, где d₁ = ac и d₂ = CBS — это оружие власти₁ и₂ Поэтому.

Равенство (8.3.2) определяет положение центра тяжести тела. Точки реализации параллельно генерируемых гравитационных сил делят расстояние между точками приложения этих сил на участки, обратно пропорциональные характеристикам сил.

Нахождение центра веса тела является важной технической проблемой, поскольку положение центра веса определяет устойчивость мостов, плотин, зданий, телебашен, автомобилей и ракет при запуске. Поэтому необходимо ознакомиться с тем, как располагаются различные формы весовых центров.

Нахождение центра тяжести тел

Технологии и повседневная жизнь представляют тело в совершенно разных формах. Часто они состоят из турника и диска (осевого колеса, спортивного турника и т.д.). Многие плоские формы состоят из прямоугольных и треугольных пластин. При определении положения центра тяжести таких тел легко определить положение центра тяжести отдельных частей простой формы. Для простых форм положение центра тяжести можно быстро определить с учетом симметрии.

Например, центр тяжести однородного стержня находится четко в центре стержня (рис. 8.5). Все однородные формы с центром симметрии имеют центр тяжести, совпадающий с этим центром. Круги имеют прямоугольники, включая их геометрические центры и пересечения диагоналей. Однако центр тяжести может находиться и вне тела (например, в кольце или полой сфере).

Определив положение центров тяжести компонентов тела в сложной геометрии, можно найти, где находится центр тяжести всего тела. Это делается путем замены тела системой материальных точек. Каждый из них расположен в центре тяжести соответствующей части тела и массы этой части (рис. 8.6).

ПРИМЕЧАНИЯ. Силовое поле — это область пространства в каждой точке, где к материальной частице приложена сила, зависящая от положения этой частицы. Например, поле, создаваемое магнитом, действует на движение заряженной частицы.

2. Способы нахождения центра тяжести

Метод симметрии. Этот метод основан на том, что Если однородное тело имеет элемент симметрии (зеркало, вал или уровень центральной симметрии), то его центр тяжести должен находиться на этом элементе.

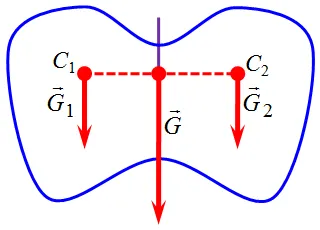
Действительно, предположим, что тело имеет уровень симметрии P. Тогда две его «половинки» имеют эквивалентные по модулю и совместному действию притяжения ɛ (ɛ vec g_ ) и ɛ (ɛ vec g_ ), с точками c₁ и в₂ (полуцентры тяжести) симметричны относительно плоскости зеркала (рис. 8.4).

Рисунок 8.4. позиционная симметрия центра тяжести зеркала

Гравитация ĩ (ĩ vec g ), практикуемая во всем теле, является результатом линейной ĩ (ĩ vec g_ ) и ĩ (ĩ vec g_ ) и должна применяться вдоль линии, проходящей через центральную часть.₁ c₂ принадлежит уровню P. Поэтому центр тяжести тела на линии действия ⌘ (⌘ vec g_ ) находится на том же уровне.

Путем аналогичных рассуждений можно доказать, например, что центры тяжести образующих измерительных тел находятся на одной оси.

Пример. Пересечение диагоналей прямоугольника является его центром симметрии. Поэтому центр тяжести однородного («компактного») прямоугольника находится в точке пересечения его диагоналей (рис. 8.5).

Рисунок 8.5.Центр тяжести параллелограмма.

То же самое относится к прямоугольнику, составленному из двух пар брусков одинаковой длины и одинаковой плотности.

Если однородное тело имеет много уровней или осей симметрии, его центр тяжести находится на их пересечении. Это связано с тем, что он должен принадлежать каждому из этих уровней (осей).

Пример. Корабль с загруженными трюмами можно рассматривать как тело, разделенное на части. Сам корпус судна выступает в качестве одного из них, а некоторые позиции груза — в качестве других. Во время обрезки координаты центра изменяются — согласно (8.3a), положение центра тяжести всего грузового контейнера также изменяется. С его помощью можно добиться максимальной устойчивости лодки и избежать ее опрокидывания при сильных толчках. Напротив, неспособность зафиксировать вес может сделать центр тяжести нежелательным и опрокинуть лодку.

Для упрощения расчетов исследуемое тело делится на небольшое количество частей максимально простой формы.

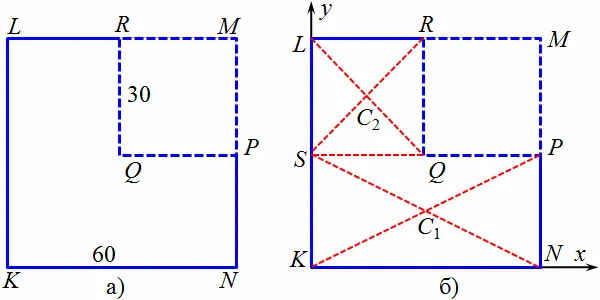
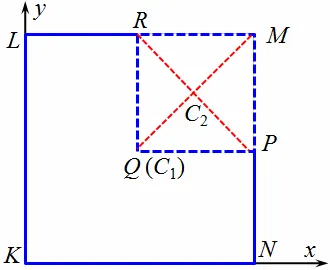
Пример. Из квадрата клмн размером 60 см вырежьте квадрат MPQR со стороной 30 см (рис. 8.6 A). Найдите полученный центр тяжести.

Разделите исходное тело на две части: прямоугольник kspn и квадрат slrq. Разрежьте исходное тело на две части: с₁ и в₂ — их центры тяжести. Введите систему координат в начало точки k, при этом ось x направьте вдоль стороны kn, а ось y — вдоль kl (рис. 8.6 b).

Исходя из вышеизложенного, c₁ пересечение диагоналей KSPN. В указанной системе координат x заканчивается на.₁ = 30 см и размещение y₁ = 15 см. Аналогично, c₂ (диагональное пересечение SLRQ) находится на расстоянии sq /2 = 15 см от оси y и ks + sl /2 = 45 см от оси x, x₂ = 15 см, y₂ = 45 см. площадь s₁ и с₂KSPN и SLPQ равны соответственно 60-30 = 1800 см2 и 30-30 = 900 см2. Используя формулу (8.3a), найдите координаты точки C — центра тяжести большого квадрата с разрезом:

3. Центры тяжести некоторых однородных тел

Центр тяжести стержня находится в его середине. Это следует из того, что стержень симметричен относительно этой точки (рис. 8.10).

Рис. 8.10. Центр тяжести однородного стержня

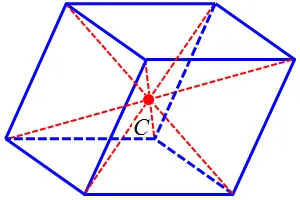
Как было сказано ранее, центр тяжести параллелограмма находится в точке пересечения его диагоналей. Аналогично, центр тяжести параллелепипеда (однородного или «собранного» из плоских поверхностей равной поверхностной плотности или ребер равной единичной плотности) также находится на пересечении его диагоналей (рис. 8.11).

Рис. 8.11. Центр тяжести однородного параллелепипеда

Центр тяжести площади треугольника находится на пересечении его медиан (рис. 8.12).

Рис. 8.12. Центр тяжести однородного треугольника

それを証明しましょう。 Разрежьте треугольник на полоски, параллельные одной стороне. Сделайте полоски настолько тонкими, чтобы каждую из них можно было приблизить к сегменту. В этом случае сила тяжести, действующая на треугольник в целом, будет эквивалентна системе сил, действующих на середины полос (рис. 8.13).

Эти средние точки заполняют медиану треугольника, проведенную по выбранной стороне. Следовательно, центр тяжести (точка приложения равнодействующей гравитационных сил, действующих на все полосы) находится на этой медиане.

Разрезав исходный треугольник на тонкие полоски, параллельные другой стороне, мы можем показать, что его центр тяжести принадлежит другой медиане. Но все диаметры треугольника пересекаются в одной точке. Таким образом, это точное положение центра тяжести, которое мы ищем.

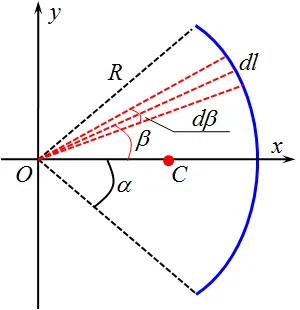
Далее найдите положение центра тяжести равномерной дуги окружности с центральным углом 2 a и радиусом R. Давайте введем систему координат, как показано на рисунке 8.14.

Рис. 8.14. Определение центра тяжести равномерной дуги окружности

Используя метод симметрии, можно легко убедиться, что искомая точка C расположена на Ox, т.е. y_c = 0. Остается найти координату x_c 。 Для этого разделите дугу на небольшие отрезки и соедините их концы с вершиной угла. Затем он будет разделен на небольшие углы. Поскольку длины отрезков, разделяющих дугу, малы, каждый из них можно рассматривать как отрезок прямой длиной dl = R dβ, где dβ — радиальная мера соответствующего угла.

Пусть β — угол между осью Ox и отрезком, соединяющим точку O с центром сегмента раздела (см. рис. 8.14). Тогда отклонение x центра тяжести этой дуги приблизительно равно R cos β. Подставим это значение x в формулу (8.3 b). Вместо объема V используем длину дуги R -2 α, вместо множителя dV под интегралом используем найденное ранее значение dl, а угол β лежит в пределах от — α до α :

Таким образом, центр тяжести однородной дуги расположен на ее оси симметрии на расстоянии ( R sin α )/α от ее центра.

4. Пример расчета координат центра тяжести

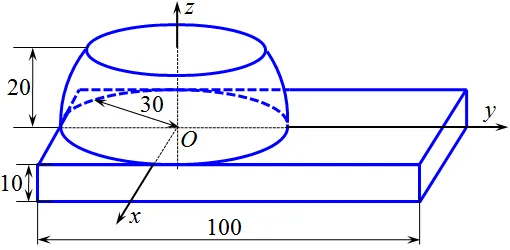
Полусфера с усеченной вершиной помещена на коробчатое основание в форме прямоугольного параллелепипеда, состоящего из плоских поверхностей. Срезанная часть заменяется плоской «крышкой» в форме круга. Определите положение центра тяжести полученного тела, предполагая, что все его элементы однородны и имеют одинаковую поверхностную плотность. Размеры указаны в см (рис. 8.18).

Исследуемый объект состоит из четырех других объектов более простой формы — параллелепипеда, круга и поверхности полусферы, от которой «отрезается» отрезок. Радиус полусферы равен R = 30 см, а высота полученного отрезка 20 см, поэтому высота отрезанного отрезка равна 10 см.

Введем систему координат, начиная с центра полусферы O, как показано на рисунке 8.18. Ось Ox расположена вдоль короткого горизонтального ребра параллелограмма, ось Oy — вдоль длинного ребра, а ось Oz — вертикально вверх. Поскольку объект симметричен относительно плоскости Oyz, дистальное положение центра тяжести C равно нулю. Необходимо найти растяжение и ширину этой точки. Используя методы деления и отрицательного объема, эти координаты можно найти по следующему уравнению.

$y_=fracy_+S_y_+S_y_-S_y_>+S_+S_-S_>,; z_=fracz_+S_z_+S_z_-S_z_>+S_+S_-S_>.$

(8.5)

Указатель «1» обозначает параллелограмм, «2» — полусферу, «3» — круг и «4» — усеченный сегмент (его площадь обозначается символом «-«). Поскольку структура состоит из поверхностных элементов, вышеуказанные типы относятся к площадям, а не к объемам.

Второе по величине ребро параллельного шестигранника равно диаметру полусферы, поэтому его поверхность равна S.₁ = 2- (100-60 + 100-10 + 60-10) = 15200 см2; центр тяжести на этой диаграмме находится на расстоянии 100/2 = 50 см от левой стороны и 20/2 = 10 см от вершины. Начало координат O находится на 30 см выше левого края параллелограмма, поэтому координаты центра тяжести на рис. 1 равны y₁ = 20 см, z₁ = -5 см.

На рис. 2 показано сечение сферы высотой H = R. Центр находится в точке O, ось симметрии — Oz. Площадь s₂ = 4π — 302/2 = 1800π см2 и координаты его центра тяжести y₂ = 0 см, z₂ = 30-30/2= 15 см.

Очевидно, что центр тяжести окружности находится в точке (0; 0; 20). Радиус этой окружности равен (Lo_SQRT = sqrt ) см, поэтому площадь S равна.₃ = 500πcm2.

Площадь купола разрезанной сферы равна S₄ = 2π — 30 — 10 = 600π см2. Линия центра тяжести y₄ = 0 см, ширина z₄ = 30-10 / 2 = 25 см.

（ Подставляя параметры, найденные в (8.5), получаем_c ≈ 14,80 см, z_c ≈ -0,34 см; следовательно, C (0; 14,80; -0,34). Как и ожидалось, центр тяжести с самого начала сместился вправо (поскольку рис. 1 асимметричен относительно Oz) и вниз (площадь, а значит и вес параллелепипеда, приходится на сферическое сечение).

Построение состояния задачи показывает, что треугольник является прямоугольным и что центр тяжести лежит на горизонтальной линии, проходящей через центр диска. Предполагается, что ось x является осью x. Чтобы решить эту проблему, сложную форму необходимо разделить на несколько частей. В каждой части можно найти нужную точку.

Понятие центра тяжести

Рассмотрим плоский однородный диск. Подвешенные на нити, они начинают вращаться под действием силы тяжести, за исключением одного. Только если нить соединена с центром диска, вращения не происходит и устанавливается равновесие.

Точка, в которой суммарный гравитационный момент всех частей тела равен нулю, называется центром тяжести. Когда объект рассматривается в однородном гравитационном поле, центр тяжести твердого тела совпадает с центром тяжести. В общем случае это не так.

Рисунок 1: Центр тяжести в неоднородном гравитационном поле.

Центр тяжести используется только по отношению к твердым телам в гравитационном поле. В противном случае его использование бессмысленно.

Рассмотрим два тела, прикрепленных к голому стержню. Система висит на нити и находится в равновесии. Следующей точкой, в которой закрепляется нить, является центр тяжести. Равенство моментов силы дает отношения:.

Рисунок 2. Два центра тела закреплены стержнями.

По полученным результатам можно определить положение центров некоторых нормальных однородных тел. Например, центр тяжести стержня находится в его центре, а центр тяжести сферы описывается центром тяжести параллельности ее поверхности и пересечением ее диагоналей.

Способы определения центра тяжести

Аналитический метод часто используется для однородных тел простой геометрии. Человек вычисляет центр тяжести трехмерной фигуры следующим образом.

$ r_c = frac cdot iiint limits_v r dv $, где v — объем тела.

Для плоских форм:.

$ r_c = frac cdot iiint limits_s r ds $, где s — поверхность тела.

Для равномерных линий:.

$ r_c = frac cdot iiint limits_l r dl $, где l — длина линии.

Общий случай, когда тело может иметь неоднородную и сложную форму, очень сложен. Используются следующие методы.

Первый способ осуществляется путем подвешивания к телу нитей из разных частей (вдоль нитей проводятся линии с пересекающимися центрами тяжести) или гирь (например, через весы разрешается автомобиль). (Существуют задачи, аналогичные тем, которые решаются для двух тел, закрепленных друг с другом стержнями).

Второй метод заключается в разделении всего тела на участки, где можно легко найти центр тяжести, используя следующие типы

Рисунок 3.Метод разделения.

Наконец, третий метод основан на принципе, что центр тяжести симметричного тела находится на уровне вала или симметрии. В принципе, этот метод используется для упрощения предыдущих методов.

Центр тяжести человека находится вблизи пятого поясничного позвонка. В этом случае вертикальное положение считается неустойчивым. Стремление тела вперед или назад создает гравитационный момент и вызывает нарушения равновесия. Поэтому нормальное мышечное напряжение необходимо для того, чтобы стоять прямо на одном месте.

Источник

Секция Физика

Определение местоположения центра тяжести твердых тел

Исследовательская работа

Дыбулина Ксения Сергеевна и Коровин Дмитрий Алексеевич,

обучающиеся 9 «А» класса Некрасовской СОШ

п. Некрасовское Ярославской области

Научный руководитель – Глазкова Светлана Борисовна,

учитель физики МБОУ Некрасовской СОШ

п. Некрасовское Ярославской области

г. Ярославль, 2019 г.

Оглавление:

Введение 3
Теоретическая часть 3

Понятие о центре тяжести 3
Методы определения центра тяжести 3
Виды равновесия твердых тел 6
Условия равновесия 6

Практическая часть 7

Ι. Экспериментальная проверка условий устойчивого равновесия тела, опирающегося

на твердую поверхность 7

Исследование зависимости устойчивости тела, опирающегося на твердую

поверхность от положения центра тяжести. 7

Исследование зависимости устойчивости тела, опирающегося на твердую

поверхность от высоты предмета 7

Исследование зависимости устойчивости тела, опирающегося на твердую

поверхность от величины площади опоры 7

ΙΙ. Определение центра тяжести плоской пластины сложной формы используя

разные методы. 8

Определение центра тяжести методом разбиения и методом отрицательных

площадей 8

Определение центра тяжести методом подвешивания 9

ΙΙΙ. Определение центра тяжести системы из двух шаров разной массы, соединенных

стержнем 9

ΙV. Определение центра тяжести тела правильной формы с полостью и установление устойчивого равновесия проволочного уголка 10

Заключение 10

5. Список использованных источников и литературы 11

6. Приложения 12

Введение

При создании машин, механизмов и различных конструкций зданий, мостов, телевизионных вышек и т.д. важно знать, при каких условиях они будут устойчивыми, т.е. находиться в равновесии. Равновесие тела неразрывно связано с его центром тяжести. Центр тяжести имеется у каждого тела. Определение центра тяжести тел и выяснение устойчивости их положения имеет большое практическое значение. Понятие центра тяжести в школьном курсе обучения физике даётся в седьмом классе и отводится всего один урок. В десятом классе эту тему изучают всего два часа. Поэтому этих знаний у учащихся недостаточно для изучения темы «Статика» при подготовке к ЕГЭ. Этим мотивируется выбор темы нашего исследования.

Цель: определение центра тяжести тел аналитическим и опытным путями.

Задачи:
1. Изучить научную литературу по теме «Центр тяжести тел» из раздела «Статика».

2. Узнать методы определения центра тяжести тел различной формы.

3. Выяснить условия устойчивости твердых тел.

Методы исследования: теоретические, экспериментальные, практические, анализ.

Объект исследования: центр тяжести.

Предмет исследования: нахождение центра тяжести у твердых тел.

Средства и приборы для измерения: штатив с лапкой и муфтой, линейка, транспортир, нить, иголка, картон, циркуль, бруски деревянные, бруски железные, проволока медная разного поперечного сечения, шарик пластмассовый, шарик металлический, стержень из пластмассы.

2. Теоретическая часть

2.1 Понятие о центре тяжести Каждое тело можно представить, как систему материальных частиц, взаимодействующих с Землей. Суммарный результат этого взаимодействия—равнодействующая элементарных сил тяжести. Точка приложения этой равнодействующей называется центром тяжести тела. Поскольку элементарные силы тяжести образуют систему параллельных сил, то центр тяжести обладает всеми свойствами центра параллельных сил. Следовательно, при любом положении тела в пространстве положение центра тяжести остается неизменным. Центр тяжести — это геометрическая точка, которая может быть расположена и вне тела (например, диск с отверстием, полый шар и т.п.). (1) 2.2 Методы определения центра тяжести: метод симметрии, метод разбиения, метод отрицательных масс, метод подвешивания. Метод симметрии опирается на положения: 1. Если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости; 2. Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси. 3.Если однородное тело имеет две оси симметрии, то центр тяжести тела лежит в точке пересечения диагоналей.

4. Центр тяжести однородного тела вращения лежит на оси вращения.

Метод разбиения заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны. (3) Составить формулы для определения координат центра тяжести сечения: Пусть сила тяжести равна приложена в точке С (рис.1) с координатами x, у, z. Приложим теперь к телу в другой точке внешнюю силу F такую, чтобы тело находилось в равновесии (подвесить тело в точке D). На тело действуют только две силы и , то согласно условию равновесия: +=0. Сила равна по модулю и противоположна по направлению силе . Разобьем тело на элементы (материальные точки) и запишем условие равновесия, заменяя равнодействующей совокупность элементарных сил тяжести: =0, где =— сила тяжести, действующая на произвольный малый элемент массой . === ( m=— масса тела).Таким образом, равнодействующая направлена вниз и равна сумме всех элементарных сил тяжести.

Выполняется и II условие равновесия для моментов всех сил относительно любой неподвижной оси. (ось ОZ) (рис. 2). Момент М равнодействующей и момент М’ силы должны в сумме давать при равновесии нуль: М’ + М = 0 Момент равнодействующей относительно какой-нибудь неподвижной оси равен сумме моментов всех элементарных сил тяжести относительно той же оси. Момент силы равен произведению силы на плечо. Для силы плечом является координата элемента малой массы . Поэтому момент силы равен: , а общий момент всех сил тяжести равен: Точка, в которой приложена суммарная сила , имеет координату х. Тогда суммарная сила создает момент относительно той же оси ОZ, равный , то Координаты точки приложения равнодействующей всех параллельных сил тяжести:, где — масса тела. Вторая и третья координаты точки приложения суммарной силы:

(6). Преобразуем числитель и знаменатель дроби:

ΣΔmi xi=m1x1 +m2x2 +…= ρV1x1 +ρV2x2 +…=ρS1h x1+ρS2h x2+…; m=m1+m2+…=ρV1+ ρV2+…= =ρS1h+ρS2h +… Числитель и знаменатель сократить на ρh, тогда имеем формулы вида:

Где S 1, S2, S3 – площади профилей, мм2; х1, х2, х3, …у1, у2, у3, мм — координаты их центров тяжести относительно выбранных осей координат.

Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба, и показать расстояние от центра тяжести до координатных осей.

Выполнить проверку правильности решения, для чего можно изменить положение координатных осей (или одной оси) и найти координаты центра тяжести относительно новых осей. Положение центра тяжести не зависит от того, как выбрана система координатных осей. (2)

Метод отрицательных масс или отрицательных площадей, отрицательных объемов. Этот метод заключается в том, что тело, имеющее свободные полости, полагают сплошным, а массу свободных полостей считают отрицательной. Вид формул для определения координат центра тяжести при этом не меняется. Зная величину F1 площади фигуры с контуром А и координаты х1 и у1 её центра тяжести С1, а также площадь F2 части, вырезанной по контуру В, и координаты х2 и у2 её центра тяжести С2, можно вычислить координаты центра тяжести оставшейся части фигуры. При этом площадь оставшейся части должна быть равна разности площадей F1 и F2.

ХС= ( F1х1 — F2х2) / F1 — F2 уС = ( F1у1 — F2 у2) / F1 — F2

Метод подвешивания. Плоская фигура подвешивается на иглу сначала в точке А, а потом в точке В. С помощью отвеса, закреплённого на той же игле, на фигуре прочерчивают линию, соответствующую нити отвеса. Центр тяжести т. С будет находиться в точке пересечения вертикальных линий, нанесённых при подвешивании фигуры в точках А и В. (5)

Виды равновесия твердых тел: устойчивое, неустойчивое и безразличное.

– Устойчивое равновесие — это равновесие, при котором выведенное из положения равновесия тело вновь к нему возвращается. При таком равновесии, центр тяжести тела располагается ниже оси вращения и находится на вертикальной прямой, проходящей через эту ось. Равновесие устойчиво, если при малом отклонении от положения равновесия есть сила, стремящаяся вернуть его в это положение. Устойчиво такое положение, в котором его потенциальная энергия минимальна.

– Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия, не возвращается в начальное положение. При неустойчивом равновесии центр тяжести тела расположен выше оси вращения и находится на вертикальной прямой, проходящей через эту ось.

–Безразличное равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, не меняет своего положения (состояния). При безразличном равновесии ось вращения тела проходит через центр тяжести.

Тело, не имеющее ось вращения (шар, лежащий на выпуклой, вогнутой и горизонтальной поверхностях, изображенный на рис. а).

Рис а (1) — неустойчивое положение равновесия

Рис а (2) — устойчивое положение равновесия

Рис а (3) – безразличное положение равновесия

Тело, имеющее ось вращения (например, однородная линейка, которая может вращаться вокруг оси, проходящей через точку О, изображенная на рисунке б)

Рис б (1) — неустойчивое положение равновесия, т.к. центр тяжести С выше оси вращения.

Рис б (2) — равновесие устойчивое, т.к. центр тяжести находится ниже оси вращения

Рис б (3) — равновесия безразличное, т.к. центр тяжести и ось вращения совпадают. (6)

Условия равновесия.

I условие равновесия: Тело находится в равновесии, если геометрическая сумма внешних сил, приложенных к телу, равна нулю. ∑ F=0. II условие равновесия: Сумма моментов сил, действующих по часовой стрелке, должна равняться сумме моментов сил, действующих против часовой стрелки. ∑ M по часовой =∑ M против часовой. М = F d, где М – момент силы, F — сила, d – плечо силы – кратчайшее расстояние от точки опоры до линии действия силы. (2)

Практическая часть

Ι. Экспериментальная проверка условий устойчивого равновесия тела, опирающегося на твердую поверхность.

Исследование зависимости устойчивости тела, опирающегося на твердую поверхность от положения центра тяжести.

Цель: Проверить зависимость устойчивости тела от положения центра тяжести тела.

Ход работы: 1) Собрать установку из наклонной плоскости, закрепленной в штативе. Упор закрепить к наклонной плоскости при помощи скотча, в виде спички (приложение 1 рис. 1)

2) Склеить несколько 3 деревянных бруска и один железный брусок двойным скотчем и установить полученное тело у упора (железный брусок внизу).

3) Аккуратно поднимать край наклонной плоскости до тех пор, пока бруски не опрокинутся.

4) Измерить высоту подъема края наклонной плоскости мерной лентой и результаты записать в таблицу 1(приложение 1).

5) Повторить опыты для тела, состоящего из того же количества брусков, изменяя только положение железного бруска (железный брусок вверху). Результаты записать в таблицу 1.

Вывод: Чем выше располагается железный брусок в теле (центр тяжести на большей высоте от наклонной плоскости), тем тело менее устойчиво, угол наклона плоскости наименьший. При более низком положении железного бруска (центр тяжести на меньшей высоте от наклонной плоскости), тело было более устойчиво. Падало тело в тот момент, когда точка центра тяжести располагалась не над площадью опоры тела, а выходила за ее пределы.

Исследование зависимости устойчивости тела, опирающегося на твердую поверхность от высоты предмета.

Цель: выяснить как зависит устойчивость тела от его высоты.

Ход работы: 1) Скрепить 2 деревянных бруска вместе двухсторонним скотчем и установить их у упора (приложение 2 рис.1)

2) Поднимать край наклонной плоскости до тех пор, пока бруски не опрокинутся.

3) Измерить высоту подъема края наклонной плоскости мерной лентой и результаты записать в таблицу 2 (приложение 2).

4) Выполнить опыты для тел, состоящих из разного количества брусков (четырех, восьми), изменяя тем самым высоту тела. Результаты занести в таблицу 2.

Вывод: Чем больше высота предмета, тем угол наклона плоскости был меньшим. Чем ниже было тело, тем оно более устойчиво. Так как тело было однородным, то центр тяжести находился в его центре.

Исследование зависимости устойчивости тела, опирающегося на твердую поверхность от величины площади опоры. Цель: выяснить зависимость устойчивости тела от площади его опоры.

Ход работы: 1) Скрепить 4 одинаковые столбика деревянных брусков вместе скотчем и установить их у упора (приложение 3 рис.1).

2) Поднимать край наклонной плоскости до тех пор, пока бруски не опрокинутся.

3) Измерить высоту подъема края наклонной плоскости мерной лентой и результаты записать в таблицу 3.

4) Выполнить опыты для тела, состоящего из 2 рядов деревянных брусков, изменяя тем самым площадь опоры тела. Результаты занести в таблицу 3 (приложение 3).

Вывод: Чем больше площадь опоры предмета, тем угол наклона плоскости был большим, тело более устойчиво. Центр тяжести тела в данном эксперименте находился в его центре.

Вывод: тело, опирающееся на горизонтальную плоскость, находится в равновесии, пока вертикальная линия, проходящая через центр тяжести, проходит внутри площади опоры; устойчивость тела зависит от положения центра тяжести, от величины площади опоры, от высоты предмета.

ΙΙ. Определение центра тяжести плоской пластины сложной формы используя разные методы.

Определение центра тяжести методом разбиения и методом отрицательных площадей.

Ход выполнения работы: 1) Выбрать сложную фигуру рис. 1

2) Разбить фигуру на простые фигуры:

2 прямоугольных треугольника, прямоугольник, круг.

Рис.1

Центры тяжести простых фигур С1, С2 — у прямоугольных треугольников это пересечение медиан, С3 – у прямоугольника это пересечение диагоналей.
Ось ОХ проходит по нижнему основанию фигуры от её начала, ось ОУ проходит перпендикулярно оси ОХ.
Вычисление площади простых фигур и координат центров тяжести:

Прямоугольного треугольника S1 = 0,5•5•45=112,5 (мм2), х1=3,4 мм, у1=45/3=15 мм

Прямоугольного треугольника S2 = 0,5•5•45=112,5 (мм2), х2=16,6 мм, у2=45/3 = 15 мм
Прямоугольника S3=10•45=450 (мм2), х3=10 мм, у3= 45/2= 22,5 мм
Круг S4 = πd2/4, А4 =3,14•82/4=50,24 (мм2), х4=10 мм, у4=15 мм

Вычисление координат центра тяжести сложной фигуры:

S 1 X1 + S2х2 + S3х3 – S4х4 =112,5•3,4 + 112,5•16,6 + 450•10 – 50,24•10 = 6247,6

S 1y1 + S 2y2 +S 3y3 –S4у4 =112,5•15+ 112,5•15+450•22,5 – 50,24•15 = 12746,4

S 1+S2+S3-S4 = 112,5+112,5+450-50,24 =624,76;

ХС = 6247,6/624,76 =10,0 мм, УС =12746,4/624,76 = 20,4 мм. Координаты центра тяжести фигуры: (10,0; 20,4). Погрешность измерения: ΔХ=1 мм+0,5 мм=1,5 мм, ΔУ=1мм+0,5мм=1,5 мм.

Правильность определения центра тяжести проверяется экспериментально: геометрический центр фигуры помещают на остриё иглы. Фигура находится в равновесии, значит, расчеты верны.

Определение центра тяжести методом подвешивания (фигура из опыта 2.1)

Ход работы: 1) Выполнить отверстия в фигуре. Просверлить три отверстия, края отверстий должны быть гладкими, а диаметр отверстий несколько больше диаметра иглы для подвешивания фигуры.

Подвесить фигуру сначала в одной точке (отверстии), прочертить карандашом линию, совпадающую с нитью отвеса. То же повторить при подвешивании фигуры в других точках.
Центр тяжести т. С будет находиться в точке пересечения вертикальных линий, нанесённых при подвешивании фигуры в этих точках (приложение 4).

Вывод: центр тяжести фигуры, найденный методами разбиения, и подвешивания совпал. Фигура находится в равновесии, значит, центр тяжести вычислен верно.

ΙΙΙ. Определение центра тяжести системы из двух шаров разной массы, соединенных стержнем.

Ход работы: 1) Соединить стержнем, массой которого можно пренебречь по сравнению с массами шаров, шары различных масс. Длина стержня значительно превышает радиусы шаров. Тогда шары можно считать материальными точками.

Точка приложения равнодействующей параллельных сил тяжести делит расстояние между точками приложения этих сил на отрезки, обратно пропорциональные модулям сил. Данное равенство определяет положение центра тяжести рассматриваемого тела. (5)
Измерили длину стержня: l=12,00+_0,15 см, массу шаров: m1=7,00+_0,01 г, m2=49,17+_0,01 г.

Вычисление местоположения центра тяжести: F1=m1g, F1=0,0686Н F2=m2g, F2=0,4819Н.

d1=0,105м=10,50 см d1=10,50+-0,15 см d2=12,00-10,50=1,50 см, d2=1,50+-0,15см.

По расчётам получили, что центр тяжести системы, состоящей из двух шаров, находится на расстоянии 10,5 см от центра шара меньшей массы. Закрепив систему на нити в данной точке, убедились, что стержень принимает горизонтальное положение, следовательно, система находится в равновесии. Погрешность измерения: Δd=1 мм+0,5 мм=1,5 мм=0,15см (приложение 5).

Вывод: Точка приложения равнодействующей параллельных сил тяжести делит расстояние между точками приложения этих сил на отрезки, обратно пропорциональные модулям сил.

ΙV. Определение центра тяжести тела правильной формы, у которой центр тяжести лежит вне фигуры и установление устойчивого равновесия проволочного уголка.

Ход работы: 1) Центр тяжести угольника т. С расположен в середине отрезка, соединяющего центры прямоугольников.

Определив положение центра тяжести относительно сторон уголка, рассчитать угол отклонения от вертикали при устойчивом равновесии для медных проволок, длиной м, имеющих разное поперечное сечение.
Проволока однородна и имеет одинаковое поперечное сечение вдоль всей длины, следовательно, центр тяжести находится в точке C, расположенной посередине отрезка C1C2 (см. рис.10). Из прямоугольного равнобедренного треугольника C 1 СВ с учётом, что C 1B= l/4 (l- полная длина проволоки). . Из треугольника C 1CA по теореме синусов , следует . , . , то sin α = 0,342. Следовательно, α = 200. Проведя эксперимент по установлению устойчивого равновесия проволочного уголка для медных проволок разного поперечного сечения, измерили угол отклонения от отвеса, угол равен 200. Вывод: угол отклонения проволочного уголка, занимающего устойчивое равновесие, вычисленный теоретическим и опытным путями оказался одинаковым. Если проволока имеет постоянное поперечное сечение и сделана из однородного материала, то результат не зависит от площади поперечного сечения проволоки (приложение 6).

Заключение

Нахождение центров тяжести тел является важной технической задачей, так как от положения центров тяжести зависит устойчивость мостов, плотин, зданий, телевизионных вышек, автомашин, ракет на старте и т.п. Поэтому необходимо знать методы нахождения центров тяжести тел. В технике и повседневной жизни мы встречаемся с телами самой различной формы. Часто они состоят из стержней и дисков (колесо на оси, спортивная штанга и т. д). Многие плоские фигуры состоят из прямоугольных и треугольных пластин. При определении положения центра тяжести подобных тел проще всего вначале определить положение центров тяжести отдельных его частей простой формы. У тел простой формы можно сразу указать положение центра тяжести, руководствуясь соображениями симметрии. У всех однородных фигур, имеющих центр симметрии, центр тяжести совпадает с этим центром.

Определив положения центров тяжести составных частей тела сложной формы, можно найти, где расположен центр тяжести всего тела. Для этого надо заменить тело системой материальных точек, каждая из которых помещается в центре тяжести соответствующей части тела и имеет массу этой части.

Если тело имеет неправильную форму или если оно неоднородно (например, в нем есть пустоты), то расчет положения центра тяжести часто затруднителен, и это положение удобнее найти посредством опыта. Подвешивая тело в разных точках и проводя вертикальные прямые, то все они пересекутся в одной точке. Эта точка и есть центр тяжести тела.

Вывод: 1. Тело, опирающееся на горизонтальную плоскость, находится в равновесии, пока вертикальная линия, проходящая через центр тяжести, проходит внутри площади опоры; устойчивость тела зависит от положения центра тяжести, от величины площади опоры, от высоты предмета.

Методы для определения центра тяжести тел: метод симметрии, метод разбиения, метод отрицательных масс, метод подвешивания.
Если центр тяжести тела занимает наинизшее положение по сравнению со всеми возможными соседними положениями, то равновесие устойчивое.

5.Список использованных источников и литературы

Билимович Б.Ф. Законы механики в технике. Пособие для учащихся. М., «Просвещение», 1975.
Иванов А.С., Проказа А.Т. Мир механики и техники: Кн. Для учащихся. – М.: Просвещение, 1993. – 223 с.: ил.
Лукьянов А.А. Нахождение центров тяжести плоских фигур разной формы. Потенциал, март, 2015 № 3 стр.48 -56.
Наумчик В.Н. Физика. Решение задач повышенной сложности. Мн.: «Мисанта», 2003. -320 с.
Элементарный учебник физики под редакцией академика Г.С. Ландсберга. Том 1. Механика. Теплота. Молекулярная физика. М., 1995 г., 656 стр. с ил.
Физика. 10 кл. Профильный уровень: учебн. для общеобразоват. учреждений / В.А. Касьянов. – 8-е изд., перераб. И доп. – М.: Дрофа, 2005. – 431, с.: ил.

6.Приложения

Приложение 1

Рис.1

Таблица 1 Зависимость устойчивости тела от положения центра тяжести тела

№ опыта	Положение железного груза	Высота подъема планки h, см	Среднее значение h, см
1	Самый нижний	26,0
2	Самый нижний	26, 5	26,27
3	Самый нижний	26,3
4	Самый верхний	14,5
5	Самый верхний	14,4	14,37
6	Самый верхний	14,2

Погрешность измерения: Δd=1 мм+0,5 мм=1,5 мм=0,15см

Приложение 2

Рис. 1

Таблица 2 Зависимость устойчивости тела, опирающегося на твердую поверхность от высоты предмета.

№ опыта	Количество брусков n шт	Высота h, см	Среднее значение h, см
1	2	25,5
2	2	25,3	25,3
3	2	25,1
4	4	19,6
5	4	19,4	19,4
6	4	19,3
7	8	11,0
8	8	11,2	11,2
9	8	11,4

Погрешность измерения: Δd=1 мм+0,5 мм=1,5 мм=0,15см

Приложение 3

Рис.1

Таблица 3 Зависимость устойчивости тела, опирающегося на твердую поверхность от величины площади опоры.

№ опыта	Площадь основания, см2	Высота подъема планки h, см	Среднее значение h, см
1	6	19,5
2	6	19,4	19,4
3	6	19,3
4	12	25,0
5	12	25,2	25,17
6	12	25,3

Погрешность измерения: Δd=1 мм+0,5 мм=1,5 мм=0,15см

Приложение 4

Приложение 5

Приложение 6

Источник