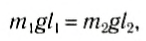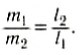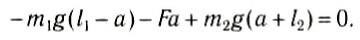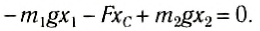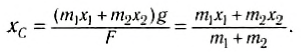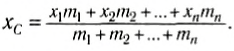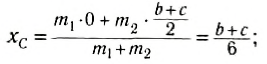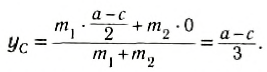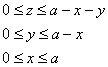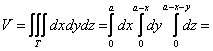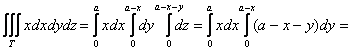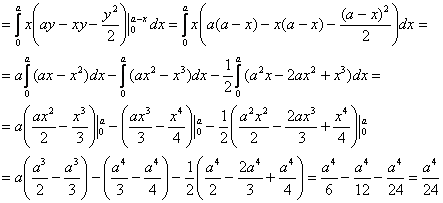Центр тяжести (центр масс):
Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.
Центр тяжести — геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.
На каждую точку тела в поле сил тяжести действует сила, а на все тело — равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.
Центр масс (центр инерции) — точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.
При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.
Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.
При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, — параллельными.
Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.
Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.
Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.
Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.
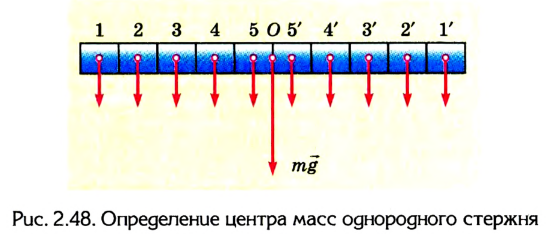
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О — середине стержня.
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.
Центр тяжести однородного стержня расположен в середине стержня.
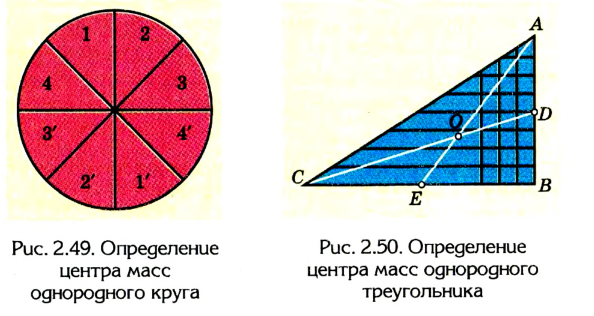
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.
Центр тяжести однородного круга совпадает с его центром.
Центр тяжести однородного треугольника находится в точке пересечения его медиан.
3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.
Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.
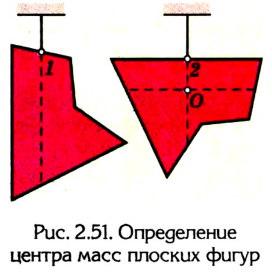
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.
Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.
Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.
- Заказать решение задач по физике
Центр тяжести тела и центр масс тела
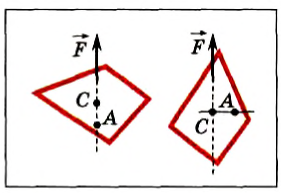
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.
Рис. 151
Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.
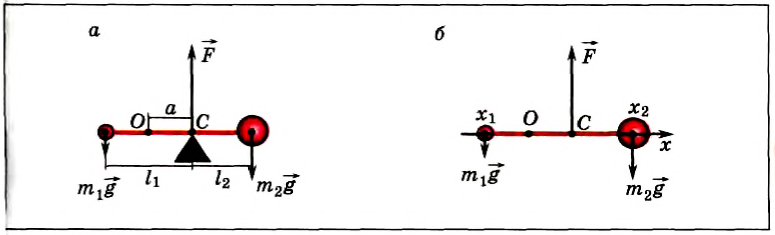
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:
или
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:
Рис. 152
Поскольку F=(m1 + m2)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х1, хс и х2. Запишем условие моментов относительно точки О:
Отсюда
При выводе этой формулы было использовано значение силы F = (m1 + m2) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии хс, определенном формулой (2).
Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.
Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.
Если произвольное тело можно разбить на n элементов, массы которых m1, m2…, mn, и если известны координаты центров масс этих элементов x1, x2…, xn относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:
Естественно, что такие же соотношения можно записать и для ус и zc. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m1 = 2m2). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C1) и линейки (C2).
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х1 = 0, y1 =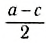
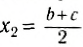
По формуле (3): .
Таким образом, центр масс угольника находится вне тела.
Главные выводы:
- Центр тяжести — точка, в которой приложена сила тяжести.
- Центр масс симметричных однородных тел находится в их геометрическом центре.
- Координаты центра масс тела можно вычислить по формуле (3).
- Импульс тела в физике
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
Центр тяжести тела, теория и онлайн калькуляторы
Центр тяжести тела
Как известно, сила тяжести тела равна векторной сумме сил тяжести, которые действуют на все материальные точки, на которые можно разбить рассматриваемое тело. Точку, к которой приложена результирующая сила тяжести, называют центром тяжести. Если известно положение центра тяжести, то можно считать, что на тело действует только одна сила тяжести, приложенная к центру тяжести.
Следует учитывать, что силы тяжести, действующие на отдельные элементы тела, направлены к центру Земли и не являются строго параллельными. Но так как размеры большинства тел на Земле много меньше ее радиуса, поэтому эти силы считают параллельными.
Определение центра тяжести тела
Определение
Центром тяжести называют точку, через которую проходит равнодействующая всех сил тяжести, действующих на материальные точки, на которые разбито рассматриваемое тело, при любом положении тела в пространстве.
Центр тяжести — это точка, относительно которой суммарный момент сил тяжести равен нулю при любом положении тела.
От положения центра тяжести зависит устойчивость всех конструкций.
Как найти центр тяжести?
Для нахождения центра тяжести тела сложной формы необходимо мысленно разбить тело на части простой формы и определить место нахождения центров тяжести для них. У тел простой формы центр тяжести определяют, используя их симметрию. Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.
Определив, где расположены центры тяжести отдельных частей тела, переходят к поиску места расположения центра тяжести тела в целом. Тело представляют в виде системы материальных точек. При этом каждая точка имеет массу своей части тела и располагается в ее центре тяжести.
Координаты центра тяжести тела
В трехмерном пространстве координаты центра тяжести для твердого тела нахояд как:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_c=frac{sumlimits_i{Delta m_iy_i}}{m};; \
z_c=frac{sumlimits_i{Delta m_iz_i}}{m} end{array}
right.left(1right),]
где $m$ — масса тела.$;;x_i$ — координата на оси X элементарной массы $Delta m_i$; $y_i$ — координата на оси Y элементарной массы $Delta m_i$; ; $z_i$ — координата на оси Z элементарной массы $Delta m_i$.
В векторной форме записи система уравнений (1) представляется как:
[{overline{r}}_c=frac{1}{m}sumlimits_i{m_i{overline{r}}_ileft(2right),}]
${overline{r}}_c$ — радиус — вектор, определяющий положение центра тяжести; ${overline{r}}_i$ — радиус-векторы, которые определяют положения элементарных масс.
Центр тяжести, центр масс и центр инерции тела
Считают, что центр тяжести тела совпадают с центром масс тела, если его размеры малы в сравнении с расстоянием до центра Земли. При этом формулы, которые определяют положение цента тяжести и центра масс тела совпадают с выражениями (1) и (2). В основной массе задач центр тяжести принимают совпадающим с центром масс тела.
Сила инерции в неинерциальных системах отсчета, движущихся поступательно, приложена к центру тяжести тела.
Но центробежная сила инерции (в общем случае) не приложена к центру тяжести, поскольку в неинерциальной системе отсчета на элементы тела действуют разные центробежные силы инерции (даже если массы элементов равны), так как расстояния до оси вращения разные.
Примеры задач с решением
Пример 1
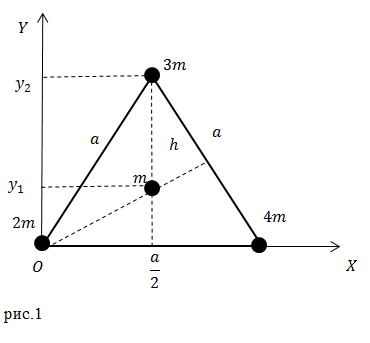
Задание: Каковы координаты центра тяжести системы из трех точечных масс, расположенных в вершинах и одной в центре равностороннего треугольника, со стороной равной $a (м)$ (рис.1)?
Решение: Определение для координат $x_c и y_c$ центра тяжести в нашем случае запишем в виде:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}(1.1);;]
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}(1.2).]
Из рис.1 мы видим, что соответствующие абсциссы точек равны:
[left{ begin{array}{c}
m_1=2m, x_1=0;; \
{rm }m_2=3m, x_2=frac{a}{2};; \
m_3=m, x_3=frac{a}{2};; \
m_4=4m, x_4=a. end{array}
right.left(1.3right).]
Тогда абсцисса центра тяжести получается равной:
[x_c=frac{2mcdot 0+3mcdot frac{a}{2}+mcdot frac{a}{2}+4mcdot a}{2m+3m+m+4m}=frac{6ma}{10m}=0,6a (м);]
Найдем ординаты точек.
[ begin{array}{c}
m_1=2m, y_1=0;; \
{rm }m_2=3m, y_2=frac{asqrt{3}}{2};; \
m_3=m, y_3=frac{asqrt{3}}{6};; \
m_4=4m, y_4=0. end{array}
left(1.4right).]
Для того чтобы найти ординату $y_2$ найдем, высоту в равностороннем треугольнике:
[h=sqrt{a^2-frac{a^2}{4}}=frac{asqrt{3}}{2}=y_2left(1.5right).]
Ординату $y_3$ найдем, учитывая, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, имеем:
[y_3=hcdot frac{1}{3}=frac{asqrt{3}}{6} left(1.6right).]
Вычислим ординату центра тяжести:
[y_c=frac{2mcdot 0+3mcdot frac{asqrt{3}}{2}+mcdot frac{asqrt{3}}{6}+4mcdot 0}{2m+3m+m+4m}=frac{10mfrac{asqrt{3}}{6}}{10m}=frac{asqrt{3} }{6}(м).]
Ответ: $x_c=0,6a {rm }{rm м}$; $y_c=frac{asqrt{3} }{6}$ м
Пример 2
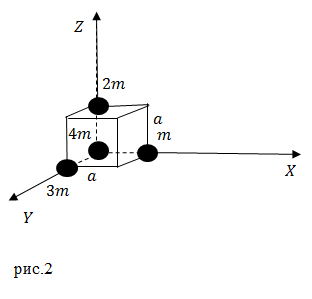
Задание: Каковы координаты центра тяжести системы из четырех элементарных масс, расположенных в вершинах куба со стороной равной $a$ (рис.2)?
Решение: Координату $x_c$ центра тяжести найдем как:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}=frac{mcdot a+2mcdot 0+3mcdot 0+4mcdot 0}{m+2m+3m+4m}=frac{am}{10m}=0,1 aleft(мright).]
Ординату центра тяжести вычислим как:
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}=frac{mcdot 0+2mcdot 0+3mcdot a+4mcdot 0}{m+2m+3m+4m}=frac{acdot 3m}{10m}=0,3a left(мright).]
Для координаты $z_c$ получаем:
[z_c=frac{m_1z_1+m_2z_2+m_3z_3+m_4z_4}{m_1+m_2+m_3+m_4}=frac{mcdot 0+2mcdot a+3mcdot 0+4mcdot 0}{m+2m+3m+4m}=frac{acdot 2m}{10m}=0,2a left(мright).]
Ответ: ($x_{c, }y_c, z_c$)=($ 0,1 a$, $0,3a$, $0,2a$)(м)
Читать дальше: циклическая частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
2.6.2. Центр тяжести тела
Подобно тому, как задача о вычислении центра тяжести плоской фигуры решалась с
помощью двойного интеграла, задача об отыскании центра тяжести тела
решается аналогичным способом – с помощью тройного интеграла.
Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести,
то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени это не
реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил
дать ему точку опоры, чтобы с помощью рычага перевернуть Землю.
Центр тяжести неоднородного тела
рассчитывается по формулам:
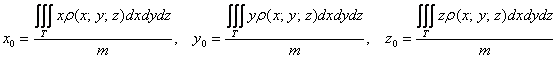
– функция плотности тела, а
– масса тела.
Если же тело однородно (стеклянное, оловянное, пластмассовое и т.д.), то формулы упрощаются. Так как плотность постоянна, и масса
– есть произведение плотности на объём, получаем:
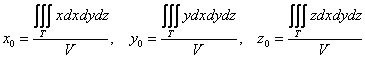
.
Для центра тяжести однородного тела справедливы следующие утверждения:
– если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара);
– если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии;
– если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости.
Как видите, практически полная аналогия с центром тяжести плоской фигуры.
Ну и, само собой, не могу не порадовать вас тематической задачей:
Пример 42
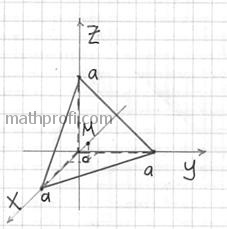
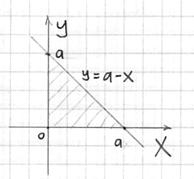
Найти центр тяжести однородного тела, ограниченного поверхностями ,
. Выполнить чертежи данного тела и его проекции на плоскость
.
Решение: искомое тело ограничено координатными плоскостями и плоскостью , которую в целях последующего построения удобно представить в
отрезках: . Выберем «а» за единицу
масштаба и выполним трёхмерный чертёж:
На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.
Проекция тела на плоскость очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие
простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости нужно решить систему, составленную из их уравнений:
Подставляем значение в 1-е
уравнение системы: и получаем
уравнение «плоской» прямой:
Для взятия грядущих интегралов выберем «классический» порядок обхода тела:
Координаты центра тяжести
тела
вычислим по формулам:
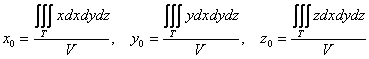
– объём данного тела. И понеслась песня:
1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме
тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем
случае параллелепипед представляет собой куб с ребром «а», а посему: .
Осталось аккуратно провести штатные вычисления:
В примерах с громоздкими преобразованиями рекомендую записывать решение «столбиком» – меньше шансов запутаться:

в средний интеграл)
, и дело за тремя тройными
интегралами:
2) Вычислим «иксовый» интеграл, …и местечка у меня тут не хватает, поэтому решение в столбик отменяется:
Таким образом, «иксовая» координата центра тяжести: 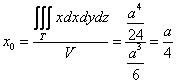
Учитывая симметрию тела, две другие координаты должны получиться такими же. Теперь ошибочный финал практически исключён! И
я вам предлагаю рассчитать самостоятельно, после чего можно записать красивый ответ.
…А вы, наверное, не так давно и представить себе не могли, что окажетесь в эпицентре такого кошмара =)


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
ЦЕНТР
ТЯЖЕСТИ – неизменно
связанная с данным телом точка, через
которую проходит линия действия
равнодействующей сил тяжести, действующих
на частицы данного тела, при любом
положении тела в пространстве.
ЦЕНТРЫ
ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ:
ЦЕНТРА
ТЯЖЕСТИ ДУГИ ОКРУЖНОСТИ – Рассмотрим
дугу
радиуса R
с центральным углом АОВ = 2α. В силу
симметрии центр тяжести этой дуги лежит
на оси ОХ
(рис.109).
Найдем
координату ХС
по формулам:
(1)
Для
этого выделим на дуге
элемент ММ’ длиной d
= R
dϕ,
положение которого определяется углом
ϕ. Координата х элемента ММ’ будет х = R
cosϕ.
Подставляя эти значения х и d
в первую из формулы (1)
и
имея в виду, что интеграл должен быть
распространен на всю длину дуги, получим:
(2)
Где L
– длина дуги
,
равная R*2α.
Отсюда окончательно находим, что центр
тяжести дуги окружности лежит на ее оси
симметрии на расстоянии от центра О,
равном
ХС
= (Rsinα)/α
(3)
Где
угол α измеряется в радианах.
-
Ц
ЕНТР
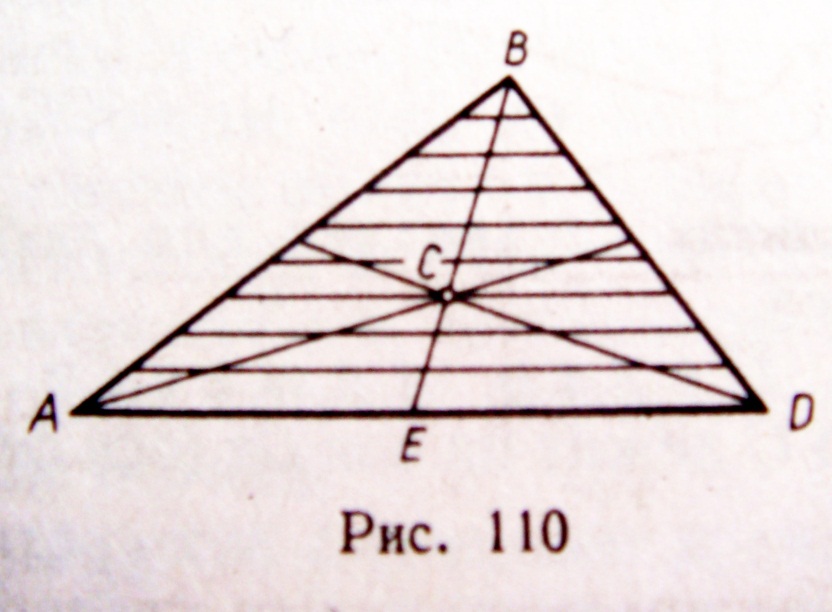
ТЯЖЕСТИ ПЛОЩАДИ ТРЕУГОЛЬНИКА – Разобьём
площадь треугольника ABD
(рис.110)прямыми, параллельными стороне
AD,
на n
узких полосок; центры тяжести этих
полосок будут лежать на медиане ВЕ
треугольника. Следовательно, и центр
тяжести всего треугольника лежит на
этой медиане. Аналогичный результат
получается для двух других медиан.
Отсюда заключаем, что центр тяжести
площади треугольника лежит в точке
пересечения его медиан. При этом, как
известно,
СЕ =
ВЕ/3.
(4)
-
Ц
ЕНТР
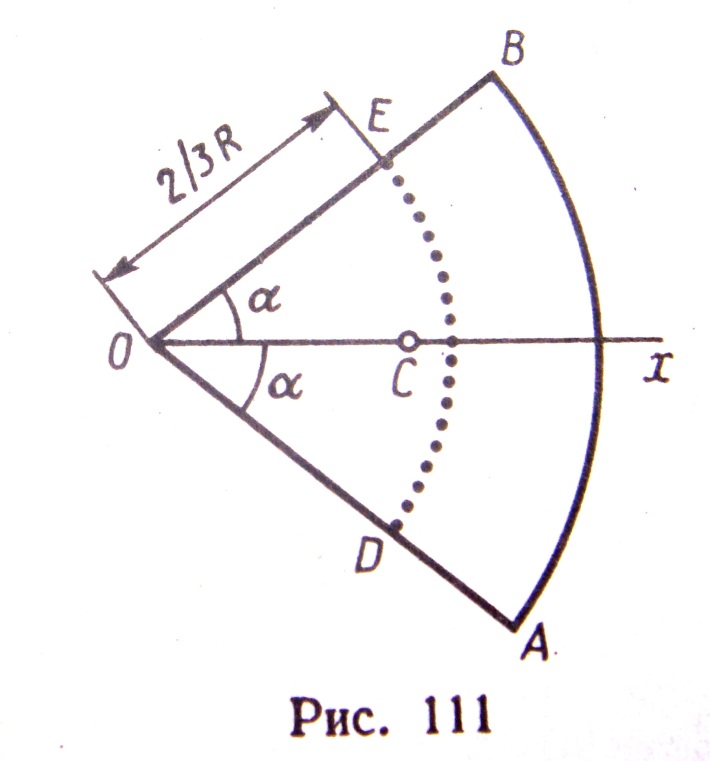
ТЯЖЕСТИ ПЛОЩАДИ КРУГОВОГО СЕКТОРА –
Рассмотрим
круговой сектор OAВ
радиуса R
с центральным углом 2α (РИС.111). Разобьём
мысленно площадь сектора ОАВ радиусами,
проведенными из центра О, на n
секторов. В пределе, при неограниченном
увеличении числа n,
эти секторы можно рассматривать как
плоские треугольники, центры тяжести
которых лежат на дуге DE
радиуса 2R/3.
Следовательно, центр тяжести секторов
ОАВ совпадает с центром тяжести дуги
DE,
положение которого найдется по формуле
(3).
Окончательно получим, что центр тяжести
площади кругового сектора лежит на его
оси симметрии на расстоянии от центра
О, равном
(5)
-
ЦЕНТР
ТЯЖЕСТИ ОБЪЁМА ПИРАМИДЫ ( ИЛИ КОНУСА)
– Этот
центр С лежит на прямой С1Е
(рис.112), где Е – вершина, а С1
– центр тяжести площади основания
пирамиды; при этом:
СС1
= ЕС1/4
Результат
справедлив для любой многоугольной
пирамиды и для конуса.
-
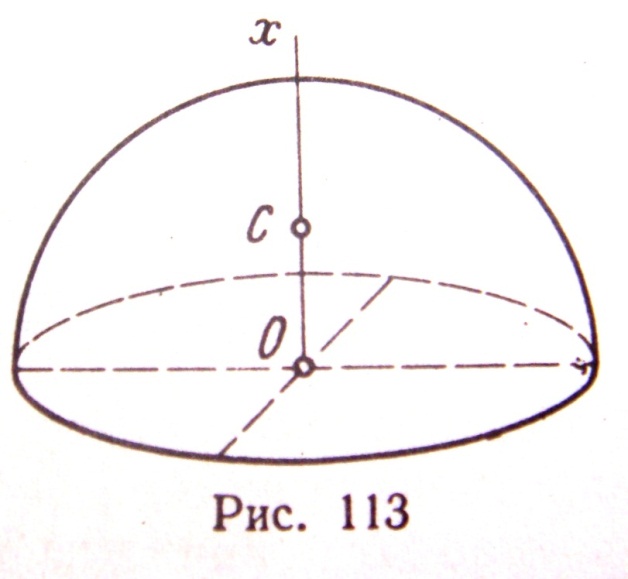
Ц
ЕНТР
ТЯЖЕСТИ ОБЪЁМА ПОЛУШАРА – Этот
центр С лежит на оси ОХ
(оси симметрии, рис.113), а его координата
ХС
=
ОС =3R/8
(7)
Где R
– радиус полушара.
Билет – 23 «способы определения центра тяжести»
ЦЕНТР
ТЯЖЕСТИ – неизменно
связанная с данным телом точка, через
которую проходит линия действия
равнодействующей сил тяжести, действующих
на частицы данного тела, при любом
положении тела в пространстве.
СИММЕТРИЯ
– Если
однородное тело имеет плоскость, ось
или центр симметрии, то его центр тяжести
лежит соответственно или в плоскости
симметрии, или на оси симметрии, или в
центре симметрии. Допустим, например,
что однородное тело имеет плоскость
симметрии. Тогда этой плоскостью оно
разбивается на две такие части, веса
которых р1
и р2,
равны друг другу, а центры тяжести
находятся на одинаковых расстояниях
от плоскости симметрии. Следовательно,
центр тяжести тела как точка, через
которую проходит равнодействующая двух
равных и параллельных сил
и
,
будет действительно лежать в плоскости
симметрии. Из свойств симметрии следует,
что центр тяжести, однородного круглого
кольца, круглой или прямоугольной
пластины, прямоугольного параллелипипида,
шара и других однородных тел, имеющих
центр симметрии, лежит в геометрическом
центре (центре симметрии) этих тел.
Р
АЗБИЕНИЕ
– Если
тело можно разбить на конечное число
таких частей, для каждой из которых
положение центра тяжести известно, то
координаты центра тяжести всего тела
можно непосредственно вычислить по
формулам:
(1)
(2)
(3)
(4)
При
этом, число слагаемых в каждой из сумм
будет равно числу частей, на которые
разбито тело.
ДОПОЛНЕНИЕ
– Этот
способ является частным случаем способа
разбиения. Он применяется к телам,
имеющим вырезы, если центры тяжести
тела без выреза и вырезанной части
известны.
И
НТЕГРИРОВАНИЕ
–
Если тело нельзя разбить на несколько
конечных частей, положения центров
тяжести которых известны, то тело
разбивают сначала на произвольные малые
объёмы
,
для которых формулы:
(5)
принимают
вид:
И Т.Д. , (6)
Г
де
– координаты некоторой точки, лежащей
внутри объёма
.
Затем в равенствах
и
т.д. переходят к пределу, устремляя все
к нулю, т.е. стягивая эти объёмы в точки.
Тогда стоящие в равенствах суммы
обращаются в интегралы, распространённые
на весь объём тела, и формулы (6)
дают в пределе:
(7)

Аналогично
для координат центров тяжести площадей
и линий получаем в пределе из формул
(3)
и (4):
(8)
(9)
-
ЭКСПЕРИМЕНТАЛЬНЫЙ
СПОСОБ – Центры
тяжести неоднородных тел сложной
конфигурации (самолётов, паровозов и
т.д.) можно определять экспериментально.
Один из возможных экспериментальных
методов (метод подвешивания) состоит
в том, что тело подвешивают на нити или
тросе за различные его точки. Направление
нити, на которой подвешено тело, будет
каждый раз давать направление силы
тяжести. Точка пересечения этих
направлений определяет центр тяжести
тела.
БИЛЕТ-24
Динамический
винт
ДИНАМИЧЕСКИЙ
ВИНТ —
совокупность действующих на твёрдое
тело силы
и
пары сил
с моментом
,
лежащей в плоскости, перпендикулярной
к силе
(векторы
и
параллельны).
К Д. в. приводится в наиб. общем случае
произвольная система действующих на
твёрдое тело сил. Дальнейшее упрощение
Д. в. невозможно, т. е. его нельзя заменить
только одной силой (равнодействующей)
или одной парой сил. Можно лишь, сложив
силу
с
одной из сил пары, привести Д. в. к двум
скрещивающимся силам.
В
общем случае для произвольной системы
сил главный вектор и главный момент
составляют между собой некоторый угол.
Главный момент MO разложим
на две составляющие, одну из них мы
обозначим MO‘ и
направим по главному вектору, а вторую
— MO» —
направим перпендикулярно первой (рис.
27, a).
Вторую
составляющую представим в виде пары,
одной из сил которой уравновесим главный
вектор (рис. 27, b). Таким образом, мы привели
систему сил к одной силе (по величине и
направлению равной главному вектору)
и к одной перпендикулярной ей паре с
моментом MO‘,
параллельным силе, равным по величине
проекции главного момента на главный
вектор (рис. 27, c и d). Такую совокупность
силы и пары сил называют динамическим
винтом,
а линию действия AL силы
в динамическом винте называют центральной
осью системы сил.
БИЛЕТ-25
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
плоскости.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
имеющей отверстие
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.