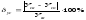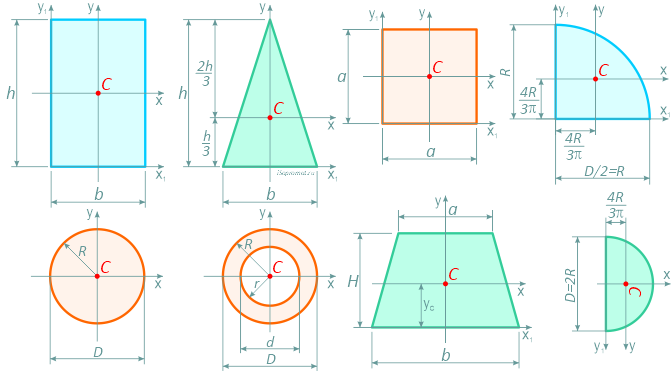
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления;
Wρ — полярный момент сопротивления
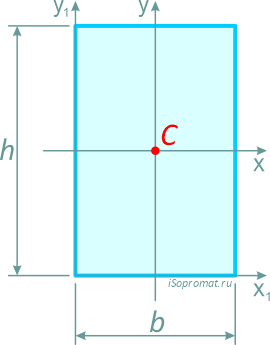
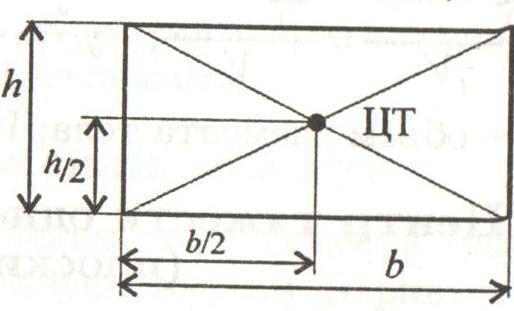
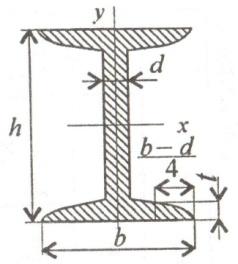
Прямоугольник
Прямоугольник высотой h и шириной b.
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
Центральные осевые моменты инерции прямоугольника
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевые моменты сопротивления прямоугольного сечения
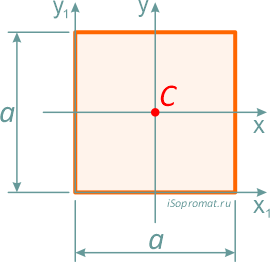
Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
Центральные осевые моменты инерции квадрата
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевой момент сопротивления квадратного сечения
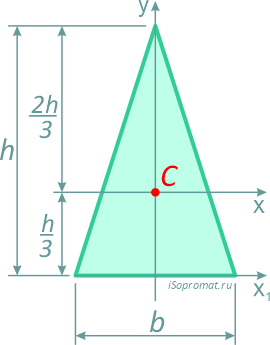
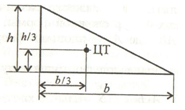
Треугольник равнобедренный
Равнобедренный треугольник высотой h и шириной основания b.
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
Центральные осевые моменты инерции треугольника
Момент инерции относительно смещенной оси x1, проходящей через его основание
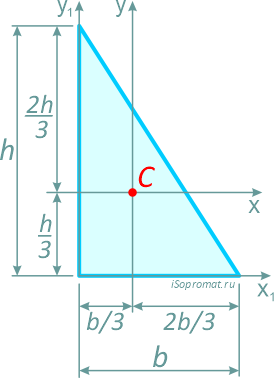
Прямоугольный треугольник
Прямоугольный треугольник высотой h и шириной основания b.
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
Центральные осевые моменты инерции прямоугольного треугольника
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
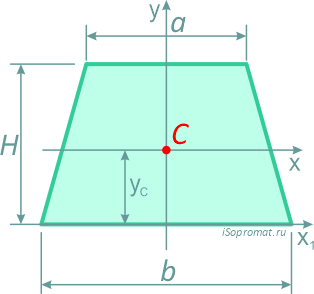
Трапеция
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
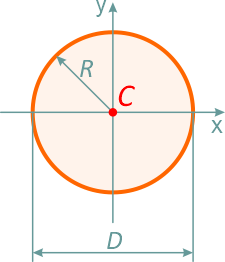
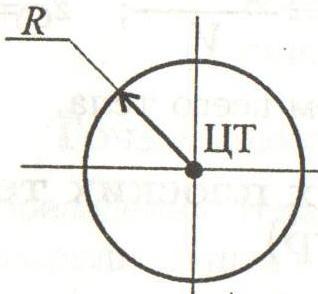
Круг
Круг диаметром D (d) или радиусом R (r)
Площадь круга через его диаметр и радиус
Центральные осевые и полярный моменты инерции круга
Осевые и полярный моменты сопротивления
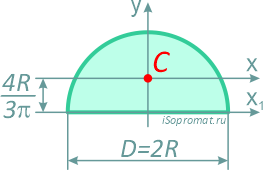
Полукруг
Половина круга диаметром D (d) или радиусом R (r)
Площадь
Осевые моменты инерции полукруга
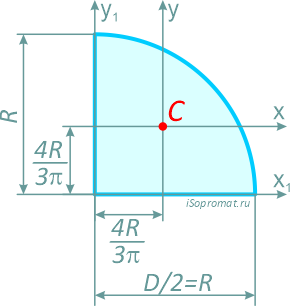
Четверть круга
Четверть круга диаметром D (d) или радиусом R (r)
Площадь
Центральные осевые моменты инерции четверти круга
Моменты инерции относительно смещенных осей x1 и y1
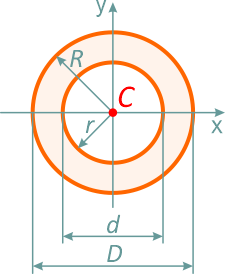
Кольцо
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
Площадь
Центральные осевые и полярный моменты инерции кольца
Осевые и полярный моменты сопротивления
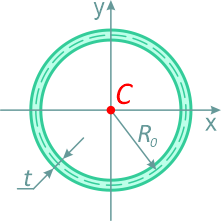
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при R0>>t
Площадь
Центральные осевые и полярный моменты инерции трубного сечения
Осевые и полярный моменты сопротивления
Пример определения координат центра тяжести сложной фигуры:
Другие видео
Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
плоскости.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
имеющей отверстие
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.
На этой странице представлена справочная информация с формулами для вычисления площадей простых фигур (сечений) с указанием положения их центров тяжестей.
Эта страничка будет полезна при расчёте более сложных фигур (составных поперечных сечений): определении положения центра тяжести, а также общей площади.
Центры тяжести
Для всех фигур, положение центра тяжести в статье обозначается буквой – C, это наиболее используемый вариант. Также иногда центр тяжести обозначают буквой – O.
Формулы для расчёта площадей
В сопромате площадь поперечного сечения обозначается буквой – A, однако, в некоторой литературе ты можешь встретить обозначения с буквой – F.
Другую справочную информацию, размещённую на сайте – ssopromat.ru, можешь найти, перейдя по указанной ссылке.
Положения центра тяжести некоторых фигур
Прямоугольник.
Так
как прямоугольник имеет две оси симметрии
, то его центр тяжести находится на
пересечении осей симметрии, т.е. в точке
пересечения диагоналей прямоугольника.
Треугольник.
Центр
тяжести лежит в точке пересечения его
медиан. Из геометрии известно, что
медианы треугольника пересекаются в
одной точке и делятся в отношении 1:2 от
основания.
Круг.
Так
как круг имеет две оси симметрии, то его
центр тяжести находится на пересечении
осей симметрии.
Полукруг.
Полукруг
имеет одну ось симметрии, то центр
тяжести лежит на этой оси. Другая
координата центра тяжести вычисляется
по формуле:
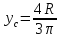
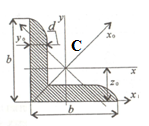
Многие
конструктивные элементы изготавливают
из стандартного проката – уголков,
двутавров, швеллеров и других. Все
размеры, а так же геометрические
характеристики прокатных профилей это
табличные данные, которые можно найти
в справочной литературе в таблицах
нормального сортамента (ГОСТ 8239-89, ГОСТ
8240-89).
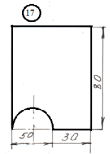
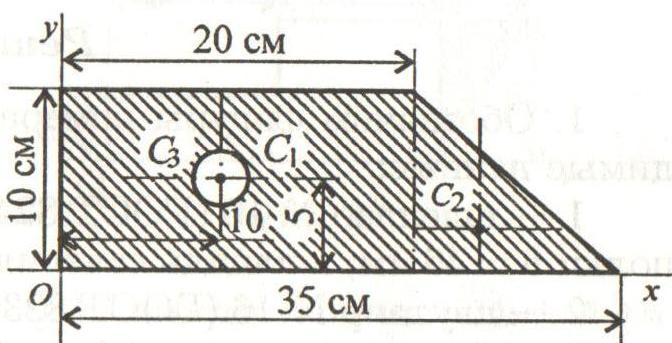
Пример
1. Определить
положение центра тяжести фигуры,
представленной на рисунке.
Решение:
-
Выбираем
оси координат, так чтобы ось Ох прошла
по крайнему нижнему габаритному размеру,
а ось Оу – по крайнему левому габаритному
размеру. -
Разбиваем
сложную фигуру на минимальное количество
простых фигур:
-
прямоугольник
20х10; -
треугольник
15х10; -
круг
R=3
см.
-
Вычисляем
площадь каждой простой фигуры, её
координаты центра тяжести. Результаты
вычислений заносим в таблицу
|
№ фигуры |
Площадь |
Координаты |
|
|
Х, |
У, |
||
|
1 |
|
20:2=10 |
10:2=5 |
|
2 |
|
|
|
|
3 |
|
10 |
5 |
-
Вычисляем
координаты центра тяжести фигуры по
формулам:
Ответ:
С(14,5; 4,5)
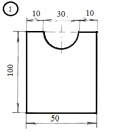
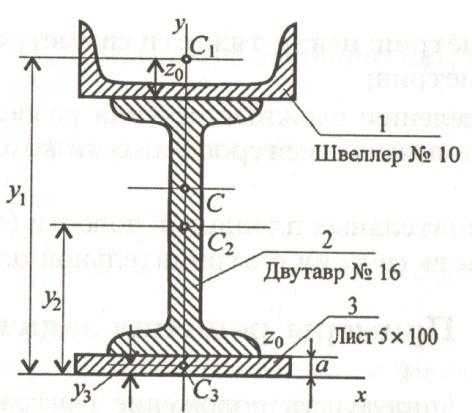
Пример
2.
Определить координаты центра тяжести
составного сечения, состоящего из листа
и прокатных профилей.
Решение.
-
Выбираем
оси координат, так как показано на
рисунке. -
Обозначим
фигуры номерами и выпишем из таблицы
необходимые данные:
-
– швеллер
№10; высота h=100
мм; ширина b=46
мм; площадь сечения
;
-
—
двутавр №16; высота
h=160
мм; ширина b=81
мм; площадь сечения
;
-
– лист
5х100; толщина 5 мм; ширина 100 мм.
-
Вычисляем
координаты центра тяжести каждой
фигуры. Составное сечение симметрично,
поэтому центр тяжести находится на оси
симметрии и координата
.
Результаты
вычислений заносим в таблицу
|
№ фигуры |
Площадь |
Координаты |
|
|
Х, |
У, |
||
|
1 |
|
0 |
|
|
2 |
|
0 |
|
|
3 |
|
0 |
|
-
Вычисляем
координаты центра тяжести фигуры по
формулам:
Ответ:
С(0; 10)
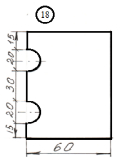
Лабораторная работа №1 «Определение центра тяжести составных плоских фигур»
Цель:
Определить центр тяжести заданной
плоской сложной фигуры опытным и
аналитическим способами и сравнить их
результаты.
Порядок выполнения работы
-
Начертить
в тетрадях свою плоскую фигуру по
размерам, с указанием осей координат. -
Определить
центр тяжести аналитическим способом.-
Разбить
фигуру на минимальное количество
фигур, центры тяжести которых, мы знаем,
как определить. -
Указать
номера площадей и координаты центра
тяжести каждой фигуры. -
Вычислить
координаты центра тяжести каждой
фигуры. -
Вычислить
площадь каждой фигуры. -
Вычислить
координаты центра тяжести всей фигуры
по формулам (положение центра тяжести
нанести на чертеж фигуры):
-
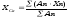
-
Записать
координаты центра тяжести.
-
Определить
центр тяжести опытным путем на установке
для определения координат центра
тяжести.-
Вырезать
данную фигуру из тонкого картона. -
Определить
центр тяжести своей фигуры на установке.
-
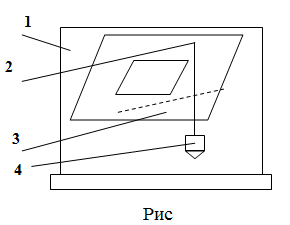
Установка
для опытного определения координат
центра тяжести способом подвешивания
состоит из вертикальной стойки 1
(см. рис.), к которой прикреплена игла 2.
Плоская фигура 3
изготовлена из картона, в котором легко
проколоть отверстие. Отверстия А
и В
прокалываются в произвольно расположенных
точках (лучше на наиболее удаленном
расстоянии друг от друга). Плоская фигура
подвешивается на иглу сначала в точке
А,
а потом в точке В.
При помощи отвеса 4,
закрепленного на той же игле, на фигуре
прочерчивают карандашом вертикальную
линию, соответствующую нити отвеса.
Центр тяжести С
фигуры будет находиться в точке
пересечения вертикальных линий,
нанесенных при подвешивании фигуры в
точках А
и В.
-
Приклеить
фигуру с определенным центром тяжести
в тетрадь. -
Записать
значения координат центра тяжести,
найденных при подвешивании фигур:
-
Сравнить
результаты:
;
-
Сделать
вывод:
Задание
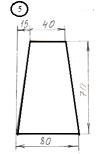
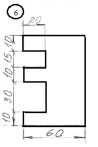
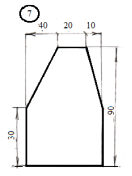
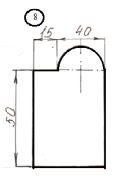
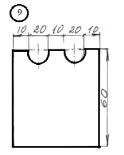
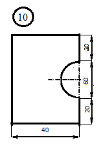
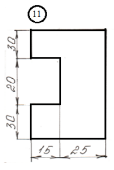
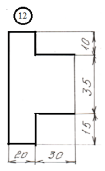
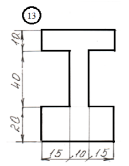
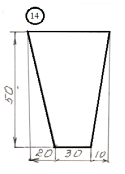
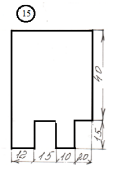
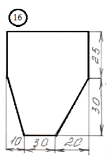
для лабораторной работы.
Номер схемы соответствует Вашему
порядковому номеру в журнале.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти центр тяжести?
Опубликовано 21 Окт 2013
Рубрика: Механика | 3 комментария

…геометрических характеристик составных поперечных сечений балок и стержней. Часто с подобными вопросами приходится сталкиваться инженерам-конструкторам вырубных штампов при определении координат центра давления, разработчикам схем погрузки различного транспорта при размещении грузов, проектировщикам строительных металлических конструкций при подборе сечений элементов и, конечно, студентам при изучении дисциплин «Теоретическая механика» и «Сопротивление материалов».
Библиотека элементарных фигур.
Для симметричных плоских фигур центр тяжести совпадает с центром симметрии. К симметричной группе элементарных объектов относятся: круг, прямоугольник (в том числе квадрат), параллелограмм (в том числе ромб), правильный многоугольник.
Из десяти фигур, представленных на рисунке выше, только две являются базовыми. То есть, используя треугольники и сектора кругов, можно скомбинировать почти любую фигуру, имеющую практический интерес. Любые произвольные кривые можно, разбив на участки, заменить дугами окружностей.
Оставшиеся восемь фигур являются самыми распространенными, поэтому они и были включены в эту своеобразную библиотеку. В нашей классификации эти элементы не являются базовыми. Прямоугольник, параллелограмм и трапецию можно составить из двух треугольников. Шестиугольник – это сумма из четырех треугольников. Сегмент круга — это разность сектора круга и треугольника. Кольцевой сектор круга — разность двух секторов. Круг – это сектор круга с углом α=2*π=360˚. Полукруг – это, соответственно, сектор круга с углом α=π=180˚.
Передавать и воспринимать информацию, рассматривая пример, всегда легче, чем изучать вопрос на чисто теоретических выкладках. Рассмотрим решение задачи «Как найти центр тяжести?» на примере составной фигуры, изображенной на рисунке, расположенном ниже этого текста.
Составное сечение представляет собой прямоугольник (с размерами a1=80 мм, b1=40 мм), к которому слева сверху добавили равнобедренный треугольник (с размером основания a2=24 мм и высотой h2=42 мм) и из которого справа сверху вырезали полукруг (с центром в точке с координатами x03=50 мм и y03=40 мм, радиусом r3=26 мм).
В помощь для выполнения расчета привлечем программу MS Excel или программу OOo Calc. Любая из них легко справится с нашей задачей!
В ячейках с желтой заливкой выполним вспомогательные предварительныерасчеты.
В ячейках со светло-желтой заливкой считаем результаты.
Синий шрифт – это исходные данные.
Черный шрифт – это промежуточные результаты расчетов.
Красный шрифт – это окончательные результаты расчетов.
Начинаем решение задачи – начинаем поиск координат центра тяжести сечения.
Исходные данные:
1. Названия элементарных фигур, образующих составное сечение впишем соответственно
в ячейку D3: Прямоугольник
в ячейку E3: Треугольник
в ячейку F3: Полукруг
2. Пользуясь представленной в этой статье «Библиотекой элементарных фигур», определим координаты центров тяжести элементов составного сечения xci и yci в мм относительно произвольно выбранных осей 0x и 0y и запишем
в ячейку D4: =80/2=40,000
xc1=a1/2
в ячейку D5: =40/2=20,000
yc1= b1/2
в ячейку E4: =24/2=12,000
xc2=a2/2
в ячейку E5: =40+42/3=54,000
yc2= b1+h2/3
в ячейку F4: =50=50,000
xc3=x03
в ячейку F5: =40-4*26/3/ПИ()=28,965
yc3= y03-4*r3/3/π
3. Рассчитаем площади элементов F1, F2, F3 в мм2, воспользовавшись вновь формулами из раздела «Библиотека элементарных фигур»
в ячейке D6: =40*80=3200
F1=a1*b1
в ячейке E6: =24*42/2=504
F2=a2*h2/2
в ячейке F6: =-ПИ()/2*26^2=-1062
F3= -π/2*r3^2
Площадь третьего элемента – полукруга – отрицательная потому, что это вырез – пустое место!
Расчет координат центра тяжести:
4. Определим общую площадь итоговой фигуры F0 в мм2
в объединенной ячейке D8E8F8: =D6+E6+F6=2642
F0=F1+F2+F3
5. Вычислим статические моменты составной фигуры Sx и Sy в мм3 относительно выбранных осей 0x и 0y
в объединенной ячейке D9E9F9: =D5*D6+E5*E6+F5*F6=60459
Sx=yc1*F1+ yc2*F2+ yc3*F3
в объединенной ячейке D10E10F10: =D4*D6+E4*E6+F4*F6=80955
Sy=xc1*F1+ xc2*F2+ xc3*F3
6. И в завершение рассчитаем координаты центра тяжести составного сечения Xc и Yc в мм в выбранной системе координат 0x — 0y
в объединенной ячейке D11E11F11: =D10/D8=30,640
Xc=Sy/F0
в объединенной ячейке D12E12F12: =D9/D8=22,883
Yc=Sx/F0
Задача решена, расчет в Excel выполнен — найдены координаты центра тяжести сечения, составленного при использовании трех простых элементов!
Заключение.
Пример в статье был выбран очень простым для того, чтобы легче было разобраться в методологии расчетов центра тяжести сложного сечения. Метод заключается в том, что любую сложную фигуру следует разбить на простые элементы с известными местами расположения центров тяжести и произвести итоговые вычисления для всего сечения.
Если сечение составлено из прокатных профилей – уголков и швеллеров, то их нет необходимости разбивать на прямоугольники и квадраты с вырезанными круговыми «π/2»- секторами. Координаты центров тяжести этих профилей приведены в таблицах ГОСТов, то есть и уголок и швеллер будут в ваших расчетах составных сечений базовыми элементарными элементами (о двутаврах, трубах, прутках и шестигранниках говорить нет смысла – это центрально симметричные сечения).
Расположение осей координат на положение центра тяжести фигуры, конечно, не влияет! Поэтому выбирайте систему координат, упрощающую вам расчеты. Если, например, я развернул бы в нашем примере систему координат на 45˚ по часовой стрелке, то вычисление координат центров тяжести прямоугольника, треугольника и полукруга превратилось бы в еще один отдельный и громоздкий этап расчетов, который «в уме» не выполнишь.
Представленный ниже расчетный файл Excel в данном случае программой не является. Скорее – это набросок калькулятора, алгоритм, шаблон по которому следует в каждом конкретном случае составлять свою последовательность формул для ячеек с яркой желтой заливкой.
Итак, как найти центр тяжести любого сечения вы теперь знаете! Полный расчет всех геометрических характеристик произвольных сложных составных сечений будет рассмотрен в одной из ближайших статей в рубрике «Механика».
Несколько слов о бокале, монете и двух вилках, которые изображены на «значке-иллюстрации» в самом начале статьи. Многим из вас, безусловно, знаком этот «трюк», вызывающий восхищенные взгляды детей и непосвященных взрослых. Тема этой статьи – центр тяжести. Именно он и точка опоры, играя с нашим сознанием и опытом, попросту дурачат наш разум!
Центр тяжести системы «вилки+монета» всегда располагается на фиксированном расстоянии по вертикали вниз от края монеты, который в свою очередь является точкой опоры. Это положение устойчивого равновесия! Если покачать вилки, то сразу становится очевидным, что система стремится занять свое прежнее устойчивое положение! Представьте маятник – точка закрепления (=точка опоры монеты на кромку бокала), стержень-ось маятника (=в нашем случае ось виртуальная, так как масса двух вилок разведена в разные стороны пространства) и груз внизу оси (=центр тяжести всей системы «вилки+монета»). Если начать отклонять маятник от вертикали в любую сторону (вперед, назад, налево, направо), то он неизбежно под действием силы тяжести будет возвращаться в исходное устойчивое состояние равновесия (это же самое происходит и с нашими вилками и монетой)!
Кто не понял, но хочет понять – разберитесь самостоятельно. Это ведь очень интересно «доходить» самому! Добавлю, что этот же принцип использования устойчивого равновесия реализован и в игрушке ванька–встань-ка. Только центр тяжести у этой игрушки расположен выше точки опоры, но ниже центра полусферы опорной поверхности.
Ссылка на скачивание файла: raschet-tsentra-tyazhesti (xls 17,0KB).
Другие статьи автора блога
На главную


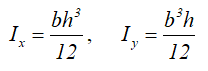
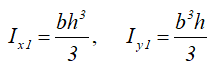
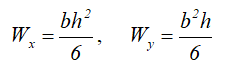
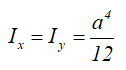
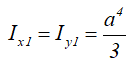
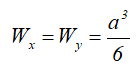
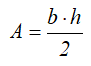
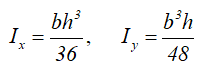
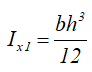
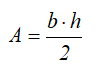
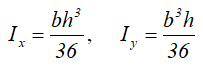
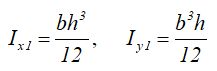
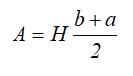
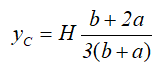
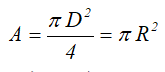
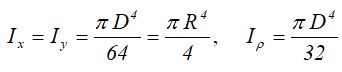
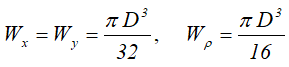
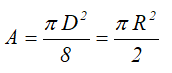
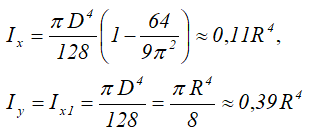
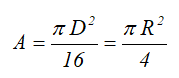
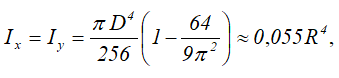
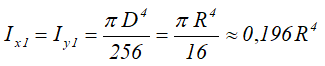
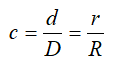
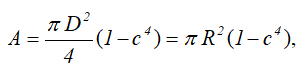
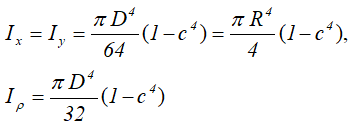
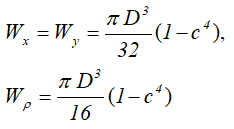
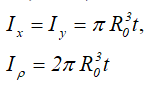
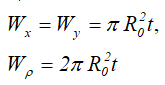
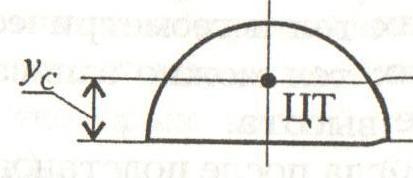
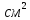
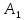 =20·10=200
=20·10=200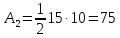
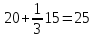
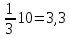
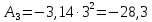
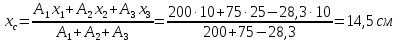
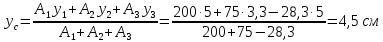
 ;
; ;
; .
.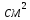
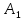 =10,9
=10,9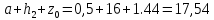
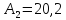
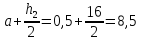
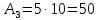
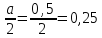
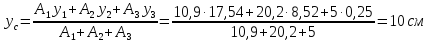
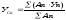
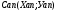
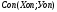
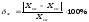 ;
;