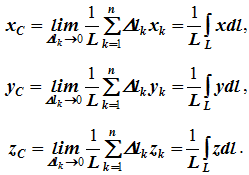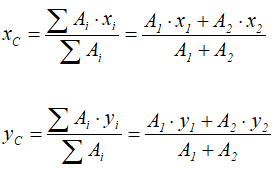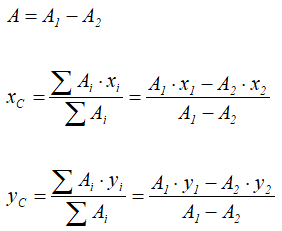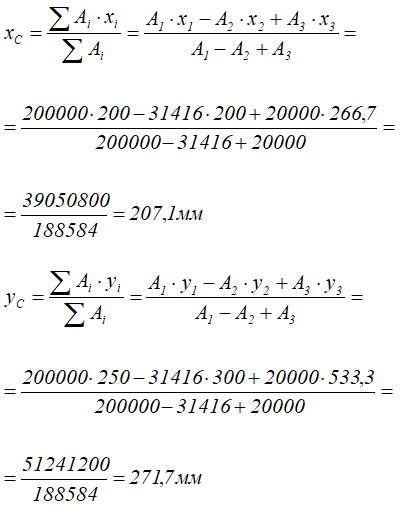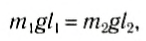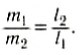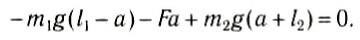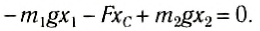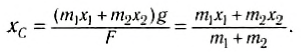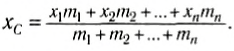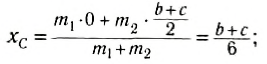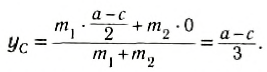Центром
тяжести твердого
тела называется геометрическая точка,
жестко связанная с этим телом, и являющаяся
центром параллельных сил тяжести,
приложенных к отдельным элементарным
частицам тела (рисунок 1.6).
Радиус-вектор
этой точки
Рисунок
1.6
Для
однородного тела положение центра
тяжести тела не зависит от материала,
а определяется геометрической формой
тела.
Если
удельный вес однородного тела γ,
вес элементарной частицы тела
Pk = γΔVk
(P = γV)
подставить в формулу для определения
rC,
имеем
Откуда,
проецируя на оси и переходя к пределу,
получаем координаты центра тяжести
однородного объема
Аналогично
для координат центра тяжести однородной
поверхности площадью S
(рисунок 1.7, а)
Рисунок
1.7
Для
координат центра тяжести однородной
линии длиной L
(рисунок 1.7, б)
Способы
определения координат центра тяжести
Исходя
из полученных ранее общих формул, можно
указать способы определения координат
центров тяжести твердых тел:
1 Аналитический (путем
интегрирования).
2 Метод
симметрии.
Если тело имеет плоскость, ось или центр
симметрии, то его центр тяжести лежит
соответственно в плоскости симметрии,
оси симметрии или в центре симметрии.
3 Экспериментальный (метод
подвешивания тела).
4 Разбиение.
Тело разбивается на конечное число
частей, для каждой из которых положение
центра тяжести C
и площадь S известны.
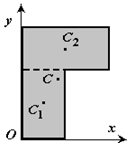
Например, проекцию тела на плоскость xOy
(рисунок 1.8) можно представить в виде
двух плоских фигур с площадями S1
и S2 (S
= S1 + S2).
Центры тяжести этих фигур находятся в
точках C1(x1,
y1) и
C2(x2, y2).
Тогда координаты центра тяжести тела
равны
Рисунок
1.8
5 Дополнение (метод
отрицательных площадей или объемов).
Частный случай способа разбиения. Он
применяется к телам, имеющим вырезы,
если центры тяжести тела без выреза и
вырезанной части известны. Например,
необходимо найти координаты центра
тяжести плоской фигуры (рисунок 1.9):
Рисунок
1.9
Центры тяжести простейших фигур
Рисунок
1.10
1
Треугольник
Центр
тяжести площади треугольник совпадает
с точкой пересечения его медиан (рисунок
1.10, а).
DM
= MB,
CM
= (1/3)AM.
2
Дуга окружности
Дуга
имеет ось симметрии (рисунок 1.10, б). Центр
тяжести лежит на этой оси, т.е. yC =
0.
dl –
элемент дуги, dl = Rdφ,
R –
радиус окружности, x
= Rcosφ,
L
= 2αR,
Следовательно:
xC =
R(sinα/α).
3
Круговой сектор
Сектор
радиуса R с
центральным углом 2α имеет
ось симметрии Ox,
на которой находится центр тяжести
(рисунок 1.10, в).
Разбиваем
сектор на элементарные секторы, которые
можно считать треугольниками. Центры
тяжести элементарных секторов
располагаются на дуге окружности радиуса
(2/3)R.
Центр
тяжести сектора совпадает с центром
тяжести дуги AB:
14.
Способы задания движения точки.
При
векторном способе задания движения
положение точки определяется
радиус-вектором, проведенным из
неподвижной точки в выбранной системе
отсчета.
При
координатном способе задания движения
задаются координаты точки как функции
времени:
Это
параметрические уравнения траектории
движущейся точки, в которых роль параметра
играет время t.
Чтобы записать ее уравнение в явной
форме, надо исключить из них t.
При
естественном способе задания движения
задаются траектория точки, начало
отсчета на траектории с указанием
положительного направления отсчета,
закон изменения дуговой координаты: s=s(t) .
Этим способом удобно пользоваться, если
траектория точки заранее известна.
15.
1.2
Скорость точки
Рассмотрим
перемещение точки за малый промежуток
времени Δt:
тогда
средняя
скорость точки за промежуток времени Dt .
Скорость точки в данный момент времени
Скорость
точки –
это кинематическая мера ее движения,
равная производной по времени от
радиус-вектора этой точки в рассматриваемой
системе отсчета. Вектор скорости
направлен по касательной к траектории
точки в сторону движения.
Определение координат центра тяжести xC и yC плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.
Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.
Способы определения координат центра тяжести
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов расчета координат положения центра тяжести:
- Аналитический (путем интегрирования).
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел. - Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
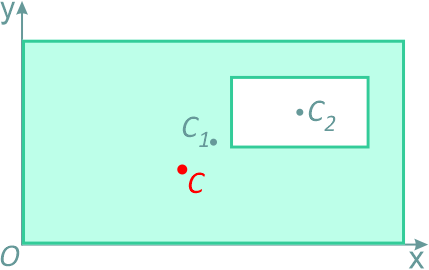
Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A1 и A2 (A = A1+ A2).
Рисунок 1.8
Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
- Дополнение (Метод отрицательных площадей или объемов).
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).
Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:
Другие видео
Пример определения координат центра тяжести плоской фигуры
Задача
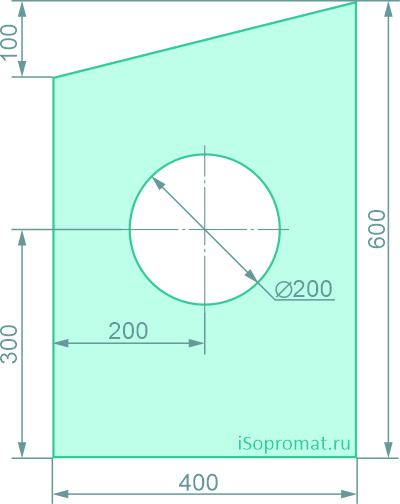
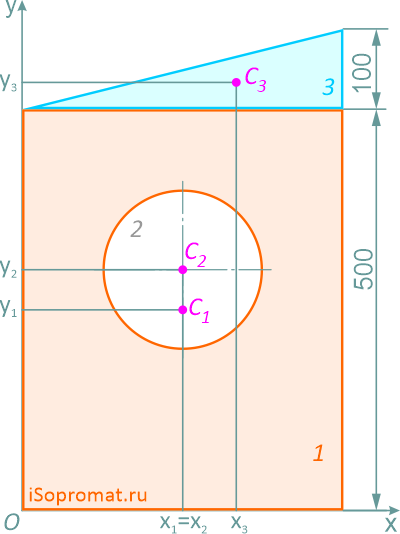
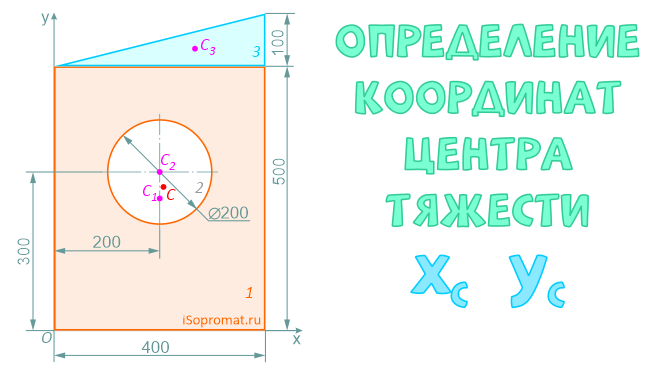
Определить координаты центра тяжести плоской фигуры с круглым отверстием
Решение
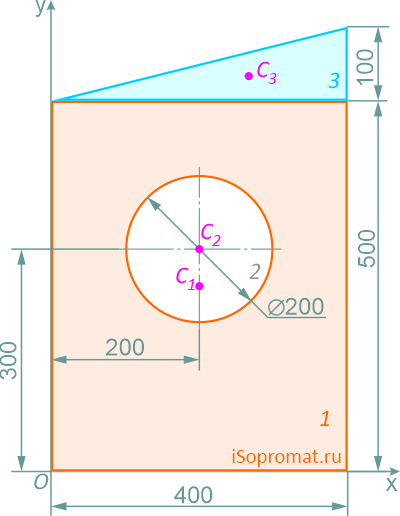
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести Ci отдельных фигур:
Прямоугольник (фигура 1)
Площадь
A1=400×500=200000 мм2
Положение центра тяжести
x1=200мм
y1=250мм
Круг (2) (вычитаемая фигура)
Площадь
A2=π×2002/4=31416 мм2
Центр тяжести
x2=200мм
y2=300мм
Прямоугольный треугольник (3)
Площадь
A3=400*100/2=20000 мм2
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x3=400×2/3=266,7мм
y3=500+100×1/3=533,3мм
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:
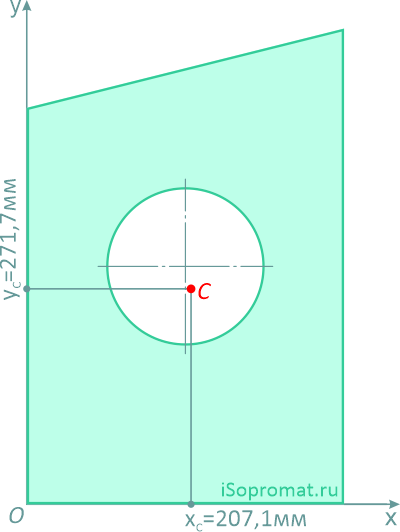
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами xC=207,1мм, yC=271,7мм.
Другие примеры решения задач >
Центры тяжести простейших фигур >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Центр тяжести (центр масс):
Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.
Центр тяжести — геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.
На каждую точку тела в поле сил тяжести действует сила, а на все тело — равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.
Центр масс (центр инерции) — точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.
При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.
Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.
При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, — параллельными.
Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.
Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.
Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.
Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.
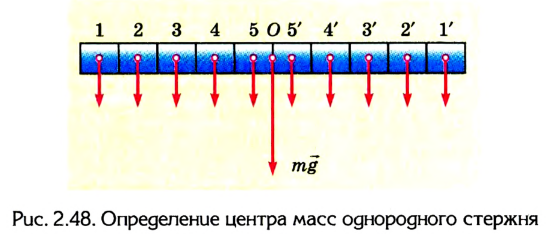
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О — середине стержня.
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.
Центр тяжести однородного стержня расположен в середине стержня.
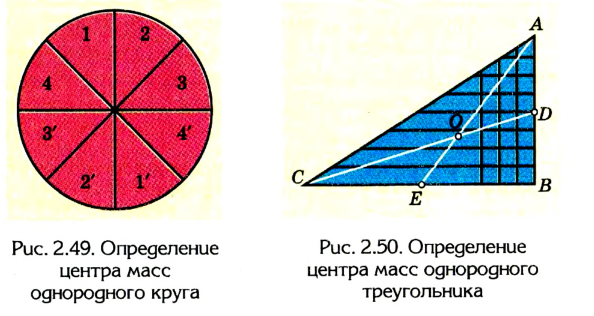
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.
Центр тяжести однородного круга совпадает с его центром.
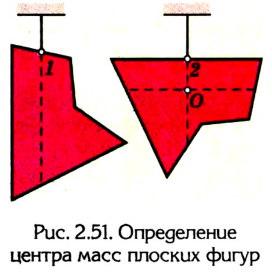
Центр тяжести однородного треугольника находится в точке пересечения его медиан.
3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.
Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.
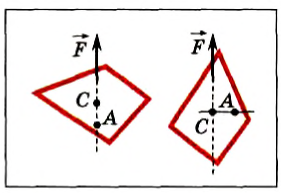
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.
Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.
Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.
- Заказать решение задач по физике
Центр тяжести тела и центр масс тела
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.
Рис. 151
Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.
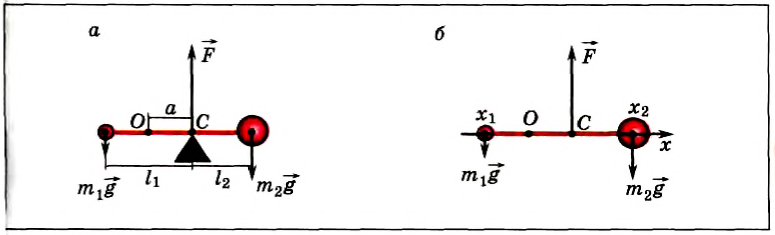
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:
или
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:
Рис. 152
Поскольку F=(m1 + m2)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х1, хс и х2. Запишем условие моментов относительно точки О:
Отсюда
При выводе этой формулы было использовано значение силы F = (m1 + m2) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии хс, определенном формулой (2).
Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.
Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.
Если произвольное тело можно разбить на n элементов, массы которых m1, m2…, mn, и если известны координаты центров масс этих элементов x1, x2…, xn относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:
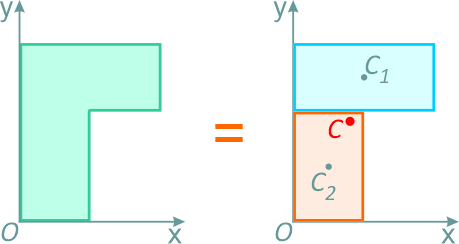
Естественно, что такие же соотношения можно записать и для ус и zc. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m1 = 2m2). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C1) и линейки (C2).
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х1 = 0, y1 =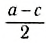
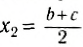
По формуле (3): .
Таким образом, центр масс угольника находится вне тела.
Главные выводы:
- Центр тяжести — точка, в которой приложена сила тяжести.
- Центр масс симметричных однородных тел находится в их геометрическом центре.
- Координаты центра масс тела можно вычислить по формуле (3).
- Импульс тела в физике
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
На каждое тело на Земле действует сила тяжести. При этом тела бывают самой разнообразной формы. Различные машины, механизмы, конструкции и строения, созданные человеком, должны быть устойчивыми для их нормального использования.
Это значит, что они должны находиться в равновесии. Каким образом мы можем добиться этого условия?
На данном уроке мы рассмотрим, как действует сила тяжести, к какой точке она приложена, чтобы мы могли говорить о равновесии тела. Мы введем определение центра тяжести тела и рассмотрим его особенности.
Центр тяжести
Давайте рассмотрим простой пример. Возьмем линейку и подвесим ее на нити (рисунок 1).
Передвигая нить по длине линейки, найдем такое положение, чтобы линейка находилась в равновесии. Мы можем сказать, что линейка подвешена в центре тяжести.
Что такое центр тяжести?
Центр тяжести тела — это точка приложения равнодействующей сил тяжести, действующих на отдельные части тела.
Если мы мысленно разделим линейку на несколько частей, то на каждую их них будет действовать сила тяжести. Сила тяжести всегда направлена вертикально вниз вне зависимости от положения тела.
Как мы увидели, у линейки центр тяжести будет находиться посередине ее длины. Но это справедливо не для всех тел. Если мы таким же образом подвесим лопату и будем искать положение, в котором она будет находиться в равновесии, то увидим другую ситуацию (рисунок 2). Лопата будет подвешена в центре тяжести ближе к началу ее черенка.
Нахождение центра тяжести тела
Вокруг нас полно твердых тел сложной формы. Если с линейкой все было достаточно просто, то как найти центр тяжести более сложного тела?
Попробуем сделать это на практике. Вырежем фигуру произвольной неправильной формы из картона. Подвесим ее, используя отвес (рисунок 3, а).
Отвес — это приспособление, состоящее из нити и маленького грузика на ее конце. Служит для определения правильного вертикального положения других тел.
На нашу фигуру действуют две силы: сила тяжести и силы упругости. Сила тяжести направлена вертикально вниз, а сила упругости — вдоль нити. Так как мы используем отвес, задающий идеальную вертикальную линию, то сила упругости будет направлена вертикально вверх.
Картонная фигура покоится. Значит, эти две силы уравновешивают друг друга. Они равны по величине и направлены в противоположные стороны. Мы можем сказать, что точки приложения этих сил находятся на одной вертикальной прямой, которую отмечает отвес. Отметим эту линию карандашом на картоне.
Теперь отцепим нашу фигуру и подвесим ее снова, но в другой точке (рисунок 3, б). Снова проведем линию по отвесу. Мы можем провести бесконечное множество линий, подвешивая фигуру в разных ее точках. Все эти линии будут пересекаться в одной точке (рисунок 3, в). Эта точка и будет центром тяжести тела C.
Это легко проверить. Возьмем фигуру из картона и поставим ее на острие карандаша а найденном центре тяжести (точка C). Фигура не будет крениться в какую-либо сторону, не упадет — она будет находится в равновесии (рисунок 3, г).
При любом положении тела его центр тяжести находится в одной и той же точке.
Где может находиться центр тяжести тела?
Для нахождения центра тяжести объемных геометрических фигур используют похожие способы. Так, центр тяжести шара находится в его геометрическом центре, а у параллелепипеда — в точке пересечения его диагоналей (рисунок 4).
Центр тяжести тела может находиться и вне самого тела. Например, у кольца (рисунок 5).
Примером тела с центром тяжести, находящимся вне тела, также могут служить разные сувениры. Например, вот эта птичка (рисунок 6). Она сделана так, что ее центр тяжести находится ровно под ее клювом. Это позволяет зрелищно держать такую игрушку на кончике пальца, создавая иллюзию полета.
В каких случаях может меняться положение центра тяжести тела?
Это возможно только в том случае, если изменяется относительное расположение частей тела. Например, при непластичной деформации.
Центр тяжести тела, теория и онлайн калькуляторы
Центр тяжести тела
Как известно, сила тяжести тела равна векторной сумме сил тяжести, которые действуют на все материальные точки, на которые можно разбить рассматриваемое тело. Точку, к которой приложена результирующая сила тяжести, называют центром тяжести. Если известно положение центра тяжести, то можно считать, что на тело действует только одна сила тяжести, приложенная к центру тяжести.
Следует учитывать, что силы тяжести, действующие на отдельные элементы тела, направлены к центру Земли и не являются строго параллельными. Но так как размеры большинства тел на Земле много меньше ее радиуса, поэтому эти силы считают параллельными.
Определение центра тяжести тела
Определение
Центром тяжести называют точку, через которую проходит равнодействующая всех сил тяжести, действующих на материальные точки, на которые разбито рассматриваемое тело, при любом положении тела в пространстве.
Центр тяжести — это точка, относительно которой суммарный момент сил тяжести равен нулю при любом положении тела.
От положения центра тяжести зависит устойчивость всех конструкций.
Как найти центр тяжести?
Для нахождения центра тяжести тела сложной формы необходимо мысленно разбить тело на части простой формы и определить место нахождения центров тяжести для них. У тел простой формы центр тяжести определяют, используя их симметрию. Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.
Определив, где расположены центры тяжести отдельных частей тела, переходят к поиску места расположения центра тяжести тела в целом. Тело представляют в виде системы материальных точек. При этом каждая точка имеет массу своей части тела и располагается в ее центре тяжести.
Координаты центра тяжести тела
В трехмерном пространстве координаты центра тяжести для твердого тела нахояд как:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_c=frac{sumlimits_i{Delta m_iy_i}}{m};; \
z_c=frac{sumlimits_i{Delta m_iz_i}}{m} end{array}
right.left(1right),]
где $m$ — масса тела.$;;x_i$ — координата на оси X элементарной массы $Delta m_i$; $y_i$ — координата на оси Y элементарной массы $Delta m_i$; ; $z_i$ — координата на оси Z элементарной массы $Delta m_i$.
В векторной форме записи система уравнений (1) представляется как:
[{overline{r}}_c=frac{1}{m}sumlimits_i{m_i{overline{r}}_ileft(2right),}]
${overline{r}}_c$ — радиус — вектор, определяющий положение центра тяжести; ${overline{r}}_i$ — радиус-векторы, которые определяют положения элементарных масс.
Центр тяжести, центр масс и центр инерции тела
Считают, что центр тяжести тела совпадают с центром масс тела, если его размеры малы в сравнении с расстоянием до центра Земли. При этом формулы, которые определяют положение цента тяжести и центра масс тела совпадают с выражениями (1) и (2). В основной массе задач центр тяжести принимают совпадающим с центром масс тела.
Сила инерции в неинерциальных системах отсчета, движущихся поступательно, приложена к центру тяжести тела.
Но центробежная сила инерции (в общем случае) не приложена к центру тяжести, поскольку в неинерциальной системе отсчета на элементы тела действуют разные центробежные силы инерции (даже если массы элементов равны), так как расстояния до оси вращения разные.
Примеры задач с решением
Пример 1
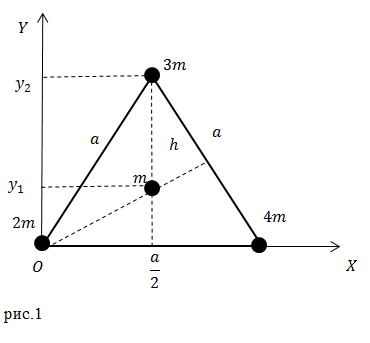
Задание: Каковы координаты центра тяжести системы из трех точечных масс, расположенных в вершинах и одной в центре равностороннего треугольника, со стороной равной $a (м)$ (рис.1)?
Решение: Определение для координат $x_c и y_c$ центра тяжести в нашем случае запишем в виде:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}(1.1);;]
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}(1.2).]
Из рис.1 мы видим, что соответствующие абсциссы точек равны:
[left{ begin{array}{c}
m_1=2m, x_1=0;; \
{rm }m_2=3m, x_2=frac{a}{2};; \
m_3=m, x_3=frac{a}{2};; \
m_4=4m, x_4=a. end{array}
right.left(1.3right).]
Тогда абсцисса центра тяжести получается равной:
[x_c=frac{2mcdot 0+3mcdot frac{a}{2}+mcdot frac{a}{2}+4mcdot a}{2m+3m+m+4m}=frac{6ma}{10m}=0,6a (м);]
Найдем ординаты точек.
[ begin{array}{c}
m_1=2m, y_1=0;; \
{rm }m_2=3m, y_2=frac{asqrt{3}}{2};; \
m_3=m, y_3=frac{asqrt{3}}{6};; \
m_4=4m, y_4=0. end{array}
left(1.4right).]
Для того чтобы найти ординату $y_2$ найдем, высоту в равностороннем треугольнике:
[h=sqrt{a^2-frac{a^2}{4}}=frac{asqrt{3}}{2}=y_2left(1.5right).]
Ординату $y_3$ найдем, учитывая, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, имеем:
[y_3=hcdot frac{1}{3}=frac{asqrt{3}}{6} left(1.6right).]
Вычислим ординату центра тяжести:
[y_c=frac{2mcdot 0+3mcdot frac{asqrt{3}}{2}+mcdot frac{asqrt{3}}{6}+4mcdot 0}{2m+3m+m+4m}=frac{10mfrac{asqrt{3}}{6}}{10m}=frac{asqrt{3} }{6}(м).]
Ответ: $x_c=0,6a {rm }{rm м}$; $y_c=frac{asqrt{3} }{6}$ м
Пример 2
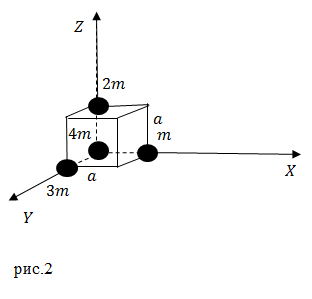
Задание: Каковы координаты центра тяжести системы из четырех элементарных масс, расположенных в вершинах куба со стороной равной $a$ (рис.2)?
Решение: Координату $x_c$ центра тяжести найдем как:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}=frac{mcdot a+2mcdot 0+3mcdot 0+4mcdot 0}{m+2m+3m+4m}=frac{am}{10m}=0,1 aleft(мright).]
Ординату центра тяжести вычислим как:
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}=frac{mcdot 0+2mcdot 0+3mcdot a+4mcdot 0}{m+2m+3m+4m}=frac{acdot 3m}{10m}=0,3a left(мright).]
Для координаты $z_c$ получаем:
[z_c=frac{m_1z_1+m_2z_2+m_3z_3+m_4z_4}{m_1+m_2+m_3+m_4}=frac{mcdot 0+2mcdot a+3mcdot 0+4mcdot 0}{m+2m+3m+4m}=frac{acdot 2m}{10m}=0,2a left(мright).]
Ответ: ($x_{c, }y_c, z_c$)=($ 0,1 a$, $0,3a$, $0,2a$)(м)
Читать дальше: циклическая частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!