Как найти центр вписанной окружности прямоугольного треугольника

Окружность, вписанная в треугольник. Теоремы и их рассмотрение

Еще в Древнем Египте появилась наука, с помощью которой можно было измерять объемы, площади и другие величины. Толчком к этому послужило строительство пирамид. Оно предполагало значительное число сложных расчетов. И кроме строительства, было важно правильно измерить землю. Отсюда и появилась наука «геометрия» от греческих слов «геос» — земля и «метрио» — измеряю.

Исследованию геометрических форм способствовало наблюдение астрономических явлений. И уже в 17-м веке до н. э. были найдены начальные способы расчета площади круга, объема шара и главнейшее открытие — теорема Пифагора.

Вам будет интересно: Казахская академия спорта и туризма. Факультеты, структура вуза

Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:

В треугольник можно вписать только одну окружность.

При таком расположении окружность — вписанная, а треугольник — описанный около окружности.

Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:

Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.

Окружность, вписанная в равнобедренный треугольник

Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.

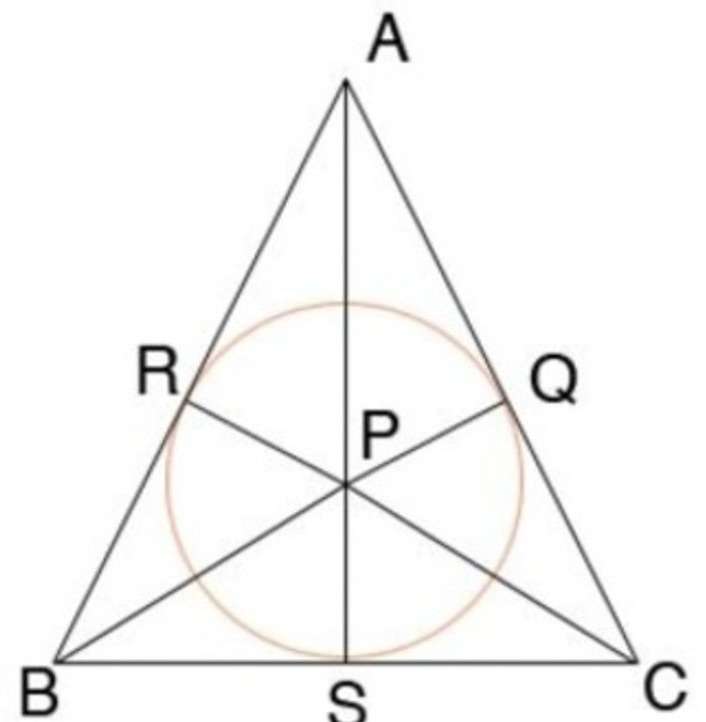
На фото ниже показана окружность, находящаяся внутри равнобедренного треугольника. Условие теоремы об окружности, вписанной в треугольник, соблюдено — она касается всех сторон треугольника AB, ВС И СА в точках R, S, Q соответственно.

Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).

Свойства теоремы об окружности, вписанной в треугольник:

• Отрезки, выходящие из одной вершины треугольника к точкам касания с окружностью, равны. На рисунке AR = AQ, BR = BS, CS = CQ.
• Радиус окружности (вписанной) — это площадь, деленная на полупериметр треугольника. Как пример, нужно начертить равнобедренный треугольник с теми же буквенными обозначениями, что на картинке, следующих размеров: основание ВС = 3 см, высота AS = 2 см, стороны АВ=ВС, соответственно, получаются по 2,5 см каждая. Проведем из каждого угла биссектрису и место их пересечения обозначим как Р. Впишем окружность с радиусом PS, длину которого нужно найти. Узнать площадь треугольника можно, умножив 1/2 основания на высоту: S = 1/2 * DC * AS = 1/2 * 3 * 2 = 3 см2. Полупериметр треугольника равен 1/2 суммы всех сторон: Р = (АВ + ВС + СА) / 2 = (2,5 + 3 + 2,5) / 2 = 4 см; PS = S/P = 3/4 = 0,75 см2, что полностью соответствует действительности, если измерить линейкой. Соответственно, верно свойство теоремы об окружности, вписанной в треугольник.

Окружность, вписанная в прямоугольный треугольник

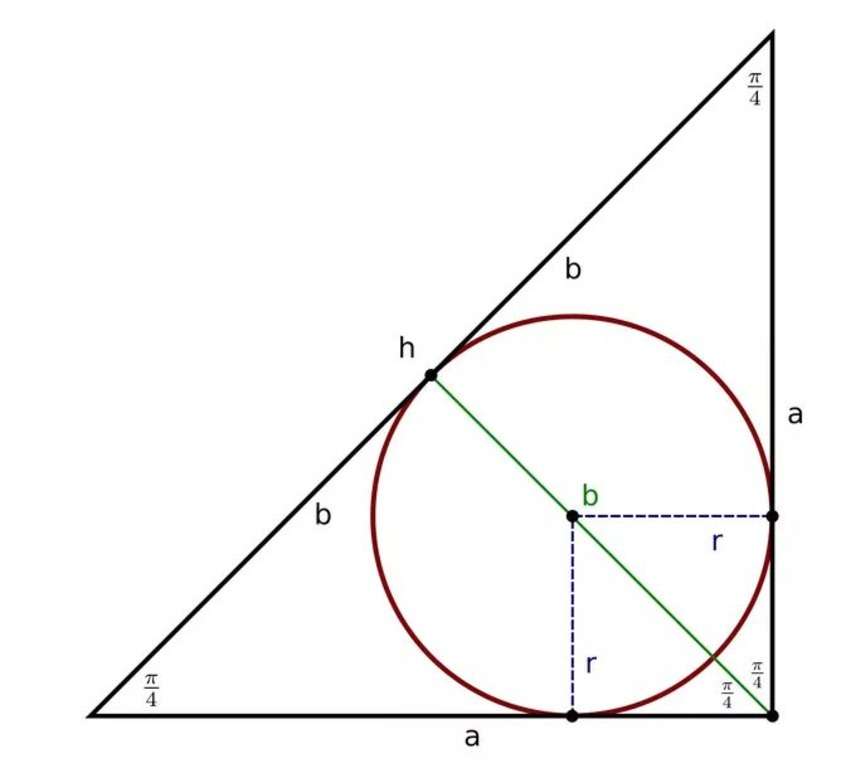
Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.

Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.

Есть хорошая формула, которая поможет высчитать площадь треугольника — периметр умножить на радиус вписанной в этот треугольник окружности.

Формулировка теоремы о вписанной окружности

В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:

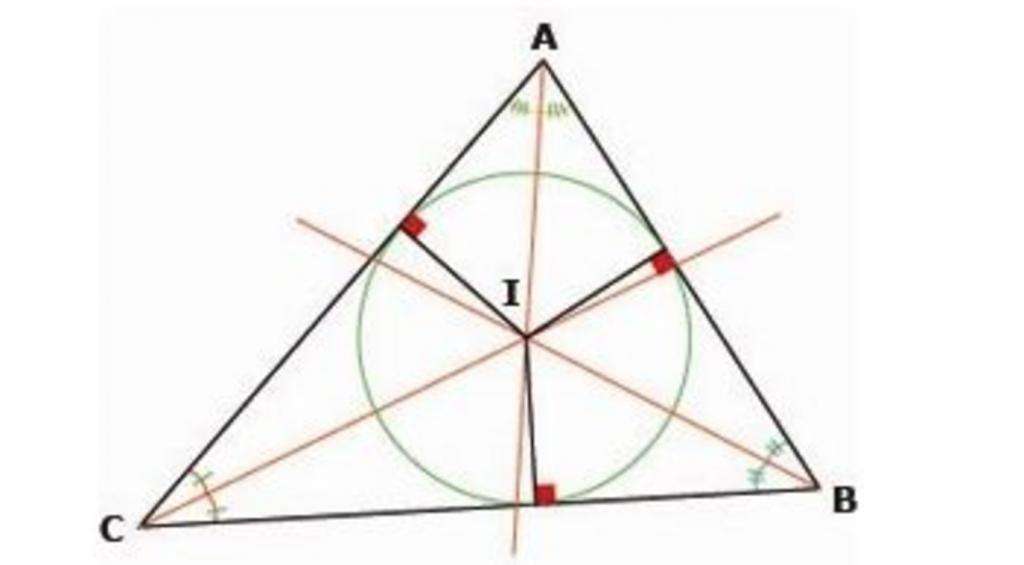
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.

На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.

Теорема о центре окружности, вписанной в треугольник

Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.

Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.

Узнать ещё

Знание — сила. Познавательная информация

Окружность, вписанная в прямоугольный треугольник

Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.

Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле

где a и b — длины катетов, c — гипотенузы.

Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.

Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.

Дано: ∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

1) По свойству отрезков касательных, проведенных из одной точки,

AK=AM=6 см,

2) AB=AM+BM=6+4=10 см,

3) По теореме Пифагора:

Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.

Ответ: 24 см, 24 см², 2 см.

Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.

Дано:∆ ABC, ∠C=90º,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AC, AB, BC,

1) Проведем отрезки OK и OF.

(как радиусы, проведенные в точки касания).

Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).

А так как OK=OF (как радиусы), то OKCF — квадрат.

2) По свойству касательных, проведенных из одной точки,

3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла

Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.

Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).

Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.

Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.

Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).

Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно

что и требовалось доказать.

Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.

Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.

Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.

Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).

Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать

Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .

Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.

Формулы для радиуса окружности, вписанной в треугольник

Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.

a, b, c – стороны треугольника,
S – площадь,
r – радиус вписанной окружности,
p – полупериметр

.

a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Фигура	Рисунок	Формула	Обозначения
Произвольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Прямоугольный треугольник

где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
.

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
.

где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Произвольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Прямоугольный треугольник

Произвольный треугольник

где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
.

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
.

Равнобедренный треугольник

Равносторонний треугольник

где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Прямоугольный треугольник

Вывод формул для радиуса окружности, вписанной в треугольник

Теорема 5 . Для произвольного треугольника справедливо равенство

где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).

с помощью формулы Герона получаем:

что и требовалось.

Теорема 6 . Для равнобедренного треугольника справедливо равенство

где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).

то, в случае равнобедренного треугольника, когда

что и требовалось.

Теорема 7 . Для равностороннего треугольника справедливо равенство

где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

то, в случае равностороннего треугольника, когда

что и требовалось.

Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.

Теорема 8 . Для прямоугольного треугольника справедливо равенство

Доказательство . Рассмотрим рисунок 9.

Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,

В силу теоремы 3 справедливы равенства

Следовательно, принимая также во внимание теорему Пифагора, получаем

что и требовалось.

Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.

Как вписать круг в прямоугольный треугольник

Прямоугольным называют треугольник, один из углов которого равен 90°. Как и в любой другой, в него можно вписать круг. Такой круг может быть только один, радиус его определяется длинами сторон, а центр лежит в точке пересечения биссектрис углов. Построить вписанную окружность можно несколькими способами — как с использованием формул и вычислений, так и без них.

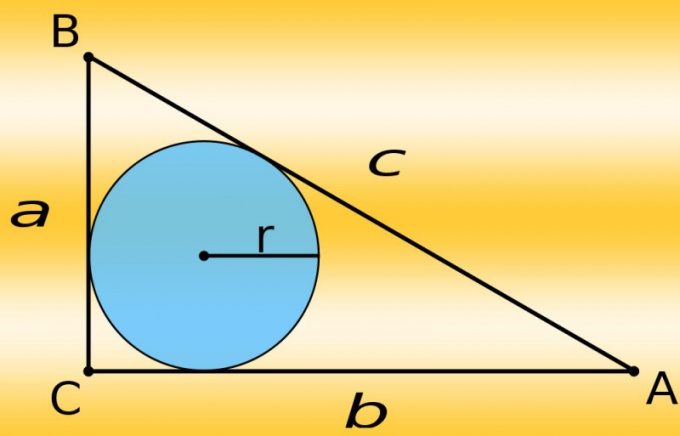
Вам понадобится

• Чертеж с треугольником, транспортир, циркуль, линейка, карандаш.

Инструкция

Найдите точку, которая будет центром вписанной окружности. Она должна лежать на пересечении биссектрис углов в вершинах треугольника, поэтому сначала приложите транспортир к одному из углов, определите его величину и поставьте вспомогательную точку на отметке, равной половине этой величины. Проведите отрезок из вершины этого угла — он должен пройти через вспомогательную точку и закончиться на противолежащей стороне. Таким же способом постройте биссектрису другого угла. Точка пересечения двух вспомогательных отрезков будет центром вписанной окружности.

Определите радиус круга. Для этого проведите еще один вспомогательный отрезок. Он должен начинаться в найденной точке, заканчиваться на одном из катетов и быть параллельным другому катету. Длина этого отрезка и будет радиусом вписанной окружности — отложите ее на циркуле и начертите круг с центром в найденной точке. На этом построение будет завершено.

Можно начертить вписанную окружность по-другому — с использованием формулы из курса элементарной геометрии. Для этого вам нужно знать длины всех сторон — измерьте их. Затем рассчитайте радиус (r) — сложите длины катетов (a и b), отнимите от результата длину гипотенузы (c), а то, что получилось, поделите пополам: r = (a+b-c)/2. Отложите найденную величину на циркуле и до конца построения не меняйте этого расстояния.

Установите циркуль в вершину прямого угла и начертите вспомогательную дугу — она должна пересекать оба катета. Собственно, только точки пересечения вам и нужны, поэтому вместо дуги можно просто поставить метки на катетах. Эти метки указывают точки касания вписанной окружности и сторон треугольника.

Установите циркуль в каждую из точек касания и проведите два полукруга, лежащих внутри треугольника. Точка их пересечения будет центром вписанной окружности — установите в нее циркуль и проведите вписанный в прямоугольный треугольник круг.

Источники:

• Как найти радиус вписанной в треугольник окружности?

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

с – гипотенуза треугольника.

Радиус вписанной в
прямоугольный треугольник окружности

равен произведению катетов, делённому на сумму
катетов и гипотенузы,

где  r –
искомый радиус, а  и  b – катеты,

с – гипотенуза треугольника.

Радиус вписанной в
прямоугольный треугольник окружности равен площади этого треугольника, делённой
на полупериметр:

где  р – полупериметр

ЗАДАЧА:

Точка касания окружности, вписанной в прямоугольный треугольник,
делит один из катетов на отрезки  2 см  и  8 см,
отсчитывая от вершины прямого угла. Найдите периметр треугольника.

РЕШЕНИЕ:

Начертим чертёж:

ВМ
= ВN = х.

(2 + х)² + (2 + ² = (8
+ х)²,

х² + 4х + 4
+ 100 =

= х² + 16х + 64,

12х = 40,

х =
¹⁰/₃ (см).

Р = (2 + + (8 + ¹⁰/₃) + (¹⁰/₃ + 2) = 26²/₃ (см).

ЗАДАЧА:

Вписанная окружность прямоугольного треугольника  АВС  касается гипотенузы  АВ  в точке 
К. Найдите радиус
вписанной окружности, если  АК = 4 см, ВК
= 6 см.

РЕШЕНИЕ:

За свойством касательных имеем:

АК = АМ = 4 см, 
ВК = ВN = 6 см.


Обозначим радиус вписанной окружности
через  х:

СN = СM = NО = МО = х.

Тогда 

АС =
(4 + х) см. 
ВС = (6 + х) см,

АВ =
4 см +
6 см =
10 см.

По теореме Пифагора для треугольника  АВС
можно записать соотношение:

(4 + х)² + (6 + х)² = 10².

Решим это квадратное уравнение:

16 + 8x + x²
+ 36 + 12x + x² = 100,

2x² + 20x + 52 – 100 = 0,

2x² + 20x – 48 = 0,

x² + 10x – 24 = 0,

x₁ = 2,  x₂ = –10.

x₂  не
удовлетворяет условию задачи.

ОТВЕТ:  2 см.

ЗАДАЧА:

Точка касания окружности, вписанной в прямоугольный треугольник,
делить гипотенузу на отрезки  8 см  и  12
см. Найдите периметр треугольника.

РЕШЕНИЕ:

Начертим чертёж:

(8 + 12)²
= (8 + х)² + (12 + х)²,

400 = 64 + 16x + x²
+ x² + 24x + 144,

2x² + 40x – 192 = 0,

x² + 20x – 96 = 0,

x₁ = 4,  x₂ = –24.

x₂  не
подходит.

Р
= 8 + 12 + 12 + 4 + 4 + 8 = 48 (см).

ОТВЕТ:  48 см.

Описанная окружность
прямоугольного треугольника.

Центром окружности, описанной
вокруг прямоугольного треугольника, будет середина его гипотенузы.

Диаметр окружности,
описанной вокруг прямоугольного треугольника, равен его гипотенузе.

Медиана прямоугольного
треугольника, проведённая к его гипотенузе, равна половине гипотенузы и
является радиусом окружности, описанной около этого треугольника.

ОА = ОВ = ОС = R

Радиус описанной окружности равен половине
гипотенузы:

ЗАДАЧА:

Отрезок  ВС – диаметр окружности, изображённой на рисунку.

Угол  АВС = 55°.

Найдите
величину
угла  АСВ
?

РЕШЕНИЕ:

ВС – диаметр,
поэтому  ∠ ВАС = 90°,

∠ АСВ = 180° – (90° + 55°) = 35°.

ЗАДАЧА:

Перпендикуляр,
опущенный из точки окружности на его диаметр, делит диаметр на отрезки, разность
между которыми равна  5 см. Найдите радиус окружности, если длина перпендикуляра равна  6 см.

РЕШЕНИЕ:

Пусть  АВ – диаметр окружности с
центром в точке  О, СD ⊥ АВ,

где  С – точка окружности,

СD = 6 см, АD = х см,

ВD – АD = 5 см.

Тогда 

DВ = (х + 5) см.

Треугольник  АСВ – прямоугольный (угол  С  прямой, так как
он вписанный и опирается на диаметр).

СD – перпендикуляр, проведений из вершины прямого угла на
гипотенузу. Тогда:

АD ∙ DВ = СD²,

х(х + 5) = 6²,

х²
+ 5х – 36 = 0,

x₁ = –9,  x₂ = 4.

x₁  не подходит.

Поэтому, АD = 4 см,

DВ = 4 + 5 = 9 (см).

АВ
= АD
+ DВ
=

=
4
+ 9 = 13 (см).

Тогда

r = АВ :
2 = 13 : 2 = 6,5 (см).

ОТВЕТ:  6,5 см

ЗАДАЧА:

Из точки на окружности проведены две перпендикулярные
хорды, разность между которыми равна  4 см. Найдите эти хорды, если радиус окружности равен  10
см.

РЕШЕНИЕ:

Пусть задана окружность радиуса  R,

в
которой
проведены
хорды  АВ  и 
АС (АВ ⊥ АС),

R = АО = ВО = СО =
10 см,

АС – АВ =
4
см.

Пусть  АВ = х см, тогда 

АС = (4
+ х) см.

Так как  ∠ А = 90°, то треугольник 
ВАС – 
прямоугольный,
в
котором 

ВС = 2ОВ= 2 ∙ 10 = 20 см.

Из
прямоугольного треугольника  ВАС  имеем:

АВ² + АС²
= ВС²,

х² + (4 + х)²
= 20²,

х² + 16 + 8х
+ х² = 400,

х² + 4х –
192 = 0,

х₁ = 12, 

х₂
= –16 – не подходит.

Поэтому,
АВ = 12 см,

АС
= 4 + 12 = 16 (см).

ОТВЕТ:  12
см, 16 см

ЗАДАЧА:

Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен  14°.
Найдите меньший угол этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

Так как треугольник
прямоугольный и медиана  ВМ  иcходит
из прямого угла  В, то точка  М  является центром
описанной окружности вокруг треугольника 
АВС.
Следовательно,

АМ
= МС = МВ = R,

где  R –
радиус описанной окружности.

Найдём сначала угол  МВС.
Учитывая, что  BD – биссектриса, то

∠ DВС = ⁹⁰/₂ = 45°. Тогда

∠ МВС = ∠ МВD + ∠ DВС,

∠ МВС = 14° + 45° = 59°.

Рассмотрим
равнобедренный треугольник  МВС  со сторонами 

МВ = МС,

в
котором углы при основании  ВС  равны, то есть

∠ С = ∠ МВС
 = 59°.

Так
как сумма острых углов в прямоугольном треугольнике равна  90°, то

∠ А + ∠ С  = 90°,

∠ А = 90° – ∠ С =

= 90° – 59° = 31°.

ЗАДАЧА:

Периметр
прямоугольного треугольника равен  72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.

РЕШЕНИЕ:

DO = OF = OE = r = 6 м.    

Поэтому  AD =
AF =
6 м.

FC = EC, BD = BE (отрезки касательных, проведённых из
одной точки)

Пусть  


BD = BE = x, 

FC = EC = y,

Тогда  


AB
= x + 6, AC = y + 6, 

BC = x + y.

AB + AC + BC = 

= x + 6 + y + 6
+ x + y = 72.

2x + 2y + 12 = 72,

2x + 2y = 60,

x + y = 30.

(x + y) – гипотенуза, или диаметр описанной окружности.

ОТВЕТ:  30 м.

ЗАДАЧА:

В окружности на расстоянии  6
см  от его центра проведена хорда длинной  16
см. Найдите радиус окружности.

РЕШЕНИЕ:

Начертим чертёж:

Пользуясь теоремой
Пифагора, находим радиус.

ЗАДАЧА:

Две окружности, радиусы которых равны  4 см  и  9 см, имеют внешнее касание. Найдите расстояние между
точками касания данных окружностей с их общей внешней касательной.

РЕШЕНИЕ:

ВК ⊥ АD, АК = 9 – 4 = 5 см.

Из  ∆ ВКА:

Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.

Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.

Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.

В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.

Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.

Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.

Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.

Всего различают четыре вида треугольников:

• Разносторонний / любой
• Правильный / равносторонний
• Равнобедренный /  равнобочный
• Прямоугольный / прямой

---

Радиус вписанной окружности в любой треугольник

1. Радиус вписанной окружности в любой треугольник через площадь и полупериметр

   [ r = frac{S}{p} ]

   S — площадь; p — полупериметр;

2. Радиус вписанной окружности в любой треугольник через все стороны и полупериметр

   [ r = sqrtfrac{{(p-a)(p-b)(p-c)}}{p} ]

   a, b, c — стороны; p — полупериметр;

3. Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр

   [ r = frac{frac{1}{2}a cdot h}{p} ]

   a — основание, сторона на которую падает высота; h — высота; p — полупериметр;

4. Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности

   [ r = frac{D}{2} ]

   D — диаметр вписанной окружности;

---

Радиус вписанной окружности в правильный треугольник

1. Радиус вписанной окружности в правильный треугольник через сторону

   [ r = frac{a}{2sqrt 3} ]

   a — сторона;

2. Радиус вписанной окружности в правильный треугольник через радиус описанной окружности

   [ r = frac{R}{2} ]

   R — радиус описанной окружности;

3. Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности

   [ r = frac{D}{2} ]

   D — диаметр вписанной окружности;

---

Радиус вписанной окружности в равнобедренный треугольник

1. Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание

   [ r = frac{b}{2} cdot sqrt{frac{2a-b}{2a+b}} ]

   a — боковая сторона; b — основание;

2. Радиус вписанной окружности в равнобедренный треугольник через высоту и основание

   [ r = frac{bh}{b + sqrt{4h^2+b^2}} ]

   b — основание; h — высота;

3. Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности

   [ r = frac{D}{2} ]

   D — диаметр вписанной окружности;

---

Радиус вписанной окружности в прямоугольный треугольник

1. Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу

   [ r = frac{a+b-c}{2} ]

   a, b — катеты; с — гипотенуза.

2. Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета

   [ r = frac{ab}{a+b+c} ]

   c — гипотенуза; a, b — катеты;

3. Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности

   [ r = frac{D}{2} ]

   D — диаметр вписанной окружности;

   ---

Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.

Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.

Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.

В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.