Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение точки, движущейся по окружности
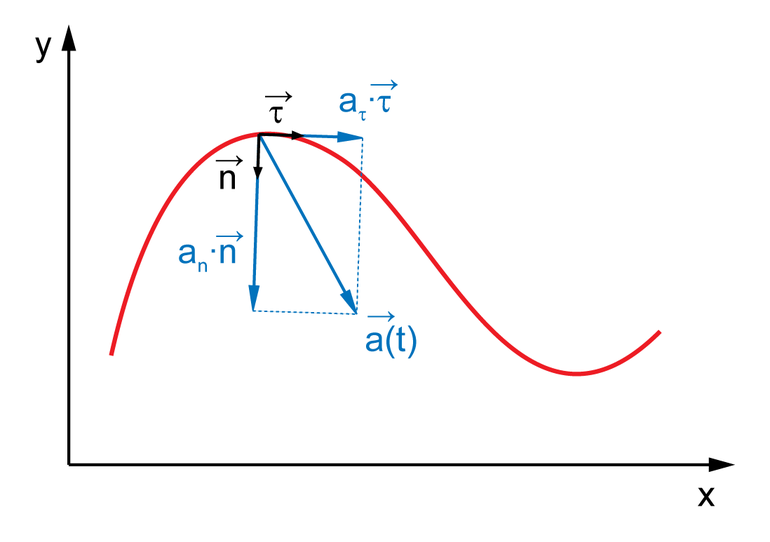
Полное ускорение точки, движущейся по окружности, складывается из двух составляющих:
- тангенциального ускорения, направленного по касательной к данной окружности;
- центростремительного ускорения, направленного по радиусу от точки к центру окружности.
Замечание 1
Тангенциальное ускорение отражает изменение величины скорости движения, центростремительное, называемое также нормальным и обозначаемое обычно как $a_n$, — измерение направления вектора скорости.
Центростремительное ускорение
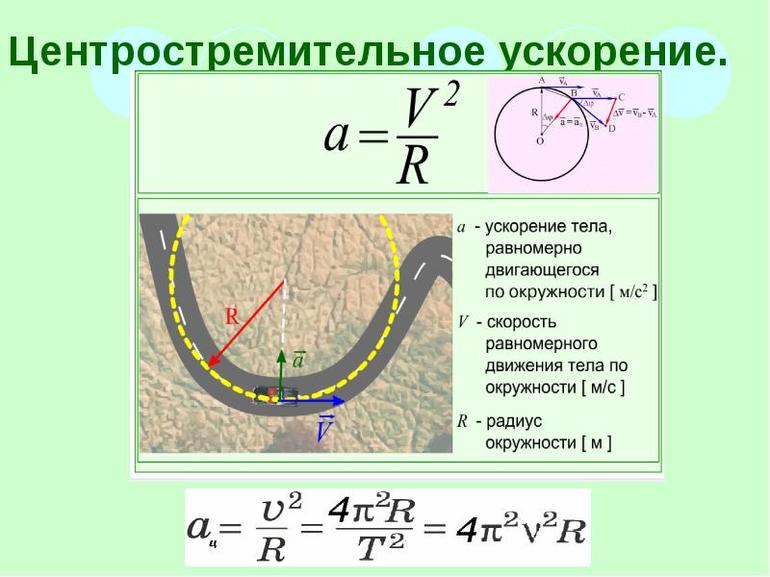
Формула для расчета центростремительного ускорения:
$a_n = frac{v^2}{R}$,
где $v$ — мгновенная скорость, $R$ — радиус кривизны траектории.
Выразив мгновенную скорость из угловой как
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
$v = omega cdot R$
и подставив в формулу, найдем центростремительное ускорение как
$a_n = frac{(omega cdot R)^2}{R} = omega^2 cdot R$
Основы теории о центростремительном ускорении заложил голландский физик Христиан Гюйгенс (1629 — 1695 гг.). В своем сочинении «Маятниковые часы» он не только изложил инженерные расчеты, необходимые для изготовления хронометров, но и сформулировал физические законы циклического движения. В частности, Гюйгенс открыл зависимость периодичности колебаний маятника от длины подвеса, описал явление изохронности ввел понятие центробежной силы и центростремительного ускорения. Это дало толчок не только прикладной механике, но и развитию теории о движении небесных тел, повлиявшей, в частности, на научные взгляды Исаака Ньютона.
Особенностью кругового движения является то, что даже если точка движется по окружности со скоростью неизменной величины (тангенциальное ускорение равно нулю), ее суммарное ускорение не равно нулю, поскольку направление вектора скорости всё время меняется. В этом заключается физический смысл центростремительного ускорения.
«Формула центростремительного ускорения в физике» 👇
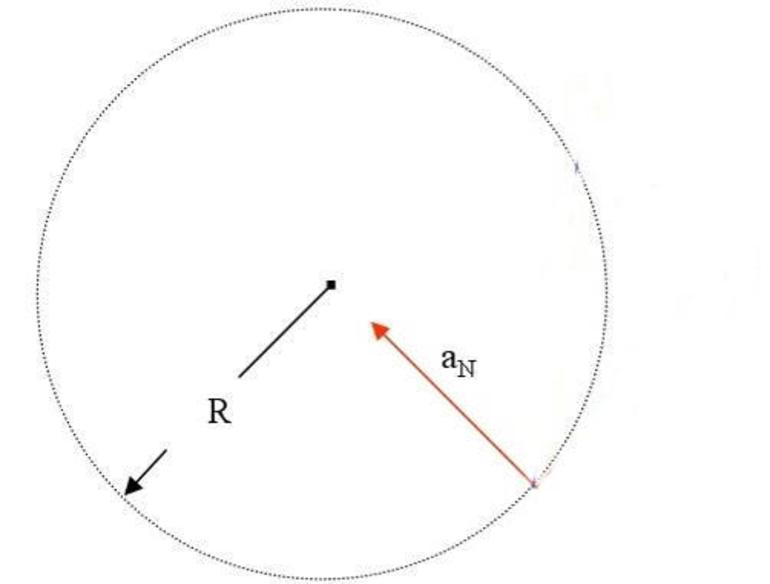
Геометрически центростремительное ускорение можно выразить следующим образом. Рассмотрим окружность, по которой движется точка.
Рисунок 1. Центростремительное ускорение. Автор24 — интернет-биржа студенческих работ
Выберем в качестве ее начального положения верхнюю точку. При этом вектор мгновенной скорости $vec{v_1}$ будет направлен горизонтально. Когда точка пройдет некоторую дугу, вектор мгновенной скорости $vec{v_2}$ окажется наклоненным к первому под углом $varphi$, который равен пройденному угловому расстоянию. Таким образом, центростремительный вектор окажется основанием равнобедренного треугольника с углом при вершине $varphi$ и стороной $bar{v_A} = bar{v_B}$. Обозначим длину основания этого треугольника как $Delta v$. Подобный треугольник со стороной $R$ мы видим внутри окружности. Его вершина соответствует ее центру. Приняв, что при достаточно малом $varphi$ длины дуги и хорды между точками $A$ и $B$ приблизительно совпадают, найдем из подобия треугольников, что
$frac{R}{v cdot Delta t} approx frac{v}{Delta v}$,
где $v cdot Delta t$ — путь, пройденный точкой по дуге, почти совпадающей с хордой.
Формулу можно преобразовать следующим образом:
$frac{Delta v}{Delta t} approx frac{v^2}{R}$
Учитывая малое пройденное угловое расстояние (при $Delta t$ стремящемся к нулю), можно считать вектор $vec{Delta v}$ направленным к центру окружности. Следовательно,
$vec{a_n} = frac{Delta vec{v}}{Delta t}; Delta t to 0; a_n = frac{v^2}{R}$
Замечание 2
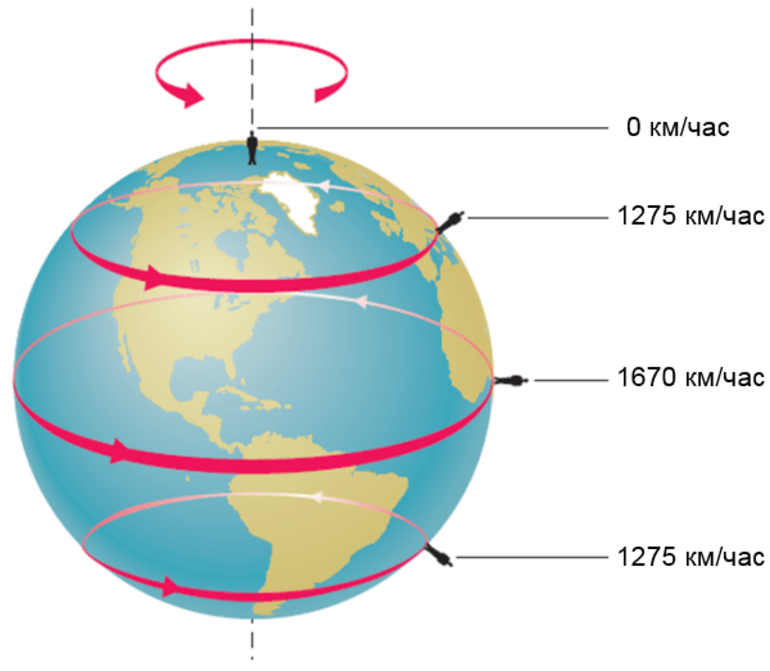
Хорошим способом представить себе центростремительное ускорение является конкретный пример. Центростремительное ускорение Земли, вращающейся вокруг своей оси, составляет $0,03 м/с^2$. Это значит, что в его отсутствие почва «уходила бы у нас из под ног» со скоростью 3 см/с.
Пример 1
Велосипедист едет по дороге со скоростью 10 м/с. Какое центростремительное ускорение точки обода колеса, если его радиус 35 см?
Подставим в формулу центростремительного ускорения числовые значения:
$a_n = frac{{10}^2}{0,35} = 285 m/c^2$
Ответ: 285 метров в секунду.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Что такое центростремительное ускорение
Определение
Центростремительным ускорением называется ускорение тела при движении тела по окружности.
Данная величина характеризует, насколько быстро изменяется направление линейной скорости объекта при его движении по окружности.
Обозначается центростремительное ускорение латинской буквой a, так как это векторная величина, обычно ее обозначение условно выглядит так: (vec a)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Единицами измерения в международной системе СИ является м/с2.
Силы центростремительная и центробежная, в чем отличия
Определение
На любое тело, передвигающееся по круговой траектории, воздействует постоянная сила, которая направлена к центру окружности, описывающей траекторию движения. Эта сила получила название центростремительной.
Определение
Центробежная сила представляет собой силу инерции. По третьему закону Исаака Ньютона, на каждое действие приходится равное ему по силе, но противоположное по направлению противодействие. И центробежная сила является той самой силой, которая противоположна центростремительной силе.
Сходства центростремительной и центробежной силы:
- Они являются инерциальными.
- Возникают всегда при движении тела.
- Появляются только парами и всегда уравновешивают друг друга.
Их различия заключаются в следующем:
- Центростремительная сила всегда направлена к центру окружности, в то время как центробежная сила противоположна центростремительной по направлению.
- Слово «центростремительная» с латинского языка переводится как «искать центр», а «центробежная» — «бежать от центра».
Куда направлен вектор центростремительного ускорения
При передвижении точки по окружности ее скорость направлена по касательной к окружности, а ускорение — по радиусу к центру окружности. Т.е. центростремительное ускорение всегда перпендикулярно скорости.
Вывод формулы центростремительного ускорения
Как найти через угловую и линейную скорость
Центростремительное ускорение, при условии равномерного движения по окружности, можно вычислить с помощью линейной скорости движения.
Центростремительное ускорение можно вычислить через угловую скорость.
Определение
Угловой скоростью (omega) называется физическая величина, численно равная отношению угла поворота (varphi) к тому интервалу времени (t), за который этот поворот произошел:
(omega =fracvarphi t)
Измеряется величина в рад/с.
Зависимость ускорения от скорости математически выглядит так:
(a=omega^2times R)
Расчет центростремительного ускорения через радиус
План урока:
Закон сложения скоростей
Мгновенная скорость, направление мгновенной скорости
Ускорение. Касательное ускорение. Центростремительное ускорение
Равноускоренное движение
Свободное падение
Равномерное движение точки по окружности
Закон сложения скоростей
Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью 

Рисунок 1 – Первоначальная скорость пчелы и ветра
Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):
Рисунок 2 – Изменившаяся скорость пчелы
Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v2 системе отсчета.
Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре
Мгновенная скорость, направление мгновенной скорости
Средняя скорость. Средняя путевая скорость
Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.
Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.
Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:
Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.
То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.
Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt1, Δt2,…Δtn, и найти средние скорости за эти отрезки времени:
А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δtb направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.
Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:
Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.
Ускорение. Касательное ускорение. Центростремительное ускорение
Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.
Единицы измерения ускорения:
Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)
Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.
Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).
Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2
Равноускоренное движение
Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении
Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:
Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.
При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:
v = v0 + a * t
Если же ускорение противонаправлено начальной скорости, это выражение станет таким:
v = v0 — a * t
Рассмотрим график зависимости скорости от времени при равноускоренном движении (см. рисунок 8). Считаем, что тело совершает движение вдоль оси ОХ, а все величины – начальная скорость (vox) , ускорение (ax) – взяты в проекции на эту ось.
Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении
Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.
Свободное падение
Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение
Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.
- Свободное падение
Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).
Рисунок 9 – Свободное падение тела
Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:
- Движение тела, брошенного вертикально вверх
Представим, что тело подкинули вертикально наверх с начальной скоростью v0 (см. рисунок 10).
Рисунок 10 – Тело бросили вертикально вверх
Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v0 (вообще нужно было бы писать voy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).
Отсюда можно найти полное время полета:
- Движение тела, брошенного под углом к горизонту
Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью под углом α к горизонту.
Рисунок 11 – Тело брошено под углом к горизонту
Уравнения движения в общем виде по двум осям выглядят так:
Еще время полета можно посчитать, учитывая что в двух моментах – в начале полета и в конце. Значит можно посчитать:
Равномерное движение точки по окружности
Центростремительное ускорение
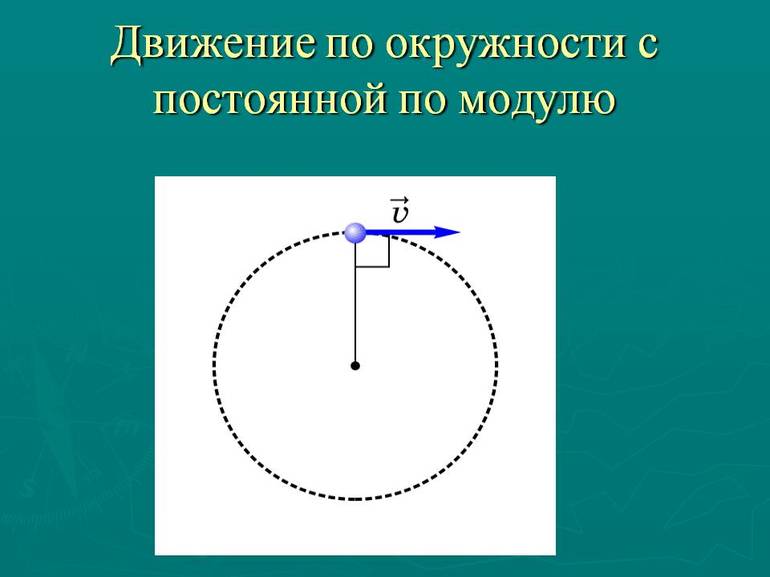
Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).
Рисунок 12 – Изменение направления скорости при равномерном движении по окружности
За изменение направления скорости отвечает центростремительное ускорение ( Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:
где R – радиус окружности, по которой циклически движется тело.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Связь со вторым законом Ньютона
Как вывести формулу центростремительного ускорения
Движение по циклоиде*
Общие сведения
Явления, происходящие в окружающем мире, описываются рядом изменений, зависящих от времени и пространства. Простейшим видом такого процесса является движение, то есть изменение положения материальной точки относительно других окружающих объектов. Кинематика изучает любое перемещение, но при этом не выясняет вызвавших его причин. Несмотря на то что любое физическое тело имеет размеры, ими обычно пренебрегают, считая любое тело точкой.
Движение представляет собой векторную величину и является отрезком, соединяющим начальное положение с конечным. Путь же, пройденный точкой, считается скалярным и определяется как дуга траектории, пройденная телом за установленный промежуток времени.
Быстрота перемещения определяется скоростью, рассчитываемой от выбранной начальной системы отсчёта. Первую производную скорости, взятой по времени, называют ускорением.
Обозначать ускорение в физике условились латинской буквой «a». Находят параметр по формуле: a = dv / dt, где dV и dt — изменение скорости и времени. Существует несколько видов физической величины:
- Тангенциальное (касательное) — характеризует изменение быстроты, направленной по касательной.
- Центростремительное (нормальное) — наблюдается при перемещении как по окружности, так и по траектории, описываемой ненулевой кривизной.
- Угловое — показывает, как изменяется угловая скорость за определённый промежуток времени, то есть относительно центра вращения к радиусу окружности.
- Полное — складываемое из предыдущих видов ускорения.
Пусть имеется тело, которое движется по окружности. В начальный момент оно находилось в точке один, а после переместилось в точку два. Произошло это за время, равное Δt. За этот промежуток физический объект повернулся на угол f. Для описания процесса вводится понятие «угловая скорость». Обозначается она буквой гамма (w) и равняется углу, на который повернулось тело за единицу времени: w = f / Δt.
Простым примером нормального ускорения является движение по окружности. Вызывается оно силами, приложенными ортогонально вектору скорости. На чертеже его можно изобразить как вектор, перпендикулярный касательной пути в выбранной точке. Рассчитывается центростремительное ускорение по формуле: an = w 2 * R, где w — угловая скорость, R — радиус кривизны. В векторном виде формула принимает вид: an = (V2 / R) * e, где e — единичный вектор, рассчитываемый от центра кривизны к точке.
Вывод формулы
Математическое обоснование формулы для нахождения центростремительного ускорения при движении по окружности либо другой кривой траектории строится следующим образом. Величина убыстрения вычисляется, когда направление ускорения меняется, а вектор же всегда направлен к центру, причём его модуль равняется квадрату скорости, делённому на радиус: a = V2 / r.
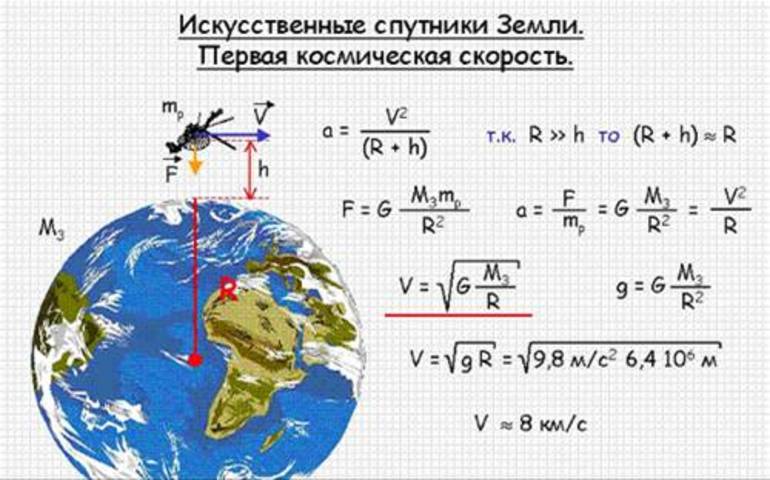
Можно представить спутник, который движется по круговой орбите вокруг Земли. Некоторые космические тела описывают окружность и вращаются против часовой стрелки. Радиус-вектор удобно определить как функцию времени. Он изменяется при вращении тела по окружности P(t). Итак, за начало координат можно взять точку, обозначающую планету Земля и провести через неё координатные оси.
Нужно определить вектор между положительной полуосью P(x) и радиус-вектором Q. Орбита имеет радиус R, величина которого постоянна. Модуль изменяющегося радиус-вектора будет равняться r || p (+)|| = r. Чтобы записать вектор через компоненты, используются основы тригонометрии, позволяющие выполнить разложение по базису.
В какой-то момент времени радиус-вектор будет обладать модулем r. Его угол равняется по иксу компоненте r * cosQ, а по игреку — r * sinQ. Параметр в любой момент может быть выражен через сумму икс и игрек компонентов: p (t) = r * cosQ (t) * I + r * sinQ (t) * j, где I — базис для икса компоненты, направленной вдоль оси ординаты, а j — параллельно оси абсциссы.
Производная от всего этого выражения и будет вектором скорости как функция от времени: V (t) = dp / dt = r (-sinQ (t)) * w * I + r * cosQ (t) * w * j. Сделав преобразования, можно получить выражение следующего вида: V (t) = -w * r (sinQ (t) * I — cos Q (t) * j). Теперь нужно взять производную от скорости, что является ускорением по времени: a (t) = dV / dt = =w * r * (cos (Q (t) * w * I + sin (Q (t) * w * j) = — w2 * r * (cos (Q (t) * I + sinQ (t) * j) = — w2 * p (t).
Таким образом, вектор ускорения как функция времени равняется отрицательному квадрату угловой скорости на радиус вектор. Теперь необходимо взять модуль обеих частей.
В итоге получится: ac = w 2 * r = (V/r)2 * r. Следует заметить, что направление центростремительного ускорения будет внутрь. В полученной формуле r сокращается и получается доказываемая формула: ac = V2 / r.
Фактическое понятие
Пусть имеется физическая точка, совершающая равномерное движение по окружности. Чтобы найти направление, следует принять, что за промежуток времени t рассматриваемое тело переместится из точки А в точку Б. При этом скорость перемещения будет постоянной по модулю. Если нарисовать вектора скорости в точках А и Б, то можно найти вектор изменения скорости дельта V.
Для этого нужно рассмотреть треугольники АБО и БОВ. Так как они равнобедренные, то углы при их вершинах идентичные, согласно теореме о взаимно перпендикулярных сторонах. Отсюда следует, что треугольники подобны. Используя правило подобия, верным будет записать пропорцию: БС / ОА = БВ / АБ. Каждому отрезку соответствует свой физический параметр. Переходя к их обозначениям, полученное соотношение можно переписать в виде: V / r = ΔV / Δr. Следовательно, v = v * Δr / r. Если обе части равенства разделить на промежуток времени, определяющий, за сколько произойдёт смена положения с учётом того, что a = ΔV / t; V = r / t, то равенство примет вид: a = V * V / r = V2 / r.
Если всё это изобразить на рисунке, то видно, что для определения ускорения нужно брать предел от Δt до бесконечности. Так как момент вращательный, то это значит, что угол w будет стремиться к нулю. Отсюда отрезок АБ стремится совместиться с АО, то есть вектор ускорения сонаправлен с изменением скорости.
Поэтому можно дать определение, что вектор ускорения при равномерном обращении всегда направлен к центру вращения, являясь, по сути, центростремительным.
Такого рода ускорение изменяет направление скорости, но оставляет неизменным её величину и является перпендикулярным вектору скорости. Как и любое убыстрение, за единицу измерения центростремительного ускорения берётся метр на секунду в квадрате, то есть единицы длины, делённые на квадрат единиц времени.
При решении задач часто также используется связь между угловой скоростью и линейной: a = V2 / r = (w * r) / r = w2 * r. Если провести аналогию дальше, то можно найти зависимость с равнопеременным прямолинейным движением: a = V — V 0 / t и равнопеременным перемещением по окружности: b = (w — w 0) / t = (v — v 0) / (r * t) = a / r .
Решение простых задач
После изучения теоретического материала важным этапом понимания темы является решение практических заданий. Существующие задачи можно разделить на элементарные и повышенного уровня. Учащимся в седьмом классе преподаватель задаёт для самостоятельного решения обычно несколько типовых заданий, научившись решать которые ученик получает не только практический опыт, но и понимает смысл изучения равнопеременного или равноускоренного движения.
Из наиболее типовых заданий можно выделить следующие:
- На велотреке спортсмен проходит закруглённый поворот радиусом 25 метров. Необходимо рассчитать скорость велосипедиста, если известно, что его центростремительная скорость равняется четыре метра в секунду. Решение задачи выполняется по формуле ускорения: a = V2 / R. Из неё можно выразить скорость: v = (4 * 25)½ = 10 м/с.
- С какой скоростью должен ехать автомобилист, чтобы пройти середину подъёма, имеющего доцентровое расстояние 22,5 метра, если его центростремительное ускорение и свободного падения должны равняться друг другу? Известно, что скорость связана с ускорением через формулу: V = √(a * R). Так как ускорение равняется величине свободного падения, то исходных данных хватает, чтобы их подставить в формулу и найти ответ: V = 10 * 22,5 = 15 м/с.
- Скорость на экваторе земной поверхности при вращении Земли вокруг своей оси составляет два километра в секунду. Необходимо определить период вращения Земли и центростремительное ускорение физического тела, располагающегося на экваторе. Центробежной силой пренебречь. Для решения задачи необходимо знать радиус Земли. Он составляет приблизительно 6300 км. Используя основную формулу, можно вычислить ускорение: a = V2 / R = 22 / 6 300 = 5,3 * 10-3 км/с. Так как V = 2pR / V, то из формулы можно выразить период: T = 2 pR / V = (2 * 3,14 * 6,3 * 108) / 2 * 103 = 575 ч = 24 сут.
-
Как должен измениться радиус поворота колеса в автомобиле, если скорость движения машины составляет три метра в секунду, а ускорение — пять метров в секунду? Для удобства можно изобразить зависимость траектории движения на рисунке. На нём обозначить скорость и ускорение, указать начало системы координат в точке нахождения колеса. Одна ось получится направленной вдоль радиуса, а вторая — по касательной к окружности. Для решения задачи понадобится формула, связывающая скорость и ускорение: V2 = a * R. Из неё можно выразить искомый радиус: R = V2 / a = 32 / 5 = 1,8 метров.
Сложные задания
Элементарные задачи решать просто, понимая суть ускорения и зная формулы. Сложнее проводить вычисления, когда необходимо использовать несколько выражений и знать зависимость параметров между собой, а также единицы их измерения. Вот некоторые из таких примеров повышенного уровня.
Движение тела описано уравнением: k(t) = N (I * coswt + j * sinwt). Известно, что N равняется 0,5 метров, а w составляет пять радианов в секунду. Нужно вычислить скорость по модулю и модульное значение нормального ускорения. Решение задачи следует выполнять по следующему алгоритму:
- Найти вектор скорости: V(t) = I * (drx / dt) + j * (dry / dt) = — i * Nw * coswt + j * Nw * sinwt.
- Определить значение скорости, согласно начальным координатам: Vx = — i * Nw * coswt; Vy = j * Nw * sinwt.
- Вычислить скорость по формуле: V = ( Vx 2 + Vy 2)1/2 = ((- Nw * cos2wt)2 + (Nw * sinwt)2)1/2 = ( N 2 w 2)1/2 = N * w = 2,5 метров в секунду.
- Используя формулу ускорения, рассчитать ответ: a = I * Nw2 * sinwt + j * Nw2 coswt = A * w2 = 12,5 метров, делённых на секунды в квадрате.
Пусть имеется точка, движущаяся по окружности с радиусом, равным двум метрам. Её путь описывается уравнением: j = At2. Найти, в какой момент нормальное ускорение сравняется с тангенциальным и вычислить полное убыстрение тела. При этом А = 2 м/с2, а центробежный момент мал и его можно не учитывать.
Для решения примера следует сначала выписать необходимые формулы.
Так, центростремительное ускорение точки определяется с помощью выражения: a = V 2 / R = ( dS ( t )/ dt )2 / R = (3 At 2)2 / R. Тангенциальное ускорение вычисляется из выражения: at = d 2 S ( t ) / d 2= A * t. Так как по условию ускорения равны, то можно записать равенство: ((3 At2)2) / R = 6 At. Отсюда можно выразить время: t = √(2 R /3 A ) = 0,874 секунды.
Полное ускорение точки вычисляется по формуле: a = √ a2 n + a2 t = √ 2 at = √ 2 * 6 * At = 14,82 м / с2. Теперь можно рассчитать угловую скорость точки, она составит: w = (1/r) * ds(t) / dt = 3At2 / R = 2,289 и будет измеряться в радианах, делённых на секунду. Угловое же ускорение находится по формуле є = a / R = (6 * At) / t = 5,241 рад / с2. Задача решена.