Introduction
Central Force, in physics, refers to a force that acts on every particle of the system, with the same magnitude and direction. Central forces are encountered often in physics, particularly when studying celestial mechanics and electromagnetism, where they appear as gravity and Coulomb’s law, respectively.
In this tutorial, we will discuss what a central force is and how it works.
What is Central Force?
A central force is a force that emanates from a single source and acts on all particles in a system. This force acts as an attractor on other objects that are nearby, like gravity and electromagnetism. The term central refers to the fact that these forces can originate from the center of an object, rather than its edge or surface, just like the word center refers to the middle of something.
Example
One of the most well-known examples of a central force comes from Isaac Newton’s law of universal gravitation, which says that all objects with mass in the universe exert a gravitational force on one another that is directly proportional to their masses and inversely proportional to the square of their distances apart; these properties are common to any central force.
The concept of central forces was introduced by French mathematician Joseph-Louis Lagrange in 1788 as an extension of Newton’s laws of motion. In Lagrange’s formulation, forces are not dependent on where an object is located within a system; they only depend on its mass and position relative to other objects within that system.
Equation of Central Force
The mathematical equation of central force is as follows:
F = F(r) r^
Where,
F = Conservative central force
r = Vector magnitude |r| is the distance to the center of force.
r^ = r/r
Here,
r^=r/r is a unit vector in the direction of r.
The central force is a conservative force, represented as follows:
$mathrm{F(r):=:dU / dr}$
Here,
F(r) is the magnitude of the central force.
U(r) is time-independent potential energy.
To result in the particle’s motion being uniformly circular under the central force, the centripetal force should be as follows:
$mathrm{mv^2r:=:F(r)}$
Where:
m = mass of the body
v = speed at which the centripetal force equation holds
r = Original Radius
Types of Motions in Central Force
The Central Force is comprised of two different types of motions:
- Bounded motion
- Unbounded motion.
Let’s have a look.
Bounded Motion
Bounded motion is a special property of a central force. It means that an object under its influence can only travel along a conic section. A conic section is any curve traced out by a plane slicing through a cone. The standard orbits of central forces are ellipses, parabolas, and hyperbolas. These three curves are all examples of conic sections.
Example
One example is the motion of the planets around the sun. All of these objects follow elliptical orbits because they are affected by a central force (gravity). In fact, every planet in our solar system follows an elliptical orbit around our star.
Unbounded Motion
During the initial and final phases of this motion, the distance between the two bodies or objects is infinite. The force of attraction that keeps them together is not constant; it varies with time. This type of motion was studied by Sir Isaac Newton and his contemporary Gottfried Leibniz.
FAQs
Q1. In which factors do central forces depend?
Ans: A Central Force is one that depends only upon the distance between two objects and not upon their intrinsic properties. It is also called an Attractive or Repulsive force depending upon whether it attracts or repels objects towards each other or away from each other, respectively.
Q2. What is the Central Force? Are all Conservative forces central?
Ans: In physics, a central force is a force that acts on a body due to its position with respect to others in a system of bodies. When used without qualification, it usually means central gravitational force. When defined more broadly, however, it can also refer to other forces that act on bodies because of their relative positions.
According to classical mechanics, we think of an object as either a central or conservative force. All forces can be described as central forces or conservative forces. But not all central forces are conservative and not all conservative forces are central.
Q3. What is the purpose of an elliptical orbit around the sun that does not have a constant angular momentum?
Ans: An elliptical orbit is defined by two extreme points at which an object passes in its transit. A central force is any phenomenon that attracts or repels a celestial body towards another celestial body. The Sun exerts a central force on all planets and other objects that orbit it, creating elliptical orbits.
This can be seen through Newton’s law of universal gravitation. It states that every particle attracts every other particle with a force proportional to their masses and inversely proportional to their distance squared from each other. This results in elliptical orbits around the sun for all objects because they are not infinitely massive (as would be required for circular motion) but are subject to gravitational forces from both ends of their orbit.
Q4. What are some examples of central force?
Ans: Following are some examples of central force:
-
Projectile Motion: Projectile motion is the best example of central motion. This motion is any motion of an object in which gravity is a significant force. In everyday terms, a projectile is an object thrown or shot at some target (such as in sports or games).
-
Simple harmonic Motion: It is an example of central motion. The point mass (the particle) moves in a circle around a fixed point. The force that causes it to move in a circle comes from a single source (the center). In other words, there is only one force acting on it. This type of motion is also called uniform circular motion or simple harmonic motion.
-
Force due to Gravitation: The gravitational force between two bodies is proportional to their masses and inversely proportional to the square of their separation. It is also directed along a line that passes through both bodies and is bisected by their center of mass.
В классической теории потенциала проблема центральной силы заключается в том, чтобы определить движение частицы в единственном центральном потенциальном поле. Центральная сила — это сила (возможно, отрицательная), которая направлена от частицы прямо к фиксированной точке в пространстве, центру, и величина которой зависит только от расстояния объекта до центра. Во многих важных случаях проблема может быть решена аналитически, т. Е. С помощью хорошо изученных функций, таких как тригонометрические функции.
Решение этой проблемы важно для классической механики, поскольку многие естественные силы являются центральными. Примеры включают гравитацию и электромагнетизм, описанные законом всемирного тяготения Ньютона и законом Кулона соответственно. Проблема важна еще и потому, что некоторые более сложные задачи классической физики (такие как задача двух тел с силами вдоль линии, соединяющей два тела) могут быть сведены к задаче центральной силы. Наконец, решение проблемы центральной силы часто дает хорошее начальное приближение к истинному движению, как при вычислении движения планет в Солнечной системе.
Содержание
- 1 Основы
- 1.1 Определение центральной силы
- 1.2 Потенциальная энергия
- 1.3 Одномерная задача
- 1.4 Равномерное круговое движение
- 1.5 Связь с классической задачей двух тел
- 2 Качественные свойства
- 2.1 Плоское движение
- 2.2 Полярные координаты
- 2.3 Удельный угловой момент
- 2.4 Постоянная пространственная скорость
- 2.5 Эквивалентное параллельное силовое поле
- 3 Общее решение
- 3.1 Уравнение Бине
- 3.2 Орбита частицы
- 3.3 Точки поворота и замкнутые орбиты
- 4 Конкретные решения
- 4.1 Проблема Кеплера
- 4.2 Центральные силы с точными решениями
- 4.3 Вращающиеся орбиты
- 5 Историческое развитие
- 5.1 Вывод Ньютона
- 6 Альтернатива вывод уравнений движения
- 6.1 Лагранжева механика
- 6.2 Гамильтонова механика
- 6.3 Гамильтон-Якоби е quation
- 7 См. также
- 8 Примечания
- 9 Ссылки
- 10 Библиография
- 11 Внешние ссылки
Основы
Суть проблемы центральной силы состоит в том, чтобы решить положение rчастицы, движущейся под действием центральной силы F, либо как функция времени t, либо как функция угла φ относительно центра силы и произвольного ось.
Определение центральной силы

Консервативная центральная сила F имеет два определяющих свойства. Во-первых, он должен направлять частицы либо прямо к, либо прямо от фиксированной точки в пространстве, центра силы, который часто обозначается O . Другими словами, центральная сила должна действовать вдоль линии, соединяющей O с текущим положением частицы. Во-вторых, консервативная центральная сила зависит только от расстояния r между O и движущейся частицей; он не зависит явно от времени или других дескрипторов положения.
Это двойное определение может быть выражено математически следующим образом. Центр силы O может быть выбран в качестве начала системы координат. Вектор r, соединяющий O с текущим положением частицы, известен как вектор положения . Следовательно, центральная сила должна иметь математическую форму
- F = F (r) r ^ { displaystyle mathbf {F} = F (r) { hat { mathbf {r}}}}
где r — величина вектора | r | (расстояние до центра силы) и r̂= r/ r — это соответствующий единичный вектор. Согласно второму закону движения Ньютона, центральная сила F создает параллельное ускорение a, масштабируемое массой m частицы
- F = F ( г) р ^ знак равно ма = г-н ¨ { Displaystyle mathbf {F} = F (г) { шляпа { mathbf {r}}} = m mathbf {a} = m { ddot { mathbf {r }}}}
Для сил притяжения F (r) отрицательно, потому что оно сокращает расстояние r до центра. И наоборот, для сил отталкивания F (r) положительно.
Потенциальная энергия
Если центральная сила является консервативной силой, то величина F (r) центральной силы всегда может быть выражена как производная от времени -независимая потенциальная энергия функция U (r)
- F (r) = — d U dr { displaystyle F (r) = — { frac {dU} {dr}}}
Таким образом, полная энергия частицы — сумма ее кинетической энергии и ее потенциальной энергии U — является постоянной величиной; энергия называется сохраненной. Чтобы показать это, достаточно того, что работа W, выполняемая силой, зависит только от начального и конечного положений, а не от пути, пройденного между ними.
- W знак равно ∫ р 1 р 2 F ⋅ dr = ∫ r 1 r 2 F (r) r ^ ⋅ dr = ∫ r 1 r 2 F dr = U (r 1) — U (r 2) { displaystyle W = int _ { mathbf {r} _ {1}} ^ { mathbf {r} _ {2}} mathbf {F} cdot d mathbf {r} = int _ { mathbf {r } _ {1}} ^ { mathbf {r} _ {2}} F (r) { hat { mathbf {r}}} cdot d mathbf {r} = int _ {r_ {1} } ^ {r_ {2}} Fdr = U (r_ {1}) — U (r_ {2})}
Эквивалентно, достаточно, чтобы curl силового поля F равно нулю; используя формулу для локона в сферических координатах,
- ∇ × F = 1 r sin θ (∂ F ∂ φ) θ ^ — 1 r (∂ F ∂ θ) φ ^ = 0 { displaystyle nabla times mathbf {F} = { frac {1} {r sin theta}} left ({ frac { partial F} { partial varphi}} right) { hat { boldsymbol { theta}}} — { frac {1} {r}} left ({ frac { partial F} { partial theta}} right) { hat { boldsymbol { varphi}}} = 0}
, поскольку частные производные равны нулю для центральной силы; величина F не зависит от угловых сферических координат θ и φ.
Поскольку скалярный потенциал V (r) зависит только от расстояния r до начала координат, он имеет сферическую симметрию. В этом отношении проблема центральной силы аналогична геодезическим Шварцшильда в общей теории относительности и квантово-механической трактовке частиц в потенциалах сферическая симметрия.
Одномерная задача
Если начальная скорость v частицы выровнена с вектором положения r, то движение навсегда останется на линии определяется r . Это следует потому, что сила — а по второму закону Ньютона также ускорение a — также совпадает с r . Чтобы определить это движение, достаточно решить уравнение
- mr ¨ = F (r) { displaystyle m { ddot {r}} = F (r)}
Один из методов решения — использовать сохранение полная энергия
- | r ˙ | = | д р д т | Знак равно 2 м E tot — U (r) { displaystyle | { dot {r}} | = { Big |} { frac {dr} {dt}} { Big |} = { sqrt { frac {2} {m}}} { sqrt {E _ { mathrm {tot}} -U (r)}}}
Взяв обратное и интегрируя, получаем:
- | т — т 0 | = m 2 ∫ | d r | E tot — U (г) { displaystyle | t-t_ {0} | = { sqrt { frac {m} {2}}} int { frac {| dr |} { sqrt {E _ { mathrm {tot}} -U (r)}}}}
В оставшейся части статьи предполагается, что начальная скорость v частицы не выровнена с вектором положения r, то есть, что вектор углового момента L= r× m v не равен нулю.
Равномерное круговое движение
Каждая центральная сила может вызывать равномерное круговое движение при условии, что начальный радиус r и скорость v удовлетворяют уравнению для центростремительной силы
- mv 2 r = F (r) { displaystyle { frac {mv ^ {2}} {r}} = F (r)}
Если это уравнение выполняется в начальные моменты, оно будет выполняться во всех последующих случаях; частица будет продолжать двигаться по кругу радиуса r со скоростью v бесконечно.
Связь с классической задачей двух тел

Проблема центральной силы касается идеальной ситуации («проблема одного тела»), в которой одиночная частица притягивается или отталкивается от неподвижной точки O, центра силы. Однако физические силы обычно действуют между двумя телами; и по третьему закону Ньютона, если первое тело прикладывает силу ко второму, второе тело прикладывает равную и противоположную силу к первому. Следовательно, оба тела ускоряются, если между ними присутствует сила; нет совершенно неподвижного центра силы. Однако, если одно тело в подавляющем большинстве массивнее другого, его ускорением относительно другого можно пренебречь; центр более массивного тела можно рассматривать как приблизительно неподвижный. Например, Солнце намного массивнее планеты Меркурий; следовательно, Солнце можно представить как неподвижный центр силы, сводя проблему к движению Меркурия в ответ на силу, приложенную Солнцем. В действительности, однако, Солнце также движется (хотя и незначительно) в ответ на силу, приложенную планетой Меркурий.

Однако такие приближения не нужны. Законы движения Ньютона позволяют преобразовать любую классическую задачу двух тел в соответствующую точную задачу одного тела. Чтобы продемонстрировать это, пусть x1и x2будут положениями двух частиц, а r= x1− x2- их относительным положением. Тогда, согласно второму закону Ньютона,
- r ¨ = x ¨ 1 — x ¨ 2 = (F 21 m 1 — F 12 m 2) = (1 m 1 + 1 m 2) F 21 { displaystyle { ddot { mathbf {r}}} = { ddot { mathbf {x}}} _ {1} — { ddot { mathbf {x}}} _ {2} = left ({ frac { mathbf {F} _ {21}} {m_ {1}}} — { frac { mathbf {F} _ {12}} {m_ {2}}} right) = left ({ frac {1} {m_ {1}}} + { frac {1} {m_ {2}}} right) mathbf {F} _ {21}}
Окончательное уравнение выводится из третьего закона Ньютона ; сила второго тела на первое тело (F21) равна силе первого тела на второе (F12) и противоположна ей. Таким образом, уравнение движения для r можно записать в виде
- μ r ¨ = F { displaystyle mu { ddot { mathbf {r}}} = mathbf {F} }
где μ { displaystyle mu}
- μ = 1 1 м 1 + 1 м 2 = m 1 м 2 м 1 + м 2 { displaystyle mu = { frac {1} {{ frac {1} {m_ {1}}} + { frac {1} {m_ {2}}}}} = { frac {m_ {1} m_ {2}} {m_ {1} + m_ {2}}}}
В качестве частного случая проблема двух тел, взаимодействующих с помощью центральной силы, может быть уменьшена к проблеме центральной силы одного тела.
Качественные свойства
Плоское движение

. Движение частицы под действием центральной силы F всегда остается в плоскости, определяемой его начальным положением и скоростью. Это можно увидеть по симметрии. Поскольку положение r, скорость v и сила F лежат в одной плоскости, никогда не бывает ускорения, перпендикулярного этой плоскости, потому что это нарушит симметрия между «над» плоскостью и «под» плоскостью.
Чтобы продемонстрировать это математически, достаточно показать, что угловой момент частицы постоянен. Этот угловой момент Lопределяется уравнением
- L = r × p = r × mv { displaystyle mathbf {L} = mathbf {r} times mathbf {p} = mathbf {r} times m mathbf {v}}
где m — масса частицы, а p — ее линейный импульс. Следовательно, вектор углового момента L всегда перпендикулярен плоскости, определяемой вектором положения частицы r и вектором скорости v.
В общем случае скорость изменения углового момента L равняется чистому крутящему моменту r× F
- d L dt = r ˙ × mv + r × mv ˙ = v × mv + r × F = r × F, { displaystyle { frac {d mathbf { L}} {dt}} = { dot { mathbf {r}}} times m mathbf {v} + mathbf {r} times m { dot { mathbf {v}}} = mathbf {v} times m mathbf {v} + mathbf {r} times mathbf {F} = mathbf {r} times mathbf {F} ,}
Первый член m v× vвсегда равен нулю, потому что вектор cross product всегда равен нулю для любых двух векторов, указывающих в одном или противоположных направлениях. Однако, когда F представляет собой центральную силу, оставшийся член r× Fтакже равен нулю, поскольку векторы r и F указывают в одном или противоположных направлениях. Следовательно, вектор L углового момента является постоянным. Тогда
- р ⋅ L = р ⋅ (r × p) = p ⋅ (r × r) = 0 { displaystyle mathbf {r} cdot mathbf {L} = mathbf {r} cdot ( mathbf {r} times mathbf {p}) = mathbf {p} cdot ( mathbf {r} times mathbf {r}) = 0}
Следовательно, положение частицы r (и, следовательно, скорость v ) всегда лежит в плоскости, перпендикулярной L.
полярным координатам

Поскольку движение является плоским, а сила радиальная, обычно переключают на полярные координаты. В этих координатах вектор положения r представлен в виде радиального расстояния r и азимутального угла φ.
- р знак равно (Икс, Y) знак равно р (соз φ, грех φ) { Displaystyle mathbf {r} = (х, y) = г ( соз varphi, sin varphi) }
Взяв первую производную по времени, получаем вектор скорости частицы v
- v = drdt = r ˙ (cos φ, sin φ) + r φ ˙ (- sin φ, cos φ) { displaystyle mathbf {v} = { frac {d mathbf {r}} {dt}} = { dot {r}} ( cos varphi, sin varphi) + r { dot { varphi}} (- sin varphi, cos varphi)}
Аналогично, вторая производная положения частицы r равна ее ускорению a
- a = r ¨ (cos φ, sin φ) + 2 r ˙ φ ˙ (- sin φ, cos φ) + r φ ¨ (- sin φ, cos φ) — r φ ˙ 2 (cos φ, sin φ) { displaystyle mathbf {a} = { ddot {r}} ( cos varphi, sin varphi) +2 { dot {r}} { dot { varphi}} (- sin varphi, cos varphi) + r { ddot { varphi}} (- sin varphi, cos varphi) -r { dot { varphi}} ^ {2} ( cos varphi, sin varphi)}
Скорость v и ускорение a могут быть выражены через радиальное a nd азимутальные единичные векторы. Радиальный единичный вектор получается делением вектора положения r на его величину r, как описано выше
- r ^ = (cos φ, sin φ) { displaystyle mathbf { hat { r}} = ( соз varphi, sin varphi)}
Азимутальный единичный вектор задается как
- φ ^ = (- sin φ, cos φ) { displaystyle { hat { boldsymbol { varphi}}} = (- sin varphi, cos varphi)}
Таким образом, скорость можно записать как
- v = vrr ^ + v φ φ ^ = r ˙ r ^ + р φ ˙ φ ^ { displaystyle mathbf {v} = v_ {r} mathbf { hat {r}} + v _ { varphi} { hat { boldsymbol { varphi}}} = { dot {r}} mathbf { hat {r}} + r { dot { varphi}} { hat { boldsymbol { varphi}}}}
, тогда как ускорение равно
- a = arr ^ + a φ φ ^ знак равно (r ¨ — r φ ˙ 2) r ^ + (2 r ˙ φ ˙ + r φ ¨) φ ^ { displaystyle mathbf {a} = a_ {r} mathbf { hat {r}} + a _ { varphi} { hat { boldsymbol { varphi}}} = ({ ddot {r}} — r { dot { varphi}} ^ {2}) mathbf { hat {r}} + (2 { dot {r}} { dot { varphi}} + r { ddot { varphi}}) { hat { boldsymbol { varphi}}}}
Удельный угловой момент

Поскольку F = m a по второму закону движения Ньютона, и поскольку F является центральной силой, тогда только радиальная составляющая ускорения a может быть ненулевой; угловая составляющая a φ должна быть равна нулю
- a φ = 2 r ˙ φ ˙ + r φ ¨ = 0 { displaystyle a _ { varphi} = 2 { dot {r}} { dot { varphi}} + r { ddot { varphi}} = 0}
Следовательно,
- ddt (r 2 φ ˙) = r (2 r ˙ φ ˙ + r φ ¨) = ra φ Знак равно 0 { displaystyle { frac {d} {dt}} left (r ^ {2} { dot { varphi}} right) = r (2 { dot {r}} { dot { varphi}} + r { ddot { varphi}}) = ra _ { varphi} = 0}
Это выражение в скобках обычно обозначается h
- h = r 2 φ ˙ = rv φ = | r × v | знак равно vr ⊥ знак равно L м { displaystyle h = r ^ {2} { dot { varphi}} = rv _ { varphi} = left | mathbf {r} times mathbf {v} right | = vr _ { perp} = { frac {L} {m}}}
что равно скорости v, умноженной на r ⊥, компонент радиус-вектора, перпендикулярный скорость. h — величина удельного углового момента , поскольку она равна величине L углового момента, деленной на массу m частицы.
Для краткости угловая скорость иногда обозначается как ω
- ω = φ ˙ = d φ dt { displaystyle omega = { dot { varphi}} = { frac {d varphi} {dt}}}
Однако не следует предполагать, что ω постоянна. Поскольку h константа, ω изменяется с радиусом r в соответствии с формулой
- ω = hr 2 { displaystyle omega = { frac {h} {r ^ {2}}}}
Поскольку h постоянна и r положительно, угол φ изменяется монотонно в любой задаче о центральной силе, непрерывно увеличиваясь (h положительный) или непрерывно уменьшаясь (h отрицательный).
Постоянная пространственная скорость
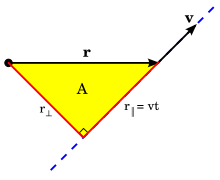
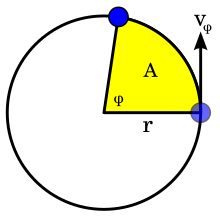
Величина h также равна удвоенному площади скорость, которая представляет собой скорость, с которой область выметается частицей относительно центра. Таким образом, поверхностная скорость постоянна для частицы, на которую действует центральная сила любого типа; это второй закон Кеплера. И наоборот, если движение под действием консервативной силы F является плоским и имеет постоянную площадную скорость для всех начальных условий радиуса r и скорости v, то азимутальный ускорение a φ всегда равно нулю. Следовательно, согласно второму закону Ньютона, F = m a, сила является центральной силой.
Постоянство пространственной скорости может быть проиллюстрировано равномерным круговым и линейным движением. При равномерном круговом движении частица движется с постоянной скоростью v по окружности радиуса r. Поскольку угловая скорость ω = v / r постоянна, площадь заметания за время Δt равна ω rΔt; следовательно, равные площади выметаются за равное время Δt. При равномерном линейном движении (т. Е. Движении в отсутствие силы согласно первому закону движения Ньютона) частица движется с постоянной скоростью, то есть с постоянной скоростью v вдоль линии. За время Δt частица выметает область ⁄ 2 vΔtr ⊥ (прицельный параметр ). Расстояние r ⊥ не меняется при движении частицы вдоль линии; он представляет собой расстояние наибольшего сближения линии с центром O (прицельный параметр ). Так как скорость v также не меняется, то пространственная скорость ⁄ 2vr⊥является константой движения; частица сметает равные площади за равное время.
Эквивалентное параллельное силовое поле
Путем преобразования переменных любую задачу центральной силы можно преобразовать в эквивалентную задачу параллельной силы. Вместо обычных декартовых координат x и y определены две новые переменные положения ξ = x / y и η = 1 / y, а также новая координата времени τ
- τ = ∫ dty 2 { displaystyle tau = int { frac {dt} {y ^ {2}}}}
Соответствующие уравнения движения для ξ и η задаются следующим образом:
- d ξ d τ = ddt (xy) dtd τ = (x ˙ y — y ˙ xy 2) y 2 = — час { displaystyle { frac {d xi} {d tau}} = { frac {d} {dt}} left ({ frac {x} { y}} right) { frac {dt} {d tau}} = left ({ frac {{ dot {x}} y — { dot {y}} x} {y ^ {2}) }} right) y ^ {2} = — h}
- d η d τ = ddt (1 y) dtd τ = — y ˙ y 2 y 2 = — y ˙ { displaystyle { frac {d eta} {d tau}} = { frac {d} {dt}} left ({ frac {1} {y}} right) { frac {dt} {d tau}} = — { frac { dot {y}} {y ^ {2}}} y ^ {2} = — { dot {y}}}
Поскольку скорость изменения ξ постоянна, его вторая производная равна нулю
- d 2 ξ d τ 2 = 0 { displaystyle { frac {d ^ {2} xi} {d tau ^ {2}}} = 0}
Поскольку это ускорение в ξ направления и поскольку F = ma по второму закону Ньютона, следует, что сила в Направление ξ равно нулю. Следовательно, сила действует только в направлении η, что является критерием для задачи параллельной силы. Явно ускорение в направлении η равно
- d 2 η d τ 2 = dtd τ ddt (d η d τ) = — y 2 y ¨ = — y 3 mr F (r) { displaystyle { frac { d ^ {2} eta} {d tau ^ {2}}} = { frac {dt} {d tau}} { frac {d} {dt}} left ({ frac {d eta} {d tau}} right) = — y ^ {2} { ddot {y}} = — { frac {y ^ {3}} {mr}} F (r)}
потому что ускорение в направлении y равно
- y ¨ = 1 m F y = 1 m F (r) yr { displaystyle { ddot {y}} = { frac {1} {m}} F_ {y } = { frac {1} {m}} F (r) , { frac {y} {r}}}
Здесь F y обозначает y-компоненту центрального сила, а y / r равно косинусу угла между осью y и радиальным вектором r.
Общее решение
уравнение Бине
Поскольку центральная сила F действует только по радиусу, только радиальная составляющая ускорения отлична от нуля. Согласно второму закону движения Ньютона величина F равна массе m частицы, умноженной на величину ее радиального ускорения
- F (r) = mr ¨ — mr ω 2 = md 2 rdt 2 — mh 2 r 3 { displaystyle F (r) = m { ddot {r}} — mr omega ^ {2} = m { frac {d ^ {2} r} {dt ^ {2}}} — { frac {mh ^ {2}} {r ^ {3}}}}
Это уравнение имеет коэффициент интегрирования drdt { displaystyle { frac {dr} {dt}}}
- F (r) dr = F (r) drdtdt = m (drdtd 2 rdt 2 — h 2 r 3 drdt) dt = m 2 d [(drdt) 2 + (hr) 2] { displaystyle { begin {align} F (r) , dr = F (r) { frac {dr} {dt}} , dt \ = m left ({ frac {dr} {dt}} { frac {d ^ {2 } r} {dt ^ {2}}} — { frac {h ^ {2}} {r ^ {3}}} { frac {dr} {dt}} right) , dt \ = { frac {m} {2}} , d left [ left ({ frac {dr} {dt}} right) ^ {2} + left ({ frac {h} {r}} right) ^ {2} right] end {align}}}
Интегрирование доходностей
- ∫ r F (r) dr = m 2 [(drdt) 2 + (hr) 2] { displaystyle int ^ {r} F (r) , dr = { frac {m} {2}} left [ left ({ frac {dr} {dt}} right) ^ {2} + left ( { frac {h} {r}} right) ^ {2} right ]}
Если h не равно нулю, независимую переменную можно изменить с t на ϕ
- ddt = ω dd φ = hr 2 dd φ { displaystyle { frac {d} {dt}} = omega { frac {d} {d varphi}} = { frac {h} {r ^ {2}}} { frac {d} {d varphi}}}
, что дает новое уравнение движения
- ∫ р F (r) dr = mh 2 2 [(- 1 r 2 drd φ) 2 + (1 r) 2] { displaystyle int ^ {r} F (r) , dr = { frac {mh ^ {2}} {2}} left [ left (- { frac {1} {r ^ {2}}} { frac {dr} {d varphi}} right) ^ {2 } + left ({ frac {1} {r}} right) ^ {2} right]}
Замена переменных на обратный радиус u = 1 / r дает
-
(dud φ) 2 знак равно C — u 2 — G (u) { displaystyle left ({ frac {du} {d varphi}} right) ^ {2} = Cu ^ {2} -G left (u right)} (1)
где C — постоянная интегрирования, а функция G (u) определяется как
- G (u) = — 2 mh 2 ∫ 1 u F (r) dr { displaystyle G (u) = — { frac {2} {mh ^ {2}}} int ^ { frac {1} {u}} F (r) , dr}
Это уравнение становится квазилинейным при дифференцировании по ϕ
- d 2 ud φ 2 + u = — 1 mh 2 u 2 F (1 / u) { displaystyle { frac {d ^ {2} u} {d varphi ^ {2}}} + u = — { frac {1} {mh ^ {2} u ^ {2}}} F (1 / u)}
Это известно как уравнение Бине. Интегрирование (1) дает решение для ϕ
- φ = φ 0 + ∫ 1 rdu C — u 2 — G (u) { displaystyle varphi = varphi _ {0} + int ^ { frac {1} {r}} { frac {du} { sqrt {Cu ^ {2} -G (u)}}}}
где ϕ 0 — другая постоянная интегрирования. Проблема центральной силы называется «интегрируемой», если это окончательное интегрирование может быть решено в терминах известных функций.
Орбита частицы
Полная энергия системы E tot равна сумме потенциальной энергии и кинетической энергии
- E tot = 1 2 mr ˙ 2 + 1 2 мр 2 φ ˙ 2 + U (г) = 1 2 мр ˙ 2 + мч 2 2 р 2 + U (г) { Displaystyle E _ { mathrm {tot}} = { frac {1} {2}} m { dot {r}} ^ {2} + { frac {1} {2}} mr ^ {2} { dot { varphi}} ^ {2} + U (r) = { frac {1} {2}} m { dot {r}} ^ {2} + { frac {mh ^ {2}} {2r ^ {2}}} + U (r)}
Поскольку полная энергия постоянна, скорость изменения r может быть рассчитана
- r ˙ = drdt = 2 m E tot — U (r) — mh 2 2 r 2 { displaystyle { dot {r}} = { frac {dr} {dt}} = { sqrt { frac {2} {m}}} { sqrt {E _ { mathrm {tot}} -U (r) — { frac {mh ^ { 2}} {2r ^ {2}}}}}}
который может быть преобразован (как и раньше) в производную от r по азимутальному углу φ
- drd φ = r 2 hdrdt { displaystyle { frac {dr} {d varphi}} = { frac {r ^ {2}} {h}} { frac {dr} {dt}}}
Интегрирование и использование формулы углового момента L = mh дает формулу
- φ = φ 0 + L 2 m ∫ rdrr 2 E tot — U (r) — L 2 2 mr 2 { displaystyle varphi = varphi _ {0} + { frac {L} { sqrt {2m}}} int ^ {r} { frac {dr} {r ^ {2} { sqrt {E _ { mathrm {tot}} -U (r) — { frac {L ^ {2}} {2mr ^ {2}}}}}}}}
что указывает на то, что угловой момент способствует эффективной потенциальной энергии
- U eff = U (r) + L 2 2 mr 2 { displaystyle U _ { mathrm {eff}} = U (r) + { frac {L ^ {2}} {2mr ^ {2}}}}
Изменение переменной интегрирования на обратный радиус дает интеграл
- φ = φ 0 + ∫ udu 2 m L 2 E tot — 2 m L 2 U (1 / u) — u 2 { displaystyle varphi = varphi _ {0} + int ^ {u} { frac {du} { sqrt {{ frac {2m} {L ^ {2}} } E _ { mathrm {tot}} — { frac {2m} {L ^ {2}}} U (1 / u) -u ^ {2}}}}}
, который выражает указанные выше константы C = 2mE tot / L и G (u) = 2mU (1 / u) / L, указанное выше, в терминах полной энергии E tot и потенциальной энергии U (r).
Точки поворота и замкнутые орбиты
Скорость изменения r равна нулю, когда эффективная потенциальная энергия равна полной энергии
- E tot = U (r) + L 2 2 mr 2 { displaystyle E _ { mathrm {tot}} = U (r) + { frac {L ^ {2}} {2mr ^ {2}}}}
Точки, в которых выполняется это уравнение, называются поворотными точки. Орбита по обе стороны от точки поворота симметрична; иными словами, если азимутальный угол определен таким образом, что φ = 0 в точке поворота, то орбита будет такой же в противоположных направлениях, r (φ) = r (−φ).
Если есть две точки поворота, так что радиус r ограничен между r min и r max, тогда движение содержится в кольцевом пространстве с этими радиусами. Поскольку радиус изменяется от одной точки поворота к другой, изменение азимутального угла φ равно
- Δ φ = L 2 м ∫ rminrmaxdrr 2 E — U (r) — L 2 2 mr 2 { displaystyle Delta varphi = { frac {L} { sqrt {2m}}} int _ {r _ { mathrm {min}}} ^ {r _ { mathrm {max}}} { frac {dr} {r ^ { 2} { sqrt {EU (r) — { frac {L ^ {2}} {2mr ^ {2}}}}}}}
Орбита замыкается сама на себя при условии, что Δφ равно рациональной дроби 2π, то есть
- Δ φ = 2 π mn { displaystyle Delta varphi = 2 pi { frac {m} {n}}}
, где m и n — целые числа. В этом случае радиус колеблется ровно m раз, а азимутальный угол φ совершает ровно n оборотов. В общем, однако, Δφ / 2π не будет таким рациональным числом, и, таким образом, орбита не будет замкнутой. В этом случае частица в конечном итоге пройдет сколь угодно близко к каждой точке в кольцевом пространстве. Два типа центральной силы всегда создают замкнутые орбиты: F (r) = αr (линейная сила) и F (r) = α / r (закон обратных квадратов ). Как показал Бертран, эти две центральные силы — единственные, которые гарантируют замкнутые орбиты.
В общем, если угловой момент L отличен от нуля, член L / 2mr предотвращает падение частицы в начало координат, если только эффективная потенциальная энергия стремится к отрицательной бесконечности в пределе r, стремящегося к нулю. Следовательно, если есть единственная точка поворота, орбита обычно уходит в бесконечность; точка поворота соответствует точке минимального радиуса.
Конкретные решения
Проблема Кеплера

В классической физике многие важные силы подчиняются закону обратных квадратов, например гравитация или электростатика. Общая математическая форма таких центральных сил, обратных квадрату:
- F = α r 2 = α u 2 { displaystyle F = { frac { alpha} {r ^ {2}}} = alpha u ^ { 2}}
для константы α { displaystyle alpha}
Этот частный случай классической проблемы центральной силы называется проблемой Кеплера. Для силы, обратно пропорциональной квадрату, полученное выше уравнение Бине является линейным
- d 2 u d φ 2 + u = — α m h 2. { displaystyle { frac {d ^ {2} u} {d varphi ^ {2}}} + u = — { frac { alpha} {mh ^ {2}}}.}
Решение этого уравнения имеет вид
- u (φ) = — α mh 2 [1 + e cos (φ — φ 0)] { displaystyle u ( varphi) = — { frac { alpha} {mh ^ { 2}}} left [1 + e cos left ( varphi — varphi _ {0} right) right]}
, что показывает, что орбита представляет собой конический участок эксцентриситет е; здесь φ 0 — начальный угол, а центр силы находится в фокусе конического участка. Используя формулу полуугла для синуса, это решение также можно записать как
- u (φ) = u 1 + (u 2 — u 1) sin 2 (φ — φ 0 2) { displaystyle u ( varphi) = u_ {1} + (u_ {2} -u_ {1}) sin ^ {2} left ({ frac { varphi — varphi _ {0}} {2 }} right)}

где u 1 и u 2 — константы, причем u 2 больше чем u 1. Две версии решения связаны уравнениями
- u 1 + u 2 = — 2 α mh 2 { displaystyle u_ {1} + u_ {2} = { frac {-2 alpha} {mh ^ {2}}}}
и
- e = u 2 — u 1 u 2 + u 1 { displaystyle e = { frac {u_ {2} -u_ {1}} {u_ {2} + u_ {1}}}}
Поскольку функция sin всегда больше нуля, u 2 — это наибольшее возможное значение u и обратное наименьшее возможное значение r, т. е. расстояние ближайшего доступа (периапсис ). Поскольку радиальное расстояние r не может быть отрицательным числом, равно как и обратное ему u; следовательно, u 2 должно быть положительным числом. Если u 1 также положительно, это наименьшее возможное значение u, которое соответствует наибольшему возможному значению r, расстоянию наибольшего сближения (апоапсис ). Если u 1 равно нулю или отрицательно, то наименьшее возможное значение u равно нулю (орбита уходит в бесконечность); в этом случае единственными значимыми значениями φ являются те, которые делают u положительным.
Для силы притяжения (α < 0), the orbit is an эллипс, гипербола или парабола, в зависимости от того, является ли u 1 положительным, отрицательное или нулевое соответственно; это соответствует эксцентриситету e меньше единицы, больше единицы или равному единице. Для силы отталкивания (α>0) u 1 должно быть отрицательным, поскольку u 2 положительны по определению, а их сумма отрицательна; следовательно, орбита является гиперболой. Естественно, если нет силы (α = 0), орбита является прямой линией.
Центральные силы с точными решениями
Уравнение Бине для u (φ) может быть решено численно почти для любой центральной силы F (1 / u). Однако лишь небольшая часть сил приводит к формулам для u в члены известных функций. Как было показано выше, решение для φ может быть выражено как интеграл по u
- φ = φ 0 + L 2 m ∫ udu E tot — U (1 / u) — L 2 u 2 2 m { displaystyle varphi = varphi _ {0} + { frac {L} { sqrt {2m}}} int ^ {u} { frac {du} { sqrt {E _ { mathrm {tot} } -U (1 / u) — { frac {L ^ {2} u ^ {2}} {2m}}}}}}
Проблема центральной силы называется «интегрируемой», если это интегрирование может быть решено в терминах известных функций.
Если сила является степенной, т. Е. Если F (r) = α r, то u может быть выражено через круговые функции и / или эллиптические функции, если n равно 1, -2, -3 (круговые функции) и -7, -5, -4, 0, 3, 5, -3/2, -5/2, -1/3, -5 / 3 и -7/3 (эллиптические функции). Точно так же только шесть возможных линейных комбинаций степенных законов дают решения в терминах круговых и эллиптических функций
- F (r) = A r — 3 + B r + C r 3 + D r 5 { displaystyle F (r) = Ar ^ {- 3} + Br + Cr ^ {3} + Dr ^ {5}}
- F (r) = A r — 3 + B r + C r — 5 + D r — 7 { displaystyle F (r) = Ar ^ {- 3} + Br + Cr ^ {- 5} + Dr ^ {- 7}}
- F (r) = A r — 3 + B r — 2 + C r + D { Displaystyle F (r) = Ar ^ {- 3} + Br ^ {- 2} + Cr + D}
- F (r) = A r — 3 + B r — 2 + C r — 4 + D r — 5 { displaystyle F (r) = Ar ^ {- 3} + Br ^ {- 2} + Cr ^ {- 4} + Dr ^ {- 5}}
- F (r) = A r — 3 + B r — 2 + C r — 3/2 + D r — 5/2 { displaystyle F (r) = Ar ^ {- 3} + Br ^ {- 2} + Cr ^ {- 3/2} + Dr ^ {- 5/2}}
- F (r) = A r — 3 + B r — 1/3 + C r — 5/3 + D r — 7/3 { displaystyle F (r) = Ar ^ {- 3} + Br ^ {- 1/3} + Cr ^ {- 5/3} + Dr ^ {- 7/3}}
Следующие особые случаи первых двух типов силы всегда приводят к круговые функции.
- F (r) = A r — 3 + B r { displaystyle F (r) = Ar ^ {- 3} + Br}
- F (r) = A r — 3 + B r — 2 { Displaystyle F (r) = Ar ^ {- 3} + Br ^ {- 2}}
Особый случай
- F (r) = A r — 5 { displaystyle F (r) = Ar ^ { -5}}
упоминается Ньютоном в следствии 1 предложения VII принципов как сила, возникающая при круговых орбитах, проходящих через точку притяжения.
Вращающиеся орбиты
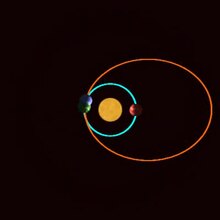
Термин r встречается во всех приведенных выше законах силы, указывая на то, что добавление силы обратного куба не влияет на разрешимость проблемы. с точки зрения известных функций. Ньютон показал, что с корректировкой начальных условий добавление такой силы не влияет на радиальное движение частицы, а умножает ее угловое движение на постоянный коэффициент k. Расширение теоремы Ньютона было открыто в 2000 году Магомедом и Вавда.
Предположим, что частица движется под произвольной центральной силой F 1 (r), и пусть ее радиус r и азимутальный угол φ обозначается как r (t), а φ 1 (t) как функция времени t. Теперь рассмотрим вторую частицу с той же массой m, которая совершает такое же радиальное движение r (t), но та, чья угловая скорость в k раз больше, чем у первой частицы. Другими словами, азимутальные углы двух частиц связаны уравнением φ 2 (t) = k φ 1 (t). Ньютон показал что сила, действующая на вторую частицу, равна силе F 1 (r), действующей на первую частицу, плюс центральная сила обратного куба
- F 2 (r) = F 1 (r) + L 1 2 мр 3 (1 — к 2) { displaystyle F_ {2} (r) = F_ {1} (r) + { frac {L_ {1} ^ {2}} {mr ^ {3}} } left (1-k ^ {2} right)}
где L 1 — величина углового момента первой частицы.
Если k больше единицы, F 2−F1- отрицательное число; таким образом, добавленная сила обратного куба привлекательна. И наоборот, если k меньше единицы, F 2−F1- положительное число; добавленная сила обратного куба является отталкивающей. Если k — целое число, такое как 3, орбита второй частицы называется гармоникой орбиты первой частицы; напротив, если k является обратным целому числу, например ⁄ 3, вторая орбита называется субгармоникой первой орбиты.
Историческое развитие

Вывод Ньютона
Классическая проблема центральной силы была геометрически решена Исааком Ньютоном в его Philosophiæ Naturalis Principia Mathematica, в которой Ньютон представил свои законы движения. Ньютон использовал эквивалент интегрирования чехарда для преобразования непрерывного движения в дискретное, чтобы можно было применять геометрические методы. В этом подходе положение частицы рассматривается только в равномерно распределенные моменты времени. Для иллюстрации частица на Фиг.10 расположена в точке A в момент времени t = 0, в точке B в момент времени t = Δt, в точке C в время t = 2Δt и так далее для всех времен t = nΔt, где n — целое число. Предполагается, что между этими временными точками скорость постоянна. Таким образом, вектор rAB= rB− rAравен Δt, умноженному на вектор скорости vAB(красная линия), тогда как rBC= rC− rBравен vBCΔt (синяя линия). Поскольку скорость постоянна между точками, предполагается, что сила действует мгновенно в каждой новой позиции; например, сила, действующая на частицу в точке B, мгновенно изменяет скорость с vABна vBC. Вектор разности Δ r= rBC− rABравен Δ v Δt (зеленая линия), где Δ v= vBC− vAB- изменение скорости в результате действия силы в точке B . Поскольку ускорение a параллельно Δ v и поскольку F = m a, сила F должна быть параллельным Δ v и Δ r . Если F является центральной силой, она должна быть параллельна вектору rBот центра O до точки B (пунктирная зеленая линия); в этом случае Δ r также параллельно rB.
. Если в точке B не действует сила, скорость не изменяется, и частица достигает точки K в момент времени t = 2Δt. Площади треугольников OAB и OBK равны, потому что у них одинаковое основание (r AB) и высота (r ⊥). Если Δ r параллельно rB, треугольники OBK и OBC также равны, потому что они имеют одно и то же основание (r B), а высота не изменяется. В этом случае площади треугольников OAB и OBC одинаковы, и частица выметает равные площади за равное время. И наоборот, если площади всех таких треугольников равны, то Δ r должно быть параллельно rB, из чего следует, что F является центральной силой. Таким образом, частица сметает равные площади за равное время тогда и только тогда, когда F является центральной силой.
Альтернативные выводы уравнений движения
Лагранжева механика
Формула для радиальной силы также может быть получена с помощью лагранжевой механики. В полярных координатах лагранжиан L отдельной частицы в поле потенциальной энергии U (r) задается формулой
- L = 1 2 mr ˙ 2 + 1 2 mr 2 φ ˙ 2 — U (r) { displaystyle L = { frac {1} {2}} m { dot {r}} ^ {2} + { frac {1} {2}} mr ^ {2} { dot { varphi}} ^ {2 } -U (r)}
Тогда уравнения движения Лагранжа
- ddt (∂ L ∂ r ˙) = ∂ L ∂ r { displaystyle { frac {d} {dt}} left ({ frac { partial L} { partial { dot {r}}}} right) = { frac { partial L} { partial r}}}
принимает вид
- mr ¨ = mr φ ˙ 2 — d U dr = mh 2 r 3 + F (r) { displaystyle m { ddot {r}} = mr { dot { varphi}} ^ {2} — { frac {dU} {dr }} = { frac {mh ^ {2}} {r ^ {3}}} + F (r)}
, поскольку величина F (r) радиальной силы равна отрицательной производной потенциальной энергии U (r) в радиальном направлении.
Гамильтонова механика
Формула радиальной силы также может быть получена с использованием гамильтоновой механики. В полярных координатах гамильтониан можно записать как
- H = 1 2 m (pr 2 + p φ 2 r 2) + U (r) { displaystyle H = { frac {1} {2m}} left (p_ {r} ^ {2} + { frac {p _ { varphi} ^ {2}} {r ^ {2}}} right) + U (r)}
Поскольку азимутальный угол φ не входит в гамильтониан, его сопряженный импульс p φ является константой движения. Этот сопряженный импульс является величиной L углового момента, как показано гамильтоновым уравнением движения для φ
- d φ dt = ∂ H ∂ p φ = p φ mr 2 = L mr 2 { displaystyle { frac { d varphi} {dt}} = { frac { partial H} { partial p _ { varphi}}} = { frac {p _ { varphi}} {mr ^ {2}}} = { frac {L} {mr ^ {2}}}}
Соответствующее уравнение движения для r:
- drdt = ∂ H ∂ pr = prm { displaystyle { frac {dr} {dt}} = { frac { partial H} { partial p_ {r}}} = { frac {p_ {r}} {m}}}
Взяв вторую производную от r по времени и используя уравнение движения Гамильтона для p r дает уравнение радиальной силы
- d 2 rdt 2 = 1 mdprdt = — 1 m (∂ H ∂ r) = p φ 2 m 2 r 3 — 1 md U dr = L 2 м 2 р 3 + 1 м F (r) { displaystyle { frac {d ^ {2} r} {dt ^ {2}}} = { frac {1} {m}} { frac {dp_ { r}} {dt}} = — { frac {1} {m}} left ({ frac { partial H} { partial r}} right) = { frac {p _ { varphi} ^ {2}} {m ^ {2} r ^ {3}}} — { frac {1} {m}} { frac {dU} {dr}} = { frac {L ^ {2}} { m ^ {2} r ^ {3}}} + { frac {1} {m}} F (r)}
Гамиль Уравнение Тона-Якоби
Орбитальное уравнение может быть получено непосредственно из уравнения Гамильтона – Якоби. Принимая радиальное расстояние r и азимутальный угол φ в качестве координат, уравнение Гамильтона-Якоби для задачи центральной силы может быть записано
- 1 2 m (d S rdr) 2 + 1 2 mr 2 (d S φ d φ) 2 + U (г) = E tot { displaystyle { frac {1} {2m}} left ({ frac {dS_ {r}} {dr}} right) ^ {2} + { frac {1} {2mr ^ {2}}} left ({ frac {dS _ { varphi}} {d varphi}} right) ^ {2} + U (r) = E _ { mathrm {tot }}}
где S = S φ (φ) + S r (r) — E tot t является главной функцией Гамильтона, E tot и t представляют собой полную энергию и время соответственно. Это уравнение может быть решено путем последовательного интегрирования обыкновенных дифференциальных уравнений, начиная с уравнения φ
- d S φ d φ = p φ = L { displaystyle { frac {dS _ { varphi}} {d varphi}} = p _ { varphi} = L}
где p φ — константа движения, равная величине углового момента L. Таким образом, S φ (φ) = Lφ, и уравнение Гамильтона – Якоби принимает вид
- 1 2 m (d S rdr) 2 + L 2 2 mr 2 + U (r) = E tot { displaystyle { frac {1} {2m}} left ({ frac {dS_ {r}} {dr}} right) ^ {2} + { frac {L ^ {2}} {2mr ^ {2} }} + U (r) = E _ { mathrm {tot}}}
Интегрирование этого уравнения для S r дает
- S r (r) = 2 m ∫ dr E tot — U (r) — L 2 2 mr 2 { displaystyle S_ {r} (r) = { sqrt {2m}} int dr { sqrt {E _ { mathrm {tot}} -U (r) — { frac {L ^ {2}} {2mr ^ {2}}}}}}
Взяв производную S по L, получаем уравнение орбиты, полученное выше
- φ 0 = ∂ S ∂ L = ∂ S φ ∂ L + ∂ S р ∂ L знак равно φ — L 2 м ∫ rdrr 2 E tot — U (r) — L 2 2 mr 2 { displaystyle varphi _ {0} = { frac { partial S} { partial L}} = { frac { partial S _ { varphi}} { partial L}} + { frac { partial S_ {r }} { partial L}} = varphi — { frac {L} { sqrt {2m}}} int ^ {r} { frac {dr} {r ^ {2} { sqrt {E_ { mathrm {tot}} -U (r) — { frac {L ^ {2}} {2mr ^ {2}}}}}}}
См. также
- Геодезические Шварцшильда, проблема центральной силы в общей теории относительности
- Частица в сферически-симметричном потенциале, квантово-механический аналог проблемы центральной силы
- водородоподобный атом, проблема Кеплера в квантовая механика
- потенциал обратного квадрата
Примечания
- ^В этой статье жирным шрифтом используется для обозначения таких величин, как r и F, равных векторы, тогда как обычные числа написаны курсивом. Вкратце, вектор v — это величина, которая имеет величину v (также обозначаемую | v |) и направление. Векторы часто задаются их компонентами. Например, вектор положения r= (x, y) в декартовых координатах описывается как упорядоченная пара его координат x и y.
- ^В этой статье ньютоновская нотация для производных («точечная нотация») иногда используется для облегчения чтения формул; это не имеет другого значения. В этой записи точка над переменной обозначает ее первую производную по времени, например,
- r ˙ = drdt { displaystyle { dot {r}} = { frac {dr} {dt}}}
Аналогично, двойная точка над переменной означает ее вторую производную по времени, например,
- r ¨ = d 2 rdt 2 { displaystyle { ddot {r}} = { frac {d ^ { 2} r} {dt ^ {2}}}}
- r ˙ = drdt { displaystyle { dot {r}} = { frac {dr} {dt}}}
- ^Здесь символ умножения × указывает на векторное векторное произведение, а не на простое умножение.
- ^Если a и b являются трехмерными векторами, их векторное векторное произведение c= a× bвсегда перпендикулярно плоскости, определяемой a и b.
- ^Эта формула для азимутального единичного вектора может быть проверена расчетом; его величина равна единице
- φ ^ ⋅ φ ^ = (- sin φ) 2 + (cos φ) 2 = 1 { displaystyle { hat { boldsymbol { varphi}}} cdot { hat { boldsymbol { varphi}}} = (- sin varphi) ^ {2} + ( cos varphi) ^ {2} = 1}
и его скалярное произведение с r равно нулю
- φ ^ ⋅ r ^ = — sin φ cos φ + cos φ sin φ = 0 { displaystyle { hat { boldsymbol { varphi}}} cdot mathbf { hat { r}} = — sin varphi cos varphi + cos varphi sin varphi = 0}
Следовательно, это единичный вектор, перпендикулярный радиальному вектору r.
- φ ^ ⋅ φ ^ = (- sin φ) 2 + (cos φ) 2 = 1 { displaystyle { hat { boldsymbol { varphi}}} cdot { hat { boldsymbol { varphi}}} = (- sin varphi) ^ {2} + ( cos varphi) ^ {2} = 1}
- ^Площадь треугольника равна единице половина основания умножена на его высоту. В этом случае основание задается как vΔt, а высота равна прицельному параметру r ⊥.
- ^Задача параллельных сил — это задача, в которой сила точно равна нулю в одном направлении.
- ^Замкнутая орбита — это орбита, которая возвращается в исходное положение через конечное время с точно такой же скоростью. Следовательно, он выполняет одно и то же движение снова и снова.
Ссылки
Библиография
- Goldstein, H. (1980). Классическая механика (2-е изд.). Ридинг, Массачусетс: Эддисон-Уэсли. ISBN 0-201-02918-9 .
- Ландау, Л. Д. и Лифшиц, Э. М. (1976). Механика. Курс теоретической физики (3-е изд.). Нью-Йорк: Pergamon Press. ISBN 0-08-029141-4 . CS1 maint: несколько имен: список авторов (ссылка )
- Misner, CW, Торн, К. и Уиллер, JA (1973). Gravitation. Сан-Франциско: WH Freeman. ISBN 978-0- 7167-0344-0 . CS1 maint: несколько имен: список авторов (ссылка )
- Зоммерфельд, А. (1970). Механика. Лекции по теоретической физике, Том I (4-й изд.). Нью-Йорк: Academic Press. ISBN 978-0-12-654670-5 .
- Саймон К.Р. (1971). Механика (3-е изд.). Ридинг, Массачусетс: Addison -Wesley. ISBN 0-201-07392-7 .
- Whittaker, ET (1937). Трактат по аналитической динамике частиц и твердых тел с Введение в проблему трех тел (4-е изд.). Нью-Йорк: Dover Publications. ISBN 978-0-521-35883-5 .
Внешние ссылки
- Два -body Central Force Problems от DE Gary из Технологического института Нью-Джерси
- Движение в центральном силовом поле А. Бризарда из Колледжа Святого Михаила
- Движение под воздействием центральной силы Дж. Коллинза, II из Западного резервного университета Кейса
- Видеолекция WHG Левин из Массачусетского технологического института
Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы (точка 
Примерами центральных сил являются силы тяготения и Кулона, направленные вдоль линии, соединяющей точечные массы или точечные заряды.
Проще всего центральные силы вводятся для физических систем, состоящих из конечного числа объектов, размерами которых можно пренебречь (материальных точек), или, иногда, некоторых эквивалентных им, состоящих из протяжённых объектов с фиксированной внутренней структурой[2]. Распределенные системы, в которых действуют центральные силы, в общем случае[3] не могут быть представлены конечным количеством материальных точек. В случае распоеделенных систем общим подходом является разбиение их на очень большое (впределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый, которые и рассматриваются как материальные точки — между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией)) таких элементарных сил.
Kлассическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы. [4]
Рис.1 К определению центральной силы: 
(где 
Содержание
- 1 Силовые поля
- 1.1 Интенсивность силового поля
- 1.2 Потенциальные центральные поля
- 1.2.1 Работа центральной силы
- 1.2.2 Потенциал поля
- 1.2.3 Поле как градиент потенциала
- 1.2.4 Кулоновское поле
- 1.2.5 Кулоновские силы
- 1.2.6 Поле гравитации
- 1.2.7 Силы гравитации
- 1.2.8 Потенциал поля гравитации
- 1.3 Движение под действием центральной силы
- 2 Примечания
Силовые поля
Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения. Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.
При сохранении подобия в геометрических размерах тел и их взаимного расстояния, силы взаимного тяготения, равно как и силы электростатические (кулоновские) растут пропорционально 4-й степени абсолютных размеров рассматриваемой модели. В то же самое время в случае электрического взаимодействия, где между величиной заряда и размерами тел, несущих эти заряды, нет определённой связи, силы взаимодействия ослабляются пропорционально 2-й степени абсолютных размеров . Поэтому при сравнении этих сил в микромире доминируют Кулоновские силы, а в масштабах Вселенной — силы Всемирного тяготения.
Интенсивность силового поля
В ряде случаев в рассматриваемом силовом поле оказывается возможным определить пространственно локализованный его источник (нем. Quelle).
Одним из основных свойств рассматриваемых здесь полей является их экспериментально подтверждаемая аддитивность, иначе называемая принципом суперпозиции, заключающегося в том, что действие поля, создаваемого несколькими источниками на объект своего воздействия независимы друг от друга при любом значении их интенсивности. Это позволяет ввести в рассмотрение понятие о «точечном источнике» с чётко определённым его пространственным расположении и сформулировать понятие об суммарной интенсивности поля нескольких источников как сумму этих воздействий с учётом геометрии конкретной задачи.
Интенсивность определяется в заданной точке пространства силой, которая могла бы подействовать на единичный «пробный объект» с заданным свойством, который мог бы находиться в этой точке или же в действительности находящийся в ней. Выбор «пробного объекта» есть предмет договорённости. При необходимости источник поля и объект его воздействия могут поменяться местами.
Величина, характеризующая интенсивность центрального силового поля представляет собой вектор направленный по линии соединяющей точечный источник и заданную точку поля.
Потенциальные центральные поля
Работа центральной силы
Элементарная работа 



где 

При перемещении на расстояние от 




Рассматривая движение в Декартовой системе координат центральную силу можно представить в виде геометрической суммы её проекций на координатные оси:
где 


Потенциал поля
Не для всякого поля силы совершаемая ею работа зависит лишь от положения начальной и конечной точек движения . Иными словами, не зависит от формы пути.
Упомянутый интеграл не будет зависеть от формы пути лишь в том случае, если будет существовать некая первообразная функция 
её частные производные будут соответствовать проекциями силы (по существующему обычному соглашению — с точностью до знака):
В этом случае функция 
Но это станет возможным лишь при одновременном выполнении равенств:
Для центральных сил это условие выполняется. Поле, в котором выполнены эти условия, называется безвихревым полем. Поэтому потенциальные поля суть поля безвихревые.[5]
Знак минус в формуле, связывающей потенциальную функцию и силу, определяется желанием отождествить потенциальную функцию с потенциальной энергией[6] (в противном случае можно было бы обойтись без знака минус, что иногда и делается при введении потенциальной функции чисто формально, особенно для векторного поля, не имеющего характера силы).
Связь с потенциальной энергией естественно осуществляется через работу.
Представляется естественным считать, что вектор напряжённости поля направлен ОТ источника поля, (что привычно принимается при описании электростатического поля при взаимодействии одноимённых зарядов [7] )Тогда, зафиксировав точку, находящуюся на расстоянии 

То же можно сказать и в случае, если поле продвинуло тело дальше 
И эти работы может быть названа с точностью до постоянной потенциалом точки : 

Тогда совершённая полем работа будет равна разности потенциалов , взятой со знаком «минус»
Таким образом работа силы на пути из начальной точки в конечную равна изменению потенциальной функции, являющейся скалярной функцией расстояния. В таком случае для каждой точки пути можно с точностью до постоянной величины приписать свой потенциал:
Поле как градиент потенциала
В поле центральной силы её составляющая по данной оси представляет собой скорость изменения потенциальной функции по этой же оси или же градиент функции по заданному направлению.
Для описания изменения потенциальной функции по произвольному направлению в теории поля введён векторный дифференциальный оператор, имеющий вид:
Применяя этот оператор к потенциальной функции получаем, что в данной точке поля сила является (с точностью до знака) градиентом потенциала:
Знак минус, по обычному соглащению присутстсвующий в этой формуле, связан с тем, чтобы функция U могла быть отождествлена с потенциальной энергией (хотя чиcто формально потенциальная функция могла бы быть выбрана и с другим знаком, если такого отождествления не предполагается).
Кулоновское поле
Напряженность кулоновского поля определяется вектором 
или, переходя, к скалярной форме записи:
Здесь 








Кулоновские силы
Объектом действия кулоновского поля является материальное тело, несущее заряд
В таком случае на него действует механическая (ньютонова) сила электрического происхождения, равная произведению величины заряда на напряжённость поля:
или, с учётом ():

Специфической особенностью кулоновского поля является то, что вектор его напряжённости направлен либо ОТ источника поля в случае совпадение знака заряда источника и объекта взаимодействия, либо направлен К источнику в случае разноимённости зарядов. Это значит, что заряжённые материальные тела в первом случае будут испытывать отталкивающую силу, а в противоположном — силу сближающую их.
Ещё одним свойством кулоновского поля является техническая возможность выделить область пространства, в котором оно будет в требуемой степени отсутствовать (клетка Фарадея)
Поле гравитации
В русскоязычной литературе интенсивность поля тяготения называют «ускорением свободного падения» 
Или, переходя, к скалярной форме записи:
Здесь 




Силы гравитации
Объектом действия поля гравитации является материальное тело,имеющее массу
В таком случае на него действует механическая сила, равная произведению массы 
или, в скалярном представлении:
Специфической особенностью сил гравитации является то, что они всегда являются силами притяжения. Кроме того, силы гравитации всепроникающи и от них невозможно защититься никаким экраном. Это свойство объединяет силы гравитации с фиктивными силами инерции, существующими в любой неинерциальной системе отсчёта. Подобная аналогия имеет своей основой фундаментальные свойства пространства, изучения которых выходит за рамки классической физики.[10]
Потенциал поля гравитации
Подставляя в (6) значение силы Всемирного тяготения из (20), получаем с учётом того, что работа была совершена против поля:

Таким образом каждой точке гравитационного поля можно с точностью до постоянной присвоить свой потенциал, как:

Движение под действием центральной силы
В общем случае любую траекторию тела, рассматриваемого как материальная точка, можно представить в виде пространственной кривой, состоящей из сопряжённых поворотов в различных плоскостях вокруг мгновенных центров поворота C с различными значениями радиуса поворота 
Но кривизна траектории отнюдь не значит, что на тело действует некая сила, для каждого момента являющейся силой центростремительной.
Замечание
Последняя оговорка весьма существенна. Так, например, для земного наблюдателя бомба, сброшенная с летящего равномерно и прямолинейно летательного аппарата движется по параболе. Но для пилота она падает вертикально под действием единственной в данном случае силы тяжести (Если не принимать во внимание снос из-за сопротивления воздуха).Никаких сил, вызывающих искривление траектории здесь нет. Центростремительные силы возникают не потому, что траектория крива,но потому, что они являются выражением реально имеющего место силового взаимодействия движущегося объекта со своим окружением.
Считается, что в центре силы находится источник силы которым может быть тяготеющая масса, либо электрический заряд в случае, если рассматриваемая сила есть характеристика соответствующего силового поля. Центр силы в общем случае не совпадает с мгновенным центром поворота — точка 
Как видно на Рис.1 единственная действующая между телами 



При этом 

Непосредственно из определения понятий о моментах силы и момента количества движения (момента импульса)следует экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела 

Однако в поле центральной силы её момент всегда равен нулю (Формула (1)).Из этого непосредственно следует, что при любом движении тела в поле центральной силы момент количества движения движущегося под её действием тела остаётся постоянным:

Наиболее часто движение тел в гравитационном поле изучают в области небесной механики, где гравитационное воздействия преоблаают и потому изучаемая система взаимодействующих сил может рассматриваться, как консервативная система , т.е. такая, в которой сохраняется полная энергия тела в виде суммы потенциальной и кинетической энергии.[4]




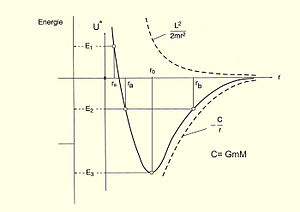
Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планеты
Воспользовавшись определением кинетического момента:

А для движения по нормали к траектории:
Тогда выражение для полной энергии тела будет иметь вид:
Введя в рассмотрение эффективный потенциал 
Получаем возможость связать диапазон изменения длины радиуса -вектора траектории тела с запасённой им энергией, что представлено на рис.2 [13]
Так при минимальной энергии движущегося тела 
Если энергия движения тела больше, скажем 


Наконец, при энергии 
Примечания
- ↑ Иногда бывает удобно — и удаётся — рассматривать как центр силы не её физический источник, а некоторую фиктивную точку. Так например при изучении движения двух точечных тел, между которыми действуют центральные силы, удобно рассматривать в качестве такого центра центр масс системы — потому что он неподвижен.
- ↑ Имеются в виду сферически симметричные объекты (или объекты, досаточно мало отличающиеся от сферически симметричных, так чтобы можно было считать их сферически симметричными в рамках рабочего приближения).
- ↑ По сути — почти в любом случае кроме описанных выше; даже в таком простом случае, как кулоновское взаимодействие абсолютно твердых тел несферической формы с фиксированными на них распределенными зарядами, обычно невозможно свести вычисление сил к силам между небольшим количеством материальных точек.
- ↑ 1 2 3 Физический энциклопедический словарь/ Гл. ред. А.М.Прохоров. Ред.кол. Д.М.Алексеев, А.М. Бонч-Бруевич,А.С.Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил.
- ↑ 1 2 Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
- ↑ Поскольку сохраняться должна сумма потенциальной и кинетической энергий, в направлении действия силы (которая может разгонять в этом направлении частицу, увеличивая тем самым ее кинетическую энергию) потенциальная энергия убывает.
- ↑ Тамм,И.Е. Основы теории электричества
- ↑ ГОСТ 8.417-2002. Единицы величин
- ↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
- ↑ Хайкин, Семён Эммануилович|С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука».Главная редакция физико-математической литературы.
- ↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
- ↑ Klaus Dransfeld, Paul Kleine, Georg Michael Kalvius. Physik I. Oldenbourg Wissenschaftsverlag GmbH 2001 ISBN 3-486-25416-2
- ↑ ‘
Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы (точка 
Примерами центральных сил являются силы тяготения и Кулона, направленные вдоль линии, соединяющей точечные массы или точечные заряды.
Проще всего центральные силы вводятся для физических систем, состоящих из конечного числа объектов, размерами которых можно пренебречь (материальных точек), или, иногда, некоторых эквивалентных им, состоящих из протяжённых объектов с фиксированной внутренней структурой[2]. Распределенные системы, в которых действуют центральные силы, в общем случае[3] не могут быть представлены конечным количеством материальных точек. В случае распределённых систем общим подходом является разбиение их на очень большое (в пределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый (которые и рассматриваются как материальные точки), между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией)) таких элементарных сил.
Классическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы.
[4]
Рис.1 К определению центральной силы: 
(где M — видимо, момент сил, 
свидетельствующее о равенстве нулю момента силы относительно центра силы:
Содержание
- 1 Силовые поля
- 1.1 Потенциальные центральные поля
- 1.1.1 Работа центральной силы
- 1.1.2 Потенциал поля
- 1.1.3 Поле как градиент потенциала
- 1.1.4 Кулоновское поле
- 1.1.5 Кулоновские силы
- 1.1.6 Поле гравитации
- 1.1.7 Силы гравитации
- 1.1.8 Потенциал поля гравитации
- 1.2 Движение под действием центральной силы
- 1.1 Потенциальные центральные поля
- 2 Примечания
Силовые поля
Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения). Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.
Величина, характеризующая интенсивность центрального силового поля, представляет собой вектор, направленный по линии, соединяющей точечный источник и заданную точку поля.
Потенциальные центральные поля
Работа центральной силы
Элементарная работа 
(в общем случае изменяющей свою величину и направление), при перемещении на столь малый отрезок своей траектории, что на нём вектор силы может считаться неизменным, то есть на расстояние 

где 

При перемещении на расстояние от 





Рассматривая движение в декартовой системе координат, центральную силу можно представить в виде геометрической суммы её проекций на координатные оси:

где 


Потенциал поля
Не для всякого поля силы совершаемая ею работа зависит лишь от положения начальной и конечной точек движения. Иными словами, не зависит от формы пути.
Упомянутый интеграл не будет зависеть от формы пути лишь в том случае, если будет существовать некая первообразная функция 
её частные производные будут соответствовать проекциями силы (по существующему обычному соглашению — с точностью до знака):
В этом случае функция 
Но это станет возможным лишь при одновременном выполнении равенств:

Для центральных сил это условие выполняется. Поле, в котором выполнены эти условия, называется безвихревым полем. Поэтому потенциальные поля суть поля безвихревые.[5]
Знак минус в формуле, связывающей потенциальную функцию и силу, определяется желанием отождествить потенциальную функцию с потенциальной энергией[6] (в противном случае можно было бы обойтись без знака минус, что иногда и делается при введении потенциальной функции чисто формально, особенно для векторного поля, не имеющего характера силы).
Связь с потенциальной энергией естественно осуществляется через работу.
Представляется естественным считать, что вектор напряжённости поля направлен ОТ источника поля, (что привычно принимается при описании электростатического поля при взаимодействии одноимённых зарядов[7]) Тогда, зафиксировав точку, находящуюся на расстоянии 

То же можно сказать и в случае, если поле продвинуло тело дальше 
И эти работы может быть названа с точностью до постоянной потенциалом точки: 

Тогда совершённая полем работа будет равна разности потенциалов, взятой со знаком «минус»

Таким образом работа силы на пути из начальной точки в конечную равна изменению потенциальной функции, являющейся скалярной функцией расстояния. В таком случае для каждой точки пути можно с точностью до постоянной величины приписать свой потенциал:
Поле как градиент потенциала
В поле центральной силы её составляющая по данной оси представляет собой скорость изменения потенциальной функции по этой же оси или же градиент функции по заданному направлению.
Для описания изменения потенциальной функции по произвольному направлению в теории поля введён векторный дифференциальный оператор, имеющий вид:
Применяя этот оператор к потенциальной функции получаем, что в данной точке поля сила является (с точностью до знака) градиентом потенциала:
Знак минус, по обычному соглашению присутствующий в этой формуле, связан с тем, чтобы функция U могла быть отождествлена с потенциальной энергией (хотя чисто формально потенциальная функция могла бы быть выбрана и с другим знаком, если такого отождествления не предполагается).
Кулоновское поле
Напряженность кулоновского поля определяется вектором 

или, переходя, к скалярной форме записи:

Здесь 








Кулоновские силы
Объектом действия кулоновского поля является материальное тело, несущее заряд 
В таком случае на него действует механическая (ньютонова) сила электрического происхождения, равная произведению величины заряда на напряжённость поля:
или, с учётом ():


Специфической особенностью кулоновского поля является то, что вектор его напряжённости направлен либо ОТ источника поля в случае совпадение знака заряда источника и объекта взаимодействия, либо направлен К источнику в случае разноимённости зарядов. Это значит, что заряженные материальные тела в первом случае будут испытывать отталкивающую силу, а в противоположном — силу сближающую их.
Ещё одним свойством кулоновского поля является техническая возможность выделить область пространства, в котором оно будет в требуемой степени отсутствовать (клетка Фарадея)
Поле гравитации
В русскоязычной литературе интенсивность поля тяготения называют «ускорением свободного падения» 

Или, переходя к скалярной форме записи:

Здесь 




[9]
Силы гравитации
Объектом действия поля гравитации является материальное тело, имеющее массу 
В таком случае на него действует механическая сила, равная произведению массы 
Тогда, с учётом ():

или, в скалярном представлении:

Специфической особенностью сил гравитации является то, что они всегда являются силами притяжения. Кроме того, силы гравитации всепроникающи, и от них невозможно защититься никаким экраном. Это свойство объединяет силы гравитации с фиктивными силами инерции, существующими в любой неинерциальной системе отсчёта. Подобная аналогия имеет своей основой фундаментальные свойства пространства, изучения которых выходит за рамки классической физики.[10]
Потенциал поля гравитации
Подставляя в (6) значение силы Всемирного тяготения из (20), получаем с учётом того, что работа была совершена против поля:

Таким образом каждой точке гравитационного поля можно с точностью до постоянной присвоить свой потенциал, как:

Движение под действием центральной силы
В общем случае любую траекторию тела, рассматриваемого как материальная точка, можно представить в виде пространственной кривой, состоящей из сопряжённых поворотов в различных плоскостях вокруг мгновенных центров поворота с различными значениями радиуса поворота 
Но кривизна траектории отнюдь не значит, что на тело действует некая сила, для каждого момента являющейся силой центростремительной.
Замечание
Последняя оговорка весьма существенна. Так, например, для земного наблюдателя бомба, сброшенная с летящего равномерно и прямолинейно летательного аппарата движется по параболе. Но для пилота она падает вертикально под действием единственной в данном случае силы тяжести (если не принимать во внимание снос из-за сопротивления воздуха). Никаких сил, вызывающих искривление траектории, здесь нет. Центростремительные силы возникают не потому, что траектория крива, но потому, что они являются выражением реально имеющего место силового взаимодействия движущегося объекта со своим окружением.
Считается, что в центре силы находится источник силы, которым может быть тяготеющая масса, либо электрический заряд в случае, если рассматриваемая сила есть характеристика соответствующего силового поля. Центр силы в общем случае не совпадает с мгновенным центром поворота — точка 
[4]
Как видно на Рис.1 единственная действующая между телами 



При этом


Непосредственно из определения понятий о моментах силы и момента количества движения (момента импульса) следует экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела 


Однако в поле центральной силы её момент всегда равен нулю (Формула (1)). Из этого непосредственно следует, что при любом движении тела в поле центральной силы момент количества движения движущегося под её действием тела остаётся постоянным:

Но, поскольку постоянство вектора есть одновременно и сохранение его направления в пространстве, то заметаемая при движении тела площадка всегда лежит в одной и той же плоскости. Из этого следует, что любая траектория движения тела под действием центральной силы есть плоская кривая.
Наиболее часто движение тел в гравитационном поле изучают в области небесной механики, где преобладают гравитационные воздействия, и потому изучаемая система взаимодействующих сил может рассматриваться как консервативная система, то есть такая, в которой сохраняется полная энергия тела в виде суммы потенциальной и кинетической энергии.[4]

причём 

Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планеты
Воспользовавшись определением кинетического момента:

А для движения по нормали к траектории:


Тогда выражение для полной энергии тела будет иметь вид:

Введя в рассмотрение эффективный потенциал 

Получаем возможость связать диапазон изменения длины радиус-вектора траектории тела с запасённой им энергией, что представлено на рис.2[13]
Так при минимальной энергии движущегося тела 

Если энергия движения тела больше, скажем 


Наконец, при энергии 

Примечания
- ↑ Центральная сила // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — С. 425—426. — 760 с. — ISBN 5-85270-101-7.
- ↑ Имеются в виду сферически симметричные объекты (или объекты, достаточно мало отличающиеся от сферически симметричных, так чтобы можно было считать их сферически симметричными в рамках рабочего приближения).
- ↑ По сути — почти в любом случае, кроме описанных выше; даже в таком простом случае, как кулоновское взаимодействие абсолютно твёрдых тел несферической формы с фиксированными на них распределёнными зарядами, обычно невозможно свести вычисление сил к силам между небольшим количеством материальных точек.
- ↑ 1 2 3 Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил.
- ↑ 1 2 Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
- ↑ Поскольку сохраняться должна сумма потенциальной и кинетической энергий, в направлении действия силы (которая может разгонять в этом направлении частицу, увеличивая тем самым её кинетическую энергию) потенциальная энергия убывает.
- ↑ Тамм И. Е. Основы теории электричества
- ↑ ГОСТ 8.417-2002. Единицы величин
- ↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
- ↑ Хайкин, Семён Эммануилович|С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
- ↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
- ↑ Klaus Dransfeld, Paul Kleine, Georg Michael Kalvius. Physik I. Oldenbourg Wissenschaftsverlag GmbH 2001 ISBN 3-486-25416-2
- ↑ ‘
Сила F, действующая на точку P, называется центральной с центром в точке O, если во всё время движения она действует вдоль линии, соединяющей точки O и P.
Основные свойства
- Если материальная точка совершает движение под действием центральной силы с центром O, то момент количества движения точки сохраняется, а она сама совершает движение в плоскости, перпендикулярной вектору момента количества движения относительно точки O и проходящей через эту точку O.
- Если система материальных точек совершает движение под действием центральных сил c общим центром O, то момент количества движения системы сохраняется.
- Если действующая на точку P центральная сила зависит лишь от её расстояния
до центра O, то такая центральная сила потенциальна: существует функция U, называемая потенциалом, такая, что
- Формула Бине позволяет определить центральную силу, если известно уравнение траектории материальной точки, движущейся под её действием, или по заданной центральной силе определить траекторию.
Примеры центральных сил
- Центральная сила ньютоновского притяжения (величина силы F(r) пропорциональна 1/r2)
- Сила Кулона (величина силы F(r) пропорциональна 1/r2)
- Сила Гука (величина силы F(r) пропорциональна r)
Движение под действием центральной силы
Как видно на Рис.1 единственная действующая между телами 



При этом


Непосредственно из определения понятий о моментах силы и момента количества движения (момента импульса) следует экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела 


Однако в поле центральной силы её момент всегда равен нулю (Формула (1)). Из этого непосредственно следует, что при любом движении тела в поле центральной силы момент количества движения движущегося под её действием тела остаётся постоянным:

Но, поскольку постоянство вектора есть одновременно и сохранение его направления в пространстве, то заметаемая при движении тела площадка всегда лежит в одной и той же плоскости. Из этого следует, что любая траектория движения тела под действием центральной силы есть плоская кривая.
Наиболее часто движение тел в гравитационном поле изучают в области небесной механики, где преобладают гравитационные воздействия, и потому изучаемая система взаимодействующих сил может рассматриваться как консервативная система, то есть такая, в которой сохраняется полная энергия тела в виде суммы потенциальной и кинетической энергии.[2]

причём 


Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планеты
Воспользовавшись определением кинетического момента:

А для движения по нормали к траектории:


Тогда выражение для полной энергии тела будет иметь вид:

Введя в рассмотрение эффективный потенциал 

Получаем возможность связать диапазон изменения длины радиус-вектора траектории тела с запасённой им энергией, что представлено на рис.2[1][3].
Так при минимальной энергии движущегося тела 

Если энергия движения тела больше, скажем 


Наконец, при энергии 

См. также
- Формула Бине (механика)
Примечания
- ↑ 1 2 Klaus Dransfeld, Paul Kleine, Georg Michael Kalvius. Physik I. Oldenbourg Wissenschaftsverlag GmbH 2001 ISBN 3-486-25416-2
- ↑ Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил.
- ↑ Peter Rennert, Herbert Schmiedel .Physik. Wissenschaftsverlag. Leipzig, Mannheim, Zürich 1995. ISBN 3-411-15821-2
Литература
- Поль Аппель, Теоретическая механика. Том 1. Статика. Динамика точки. М.: Физматлит, 1960 .
Эта страница в последний раз была отредактирована 21 мая 2021 в 20:06.
Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.




































![{ begin {align} F (r) , dr = F (r) { frac {dr} {dt}} , dt = m left ({ frac {dr} {dt}} { frac {d ^ {{2}} r} {dt ^ {{2}}}}} - { frac {h ^ {{2 }}} {r ^ {{3}}}} { frac {dr} {dt}} right) , dt \ = { frac m2} , d left [ left ({ frac {dr} {dt}} right) ^ {2} + left ({ frac hr} right) ^ {2} right] end {align}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26e59b4b76c0a42cc89c842afa0563c4a6d2ff20)
![int ^ {{r}} F (r) , dr = { frac m2} left [ left ({ frac {dr} {dt}} right) ^ {2} + left ({ frac hr} right) ^ {2} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e10a467bb0dce3d92b1826c73e13f580c30db95)

![int ^ {{r}} F (r) , dr = { frac {mh ^ {2}} 2} left [ left (- { frac 1 {r ^ {2}}} { frac {dr} {d varphi}} right) ^ {2} + left ({ frac 1r} right) ^ {2} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6fdd7a0a24825cd61f57b5f2a34446ac449f6b8)















![{ displaystyle u ( varphi) = - { frac { alpha} {mh ^ {2}}} left [1 + e cos left ( varphi - varphi _ {0} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d346a044e3603002a2d0a12ae4bf88984c4e7d7)