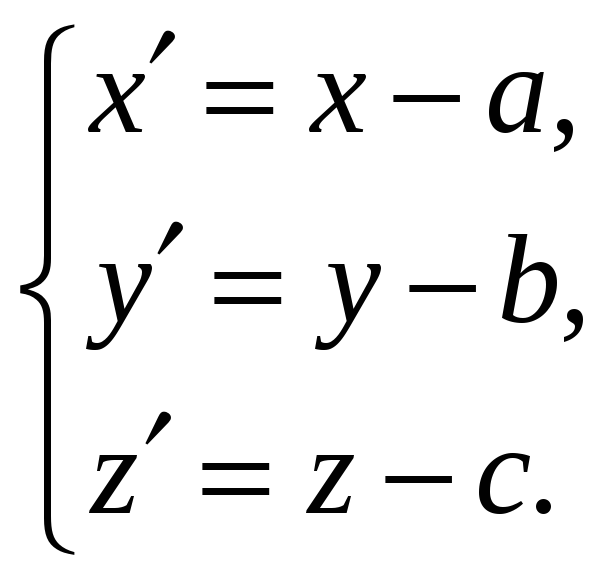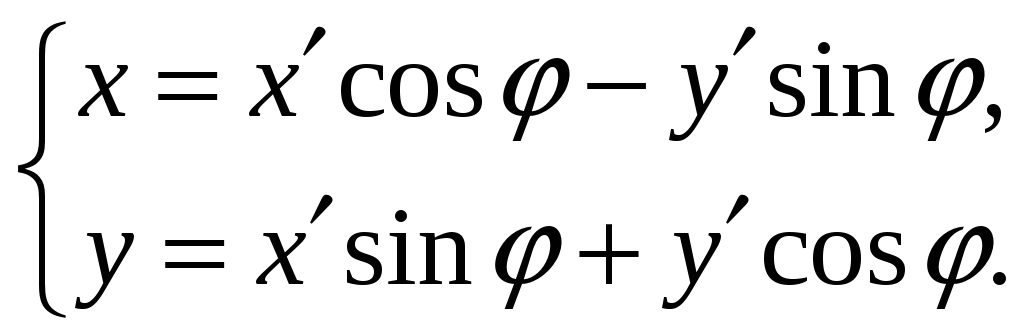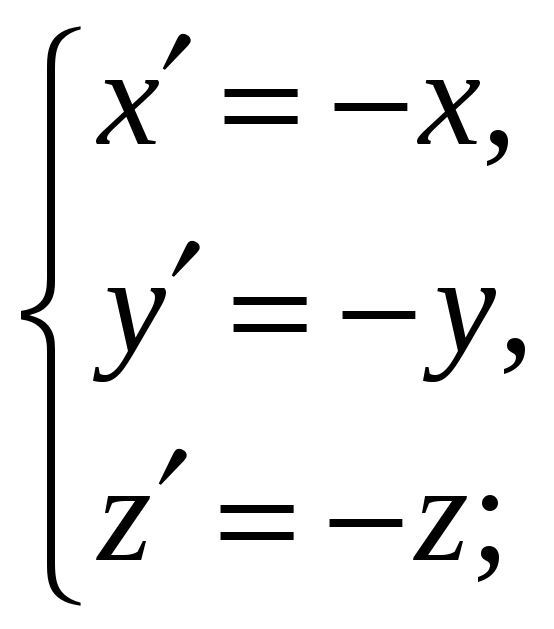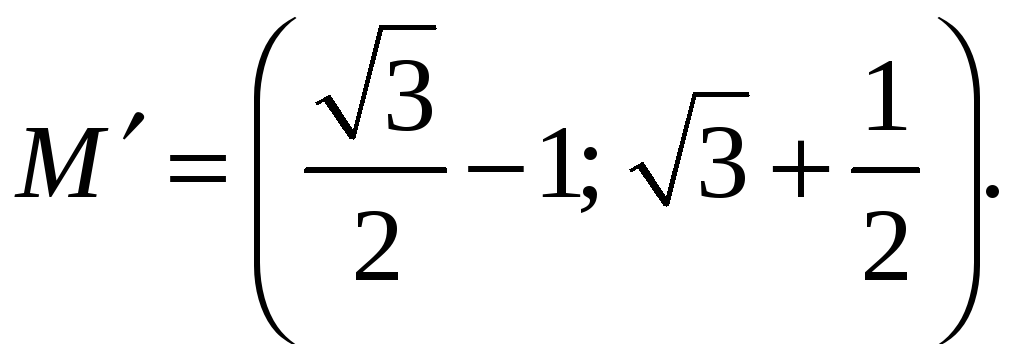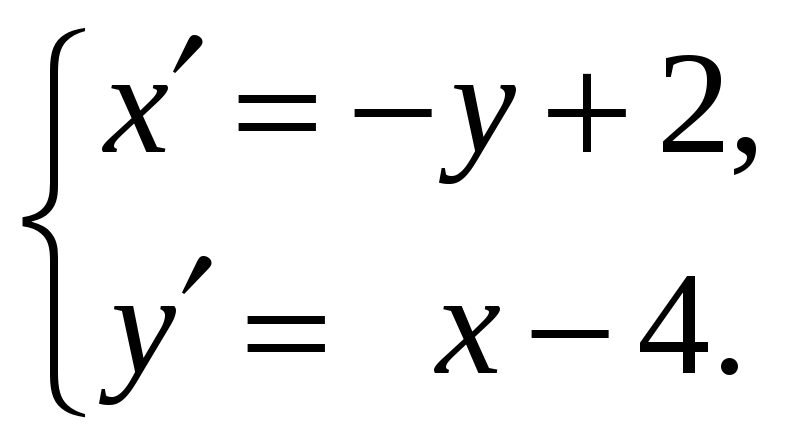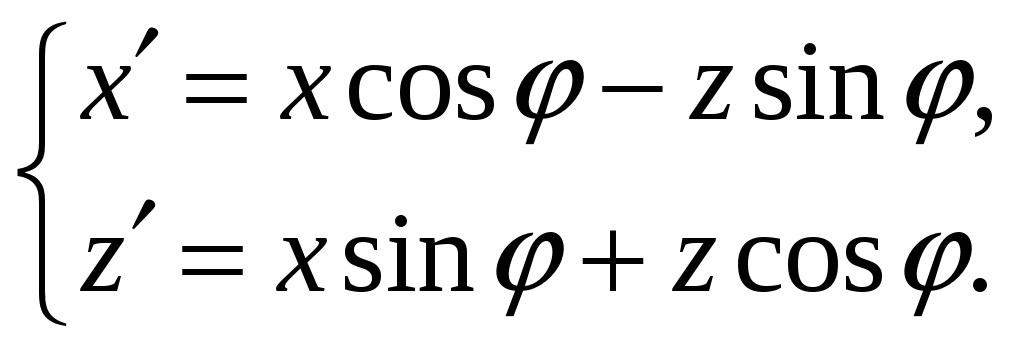Задание преобразований в координатах.
Говорят, что преобразование пространства задано в координатах, если каждой точке М(x; y; z) пространства ставится в соответствие точка M‘(x‘; y‘; z’) такая, что $begin{cases}x^{‘} = f_{1}(x;y;z),\y^{‘} = f_{2}(x;y;z),\z^{‘} = f_{3}(x;y;z).end{cases}$
Тождественное преобразование задается формулами: $begin{cases}x^{‘} = x\y^{‘} = y,\z^{‘} = z.end{cases}$
Центральная симметрия относительно начала координат задается формулами: $begin{cases}x^{‘} = −x\y^{‘} = −y,\z^{‘} = −z.end{cases}$
Осевая симметрия относительно координатной оси ОХ задается формулами: $begin{cases}x^{‘} = x\y^{‘} = −y,\z^{‘} = −z.end{cases}$
Зеркальная симметрия относительно координатной плоскости XOY задается формулами: $begin{cases}x^{‘} = x\y^{‘} = y,\z^{‘} = −z.end{cases}$
Параллельный перенос на вектор $overrightarrow{a}(x_{a};y_{a};z_{a})$ задается формулами: $begin{cases}x^{‘} = x + x_{a}\y^{‘} = y + y_{a},\z^{‘} = z + z_{a}.end{cases}$
Сегодня на уроке мы вспомним понятия отображения
плоскости на себя, движение плоскости, вспомним основные понятия центральной
симметрии. Введём понятия отображения пространства и движение пространства,
центральной симметрии в пространстве. Определим, будет ли центральная симметрия
в пространстве – движением пространства.
Мы уже с вами знакомы с таким понятием, как
движение. Давайте вспомним, что мы называли движением.
Движением
мы называли любое отображение плоскости, которое сохраняет расстояние между
точками.
Отображение
плоскости на себя определяли так: если каждой точке плоскости
ставится в соответствие какая-то точка этой же плоскости, причём любая точка
плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение
плоскости на себя.
Эти определения мы давали для движения на плоскости.
Но в стереометрии мы говорим о пространстве, значит, надо определить, что
называется движением пространства.
Но сначала давайте определим, что такое отображение
пространства на себя.
Определение:
Пусть каждой точке пространства
поставлена в соответствие некоторая точка ,
причем любая точка пространства
оказалась поставленной в соответствие какой-то точке .
Тогда говорят, что задано отображение пространства на себя. При
данном отображении точка переходит
(отображается) в точку .
Определение:
Под движением пространства понимается
отображение пространства на себя, при котором любые две точки пространства и
отображаются
в какие-то точки и
так,
что .
По-другому можно сказать, что движение
пространства – это отображение пространства на себя, сохраняющее
расстояние между точками.
Теперь давайте вспомним, какие фигуры обладают центральной
симметрией.
Определение:
Фигура называется симметричной относительно
точки ,
если для каждой точки фигуры симметричная ей точка относительно точки также
принадлежит этой фигуре. Точка называется
центром симметрии фигуры.
Примерами
центрально симметричных фигур можно назвать некоторые цветы:
В геометрии яркими примерами центрально симметричных
фигур являются окружность (центр симметрии – центр окружности) и параллелограмм
(центром симметрии является точка пересечения диагоналей).
Ещё мы давали такое определение:
Точки и
называются
симметричными относительно точки ,
если –
середина отрезка .
Точка называется
центром симметрии.
Точка считается
симметричной сама себе.
В курсе планиметрии мы доказывали, что центральная
симметрия является движением.
Напомним это доказательство.
Рассмотрим точки М и N
и точки М1 и N
1
симметричные точкам М и N
относительно точки О.
Рассмотрим треугольники М NО
и М1ОN1.
То есть при центральной симметрии сохраняется
расстояние между точками. Тогда по определению движения, получим, что и центральная
симметрия является движением.
Определение:
В пространстве центральной симметрией
мы назовём отображение пространства на себя, при котором любая точка переходит
в симметричную ей точку относительно
данного центра .
Теперь давайте докажем, что и в пространстве
центральная симметрия является движением.
Пусть О – центр симметрии. Введём прямоугольную
систему координат Оxyz с началом в
точке О. Теперь давайте попробуем установить связь между координатами двух
точек М (x, y,
z) и М1(x1,
y1,
z1),
симметричных относительно точки О.
Если точка М не совпадает с точкой О, то по
определению центральной симметрии О – середина отрезка ММ1. Тогда
координаты точки О можно вычислить по формулам координат середины отрезка. С
другой стороны, поскольку О – начало координат, значит, точка О имеет
координаты 0, 0, 0. То есть получим, что ,
,
.
Если точки М и О совпадают, тогда точка М1
также совпадает с точкой О, потому что точка О – центр симметрии, а, значит,
она отображается сама на себя. И в этом случае будут выполнятся равенства,
,
.
Теперь давайте рассмотрим две точки и
.
По только что доказанным формулам для координат
симметричных точек получим, что точка .
Точка .
Теперь давайте найдём расстояние .
Получим, что расстояние между точками ,
равно:
Теперь давайте найдём расстояние между точками и
.
Очевидно, что оба эти выражения равны, то есть
получим, что .
Вывод: расстояние между
точками при центральной симметрии в пространстве сохраняется, значит,
центральная симметрия в пространстве также является движением, но
уже не плоскости, а пространства.
Рассмотрим несколько задач.
Задача:
найти координаты точек, в которые переходят точки ,
,
при
центральной симметрии относительно начала координат.
Решение: воспользуемся
формулами для вычисления координат симметричных точек.
Если точка симметрична
точке то
справедливы формулы:
.
Тогда получим, что точка отобразится
в точку .
Точка отобразится
в точку .
Точка отобразится
в точку .
Решим ещё одну задачу.
Задача:
доказать, что при центральной симметрии прямая, не проходящая через центр
симметрии, отображается на параллельную ей прямую.
Доказательство. Пусть
прямая не
проходит через центр симметрии О. Построим точки симметричные точкам и
относительно
точки О.
Рассмотрим и
.
По определению центральной симметрии точка О – середина отрезков АА1
и ВВ1, то есть и
.
Углы как вертикальные, то
есть треугольники равны по двум сторонам и углу между ними.
Тогда получим, что .
Эти углы являются накрестлежащими для прямых и
при
секущей .
Тогда по признаку параллельности прямых получим, что прямые .
Что и требовалось доказать.
Итоги:
Сегодня на уроке мы вспомнили понятия отображения
плоскости на себя, движение плоскости, вспомнили основные понятия центральной
симметрии. Ввели понятия отображения пространства и движение пространства,
центральной симметрии в пространстве. Показали, что и в пространстве
центральная симметрия будет примером движения.
План урока
- Центральная симметрия;
- Осевая симметрия;
- Зеркальная симметрия;
- Параллельный перенос.
Цели урока
- Знать определение движения;
- Знать основные виды движений.
Разминка
- Как вычислить расстояние между точками?
- Какие фигуры называются равными?
- Какие прямые называются параллельными?
Центральная симметрия
Определение 1
Движением
называется преобразование, при котором сохраняется расстояние между точками.
При движении прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, плоскость – в плоскость. Можно доказать, что при движении сохраняются и углы между прямыми.
Определение 2
Центральная симметрия
– это преобразование, при котором любая точка M переходит в симметричную ей точку M1 относительно данной точки O. Точка O при этом называется
центром симметрии
.
Докажем, что центральная симметрия является движением.
Пусть точка O является центром симметрии. Введём прямоугольную систему координат Oxyz с началом в точке O. При центральной симметрии с центром O (0;0;0), точка M (x;y;z) перейдёт в симметричную ей точку M1 (x1;y1;z1). Если точки M и O не совпадают, то точка O является срединой отрезка MM1.
По формулам координат середины отрезка, получаем
x+x12=0, y+y12=0, z+z12=0.
Отсюда следует, что x1=-x, y1=-y, z1=-z.
Эти формулы верны и в случае, когда точки M и O совпадают (объясните самостоятельно почему). Таким образом, при центральной симметрии соответствующие координаты симметричных точек противоположны.
Рассмотрим теперь две произвольные точки A (x1;y1;z1) и B (x2;y2;z2).
При центральной симметрии они перейдут соответственно в A1 (-x1;-y1;-z1) и B1 (-x2;-y2;-z2). Докажем, что AB=A1B1.
Найдем расстояния AB и A1B1.
AB=x2-x12+y2-y12+z2-z12
A1B1=-x2—x12+-y2—y12+-z2—z12=
=-x2+x12+-y2+y12+-z2+z12=AB.
Таким образом, центральная симметрия является движением. Что и требовалось доказать.
Упражнение 1
1. Найдите координаты точек, в которые переходят точки A (0;3;4), B (4;-2;5), C (2;0;-3) при центральной симметрии относительно начала координат.
2. Докажите, что при центральной симметрии:
а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую;
б) прямая, проходящая через центр симметрии, отображается на себя.
3. Докажите, что при центральной симметрии:
а) плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость;
б) плоскость, проходящая через центр симметрии, отображается на себя.
Осевая симметрия
Определение 3
Осевая симметрия с осью a – это преобразование, при котором любая точка M переходит в симметричную ей точку M1 относительно оси a.
Докажем, что
осевая симметрия является движением
.
Пусть в прямоугольной системе координат Oxyz ось Oz является осью симметрии. Тогда некоторая точка M (x;y;z) перейдёт в симметричную относительно оси Oz точку M1 (x1;y1;z1). Если точка M не лежит на оси Oz, то ось Oz проходит через середину отрезка MM1 и перпендикулярна к нему. Из этого следует
x+x12=0, y+y12=0, z1=z⇒x1=-x, y1=-y, z1=z.
Эти формулы верны и в случае, когда точка M лежит на оси Oz (объясните самостоятельно почему).
Рассмотрим теперь две произвольные точки A (x1;y1;z1) и B (x2;y2;z2).
При осевой симметрии они перейдут соответственно в
A1 (-x1;-y1; z1) и B1 (-x2;-y2; z2). Найдем расстояния AB и A1B1.
AB=x2-x12+y2-y12+z2-z12
A1B1=-x2—x12+-y2—y12+z2-z12=
=-x2+x12+-y2+y12+z2-z12.
Видим, что AB=A1B1. Значит, осевая симметрия является движением. Что и требовалось доказать.
Упражнение 2
- Найдите координаты точек, в которые переходят точки A (0;5;2), B (7;-4;3), C (-3;0;-2) при осевой симметрии относительно оси Ox.
- Докажите, что при осевой симметрии прямая, параллельная оси симметрии, отображается на параллельную ей прямую.
Зеркальная симметрия
Определение 4
Зеркальной симметрией (симметрией относительно плоскости α) называется такое преобразование, при котором любая точка M переходит в симметричную ей относительно плоскости α точку M1.
Докажем, что зеркальная симметрия является движением.
Пусть в прямоугольной системе координат Oxyz плоскость Oxy является плоскостью симметрии. Тогда некоторая точка M (x;y;z) перейдёт в симметричную относительно плоскости Oxy точку M1 (x1;y1;z1). Если точка М не лежит в плоскости Oxy, то плоскость Oxy проходит через середину отрезка MM1 и перпендикулярна к нему (MM1 параллелен оси Oz). Из этого следует
x1=x, y1=y, z+z12=0⇒x1=x, y1=y, z1=-z.
Полученные формулы верны и в случае, когда точка М лежит в плоскости Oxy (объясните самостоятельно почему).
Рассмотрим теперь две произвольные точки A (x1;y1;z1) и B (x2;y2;z2).
При зеркальной симметрии они перейдут соответственно в A1 (x1;y1;-z1)
и B1 (x2;y2;-z2). Найдем расстояния AB и A1B1.
AB=x2-x12+y2-y12+z2-z12
A1B1=x2-x12+y2-y12+-z2—z12=
=x2-x12+y2-y12+-z2+z12.
Получили, что AB=A1B1. Значит, зеркальная симметрия является движением. Что и требовалось доказать.
Упражнение 3
- Найдите координаты точек, в которые переходят точки A (0;-3;5), B (-7;2;8), C (4;0;-3) при зеркальной симметрии относительно плоскости Oyz.
- Докажите, что при зеркальной симметрии прямая переходит в параллельную ей прямую.
Параллельный перенос
Определение 5
Рис. 1.
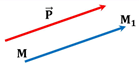
Параллельным переносом на вектор p→ называется такое преобразование, при котором любая точка М переходит в точку M1 такую, что MM1→=p→ (Рис. 1).
Рис. 2.
Докажем, что
параллельный перенос является движением
.
Рассмотрим две произвольные точки A и B. При параллельном переносе на вектор p→ эти точки перейдут в точки A1 и B1 такие, что AA1→=p→, BB1→=p→ (рис. 2).
По правилу треугольника AB1→=AA1→+A1B1→ и AB1→=AB→+BB1→.
При этом AA1→=BB1→⇒A1B1→=AB→⇒A1B1=AB. Таким образом, при параллельном переносе сохраняется между точками. Следовательно, параллельный перенос является движением. Что и требовалось доказать.
Упражнение 4
Найдите координаты точек, в которые переходят точки A (0;-3;5), B (-7;2;8), C (4;0;-3) при параллельном переносе на вектор p→ 3;4;-2.
Контрольные вопросы
- Сформулируйте определение движения.
- Перечислите основные виды движений и дайте определения этих преобразований.
Ответы
Упражнение 1
1. A1 (0;-3;-4), B1 (-4;2;-5), C1 (-2;0;3).
Упражнение 2
1. A1 (0;-5;-2), B1 (7;4;-3), C1 (-3;0;2).
Упражнение 3
1. A1 (0;-3;5), B1 (7;2;8), C1 (-4;0;-3).
Упражнение 4
A1 (3;1;3), B1 (-4;6;6), C1 (7;4;-5).
Введение
В курсе планиметрии мы познакомились с движениями плоскости, т.е. отображениями плоскости на себя, сохраняющими расстояния между точками. Введем теперь понятие движения пространства. Допустим, что каждой точке пространства поставлена в соответствие некоторая точка
(Рис. 1).
Рис. 1. Каждой точке пространства поставлена в соответствие некоторая точка
Причем любая точка пространства оказалась поставленной в соответствие какой-то точке
(Рис. 2).
Рис. 2. Каждой точке пространства поставлена в соответствие некоторая точка
Тогда говорят, что задано отображение пространства на себя. При данном отображении точка переходит (отображается) в точку
.
Движение
Под движением пространствапонимается отображение пространства на себя, при котором любые две точки и
переходят (отображаются) в какие-то точки
и
так, что
(Рис. 3).
Рис. 3. Иллюстрация к определению термина «движение»
То есть движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками (расстояние между исходными точками равно расстоянию между их образами).
Центральная симметрия
Примером движения может служить центральная симметрия (симметрия относительно точки). Возьмем точку и произвольную точку
нашего пространства. Отразим точку
относительно точки
симметрично. Для этого проведем прямую через данные две точки и отложим за точку
точку
так, чтобы
(Рис. 4).
Рис. 4. Центральная симметрия
Если говорить векторным языком, то (Рис. 5).
Рис. 5. Центральная симметрия на векторном языке
Если каждую точку пространства отразить таким образом, то это и называется центральной симметрией относительно точки .
Докажем, что центральная симметрия является движением.
Доказательство геометрическим методом: пусть даны точки и
, точка
– центр,
– образы исходных точек,
. Доказать, что
(Рис. 6).
Рис. 6. Иллюстрация к условию доказательства
Рассмотрим и
. По первому признаку равенства треугольника
:

(Рис. 7).
Рис. 7. Равные треугольники
Доказательство методом координат: пусть – центр симметрии,
и
– произвольные точки в декартовой системе координат. Доказать, что
. Найдем координаты точек
и
(образов точек
и
) (Рис. 8).
Рис. 8. Иллюстрация к условию доказательства
Раз симметрична
относительно начала координат, то все координаты точки
меняют знак на противоположный, то есть
. Аналогично с точками
и
. Получаем, что
.
Тогда ;

В свою очередь:
Отсюда следует, что . Значит, центральная симметрия сохраняет расстояние, а значит, является движением.
У движений есть ряд свойств, например, наиболее важное для нас то, что любую фигуру в пространстве движение переводит в равную ей фигуру (Рис. 9). Но мы не будем доказывать этот весьма непростой факт, а просто будем его использовать.
Рис. 9. Свойство движения
Задачи на центральную симметрию
Задача . В какую точку перейдет точка
при центральной симметрии относительно точки
? Найти координаты получившейся точки
.
Решение
Вариант . Если точка
переходит в некоторую точку
, то
– середина
. Значит, координаты точки
есть полусумма координат
и
:
То есть точка имеет координаты
.
Вариант .
Получаем: 
.
Ответ: .
Задача . Докажите, что при центральной симметрии прямая, не проходящая через центр симметрии, перейдет в прямую, параллельную исходной.
Решение
Пусть . Нужно доказать, что
(Рис. 10).
Рис. 10. Иллюстрация к условию
Точка перешла в точку
, а точка
– в точку
. Образовалась прямая
, т.к. образом прямой при движении является прямая.
Распишем вектор :
(коллинеарные векторы). Значит,
.
Осевая симметрия
Другим примером движения является осевая симметрия (симметрия относительно прямой).
Рассмотрим прямую и произвольную точку
. Опустим из
перпендикуляр на
. Продлим этот перпендикуляр на его длину и получим точку
. Значит,
, тогда
– серединный перпендикуляр отрезка
. Аналогично сделаем для точки
(Рис.11).
Рис. 11. Иллюстрация к объяснению
При этом точки не обязаны лежать в одной плоскости (Рис. 12).
Рис. 12. Точки и
лежат в разных плоскостях
Нужно доказать, что (чтобы осевая симметрия являлась движением).
Для этого введем прямоугольную систему координат так, чтобы ось
совпала с осью симметрии. Координаты точек:
;
. Найдем координаты образов точек. Координаты по оси
не изменятся, а остальные координаты поменяют свой знак на противоположный, то есть
;
(Рис. 13).
Рис. 13. Визуальное пояснение нахождения координат образов точек
Найдем длины отрезков и
:
;
.
Из полученных формул видно, что , значит, при осевой симметрии расстояния между точками
,
и их отображениями
,
равны. Значит, осевая симметрия является движением, что и требовалось доказать.
Есть и более общее понятие – поворот вокруг прямой, когда мы каждую точку поворачиваем вокруг данной прямой на некоторый фиксированный угол (Рис. 14).
Рис. 14. Поворот вокруг прямой
Тогда осевая симметрия – это поворот на .
Задачи на осевую симметрию
Задача . Есть ли ось симметрии у прямоугольного параллелепипеда? (Рис. 15)
Рис. 15. Параллелепипед
Решение
Рассмотрим прямую, проходящую через центр любой грани параллелепипеда, перпендикулярно ей (Рис. 16).
Рис. 16. Перпендикулярная прямая, проходящая через центр грани
Тогда очевидно, что каждое перпендикулярное сечение будет симметрично относительно этой оси (повернув прямоугольник на , получим такой же прямоугольник), а значит, и вся фигура также будет симметрична.
Ответ: да, есть.
Задача . Рассмотрим правую перчатку. Проведем через средний палец ось параллельно пальцу и сделаем осевую симметрию перчатки относительно этой оси. В какую перчатку: правую или левую перейдет исходная перчатка?
Ответ: В правую перчатку, ведь это просто поворот относительно прямой на .
Заключение
На этом уроке мы познакомились с понятием «движение в пространстве» и двумя видами движения – центральной симметрией (симметрией относительно точки) и осевой симметрией (симметрией относительно прямой); выяснили, как можно находить координаты образов с помощью векторов; доказали, что эти симметрии являются движением, и выяснили, что осевая симметрия – это поворот относительно оси на .
Список рекомендованной литературы
1. Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. — М.: Просвещение, 2009. – 255 с.
2. Геометрия 11 класс, А.В. Погорелов, М.: Просвещение, 2002.
3. Рабочая тетрадь по геометрии 11 класс, В.Ф. Бутузов, Ю.А. Глазков.
Рекомендованные ссылки на ресурсы сети Интернет
1. Интернет портал «ЯКласс» (Источник)
2. Интернет портал «Geometry2006.narod.ru» (Источник)
3. Интернет портал «Belmathematics.by» (Источник)
Домашнее задание
1. В координатной системе дана точка . Определите координаты точек, в которые переходит точка
при центральной симметрии относительно начала координат.
2. Точки и
симметричны относительно плоскости
. Найдите длину отрезка
.
3. Постройте фигуру, симметричную кубу относительно прямой .
Глава
3. Геометрические преобразования
Пусть
дана прямоугольная система координат
на плоскости или
в пространстве. В теории геометрических
преобразований рассматриваются две
основные задачи, которые мы назовём
задачами А и Б. Сформулируем эти задачи
для случая плоскости, для пространства
они формулируются аналогично.
Задача
А. Пусть
система координат изменилась (например,
претерпела сдвиг или поворот на некоторый
угол) и
– новая система координат. Каждая точка
имеет определённые координаты
в старой (исходной) системе координат
и какие-то координаты
в новой системе координат
Требуется найти связь между новыми и
старыми координатами точки.
Задача
Б. Пусть
система координат
неизменна, а сама плоскость преобразуется,
т.е. точка
переходит в точку
Требуется установить связь между
координатами
и
В
каждом случае надо чётко представлять
себе, о какой задаче идёт речь. В задаче
А надо найти связь между координатами
и
одной и той
же точки в
разных
системах
координат, а в задаче Б – связь между
координатами
произвольной точки и координатами
её образа
при данном преобразовании. В обеих
задачах целью является получение формул,
выражающих
через
а также обратных
формул –
через
Позже средствами линейной алгебры эти
задачи будут разбираться в более общей
ситуации – для п-мерного
пространства.
Параллельный
перенос
системы координат
– преобразование, при котором начало
координат переходит в точку
а направления координатных осей
сохраняются. Связь между старыми и
новыми координатами произвольной точки
(решение задачи А) даётся формулами
(1)
Аналогичные формулы
справедливы для плоскости (см. рис. 1):
(2)
Рис.1.
Поворот
осей
координат
вокруг начала координат на угол
(решение задачи А) даётся формулами:
(3)
(см. рис. 2).
Рис.2.
Обратные
формулы получаются заменой
на
Приведём теперь
формулы для задачи Б.
Параллельный
перенос пространства
на вектор
задаётся формулами
(4)
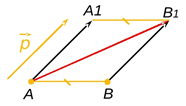
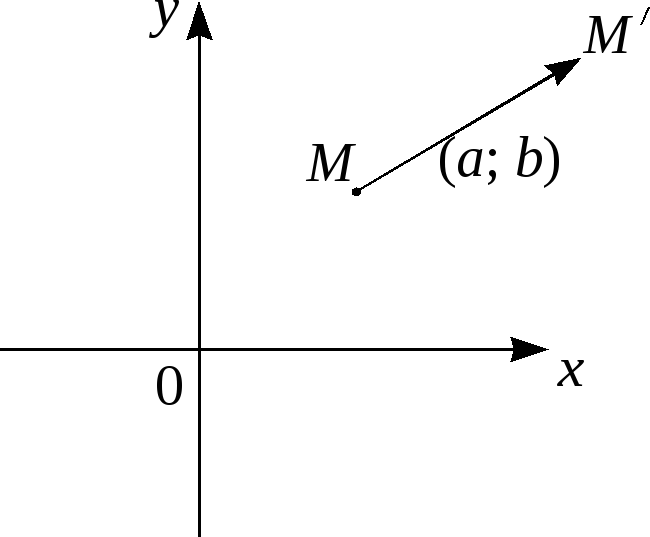
Параллельный
перенос плоскости
(см. рис. 3) – формулами
(5)
Рис.3.
Поворот
плоскости
на угол
вокруг начала координат
– преобразование плоскости, при котором
каждая точка
переходит в такую точку
что угол между векторами
и
равен
(см. рис. 4).
Формулы поворота:
(6)
Примечание:
здесь речь идёт о направленном
угле, т.е. об
угле от
к
Поворот
плоскости на угол
вокруг точки
(7)
Симметрии
плоскости (или пространства) – это такие
преобразования плоскости (пространства),
при которых каждая точка
переходит в точку
симметричную точке
относительно точки, прямой или плоскости.
Разумеется, это является задачей Б.
Переход от системы координат к симметричной
системе (задача А) встречается весьма
редко и здесь рассматриваться не будет.
Формулы
симметрии плоскости: а) симметрия
относительно начала координат, б)
относительно оси
в) относительно точки
г) относительно прямой
а)
б)
в)
г)
формулы
симметрии пространства: а) относительно
начала координат, б) относительно оси
в) относительно плоскости
г) относительно плоскости
а)
б)
в)
г)
Для
симметрий относительно других осей
координат (координатных плоскостей) и
параллельных им прямых (соотв., плоскостей)
формулы пишутся аналогичным образом.
Приведём ещё формулу поворота пространства
на угол
вокруг оси
Симметрия
относительно прямой
(или
осевая
симметрия)
– преобразование плоскости, при котором
каждая точка
переходит в точку
,
расположенную симметрично
относительно
,
т.е.
и
лежат по разные стороны от
на одинаковом расстоянии от
на одном перпендикуляре к
.
Центральная
симметрия
(симметрия
относительно точки
):
если
то
Симметрия относительно точки
– это поворот плоскости на угол
вокруг точки
.
Решим две задачи
на преобразование координат.
Задача
1. Кривая
задана уравнением
Написать уравнение этой кривой в системе
координат: (а) параллельно перенесённой
на 2 единицы вправо и на 3 единицы вниз;
(б) повёрнутой относительно начала
координат на угол
Решение.
(а) Используя формулы (2), получим:
Напишем обратные формулы:
Подставим в уравнение кривой:
Это и будет уравнением кривой в новой
системе координат.
Задача
2. Написать
уравнение параболы
в системе координат, повёрнутой на
вокруг начала координат.
Решение.
Взяв в формулах
получим:
Подставим в уравнение
Отсюда получаем, что уравнение параболы
в новой системе координат таково:
Теперь
решим несколько задач на преобразование
плоскости или пространства.
Задача
3. Кривую
сдвинули на 4 единицы вправо, а затем на
4 единицы вверх. Написать уравнение
новой кривой.
Решение.
По формулам (5) получаем:
Отсюда получаем:
или
Таким образом, новая кривая имеет
уравнение
Задача
4. Найти образ
точки
при повороте плоскости на угол
вокруг начала координат.
Решение.
Пусть
– образ точки
Запишем формулы поворота (6) для угла
Подставим
в эти формулы
Получим:
Следовательно,
Задача
5. Дана прямая
Составить уравнение прямой, симметричной
прямой
а) относительно начала координат; б)
относительно оси
в) относительно прямой
г) относительно прямой
Решение.
Симметрия
относительно начала координат задаётся
формулами
(формулы (8а)). Подставим в уравнение
прямой
вместо
и
вместо
Получим:
Отсюда следует, что
Значит, уравнение симметричной прямой
таково:
б) Применяя формулы (8б), получим:
в) Симметрия относительно прямой
задаётся формулами
Поэтому следует подставить в уравнение
прямой
вместо
и
вместо
Мы получим:
Окончательно получаем:
г) Симметрия относительно прямой
определяется формулами
Отсюда нетрудно получить уравнение
симметричной прямой:
Задача
6. Найти образ
прямой
а) при повороте плоскости на угол
вокруг точки
б) при симметрии плоскости относительно
точки
в) при симметрии плоскости относительно
прямой
Решение.
а) Применяя формулы, обратные формулам
(7), получим:
Подставим в уравнение прямой:
Приводя
подобные члены и убирая штрихи, получим
окончательно:
б)
Используя формулы (8в), получим:
Подставим в уравнение прямой:
т.е.
Убирая штрихи, получим окончательно:
в) Заменим
на
на
получим:
После приведения подобных членов и
удаления штрихов получим:
Задача
7. Написать
формулы симметрии плоскости относительно
прямой
Решение.
Пусть
– произвольная точка плоскости,
– её образ при симметрии относительно
прямой
Тогда
Очевидно,
– направляющий вектор этой прямой.
Точку
можно найти из следующих условий: 1)
точка с координатами
(середина отрезка
)
принадлежит прямой
2)
Запишем эти условия в виде системы
уравнений:
Решив
эту систему, получим:
Это и есть формулы симметрии.
Задача
8. Дан центр
квадрата:
и уравнение
одной его стороны:
Составить уравнения других сторон
квадрата.
Решение.
Две стороны (смежные) получаются
поворотом плоскости вокруг точки
на
и
а
третья сторона (противоположная) –
поворотом на
или, что то же самое, – симметрией
относительно точки
Найдём сначала уравнения смежных сторон.
Запишем формулы поворота:
Отсюда
получаем:
т.е.
или
Подставим
оба варианта в уравнение прямой: а)
б)
Упростив и удалив штрихи, получим: а)
б)
Найдём
теперь уравнение противоположной
стороны. Запишем формулы симметрии
плоскости относительно точки
Подставим эти формулы в уравнение
прямой:
Упростив и удалив штрихи, получим:
Задача
9. Найти образ
точки
при повороте пространства на угол
вокруг оси ординат.
Решение.
Формулы поворота пространства вокруг
оси
на плоскости
совпадают с формулами поворота этой
плоскости вокруг начала координат, т.е.
мы имеем:
Добавив
уравнение
и подставив
получим:
Взяв
вычислим
Следовательно, точка
– образ точки
при повороте.
Задача
10. Поверхность
задана уравнением
Составить уравнение поверхности,
симметричной данной относительно
плоскости
Решение.
Симметрия относительно плоскости
задаётся формулами
Подставим в уравнение поверхности:
Убрав штрихи, получим искомое уравнение:
Задачи для
самостоятельного решения
-
Точка
имеет координаты
в одной системе координат и
в другой, получающейся из первоначальной
параллельным переносом. Написать
формулы, выражающие новые координаты
произвольной точки через старые. Ответ:
-
Система
координат повернулась на угол
вокруг начала координат. Написать
формулы поворота и уравнение прямой
в новой системе координат. Ответ:
-
Плоскость
повернулась на
вокруг точки
Написать формулы поворота. Ответ:
-
Написать
формулы параллельного переноса
пространства, при котором точка
переходит в точку
Ответ:
-
Написать
уравнение кривой, полученной из кривой
а) параллельным переносом на 2 вправо
и на 3 вниз; б) симметрией относительно
точки
в) симметрией относительно прямой
г) симметрией относительно прямой
Ответ: а)
б)
в)
г)
-
Поверхность
задана уравнением
Написать уравнение поверхности,
полученной из данной: а) симметрией
относительно оси
б)симметрией относительно плоскости
в) симметрией относительно точки
Ответ: а)
б)
в) -
Преобразование
плоскости задано формулами
Доказать, что это поворот; найти центр
и угол поворота. Ответ: центр:
угол:
-
Дан
центр правильного треугольника:
и уравнение
одной его стороны:
Составить уравнения двух других
сторон. Ответ:
-
Написать
формулы симметрии плоскости относительно
прямой
Ответ:
-
Какое
преобразование плоскости получится,
если сначала сделать поворот на
вокруг начала координат, а затем на
вокруг точки
Ответ: параллельный перенос на вектор
-
Соседние файлы в папке СРС
- #
- #
- #
- #
- #
- #
- #
- #
- #