Определение.
Центральный угол правильного многоугольника — это угол, под которым сторона многоугольника видна из его центра.

∠AOB — центральный угол правильного восьмиугольника.
Около любого правильного многоугольника можно описать окружность, центр которой совпадает с центром этого многоугольника. Если у многоугольника n сторон, то центральных углов у него также n и все они равны между собой.
Градусная мера всей окружности — 360º, следовательно, градусная мера каждой дуги окружности, на которую окружность разбивают вершины n-угольника, равна
Так как центральный угол равен дуге, на которую от опирается, то и каждый из центральных углов равен 360º:n.
Примеры

равен 360º:3=120º.

равен 360º:4=90º.

равен 360º:6=60º.

равен 360º:8=45º.
Углы правильного многоугольника делятся на :
- центральный угол;
- внутренний угол;
- внешний угол.
Сумма внутреннего и внешнего угла равна (180°).
Сумма внутренних углов правильного многоугольника с (n) сторонами равна:
((n — 2)180°)
Для нахождения внутреннего угла используют формулу:
(alpha = frac{{{{180}^o}(n — 2)}}{n})
(n)— число сторон
Для нахождения внешнего угла используют формулу:
(varphi = frac{{{{360}^o}}}{n})
(n)— число сторон
Для нахождения центрального угла используют формулу:
(beta = frac{{{{360}^o}}}{n})
(n)— число сторон
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
ВИДЕОУРОК
Правильным
многоугольником называют выпуклый многоугольник, у которого все стороны и все углы
равны.
Сумма углов
правильного многоугольника, как и произвольного многоугольника, равна 180° (n – 2).
Величина
угла αn правильного n – угольника
равна:
Многоугольник
называют вписанным в окружность, если все его вершины лежат на этой окружности.
Многоугольник
называют описанным вокруг окружности, если все его стороны касаются окружности.
Около любого правильного
многоугольника можно описать окружность: в любой правильный многоугольник можно
вписать окружность, к тому же центры вписанной и описанной окружности совпадают.
где R – радиус описанной окружности, r –
радиус вписанной окружности, a – сторона правильного n-угольника.
Формулы для нахождения
стороны an радиуса
R описанной
и радиуса r вписанной
окружности для правильных n-угольников.
Общий центр описанной и вписанной окружности
называют центром правильного многоугольника.
Апофемою
правильного многоугольника называется перпендикуляр, проведенный с центра
правильного многоугольника до его стороны.
Апофема – это радиус
вписанной окружности.
Центральным
углом правильного многоугольника
называют угол, образованный двумя радиусами, проведенными до соседних вершин.
Центральный угол правильного n – угольника вычисляют по
формуле:
ЗАДАЧА:
Найдите внешний угол при вершине правильного шестиугольника.
РЕШЕНИЕ:
Внутренний угол правильного шестиугольника равен 120°. Поэтому внешний его угол равен
180° – 120° = 60°.
ЗАДАЧА:
Определите количество сторон правильного многоугольника, внутренний
угол которого равен 150°.
РЕШЕНИЕ:
180°n – 360° = 150°n,
30°n = 360°,
n = 360° : 30°,
n = 12.
ЗАДАЧА:
Центральный угол правильного многоугольника равен 30°. Определите количество сторон многоугольника.
РЕШЕНИЕ:
Центральный угол
откуда
ЗАДАЧА:
Как найти диагонали правильного
шестиугольника, если известна длина его стороны ?
РЕШЕНИЕ:
СЕ – одна из коротких диагоналей шестиугольника, ВЕ – одна из длинных диагоналей.
Учитывая, что углы правильного шестиугольника равны 120°, легко найти прямоугольный треугольник, в котором есть угол 30°, и воспользоваться соотношениями в этом треугольнике.
ОТВЕТ: а√͞͞͞͞͞3, 2а.
ЗАДАЧА:
Радиус окружности,
вписанной в правильный многоугольник, равен
2√͞͞͞͞͞3 см, а радиус окружности,
описанной вокруг него 4 см. Найдите периметр многоугольника.
РЕШЕНИЕ:
Пусть n – количество сторон правильного
многоугольника. По известной формуле имеем:
Учитывая
From Wikipedia, the free encyclopedia
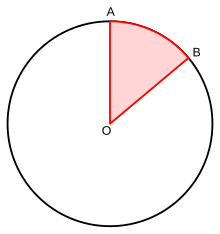
Angle AOB is a central angle
A central angle is an angle whose apex (vertex) is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points A and B. Central angles are subtended by an arc between those two points, and the arc length is the central angle of a circle of radius one (measured in radians).[1] The central angle is also known as the arc’s angular distance. The arc length spanned by a central angle on a sphere is called spherical distance.
The size of a central angle Θ is 0° < Θ < 360° or 0 < Θ < 2π (radians). When defining or drawing a central angle, in addition to specifying the points A and B, one must specify whether the angle being defined is the convex angle (<180°) or the reflex angle (>180°). Equivalently, one must specify whether the movement from point A to point B is clockwise or counterclockwise.
Formulas[edit]
If the intersection points A and B of the legs of the angle with the circle form a diameter, then Θ = 180° is a straight angle. (In radians, Θ = π.)
Let L be the minor arc of the circle between points A and B, and let R be the radius of the circle.[2]
Central angle. Convex. Is subtended by minor arc L
If the central angle Θ is subtended by L, then
Proof (for degrees)
The circumference of a circle with radius R is 2πR, and the minor arc L is the (Θ/360°) proportional part of the whole circumference (see arc). So:
Central angle. Reflex. Is not subtended by L
Proof (for radians)
The circumference of a circle with radius R is 2πR, and the minor arc L is the (Θ/2π) proportional part of the whole circumference (see arc). So
If the central angle Θ is not subtended by the minor arc L, then Θ is a reflex angle and
If a tangent at A and a tangent at B intersect at the exterior point P, then denoting the center as O, the angles ∠BOA (convex) and ∠BPA are supplementary (sum to 180°).
Central angle of a regular polygon[edit]
A regular polygon with n sides has a circumscribed circle upon which all its vertices lie, and the center of the circle is also the center of the polygon. The central angle of the regular polygon is formed at the center by the radii to two adjacent vertices. The measure of this angle is 
See also[edit]
- Inscribed angle
- Great-circle navigation
References[edit]
- ^ Clapham, C.; Nicholson, J. (2009). «Oxford Concise Dictionary of Mathematics, Central Angle» (PDF). Addison-Wesley. p. 122. Retrieved December 30, 2013.
- ^ «Central angle (of a circle)». Math Open Reference. 2009. Retrieved December 30, 2013. interactive
External links[edit]
- «Central angle (of a circle)». Math Open Reference. 2009. Retrieved December 30, 2013. interactive
- «Central Angle Theorem». Math Open Reference. 2009. Retrieved December 30, 2013. interactive
- Inscribed and Central Angles in a Circle
���������� �������������
�������� �����: �������������, ���������� �������������, �������, ����, ���������, ��������� ����������
�������� ������������� ���������� ����������, ���� � ���� ��� ������� ����� � ��� ���� �����.
������� ����������� �������������� ���������� �����, �������������� �� ���� ��� ������ � ���� ��� ������.
����������� ����� ����������� �������������� ���������� ����, ��� ������� ����� ������� �� ��� ������.
 |
�������� ����������� ��������������.
|
�������
- ����� R — ������ ��������� ������ ����������� �������������� ����������, ����� ������ ��������� ���������� ����� $$r = R cdot cosfrac{pi}{n}$$, � ����� ������� �������������� ����� $$a = 2R cdot sinfrac{pi}{n}$$.
- ������� ����������� �������������� � ������ ������ n � ������ ������� a ���������� $$S = frac{n}{4}a^{2} cdot ctgfrac{pi}{n}$$.
- ������� ����������� �������������� � ������ ������ n, ���������� � ���������� ������� R ���������� $$S = frac{n}{2}R^{2} cdot sinfrac{2pi}{n}$$.
- ������� ����������� �������������� � ������ ������ n, ���������� ������ ���������� ������� r ���������� $$S = nr^{2} cdot tgfrac{pi}{n}$$.

��. �����:
��������� ����������,
��������� ����������,
�������� ����ң���������,
������������ �������� �������������