Как найти центростремительное ускорение если нет радиуса

Что такое центростремительное ускорение

Данная величина характеризует, насколько быстро изменяется направление линейной скорости объекта при его движении по окружности.

Обозначается центростремительное ускорение латинской буквой a, так как это векторная величина, обычно ее обозначение условно выглядит так: (vec a)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Единицами измерения в международной системе СИ является м/с².

Силы центростремительная и центробежная, в чем отличия

Сходства центростремительной и центробежной силы:

1. Они являются инерциальными.
2. Возникают всегда при движении тела.
3. Появляются только парами и всегда уравновешивают друг друга.

Их различия заключаются в следующем:

1. Центростремительная сила всегда направлена к центру окружности, в то время как центробежная сила противоположна центростремительной по направлению.
2. Слово «центростремительная» с латинского языка переводится как «искать центр», а «центробежная» — «бежать от центра».

Куда направлен вектор центростремительного ускорения

При передвижении точки по окружности ее скорость направлена по касательной к окружности, а ускорение — по радиусу к центру окружности. Т.е. центростремительное ускорение всегда перпендикулярно скорости.

Вывод формулы центростремительного ускорения

Как найти через угловую и линейную скорость

Центростремительное ускорение, при условии равномерного движения по окружности, можно вычислить с помощью линейной скорости движения.

Центростремительное ускорение можно вычислить через угловую скорость.

Измеряется величина в рад/с.

Зависимость ускорения от скорости математически выглядит так:

(a=omega^2times R)

Расчет центростремительного ускорения через радиус

Тело изменяет направление движения, когда движется по окружности. Это говорит о том, что подобное движение происходит под действием некоторой силы. Такую силу называют центростремительной. С ней связано центростремительное ускорение.

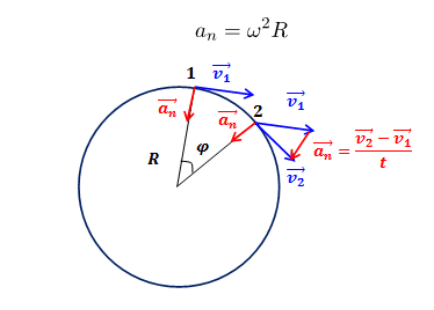
Линейная скорость меняется от точки к точке

При движении по окружности вектор линейной скорости (vec{v}) изменяет свое направление (рис. 1). Значит, направления векторов (vec{v}) для соседних точек будут различаться! Но в каждой точке окружности вектор (vec{v}) направлен перпендикулярно радиусу.

Тело, двигаясь по кругу, изменяет направление, в котором движется. А если меняется направление движения, изменяется вектор скорости тела.

Примечания:

1. Характеристики вектора – это его длина и его направление. Если изменится хотя бы одна из них, говорят, что изменился вектор.
2. Через красную точку на рисунке 1 проходит ось вращения. По правилу правого винта вдоль оси вращения направлена угловая скорость.

Центростремительная сила – причина движения по окружности

Первый закон Ньютона гласит: пока на тело не действуют другие тела, оно сохраняет свою скорость неизменной. То есть, тело покоится, или движется с постоянной скоростью по прямой.

Тело изменит скорость своего движения по направлению или по модулю, только если на него подействует сила (другое тело).

При движении тела по окружности вектор скорости изменяется по направлению. Значит, на движущееся по окружности тело действует сила.

Эта сила притягивает тело к центру окружности (рис. 2), заставляя тело поворачивать. Поэтому, силу называют центростремительной (стремится к центру). Она направлена к центру окружности по радиусу.

А если эту силу убрать, тело начнет двигаться по прямой с постоянной (одной и той же) скоростью.

Примечание: На любое тело, движущееся по окружности, действует центростремительная сила. Она в каждой точке этой окружности направлена к ее центру по радиусу.

Центростремительное ускорение

Второй закон Ньютона утверждает: если есть сила, появится ускорение.

Сила и ускорение связаны так:

[ large vec{F_{text{ц}}} = m cdot vec{a_{text{ц}}} ]

Это ускорение (vec{a_{text{ц}}}) сонаправлено (рис. 3) с вектором силы (vec{ F_{text{ц}} }), поэтому, его называют центростремительным ускорением.

Длина центростремительного ускорения отличается от длины вектора силы в (m) раз. Где (m) – это масса точки.

Вектор ускорения (vec{a_{text{ц}}}) направлен по радиусу к центру окружности. Значит, он перпендикулярен вектору (vec{v}) линейной скорости.

Поэтому центростремительное ускорение иногда называют нормальным ускорением.

[ vec{a_{text{ц}}} = vec{a_{n}} ]

Примечание: Нормаль – это перпендикуляр. Нормальное, значит, перпендикулярное.

Нормальное ускорение можно вычислить, пользуясь выражением:

[ large boxed{ left|vec{a_{n}} right| = frac{v^{2}}{R} }]

​( vec{a_{n}} left( frac{text{м}}{c^{2}} right) )​ — центростремительное ускорение;

(v left( frac{text{м}}{c} right)) — линейная скорость точки;

(R left( text{м}right)) – радиус окружности, по которой движется точка.

[ large boxed{vec{F_{text{ц}}} = m cdot vec{a_{text{ц}}} = m cdot frac{v^{2}}{R} }]

(m left( text{кг}right)) – масса точки.

Чем быстрее движется тело, и чем меньше радиус окружности, тем больше нормальное ускорение и центростремительная сила, действующая на тело.

Примечание: Нормальное ускорение есть всегда, когда есть движение по окружности, при этом не важно, меняется ли скорость тела по модулю, или не меняется.

Что такое центростремительное ускорение

Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка.

Чему равно центростремительное ускорение

Модуль центростремительного ускорения определяется формулой:

[a_{n}=frac{v^{2}}{R}]

Модуль a_n остается постоянным, однако направление вектора a_n все время меняется, поэтому движение по окружности не является равноускоренным.

Центростремительное ускорение также можно определить через угловую скорость:

В общем случае ускорение движущейся по окружности точки можно представить в виде двух составляющих – нормальной и тангенциальной. Первая составляющая направлена по касательной к траектории, вторая по радиусу непосредственно к центру круга. Всё это можно представить в виде формулы:

[mathbf{a}=mathbf{d} v / d t=(d v / d t) * boldsymbol{tau}+v *(d tau / d t)=(mathrm{dv} / mathrm{dt}) * boldsymbol{tau}+left(mathrm{v}^{2} / mathrm{R}right) * mathbf{n}]

Где R – радиус окружности, n – единичный вектор нормали к траектории.

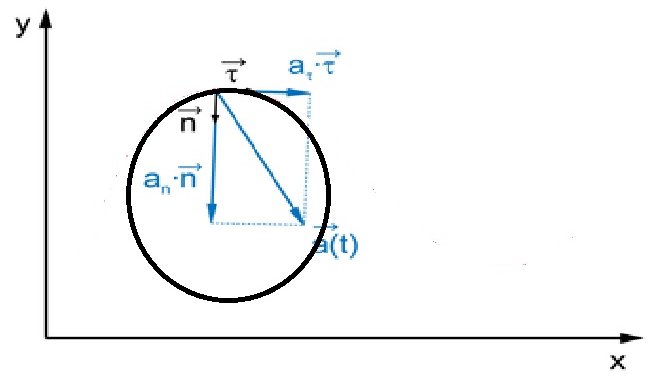
Тангенциальное ускорение 

Это ускорение (dv/dt) * τ, оно характеризует изменение скорости по величине за единицу времени и является её производной. В системе СИ тангенциальное ускорение измеряется в м/c². Оно может быть, как положительным, так и отрицательным. При положительных значениях тангенциального ускорения модуль скорости движущейся по окружности точки возрастает и движение именуют ускоренным. При отрицательных значениях величина скорости понижается и движение называют замедленным. Если тангенциальное ускорение постоянно, то к словам ускоренный и замедленный добавляется приставка «равно».

Нормальное или центростремительное ускорение

Это вторая составляющая разложенного нами движения (v²/R)*n. Обозначим её как a_n Поясним, откуда взялись квадрат скорости, радиус и n.

Одновременно умножаем и делим v * (dτ/dt) на стремящийся к нулю элемент длины траектории, т. е. v*(dτ/dl)(dl/dt). Последний множитель в этом выражении есть скорость, его можно записать как v *(dτ/dl)*v. Отсюда v²*(dτ/dl). dl допустимо представить как R*dϕ. dϕ здесь есть малый угол поворота вокруг центра окружности.

n = dϕ/dτ. Это ясно из геометрических соображений. Δτ = τ ′- τ есть разность единичных касательных векторов в рассматриваемой нами точке (τ) и бесконечно близкой к ней точке (τ ′). По величине она равна 2sin(dϕ/2). Здесь dϕ есть угол между τ и τ ′. Эта разность в рассматриваемой точке имеет направление к нормали n под углом dϕ/2. Из-за малости dϕ становится возможным совпадение его с вектором нормали n. Также из-за малости dϕ синус допустимо разложить в ряд Тейлора. В результате всего этого мы приходим к тому, что Δτ = Δϕ * n. Для бесконечно малых это выражение переходит в dτ = dϕ * n.

Мгновенную скорость можно выразить соотношением v =ω*R. После этого формула центростремительного ускорения приобретает у нас вид a_n = (ω*R)²/R = ω²*R.

Теперь о том, в чем измеряется центростремительное ускорение в физике. Хотя некоторым может показаться странным, но меряется оно, также как и тангенциальное ускорение в метрах на секунду квадрат, т. е. м/c².

Первым (или одним из первых), кто стал пользоваться понятием центростремительного ускорения, был по-видимому Христиан Гюйгенс. Именно с его времени понятие нормального ускорения в физике начали повсеместно применять при решении самых разных механических задач.

Примеры решения задач

Прежде чем научиться рассчитывать центростремительную силу, давайте посмотрим, что такое центростремительная сила и как она получается. Объект, движущийся по круговой траектории, ускоряется, даже если он поддерживает постоянную скорость. Ускорение, испытываемое таким объектом, называется центростремительным ускорением, и оно всегда указывает на центр кругового пути. Согласно второму закону Ньютона, должна быть центростремительная сила, указывающая на центр круговой траектории, которая отвечает за круговое движение. Мы рассмотрим несколько примеров того, как рассчитать центростремительную силу.

Как найти центростремительную силу

Получение центростремительной силы довольно просто, если вы знакомы с понятиями центростремительного ускорения и вторым законом Ньютона.

Центростремительное ускорение тела, движущегося с постоянной скоростью

в круговой дорожке с радиусом

дан кем-то

Если угловая скорость тела

Тогда центростремительное ускорение можно записать как

Теперь, чтобы перейти от центростремительной силы к центростремительному ускорению, мы просто используем второй закон движения Ньютона,

, Затем центростремительное ускорение

для тела, имеющего массу

является,

а также,

Как рассчитать центростремительную силу

Пример 1

К струне прикреплен небольшой шарик массой 0, 5 кг, который вращается с постоянной скоростью по горизонтальному кругу радиусом 0, 4 м. Круговое движение мяча имеет частоту 1, 8 Гц.

а) Найти центростремительную силу.

б) Рассчитайте, сколько силы потребуется для перемещения мяча по тому же кругу, но с удвоенной скоростью.

Как рассчитать центростремительную силу — Пример 1

Примеры центростремительной силы

Теперь мы рассмотрим несколько ситуаций, в которых применимы концепции, которые мы узнали о круговом движении. Ключом к решению этих типов проблем является определение круговой траектории, а затем поиск результирующей силы, указывающей на центр круговой траектории . Эта результирующая сила является центростремительной силой.

Круговое движение конического маятника

Предположим, масса

прикреплен к концу строки длины

сделано, чтобы двигаться в горизонтальном круге с радиусом

так, что струна составляет угол

к вертикали. Ситуация иллюстрируется ниже:

Как рассчитать центростремительную силу — конический маятник

Здесь важно отметить, что маятник нельзя качать по горизонтальному кругу, а струна должна быть параллельна земле . Гравитация всегда тянет маятник вниз, поэтому всегда должна быть вертикальная сила, чтобы уравновесить это. Вертикальная сила должна исходить от натяжения, которое действует вдоль струны. Поэтому, чтобы натяжение могло уравновесить нисходящее тяговое усилие, нить маятника всегда должна находиться под углом к ​​земле.

Круговое движение и банковское дело

Банковское дело происходит, когда, например, автомобиль движется по наклонной дорожке по круговой траектории или когда пилот преднамеренно наклоняет летательный аппарат для поддержания круговой траектории. Диаграмма свободного тела в обоих случаях выглядит одинаково, поэтому я буду использовать только одну диаграмму, чтобы найти центростремительную силу в обоих случаях. Разница лишь в том, что сила по имени

для автомобиля — сила реакции между шинами автомобиля и дорожным покрытием, тогда как для самолета

«Поднимите» силу с крыльев. В обоих случаях,

относится к массе автомобиля / самолета.

Как рассчитать центростремительную силу — банковское дело

Пример 2

Автомобиль движется со скоростью 20 мс ^-1 по наклонному участку дороги. Если радиус горизонтальной круговой траектории составляет 200 м, рассчитайте угол крена, необходимый для того, чтобы автомобиль двигался с этой скоростью без какого-либо трения между шинами и дорогой.

Если есть трение, это будет способствовать центростремительной силе, и транспортное средство сможет двигаться с большей скоростью. Однако мы предполагаем, что трение здесь равно 0 (представьте, очень скользкая дорога).

Как рассчитать центростремительную силу — Пример 2