В предыдущем посте мы кратко объяснили связь между центростремительным ускорением и гравитацией. Этот пост посвящен подробному описанию центростремительного ускорения при равномерном круговом движении.
Равномерное круговое движение означает, что при движении по круговой траектории будет постоянная скорость. Тогда давайте узнаем о центростремительном ускорении с постоянной скоростью при равномерном круговом движении в следующем разделе.
Чему равно центростремительное ускорение при равномерном круговом движении?
Центростремительное ускорение при равномерном круговом движении — это движение объекта, ускорение которого направлено к центру траектории вращения с постоянной скоростью и действует перпендикулярно мгновенной скорости.
Изображение кредита: Wikimedia Commons
Интересен тот факт, что тангенциальное ускорение равно нулю при равномерном круговом движении, поскольку угловая скорость постоянна. Все еще, центростремительное ускорение обусловлен ориентацией направления движения объекта.
Изображение кредита: Wikimedia Commons
Постоянно ли центростремительное ускорение при равномерном круговом движении?
Равномерное круговое движение сосредоточено только на центростремительных компонентах, которые соответствуют скорости объекта и радиусу кругового пути. Поскольку радиус постоянен при равномерном круговом движении и даже изменение скорости постоянно, центростремительное ускорение непостоянно.
Поскольку мы знаем, что при равномерном круговом движении скорость всегда постоянна, постоянна только величина движения, а не направление. Таким образом, говорят, что мы можем достичь постоянного линейного ускорения при равномерном круговом движении, но не центростремительного ускорения.
В другом аспекте возникает центростремительное ускорение центростремительной силой, действующей на объект, движущийся по окружности. Если центростремительная сила поддерживается постоянной, то центростремительное ускорение при равномерном движении по окружности будет постоянным, чего действительно трудно достичь. Центростремительная сила постоянна только при вертикальном круговом движении.
Почему центростремительное ускорение не постоянно при равномерном круговом движении?
Хотя скорость и радиус постоянны, центростремительное ускорение непостоянно, потому что центростремительное ускорение в основном связано с направлением.
Постоянная скорость и радиус относятся только к величине движения, но не к направлению. Каждое круговое движение связано с двумя компонентами: тангенциальной и центростремительной. Тангенциальные компоненты всегда зависят от величины движения, а центростремительные компоненты связаны с направлением.
Таким образом, мы можем наблюдать постоянное тангенциальное ускорение, поскольку скорость и радиус демонстрируют тангенциальное поведение, но центростремительное ускорение при равномерном круговом движении непостоянно.
Изображение кредита: Wikimedia Commons
Найти центростремительное ускорение при равномерном круговом движении.
Центростремительное ускорение можно также определить как скорость изменения тангенциальной скорости тела при круговом движении. Таким образом, чтобы найти центростремительное ускорение, требуется тангенциальная скорость. Так как тело совершает круговое движение, то для процесса важен и радиус круговой орбиты.
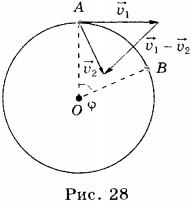
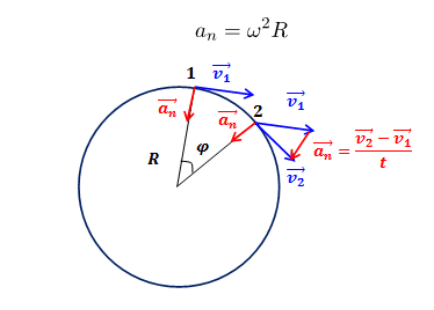
Рассмотрим движение тела массы m при равномерном круговом движении, скорость которого v1 меняется на v2 производить ускорение. Радиус кругового пути равен ‘r’. Чтобы сохранить движение тела по круговой траектории, требуется небольшая сила, поэтому, используя второй закон движения Ньютона, силу можно записать как F = ma. Поскольку сила направлена к центру оси вращения, сила называется центростремительной силой, а результирующее ускорение — центростремительным.
Изменение скорости можно записать как Δv=v2-v1.
Но мы знаем, что ускорение тела при любом движении дается выражением
Для решения рассмотрим приведенную ниже схему.
На приведенной выше диаграмме рассмотрим ΔOAB и ΔXYZ, которые подобны. Из обоих треугольников
Но АВ=vΔt
Переставляя термины, получаем
Мы можем переписать приведенное выше уравнение из первого уравнения как центростремительное ускорение.
Но скорость v можно записать как v=ωr, где ω — угловая скорость. Подставив полученное значение,
ac= ω2r
Направление центростремительного ускорения при равномерном круговом движении
Направление центростремительного ускорения при равномерном круговом движении всегда направлено внутрь, направленное к центру окружности. Просто похоже на движение планет, где солнце находится в центре, а движение планеты сосредоточено к солнцу.
Например, мы знаем, что гравитация работает как центростремительная сила. Когда объект должен свободно падать из пространства, центростремительное ускорение направлено к центру тяжести, и таким образом объект притягивается к земле.
Многие думают, что центростремительное ускорение действует по касательной наружу, что неверно. центростремительное ускорение при равномерном круговом движении ориентировано радиально внутрь. Центростремительное ускорение — это центральное ускорение, необходимое для того, чтобы объект двигался вдоль оси окружности. Если ускорение направлено наружу, то объект может уйти с кругового пути.
Решенные задачи о центростремительном ускорении при равномерном круговом движении
Диск массой 8 кг вращается со скоростью 12 м/с вокруг оси окружности радиусом 3 м. Вычислите центростремительное ускорение диска и найдите центростремительную силу, действующую на диск, чтобы он оставался на оси окружности.
Решение:
Дано –масса диска m=8кг
Скорость диска v=12м/с
Радиус кругового пути r=3м.
Центростремительное ускорение определяется выражением
ac= 48 м / с2
Центростремительная сила Fc=маc
Fc=(12×48)
Fc=576 Н.
Вычислите центростремительное ускорение тела массой 4 кг, вращающегося с угловой скоростью 3 м/с и радиусом оси вращения 8 м. А также найти линейную скорость и силу, приложенные для удержания тела во вращении.
Решение:
Дано – угловая скорость объекта ω=3м/с
Радиус оси вращения r=8м.
Масса объекта m=4кг.
центростремительное ускорение аc= ω2r
ac=(3)2(8)
ac= 72 м / с2
Центростремительная сила Fc=маc
Fc=(4×72)
Fc=288 Н.
Линейная скорость v=ωr
v=3×8
v=24 м/с.
Центростремительная сила, действующая на тело массой 45 кг, равна 583 Н. Вычислите центростремительное ускорение и скорость тела. Радиус оси вращения 16м.
Решение:
Дано – масса тела, m=45кг.
Радиус оси вращения r=16м.
Действующая центростремительная сила Fc= 583Н.
Центростремительное ускорение можно рассчитать, используя второй закон Ньютона F.c=маc
ac= 12.95 м / с2.
Скорость тела определяется перестановкой уравнения центростремительного ускорения.
v2=acr
v=14.99 м/с.
Заключение
В этом посте мы узнали, что центростремительное ускорение при равномерном круговом движении является переменной величиной, часто определяемой как изменение направления, связанное с объектом, движущимся по круговой орбите.
Равномерное движение тела по окружности
1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ( T ) — время, в течение которого тело совершает один полный оборот. Единица периода — ( [,T,] ) = 1 с.
Частота обращения ( (n) ) — число полных оборотов тела за одну секунду: ( n=N/t ). Единица частоты обращения — ( [,n,] ) = 1 с-1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: ( n=1/T ).
Пусть некоторое тело, движущееся по окружности, за время ( t ) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ( varphi ).
Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость ( omega ) — физическая величина, равная отношению угла поворота ( varphi ) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ( omega=varphi/t ). Единица угловой скорости — радиан в секунду, т.е. ( [,omega,] ) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ( 2pi ). Поэтому ( omega=2pi/T ).
Линейная скорость тела ( v ) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ( vec{v}=l/t ). За один оборот точка проходит путь, равный длине окружности. Поэтому ( vec{v}=2pi!R/T ). Связь между линейной и угловой скоростью выражается формулой: ( v=omega R ).
Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ( vec{a}=frac{Deltavec{v}}{t} ) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.
Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ( a=frac{v^2}{R} ). Так как ( v=omega R ), то ( a=omega^2R ).
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии ( R_1 ) от центра вращающегося колеса, равна ( v_1 ). Чему равна скорость ( v_2 ) точки 2, находящейся от центра на расстоянии ( R_2=4R_1 )?
1) ( v_2=v_1 )
2) ( v_2=2v_1 )
3) ( v_2=0,25v_1 )
4) ( v_2=4v_1 )
3. Период обращения точки по окружности можно вычислить по формуле:
1) ( T=2pi!Rv )
2) ( T=2pi!R/v )
3) ( T=2pi v )
4) ( T=2pi/v )
4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:
1) ( omega=a^2R )
2) ( omega=vR^2 )
3) ( omega=vR )
4) ( omega=v/R )
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с
2) 3300 с
3) 3·10-4 с
4) 5·10-6 с
9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?
1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц
10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?
1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с
11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения
ФОРМУЛА
1) ( 1/T )
2) ( v^2/R )
3) ( v/R )
4) ( omega R )
5) ( 1/n )
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
Ответы
Равномерное движение тела по окружности
3.2 (64%) 50 votes
Центростремительное ускорение, теория и онлайн калькуляторы
Центростремительное ускорение
Центростремительное ускорение при равномерном движении по окружности
Пусть материальная точка равномерно движется по окружности. Тогда модуль ее скорости не изменяется ($v=const$). Но это не значит, что ускорение материальной точки равно нулю. Вектор скорости направлен по касательной к траектории движения точки. При перемещении по окружности скорость изменяет свое направление постоянно. Значит, точка движется с ускорением.
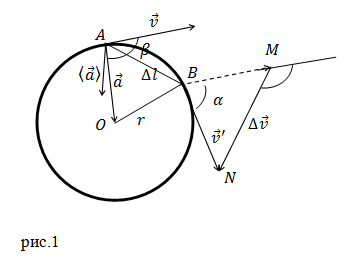
Рассмотрим точки A и B принадлежащие траектории движения рассматриваемого тела. Вектор изменения скорости для этих точек равен:
[Delta overline{v}={overline{v}}’-overline{v}left(1right).]
Если время движения, между точками A и B мало, то дуга AB мало отличается от хорды AB. Треугольники AOB и BMN подобны, следовательно:
[frac{Delta v}{v}=frac{Delta l}{r}=alpha left(2right).]
Модуль среднего ускорения найдем как:
[leftlangle arightrangle =frac{Delta v}{Delta t}=frac{vDelta l}{rDelta t}left(3right).]
Величину мгновенного ускорения можно получить, перейдя к пределу при $Delta tto 0 $ от $leftlangle arightrangle $:
[a={mathop{lim }_{Delta tto 0} leftlangle arightrangle }={mathop{lim }_{Delta tto 0} frac{vDelta l}{rDelta t}=frac{v}{r} }mathop{{rm lim}}_{Delta tto 0}frac{Delta l}{Delta t}=frac{v}{r}v=frac{v^2}{r}left(4right).]
Вектор среднего ускорения составляет с вектором скорости угол равный:
[beta =frac{pi +alpha }{2}left(5right).]
При $Delta tto 0 $ угол $alpha to 0.$ Получается, что вектор мгновенного ускорения составляет с вектором скорости угол $frac{pi }{2}$.
Мы получили, что материальная точка, равномерно движущаяся по окружности, имеет ускорение, направленное к центру траектории движения (перпендикулярное вектору скорости), его модуль равен скорости в квадрате, деленной на радиус окружности.
Такое ускорение называют центростремительным или нормальным, обозначают его обычно ${overline{a}}_n$.
[a_n=frac{v^2}{r}={omega }^2r left(6right),]
где $omega $ — угловая скорость движения материальной точки ($v=omega cdot r$).
Определение центростремительного ускорения
Определение
И так, центростремительное ускорение (в общем случае) — это составляющая полного ускорения материальной точки, которая характеризует,
как быстро изменяется направление вектора скорости при криволинейном перемещении.
Другой компонентой полного ускорения является тангенциальное ускорение, оно отвечает за изменение величины скорости.
Центростремительное ускорение равно:
[{overline{a}}_n=frac{v^2}{r^2}overline{r }left(7right),]
где $e_r=frac{overline{r }}{r}$ — единичный вектор, направленный от центра кривизны траектории к рассматриваемой точке.
Впервые верные формулы для центростремительного ускорения были получены Х. Гюйгенсом.
Единицей измерения центростремительного ускорения в Международной системе единиц является метр, деленный на секунду в квадрате:
[left[a_nright]=frac{м}{с^2}.]
Примеры задач с решением
Пример 1
Задание. Диск вращается вокруг неподвижной оси. Закон изменения угла поворота радиуса диска задает уравнение: $varphi =5t^2+7 (рад)$. Чему равно центростремительное ускорение точки A диска, которая находится на расстоянии $r=$0,5 м от оси вращения к окончанию четвертой секунды от начала вращения?
Решение. Сделаем рисунок.
Модуль центростремительного ускорения равен:
[a_n=frac{v^2}{r}={omega }^2rleft(1.1right).]
Угловую скорость вращения точки найдем как:
[omega =frac{dvarphi }{dt} (1.2)]
уравнение изменения угла поворота в зависимости о времени:
[omega =frac{dleft(5t^2+7right)}{dt}=10t left(1.3right).]
В конце четвертой секунды угловая скорость равна:
[omega left(t=4right)=10cdot 4=40 left(frac{рад}{с}right).]
Используя выражение (1.1) найдем величину центростремительного ускорения:
[a_n={(40)}^2cdot 0,5=800 left(frac{м}{с^2}right).]
Ответ. $a_n=800frac{м}{с^2}$.
Пример 2
Задание. Движение материальной точки задается при помощи уравнения: $overline{r}left(tright)=0,5 (overline{i}{cos left(omega tright)+overline{j}{sin (omega t) } })$, где $omega =2 frac{рад}{с}$. Какова величина нормального ускорения точки?
Решение. За основу решения задачи примем определение центростремительного ускорения в виде:
[a_n=frac{v^2}{R}left(2.1right).]
Из условий задачи видно, что траекторией движения точки является окружность. В параметрическом виде уравнение: $overline{r}left(tright)=0,5 (overline{i}{cos left(omega tright)+overline{j}{sin (omega t) } })$, где $omega =2 frac{рад}{с}$ можно представить как:
[left{ begin{array}{c}
x=0,5{cos left(2tright);; } \
y=0,5{sin left(2tright). } end{array}
right.]
Радиус траектории можно найти как:
[R=sqrt{x^2+y^2}=sqrt{{(0,5{cos (2t) })}^2+{(0,5{sin (2t)) }}^2}=sqrt{{left(0,5right)}^2(c{os}^2left(2tright)+{sin}^2(2t))}=0,5.]
Компоненты скорости равны:
[v_x=frac{dx}{dt}=-0,5cdot 2{sin left(2tright) }left(2.2right).]
[v_y=frac{dy}{dt}=0,5cdot 2{cos left(2tright) }left(2.3right).]
Получим модуль скорости:
[v=sqrt{v^2_x+v^2_y}=sqrt{{{sin}^2 left(2tright)+{cos}^2(2t) }}=1 left(frac{м}{с}right)(2.4).]
Подставим величину скорости и радиус окружности в выражение (2.2), имеем:
[a_n=frac{1^2}{0,5}=2left(frac{м}{с^2}right).]
Ответ. $a_n=2frac{м}{с^2}$.
Читать дальше: сила тяги.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Равномерное движение по окружности.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна
. Скорость
называется линейной скоростью точки.
Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:
. (1)
Частота обращения — это величина, обратная периоду:
.
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).
Пусть, например, . Это означает, что за время
точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
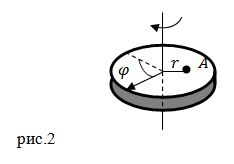
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).
 |
| Рис. 1. Равномерное движение по окружности |
Пусть — начальное положение точки; иными словами, при
точка имела координаты
. Пусть за время
точка повернулась на угол
и заняла положение
.
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
. (2)
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол
. Поэтому
. (3)
Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:
. (4)
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что
.
Но из формулы (2) имеем: . Следовательно,
. (5)
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):
С учётом формул (5) имеем:
(6)
Полученные формулы (6) можно записать в виде одного векторного равенства:
(7)
где — радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
(8)
Выразим угловую скорость из (4)
и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:
.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Равномерное движение по окружности.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Что такое центростремительное ускорение
Центростремительное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.
Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка.
Чему равно центростремительное ускорение
Модуль центростремительного ускорения определяется формулой:
[a_{n}=frac{v^{2}}{R}]
Модуль an остается постоянным, однако направление вектора an все время меняется, поэтому движение по окружности не является равноускоренным.
Центростремительное ускорение также можно определить через угловую скорость:
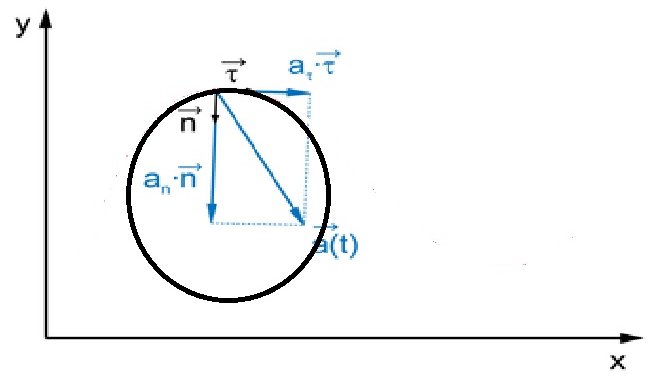
В общем случае ускорение движущейся по окружности точки можно представить в виде двух составляющих – нормальной и тангенциальной. Первая составляющая направлена по касательной к траектории, вторая по радиусу непосредственно к центру круга. Всё это можно представить в виде формулы:
[mathbf{a}=mathbf{d} v / d t=(d v / d t) * boldsymbol{tau}+v *(d tau / d t)=(mathrm{dv} / mathrm{dt}) * boldsymbol{tau}+left(mathrm{v}^{2} / mathrm{R}right) * mathbf{n}]
Где R – радиус окружности, n – единичный вектор нормали к траектории.
Тангенциальное ускорение
Это ускорение (dv/dt) * τ, оно характеризует изменение скорости по величине за единицу времени и является её производной. В системе СИ тангенциальное ускорение измеряется в м/c2. Оно может быть, как положительным, так и отрицательным. При положительных значениях тангенциального ускорения модуль скорости движущейся по окружности точки возрастает и движение именуют ускоренным. При отрицательных значениях величина скорости понижается и движение называют замедленным. Если тангенциальное ускорение постоянно, то к словам ускоренный и замедленный добавляется приставка «равно».
Нет времени решать самому?
Наши эксперты помогут!
Нормальное или центростремительное ускорение
Это вторая составляющая разложенного нами движения (v2/R)*n. Обозначим её как an Поясним, откуда взялись квадрат скорости, радиус и n.
Одновременно умножаем и делим v * (dτ/dt) на стремящийся к нулю элемент длины траектории, т. е. v*(dτ/dl)(dl/dt). Последний множитель в этом выражении есть скорость, его можно записать как v *(dτ/dl)*v. Отсюда v2*(dτ/dl). dl допустимо представить как R*dϕ. dϕ здесь есть малый угол поворота вокруг центра окружности.
n = dϕ/dτ. Это ясно из геометрических соображений. Δτ = τ ′- τ есть разность единичных касательных векторов в рассматриваемой нами точке (τ) и бесконечно близкой к ней точке (τ ′). По величине она равна 2sin(dϕ/2). Здесь dϕ есть угол между τ и τ ′. Эта разность в рассматриваемой точке имеет направление к нормали n под углом dϕ/2. Из-за малости dϕ становится возможным совпадение его с вектором нормали n. Также из-за малости dϕ синус допустимо разложить в ряд Тейлора. В результате всего этого мы приходим к тому, что Δτ = Δϕ * n. Для бесконечно малых это выражение переходит в dτ = dϕ * n.
Мгновенную скорость можно выразить соотношением v =ω*R. После этого формула центростремительного ускорения приобретает у нас вид an = (ω*R)2/R = ω2*R.
Теперь о том, в чем измеряется центростремительное ускорение в физике. Хотя некоторым может показаться странным, но меряется оно, также как и тангенциальное ускорение в метрах на секунду квадрат, т. е. м/c2.
Первым (или одним из первых), кто стал пользоваться понятием центростремительного ускорения, был по-видимому Христиан Гюйгенс. Именно с его времени понятие нормального ускорения в физике начали повсеместно применять при решении самых разных механических задач.
Примеры решения задач
Примеры
Задача №1.
Поезд движется со скоростью 54 километра в час по закруглению, радиус которого равен 1 километру.
Найти чему равно его центростремительное ускорение.
Дано:
Радиус R = 1 км = 1000 м.
Скорость v = 54 км/ч = 15 м/с.
Найти нужно нормальное ускорение [a_{n}].
Решение:
Формула центростремительного ускорения в физике нам известна [a_{n}=v^{2} / R]. Подставляем в неё наши
числовые значения и находим [a_{n}=(15 м/с)^{2} / 1000=0,225 м/
с^{2}].
Ответ: [a_{n}=0,225 м/с^{2}].
Задача №2.
Тело движется по траектории радиусом 5 метров с угловой скоростью 0,3 радиан в секунду. Требуется найти его
центростремительное ускорение.
Дано:
Радиус R = 5 м.
Угловая скорость [omega=0,3 text { рад/с }]
Найти центростремительное ускорение [a_{n}].
Решение:
Опять подставляем числовые значения, но уже в формулу [a_{n}=omega^{2} * R].
[a_{n}=5^{2 *} 0,3=0,45 м/с^{2}].
Ответ: [a_{n}] равно [0,45 м/с^{2}]
Задача №3.
Диск вращается вокруг неподвижной оси. Угол поворота диска изменяется в соответствие с уравнением ϕ = 5t+7.
Нужно вычислить, чему равно центростремительное ускорение очки диска, расположенной на расстоянии R от оси
вращения равном 0,5 м на 4 секунду от времени начала вращения.
Дано:
Радиус R = 0,5 м.
Время t = 4 c.
Закон движения ϕ = 5t+7 .
Найти [a_{n}].
Решение:
Формула центростремительного ускорения, включающая угловую скорость [a_{n}=omega^{2 *} R].
Угловую скорость можно найти по формуле [omega=d phi / d t].
Подставляем вместо ϕ уравнение изменения угла поворота [omega=d(5 t+7) / d t].
Производная этого выражения равна 10t.
Теперь нужно подставить вместо t конкретное числовое значение, т.е. 4 секунды.
Получаем [a_{n}=10 * 4=40 м/с^{2}].
Ответ: [a_{n}] точки на диске равно [40 м/с^{2}].