From Wikipedia, the free encyclopedia
The digital root (also repeated digital sum) of a natural number in a given radix is the (single digit) value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached. For example, in base 10, the digital root of the number 12345 is 6 because the sum of the digits in the number is 1 + 2 + 3 + 4 + 5 = 15, then the addition process is repeated again for the resulting number 15, so that the sum of 1 + 5 equals 6, which is the digital root of that number. In base 10, this is equivalent to taking the remainder upon division by 9 (except when the digital root is 9, where the remainder upon division by 9 will be 0), which allows it to be used as a divisibility rule.
Formal definition[edit]
Let 


where 

is the value of each digit of the number. A natural number 


All natural numbers 


and therefore
because 
If 
Therefore, the only possible digital roots are the natural numbers 

Example[edit]
In base 12, 8 is the additive digital root of the base 10 number 3110, as for 
This process shows that 3110 is 1972 in base 12. Now for 
shows that 19 is 17 in base 12. And as 8 is a 1-digit number in base 12,
Direct formulas[edit]
We can define the digit root directly for base 

Congruence formula[edit]
The formula in base 
or,
In base 10, the corresponding sequence is (sequence A010888 in the OEIS).
The digital root is the value modulo 





.
To obtain the modular value with respect to other numbers 



Also of note is the modulus 



Using the floor function[edit]
It helps to see the digital root of a positive integer as the position it holds with respect to the largest multiple of 




With this in mind the digital root of a positive integer 

Properties[edit]
Additive persistence[edit]
The additive persistence counts how many times we must sum its digits to arrive at its digital root.
For example, the additive persistence of 2718 in base 10 is 2: first we find that 2 + 7 + 1 + 8 = 18, then that 1 + 8 = 9.
There is no limit to the additive persistence of a number in a number base 



- 0, 10, 19, 199, 19 999 999 999 999 999 999 999, … (sequence A006050 in the OEIS)
The next number in the sequence (the smallest number of additive persistence 5) is 2 × 102×(1022 − 1)/9 − 1 (that is, 1 followed by 2 222 222 222 222 222 222 222 nines). For any fixed base, the sum of the digits of a number is proportional to its logarithm; therefore, the additive persistence is proportional to the iterated logarithm.[1]
Programming example[edit]
The example below implements the digit sum described in the definition above to search for digital roots and additive persistences in Python.
def digit_sum(x: int, b: int) -> int: total = 0 while x > 0: total = total + (x % b) x = x // b return total def digital_root(x: int, b: int) -> int: seen = set() while x not in seen: seen.add(x) x = digit_sum(x, b) return x def additive_persistence(x: int, b: int) -> int: seen = set() while x not in seen: seen.add(x) x = digit_sum(x, b) return len(seen) - 1
In popular culture[edit]
Digital roots are used in Western numerology, but certain numbers deemed to have occult significance (such as 11 and 22) are not always completely reduced to a single digit.
Digital roots form an important mechanic in the visual novel adventure game Nine Hours, Nine Persons, Nine Doors.
See also[edit]
- Arithmetic dynamics
- Base 9
- Casting out nines
- Digit sum
- Divisibility rule
- Hamming weight
- Multiplicative digital root
References[edit]
- ^ Meimaris, Antonios (2015), On the additive persistence of a number in base p, Preprint
- Averbach, Bonnie; Chein, Orin (27 May 1999), Problem Solving Through Recreational Mathematics, Dover Books on Mathematics (reprinted ed.), Mineola, NY: Courier Dover Publications, pp. 125–127, ISBN 0-486-40917-1 (online copy, p. 125, at Google Books)
- Ghannam, Talal (4 January 2011), The Mystery of Numbers: Revealed Through Their Digital Root, CreateSpace Publications, pp. 68–73, ISBN 978-1-4776-7841-1, archived from the original on 29 March 2016, retrieved 11 February 2016 (online copy, p. 68, at Google Books)
- Hall, F. M. (1980), An Introduction into Abstract Algebra, vol. 1 (2nd ed.), Cambridge, U.K.: CUP Archive, p. 101, ISBN 978-0-521-29861-2 (online copy, p. 101, at Google Books)
- O’Beirne, T. H. (13 March 1961), «Puzzles and Paradoxes», New Scientist, Reed Business Information, 10 (230): 53–54, ISSN 0262-4079 (online copy, p. 53, at Google Books)
- Rouse Ball, W. W.; Coxeter, H. S. M. (6 May 2010), Mathematical Recreations and Essays, Dover Recreational Mathematics (13th ed.), NY: Dover Publications, ISBN 978-0-486-25357-2 (online copy at Google Books)
External links[edit]
- Patterns of digital roots using MS Excel
- Weisstein, Eric W. «Digital Root». MathWorld.
Нумерология: никакого гадания, только теория чисел
Время на прочтение
8 мин
Количество просмотров 19K
В данной статье речь пойдёт о таких понятиях теории чисел, как цифровой корень и ведический квадрат.
Данная статья ничего не говорит о нумерологии, кроме того, что это псевдонаучная концепция.
Цель данной статьи: показать математические закономерности вокруг вычисления цифрового корня и его связь с циклическими числами.
Введение
Несколько дней назад я решил написать незатейливую статью про нумерологическое сложение. Моей целью было показать, что даже такая незамысловатая операция может иметь большое количество интересных закономерностей. Многие из этих закономерностей я нашёл ещё в школьное время, когда скучал на уроках географии. При внимательном рассмотрении я нашёл больше закономерностей, чем ожидал, и это привело меня назад к моей любимой теме full reptend prime.
После я внимательно изучил то, что нашёл, узнал, что многие из этих понятий уже существуют, и решил переписать статью заново, чтобы опираться на общеизвестные понятия. Помимо известных понятий я добавил собственные визуализации, чтобы сделать чтение немного более увлекательным.
Сумма цифр и цифровой корень
Цифровой корень натурального числа в заданной системе счисления — это значение, получаемое итеративным расчётом суммы цифр, где на первой итерации происходит расчёт суммы цифр натурального числа, а на каждой следующей — расчёт суммы цифр результата предыдущей итерации. Операция выполняется до тех пор, пока вычисленное значение не становится меньше заданной системы счисления, т.е. до тех пор, пока оно не равняется одной-единственной цифре.
Аддитивная стойкость натурального числа — это количество итераций, на которых нужно применить операцию суммы цифр, для того чтобы получить цифровой корень.
Пример: Цифровая сумма числа 142857 равна 1 + 4 + 2 + 8 + 5 + 7 = 27
Цифровая сумма числа 27 равна 2 + 7 = 9
Как следствие, цифровой корень числа 142857 = 9, аддитивная стойкость 142857 = 2.
Код для вычисления цифрового корня в произвольной системе счисления на языке Python:
def digitalRootRecurrent(number, base):
digitSum = 0
while number > 0:
digitSum += number % base
number //= base
if digitSum >= base:
digitSum = digitalRootRecurrent(digitSum, base)
return digitSumПрименение цифровой суммы
Цифровые суммы применялись при расчёте контрольных сумм для проверки арифметических операций ранних компьютеров. Ранее, в эпоху ручного счета, Фрэнсис Исидор Эджуорт предложил использовать суммы 50 цифр, взятых из математических таблиц логарифмов, в качестве формы генерации случайных чисел; если предположить, что каждая цифра случайна, то по центральной предельной теореме эти цифровые суммы будут иметь случайное распределение, близкое к гауссову распределению.
Цифровая сумма двоичного представления числа известна как вес Хэмминга или численность населения. Алгоритмы выполнения этой операции были изучены, и она была включена в качестве встроенной операции в некоторые компьютерные архитектуры и некоторые языки программирования. Эти операции используются в вычислительных приложениях, включая криптографию, теорию кодирования и компьютерные шахматы.
Улучшение алгоритма вычисления цифрового корня
При расчёте цифрового корня можно воспользоваться небольшой хитростью: если значение не равно нулю, и не равно основанию системы счисления — 1, можно получить значение цифрового корня просто операцией взятия остатка от деления на основание системы счисления — 1.
Модифицированный код:
def digitalRoot(number, base):
if number == 0:
return 0
dR = number % (base - 1)
if dR == 0:
dR = base - 1
return dRСвойства цифрового корня
Операция сложения
Сделаем небольшую таблицу, для того чтобы изучить закономерности, каким образом вычисляется цифровой корень суммы двух чисел:
Код для построения таблицы суммы:
firstTermRangeStart = 2
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10
for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
print()
for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
if i % (secondTermRangeEnd + 1) == 0:
print()
print('dr(',j,'+', i, ') =', digitalRoot(j + i, base), ' ', end='')Как можно увидеть, цифровой корень суммы чисел равен цифровому корню суммы цифровых корней этих чисел:
Операция вычитания
Формула похожа на предыдущую, однако совпадает не полностью.
Приведем контрпример: 455 — 123 = 332.
Как можно отметить, выражение 4 — 6 не даёт в результате 8, потому формулу сложения нужно модифицировать, чтобы она работала для операции вычитания:
Операция умножения
Выведем вариацию таблицы умножения, для того чтобы исследовать эту операцию:
Код для вывода таблицы умножения:
firstTermRangeStart = 1
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10
for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
print()
for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
print('dr(',j,'*', i, ') =', digitalRoot(i * j, base), ' ', end='') Запишем значения для каждого множителя:
1) [1, 2, 3, 4, 5, 6, 7, 8, 9]
2) [2, 4, 6, 8, 1, 3, 5, 7, 9]
3) [3, 6, 9, 3, 6, 9, 3, 6, 9]
4) [4, 8, 3, 7, 2, 6, 1, 5, 9]
5) [5, 1, 6, 2, 7, 3, 8, 4, 9]
6) [6, 3, 9, 6, 3, 9, 6, 3, 9]
7) [7, 5, 3, 1, 8, 6, 4, 2, 9]

9) [9, 9, 9, 9, 9, 9, 9, 9, 9]
Можно увидеть, что последовательности разбиваются на пары 1 и 8, 2 и 7, 3 и 6, 4 и 5. В каждой из пар сохраняется та же самая последовательность, но они представляют собой реверсированные копии друг друга, за исключением последнего элемента, который связан с множителем, равным основанию системы счисления — 1.
Также отметим, что при умножении на основание системы счисления -1 цифровой корень будет равен основанию системы счисления — 1. При умножении на 1 значение цифрового корня второго множителя сохраняется.
Визуализация последовательностей:
Последовательности можно рассмотреть как множество всех возможных замкнутых фигур с количеством точек, равным основанию системы счисления — 1, начиная с правильного n-угольника. Исключением является множитель, который не является взаимно простым с основанием системы счисления — 1, в данном случае это 3 и 6.
Для нахождения последовательности любой линии можно записать формулу:
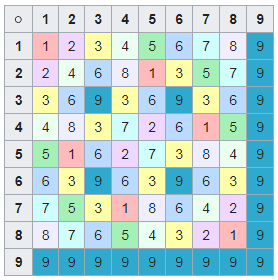
Если записать эти значения как множество пересечений всех множителей, мы получим в результате ведический квадрат.
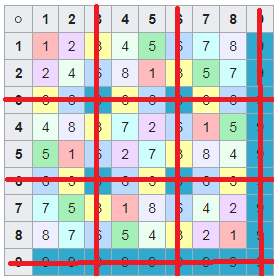
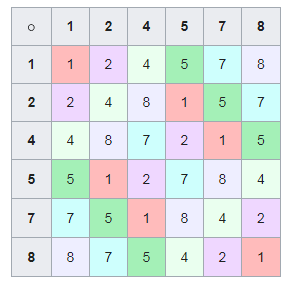
Подмножество данного ведического квадрата формирует собой латинский квадрат. Чтобы получить его, нужно вычеркнуть элементы, равные основанию системы счисления — 1.
В результате мы получим:
Если переставить некоторые из его строчек местами, мы получим последовательность циклических чисел. О том, каким образом должны быть осуществлены перестановки строчек, будет рассказано ниже при исследовании других операций с цифровым корнем.
Ниже приведена ещё одна картинка ведических квадратов для систем счисления 100 и 1000. Белым отмечены самые большие значения клеток — соответствующие основанию системы счисления — 1, черным — самые маленькие, соответствующие 1.
Теперь вернемся к произведению. Цифровой корень произведения одиночных цифр в заданной системе счисления вычисляется при помощи соответствующего ведического квадрата.
Для вычисления цифрового корня произведения двух чисел, которые содержат больше одной цифры, для начала нужно вычислить цифровой корень каждой из этих цифр, и после этого воспользоваться ведической площадью.
Операция деления
Рассмотрим те числа, которые дают при делении непериодические дроби, это 2, 5, 4, 8.
Для того чтобы быть уверенными, что мы не допускаем ошибок, воспользуемся уже выведенными правилами и умножим результат деления на 1000; так как цифровой корень 1000 равен 1, то произведение будет иметь тот же самый цифровой корень.
base = 10
divisors = [2, 4, 5, 8]
for j in divisors:
print()
for i in range(1, base):
value = (digitalRoot(int((i / j) * (base ** 3)), base))
print('dr(',i, '/', j, ') =', value, ' ', end='') Тут бросаются в глаза несколько закономерностей. Число 9 не только при умножении, но и при делении приводит к значению цифрового корня, равному 9. Интересное происходит также с числами 3 и 6, эти числа как при умножении, так и при делении дают абсолютно одинаковые значения цифрового корня.
Запишем в таблицу череду делений:
2) [5, 1, 6, 2, 7, 3, 8, 4, 9] — Эта последовательность встречалась в множителе 5
4) [7, 5, 3, 1, 8, 6, 4, 2, 9] — Эта последовательность встречалась в множителе 7
5) [2, 4, 6, 8, 1, 3, 5, 7, 9] — Эта последовательность встречалась в множителе 2

Операция деления для цифрового корня определена только для делителей, которые не являются взаимно простыми с основанием системы счисления.
Операция возведения в степень
Таблица возведения в степень:
base = 10
.
for i in range(2, base - 2):
print()
for j in range(1, base - 1):
print('dr(', j ,'^', i, ') =', digitalRoot(i ** j, base), ' ', end='') Здесь мы можем наблюдать цикличность.
При внимательном рассмотрении других систем счисления можно сделать вывод, что эта череда связана с формированием остатков от деления, и таким образом она связалась с моим любимым классом простых чисел — full reptend prime.
Для того чтобы пояснить это, рассмотрим операции возведения в степень в других системах счисления. Забегая вперед, скажу: наиболее интересными будут являться такие степени счисления, которые равны p^n + 1, где p — это простое число, а n — натуральное.
Рассмотрим систему счисления 8, череда его значений будет равна [1, 3, 2, 6, 4, 5]. Именно такие же остатки от деления мы получаем при делении числа в десятичной системе счисления.
Это свойство связано с тем, что вычисление цифрового корня можно осуществить при помощи альтернативной формулы расчета цифрового корня:
Ещё визуализации
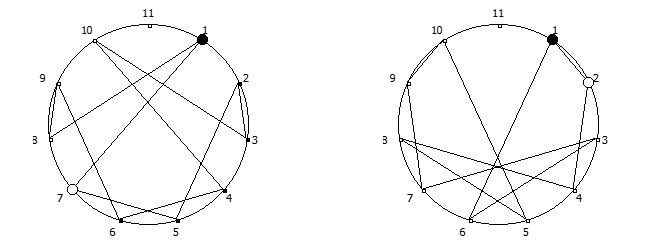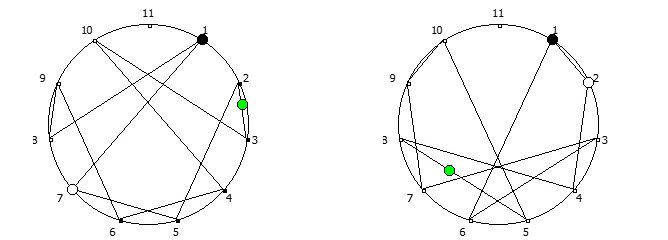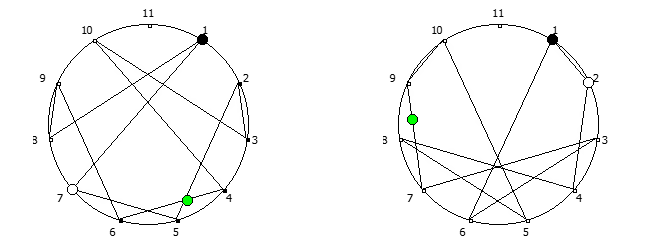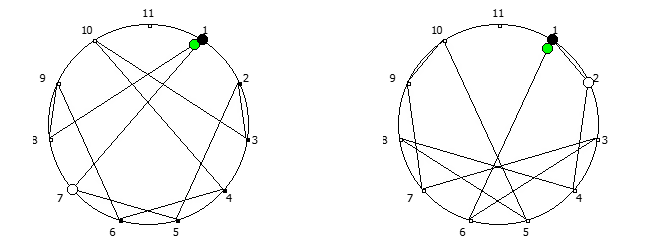
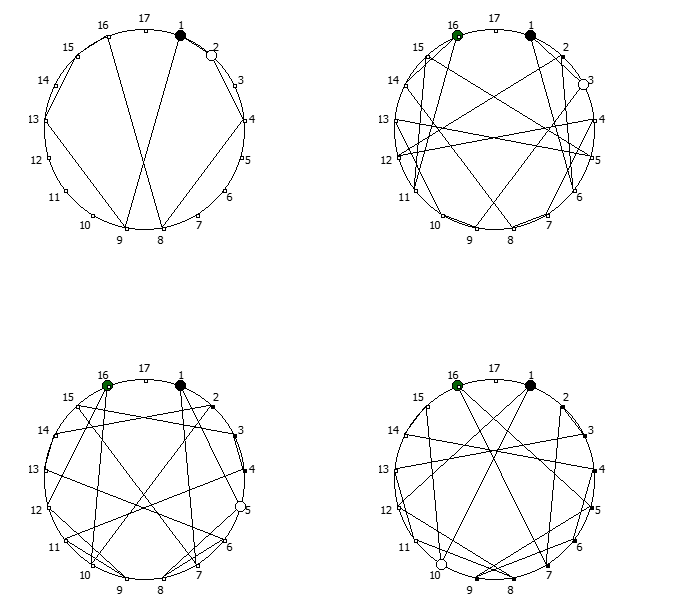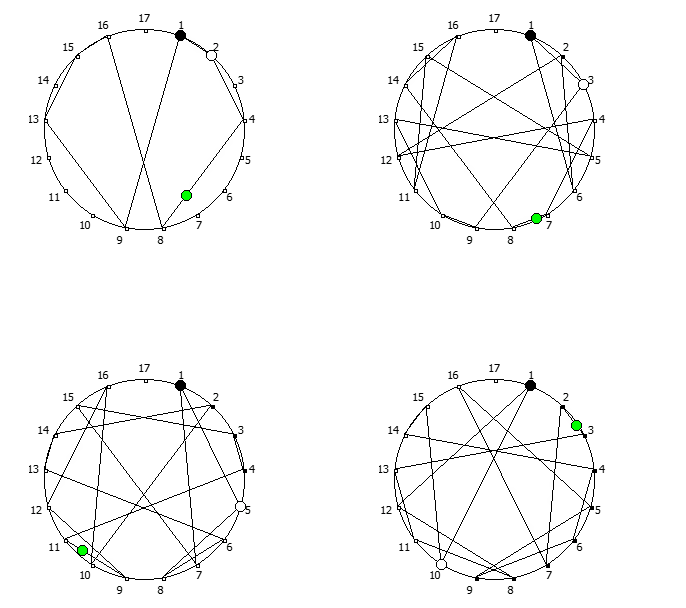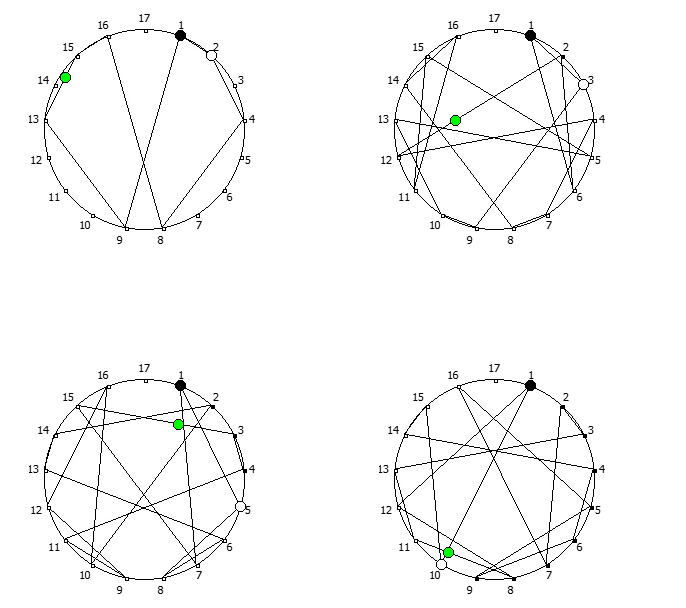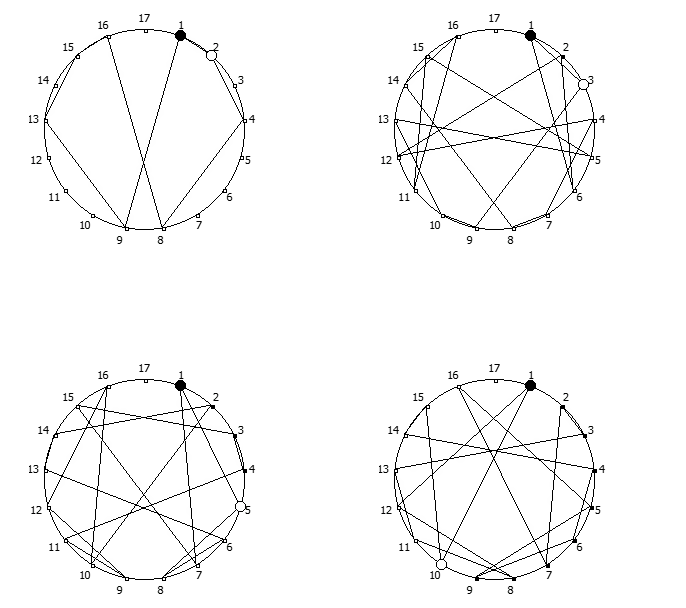
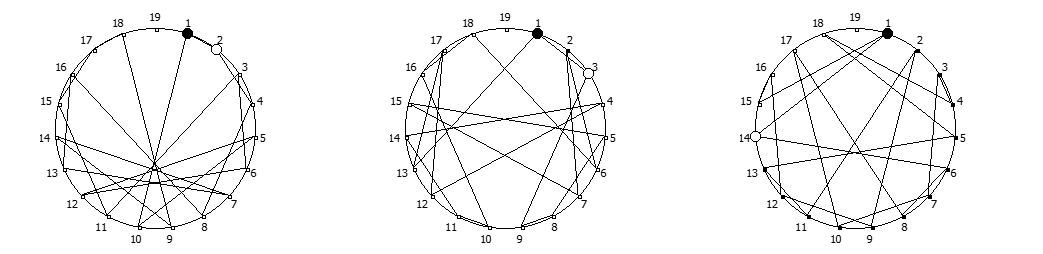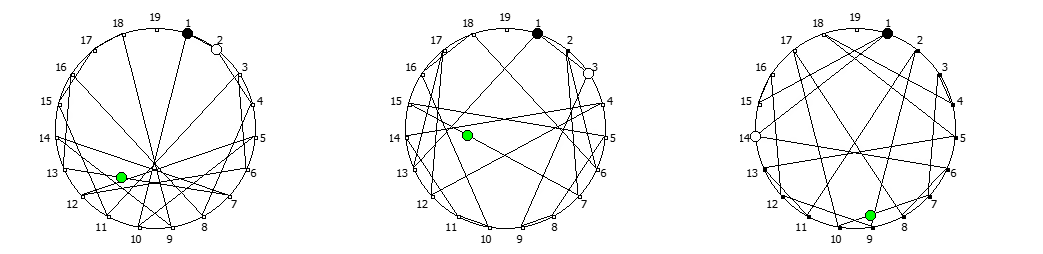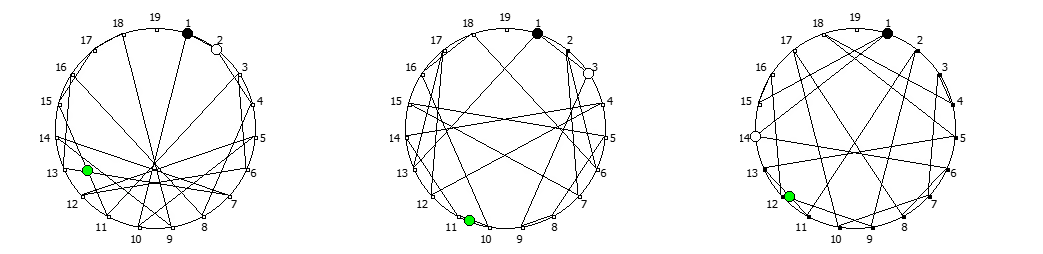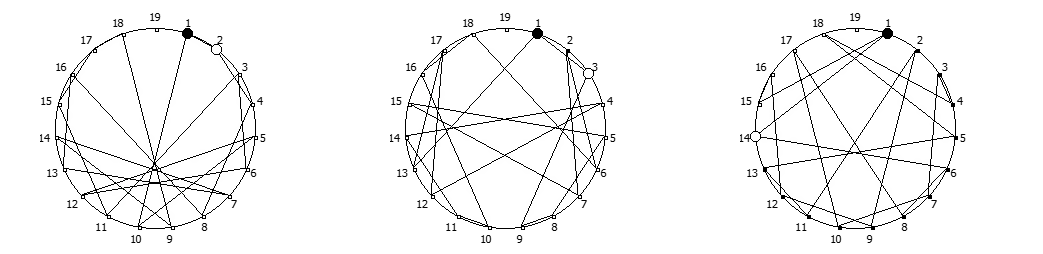
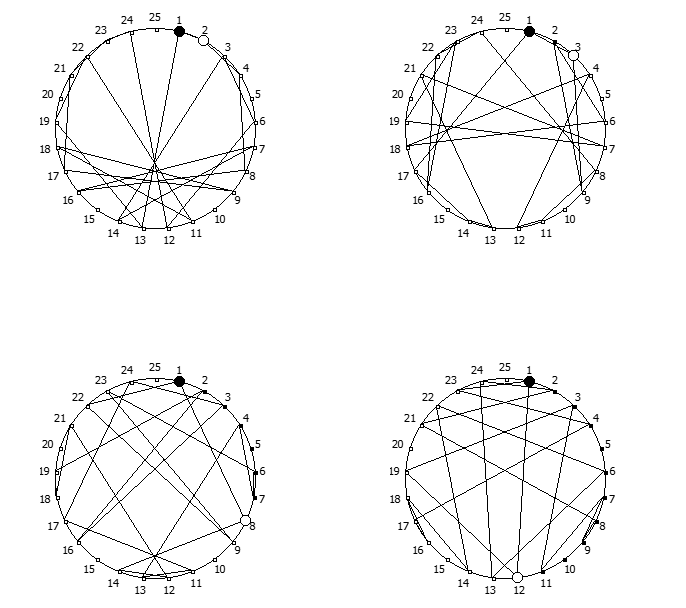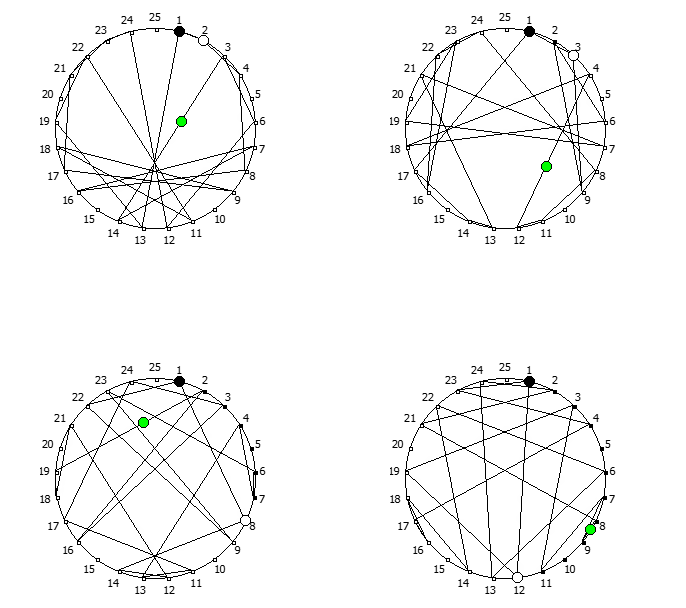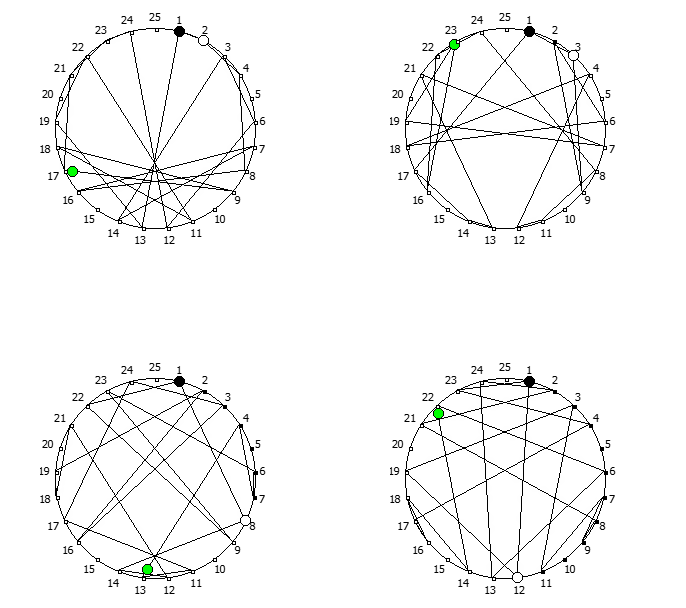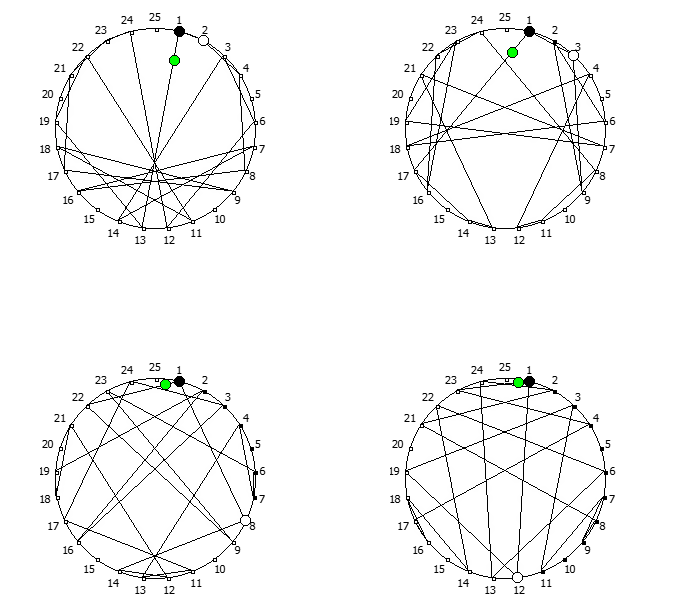
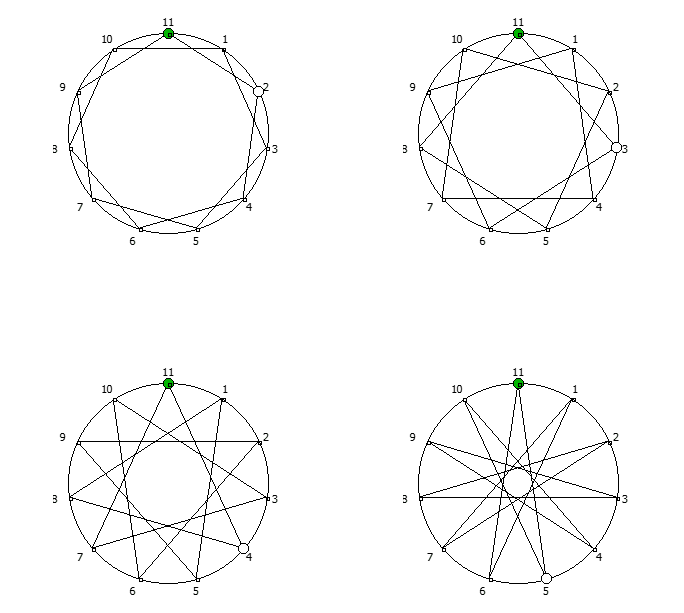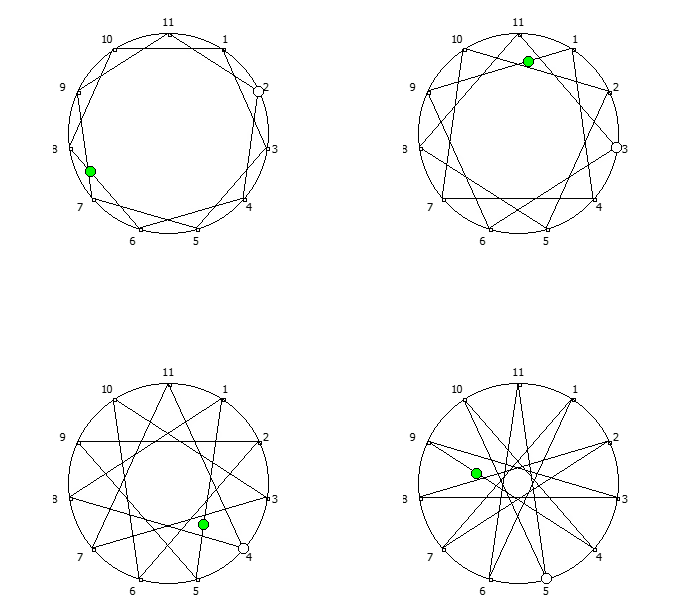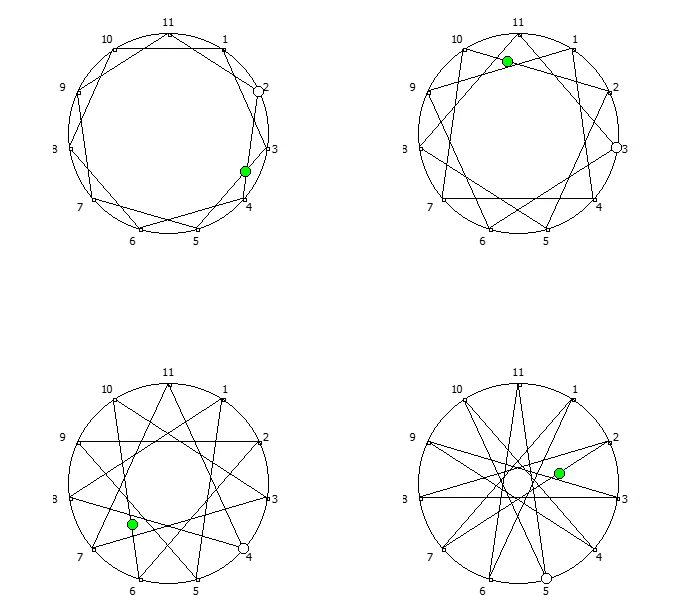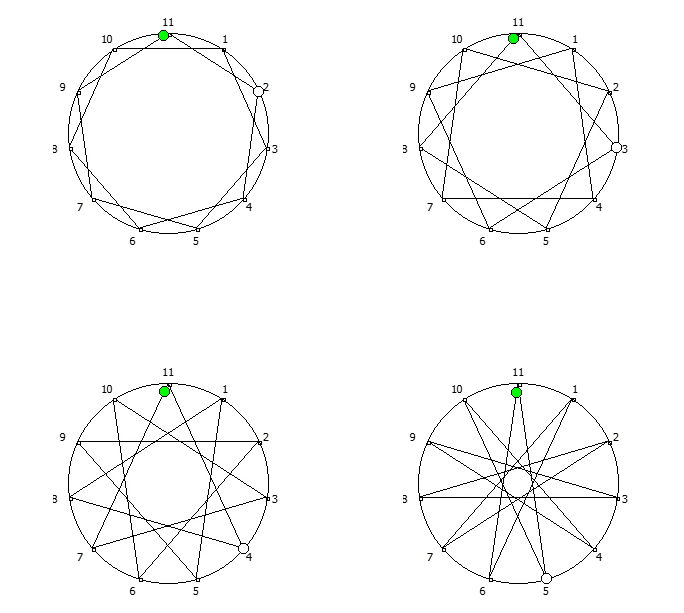
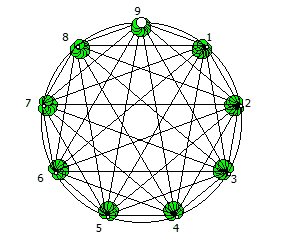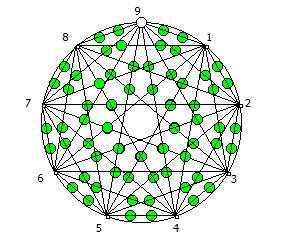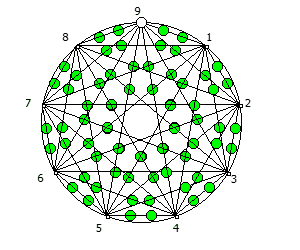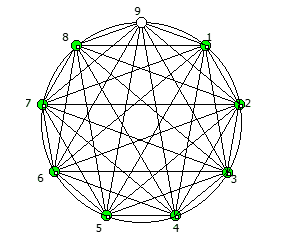
Приведём ниже визуализации для операции возведения в степень для разных систем счисления, все они будут связанны с паттернами, образующимися в рациональных дробях 1/P, где P — это full reptend prime.
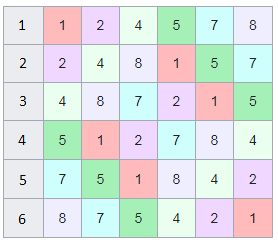
Теперь приведём несколько картинок из ведических квадратов, принцип их формирования очень прост, потому ограничимся небольшим количеством:
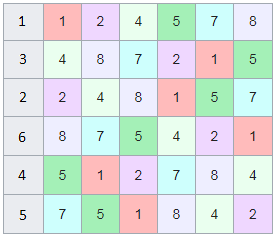
Образование циклических чисел при помощи ведической площади и остатков от деления
После того как мы получили латинский квадрат из ведического квадрата, пронумеруем его строки последовательно:
Теперь мы можем переставить строки на основании череды остатков от деления, таким образом мы получим последовательность циклических чисел. Напомню, остатки от деления были равны [1, 3, 2, 6, 4, 5]. В результате у нас получится следующая картина:
Как можно наблюдать, первый столбец теперь представляет собой циклическое число 142857.
Выводы
Несмотря на плохую репутацию нумерологии, операции суммы цифр и цифрового корня имеют пусть не широкое, но всё же практическое применение.
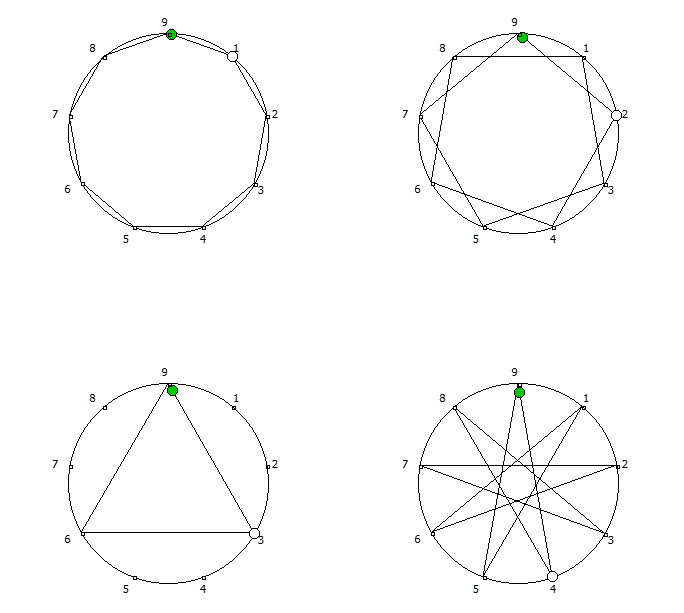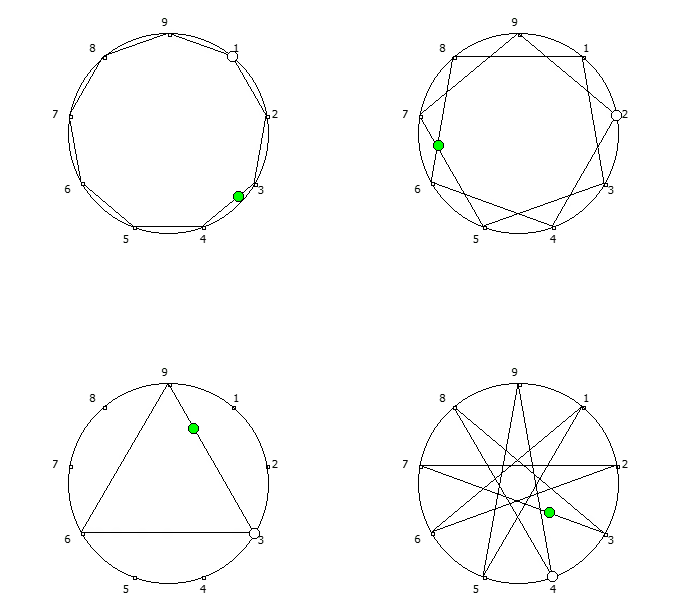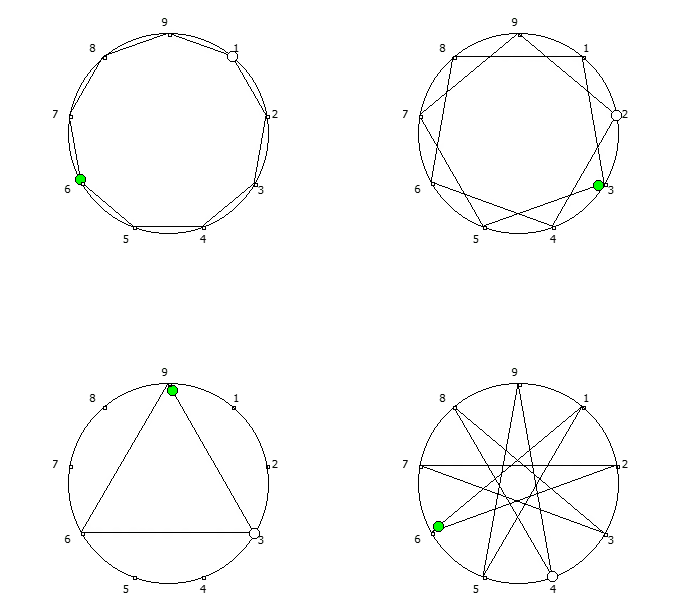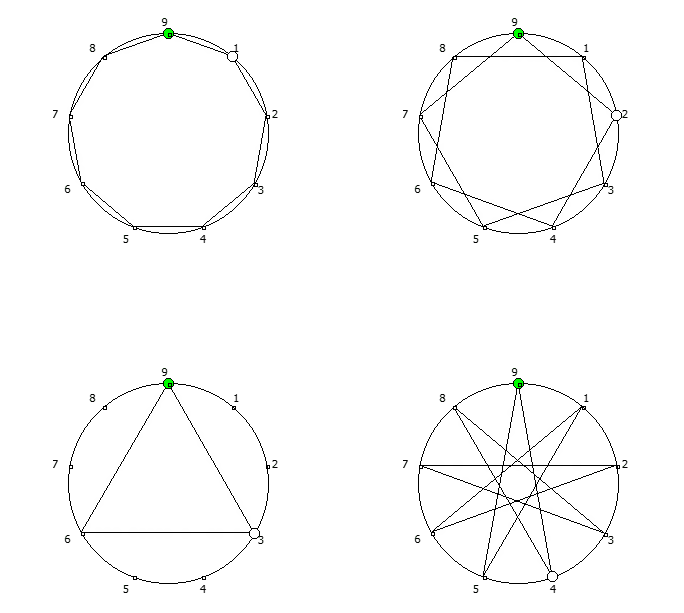
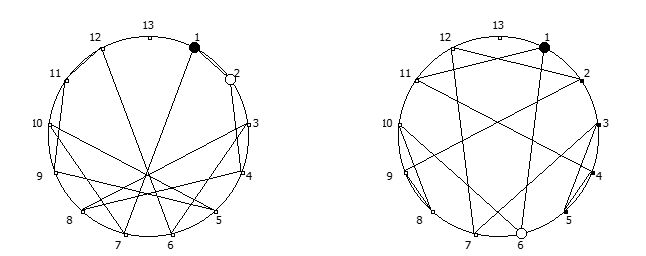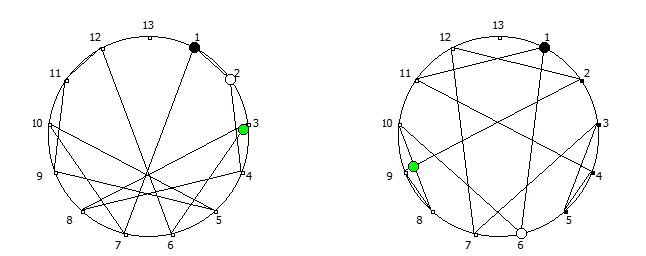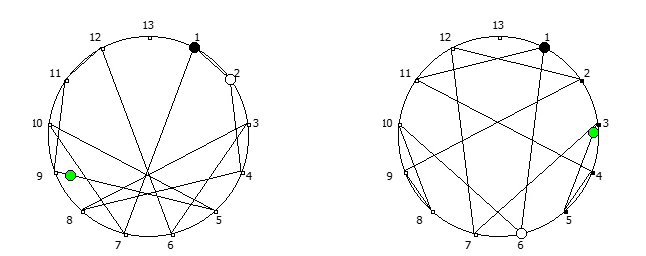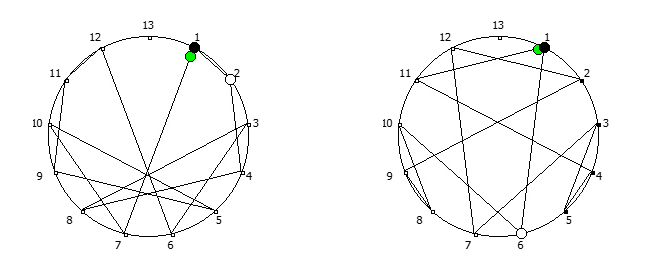
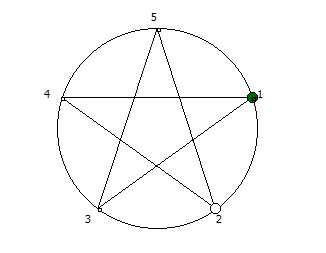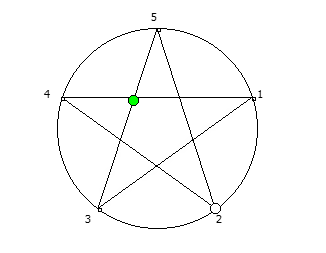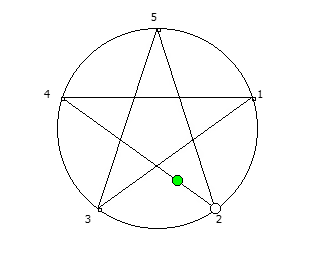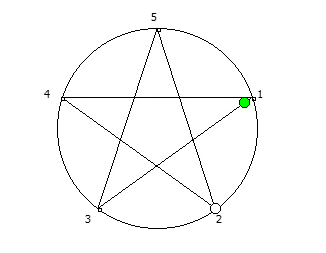
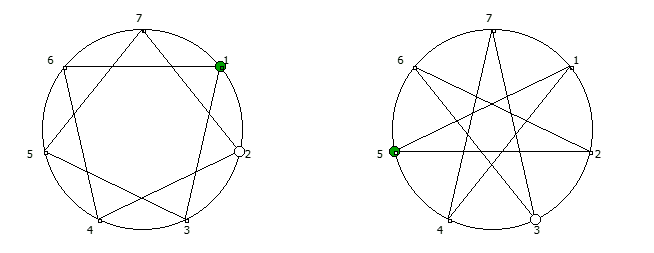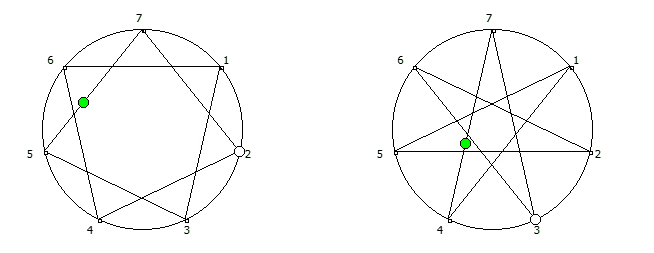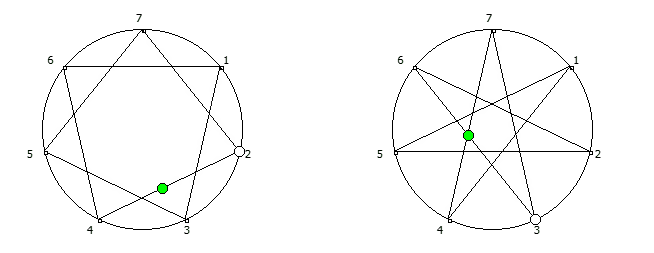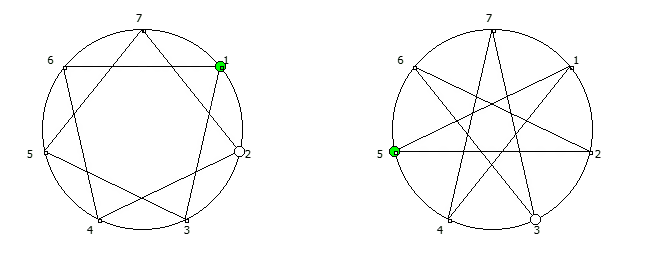
Например, с помощью цифрового корня можно сформировать множество замкнутых n-вершинных звезд, многие из которых очень любят современные рокметал группы 

Как можно видеть, многие метал группы тоже любят теорию чисел!
Но лично я для своей метал группы решил выбрать анимированный логотип, составленный из одновременной визуализации периодических дробей, образованных из 90 рациональных дробей 1/91..90/91:

Если у кого-то есть дополнительная информация об описанных выше понятиях, пожалуйста присылайте её в комментарии, я буду очень благодарен!
Надеюсь, что вам было интересно, большое спасибо за внимание!
Всем привет.
Недавно мне посчастливилось подготовить задачу про цифровой корень на Russian Code Cup. В результате прорешивания, а также комментариев к разбору, я заметил, что, к сожалению, отнюдь не каждый осведомлен о свойствах данной функции. Я просто не мог остаться равнодушным к этой проблеме.
Для начала рассмотрим определение цифрового корня, взятое с англоязычной Википедии с моим переводом:
Цифровой корень натурального числа — это цифра, полученная в результате итеративного процесса суммирования цифр, на каждой итерации которого для подсчета суммы цифр берут результат, полученный на предыдущей итерации. Этот процесс повторяется до тех пор, пока не будет получена одна цифра.
Например цифровой корень 65,536 это 7, потому что 6 + 5 + 5 + 3 + 6 = 25 и 2 + 5 = 7.
Для начала заметим очевидное свойство (dr(n) — цифровой корень числа n):
dr(n) = n, n ≤ 9
Дальше докажем следующий факт: Сумма цифр числа n имеет такой же остаток при делении на 9, как и число n.
В доказательстве нам понадобится формула 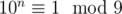
База: 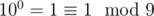
Переход: 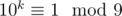
Нужно доказать 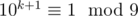
Таким образом мы доказали по индукции, что 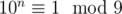
Вернемся к основному доказательству. Пусть 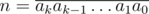
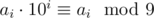
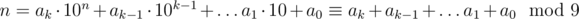
Теперь по только что доказанному утверждению понятно, что остаток при делении на 9 — инвариант относительно взятия цифрового корня, а поскольку сумма цифр числа меньше самого числа, если число больше 9, справедливы следующие две формулы:
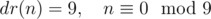
Эти две формулы можно собрать объединить формулой:
Из этой формулы, например, следует периодичность цифрового корня.
Любая задача про цифровой корень становится легче при знании этого несложного факта, надеюсь, что кому-нибудь этот пост покажется полезным.
Поддержано грантом для одаренной молодежи А. А. Шалыто.
|
BarbaraPeach 0 / 0 / 0 Регистрация: 17.03.2020 Сообщений: 4 |
||||
|
1 |
||||
Цифровой корень17.03.2020, 13:15. Показов 30412. Ответов 6 Метки if elseif, python 3.7, while() (Все метки)
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
17.03.2020, 13:15 |
|
Ответы с готовыми решениями: Найти цифровой корень
Появилась проблема, не могу понять в чем проблема в… Цифровой корень Цифровой корень 6 |
|
5407 / 3831 / 1214 Регистрация: 28.10.2013 Сообщений: 9,554 Записей в блоге: 1 |
|
|
17.03.2020, 13:30 |
2 |
|
Цифровой корень Твой цифровой корень уже здесь нашли. Теперь ищи ты. Ссылка внизу.
0 |
|
Заблокирован |
||||
|
17.03.2020, 13:31 |
3 |
|||
|
Решение
palva, помоги ещё с этой задачей, пожалуйста
1 |
|
palva 3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,668 Записей в блоге: 4 |
||||
|
17.03.2020, 15:18 |
4 |
|||
|
Вы применяете функцию int. Значит, она разрешена. Наверно, разрешена и функция str. Тогда можно так:
1 |
|
u235 4379 / 2489 / 525 Регистрация: 07.11.2019 Сообщений: 4,134 |
||||
|
17.03.2020, 22:13 |
5 |
|||
|
Еще вариант:
0 |
|
Status 418 3850 / 2133 / 568 Регистрация: 26.11.2017 Сообщений: 4,995 Записей в блоге: 2 |
|
|
18.03.2020, 06:49 |
6 |
|
0 |
|
1 / 1 / 0 Регистрация: 29.04.2020 Сообщений: 1 |
|
|
29.04.2020, 21:28 |
7 |
|
def digital_root(n): Держи еще решение
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
29.04.2020, 21:28 |
|
Помогаю со студенческими работами здесь
Цифровой корень числа Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 7 |
Задача:
Написать рекурсивную и нерекурсивную функцию,
которая принимает положительный целочисленный аргумент
и возвращает цифровой корень этого числа. Цифровой
корень числа вычисляется следующим образом.
Складываются все цифры числа, затем все цифры
найденной суммы и т.д. Процесс повторяется до тех пор,
пока в результате не будет получено однозначное число
(цифра), которое и является цифровым корнем.
Начнем с нерекурсивного варианта.
Весь исходный код такой:
[cpp]
#include <locale.h>
#include <conio.h>
int SumOfDigits(int N)
{
int d=0, sum = 0;
while (N != 0)
{
d = N % 10;
sum += d;
N = N / 10;
}
return sum;
}
int RootOfNumber (int k)
{
while (k>9)
{
k = SumOfDigits(k);
}
return k;
}
int main()
{
setlocale(LC_ALL, «Russian»);
int N;
printf («Введите целое число:n»);
scanf («%d», &N );
printf («Сумма цифр числа %d = %dn», N, RootOfNumber (N));
getch();
return 0;
}
[/cpp]
в функции main всё достаточно просто: сначала устанавливается русская локаль ( setlocale(LC_ALL, «Russian»);), затем пользователю выдается приглашение ввести число и это число считывается в переменную n целого типа. После этого печатается результат работы функции int RootOfNumber(int k).
Рассмотрим ее подробнее.
[cpp]
int RootOfNumber (int k)
{
while (k>9)
{
k = SumOfDigits(k);
}
return k;
}
[/cpp]
В нее передается целое число и пока оно содержит больше 1 знака (условие k > 9) выполняется вызов функции для складывания чисел внутри числа. Вызывается она с разными аргументами. У меня это k. На каждом витке цикла это число уменьшается, и рано или поздно оно станет меньше 10. Тогда функция вернет значение.
И последняя функция, которая просто вычисляет сумму цифр внутри числа:
[cpp]
int SumOfDigits(int N)
{
int d=0, sum = 0;
while (N != 0)
{
d = N % 10;
sum += d;
N = N / 10;
}
return sum;
}
[/cpp]
Принимает целое число N. И пока N не станет равным нулю делит это число на 10 (основание системы счисления) и прибавляет остаток от деления к сумме, после чего делит N на 10 еще раз, но в этот раз уже записывает не остаток от деления, а целую часть. Так как происходит округление, то рано или поздно это число станет равным нулю.
Рекурсивный вариант той же функции:
Примечание: опубликован лишь код функции, так как ее вызов идентичен описанному выше.
[cpp]
int RootOfNumber(int N)
{
int d, sum = 0;
while (N != 0)
{
d = N % 10;
sum = sum + d;
N = N / 10;
}
if(sum<10)
{
return sum;
}
else
{
RootOfNumber(sum);
}
}
[/cpp]
Фишка рекурсивных функций в том, что она вызывает сама себя внутри себя. В этом коде нет дополнительной функции, которая считала бы сумму, но код содержится внутри. Т.е сначала на функцию подается число, для которого хорошо бы посчитать корень, далее для этого числа считается сумма его чисел и проверяется условие выхода из рекурсии — является ли число однозначным, т.е меньше 10. Если да, то выходим из рекурсии и возвращаем число, иначе — вызываем еще раз эту же функцию, но уже с новой суммой.



























![Деление 1 на 7 в столбик. Здесь мы можем наблюдать остатки от деления [1, 3, 2, 6, 4, 5]. Деление 1 на 7 в столбик. Здесь мы можем наблюдать остатки от деления [1, 3, 2, 6, 4, 5].](https://habrastorage.org/getpro/habr/upload_files/740/9dc/7d8/7409dc7d835e4080385e4973454b939c.png)
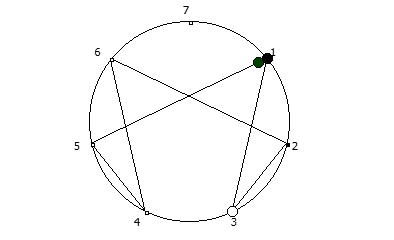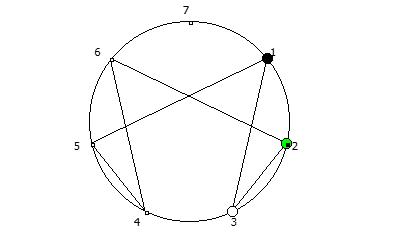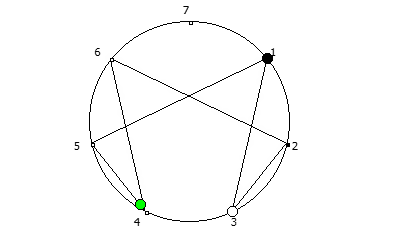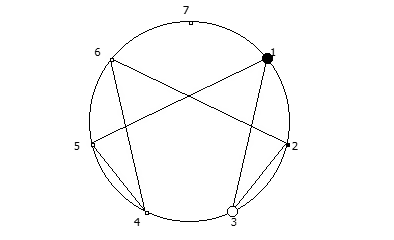





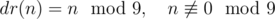
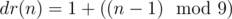

 Простой цифровой корень (ПЦК) натурального числа
Простой цифровой корень (ПЦК) натурального числа