Числовая окружность
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac<π><2>, frac<π><3>, frac<7π><4>, 10π, -frac<29π><6>)) разбирается в этой статье .
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки — положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).
Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.
Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).
Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?
Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.
При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.
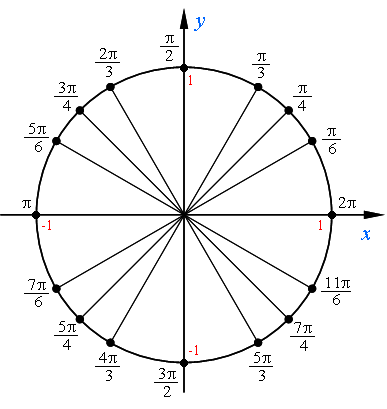
К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac<π><2>),(-frac<π><2>),(frac<3π><2>), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .
Что надо запомнить про числовую окружность:
Урок «Числовая окружность»
Краткое описание документа:
Видеоуроки относятся к наиболее эффективным средствам обучения, особенно таких школьных дисциплин, как математика. Поэтому автор данного материала собрал в единое целое только полезную, важную и грамотную информацию.
Данный урок рассчитан на 11:52 минут. Практически столько же времени требуется учителю на уроке для объяснения нового материала по данной теме. Хотя главным достоинством видеоурока будет тот факт, что обучающиеся будут внимательно слушать то, о чем говорит автор, не отвлекаясь на посторонние темы и разговоры. Ведь если обучающиеся будут слушать не внимательно, то упустят важный момент урока. А если материал будет объяснять учитель сам, то его обучающиеся смогут легко отвлечь от главного своими разговорами на отвлеченные темы. И, конечно, становится понятно, какой способ будет боле рационален.
Начало урока автор посвящает повторению тех функций, с которыми обучающиеся знакомились ранее в курсе алгебры. И первыми предлагается начать изучать – тригонометрические функции. Чтобы их рассматривать и изучать требуется новая математическая модель. И этой моделью становится числовая окружность, которая, как раз, и заявлена в теме урока. Для этого вводится понятие единичной окружности, задается ее определение. Далее на рисунке автор показывает все компоненты такой окружности, и что пригодится обучающимся для дальнейшего обучения. Дугами обозначаются четверти.
Затем автор предлагает рассмотреть числовую окружность. Здесь же он делает замечание, что удобнее использовать единичную окружность. На этой окружности показано, как получается точка M, если t>0, t 0(тэ больше нуля), то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ (а эм) длины t. Точка М и будет искомой точкой М(t) (эм от тэ).
1. Конспект для учителя по теме «Числовая окружность»
Что такое числовая окружность? Для чего она нужна?
Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Сегодня мы будем учиться использовать единичную окружность.
Для успешной работы с единичной окружностью нужно знать всего три вещи.
Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику.
Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность.
Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов.
- Какой угол называется углом поворота?
Угол поворота – это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.
- Какой угол называется углом в 1?
Угол в 1— это центральный угол, опирающийся на дугу, длина которой равна части окружности.
- Какой угол называется углом в 1 радиан?
Угол в 1 радиан — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
- Как выразить градусную меру угла в радианной?
- Как определить какой четверти принадлежит угол?
В зависимости от того в какой координатной четверти окажется начальный радиус, угол α называют углом этой четверти:
0 Главная
http://urokimatematiki.ru/urok-chislovaya-okruzhnost-831.html
http://shkolnik.pro/publikacii/matematika/desyati_klass/1-algebra-10-klass/chislovaya-okruzhnost-10/konspekt-dlya-uchitelya-po-teme-chisl-okr-t.html
В этом круге многие видят разные цифры, а некоторые вообще ничего. Давайте посмотрим, каково ваше предположение.
Сегодня мы подобрали для вас интересную оптическую иллюзию, которая успела покорить уже миллионы пользователей сети интернет.
Это довольно простой тест: иллюзия показывает число, скрытое в черно-сером полосатом круге. Задача – суметь увидеть числа внутри круга.
Поначалу это кажется лёгким заданием, но каждый последующий взгляд на головоломку показывает её сложность. Тот факт, что полосы расположены неровными спиралями, ещё больше усложняет вычисление чисел.
Взгляните сами и посмотрите, сможете ли вы найти ответ. Вы видите цифру?
Загрузка …
Всё ещё не можете найти правильный ответ?
Что же, хотите верьте – хотите нет, но здесь спрятано всего 7 цифр, и ответ таков: 3452839.
Вы всё правильно увидели? Если да – с вашей внимательностью всё в порядке.
Если нет, не волнуйтесь, вы не одиноки. Вот некоторые из самых забавных ответов на умопомрачительную головоломку, найденные на просторах интернета!
— «Я вижу только 528. Что-то не так с моим зрением?» (Елизавета).
— «В чём смысл этого?» (Евгений).
— «Я уже видел это раньше. Если развернуть изображение на весь экран и посмотреть на точку в центре в течение 60 секунд, затем посмотреть на потолок, то можно увидеть слово «легковерный» (Мария).
— «Я также видел только 45283. У меня дегенерация жёлтого пятна, интересно, влияет ли это на то, чего я не вижу» (Ирина).
— «Честно говоря, первые 3 цифры сложно рассмотреть. Не могу ничего с этим поделать. Легче увидеть, если покачать изображение вверх и вниз, но я не знаю почему» (Анатолий).
— Спасибо, что устроили мне экзамен, чтобы узнать, как сейчас поживает мой глаз☺» (Инна).
А какое число увидели вы? Сложно было его увидеть или запомнить? Поделитесь с нами своим опытом!
Также рекомендуем вам пройти ещё один интересный тест: Могут ли ваши глаза различать оттенки цвета?
Есть несколько способов сделать цифру в кружке.
1 способ
1) Поставьте курсор в то место документа Ворд, куда нужно вставить цифру.
2) На панели инструментов «Вставка» нажмите на «Символ», а затем — на «Другие символы».
3) В окне символов выберите «Wingdings 2».
4) Здесь и находятся нужные нам цифры в кружках — просто щёлкаем два раза на нужной цифре, и она вставится в документ.
2 способ
Можно воспользоваться Alt-кодами.
Для цифр в круге Alt-коды будут:
9312 — это ①.
9313 — это ②.
9314 — это ③.
.
9331 — это ⑳.
Эти коды вводятся так:
1) Сначала нажмите на клавишу Num Lock, чтобы включить цифровую клавиатуру (иначе ничего не получится).
2) Зажмите клавишу «Alt».
3) Последовательно нажмите нужные цифры. Например, для ⑩ это будет 9 3 2 1.
3 способ
Можно воспользоваться специальными фигурами.
1) На панели инструментов «Вставка» нажмите на «Фигуры» и выберите «Овал».
2) Теперь зажмите «Shift» (чтобы рисовался именно круг, а не овал) и нарисуйте круг нужных вам размеров.
3) Щёлкните на фигуре правой кнопкой мыши и в контекстном меню выберите «Добавить текст».
4) Печатаем цифру.
5) Теперь остаётся немного поменять шрифт, отступы и интервалы, чтобы всё было красиво.
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac{π}{2}, frac{π}{3}, frac{7π}{4}, 10π, -frac{29π}{6})) разбирается в этой статье.
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам, расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки — положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π): ( frac{π}{2}),(-frac{π}{2}),(frac{3π}{2}),(2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье).

Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
(t_0+2πn), (n∈Z),
где (t_0) — любое значение это точки.
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео.
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь.
Что надо запомнить про числовую окружность:
Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
Содержание
- Длина числовой окружности равна (2π) или примерно (6,28).
- Какие точки соответствуют числам (1), (2) и т.д?
- Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
- Главное свойство числовой окружности
- Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
- Все значения одной точки на числовой окружности можно записать с помощью формулы:
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac<π><2>, frac<π><3>, frac<7π><4>, 10π, -frac<29π><6>)) разбирается в этой статье .
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки — положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).
Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?
Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.
При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.
К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac<π><2>),(-frac<π><2>),(frac<3π><2>), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.
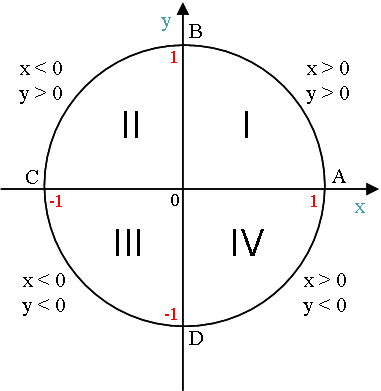
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значения x и y в четвертях числовой окружности:
x 0, y Основные величины числовой окружности:
Величина
в радианах
Величина
в радиусах
Имена и местонахождение основных точек числовой окружности:
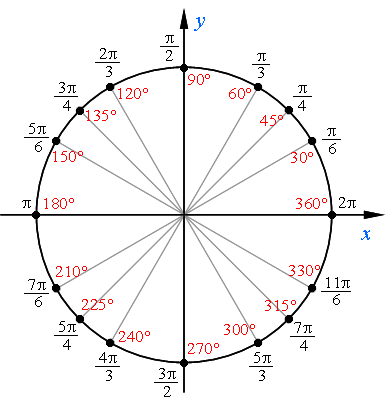
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).
Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.
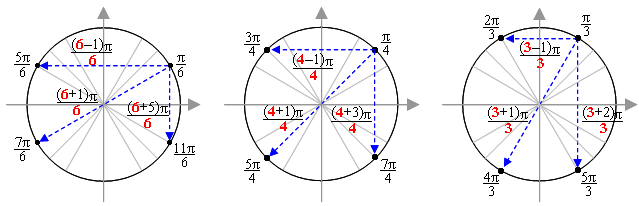
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.
Отсюда формула:
Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:
M(t) = M(t + 2πk),
где k ∈ Z.
Число k называется параметром.
Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):









Числовая окружность
Изучая курс алгебры 7—9-го классов, мы до сих пор имели дело с алгебраическими функциями, т.е. функциями, заданными аналитически выражениями, в записи которых использовались алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение квадратного корня). Но математические модели реальных ситуаций часто бывают связаны с функциями другого типа, не алгебраическими. С первыми представителями класса неалгебраических функций — тригонометрическими функциями — мы познакомимся в этой главе. Более детально изучать тригонометрические функции и другие виды неалгебраических функций (показательные и логарифмические) вам предстоит в старших классах.
Для введения тригонометрических функций нам понадобится новая математическая модель — числовая окружность, с которой вы до сих пор не встречались, зато хорошо знакомы с числовой прямой. Напомним, что числовая прямая — это прямая, на которой заданы начальная точка О, масштаб (единичный отрезок) и положительное направление. Любое действительное число мы можем сопоставить с точкой на прямой и обратно.
Как по числу х найти на прямой соответствующую точку М? Числу 0 соответствует начальная точка О. Если х > 0, то, двигаясь по прямой из точки 0 в положительном направлении, нужно пройти п^ть длиной х; конец этого пути и будет искомой точкой М(х). Если х 0, то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь длиной и конечная точка М этого пути и будет искомой точкой: М = М(x);