Как найти цикл отрицательного веса в графе

Задача:
Для заданного взвешенного графа найти кратчайшие пути из заданной вершины до всех остальных вершин.
В случае, когда в графе содержатся циклы с отрицательным суммарным весом, достижимые из , сообщить, что кратчайших путей не существует.

Содержание

  • 1 Введение
  • 2 Псевдокод
  • 3 Корректность
  • 4 Реализация алгоритма и ее корректность
  • 5 Сложность
  • 6 Нахождение отрицательного цикла
  • 7 Источники информации

Введение

Количество путей длины рёбер можно найти с помощью метода динамического программирования.
Пусть — количество путей длины рёбер, заканчивающихся в вершине . Тогда .

Аналогично посчитаем пути кратчайшей длины. Пусть — стартовая вершина. Тогда , при этом , а

Лемма:

Если существует кратчайший путь от до , то

Доказательство:
Пусть кратчайший путь состоит из ребер, тогда корректность формулы следует из динамики, приведенной ниже.

Псевдокод

Используя приведенные формулы, алгоритм можно реализовать методом динамического программирования. 

 for k = 0 to                                            // вершины нумеруются с единицы
    for 
       for 
          d[k + 1][v] = min(d[k + 1][v], d[k][u] + )     //  — вес ребра uv

Также релаксацию можно свести к одномерному случаю, если не хранить длину пути в рёбрах. Одномерный массив будем обозначать , тогда

Корректность

Лемма:

Пусть — взвешенный ориентированный граф, — стартовая вершина.
Тогда после завершения итераций цикла выполняется неравенство .
Доказательство:

Воспользуемся индукцией по :

База индукции

При выполнено:

Индукционный переход

Сначала докажем, что .
Пусть после итерации выполняется для всех .
Тогда после итераций .
Переходим ко второму неравенству.
Теперь возможно два случая:

Рассмотрим 1 случай:

2 случай расписывается аналогично.

Таким образом переход выполнен и выполняется.

Реализация алгоритма и ее корректность

bool fordBellman(s):
    for 
        d[v] = 
    d[s] = 0
    for i = 0 to 
        for 
            if d[v] > d[u] +      //  — вес ребра uv
                d[v] = d[u] + 
    for 
        if d[v] > d[u] + 
            return false
    return true

В этом алгоритме используется релаксация, в результате которой уменьшается до тех пор, пока не станет равным .
— оценка веса кратчайшего пути из вершины в каждую вершину .
— фактический вес кратчайшего пути из в вершину .

Лемма:

Пусть — взвешенный ориентированный граф, — стартовая вершина. Тогда после завершения итераций цикла для всех вершин, достижимых из , выполняется равенство .
Доказательство:

Рассмотрим произвольную вершину , достижимую из .
Пусть , где , — кратчайший ациклический путь из в . Путь содержит не более ребер. Поэтому .

Докажем следующее утверждение:

После итераций первого цикла алгоритма,

Воспользуемся индукцией по :

База индукции

Перед первой итерацией утверждение очевидно выполнено:

Индукционный переход

Пусть после итераций, верно что . Так как принадлежит кратчайшему пути от до , то . Во время итерации релаксируется ребро , следовательно по завершению итерации будет выполнено

.
Ясно, что , поэтому верно что после итерации .
Индукционный переход доказан.

Итак, выполнены равенства .

Теорема:

Пусть — взвешенный ориентированный граф, — стартовая вершина. Если граф не содержит отрицательных циклов, достижимых из вершины , то алгоритм возвращает и для всех . Если граф содержит отрицательные циклы, достижимые из вершины , то алгоритм возвращает .
Доказательство:

Пусть граф не содержит отрицательных циклов, достижимых из вершины .

Тогда если вершина достижима из , то по лемме . Если вершина не достижима из , то из несуществования пути.

Теперь докажем, что алгоритм вернет значение .

После выполнения алгоритма верно, что для всех , значит ни одна из проверок не вернет значения .

Пусть граф содержит отрицательный цикл , где , достижимый из вершины . Тогда .

Предположим, что алгоритм возвращает , тогда для выполняется .

Просуммируем эти неравенства по всему циклу: .

Из того, что следует, что .

Получили, что , что противоречит отрицательности цикла .

Сложность

Инициализация занимает времени, каждый из проходов требует времени, обход по всем ребрам для проверки наличия отрицательного цикла занимает времени. Значит алгоритм Беллмана-Форда работает за времени.

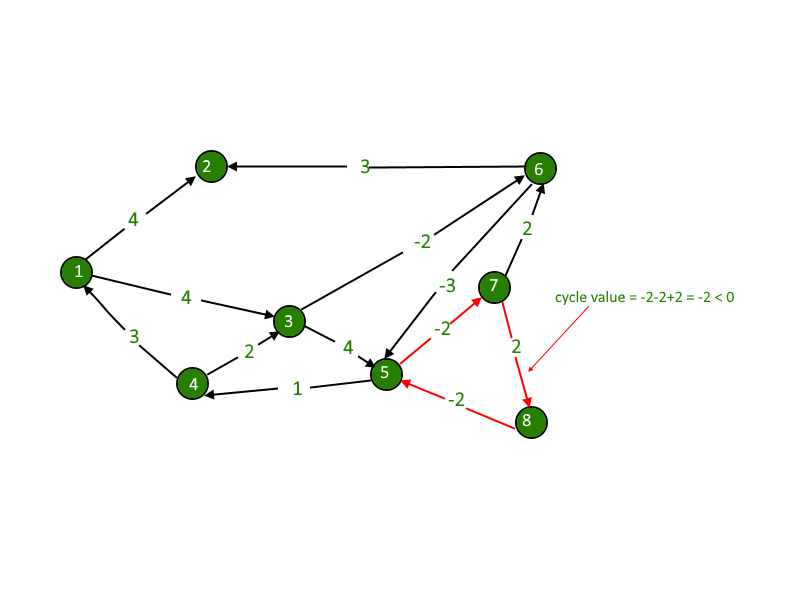
Нахождение отрицательного цикла

Приведенная выше реализация позволяет определить наличие в графе цикла отрицательного веса. Чтобы найти сам цикл, достаточно хранить вершины, из которых производится релаксация.

Если после итерации найдется вершина , расстояние до которой можно уменьшить, то эта вершина либо лежит на каком-нибудь цикле отрицательного веса, либо достижима из него. Чтобы найти вершину, которая лежит на цикле, можно раз пройти назад по предкам из вершины . Так как наибольшая длина пути в графе из вершин равна , то полученная вершина будет гарантированно лежать на отрицательном цикле.

Зная, что вершина лежит на цикле отрицательного веса, можно восстанавливать путь по сохраненным вершинам до тех пор, пока не встретится та же вершина . Это обязательно произойдет, так как в цикле отрицательного веса релаксации происходят по кругу. 

 int[] negativeCycle(s):
     for 
         d[v] = 
         p[v] = -1
     d[s] = 0
     for i = 1 to 
         for 
             if d[v] > d[u] + 
                 d[v] = d[u] + 
                 p[v] = u
     for 
         if d[v] > d[u] + 
             for i = 0 to 
                 v = p[v]
             u = v
             while u != p[v]
                 ans.add(v)            // добавим вершину к ответу
                 v = p[v]
             reverse(ans)
             break
   return ans

Источники информации

  • Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд — М.: Издательский дом «Вильямс», 2009. — ISBN 978-5-8459-0857-5.
  • MAXimal :: algo :: Алгоритм Форда-Беллмана
Источник

Improve Article

Save Article

Like Article

  • Read
  • Discuss

    • Improve Article

    Save Article

    Like Article

    We are given a directed graph. We need to compute whether the graph has a negative cycle or not. A negative cycle is one in which the overall sum of the cycle becomes negative.

    negative_cycle

    Negative weights are found in various applications of graphs. For example, instead of paying cost for a path, we may get some advantage if we follow the path.

    Examples: 

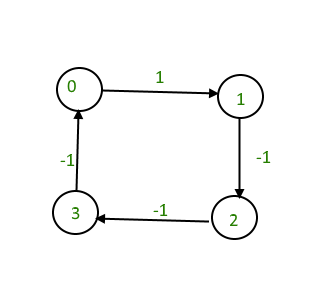
    Input : 4 4
        0 1 1
        1 2 -1
        2 3 -1
        3 0 -1

Output : Yes
The graph contains a negative cycle.

    cycle

    Recommended: Please solve it on “PRACTICE ” first, before moving on to the solution.

    The idea is to use Bellman-Ford Algorithm. 

    Below is an algorithm to find if there is a negative weight cycle reachable from the given source.

    1. Initialize distances from the source to all vertices as infinite and distance to the source itself as 0. Create an array dist[] of size |V| with all values as infinite except dist[src] where src is the source vertex.
    2. This step calculates the shortest distances. Do the following |V|-1 times where |V| is the number of vertices in the given graph. 
      1. Do the following for each edge u-v.
      2. If dist[v] > dist[u] + weight of edge uv, then update dist[v]. 
      3. dist[v] = dist[u] + weight of edge uv.
    3. This step reports if there is a negative weight cycle in the graph. Do the following for each edge u-v  
      1. If dist[v] > dist[u] + weight of edge uv, then the “Graph has a negative weight cycle” 

    The idea of step 3 is, step 2 guarantees the shortest distances if the graph doesn’t contain a negative weight cycle. If we iterate through all edges one more time and get a shorter path for any vertex, then there is a negative weight cycle.

    Implementation:

    C++

    #include <bits/stdc++.h>

    using namespace std;

    struct Edge {

        int src, dest, weight;

    };

    struct Graph {

        int V, E;

        struct Edge* edge;

    };

    struct Graph* createGraph(int V, int E)

    {

        struct Graph* graph = new Graph;

        graph->V = V;

        graph->E = E;

        graph->edge = new Edge[graph->E];

        return graph;

    }

    bool isNegCycleBellmanFord(struct Graph* graph,

                               int src)

    {

        int V = graph->V;

        int E = graph->E;

        int dist[V];

        for (int i = 0; i < V; i++)

            dist[i] = INT_MAX;

        dist[src] = 0;

        for (int i = 1; i <= V - 1; i++) {

            for (int j = 0; j < E; j++) {

                int u = graph->edge[j].src;

                int v = graph->edge[j].dest;

                int weight = graph->edge[j].weight;

                if (dist[u] != INT_MAX && dist[u] + weight < dist[v])

                    dist[v] = dist[u] + weight;

            }

        }

        for (int i = 0; i < E; i++) {

            int u = graph->edge[i].src;

            int v = graph->edge[i].dest;

            int weight = graph->edge[i].weight;

            if (dist[u] != INT_MAX && dist[u] + weight < dist[v])

                return true;

        }

        return false;

    }

    int main()

    {

        int V = 5;

        int E = 8;

        struct Graph* graph = createGraph(V, E);

        graph->edge[0].src = 0;

        graph->edge[0].dest = 1;

        graph->edge[0].weight = -1;

        graph->edge[1].src = 0;

        graph->edge[1].dest = 2;

        graph->edge[1].weight = 4;

        graph->edge[2].src = 1;

        graph->edge[2].dest = 2;

        graph->edge[2].weight = 3;

        graph->edge[3].src = 1;

        graph->edge[3].dest = 3;

        graph->edge[3].weight = 2;

        graph->edge[4].src = 1;

        graph->edge[4].dest = 4;

        graph->edge[4].weight = 2;

        graph->edge[5].src = 3;

        graph->edge[5].dest = 2;

        graph->edge[5].weight = 5;

        graph->edge[6].src = 3;

        graph->edge[6].dest = 1;

        graph->edge[6].weight = 1;

        graph->edge[7].src = 4;

        graph->edge[7].dest = 3;

        graph->edge[7].weight = -3;

        if (isNegCycleBellmanFord(graph, 0))

            cout << "Yes";

        else

            cout << "No";

        return 0;

    }

    Java

    import java.util.*;

    class GFG {

        static class Edge {

            int src, dest, weight;

        }

        static class Graph {

            int V, E;

            Edge edge[];

        }

        static Graph createGraph(int V, int E) {

            Graph graph = new Graph();

            graph.V = V;

            graph.E = E;

            graph.edge = new Edge[graph.E];

            for (int i = 0; i < graph.E; i++) {

                graph.edge[i] = new Edge();

            }

            return graph;

        }

        static boolean isNegCycleBellmanFord(Graph graph, int src) {

            int V = graph.V;

            int E = graph.E;

            int[] dist = new int[V];

            for (int i = 0; i < V; i++)

                dist[i] = Integer.MAX_VALUE;

            dist[src] = 0;

            for (int i = 1; i <= V - 1; i++) {

                for (int j = 0; j < E; j++) {

                    int u = graph.edge[j].src;

                    int v = graph.edge[j].dest;

                    int weight = graph.edge[j].weight;

                    if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v])

                        dist[v] = dist[u] + weight;

                }

            }

            for (int i = 0; i < E; i++) {

                int u = graph.edge[i].src;

                int v = graph.edge[i].dest;

                int weight = graph.edge[i].weight;

                if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v])

                    return true;

            }

            return false;

        }

        public static void main(String[] args) {

            int V = 5, E = 8;

            Graph graph = createGraph(V, E);

            graph.edge[0].src = 0;

            graph.edge[0].dest = 1;

            graph.edge[0].weight = -1;

            graph.edge[1].src = 0;

            graph.edge[1].dest = 2;

            graph.edge[1].weight = 4;

            graph.edge[2].src = 1;

            graph.edge[2].dest = 2;

            graph.edge[2].weight = 3;

            graph.edge[3].src = 1;

            graph.edge[3].dest = 3;

            graph.edge[3].weight = 2;

            graph.edge[4].src = 1;

            graph.edge[4].dest = 4;

            graph.edge[4].weight = 2;

            graph.edge[5].src = 3;

            graph.edge[5].dest = 2;

            graph.edge[5].weight = 5;

            graph.edge[6].src = 3;

            graph.edge[6].dest = 1;

            graph.edge[6].weight = 1;

            graph.edge[7].src = 4;

            graph.edge[7].dest = 3;

            graph.edge[7].weight = -3;

            if (isNegCycleBellmanFord(graph, 0))

                System.out.println("Yes");

            else

                System.out.println("No");

        }

    }

    Python3

    class Edge:

        def __init__(self):

            self.src = 0

            self.dest = 0

            self.weight = 0

    class Graph:

        def __init__(self):

            self.V = 0

            self.E = 0

            self.edge = None

    def createGraph(V, E):

        graph = Graph()

        graph.V = V;

        graph.E = E;

        graph.edge =[Edge() for i in range(graph.E)]

        return graph;

    def isNegCycleBellmanFord(graph, src):

        V = graph.V;

        E = graph.E;

        dist = [1000000 for i in range(V)];

        dist[src] = 0;

        for i in range(1, V):

            for j in range(E):

                u = graph.edge[j].src;

                v = graph.edge[j].dest;

                weight = graph.edge[j].weight;

                if (dist[u] != 1000000 and dist[u] + weight < dist[v]):

                    dist[v] = dist[u] + weight;

        for i in range(E):

            u = graph.edge[i].src;

            v = graph.edge[i].dest;

            weight = graph.edge[i].weight;

            if (dist[u] != 1000000 and dist[u] + weight < dist[v]):

                return True;

        return False;

    if __name__=='__main__':

        V = 5;

        E = 8;

        graph = createGraph(V, E);

        graph.edge[0].src = 0;

        graph.edge[0].dest = 1;

        graph.edge[0].weight = -1;

        graph.edge[1].src = 0;

        graph.edge[1].dest = 2;

        graph.edge[1].weight = 4;

        graph.edge[2].src = 1;

        graph.edge[2].dest = 2;

        graph.edge[2].weight = 3;

        graph.edge[3].src = 1;

        graph.edge[3].dest = 3;

        graph.edge[3].weight = 2;

        graph.edge[4].src = 1;

        graph.edge[4].dest = 4;

        graph.edge[4].weight = 2;

        graph.edge[5].src = 3;

        graph.edge[5].dest = 2;

        graph.edge[5].weight = 5;

        graph.edge[6].src = 3;

        graph.edge[6].dest = 1;

        graph.edge[6].weight = 1;

        graph.edge[7].src = 4;

        graph.edge[7].dest = 3;

        graph.edge[7].weight = -3;

        if (isNegCycleBellmanFord(graph, 0)):

            print("Yes")

        else:

            print("No")

    C#

    using System;

    using System.Collections;

    using System.Collections.Generic;

    class GFG {

        class Edge {

            public int src, dest, weight;

        }

        class Graph {

            public int V, E;

            public Edge []edge;

        }

        static Graph createGraph(int V, int E) {

            Graph graph = new Graph();

            graph.V = V;

            graph.E = E;

            graph.edge = new Edge[graph.E];

            for (int i = 0; i < graph.E; i++) {

                graph.edge[i] = new Edge();

            }

            return graph;

        }

        static bool isNegCycleBellmanFord(Graph graph, int src) {

            int V = graph.V;

            int E = graph.E;

            int[] dist = new int[V];

            for (int i = 0; i < V; i++)

                dist[i] = 1000000;

            dist[src] = 0;

            for (int i = 1; i <= V - 1; i++) {

                for (int j = 0; j < E; j++) {

                    int u = graph.edge[j].src;

                    int v = graph.edge[j].dest;

                    int weight = graph.edge[j].weight;

                    if (dist[u] != 1000000 && dist[u] + weight < dist[v])

                        dist[v] = dist[u] + weight;

                }

            }

            for (int i = 0; i < E; i++) {

                int u = graph.edge[i].src;

                int v = graph.edge[i].dest;

                int weight = graph.edge[i].weight;

                if (dist[u] != 1000000 && dist[u] + weight < dist[v])

                    return true;

            }

            return false;

        }

        public static void Main(string[] args) {

            int V = 5, E = 8;

            Graph graph = createGraph(V, E);

            graph.edge[0].src = 0;

            graph.edge[0].dest = 1;

            graph.edge[0].weight = -1;

            graph.edge[1].src = 0;

            graph.edge[1].dest = 2;

            graph.edge[1].weight = 4;

            graph.edge[2].src = 1;

            graph.edge[2].dest = 2;

            graph.edge[2].weight = 3;

            graph.edge[3].src = 1;

            graph.edge[3].dest = 3;

            graph.edge[3].weight = 2;

            graph.edge[4].src = 1;

            graph.edge[4].dest = 4;

            graph.edge[4].weight = 2;

            graph.edge[5].src = 3;

            graph.edge[5].dest = 2;

            graph.edge[5].weight = 5;

            graph.edge[6].src = 3;

            graph.edge[6].dest = 1;

            graph.edge[6].weight = 1;

            graph.edge[7].src = 4;

            graph.edge[7].dest = 3;

            graph.edge[7].weight = -3;

            if (isNegCycleBellmanFord(graph, 0))

                Console.Write("Yes");

            else

                Console.Write("No");

        }

    }

    Javascript

    <script>

    class Edge

    {

        constructor()

        {

            let src, dest, weight;

        }

    }

    class Graph

    {   

        constructor()

        {

            let V, E;

            let edge = [];

        }

    }

    function createGraph(V,E)

    {

        let graph = new Graph();

        graph.V = V;

        graph.E = E;

        graph.edge = new Array(graph.E);

        for(let i = 0; i < graph.E; i++)

        {

            graph.edge[i] = new Edge();

        }

        return graph;

    }

    function isNegCycleBellmanFord(graph, src)

    {

        let V = graph.V;

        let E = graph.E;

        let dist = new Array(V);

        for(let i = 0; i < V; i++)

            dist[i] = Number.MAX_VALUE;

        dist[src] = 0;

        for(let i = 1; i <= V - 1; i++)

        {

            for(let j = 0; j < E; j++)

            {

                let u = graph.edge[j].src;

                let v = graph.edge[j].dest;

                let weight = graph.edge[j].weight;

                if (dist[u] != Number.MAX_VALUE && dist[u] +

                               weight < dist[v])

                    dist[v] = dist[u] + weight;

            }

        }

        for(let i = 0; i < E; i++)

        {

            let u = graph.edge[i].src;

            let v = graph.edge[i].dest;

            let weight = graph.edge[i].weight;

            if (dist[u] != Number.MAX_VALUE &&

                dist[u] + weight < dist[v])

                return true;

        }

        return false;

    }

    let V = 5, E = 8;

    let graph = createGraph(V, E);

    graph.edge[0].src = 0;

    graph.edge[0].dest = 1;

    graph.edge[0].weight = -1;

    graph.edge[1].src = 0;

    graph.edge[1].dest = 2;

    graph.edge[1].weight = 4;

    graph.edge[2].src = 1;

    graph.edge[2].dest = 2;

    graph.edge[2].weight = 3;

    graph.edge[3].src = 1;

    graph.edge[3].dest = 3;

    graph.edge[3].weight = 2;

    graph.edge[4].src = 1;

    graph.edge[4].dest = 4;

    graph.edge[4].weight = 2;

    graph.edge[5].src = 3;

    graph.edge[5].dest = 2;

    graph.edge[5].weight = 5;

    graph.edge[6].src = 3;

    graph.edge[6].dest = 1;

    graph.edge[6].weight = 1;

    graph.edge[7].src = 4;

    graph.edge[7].dest = 3;

    graph.edge[7].weight = -3;

    if (isNegCycleBellmanFord(graph, 0))

        document.write("Yes");

    else

        document.write("No");

    </script>

    Time Complexity: O(VE), where V is the number of vertices and E is the number of edges in the graph.

    Space Complexity: O(V), where V is the number of vertices in the graph.

    How does it work? 
    As discussed, the Bellman-Ford algorithm, for a given source, first calculates the shortest distances which have at most one edge in the path. Then, it calculates the shortest paths with at-most 2 edges, and so on. After the i-th iteration of the outer loop, the shortest paths with at most i edges are calculated. There can be a maximum |V| – 1 edge on any simple path, that is why the outer loop runs |v| – 1 time. If there is a negative weight cycle, then one more iteration would give a short route.
     

    Detect a negative cycle in a Graph using Bellman Ford Algorithm

    How to handle a disconnected graph (If the cycle is not reachable from the source)? 
    The above algorithm and program might not work if the given graph is disconnected. It works when all vertices are reachable from source vertex 0.
    To handle disconnected graphs, we can repeat the process for vertices for which distance is infinite.

    Implementation:

    C++

    #include <bits/stdc++.h>

    using namespace std;

    struct Edge {

        int src, dest, weight;

    };

    struct Graph {

        int V, E;

        struct Edge* edge;

    };

    struct Graph* createGraph(int V, int E)

    {

        struct Graph* graph = new Graph;

        graph->V = V;

        graph->E = E;

        graph->edge = new Edge[graph->E];

        return graph;

    }

    bool isNegCycleBellmanFord(struct Graph* graph,

                               int src, int dist[])

    {

        int V = graph->V;

        int E = graph->E;

        for (int i = 0; i < V; i++)

            dist[i] = INT_MAX;

        dist[src] = 0;

        for (int i = 1; i <= V - 1; i++) {

            for (int j = 0; j < E; j++) {

                int u = graph->edge[j].src;

                int v = graph->edge[j].dest;

                int weight = graph->edge[j].weight;

                if (dist[u] != INT_MAX && dist[u] + weight < dist[v])

                    dist[v] = dist[u] + weight;

            }

        }

        for (int i = 0; i < E; i++) {

            int u = graph->edge[i].src;

            int v = graph->edge[i].dest;

            int weight = graph->edge[i].weight;

            if (dist[u] != INT_MAX && dist[u] + weight < dist[v])

                return true;

        }

        return false;

    }

    bool isNegCycleDisconnected(struct Graph* graph)

    {

        int V = graph->V;

        bool visited[V];

        memset(visited, 0, sizeof(visited));

        int dist[V];

        for (int i = 0; i < V; i++) {

            if (visited[i] == false) {

                if (isNegCycleBellmanFord(graph, i, dist))

                    return true;

                for (int i = 0; i < V; i++)

                    if (dist[i] != INT_MAX)

                        visited[i] = true;

            }

        }

        return false;

    }

    int main()

    {

        int V = 5;

        int E = 8;

        struct Graph* graph = createGraph(V, E);

        graph->edge[0].src = 0;

        graph->edge[0].dest = 1;

        graph->edge[0].weight = -1;

        graph->edge[1].src = 0;

        graph->edge[1].dest = 2;

        graph->edge[1].weight = 4;

        graph->edge[2].src = 1;

        graph->edge[2].dest = 2;

        graph->edge[2].weight = 3;

        graph->edge[3].src = 1;

        graph->edge[3].dest = 3;

        graph->edge[3].weight = 2;

        graph->edge[4].src = 1;

        graph->edge[4].dest = 4;

        graph->edge[4].weight = 2;

        graph->edge[5].src = 3;

        graph->edge[5].dest = 2;

        graph->edge[5].weight = 5;

        graph->edge[6].src = 3;

        graph->edge[6].dest = 1;

        graph->edge[6].weight = 1;

        graph->edge[7].src = 4;

        graph->edge[7].dest = 3;

        graph->edge[7].weight = -3;

        if (isNegCycleDisconnected(graph))

            cout << "Yes";

        else

            cout << "No";

        return 0;

    }

    Java

    import java.util.*;

    class GFG{

    static class Edge

    {

        int src, dest, weight;

    }

    static class Graph

    {

        int V, E;

        Edge edge[];

    }

    static Graph createGraph(int V, int E)

    {

        Graph graph = new Graph();

        graph.V = V;

        graph.E = E;

        graph.edge = new Edge[graph.E];

        for(int i = 0; i < graph.E; i++)

        {

            graph.edge[i] = new Edge();

        }

        return graph;

    }

    static boolean isNegCycleBellmanFord(Graph graph,

                                         int src,

                                         int dist[])

    {

        int V = graph.V;

        int E = graph.E;

        for(int i = 0; i < V; i++)

            dist[i] = Integer.MAX_VALUE;

        dist[src] = 0;

        for(int i = 1; i <= V - 1; i++)

        {

            for(int j = 0; j < E; j++)

            {

                int u = graph.edge[j].src;

                int v = graph.edge[j].dest;

                int weight = graph.edge[j].weight;

                if (dist[u] != Integer.MAX_VALUE &&

                    dist[u] + weight < dist[v])

                    dist[v] = dist[u] + weight;

            }

        }

        for(int i = 0; i < E; i++)

        {

            int u = graph.edge[i].src;

            int v = graph.edge[i].dest;

            int weight = graph.edge[i].weight;

            if (dist[u] != Integer.MAX_VALUE &&

                dist[u] + weight < dist[v])

                return true;

        }

        return false;

    }

    static boolean isNegCycleDisconnected(Graph graph)

    {

        int V = graph.V;

        boolean visited[] = new boolean[V];

        Arrays.fill(visited, false);

        int dist[] = new int[V];

        for(int i = 0; i < V; i++)

        {

            if (visited[i] == false)

            {

                if (isNegCycleBellmanFord(graph, i, dist))

                    return true;

                for(int j = 0; j < V; j++)

                    if (dist[j] != Integer.MAX_VALUE)

                        visited[j] = true;

            }

        }

        return false;

    }

    public static void main(String[] args)

    {

        int V = 5, E = 8;

        Graph graph = createGraph(V, E);

        graph.edge[0].src = 0;

        graph.edge[0].dest = 1;

        graph.edge[0].weight = -1;

        graph.edge[1].src = 0;

        graph.edge[1].dest = 2;

        graph.edge[1].weight = 4;

        graph.edge[2].src = 1;

        graph.edge[2].dest = 2;

        graph.edge[2].weight = 3;

        graph.edge[3].src = 1;

        graph.edge[3].dest = 3;

        graph.edge[3].weight = 2;

        graph.edge[4].src = 1;

        graph.edge[4].dest = 4;

        graph.edge[4].weight = 2;

        graph.edge[5].src = 3;

        graph.edge[5].dest = 2;

        graph.edge[5].weight = 5;

        graph.edge[6].src = 3;

        graph.edge[6].dest = 1;

        graph.edge[6].weight = 1;

        graph.edge[7].src = 4;

        graph.edge[7].dest = 3;

        graph.edge[7].weight = -3;

        if (isNegCycleDisconnected(graph))

            System.out.println("Yes");

        else

            System.out.println("No");

    }

    }

    Python3

    def isNegCycleBellmanFord(src, dist):

        global graph, V, E

        for i in range(V):

            dist[i] = 10**18

        dist[src] = 0

        for i in range(1,V):

            for j in range(E):

                u = graph[j][0]

                v = graph[j][1]

                weight = graph[j][2]

                if (dist[u] != 10**18 and dist[u] + weight < dist[v]):

                    dist[v] = dist[u] + weight

        for i in range(E):

            u = graph[i][0]

            v = graph[i][1]

            weight = graph[i][2]

            if (dist[u] != 10**18 and dist[u] + weight < dist[v]):

                return True

        return False

    def isNegCycleDisconnected():

        global V, E, graph

        visited = [0]*V

        dist = [0]*V

        for i in range(V):

            if (visited[i] == 0):

                if (isNegCycleBellmanFord(i, dist)):

                    return True

                for i in range(V):

                    if (dist[i] != 10**18):

                        visited[i] = True

        return False

    if __name__ == '__main__':

        V = 5

        E = 8

        graph = [[0, 0, 0] for i in range(8)]

        graph[0][0] = 0

        graph[0][1] = 1

        graph[0][2] = -1

        graph[1][0] = 0

        graph[1][1] = 2

        graph[1][2] = 4

        graph[2][0] = 1

        graph[2][1] = 2

        graph[2][2] = 3

        graph[3][0] = 1

        graph[3][1] = 3

        graph[3][2] = 2

        graph[4][0] = 1

        graph[4][1] = 4

        graph[4][2] = 2

        graph[5][0] = 3

        graph[5][1] = 2

        graph[5][2] = 5

        graph[6][0] = 3

        graph[6][1] = 1

        graph[6][2] = 1

        graph[7][0] = 4

        graph[7][1] = 3

        graph[7][2] = -3

        if (isNegCycleDisconnected()):

            print("Yes")

        else:

            print("No")

    C#

    using System;

    using System.Collections.Generic;

    public class GFG

    {

      public

        class Edge

        {

          public

            int src, dest, weight;

        }

      public

        class Graph

        {

          public

            int V, E;

          public

            Edge []edge;

        }

      static Graph createGraph(int V, int E)

      {

        Graph graph = new Graph();

        graph.V = V;

        graph.E = E;

        graph.edge = new Edge[graph.E];

        for(int i = 0; i < graph.E; i++)

        {

          graph.edge[i] = new Edge();

        }

        return graph;

      }

      static bool isNegCycleBellmanFord(Graph graph,

                                        int src,

                                        int []dist)

      {

        int V = graph.V;

        int E = graph.E;

        for(int i = 0; i < V; i++)

          dist[i] = int.MaxValue;

        dist[src] = 0;

        for(int i = 1; i <= V - 1; i++)

        {

          for(int j = 0; j < E; j++)

          {

            int u = graph.edge[j].src;

            int v = graph.edge[j].dest;

            int weight = graph.edge[j].weight;

            if (dist[u] != int.MaxValue &&

                dist[u] + weight < dist[v])

              dist[v] = dist[u] + weight;

          }

        }

        for(int i = 0; i < E; i++)

        {

          int u = graph.edge[i].src;

          int v = graph.edge[i].dest;

          int weight = graph.edge[i].weight;

          if (dist[u] != int.MaxValue &&

              dist[u] + weight < dist[v])

            return true;

        }

        return false;

      }

      static bool isNegCycleDisconnected(Graph graph)

      {

        int V = graph.V;

        bool []visited = new bool[V];

        int []dist = new int[V];

        for(int i = 0; i < V; i++)

        {

          if (visited[i] == false)

          {

            if (isNegCycleBellmanFord(graph, i, dist))

              return true;

            for(int j = 0; j < V; j++)

              if (dist[j] != int.MaxValue)

                visited[j] = true;

          }

        }

        return false;

      }

      public static void Main(String[] args)

      {

        int V = 5, E = 8;

        Graph graph = createGraph(V, E);

        graph.edge[0].src = 0;

        graph.edge[0].dest = 1;

        graph.edge[0].weight = -1;

        graph.edge[1].src = 0;

        graph.edge[1].dest = 2;

        graph.edge[1].weight = 4;

        graph.edge[2].src = 1;

        graph.edge[2].dest = 2;

        graph.edge[2].weight = 3;

        graph.edge[3].src = 1;

        graph.edge[3].dest = 3;

        graph.edge[3].weight = 2;

        graph.edge[4].src = 1;

        graph.edge[4].dest = 4;

        graph.edge[4].weight = 2;

        graph.edge[5].src = 3;

        graph.edge[5].dest = 2;

        graph.edge[5].weight = 5;

        graph.edge[6].src = 3;

        graph.edge[6].dest = 1;

        graph.edge[6].weight = 1;

        graph.edge[7].src = 4;

        graph.edge[7].dest = 3;

        graph.edge[7].weight = -3;

        if (isNegCycleDisconnected(graph))

          Console.WriteLine("Yes");

        else

          Console.WriteLine("No");

      }

    }

    Javascript

    <script>

        class Edge

        {

            constructor()

            {

                let src, dest, weight;

            }

        }

        class Graph

        {

            constructor()

            {

                let V, E;

                let edge=[];

            }

        }

        function createGraph(V,E)

        {

            let graph = new Graph();

            graph.V = V;

               graph.E = E;

            graph.edge = new Array(graph.E);

        for(let i = 0; i < graph.E; i++)

        {

            graph.edge[i] = new Edge();

        }

        return graph;

        }

    function isNegCycleBellmanFord(graph,src,dist)

    {

        let V = graph.V;

        let E = graph.E;

        for(let i = 0; i < V; i++)

            dist[i] = Number.MAX_VALUE;

        dist[src] = 0;

        for(let i = 1; i <= V - 1; i++)

        {

            for(let j = 0; j < E; j++)

            {

                let u = graph.edge[j].src;

                let v = graph.edge[j].dest;

                let weight = graph.edge[j].weight;

                if (dist[u] != Number.MAX_VALUE &&

                    dist[u] + weight < dist[v])

                    dist[v] = dist[u] + weight;

            }

        }

        for(let i = 0; i < E; i++)

        {

            let u = graph.edge[i].src;

            let v = graph.edge[i].dest;

            let weight = graph.edge[i].weight;

            if (dist[u] != Number.MAX_VALUE &&

                dist[u] + weight < dist[v])

                return true;

        }

        return false;

    }

    function isNegCycleDisconnected(graph)

    {

        let V = graph.V;

        let visited = new Array(V);

        for(let i=0;i<V;i++)

        {

            visited[i]=false;

        }

        let dist = new Array(V);

        for(let i = 0; i < V; i++)

        {

            if (visited[i] == false)

            {

                if (isNegCycleBellmanFord(graph, i, dist))

                    return true;

                for(let j = 0; j < V; j++)

                    if (dist[j] != Number.MAX_VALUE)

                        visited[j] = true;

            }

        }

        return false;

    }

    let V = 5, E = 8;

    let graph = createGraph(V, E);

    graph.edge[0].src = 0;

    graph.edge[0].dest = 1;

    graph.edge[0].weight = -1;

    graph.edge[1].src = 0;

    graph.edge[1].dest = 2;

    graph.edge[1].weight = 4;

    graph.edge[2].src = 1;

    graph.edge[2].dest = 2;

    graph.edge[2].weight = 3;

    graph.edge[3].src = 1;

    graph.edge[3].dest = 3;

    graph.edge[3].weight = 2;

    graph.edge[4].src = 1;

    graph.edge[4].dest = 4;

    graph.edge[4].weight = 2;

    graph.edge[5].src = 3;

    graph.edge[5].dest = 2;

    graph.edge[5].weight = 5;

    graph.edge[6].src = 3;

    graph.edge[6].dest = 1;

    graph.edge[6].weight = 1;

    graph.edge[7].src = 4;

    graph.edge[7].dest = 3;

    graph.edge[7].weight = -3;

    if (isNegCycleDisconnected(graph))

        document.write("Yes");

    else

        document.write("No");

    </script>

     Time complexity : O(E*V2), where V is the number of vertices and E is the number of edges.

    Space Complexity : O(V + E) which is the space required to store the graph. 

    Detecting negative cycle using Floyd Warshall

    This article is contributed by kartik. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks. 

    Last Updated :
    16 May, 2023

    Like Article

    Save Article

    Источник

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    31

    32

    33

    34

    35

    36

    37

    38

    39

    40

    41

    42

    43

    44

    45

    46

    47

    48

    49

    50

    51

    52

    53

    54

    55

    56

    57

    58

    59

    60

    61

    62

    63

    64

    65

    66

    67

    68

    69

    70

    71

    72

    73

    74

    75

    76

    77

    78

    79

    80

    81

    82

    83

    84

    85

    86

    87

    88

    89

    90

    91

    92

    93

    94

    95

    96

    97

    98

    99

    100

    101

    102

    103

    104

    105

    106

    107

    108

    109

    110

    111

    112

    113

    114

    115

    116

    117

    118

    119

    120

    121

    122

    123

    124

    125

    import java.util.ArrayList;

    import java.util.Arrays;

    import java.util.List;

    import java.util.stream.IntStream;

    // Класс для хранения ребра Graph

    class Edge

    {

        // ребро от `source` к `dest`, имеющее вес, равный `weight`

        int source, dest, weight;

        Edge(int source, int dest, int weight)

        {

            this.source = source;

            this.dest = dest;

            this.weight = weight;

        }

    }

    class Main

    {

        // Определяем бесконечность как максимальное значение целого числа

        private static final int INF = Integer.MAX_VALUE;

        // Функция для запуска алгоритма Беллмана-Форда из заданного источника

        public static boolean bellmanFord(List<Edge> edges, int source, int n)

        {

            // cost[] хранит информацию о кратчайшем пути

            int[] cost = new int[n];

            // Изначально все вершины, кроме исходной, весят бесконечность

            Arrays.fill(cost, INF);

            cost[source] = 0;

            int u, v, w;

            // Шаг релаксации (выполнить V-1 раз)

            for (int k = 1; k < n; k++)

            {

                for (Edge e: edges)

                {

                    // ребро от `u` до `v` с весом `w`

                    u = e.source;

                    v = e.dest;

                    w = e.weight;

                    // если стоимость до пункта назначения `u` может быть

                    // укорачивается за счет ребра (u, v)

                    if (cost[u] != INF && cost[u] + w < cost[v])

                    {

                        // обновить стоимость до нового меньшего значения

                        cost[v] = cost[u] + w;

                    }

                }

            }

            // Выполнить шаг релаксации еще раз в n-й раз, чтобы

            // проверка циклов с отрицательным весом

            for (Edge e: edges)

            {

                // ребро от `u` до `v` с весом `w`

                u = e.source;

                v = e.dest;

                w = e.weight;

                // если стоимость пути к месту назначения `u` можно сократить, взяв преимущество (u, v)

                if (cost[u] != INF && cost[u] + w < cost[v]) {

                    return true;

                }

            }

            return false;

        }

        public static boolean hasNegativeWeightCycle(int[][] adjMatrix)

        {

            // базовый вариант

            if (adjMatrix == null || adjMatrix.length == 0) {

                return false;

            }

            // создаем список для хранения ребер Graph

            List<Edge> edges = new ArrayList<>();

            // общее количество узлов в Graph

            int n = adjMatrix.length;

            for (int v = 0; v < n; v++)

            {

                for (int u = 0; u < n; u++)

                {

                    if (adjMatrix[v][u] != 0 && adjMatrix[v][u] != INF) {

                        edges.add(new Edge(v, u, adjMatrix[v][u]));

                    }

                }

            }

            // Запускаем алгоритм Беллмана-Форда из каждой вершины как исходной

            // и проверяем цикл с отрицательным весом

            if (IntStream.range(0, n).anyMatch(i -> bellmanFord(edges, i, n))) {

                return true;

            }

            return false;

        }

        public static void main(String[] args)

        {

            // представление смежности матрицы

            int[][] adjMatrix =

            {

                { 0,   INF, —2,   INF },

                { 4,   0,    —3,   INF },

                { INF, INF,  0,      2 },

                { INF, —1,   INF, 0 }

            };

            boolean result = hasNegativeWeightCycle(adjMatrix);

            if (result) {

                System.out.println(«Negative-weight cycle found»);

            } else {

                System.out.println(«Negative-weight cycle doesn’t exist»);

            }

        }

    }
    Источник
    title authors weight draft

    Нахождение отрицательного цикла

    Максим Иванов

    6

    true

    Дан ориентированный взвешенный граф G с n вершинами и m рёбрами. Требуется найти в нём любой цикл отрицательного веса, если таковой имеется.

    При другой постановке задачи — требуется найти все пары вершин такие, что между ними существует путь сколько угодно малой длины.

    Эти два варианта задачи удобно решать разными алгоритмами, поэтому ниже будут рассмотрены оба из них.

    Одна из распространённых «жизненных» постановок этой задачи — следующая: известны курсы валют, т.е. курсы перевода из одной валюты в другую. Требуется узнать, можно ли некоторой последовательностью обменов получить выгоду, т.е. стартовав с одной единицы какой-либо валюты, получить в итоге больше чем одну единицу этой же валюты.

    Решение с помощью алгоритма Форда-Беллмана
    Алгоритм Форда-Беллмана позволяет проверить наличие или отсутствие цикла отрицательного веса в графе, а при его наличии — найти один из таких циклов.

    Не будем вдаваться здесь в подробности (которые описаны в статье по алгоритму Форда-Беллмана), а приведём лишь итог — то, как работает алгоритм.

    Делается n итераций алгоритма Форда-Беллмана, и если на последней итерации не произошло никаких изменений — то отрицательного цикла в графе нет. В противном случае возьмём вершину, расстояние до которой изменилось, и будем идти от неё по предкам, пока не войдём в цикл; этот цикл и будет искомым отрицательным циклом.

    Реализация:

    struct edge {
    int a, b, cost;
    };

    int n, m;
    vector e;
    const int INF = 1000000000;

    void solve() {
    vector d (n);
    vector p (n, -1);
    int x;
    for (int i=0; i<n; ++i) {
    x = -1;
    for (int j=0; j<m; ++j)
    if (d[e[j].b] > d[e[j].a] + e[j].cost) {
    d[e[j].b] = max (-INF, d[e[j].a] + e[j].cost);
    p[e[j].b] = e[j].a;
    x = e[j].b;
    }
    }

    if (x == -1)
	cout << "No negative cycle found.";
else {
	int y = x;
	for (int i=0; i<n; ++i)
		y = p[y];

	vector<int> path;
	for (int cur=y; ; cur=p[cur]) {
		path.push_back (cur);
		if (cur == y && path.size() > 1)  break;
	}
	reverse (path.begin(), path.end());

	cout << "Negative cycle: ";
	for (size_t i=0; i<path.size(); ++i)
		cout << path[i] << ' ';
}

    }
    Решение с помощью алгоритма Флойда-Уоршелла
    Алгоритм Флойда-Уоршелла позволяет решать вторую постановку задачи — когда надо найти все пары вершин (i,j), между которыми кратчайшего пути не существует (т.е. он имеет бесконечно малую величину).

    Опять же, более подробные объяснения содержатся в описании алгоритма Флойда-Уоршелла, а здесь мы приведём только итог.

    После того, как алгоритм Флойда-Уоршелла отработает для входного графа, переберём все пары вершин (i,j), и для каждой такой пары проверим, бесконечно мал кратчайший путь из i в j или нет. Для этого переберём третью вершину t, и если для неё оказалось d[t][t]<0 (т.е. она лежит в цикле отрицательного веса), а сама она достижима из i и из неё достижима j — то путь (i,j) может иметь бесконечно малую длину.

    Реализация:

    for (int i=0; i<n; ++i)
    for (int j=0; j<n; ++j)
    for (int t=0; t<n; ++t)
    if (d[i][t] < INF && d[t][t] < 0 && d[t][j] < INF)
    d[i][j] = -INF;

    Источник

    Материал из Algocode wiki

    Перейти к: навигация, поиск

    Содержание

    • 1 Задача
      • 1.1 Ориентированность
    • 2 Динамическое программирование
    • 3 Переходим от вершин к рёбрам
    • 4 Избавляемся от одного из измерений
    • 5 Оставляем только один массив
    • 6 Ускоряем алгоритм (Алгоритм SPFA)
    • 7 Форд-Беллман с random_shuffle
    • 8 Поиск циклов отрицательного веса
      • 8.1 Теорема
      • 8.2 Восстановление цикла отрицательного веса
      • 8.3 Как определить кратчайшие расстояния до всех вершин с учётом отрицательных циклов

    Задача

    Дан ориентированный граф $G=(V, E)$ с выделенной вершиной $s$. Веса рёбер в графе могут быть любыми. Надо для каждой вершины найти кратчайшее расстояние до неё от $s$.

    Ориентированность

    Ориентированность графа важна, потому что поиск кратчайших путей в неориентированном графе с отрицательными весами рёбер не решается с помощью алгоритма Форда-Беллмана. Но можно свести к поиску паросочетания минимальной стоимости в графе (необязательно двудольном). Подробнее можно почитать тут

    Динамическое программирование

    Решим эту задачу с помощью динамического программирования:

    • $sp[k][v]$ — кратчайшее растояние от $s$ до $v$ по путям, в которых $k$ рёбер.
    • Начальные значения
      • $ sp[0][s] = 0 $
      • $ sp[0][V setminus {s} ] = INF $
      • $ sp[1…|V|][*] = INF $
    • $ sp[k][v] = min_{u in N(v)} sp[k-1][u] + w(u, v) $
    • Порядок пересчёта:
     
for (int k = 0; k < vertices_count; ++k) {
  for (int v = 0; v < vertices_count; ++v) {
    // ...
  }
}
    • Ответ: $dist[v] = min_{k} sp[k][v]$
    • Восстановление ответа: либо запоминаем для каждого состояния, из какого пришли, либо заново перебираем

    Переходим от вершин к рёбрам

    Заметим, что цикл по вершинам, внутри которого перебираются соседи, можно заменить на цикл по рёбрам и получить 

     
void relax(int& old_value, int new_value) {
  old_value = min(old_value, new_value);
}

// Инициализация динамики
for (int k = 1; k < vertices_count; ++k) {
  for (auto [from, to, w] : edges) {
    relax(sp[k][to], sp[k-1][from] + w); 
  }
}

    Избавляемся от одного из измерений

    Мы получили решение, в котором используется массив размера $|V| times |V|$. Мы можем изменить это и получить 2 массива длины $|V|$ — достаточно заметить, что для подсчёта $sp[k][*]$ достаточно знать $sp[k-1][*]$, поэтому нам достаточно хранить только 2 последних слоя динамики.

    Оставляем только один массив

    В предыдущем пункте можно отказаться от двух массивов и оставить только $sp[v]$. Тогда
    $sp[v] = min_{u in N(v)} sp[u] + w(u, v)$. Однако, теперь значение, хранящееся в $sp[v]$ потеряет то значение, которое мы ему придавали раньше, потому что теперь при пересчёте слоя динамики мы можем воспользоваться значениями из нового слоя.

    Однако можно доказать, что за $k$ итераций в $sp[v]$ будут точно рассмотрены пути длины хотя бы $k$ рёбер от $s$ до $v$ (плюс, возможно, пути большей длины) (доказательство по индукции, упражнение читателю). Из этого следует, что за $|V| — 1$ итераций в $sp[v]$ будут рассмотрены все возможные пути из $s$ в $v$ $implies$ в $sp[v]$ будут будет хранится кратчайшее расстояние от $s$ до $v$.

    Ускоряем алгоритм (Алгоритм SPFA)

    Заметим следующее:

    1. Если на какой-то итерации внешнего цикла $sp[*]$ не изменился, то мы уже нашли все кратчайшие расстояния и можно прекратить наш алгоритм.
    2. Достаточно на каждом шаге рассматривать не все рёбра, а только те, у которых $sp$ изменился хотя бы для одного из концов.

    Эти немудрёные рассуждения приводят нас к следующему, окончательному коду: 

     
typedef int Vertex;
typedef long long dist_t;

bool try_relax(dist_t& old_value, dist_t new_value) {
  old_value = min(old_value, new_value);
  return old_value == new_value;
}

vector<dist_t> SPFA(int start) {
  vector<dist_t> sp(n, INF);
  sp[start] = 0;
  
  vector<Vertex> updated_vertices = { start };

  for (int k = 0; k < vertices_count; ++k) {
    vector<Vertex> newly_updated_vertices;

    for (auto v : updated_vertices) {
      for (auto [to, w] : edge_from[v]) {
        if (try_relax(sp[to], sp[v] + w)) {
          newly_updated_vertices.push_back(to);
        }
      }
    }
    
    if (newly_updated_vertices.empty()) {
      break;
    }

    updated_vertices.swap(newly_updated_vertices); 
  }

 return sp;
}

    Форд-Беллман с random_shuffle

    Если вы вдруг забыли про SPFA, то вы всё ещё можете ускорить ваш алгоритм Форда-Беллмана, случайным образом перемешивая рёбра. Подробнее: http://codeforces.com/blog/entry/58825

    Поиск циклов отрицательного веса

    Теорема

    В графе есть цикл отрицательного веса, достижимый из $s$ $iff$ после $|V|$-й итерации алгоритма $updated _ vertices$ непусто.

    Доказательство:

    $implies$: пусть в графе есть отрицательный цикл $v_0 rightarrow v_1 rightarrow dots rightarrow v_k = v_0$. Если в этом цикле есть такое ребро $v_i rightarrow v_{i+1}$, что на $|V|$-м шаге $sp[v_{i+1}] > sp[v_{i}] + w(v_{i}, v_{i+1})$, то $v_{i+1}$ окажется в $updated_ vertices$ и утверждение доказано. Пусть такого ребра нет, то есть
    $$
    forall i in [0 dots k]: sp[v_{i+1}] leq sp[v_{i}] + w(v_{i}, v_{i+1})
    $$

    Сложим эти неравенства и заметим, что $sum_{0 leq i leq k-1} sp[v_{i+1}] = sum_{0 leq i leq k-1} sp[v_{i}]$ (поскольку это одна и та же сумма, в которой сделали циклический сдвиг (помним, что $v_k = v_0$)).

    Значит, если сократить, получится:
    $$
    0 leq sum_{0 leq i leq k-1} w(v_{i}, v_{i+1})
    $$

    Или, другими словами, наш цикл вовсе не имеет отрицательный вес. Противоречие.

    $impliedby$: если на $|V|$-й итерации расстояние до какой-то вершины уменьшилось, то существует последовательность из хотя бы $|V|$ рёбер из $s$ в некоторую вершину $v$, вдоль которой расстояние меньше, чем то, что было на $(|V| — 1)$-й итерации. Поскольку рёбер не меньше, чем $|V|$, то в этой последовательности есть цикл. Если этот цикл имеет неотрицательный вес, то его можно выкинуть из последовательности и получить последовательность рёбер меньшей длины, которая должна была быть рассмотрена на предыдущих шагах алгоритма $implies$ на $|V|$-й итерации расстояние не могло уменьшиться вдоль последовательности с циклом. Значит, цикл всё-таки имеет отрицательный вес, а это ровно то, чего мы хотели. ∎

    Из леммы следует, что для проверки наличия цикла отрицательного веса достаточно запустить алгоритм на ещё одну итерацию и проверить, что ничего не изменилось.

    Восстановление цикла отрицательного веса

    Чтобы восстановить цикл достаточно для каждой вершины $v$ запоминать $prev[v]$ — вершину, через которую произошла последняя релаксация ребра в $v$. Тогда для восстановления цикла отрицательного веса достаточно взять любое из рёбер, которые прорелаксировались на $|V|$-м шаге и начать от них разматывать цикл.

    Корректность этого алгоритма следует из того, что любое ребро, которое прорелаксировалось на $|V|$-м шаге лежит на цикле отрицательного веса $implies$ пойдя из конца ребра мы вернёмся в него, пройдя по нашему циклу отрицательного веса.

    Как определить кратчайшие расстояния до всех вершин с учётом отрицательных циклов

    Заметим, что updated_vertices на $|V|$-м шаге содержит два типа вершин: те, которые лежат на цикле отрицательного веса и те, которые сами достижимы из какого-то цикла отрицательного веса. При этом из доказательства леммы выше мы знаем, что от каждого (!) цикла отрицательного веса в множестве будет хотя бы по одному представителю. Из этих двух наблюдений следует корректность и полнота следующего алгоритма:

    Запускаем Форда-Беллмана на $|V|$ шагов. Если на последнем шаге до вершины расстояние не поменялось, то оно и кратчайшее. Если поменялось, то до неё и до всех вершин, достижимых из неё, расстояние от стартовой вершины равно минус бесконечности. Чтобы найти все вершины с расстоянием минус бесконечность, достаточно запустить dfs из всех вершин, расстояние до которых уменьшилось на последней итерации алгоритма.

    Автор конспекта: Александр Гришутин

    По всем вопросам пишите в telegram @rationalex

    Источник

    Понравилась статья? Поделить с друзьями:
  • Как найти ребро квадрата если известна диагональ
  • Найди мне мультик как рисовать
  • Как найти старший коэффициент параболы по графику
  • Как найти предел обнаружения
  • Как найти правду в интернете