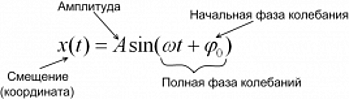Циклическая частота колебаний, теория и онлайн калькуляторы
Циклическая частота колебаний
Определение
Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.
Это скалярная физическая величина.
Циклическая частота при гармонических колебаниях
Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.
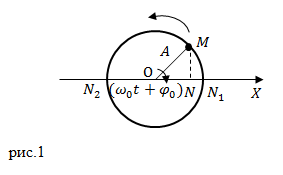
Самыми простыми колебаниями являются гармонические колебания. Рассмотрим следующую кинематическую модель. Точка M с постоянной по модулю скоростью ($v$) движется по окружности радиуса A. В этом случае ее угловую скорость обозначим ${omega }_0$, эта скорость постоянна (рис.1).
Проекция точки $M$ на диаметр окружности (точка $N$), на ось X, выполняет колебания от $N_1$ до $N_2 $и обратно. Такое колебание N ,будет гармоническим. Для описания колебания точки N необходимо записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол ${varphi }_0$. Через некоторый промежуток времени этот угол изменится на величину ${omega }_0t$ и будет равен ${omega }_0t+{varphi }_0$, тогда:
[x=A{cos left({omega }_0t+{varphi }_0right) }left(1right).]
Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.
Обратимся к выражению (1). Величина $A$ — это максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О — центра окружности), называется амплитудой колебаний.
Параметр ${omega }_0$ — циклическая частота колебаний. $varphi =({omega }_0t+{varphi }_0$) — фаза колебаний; ${varphi }_0$ — начальная фаза колебаний.
Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:
[{omega }_0=frac{?varphi }{partial t}=dot{varphi }left(2right).]
При ${varphi }_0=0$, уравнение колебаний (1) преобразуется к виду:
[x=A{cos left({omega }_0tright) }left(3right).]
Если начальная фаза колебаний равна ${varphi }_0=frac{pi }{2}$ , то получим уравнение колебаний в виде:
[x=A{{rm s}in left({omega }_0tright) }left(4right).]
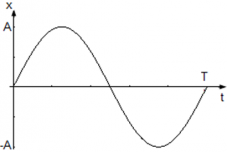
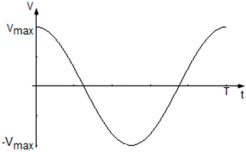
Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ — это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.
Циклическую частоту колебаний можно выразить через период (T) колебаний:
[{omega }_0=frac{2pi }{T}left(5right).]
Циклическую частоту с частотой $?$$?$ свяжем выражением:
[{omega }_0=2pi nu left(6right).]
Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Размерность циклической частоты:
[{dim left({omega }_0right)=frac{1}{t}, }]
где $t$ — время.
Частные случаи формул для вычисления циклической частоты
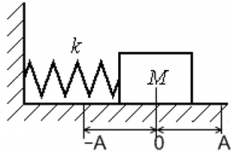
Груз на пружине (пружинный маятник — идеальная модель) совершает гармонические колебания с круговой частотой равной:
[{omega }_0=sqrt{frac{k}{m}}left(7right),]
$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.
Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:
[{omega }_0=sqrt{frac{mga}{J}}left(8right),]
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.
Примером физического маятника является математический маятник. Круговая частота его колебаний равна:
[{omega }_0=sqrt{frac{g}{l}}left(9right),]
где $l$ — длина подвеса.
Угловая частота затухающих колебаний находится как:
[omega =sqrt{{omega }^2_0-{delta }^2}left(10right),]
где $delta $ — коэффициент затухания; в случае с затуханием колебаний ${omega }_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Пример 1
Задание: Чему равна циклическая частота гармонических колебаний, если максимальная скорость материальной точки равна ${dot{x}}_{max}=10 frac{см}{с}$, а ее максимальное ускорение ${ddot{x}}_{max}=100 frac{см}{с^2}$?
Решение: Основой решения задачи станет уравнение гармонических колебаний точки, так как из условий, очевидно, что они происходят по оси X:
[x=A{cos left({omega }_0t+{varphi }_0right) }left(1.1right).]
Скорость колебаний найдем, используя уравнение (1.1) и кинематическую связь координаты $x$ и соответствующей компоненты скорости:
[v_x=frac{dx}{dt}=-A{omega }_0left({sin left({omega }_0t+{varphi }_0right) }right)left(1.2right).]
Максимальное значение скорости (амплитуда скорости) равна:
[v_{max}={dot{x}}_{max}=Aщ_0 left(1.3right).]
Ускорение точки вычислим как:
[a_x==frac{dv_x}{dt}=-A{{omega }_0}^2left({cos left({omega }_0t+{varphi }_0right) }right)left(1.4right),]
из (1.4):
[a_{max}={ddot{x}}_{max}=A{{omega }_0}^2(1.5).]
Из формулы (1.3) выразим амплитуду, подставим ее в (1.5), получим циклическую частоту:
[{dot{x}}_{max}=A{omega }_0to A=frac{{dot{x}}_{max}}{{omega }_0};; {ddot{x}}_{max}=A{щ_0}^2=frac{{dot{x}}_{max}}{щ_0}{щ_0}^2to щ_0=frac{{ddot{x}}_{max}}{{dot{x}}_{max}}.]
Вычислим циклическую частоту:
[щ_0=frac{100}{10}=10(frac{рад}{с}).]
Ответ: $щ_0=10frac{{rm рад}}{{rm с}}$
Пример 2
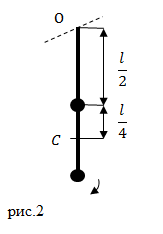
Задание: На длинном невесомом стержне закреплены два груза одинаковой массы. Один груз находится на середине стержня, другой на его конце (рис.2). Система совершает колебания около горизонтальной оси, проходящей через свободный конец стрежня. Какова циклическая частота колебаний? Длина стержня равна $l$.
Решение: Основой для решения задачи является формула нахождения частоты колебаний физического маятника:
[{omega }_0=sqrt{frac{mga}{J}}left(2.1right),]
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника. Масса маятника по условию задачи состоит из масс двух одинаковых шариков (масса одного шарика $frac{m}{2}$). В нашем случае расстояние $a$ равно расстоянию между точками O и C (см. рис.2):
[a=frac{3}{4}l left(2.2right).]
Найдем момент инерции системы из двух точечных масс. Относительно центра масс (если ось вращения провести через точку C), момент инерции системы ($J_0$) равен:
[J_0=2cdot frac{m}{2}cdot frac{l^2}{16}=frac{ml^2}{16}left(2.3right).]
Момент инерции нашей системы относительно оси, проходящей через точку О найдем по теореме Штейнера:
[J=J_0+m{(frac{3}{4}l )}^2=frac{ml^2}{16}+frac{m9l^2}{16}=frac{5}{8}ml^2left(2.4right).]
Подставим правые части выражение (2.2) и (2.4) в (2.1) вместо соответствующих величин:
[{omega }_0=sqrt{frac{mgfrac{3}{4}l }{frac{5}{8}ml^2}}=sqrt{frac{6g}{5l}}.]
Ответ: ${omega }_0=sqrt{frac{6g}{5l}}$
Читать дальше: амплитуда скорости груза.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Циклическая частота колебаний
Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.
Это скалярная физическая величина.
Циклическая частота при гармонических колебаниях
Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.
Самыми простыми колебаниями являются гармонические колебания. Рассмотрим следующую кинематическую модель. Точка M с постоянной по модулю скоростью ($v$) движется по окружности радиуса A. В этом случае ее угловую скорость обозначим $<omega >_0$, эта скорость постоянна (рис.1).
Проекция точки $M$ на диаметр окружности (точка $N$), на ось X, выполняет колебания от $N_1$ до $N_2 $и обратно. Такое колебание N ,будет гармоническим. Для описания колебания точки N необходимо записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол $<varphi >_0$. Через некоторый промежуток времени этот угол изменится на величину $<omega >_0t$ и будет равен $<omega >_0t+<varphi >_0$, тогда:
Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.
Обратимся к выражению (1). Величина $A$ — это максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О — центра окружности), называется амплитудой колебаний.
Параметр $<omega >_0$ — циклическая частота колебаний. $varphi =(<omega >_0t+<varphi >_0$) — фаза колебаний; $<varphi >_0$ — начальная фаза колебаний.
Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:
При $<varphi >_0=0$, уравнение колебаний (1) преобразуется к виду:
Если начальная фаза колебаний равна $<varphi >_0=frac<pi ><2>$ , то получим уравнение колебаний в виде:
Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ — это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.
Циклическую частоту колебаний можно выразить через период (T) колебаний:
Циклическую частоту с частотой $?$$?$ свяжем выражением:
Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:
Размерность циклической частоты:
Частные случаи формул для вычисления циклической частоты
Груз на пружине (пружинный маятник — идеальная модель) совершает гармонические колебания с круговой частотой равной:
$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.
Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.
Примером физического маятника является математический маятник. Круговая частота его колебаний равна:
где $l$ — длина подвеса.
Угловая частота затухающих колебаний находится как:
где $delta $ — коэффициент затухания; в случае с затуханием колебаний $<omega >_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Задание: Чему равна циклическая частота гармонических колебаний, если максимальная скорость материальной точки равна $<dot>_=10 frac<см><с>$, а ее максимальное ускорение $<ddot>_=100 frac<см><с^2>$?
Решение: Основой решения задачи станет уравнение гармонических колебаний точки, так как из условий, очевидно, что они происходят по оси X:
Скорость колебаний найдем, используя уравнение (1.1) и кинематическую связь координаты $x$ и соответствующей компоненты скорости:
Максимальное значение скорости (амплитуда скорости) равна:
Ускорение точки вычислим как:
Из формулы (1.3) выразим амплитуду, подставим ее в (1.5), получим циклическую частоту:
Вычислим циклическую частоту:
Задание: На длинном невесомом стержне закреплены два груза одинаковой массы. Один груз находится на середине стержня, другой на его конце (рис.2). Система совершает колебания около горизонтальной оси, проходящей через свободный конец стрежня. Какова циклическая частота колебаний? Длина стержня равна $l$.
Решение: Основой для решения задачи является формула нахождения частоты колебаний физического маятника:
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника. Масса маятника по условию задачи состоит из масс двух одинаковых шариков (масса одного шарика $frac<2>$). В нашем случае расстояние $a$ равно расстоянию между точками O и C (см. рис.2):
Найдем момент инерции системы из двух точечных масс. Относительно центра масс (если ось вращения провести через точку C), момент инерции системы ($J_0$) равен:
Момент инерции нашей системы относительно оси, проходящей через точку О найдем по теореме Штейнера:
Подставим правые части выражение (2.2) и (2.4) в (2.1) вместо соответствующих величин:
17. Механика Читать 0 мин.
17.547. Механические колебания
Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.
Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac<1>$ , где
Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac$ , где
N ― количество колебаний;
Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac<2pi>$ , где
ω ― циклическая частота [рад/с];
Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
ω ― циклическая частота [рад/с];
φ0 ― начальная фаза колебаний, [рад];
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.
Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
φ ― полная фаза колебаний [рад];
φ0 ― начальная фаза колебаний, [рад];
ω ― циклическая частота [рад/с];
Пример анализа гармонических колебаний точки
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
ω ― циклическая частота [рад/с].
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac<pi> <2>+2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac<3pi> <2>+2pi n$ , где n = 0, 1 , 2, … N.
График колебания координаты точки имеет вид:
Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где
v ― скорость движения точки [м/с];
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).
Уравнение скорости точки равно v(t) = Acos(ωt), где
v ― скорость движения точки [м/с];
ω ― циклическая частота [рад/с];
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.
График колебания скорости точки имеет вид:
Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
Ускорение ― это производная скорости по времени: a = vt‘, где
a ― ускорение движения точки [м/с2];
v ― скорость движения точки [м/с];
Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).
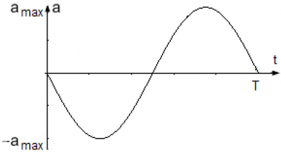
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
a ― ускорение движения точки [м/с2];
ω ― циклическая частота [рад/с];
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.
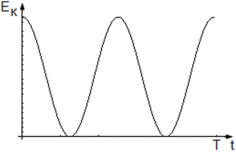
График колебания ускорения точки имеет вид:
Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где
E ― полная механическая энергия системы, E = const, [Дж];
EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).
Потенциальная энергия деформированной пружины равна EП = $frac<2>$ , где
EП ― потенциальная энергия деформированной пружины, [Дж];
k ― коэффициент упругости пружины [Н/м];
x ― деформация пружины (величина ее удлинения или сжатия) [м].
У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac<2>$ = $frac<2>$ = $frac <2>cdot A^2 sin^2 (omega t)$ .
Уравнение потенциальной энергии пружинного маятника EП = $frac <2>cdot A^2 sin^2 (omega t)$ , где
EП ― потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
ω ― циклическая частота [рад/с];
Амплитуда потенциальной энергии пружинного маятника равна EПmax = $frac<2>A^2$ , где
EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
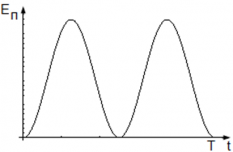
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.
График колебаний потенциальной энергии пружинного маятника:
Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac<2>$ , где
Eк ― кинетическая энергия тела, [Дж];
v ― скорость движения тела, [м/с].
У тела, которое совершает колебательные движения, скорость ― переменная величина.
Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac<2>$ = $frac <2>cdot (Aomegacos(omega t))^2$ = $frac <2>cdot A^2 omega^2 cos^2 (omega t)$ .
Уравнение кинетической энергии маятника Eк = $frac <2>cdot A^2 omega^2 cos^2 (omega t)$ , где
Eк ― кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с];
Амплитуда кинетической энергии маятника равна EКmax = $frac <2>cdot A^2 omega^2$ , где
EКmax ― максимальная кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с].
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
График колебаний кинетической энергии маятника:
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
Период колебаний математического маятника равен T = $2pi sqrt<frac>$ , где
l ― длина нити математического маятника [м];
g ― ускорение свободного падения [м/с2].
Период колебаний пружинного маятника равен T = $2pi sqrt<frac>$ , где
Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.
На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.
Механические колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .
Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :
График функции (1) , выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1 .
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:
График гармонических колебаний в этом случае представлен на рис. 2 .
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:
График колебаний представлен на рис. 3 .
 |
| Рис. 3. Закон синуса |
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1) . Дифференцируем это равенство:
Теперь дифференцируем полученное равенство (4) :
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6) , (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.
Пружинный маятник.
Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:
Если 0′ alt=’x>0′ /> (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то 0′ alt=’F_>0′ /> . Знаки и всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
Мы получили уравнение гармонических колебаний вида (6) , в котором
Циклическая частота колебаний пружинного маятника, таким образом, равна:
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10) .
Математический маятник.
Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5 ). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
и спроектируем его на ось :
Если маятник занимает положение как на рисунке (т. е. 0′ alt=’x>0′ /> ), то:
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
Итак, при любом положении маятника имеем:
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11) :
Это — уравнение гармонических колебаний вида (6) , в котором
Следовательно, циклическая частота колебаний математического маятника равна:
Отсюда период колебаний математического маятника:
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7 .
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .
http://reshutest.ru/theory/13?theory_id=334
http://ege-study.ru/ru/ege/materialy/fizika/mexanicheskie-kolebaniya/
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Гармоническими называют колебания, в которых интересующий нас параметр изменяется во времени по тригонометрическому закону (синус или косинус).
$z=z_mcos (omega_0 t+alpha) (1),$ где:
- $z_m$ — является амплитудой колебаний;
- $(omega_0 t+alpha)$ – фаза колебаний;
- $alpha $ — служит начальной фазой колебаний (фаза колебаний в момент времени, который считают начальным ($t=0$));
- $omega_0$ — обозначение циклической (или круговой) частоты процесса.
Колебания играют важную роль в разных физических процессах. Среди множества колебаний гармонические колебания занимают особое место, поскольку:
- они считаются наиболее простыми для математического описания;
- любое периодическое движение можно разложить на составляющие, которые можно считать гармоническими компонентами рассматриваемого колебательного движения.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим колебательное движение материальной точки.
Кинематическая модель гармонических колебаний
Пусть материальная точка $A$ равномерно движется по окружности (рис.1). Угловую скорость ее движения обозначим $omega_0=const$. Радиус окружности равен $R$.
Рисунок 1. Точка движется по окружности. Автор24 — интернет-биржа студенческих работ
Проектируя место наше точки в момент времени $t$ (рис.1) на ось $OZ$ мы получим точку $Z$, которая находится на расстоянии $z$ от начала координат (точки $O$). С течением времени (в ходе перемещения материальной точки $A$ по окружности) точка $Z$ будет совершать колебания от положения $Z_1$ до положения $Z_2$ и в обратную сторону.
Рассматриваемое колебание точки $Z$ будет гармоническим. Для его описания достаточно записать закон изменения расстояния $z$ (координаты $z$) от начала координат (точки $O$) в зависимости от времени, то есть получить функцию $z(t)$.
«Частота гармонических колебаний» 👇
Будем считать, что при $t=0$ радиус $ОA$ составляет угол $alpha$ с осью $OZ$. Через время $t$ данный угол изменится на величину $omega_0 t$. Из прямоугольного треугольника $OZA$ мы получим:
$z(t)=Rcos (omega_0 t+alpha)=z_mcos (omega_0 t+alpha) (2).$
Выражение (2) описывает гармонические колебания точки $A$ по оси $OZ$.
Параметр $R=z_m$ в данном случае – это наибольшее отклонение точки, выполняющей колебания от положения равновесия (точки $O$), данный параметр носит название амплитуды колебаний.
Угловая скорость вращения точки по окружности в данной модели будет играть роль циклической частоты колебаний.
- При начальной фазе колебаний равной нулю $(alpha=0),$ имеем $z(t)= z_mcos (omega_0 t );$
- При $alpha=frac{pi}{2}$ мы получим, что $z(t)= z_msin (omega_0 t ).$
Мы видим, что при гармонических колебаниях координата $z$ является функцией синуса или косинуса, зависящей от времени.
Гармонические колебания часто изображают в виде графиков. При этом по горизонтальной оси откладывают время, на вертикальной оси — координату. Получают периодическую кривую (синусоиду или косинусоиду). При этом форма кривой зависит только от амплитуды и круговой частоты гармонических колебаний. Положение данной кривой определяет начальная фаза колебаний.
Период колебаний и круговая частота
Синус (косинус) является периодической функцией, следовательно, рассматриваемое нами движение является периодическим. Период этих тригонометрических функций составляет $T=2pi$. Это означает, что по истечении времени $T$ точка, выполняющая колебания приходит в свое исходное положение, сохраняя свое направление движения. $T$ называют периодом колебаний.
Период колебаний и круговая частота колебаний связаны выражением:
$omega_0=frac{2pi}{T}(3).$
Частота колебаний
Кроме циклической частоты при описании колебаний используют линейную частоту (или просто частоту), обозначаемую $nu$.
Линейная частота является величиной обратной периоду колебаний:
$nu=frac{1}{T}(4)$.
Она измеряется в герцах (Гц), тогда как единицей измерения циклической частоты является обратная секунда.
Определение 1
Частотой (линейной частотой) называют физическую величину, которая служит характеристикой периодического процесса, равную числу колебаний (повторений) за единицу времени.
$nu=frac{n}{t}(5),$
где $n$ — количество колебаний (повторений процесса); $t$ — время наблюдения.
Линейная частота связана с круговой частотой формулой:
$nu=frac{omega_0}{2pi}(6).$
Формулы циклической частоты для гармонических осцилляторов
Классическими примерами гармонических осцилляторов в механике являются:
- груз на упругой пружине (пружинный маятник);
- математический маятник;
- физический маятник (твердое тело, выполняющее колебания (качания) относительно неподвижной горизонтальной оси, которая проходит через точку, не совпадающую с его центром масс);
- электрический $LC$ контур.
Допустим, что осцилляторы совершают свободные (без действия внешних сил) колебания при отсутствии трения.
Груз на пружине выполняет колебания с циклической частотой равной:
$omega_0=sqrt{frac{k}{m}}(7),$
где $k$ — коэффициент упругости пружины; $m$- масса тела, подвешенного к пружине.
Круговая частота малых колебаний физического маятника равна:
$omega_0=sqrt{frac{mga}{I}}(8),$
где $m$ — масса маятника; $a$ — расстояние от центра масс, до точки подвеса маятника; $I$ — момент инерции маятника.
Математический маятник — это частный случай физического маятника. У этого маятника массу считают сосредоточенной в одной точке — центре его центре масс. Чаще всего в качестве математического маятника рассматривают шарик, который выполняет колебания на длинной нити.
Циклическая частота колебаний математического маятника равна:
$omega_0=sqrt{frac{g}{l}}(9),$
где $l$ — длина нити.
Классическим примером осциллятора, который может выполнять свободные незатухающие гармонические электромагнитные колебания является идеальный электрический контур, состоящий из конденсатора и катушки индуктивности.
Циклическая частота данных колебаний определяется выражением:
$omega_0=frac{1}{sqrt{LC}}(10)$,
где $C$ — емкость конденсатора; $L$ — индуктивность катушки.
Из приведенных выше формул мы видим, что частота свободных колебаний без учета трения зависит только от свойств самих осцилляторов.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Механические колебания.
-
Гармонические колебания.
-
Уравнение гармонических колебаний.
-
Пружинный маятник.
-
Математический маятник.
-
Свободные и вынужденные колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду:
. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
к оглавлению ▴
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение
. Основная задача механики в данном случае состоит в нахождении функции
, дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому
— амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина
, равная значению фазы при
, называется начальной фазой. Начальная фаза отвечает начальной координате тела:
.
Величина называется циклической частотой. Найдём её связь с периодом колебаний
и частотой
. Одному полному колебанию отвечает приращение фазы, равное
радиан:
, откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить
. Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить
. Получаем закон синуса:
.
График колебаний представлен на рис. 3.
 |
| Рис. 3. Закон синуса |
к оглавлению ▴
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы
определяются из начальных условий — по начальным значениям координаты и скорости.
к оглавлению ▴
Пружинный маятник.
Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна
.
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось
имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и
. Наоборот, если
, то
. Знаки
и
всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
к оглавлению ▴
Математический маятник.
Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство
. Воспользуемся им в формуле (11):
,
или
.
Это — уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
к оглавлению ▴
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы:
, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний,
, а амплитуда колебаний возрастает до бесконечности при
.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023

6.Колебания
6.1.Основные понятия и законы
|
Движение называется периодическим, если |
|||||||||||||||||
|
x(t)= x(t +T ), где T |
— период. |
(6.1) |
|||||||||||||||
|
Колебание |
– |
это |
х |
||||||||||||||
|
периодическое |
движение |
около |
|||||||||||||||
|
положения равновесия. На рис.6.1 в |
|||||||||||||||||
|
качестве |
примера |
изображены |
|||||||||||||||
|
периодические |
негармонические |
0 |
|||||||||||||||
|
колебания |
около |
положения |
|||||||||||||||
|
равновесия |
x0 = 0. |
t |
|||||||||||||||
|
Период T – это время, за |
T |
||||||||||||||||
|
которое |
совершается |
одно |
полное |
||||||||||||||
|
колебание. |
|||||||||||||||||
|
Рис.6.1 |
|||||||||||||||||
|
Частота |
– число |
полных |
|||||||||||||||
|
колебаний в единицу времени |
|||||||||||||||||
|
ν = |
1 |
. |
(6.2) |
||||||||||||||
|
T |
|||||||||||||||||
Круговая (циклическая) частота |
|||||||||||||||||
|
ω= 2πν = |
2π |
. |
(6.3) |
||||||||||||||
|
T |
|||||||||||||||||
|
Гармоническими |
называются колебания, при которых смещение |
||||||||||||||||
|
точки |
от положения равновесия в зависимости от времени |
||||||||||||||||
|
изменяется по закону синуса или косинуса |
|||||||||||||||||
|
x = Asin(ω0t + α) |
, |
(6.4) |
|||||||||||||||
|
где A |
— |
амплитуда колебаний (максимальное смещение точки от |
положения равновесия), ω0 — круговая частота гармонических колебаний, ω0t + α — фаза, α— начальная фаза (при t = 0).
Система, совершающая гармонические колебания, называется
классическим гармоническим осциллятором или колебательной
|
системой. |
|||||||
|
Скорость |
и ускорение |
при |
гармонических колебаниях |
||||
|
изменяются по законам |
|||||||
|
v = |
dx |
& |
(6.5) |
||||
|
dt |
= x = Aω0 cos(ω0t + α) , |
||||||
|
d 2 x |
&& |
2 |
|||||
|
a = |
= −Aω0 sin(ω0t + α) . |
(6.6) |
|||||
|
dt |
2 |
= x |
|||||
|
Из соотношений (6.6) и (6.4) получим |
|||||||
|
a = −ω2 x , |
(6.7) |
||||||
|
0 |
99

откуда следует, что при гармонических колебаниях ускорение прямо пропорционально смещению точки от положения равновесия и направлено противоположно смещению.
Из уравнений (6,6), (6,7) получим
|
&& |
2 |
(6.8) |
|
x |
+ ω0 x = 0 . |
Уравнение (6.8) называется дифференциальным уравнением гармонических колебаний, а (6.4) является его решением. Подставив
(6.7) во второй закон Ньютона F = mar, получим силу, под действием которой происходят гармонические колебания
|
F = −mω2 x . |
(6.9) |
|
|
0 |
||
|
Обозначим mω2 |
= k . |
(6.10) |
|
0 |
||
|
Из (6.9), (6.10) получим |
||
|
Fr = −kxr. |
(6.11) |
Эта сила, прямо пропорциональная смещению точки от положения равновесия и направленная противоположно смещению, называется возвращающей силой, k называется коэффициентом возвращающей силы. Таким свойством обладает сила упругости. Силы другой физической природы, подчиняющиеся закону (6.11),
называются квазиупругими.
Колебания, происходящие под действием сил, обладающих
|
свойством |
(6.11), |
называются |
собственными |
(свободными |
|
|
гармоническими) колебаниями. |
|||||
|
Из соотношений (6.3),(6.10) получим круговую частоту и период |
|||||
|
этих колебаний |
|||||
|
ω = |
k ; |
T = 2π |
m . |
(6.12) |
|
|
0 |
m |
0 |
k |
||
При гармонических колебаниях по закону (6.4) зависимости кинетической и потенциальной энергии от времени имеют вид
|
E |
K |
= |
mv2 |
= |
mA2ω0 |
2 |
cos2 (ω t + α), |
(6.13) |
||||||
|
2 |
2 |
0 |
||||||||||||
|
U = |
kx2 |
= |
mA2ω0 |
2 |
sin2 (ω t + α) . |
(6.14) |
||||||||
|
2 |
2 |
0 |
||||||||||||
100

Полная энергия в процессе гармонических колебаний сохраняется
|
EK +U = const . |
(6.15) |
||||||
|
Подставляя в (6.15) выражения (6.4) и (6.5) для x и v, получим |
|||||||
|
E = EK max =Umax |
= |
mA2ω2 |
(6.16) |
||||
|
2 |
0 . |
||||||
|
Примером классического |
гармонического |
||||||
|
осциллятора является легкая пружина, к которой |
|||||||
|
подвешен груз массой m |
(рис.6.2). Коэффициент |
||||||
|
возвращающей силы k называется коэффициентом |
|||||||
|
жесткости пружины. |
Из второго закона Ньютона |
x |
|||||
|
для груза |
на пружине |
F = |
– kx получим |
||||
|
уравнение, |
совпадающее |
по |
форме |
с |
m |
||
|
дифференциальным |
уравнением |
гармонических |
|||||
|
колебаний (6.8) Следовательно, груз на пружине |
x |
||||||
|
при отсутствии сил сопротивления среды будет |
|||||||
|
совершать гармонические колебания (6.4). |
Рис.6.2 |
||||||
|
Гармонические |
колебания |
(6.4) |
можно |
представить в виде проекции на оси координат вектора, величина которого равна амплитуде A, вращающегося вокруг начала координат с угловой скоростью ω0 . На этом представлении основан метод
|
векторных диаграмм сложения гармонических колебаний с |
|||||||||||
|
одинаковой частотой, происходящих по одной оси |
|||||||||||
|
x1 = A1 sin(ωt + ϕ1 ), |
(6.17) |
||||||||||
|
x2 = A2 sin(ωt + ϕ2 ). |
|||||||||||
|
Амплитуда результирующего колебания определяется по |
|||||||||||
|
теореме косинусов |
− 2A A cos(ϕ −ϕ |
) . |
|||||||||
|
A = |
A2 |
+ A2 |
2 |
(6.18) |
|||||||
|
1 |
2 |
1 |
2 |
1 |
|||||||
|
Начальная фаза результирующего колебания ϕ |
может быть |
||||||||||
|
найдена из формулы |
|||||||||||
|
tg ϕ = |
A1 sin ϕ1 + A2 sin ϕ2 |
. |
(6.19) |
||||||||
|
A cosϕ + A cosϕ |
2 |
||||||||||
|
1 |
1 |
2 |
|||||||||
|
При сложении однонаправленных колебаний с близкими |
|||||||||||
|
частотами ω1 и ω2 |
возникают биения, частота которых равна ω1 − ω2 . |
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях
x = A1 sin((ωt + ϕ1 )), (6.20) y = A2 sin ωt + ϕ2
имеет вид
101

|
x2 |
+ |
y2 |
− 2 |
xy |
cos(ϕ −ϕ |
)= sin2 (ϕ |
−ϕ ). |
(6.21) |
||||||||||||||||||||||||
|
A2 |
A2 |
A A |
||||||||||||||||||||||||||||||
|
1 |
2 |
2 |
1 |
|||||||||||||||||||||||||||||
|
1 |
2 |
1 |
2 |
|||||||||||||||||||||||||||||
|
Если начальные фазы ϕ1 = ϕ2 , то уравнение траектории – прямая |
||||||||||||||||||||||||||||||||
|
y = |
A2 |
x , или y = − |
A2 |
x . |
||||||||||||||||||||||||||||
|
A |
A |
|||||||||||||||||||||||||||||||
|
1 |
1 |
ϕ = ϕ1 − ϕ2 = π 2 , |
||||||||||||||||||||||||||||||
|
Если |
разность |
фаз |
||||||||||||||||||||||||||||||
|
x2 |
y2 |
|||||||||||||||||||||||||||||||
|
точка движется по эллипсу |
+ |
=1. |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||
|
A |
A |
|||||||||||||||||||||||||||||||
|
d |
||||||||||||||||||||||||||||||||
|
1 |
2 |
|||||||||||||||||||||||||||||||
|
O |
Физический маятник – это твердое тело, |
|||||||||||||||||||||||||||||||
|
способное |
совершать |
колебания |
вокруг |
|||||||||||||||||||||||||||||
|
закрепленной оси, проходящей через точку |
О |
|||||||||||||||||||||||||||||||
|
ϕ |
||||||||||||||||||||||||||||||||
|
,не |
совпадающую |
с |
его |
центром |
масс |
С |
||||||||||||||||||||||||||
|
C |
(рис.6.3). Колебания являются гармоническими |
|||||||||||||||||||||||||||||||
|
при малых углах отклонения. |
||||||||||||||||||||||||||||||||
|
Момент силы тяжести относительно оси, |
||||||||||||||||||||||||||||||||
|
проходящей |
через |
точку |
О, |
является |
||||||||||||||||||||||||||||
|
mg |
||||||||||||||||||||||||||||||||
|
возвращающим |
моментом |
и |
выражается |
|||||||||||||||||||||||||||||
|
Рис.6.3 |
соотношением |
r |
||||||||||||||||||||||||||||||
|
M = mgd sin |
(6.22) |
|||||||||||||||||||||||||||||||
|
ϕ ≈ mgdϕ. |
Основное уравнение динамики вращательного движения имеет вид (см. формулу (4.18))
M = I ε , (6.23)
где I — момент инерции маятника относительно оси, проходящей через точку О, ε — угловое ускорение.
Из (6.23), (6.22) получим дифференциальное уравнение гармонических колебаний физического маятника
|
d 2ϕ |
+ |
mgd |
ϕ = 0 . |
(6.24) |
||
|
dt2 |
I |
|||||
|
Его решения ϕ = ϕ0 sin ω0t , |
(6.25) |
|||||
|
где |
ω = |
mgd . |
||||
|
0 |
I |
|||||
Из (6.3) получим формулу периода колебаний физического маятника
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити длиной L. Из (6.26) полагая d = l,
I = ml2 , получим формулу периода колебаний математического маятника
102

Тело, подвешенное на легкой упругой проволоке (рис.6.4) , совершает крутильные колебания вокруг оси, совпадающей с проволокой. При повороте на малый угол в проволоке возникает возвращающий момент упругих сил
Коэффициент возвращающего момента зависит от материала проволоки и ее размеров
|
c = |
πG |
r4 |
, |
(6.29) |
||
|
2 |
L |
|||||
где G — модуль сдвига, характеризующий упругие свойства материала, r — радиус проволоки, L — ее длина.
Основное уравнение динамики вращательного
движения имеетr вид
Iϕ&r& = M .
ϕ
M

Рис.6.4
(6.30)
|
Из |
(6.28), (6.30) получим |
дифференциальное уравнение |
||||
|
гармонических крутильных колебаний |
||||||
|
d 2ϕ |
+ |
c |
ϕ = 0 . |
(6.31) |
||
|
dt2 |
I |
|||||
|
Его решение имеет вид ϕ = ϕ0 sin(ω0t + α), |
(6.32) |
где ϕ — угловое смещение от положения равновесия, ϕ0 – амплитуда
колебаний.
Сравнив уравнения (6.8) и (6.32), получим значения угловой частоты и периода крутильных колебаний
|
ω = |
c , |
(6.33) |
|
0 |
I |
|
|
T = 2π |
I . |
(6.34) |
|
c |
Свободные колебания становятся затухающими из-за наличия сил сопротивления. Например, когда материальная точка колеблется в вязкой среде, при малых скоростях на нее действует сила
|
сопротивления |
r |
& |
где |
r — коэффициент |
||||||
|
среды Fсопр = −rv |
= −rx , |
|||||||||
|
сопротивления среды. Поэтому из второго закона Ньютона |
||||||||||
|
mx = −kx − rx |
||||||||||
|
&& |
& |
|||||||||
|
получим дифференциальное уравнение затухающих колебаний |
||||||||||
|
&& |
r |
& |
k |
(6.35) |
||||||
|
x |
+ m x + m x = 0 . |
r 2 |
||||||||
|
Его решение для случая, когда |
k |
|||||||||
|
> |
, |
имеет вид |
||||||||
|
m |
2m |
|||||||||
|
x = A e−βt |
sin(ωt + α), |
(6.36) |
||||||||
|
0 |
103
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #