Как найти циклы в последовательности

In computer science, cycle detection or cycle finding is the algorithmic problem of finding a cycle in a sequence of iterated function values.

For any function f that maps a finite set S to itself, and any initial value x₀ in S, the sequence of iterated function values

must eventually use the same value twice: there must be some pair of distinct indices i and j such that x_i = x_j. Once this happens, the sequence must continue periodically, by repeating the same sequence of values from x_i to x_{j − 1}. Cycle detection is the problem of finding i and j, given f and x₀.

Several algorithms for finding cycles quickly and with little memory are known. Robert W. Floyd’s tortoise and hare algorithm moves two pointers at different speeds through the sequence of values until they both point to equal values. Alternatively, Brent’s algorithm is based on the idea of exponential search. Both Floyd’s and Brent’s algorithms use only a constant number of memory cells, and take a number of function evaluations that is proportional to the distance from the start of the sequence to the first repetition. Several other algorithms trade off larger amounts of memory for fewer function evaluations.

The applications of cycle detection include testing the quality of pseudorandom number generators and cryptographic hash functions, computational number theory algorithms, detection of infinite loops in computer programs and periodic configurations in cellular automata, automated shape analysis of linked list data structures, and detection of deadlocks for transactions management in DBMS.

Example[edit]

The figure shows a function f that maps the set S = {0,1,2,3,4,5,6,7,8} to itself. If one starts from x₀ = 2 and repeatedly applies f, one sees the sequence of values

2, 0, 6, 3, 1, 6, 3, 1, 6, 3, 1, ….

The cycle in this value sequence is 6, 3, 1.

Definitions[edit]

Let S be any finite set, f be any function from S to itself, and x₀ be any element of S. For any i > 0, let x_i = f(x_{i − 1}). Let μ be the smallest index such that the value x_μ reappears infinitely often within the sequence of values x_i, and let λ (the loop length) be the smallest positive integer such that x_μ = x_{λ + μ}. The cycle detection problem is the task of finding λ and μ.^[1]

One can view the same problem graph-theoretically, by constructing a functional graph (that is, a directed graph in which each vertex has a single outgoing edge) the vertices of which are the elements of S and the edges of which map an element to the corresponding function value, as shown in the figure. The set of vertices reachable from starting vertex x₀ form a subgraph with a shape resembling the Greek letter rho (ρ): a path of length μ from x₀ to a cycle of λ vertices.^[2]

Computer representation[edit]

Generally, f will not be specified as a table of values, the way it is shown in the figure above. Rather, a cycle detection algorithm may be given access either to the sequence of values x_i, or to a subroutine for calculating f. The task is to find λ and μ while examining as few values from the sequence or performing as few subroutine calls as possible. Typically, also, the space complexity of an algorithm for the cycle detection problem is of importance: we wish to solve the problem while using an amount of memory significantly smaller than it would take to store the entire sequence.

In some applications, and in particular in Pollard’s rho algorithm for integer factorization, the algorithm has much more limited access to S and to f. In Pollard’s rho algorithm, for instance, S is the set of integers modulo an unknown prime factor of the number to be factorized, so even the size of S is unknown to the algorithm.
To allow cycle detection algorithms to be used with such limited knowledge, they may be designed based on the following capabilities. Initially, the algorithm is assumed to have in its memory an object representing a pointer to the starting value x₀. At any step, it may perform one of three actions: it may copy any pointer it has to another object in memory, it may apply f and replace any of its pointers by a pointer to the next object in the sequence, or it may apply a subroutine for determining whether two of its pointers represent equal values in the sequence. The equality test action may involve some nontrivial computation: for instance, in Pollard’s rho algorithm, it is implemented by testing whether the difference between two stored values has a nontrivial greatest common divisor with the number to be factored.^[2] In this context, by analogy to the pointer machine model of computation, an algorithm that only uses pointer copying, advancement within the sequence, and equality tests may be called a pointer algorithm.

Algorithms[edit]

If the input is given as a subroutine for calculating f, the cycle detection problem may be trivially solved using only λ + μ function applications, simply by computing the sequence of values x_i and using a data structure such as a hash table to store these values and test whether each subsequent value has already been stored. However, the space complexity of this algorithm is proportional to λ + μ, unnecessarily large. Additionally, to implement this method as a pointer algorithm would require applying the equality test to each pair of values, resulting in quadratic time overall. Thus, research in this area has concentrated on two goals: using less space than this naive algorithm, and finding pointer algorithms that use fewer equality tests.

Floyd’s tortoise and hare[edit]

Floyd’s cycle-finding algorithm is a pointer algorithm that uses only two pointers, which move through the sequence at different speeds. It is also called the «tortoise and the hare algorithm», alluding to Aesop’s fable of The Tortoise and the Hare.

The algorithm is named after Robert W. Floyd, who was credited with its invention by Donald Knuth.^[3][4] However, the algorithm does not appear in Floyd’s published work, and this may be a misattribution: Floyd describes algorithms for listing all simple cycles in a directed graph in a 1967 paper,^[5] but this paper does not describe the cycle-finding problem in functional graphs that is the subject of this article. In fact, Knuth’s statement (in 1969), attributing it to Floyd, without citation, is the first known appearance in print, and it thus may be a folk theorem, not attributable to a single individual.^[6]

The key insight in the algorithm is as follows. If there is a cycle, then, for any integers i ≥ μ and k ≥ 0, x_i = x_{i + kλ}, where λ is the length of the loop to be found, μ is the index of the first element of the cycle, and k is a whole integer representing the number of loops. Based on this, it can then be shown that i = kλ ≥ μ for some k if and only if x_i = x_2i (if x_i = x_2i in the cycle, then there exists some k such that 2i = i + kλ, which implies that i = kλ; and if there are some i and k such that i = kλ, then 2i = i + kλ and x_2i = x_{i + kλ}). Thus, the algorithm only needs to check for repeated values of this special form, one twice as far from the start of the sequence as the other, to find a period ν of a repetition that is a multiple of λ. Once ν is found, the algorithm retraces the sequence from its start to find the first repeated value x_μ in the sequence, using the fact that λ divides ν and therefore that x_μ = x_{μ + v}. Finally, once the value of μ is known it is trivial to find the length λ of the shortest repeating cycle, by searching for the first position μ + λ for which x_{μ + λ} = x_μ.

The algorithm thus maintains two pointers into the given sequence, one (the tortoise) at x_i, and the other (the hare) at x_2i. At each step of the algorithm, it increases i by one, moving the tortoise one step forward and the hare two steps forward in the sequence, and then compares the sequence values at these two pointers. The smallest value of i > 0 for which the tortoise and hare point to equal values is the desired value ν.

The following Python code shows how this idea may be implemented as an algorithm.

def floyd(f, x0) -> tuple[int, int]:
    """Floyd's cycle detection algorithm."""
    # Main phase of algorithm: finding a repetition x_i = x_2i.
    # The hare moves twice as quickly as the tortoise and
    # the distance between them increases by 1 at each step.
    # Eventually they will both be inside the cycle and then,
    # at some point, the distance between them will be
    # divisible by the period λ.
    tortoise = f(x0) # f(x0) is the element/node next to x0.
    hare = f(f(x0))
    while tortoise != hare:
        tortoise = f(tortoise)
        hare = f(f(hare))
  
    # At this point the tortoise position, ν, which is also equal
    # to the distance between hare and tortoise, is divisible by
    # the period λ. So hare moving in cycle one step at a time, 
    # and tortoise (reset to x0) moving towards the cycle, will 
    # intersect at the beginning of the cycle. Because the 
    # distance between them is constant at 2ν, a multiple of λ,
    # they will agree as soon as the tortoise reaches index μ.

    # Find the position μ of first repetition.    
    mu = 0
    tortoise = x0
    while tortoise != hare:
        tortoise = f(tortoise)
        hare = f(hare)   # Hare and tortoise move at same speed
        mu += 1
 
    # Find the length of the shortest cycle starting from x_μ
    # The hare moves one step at a time while tortoise is still.
    # lam is incremented until λ is found.
    lam = 1
    hare = f(tortoise)
    while tortoise != hare:
        hare = f(hare)
        lam += 1
 
    return lam, mu

This code only accesses the sequence by storing and copying pointers, function evaluations, and equality tests; therefore, it qualifies as a pointer algorithm. The algorithm uses O(λ + μ) operations of these types, and O(1) storage space.^[7]

Brent’s algorithm[edit]

Richard P. Brent described an alternative cycle detection algorithm that, like the tortoise and hare algorithm, requires only two pointers into the sequence.^[8] However, it is based on a different principle: searching for the smallest power of two 2ⁱ that is larger than both λ and μ. For i = 0, 1, 2, …, the algorithm compares x_2ⁱ−1 with each subsequent sequence value up to the next power of two, stopping when it finds a match. It has two advantages compared to the tortoise and hare algorithm: it finds the correct length λ of the cycle directly, rather than needing to search for it in a subsequent stage, and its steps involve only one evaluation of f rather than three.^[9]

The following Python code shows how this technique works in more detail.

def brent(f, x0) -> tuple[int, int]:
    """Brent's cycle detection algorithm."""
    # main phase: search successive powers of two
    power = lam = 1
    tortoise = x0
    hare = f(x0)  # f(x0) is the element/node next to x0.
    while tortoise != hare:
        if power == lam:  # time to start a new power of two?
            tortoise = hare
            power *= 2
            lam = 0
        hare = f(hare)
        lam += 1

    # Find the position of the first repetition of length λ
    tortoise = hare = x0
    for i in range(lam):
    # range(lam) produces a list with the values 0, 1, ... , lam-1
        hare = f(hare)
    # The distance between the hare and tortoise is now λ.

    # Next, the hare and tortoise move at same speed until they agree
    mu = 0
    while tortoise != hare:
        tortoise = f(tortoise)
        hare = f(hare)
        mu += 1
 
    return lam, mu

Like the tortoise and hare algorithm, this is a pointer algorithm that uses O(λ + μ) tests and function evaluations and O(1) storage space. It is not difficult to show that the number of function evaluations can never be higher than for Floyd’s algorithm. Brent claims that, on average, his cycle finding algorithm runs around 36% more quickly than Floyd’s and that it speeds up the Pollard rho algorithm by around 24%. He also performs an average case analysis for a randomized version of the algorithm in which the sequence of indices traced by the slower of the two pointers is not the powers of two themselves, but rather a randomized multiple of the powers of two. Although his main intended application was in integer factorization algorithms, Brent also discusses applications in testing pseudorandom number generators.^[8]

Gosper’s algorithm[edit]

R. W. Gosper’s algorithm^[10][11] finds the period , and the lower and upper bound of the starting point, and , of the first cycle. The difference between the lower and upper bound is of the same order as the period, eg. .

Advantages[edit]

The main feature of Gosper’s algorithm is that it never backs up to reevaluate the generator function, and is economical in both space and time. It could be roughly described as a concurrent version of Brent’s algorithm. While Brent’s algorithm gradually increases the gap between the tortoise and hare, Gosper’s algorithm uses several tortoises (several previous values are saved), which are roughly exponentially spaced. According to the note in HAKMEM item 132, this algorithm will detect repetition before the third occurrence of any value, i.e. the cycle will be iterated at most twice. This note also states that it is sufficient to store previous values; however, the provided implementation^[10] stores values. For example, assume the function values are 32-bit integers, and therefore the second iteration of the cycle ends after at most 2³² function evaluations since the beginning (viz. ). Then Gosper’s algorithm will find the cycle after at most 2³² function evaluations, while consuming the space of 33 values (each value being a 32-bit integer).

Complexity[edit]

Upon the -th evaluation of the generator function, the algorithm compares the generated value with previous values; observe that goes up to at least and at most . Therefore, the time complexity of this algorithm is . Since it stores values, its space complexity is . This is under the usual assumption, present throughout this article, that the size of the function values is constant. Without this assumption, the space complexity is since we need at least distinct values and thus the size of each value is .

Time–space tradeoffs[edit]

A number of authors have studied techniques for cycle detection that use more memory than Floyd’s and Brent’s methods, but detect cycles more quickly. In general these methods store several previously-computed sequence values, and test whether each new value equals one of the previously-computed values. In order to do so quickly, they typically use a hash table or similar data structure for storing the previously-computed values, and therefore are not pointer algorithms: in particular, they usually cannot be applied to Pollard’s rho algorithm. Where these methods differ is in how they determine which values to store. Following Nivasch,^[12] we survey these techniques briefly.

• Brent^[8] already describes variations of his technique in which the indices of saved sequence values are powers of a number R other than two. By choosing R to be a number close to one, and storing the sequence values at indices that are near a sequence of consecutive powers of R, a cycle detection algorithm can use a number of function evaluations that is within an arbitrarily small factor of the optimum λ + μ.^[13][14]
• Sedgewick, Szymanski, and Yao^[15] provide a method that uses M memory cells and requires in the worst case only function evaluations, for some constant c, which they show to be optimal. The technique involves maintaining a numerical parameter d, storing in a table only those positions in the sequence that are multiples of d, and clearing the table and doubling d whenever too many values have been stored.
• Several authors have described distinguished point methods that store function values in a table based on a criterion involving the values, rather than (as in the method of Sedgewick et al.) based on their positions. For instance, values equal to zero modulo some value d might be stored.^[16][17] More simply, Nivasch^[12] credits D. P. Woodruff with the suggestion of storing a random sample of previously seen values, making an appropriate random choice at each step so that the sample remains random.
• Nivasch^[12] describes an algorithm that does not use a fixed amount of memory, but for which the expected amount of memory used (under the assumption that the input function is random) is logarithmic in the sequence length. An item is stored in the memory table, with this technique, when no later item has a smaller value. As Nivasch shows, the items with this technique can be maintained using a stack data structure, and each successive sequence value need be compared only to the top of the stack. The algorithm terminates when the repeated sequence element with smallest value is found. Running the same algorithm with multiple stacks, using random permutations of the values to reorder the values within each stack, allows a time–space tradeoff similar to the previous algorithms. However, even the version of this algorithm with a single stack is not a pointer algorithm, due to the comparisons needed to determine which of two values is smaller.

Any cycle detection algorithm that stores at most M values from the input sequence must perform at least function evaluations.^[18][19]

Applications[edit]

Cycle detection has been used in many applications.

• Determining the cycle length of a pseudorandom number generator is one measure of its strength. This is the application cited by Knuth in describing Floyd’s method.^[3] Brent^[8] describes the results of testing a linear congruential generator in this fashion; its period turned out to be significantly smaller than advertised. For more complex generators, the sequence of values in which the cycle is to be found may not represent the output of the generator, but rather its internal state.
• Several number-theoretic algorithms are based on cycle detection, including Pollard’s rho algorithm for integer factorization^[20] and his related kangaroo algorithm for the discrete logarithm problem.^[21]
• In cryptographic applications, the ability to find two distinct values x_μ−-1 and x_λ+μ−-1 mapped by some cryptographic function ƒ to the same value x_μ may indicate a weakness in ƒ. For instance, Quisquater and Delescaille^[17] apply cycle detection algorithms in the search for a message and a pair of Data Encryption Standard keys that map that message to the same encrypted value; Kaliski, Rivest, and Sherman^[22] also use cycle detection algorithms to attack DES. The technique may also be used to find a collision in a cryptographic hash function.^[23]
• Cycle detection may be helpful as a way of discovering infinite loops in certain types of computer programs.^[24]
• Periodic configurations in cellular automaton simulations may be found by applying cycle detection algorithms to the sequence of automaton states.^[12]
• Shape analysis of linked list data structures is a technique for verifying the correctness of an algorithm using those structures. If a node in the list incorrectly points to an earlier node in the same list, the structure will form a cycle that can be detected by these algorithms.^[25] In Common Lisp, the S-expression printer, under control of the *print-circle* variable, detects circular list structure and prints it compactly.
• Teske^[14] describes applications in computational group theory: determining the structure of an Abelian group from a set of its generators. The cryptographic algorithms of Kaliski et al.^[22] may also be viewed as attempting to infer the structure of an unknown group.
• Fich (1981) briefly mentions an application to computer simulation of celestial mechanics, which she attributes to William Kahan. In this application, cycle detection in the phase space of an orbital system may be used to determine whether the system is periodic to within the accuracy of the simulation.^[18]
• In Mandelbrot Set fractal generation some performance techniques are used to speed up the image generation. One of them is called «period checking», which consists of finding the cycles in a point orbit. This article describes the «period checking» technique. You can find another explanation here. Some cycle detection algorithms have to be implemented in order to implement this technique.

References[edit]

External links[edit]

• Gabriel Nivasch, The Cycle Detection Problem and the Stack Algorithm
• Tortoise and Hare, Portland Pattern Repository
• Floyd’s Cycle Detection Algorithm (The Tortoise and the Hare)
• Brent’s Cycle Detection Algorithm (The Teleporting Turtle)

В этом посте будут обнаружены циклы в связанном списке с использованием хеширования и алгоритма обнаружения циклов Флойда.

Например, следующий связанный список содержит цикл:

Потренируйтесь в этой проблеме

1. Использование хеширования

Простое решение — использовать Хеширование. Идея состоит в том, чтобы пройти по заданному списку и вставить каждый встреченный узел в набор. Если текущий узел уже присутствует в наборе (т. е. он был замечен ранее), это означает, что в списке присутствует цикл.

Ниже приведена программа на C++, Java и Python, которая демонстрирует это:

Временная сложность приведенного выше решения равна O(n), куда n общее количество узлов в связанном списке. Вспомогательное пространство, необходимое программе, равно O(n).

2. Алгоритм обнаружения цикла Флойда

Алгоритм обнаружения циклов Флойда — это алгоритм указателей, использующий только два указателя, которые перемещаются по последовательности с разной скоростью. Идея состоит в том, чтобы перемещать быстрый указатель в два раза быстрее, чем медленный, а расстояние между ними увеличивается на единицу с каждым шагом. Если мы оба встретимся в какой-то момент, мы нашли цикл в списке; в противном случае цикл отсутствует, если достигнут конец списка. Его еще называют “алгоритмом черепахи и зайца”.

Алгоритм может быть реализован следующим образом на C++, Java и Python:

Временная сложность приведенного выше решения равна O(n), куда n — это общее количество узлов в связанном списке, не требующее дополнительного места.

В информатике, обнаружение цикла или поиск цикла — это алгоритмическая проблема поиска цикла в последовательности значений повторяющейся функции.

Для любой функции f, которая отображает конечный набор S на себя, и любое начальное значение x 0 в S, последовательность повторенных значения функции

x 0, x 1 = f (x 0), x 2 = f (x 1),…, xi = f (xi — 1),… { displaystyle x_ {0}, x_ {1 } = f (x_ {0}), x_ {2} = f (x_ {1}), dots, x_ {i} = f (x_ {i-1}), dots}

в конечном итоге должен использовать одно и то же значение дважды: должна существовать пара различных индексов i и j, такая, что x i = x j. Как только это произойдет, последовательность должна продолжаться периодически, повторяя ту же последовательность значений от x i до x j — 1. Обнаружение цикла — это проблема поиска i и j при заданных f и x 0.

Известно несколько алгоритмов для быстрого поиска циклов с небольшим объемом памяти. Алгоритм черепахи и зайца Роберта Флойда перемещает два указателя с разной скоростью через последовательность значений, пока они оба не укажут на равные значения. В качестве альтернативы алгоритм Брента основан на идее экспоненциального поиска. Алгоритмы как Флойда, так и Брента используют только постоянное количество ячеек памяти и выполняют ряд вычислений функций, которые пропорциональны расстоянию от начала последовательности до первого повторения. Некоторые другие алгоритмы жертвуют большим объемом памяти за меньшее количество вычислений функций.

Применения обнаружения цикла включают проверку качества генераторов псевдослучайных чисел и криптографических хеш-функций, алгоритмов теории чисел, обнаружение бесконечные циклы в компьютерных программах и периодические конфигурации в клеточных автоматах, автоматический анализ формы из структур данных связанного списка, обнаружение взаимоблокировок для управления транзакциями в СУБД.

Содержание

• 1 Пример
• 2 Определения
• 3 Компьютерное представление
• 4 Алгоритмы
  • 4.1 Черепаха и Заяц Флойда
  • 4.2 Алгоритм Брента
  • 4.3 Алгоритм Госпера
  • 4.4 Компромисс между пространством и временем
• 5 Приложения
• 6 Ссылки
• 7 Внешние ссылки

Пример

Функция от и до множества {0,1,2,3,4,5,6,7,8} и соответствующий функциональный граф

На рисунке показана функция f, которая отображает множество S = {0,1,2,3,4, 5,6,7,8} себе. Если начать с x 0 = 2 и многократно применить f, вы увидите последовательность значений

2, 0, 6, 3, 1, 6, 3, 1, 6, 3, 1,….

Цикл в этой последовательности значений равен 6, 3, 1.

Определения

Пусть S — любое конечное множество, f — любая функция от S до самой себя, и x 0 — любой элемент S. Для любого i>0 пусть x i = f (x i — 1). Пусть μ будет наименьшим индексом, так что значение x μ повторяется бесконечно часто в последовательности значений x i, и пусть λ (длина цикла) будет наименьшим положительным целым числом, таким, что x μ = x λ + μ. Задача обнаружения цикла — это задача нахождения λ и μ.

Можно рассмотреть ту же проблему теоретически, построив функциональный граф (то есть, ориентированный граф, в котором каждая вершина имеет одно исходящее ребро), вершины которого являются элементами S, а ребра которого отображают элемент на соответствующее значение функции, как показано на рисунке. Множество вершин , достижимых из начальной вершины x 0, образуют подграф с формой, напоминающей греческую букву ро (ρ): путь длиной μ от x От 0 до цикла из λ вершин.

Компьютерное представление

Как правило, f не указывается в виде таблицы значений, так как показано на рисунке выше. Напротив, алгоритму обнаружения цикла может быть предоставлен доступ либо к последовательности значений x i, либо к подпрограмме для вычисления f. Задача состоит в том, чтобы найти λ и μ, исследуя как можно меньше значений из последовательности или выполняя как можно меньше вызовов подпрограмм. Как правило, также важна пространственная сложность алгоритма для задачи обнаружения цикла: мы хотим решить эту проблему, используя объем памяти, значительно меньший, чем потребуется для хранения всей последовательности.

В некоторых приложениях, и в частности в алгоритме ро Полларда для целочисленной факторизации, алгоритм имеет гораздо более ограниченный доступ к S и к f. В алгоритме Ро Полларда, например, S — это набор целых чисел по модулю неизвестного простого множителя числа, которое нужно разложить на множители, поэтому даже размер S неизвестен алгоритму. Чтобы позволить использовать алгоритмы обнаружения цикла с такими ограниченными знаниями, они могут быть разработаны на основе следующих возможностей. Первоначально предполагается, что алгоритм имеет в своей памяти объект, представляющий указатель на начальное значение x 0. На любом этапе он может выполнить одно из трех действий: он может скопировать любой указатель, который он имеет, на другой объект в памяти, он может применить f и заменить любой из своих указателей указателем на следующий объект в последовательности, или он может применить подпрограмма для определения, представляют ли два из ее указателя равные значения в последовательности. Действие проверки на равенство может включать в себя некоторые нетривиальные вычисления: например, в алгоритме ро Полларда оно реализуется путем проверки того, имеет ли разница между двумя сохраненными значениями нетривиальный наибольший общий делитель с числом, которое нужно факторизовать. В этом контексте, по аналогии с моделью вычислений машины указателя, алгоритм, который использует только копирование указателя, продвижение в последовательности и проверки равенства, может называться алгоритмом указателя.

Алгоритмы

Если ввод задан как подпрограмма для вычисления f, проблема обнаружения цикла может быть тривиально решена с использованием только приложений функции λ + μ, просто путем вычисления последовательности значений x i и с использованием структуры данных , такой как хэш-таблица, для хранения этих значений и проверки того, было ли уже сохранено каждое последующее значение. Однако пространственная сложность этого алгоритма пропорциональна λ + μ, что неоправданно велико. Кроме того, для реализации этого метода в виде алгоритма указателя потребуется применить проверку равенства к каждой паре значений, что приведет к квадратичному времени в целом. Таким образом, исследования в этой области сосредоточены на двух целях: использование меньшего пространства, чем этот наивный алгоритм, и поиск алгоритмов указателей, которые используют меньше тестов на равенство.

Черепаха и Заяц Флойда

Алгоритм обнаружения цикла «черепаха и заяц» Флойда, примененный к последовательности 2, 0, 6, 3, 1, 6, 3, 1,…

Флойда Алгоритм поиска цикла — это алгоритм указателя, который использует только два указателя, которые перемещаются по последовательности с разной скоростью. Его также называют «алгоритмом черепахи и зайца», отсылая к басне Эзопа Черепаха и Заяц.

. Алгоритм назван в честь Роберта У. Флойда, которому приписывают его изобретение Дональда Кнута. Однако алгоритм не появляется в опубликованной работе Флойда, и это может быть неправильной атрибуцией: Флойд описывает алгоритмы для перечисления всех простых циклов в ориентированном графе в статье 1967 года, но эта статья не описывает цикл -нахождение проблемы в функциональных графах, которой и посвящена данная статья. Фактически, заявление Кнута (1969 г.), приписывающее его Флойду, без цитирования, является первым известным печатным словом, и, таким образом, может быть народной теоремой, не относящейся к одному человеку <91.>

Ключевое понимание алгоритма заключается в следующем. Если цикл существует, то для любых целых чисел i ≥ μ и k ≥ 0 x i = x i + kλ, где λ — длина найденного цикла. а μ — номер первого элемента цикла. На основании этого можно затем показать, что i = kλ ≥ μ для некоторого k тогда и только тогда, когда x i = x 2i. Таким образом, алгоритму нужно только проверить повторяющиеся значения этой специальной формы, одно в два раза дальше от начала последовательности, чем другое, чтобы найти период ν повторения, кратный λ. Как только ν найдено, алгоритм повторяет последовательность от ее начала, чтобы найти первое повторяющееся значение x μ в последовательности, используя тот факт, что λ делит ν, и, следовательно, x μ = х μ + v. Наконец, как только значение μ известно, становится тривиальным найти длину λ кратчайшего повторяющегося цикла путем поиска первой позиции μ + λ, для которой x μ + λ = x μ.

Таким образом, алгоритм поддерживает два указателя на заданную последовательность, один (черепаха) в x i, а другой (заяц) в x 2i. На каждом шаге алгоритма он увеличивает i на единицу, перемещая черепаху на один шаг вперед, а зайца на два шага вперед по последовательности, а затем сравнивает значения последовательности на этих двух указателях. Наименьшее значение i>0, для которого черепаха и заяц указывают на равные значения, является искомым значением ν.

Следующий код Python показывает, как эту идею можно реализовать в виде алгоритма.

def floyd (f, x0): # Основная фаза алгоритма: поиск повторения x_i = x_2i. # Заяц движется вдвое быстрее черепахи и # расстояние между ними увеличивается на 1 с каждым шагом. # В конце концов они оба окажутся внутри цикла, а затем, # в какой-то момент, расстояние между ними будет # делиться на период λ. черепаха = f (x0) # f (x0) - это элемент / узел рядом с x0. hare = f (f (x0)) while tortoise! ​​= hare: tortoise = f (tortoise) hare = f (f (hare)) # В этой точке положение черепахи, ν, которое также равно # расстоянию между зайцами и черепаха, делится на # период λ. Таким образом, заяц, перемещающийся по кругу по одному шагу за раз, # и черепаха (сброшен на x0), двигаясь к кругу, # пересекутся в начале круга. Поскольку # расстояние между ними постоянно и равно 2ν, кратно λ, # они согласятся, как только черепаха достигнет индекса μ. # Найдите позицию μ первого повторения. mu = 0 tortoise = x0 while tortoise! ​​= hare: tortoise = f (tortoise) hare = f (hare) # Заяц и черепаха движутся с одинаковой скоростью mu + = 1 # Найдите длину самого короткого цикла, начиная с x_μ # Заяц делает шаг за шагом, пока черепаха неподвижна. # lam увеличивается до тех пор, пока не будет найдено λ. lam = 1 hare = f (черепаха) while tortoise! ​​= hare: hare = f (hare) lam + = 1 return lam, mu

Этот код обращается к последовательности только путем сохранения и копирования указателей, оценок функций и тестов на равенство ; поэтому он квалифицируется как алгоритм указателя. Алгоритм использует O (λ + μ) операций этих типов и O (1) дискового пространства.

Алгоритм Брента

Ричард П. Брент описал альтернативный алгоритм обнаружения цикла, который, как и Алгоритм черепахи и зайца требует только двух указателей в последовательности. Однако он основан на другом принципе: поиск наименьшей степени двойки 2, которая больше, чем λ и μ. Для i = 0, 1, 2,… алгоритм сравнивает x 2−1 с каждым последующим значением последовательности до следующей степени двойки и останавливается, когда находит совпадение. Он имеет два преимущества по сравнению с алгоритмом черепахи и зайца: он находит правильную длину цикла λ напрямую, вместо того, чтобы искать ее на следующем этапе, и его шаги включают только одну оценку f, а не три.

Следующий код Python более подробно показывает, как этот метод работает.

def brent (f, x0): # основная фаза: поиск последовательных степеней двойки power = lam = 1 tortoise = x0 hare = f (x0) # f (x0) - это элемент / узел рядом с x0. while tortoise! ​​= hare: if power == lam: # пора начинать новую силу двойки? tortoise = hare power * = 2 lam = 0 hare = f (hare) lam + = 1 # Найти позицию первого повторения длины λ tortoise = hare = x0 для i in range (lam): # range (lam) производит список со значениями 0, 1,..., lam-1 hare = f (hare) # Теперь расстояние между зайцем и черепахой равно λ. # Затем заяц и черепаха движутся с одинаковой скоростью, пока не согласятся, что mu = 0, а черепаха! = Hare: tortoise = f (tortoise) hare = f (hare) mu + = 1 return lam, mu

Как черепаха и hare алгоритм, это алгоритм указателя, который использует O (λ + μ) тестов и оценок функций и O (1) дискового пространства. Нетрудно показать, что количество вычислений функций никогда не может быть больше, чем для алгоритма Флойда. Брент утверждает, что в среднем его алгоритм поиска циклов работает примерно на 36% быстрее, чем алгоритм Флойда, и что он ускоряет алгоритм Полларда примерно на 24%. Он также выполняет анализ среднего случая для рандомизированной версии алгоритма, в которой последовательность индексов, отслеживаемых более медленным из двух указателей, не является степенью двойки, а скорее рандомизированным кратным степеням. из двух. Хотя его основное предполагаемое применение было в алгоритмах целочисленной факторизации, Брент также обсуждает приложения для тестирования генераторов псевдослучайных чисел.

алгоритм Госпера

R. Алгоритм У. Госпера находит период λ { displaystyle lambda}, а также нижнюю и верхнюю границу начальной точки μ l { displaystyle mu _ {l}}и μ u { displaystyle mu _ {u}}первого цикла. Разница между нижней и верхней границей того же порядка, что и период, например. μ l + λ ∼ μ h { displaystyle mu _ {l} + lambda sim mu _ {h}}.

Основная особенность алгоритма Госпера заключается в том, что он никогда не выполняет резервное копирование для переоценки генератора функции и экономичен как в пространстве, так и во времени. Это можно примерно описать как параллельную версию алгоритма Брента. В то время как алгоритм Брента постепенно увеличивает разрыв между черепахой и зайцем, алгоритм Госпера использует несколько черепах (сохраняются несколько предыдущих значений), которые расположены примерно по экспоненте. Согласно примечанию в элементе 132 HAKMEM, этот алгоритм обнаружит повторение перед третьим появлением любого значения, например. цикл будет повторяться не более двух раз. В этом примечании также говорится, что достаточно сохранить Θ (log ⁡ λ) { displaystyle Theta ( log lambda)}предыдущие значения; однако предоставленная реализация хранит значения Θ (log ⁡ (μ + λ)) { displaystyle Theta ( log ( mu + lambda))}. Например: значения функции представляют собой 32-битные целые числа, и априори известно, что вторая итерация цикла заканчивается после не более чем двух вычислений функции с начала, т.е. μ + 2 λ ≤ 2 32 { displaystyle mu +2 lambda leq 2 ^ {32}}. Тогда достаточно сохранить 33 32-битных целых числа.

После i { displaystyle i}-ой оценки функции генератора алгоритм сравнивает сгенерированное значение с O (log ⁡ i) { displaystyle O ( log i)}предыдущие значения; обратите внимание, что i { displaystyle i}возрастает не менее μ + λ { displaystyle mu + lambda}и не более μ + 2 λ { displaystyle mu +2 lambda}. Следовательно, временная сложность этого алгоритма составляет O ((μ + λ) ⋅ log ⁡ (μ + λ)) { displaystyle O (( mu + lambda) cdot log ( mu + lambda))}. Поскольку он хранит значения Θ (log ⁡ (μ + λ)) { displaystyle Theta ( log ( mu + lambda))}, его пространственная сложность составляет Θ ( журнал ⁡ (μ + λ)) { Displaystyle Theta ( log ( mu + lambda))}. Это происходит при обычном предположении, присутствующем в этой статье, что размер значений функции постоянен. Без этого предположения сложность пространства равна Ω (log 2 ⁡ (μ + λ)) { displaystyle Omega ( log ^ {2} ( mu + lambda))}, поскольку нам нужно по крайней мере μ + λ { displaystyle mu + lambda}различных значений, и поэтому размер каждого значения составляет Ω (log ⁡ (μ + λ)) { displaystyle Omega ( log ( mu + lambda))}.

Компромисс между пространством и временем

Ряд авторов изучили методы обнаружения цикла, которые используют больше памяти, чем методы Флойда и Брента, но обнаруживают циклы быстрее. Как правило, эти методы хранят несколько ранее вычисленных значений последовательности и проверяют, равно ли каждое новое значение одному из ранее вычисленных значений. Чтобы сделать это быстро, они обычно используют хэш-таблицу или аналогичную структуру данных для хранения ранее вычисленных значений и, следовательно, не являются алгоритмами указателя: в частности, они обычно не могут быть применены к алгоритму rho Полларда.. Эти методы различаются тем, как они определяют, какие значения хранить. Следуя Nivasch, мы кратко рассмотрим эти методы.

• Брент уже описывает варианты своей техники, в которых индексы сохраненных значений последовательности являются степенями числа R, отличного от двух. Выбирая R как число, близкое к единице, и сохраняя значения последовательности в индексах, которые близки к последовательности последовательных степеней R, алгоритм обнаружения цикла может использовать ряд оценок функций, которые находятся в пределах произвольно малого коэффициента оптимального λ + μ.
• Седжвик, Шимански и Яо предлагают метод, использующий M ячеек памяти и требующий в худшем случае только (λ + μ) (1 + c M — 1/2) { displaystyle ( lambda + mu) (1 + cM ^ {- 1/2})}оценки функции для некоторой константы c, которая, по их мнению, является оптимальной. Этот метод включает поддержание числового параметра d, сохранение в таблице только тех позиций в последовательности, которые кратны d, очистку таблицы и удвоение d всякий раз, когда было сохранено слишком много значений.
• Несколько авторов описали методы выделенных точек, которые хранят значения функций в таблице на основе критерия, включающего значения, а не (как в методе Седжевика и др.) на основе их положения. Например, могут быть сохранены значения, равные нулю по модулю некоторого значения d. Проще говоря, Nivasch доверяет Д.П. Вудраффу предложение хранить случайную выборку ранее увиденных значений, делая соответствующий случайный выбор на каждом этапе, чтобы выборка оставалась случайной.
• Nivasch описывает алгоритм, который не использует фиксированный объем памяти, но для которого ожидаемый объем используемой памяти (в предположении, что функция ввода является случайной) является логарифмическим по длине последовательности. При использовании этого метода элемент сохраняется в таблице памяти, когда ни один из последующих элементов не имеет меньшего значения. Как показывает Nivasch, элементы с помощью этого метода могут поддерживаться с использованием структуры данных стека , и каждое последующее значение последовательности необходимо сравнивать только с вершиной стека. Алгоритм завершается, когда обнаруживается повторяющийся элемент последовательности с наименьшим значением. Выполнение того же алгоритма с несколькими стеками, используя случайные перестановки значений для изменения порядка значений в каждом стеке, позволяет найти компромисс между пространством и временем, аналогичный предыдущим алгоритмам. Однако даже версия этого алгоритма с одним стеком не является алгоритмом указателя из-за сравнений, необходимых для определения, какое из двух значений меньше.

Любой алгоритм обнаружения цикла, который хранит не более M значений из входной последовательности, должен выполнить не менее (λ + μ) (1 + 1 M — 1) { displaystyle ( lambda + mu) left (1 + { frac {1} {M-1}} right)}оценка функций.

Приложения

Обнаружение цикла использовалось во многих приложениях.

• Определение длины цикла генератора псевдослучайных чисел является одним из показателей его силы. Это приложение, которое цитирует Кнут при описании метода Флойда. Брент описывает результаты тестирования линейного конгруэнтного генератора таким образом; его срок оказался значительно меньше заявленного. Для более сложных генераторов последовательность значений, в которой должен быть найден цикл, может представлять не выход генератора, а его внутреннее состояние.
• Некоторые алгоритмы теории чисел являются основан на обнаружении цикла, включая алгоритм ро Полларда для целочисленной факторизации и связанный с ним алгоритм кенгуру для задачи дискретного логарифма.
• In криптографические приложения, способность находить два различных значения x μ −- 1 и x λ + μ −- 1, сопоставленных некоторой криптографической функцией ƒ с одним и тем же значением x μ может указывать на слабость ƒ. Например, Quisquater и Delescaille применяют алгоритмы обнаружения цикла при поиске сообщения и пару ключей Data Encryption Standard, которые отображают это сообщение в одно и то же зашифрованное значение; Калиски, Ривест и Шерман также используют алгоритмы обнаружения цикла для атаки на DES. Этот метод также можно использовать для поиска коллизии в криптографической хеш-функции .
• Обнаружение цикла может быть полезным как способ обнаружения бесконечных циклов в определенных типах компьютерные программы.
• Периодические конфигурации в моделировании клеточного автомата могут быть найдены путем применения алгоритмов обнаружения цикла к последовательности состояний автомата.
• Анализ формы из связан Структуры данных list — это метод проверки правильности алгоритма с использованием этих структур. Если узел в списке неправильно указывает на более ранний узел в том же списке, структура сформирует цикл, который может быть обнаружен этими алгоритмами. В Common Lisp принтер S-выражения под управлением переменной * print-circle *обнаруживает кольцевую структуру списка и печатает ее компактно.
• Теске описывает приложения в теории вычислительных групп : определение структуры абелевой группы по набору ее образующих. Криптографические алгоритмы Калиски и др. также может рассматриваться как попытка вывести структуру неизвестной группы.
• Fich (1981) кратко упоминает приложение к компьютерному моделированию небесной механики, которое она атрибуты Уильяма Кахана. В этом приложении обнаружение цикла в фазовом пространстве орбитальной системы может использоваться для определения того, является ли система периодической с точностью до точности моделирования.
• В наборе фракталов Мандельброта некоторые методы производительности используются для ускорения генерации изображения. Один из них называется «проверка периода» и в основном заключается в нахождении циклов на точечной орбите. В этой статье описывается техника «проверки периода », а здесь вы можете найти лучшее объяснение. Для реализации этого необходимо реализовать несколько алгоритмов обнаружения цикла.

Ссылки

Внешние ссылки

• Габриэль Ниваш, Проблема обнаружения цикла и алгоритм стека
• Черепаха и Заяц, Портлендский репозиторий паттернов
• Алгоритм обнаружения цикла Флойда (Черепаха и Заяц)
• Алгоритм обнаружения цикла Брента (Телепортирующаяся черепаха)

Как я простые циклы искал

Проснулся я как-то ближе к вечеру и решил — всё пора, пора уже сделать новую фичу в моей библиотеке. А за одно и проверку графа на циклы починить и ускорить. К утреннему обеду сделал новую фичу, улучшил код, сделал представление графа в удобном виде, и дошёл до задачи нахождения всех простых циклов в графе. Потягивая чашку холодной воды, открыл гугл, набрал «поиск всех простых циклов в графе» и увидел…

Увидел я не много… хотя было всего лишь 4 часа утра. Пару ссылок на алгоритмы ссылка1, ссылка2, и много намеком на то, что пора спать циклов в графе может быть много, и в общем случае задача не решаемая. И еще вопрос на хабре на эту тему, ответ на который меня тоже не спас — про поиск в глубину я и так знал.

Но раз я решил, то даже NP сложную задачу решу за P тем более я пью воду, а не кофе — а она не может резко закончиться. И я знал, что в рамках моей задачи найти все циклы должно быть возможным за маленькое время, без суперкомпьютеров — не тот порядок величин у меня.

Немного отвлечемся от детектива, и поймем зачем мне это нужно.

Что за библиотека?

Библиотека называется DITranquillity написана на языке Swift, и её задача — внедрять зависимости. С задачей внедрения зависимостей библиотека справляется на ура, имеет возможности которые не умеют другие библиотеки на Swift, и делает это с хорошей скоростью.

Но зачем мне взбрело проверять циклы в графе зависимостей?

Ради киллерфичи — если библиотека делает основной функционал на ура, то ищешь способы её улучшить и сделать лучше. А киллефича — это проверка графа зависимостей на правильность — это набор разных проверок, которые позволяют избежать проблем во время исполнения, что экономит время разработки. И проверка на циклы выделяется отдельно среди всех проверок, так как эта операция занимает гораздо больше времени. И до недавнего времени некультурно больше времени.

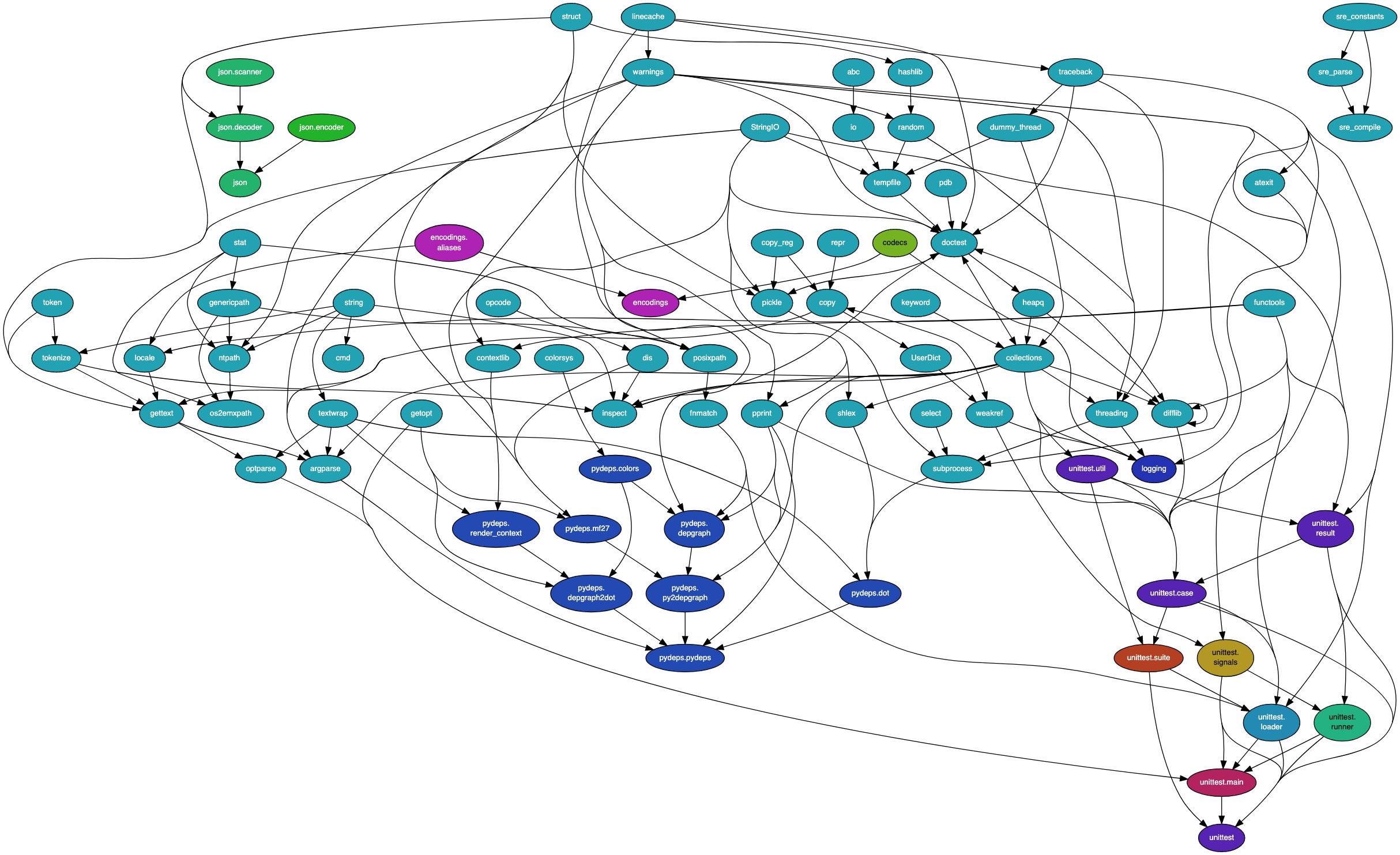
О проблеме я знал давно, но понимал, что в том виде, в каком сейчас хранится граф сделать быструю проверку сложно. Да и раз уж библиотека умеет проверять граф зависимостей, то сделать «Graph API» само напрашивается. «Graph API» — позволяет отдавать граф зависимостей для внешнего пользования, чтобы:

• Его проанализировать как-то на свой лад. Например, в своё время, для работы собрал автоматически все зависимости между нашими модулями, что помогло убрать лишние зависимости и ускорить сборку.
• Пока нет, но когда-нибудь будет — визуализация этого графа с помощью graphvis.
• Проверка графа на корректность.

Особенно ради второго — кто как, а мне нравится смотреть на эти ужасные картинки и понимать как же все плохо…

Исходные данные

Давайте посмотрим, с чем предстоит работать:

• MacBook pro 2019, 2,6 GHz 6-Core i7, 32 Gb, Xcode 11.4, Swift 5.2
• Проект на языке Swift с 300к+ строчек кода (пустые строки и комментарии не в счёт)
• Более 900 вершин
• Более 2000 ребер
• Максимальная глубина зависимостей достигает 40
• Почти 7000 циклов

Все замеры делаются в debug режиме, не в release, так как использовать проверку графа будут только в debug.

До этой ночи, время проверки составляло 95 минут.

Этап 1. Представление графа

Возвращаемся к нашему детективу. Мой графне Монте Кристо, он ориентированный.
Каждая вершина графа это компонент, ну или проще информация о классе. До появления Graph API все компоненты хранились в словаре, и каждый раз приходилось в него лазить, еще и ключ создавать. Что не очень быстро. Поэтому, будучи в здравом уме, я понимал, что граф надо представить в удобном виде.

Как человек, недалекий от теории графов, я помнил только одно представление графа — Матрица смежности. Правда моё создание подсказывало, что есть и другие, и немного поднапряг память, я вспомнил три варианта представления графа:

• Список вершин и список ребер — отдельно храним вершины, отдельно храним ребра.
• Матрица смежности — для каждой вершины храним информацию, есть ли переход в другую вершину
• Список смежности — для каждой вершины храним список переходов

Но прежде чем напрягать мозги, пальцы уже сделали своё дело, и пока я думал какой сейчас час, на экране уже успел появиться код для создания графа в виде матрицы смежности. Жалко конечно, но код пришлось переписать — для моей задачи важнее как можно быстрее находить исходящие ребра, а вот входящие меня мало интересуют. Да и память в наше время безгранична — почему бы её не сэкономить?

Переписав код, получилось что-то на подобии такого:

Graph:
    vertices: [Vertex]
    adjacencyList: [[Edge]]

Vertex:
    more information about vertex

Edge:
    toIndices: [Int]
    information about edge

Где Vertex информация о вершине, а Edge информация о переходе, в том числе и индексы, куда по этому ребру можно перейти.
Обращаю внимание что ребро хранит переход не один в один, а один в много. Это сделано специально, чтобы обеспечить уникальность рёбер, что в случае зависимостей очень важно, так как два перехода на две вершины, и один переход на две вершины означает разное.

Этап 2. Наивный поиск в глубину

Из начала статьи все же помнят, что к этому моменту было уже 4 часа утра, а значит, единственная идея, как реализовать поиск всех простых циклов была та, что я нашел в гугле, да и мой учитель всегда говорил — «прежде чем оптимизировать, убедись, что это необходимо». Поэтому первым делом я написал обычный поиск в глубину:

func findAllCycles() -> [Cycle] {
  result: [Cycle] = []
  for index in vertices {
    result += findCycles(from: index)
  }

  return result
}

func findCycles(from index: Int) -> [Cycle] {
  result: [Cycle] = []
  dfs(startIndex: index, currentIndex: index, visitedIndices: [], result: &result)

  return result
}

func dfs(startIndex: Int,
         currentIndex: Int,
         // visitedIndices каждый раз копируется
         visitedIndices: Set<Int>,
         // result всегда один - это ссылка
         result: ref [Cycle]) {
  if currentIndex == startIndex && !visitedIndices.isEmpty {
    result.append(cycle)
    return
  }

  if visitedIndices.contains(currentIndex) {
    return
  }

  visitedIndices += [currentIndex]

  for toIndex in adjacencyList[currentIndex] {
    dfs(startIndex: startIndex, currentIndex: toIndex, visitedIndices: visitedIndices, result: &result)
  }
}

Запустил этот алгоритм, подождал 10 минут… И, конечно же, ушел спать — А то уже солнце появилось из-за верхушек зданий…

Пока спал, думал — а почему так долго? Про размер графа я уже писал, но в чем проблема данного алгоритма? Судорожно вспоминая дебажные логи вспомнил, что для многих вершин количество вызовов функции dfs составляет миллион, а для некоторых по 30 миллионов раз. То есть в среднем 900 вершин * 1000000 = 900.000.000 вызовов функции dfs…

Откуда такие бешеные цифры? Будь бы это обычный лес, то все бы работало быстро, но у нас же граф с циклами… ZZzzz…

Этап 3. Наивная оптимизация

Проснулся я снова не по завету после обеда, и первым делом было не пойти в туалет, и уж точно не поесть, а посмотреть, сколько же выполнялся мой алгоритм, а ну да всего-то полтора часа… Ну, ладно, я за ночь придумал, как оптимизировать!

В первой реализации ищутся циклы, проходящие только через указанную вершину, а все подциклы, найденные при поиске основных циклов, просто игнорируются. Возникает желание перестать их игнорировать — тогда получается, что можно выкидывать из рассмотрения все вершины, через которые мы уже прошли. Сделать это не так сложно, правда, когда пальцы не попадают по клавиатуре чуть сложнее, но каких-то полчаса и готово:

func findAllCycles() -> [Cycle] {
  globalVisitedIndices: Set<Int> = []
  result: [Cycle] = []
  for index in vertices {
    if globalVisitedIndices.containts(index) {
      continue
    }
    result += findCycles(from: index, globalVisitedIndices: &globalVisitedIndices)
  }

  return result
}

func findCycles(from index: Int, globalVisitedIndices: ref Set<Int>) -> [Cycle] {
  result: [Cycle] = []
  dfs(currentIndex: index, visitedIndices: [], globalVisitedIndices, &globalVisitedIndices, result: &result)

  return result
}

func dfs(currentIndex: Int,
         // visitedIndices каждый раз копируется
         visitedIndices: Set<Int>,
         // globalVisitedIndices всегда один - это ссылка
         globalVisitedIndices: ref Set<Int>,
         // result всегда один - это ссылка
         result: ref [Cycle]) {

  if visitedIndices.contains(currentIndex) {
    // если visitedIndices упорядочен, то вырезав кусок, можно получить информацию о цикле
    result.append(cycle)
    return
  }

  visitedIndices += [currentIndex]

  for toIndex in adjacencyList[currentIndex] {
    dfs(currentIndex: toIndex, visitedIndices: visitedIndices, globalVisitedIndices: &globalVisitedIndices, result: &result)
  }
}

Дальше по заповедям программиста «Программист ест, билд идёт» я ушел есть… Ем я быстро. Вернувшись через 10 минут и увидев, что все еще нет результата, я огорчился, и решил подумать, в чем же проблема:

• Если у меня несколько больших раздельных циклов, то на каждый такой цикл тратится уйму времени, благо, всего один раз.
• Многие циклы «дублируются» — нужно проверять уникальность при добавлении, а это время на сравнение.

Интуиция мне подсказывала, что первый вариант был лучше. На самом деле он понятней для анализа, так как мы запоминаем циклы для конкретной вершины, а не для всего подряд.

Этап 4. А что если отсекать листья из поиска

Проснуться я уже успел, а значит самое время для листочка и карандаша. Посмотрев на цифры, нарисовав картинки на листочке, стало понятно, что листья обходить не имеет смысла, и даже не листья, а целые ветки, которые не имеют циклов. Смысл в них заходить, если мы ищем циклы? Вот их и будем отсекать. Пока это думал, руки уже все сделали, и даже нажали run… Ого, вот это оптимизация — глазом моргнуть не успел, а уже все нашло… Ой, а чего циклов так мало то нашлось… Эх… А всё ясно проблема в том, что я не налил себе стакан воды. На самом деле проблема вот в этой строчке:

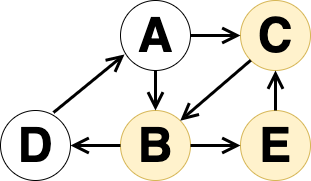
if visitedIndices.contains(currentIndex) {

Я решил, что в этом случае мы тоже наткнулись на лист, но это неверно. Давайте рассмотрим вот такой граф:

В этом графе есть под цикл B->E->C значит, этот if выполнится. Теперь предположим, что вначале мы идем так:
A->B->E->C->B!.. При таком проходе C, Е помечается как лист. После находим цикл A->B->D->A.
Но Цикл A->C->B->D->A будет упущен, так как вершина C помечена как лист.

Если это исправить и отбрасывать только листовые под ветки, то количество вызовов dfs снижается, но не значительно.

Этап 5. Делаем подготовку к поиску

Ладно, еще целых полдня впереди. Посмотрев картинки и различные дебажные логи, стало понятно, что есть ситуации, где функция dfs вызывается 30 миллионов раз, но находится всего 1-2 цикла. Такое возможно в случаях на подобии:

Где «Big» это какой-то большой граф с кучей циклов, но не имеющий цикла на A.

И тут возникает идея! Для всех вершин из Big и C, можно заранее узнать, что они не имеют переходов на A или B, а значит, при переходе на C понятно, что эту вершину не нужно рассматривать, так как из нее нельзя попасть в A.

Как это узнать? Заранее, для каждой вершины запустить или поиск в глубину, или в ширину, и не посещать одну вершину дважды. После сохранить посещенные вершины. Такой поиск в худшем случае на полном графе займет O(N^2) времени, а на реальных данных намного меньше.

Текст для статьи я писал гораздо дольше, чем код для реализации:

func findAllCycles() -> [Cycle] {
  reachableIndices: [Set<Int>] = findAllReachableIndices()
  result: [Cycle] = []
  for index in vertices {
    result += findCycles(from: index, reachableIndices: &reachableIndices)
  }

  return result
}

func findAllReachableIndices() -> [Set<Int>] {
  reachableIndices: [Set<Int>] = []
  for index in vertices {
    reachableIndices[index] = findAllReachableIndices(for: index)
  }
  return reachableIndices
}

func findAllReachableIndices(for startIndex: Int) -> Set<Int> {
  visited: Set<Int> = []
  stack: [Int] = [startIndex]
  while fromIndex = stack.popFirst() {
    visited.insert(fromIndex)

    for toIndex in adjacencyList[fromIndex] {
      if !visited.contains(toIndex) {
        stack.append(toIndex)
      }
    }
  }

  return visited
}

func findCycles(from index: Int, reachableIndices: ref [Set<Int>]) -> [Cycle] {
  result: [Cycle] = []
  dfs(startIndex: index, currentIndex: index, visitedIndices: [], reachableIndices: &reachableIndices, result: &result)

  return result
}

func dfs(startIndex: Int,
         currentIndex: Int,
         visitedIndices: Set<Int>,
         reachableIndices: ref [Set<Int>],
         result: ref [Cycle]) {
  if currentIndex == startIndex && !visitedIndices.isEmpty {
    result.append(cycle)
    return
  }

  if visitedIndices.contains(currentIndex) {
    return
  }

  if !reachableIndices[currentIndex].contains(startIndex) {
    return
  }

  visitedIndices += [currentIndex]

  for toIndex in adjacencyList[currentIndex] {
    dfs(startIndex: startIndex, currentIndex: toIndex, visitedIndices: visitedIndices, result: &result)
  }
}

Готовясь к худшему, я запустил новую реализацию, и пошел смотреть в окно на ближайшее дерево, в 5 метрах — вдаль смотреть говорят полезно. И вот счастье — код полностью исполнился за 15 минут, что в 6-7 раз быстрее прошлого варианта. Порадовавшись мини победе, и порефачив код, я начал думать, что же делать — такой результат меня не устраивал.

Этап 6. Можно ли использовать прошлые результаты?

Все время пока я писал код, и пока спал, меня мучил вопрос — а можно ли как-то использовать результат прошлых вычислений. Ведь уже найдены все циклы через некоторую вершину, наверное, что-то это да значит для других циклов.
Чтобы понять, что это значит, мне понадобилось сделать три итерации, каждая из которых была оптимальней предыдущей.
Все началось с вопроса — «Зачем начинать поиск с новой вершины, если все исходящие ребра ведут в вершины, которые или не содержат цикла, или это вершина через которую уже были построены все циклы?». Потом поток мыслей дошел до того что проверку можно делать рекурсивно. Это позволило уменьшить время до 5 минут.

И только выпив залпом весь стакан с водой, а он 250мл, я осознал, что эту проверку можно вставить, прям внутри поиска в глубину:

func findAllCycles() -> [Cycle] {
  reachableIndices: [Set<Int>] = findAllReachableIndices()
  result: [Cycle] = []
  for index in vertices {
    result += findCycles(from: index, reachableIndices: &reachableIndices)
  }

  return result
}

func findAllReachableIndices() -> [Set<Int>] {
  reachableIndices: [Set<Int>] = []
  for index in vertices {
    reachableIndices[index] = findAllReachableIndices(for: index)
  }
  return reachableIndices
}

func findAllReachableIndices(for startIndex: Int) -> Set<Int> {
  visited: Set<Int> = []
  stack: [Int] = [startIndex]
  while fromIndex = stack.popFirst() {
    visited.insert(fromIndex)

    for toIndex in adjacencyList[fromIndex] {
      if !visited.contains(toIndex) {
        stack.append(toIndex)
      }
    }
  }

  return visited
}

func findCycles(from index: Int, reachableIndices: ref [Set<Int>]) -> [Cycle] {
  result: [Cycle] = []
  dfs(startIndex: index, currentIndex: index, visitedIndices: [], reachableIndices: &reachableIndices, result: &result)

  return result
}

func dfs(startIndex: Int,
         currentIndex: Int,
         visitedIndices: Set<Int>,
         reachableIndices: ref [Set<Int>],
         result: ref [Cycle]) {
  if currentIndex == startIndex && !visitedIndices.isEmpty {
    result.append(cycle)
    return
  }

  if visitedIndices.contains(currentIndex) {
    return
  }

  if currentIndex < startIndex || !reachableIndices[currentIndex].contains(startIndex) {
    return
  }

  visitedIndices += [currentIndex]

  for toIndex in adjacencyList[currentIndex] {
    dfs(startIndex: startIndex, currentIndex: toIndex, visitedIndices: visitedIndices, result: &result)
  }
}

Изменения только тут: if currentIndex < startIndex.

Посмотрев на это простое решение, я нажал run, и был уже готов снова отойти от компьютера, как вдруг — все проверки прошли… 6 секунд? Не, не может быть… Но по дебажным логам все циклы были найдены.

Конечно, я подсознательно понимал, почему оно работает, и что я сделал. Постараюсь эту идею сформировать в тексте — Если уже найдены все циклы, проходящие через вершину A, то при поиске циклов проходящих через любые другие вершины, рассматривать вершину A не имеет смысла. Так как уже найдены все циклы через A, значит нельзя найти новых циклов через неё.

Такая проверка не только сильно ускоряет работу, но и полностью устраняет появление дублей, без необходимости их обрезать/сравнивать.
Что позволяет сэкономить время на способе хранения циклов — можно или вообще не хранить их или хранить в обычном массиве, а не множестве. Это экономит еще 5-10% времени исполнения.

Этап 6. Профайл

Результат в 5-6 секунд меня уже устраивал, но хотелось еще быстрее, на улице еще солнце даже светит! Поэтому я открыл профайл. Я понимал, что на языке Swift низкоуровневая оптимизация почти невозможна, но иногда находишь проблемы в неожиданных местах.
И какое было моё удивление, когда я обнаружил, что половину времени из 6 секунд занимают логи библиотеки… Особенно с учетом, что я их выключил. Как говорится — «ты видишь суслика? А он есть…». У меня суслик оказался большим — на пол поля. Проблема была типичная — некоторое строковое выражение считалось всегда, независимо от необходимости писать его в логи.

Запустив приложение и увидев 3 секунды, я уже хотел было остановиться, но меня мучило одно предчувствие в обходе в ширину. Я давно знал, что массивы у Apple сделаны так, что вставка в начало и в конец массива занимает константное время в силу кольцевой реализации внутри (извиняюсь, я не помню, как правильно это называется). И на языке Swift у массива есть интересная функция popLast(), но нет аналога для первого элемента. Но проще показать.

var visited: Set<Int> = []
var stack: [Int] = [startVertexIndex]
while let fromIndex = stack.first {
  stack.removeFirst()

  visited.insert(fromIndex)
  for toIndex in graph.adjacencyList[fromIndex].flatMap({ $0.toIndices }) {
    if !visited.contains(toIndex) {
      stack.append(toIndex)
    }
  }
}

return visited

var visited: Set<Int> = []
var stack: [Int] = [startVertexIndex]
while let fromIndex = stack.popLast() {
  visited.insert(fromIndex)
  for toIndex in graph.adjacencyList[fromIndex].flatMap({ $0.toIndices }) {
    if !visited.contains(toIndex) {
      stack.insert(toIndex, at: 0)
    }
  }
}

return visited

Вроде изменения не значительные и, кажется, что второй код должен работать медленнее — и на многих языках второй код будет работать медленнее, но на Swift он быстрее на 5-10%.

Итоги

А какие могут быть итоги? Цифры говорят сами за себя — было 95 минут, стало 2.5-3 секунды, да еще и добавилось новых проверок.

Три секунды тоже выглядит не шустро, но не стоит забывать, что это на большом и не красивом графе зависимостей — такие днем с огнем не сыщешь в мобильной разработке.
Да и на другом проекте, который больше похож на средний мобильный проект, время с 15 минут уменьшилось до менее секунды, при этом на более слабом железе.

Ну а появлению статьи благодарим гугл — который не захотел мне помогать, и я придумывал все из головы, хоть и понимаю, что Америку я не открыл.

Весь код на языке Swift можно найти в папке.

Немного рекламы и Планы

Кому понравилась статья, или не понравилась, пожалуйста, зайдите на страницу библиотеки и поставьте ей звёздочку.

Я каждый раз озвучиваю планы по развитию, каждый раз говорю «скоро» и всегда скоро оказывается когда-нибудь. Поэтому сроков называть не буду, но когда-нибудь это появится:

• Конвертация графа зависимостей в формат для graphvis — а он в свою очередь позволит просматривать графы визуально.
• Оптимизация основного функционала библиотеки — С появлением большого количества новых возможностей, моя библиотека хоть и осталось быстрой, но теперь она не сверх быстрая, а на уровне других библиотек.
• Переход на проверку графа и поиск проблем во время компиляции, а не при запуске приложения.

P.S. Если отключить 5 этап полностью, это который добавление доп. действия перед началом поиска, то скорость работы понизится в 1.5 раза — до 4.5 секунд. То есть в этой операции даже после всех других оптимизаций есть толк.

P.P.S. Некоторые факты из статьи выдуманные, для придания красоты картины. Но, я на самом деле пью только чистую воду, и не пью чай/кофе/алкоголь.

UPD: По просьбе добавляю ссылку на сам граф. Он описан в dot формате, имена вершин просто нумерацией. Ссылка
Посмотреть на то как это выглядит визуально можно по этой ссылке.

UPD: banshchikov нашёл другой алгоритм Donald B. Johnson. Более того есть его реализация на swift.
Я решил сравнить свой алгоритм, и этот алгоритм на имеющемся графе.
Вот что получилось:

Время измерялось только на поиск циклов. Сторонняя библиотека конвертирует входные данные в удобные ей, но подобная конвертация должна занимать не более 0.1 секунды. А как видно время отличается на порядок (а в релизе на два). И списать такую большую разницу на неоптимальную реализацию нельзя.

• Как я писал, в моей в библиотеки ребра это не просто переход из одной вершины в другую. В стороннюю реализацию подобную информацию передать нельзя, поэтому количество найденных циклов не совпадает. Из-за этого в результатах ищутся все уникальные циклы по вершинам, без учета рёбер, дабы убедиться в совпадении результата.