Цилиндрическая система координат (цилиндрические координаты)
Для введения цилиндрической системы координат в пространстве выбирается плоскость (основная плоскость) и на ней задается полярная система координат с полюсом и полярной осью
. Через точку
перпендикулярно основной плоскости проведем ось
(ось аппликат) и выберем ее направление так, чтобы возрастание полярного угла, наблюдаемое со стороны положительного направления оси
, происходило против часовой стрелки (рис.2.34,а).
В цилиндрической системе координат положение точки , не принадлежащей оси аппликат, характеризуется полярными координатами
точки
— ортогональной проекции точки
на основную плоскость, и аппликатой
— координатой точки
— ортогональной проекции точки
на ось аппликат. Таким образом, цилиндрические координаты точки
— это упорядоченная тройка чисел
— полярный радиус
, полярный угол
и аппликата
. У точек, принадлежащих оси аппликат, не определен полярный угол, они задаются указанием нулевого полярного радиуса и аппликатой.
Переход от цилиндрических координат к декартовым (прямоугольным)
С цилиндрической системой координат можно связать прямоугольную систему координат
(рис.2.34,б), у которой начало и базисные векторы
совпадают с началом цилиндрической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор
выбирается так, чтобы тройка
была правой (при этом базис оказывается стандартным).
Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим цилиндрическую систему координат (связанную с данной прямоугольной).
Поскольку аппликата точки
в прямоугольной системе координат и аппликата
в цилиндрической системе координат совпадают, то формулы, связывающие между собой прямоугольные координаты
точки
и ее цилиндрические координаты
, имеют вид, следующий из
(2.19)
Эти формулы перехода позволяют найти прямоугольные координаты по известным цилиндрическим. Обратный переход выполняется по формулам
(2.20)
Главное значение полярного угла находится по формулам (см. рис.2.29).
Пример 2.12. В цилиндрической системе координат :
а) построить координатные поверхности ;
б) найти цилиндрические координаты точки , если известны ее прямоугольные координаты
;
в) найти прямоугольные координаты точки , если известны ее цилиндрические координаты:
.
Решение. а) Координатной поверхностью , т.е. геометрическим местом точек
при фиксированном значении полярного радиуса
, является прямой круговой цилиндр, ось которого параллельна оси аппликат (рис.2.35). Этим объясняется название цилиндрической системы координат. Координатной поверхностью
, т.е. геометрическим местом точек
при фиксированном значении полярного угла
, является полуплоскость, ограниченная осью аппликат (на рис.2.35 изображены полуплоскости
и
). Координатной поверхностью
, т.е. геометрическим местом точек
при фиксированном значении аппликаты
, является плоскость, перпендикулярная оси аппликат (на рис.2.35 изображены плоскости
и
).
б) Найдем цилиндрические координаты точки . Аппликата
, полярный радиус и полярный угол находим по формулам (2.20) (см. пример 2.11):
так как и ортогональная проекция точки
на координатную плоскость
(основную плоскость) лежит в IV четверти.
в) Найдем прямоугольные координаты точки . По формулам (2.19) вычисляем (см. пример 2.10):
Также см. преобразования систем координат.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Конев В.В. Скалярные и векторные поля
Цилиндрическая система координат
Цилиндрическая система координат представляет собой трёхмерную систему координат, являющуюся обобщением полярной системы координат посредством добавления третьей координаты, которая задаёт смещение произвольной точки M вдоль оси 0z относительно координатной плоскости 0xy. Положение точки M в цилиндрической системе координат определяется тройкой чисел ρ, φ и z, где ρ – расстояние от точки M до оси 0z (
 ); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х (
); φ – угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х (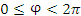 ); z – проекция точки M на ось 0z (
); z – проекция точки M на ось 0z ( ).
).
Рис. 1. Цилиндрические координаты точки M.
Связь между декартовыми и цилиндрическими координатами описывается формулами
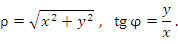
Поверхность, на которой одна из координат сохраняет постоянное значение, называется координатной поверхностью.
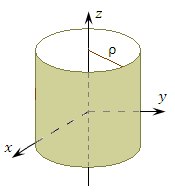
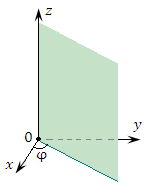
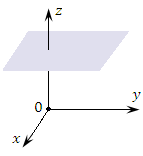
Рис. 2. Координатные поверхности цилиндрической системы координат:
круговой цилиндр (ρ = const);
полуплоскость (φ = const);
плоскость (z = const).
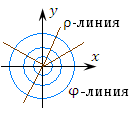
Линия, вдоль которой изменяется только одна координата, а остальные координаты остаются неизменными, называется координатной линией.
Рис. 3. Координатные ρ-линии (лучи) и φ-линии (окружности) цилиндрической системы координат.
Координатная z-линия (прямая) направлена перпендикулярно плоскости 0xy.
В цилиндрической системе координатные линии, проходящие через любую точку M пространства, пересекаются под прямым углом. Такие системы координат называются ортогональными.
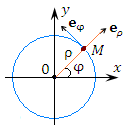
Единичный касательный вектор к координатной линии в точке М, направленный в сторону возрастания координаты, называется ортом в точке М. Поскольку цилиндрическая система координат является ортогональной, то в любой точке пространства векторы 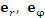
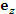
Рис. 4. Орты 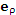
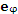
Вектор 
Отметим, что каждая координатная линия перпендикулярна соответствующей координатной поверхности.
Некоторые полезные формулы:
-
Элемент длины дуги:
-
Элемент площади поверхности:
-
Якобиан перехода от декартовой системы координат к цилиндрической:
-
Элемент объема:
Положение точки
в пространстве в момент времени
можно определить тройкой величин
,
которые являются цилиндрическими
координатами точки (рис. 2.1). Формулы
преобразования от декартовых координат
к цилиндрическим и обратно имеют вид
, (7.1)
. (8.1)
Это так называемые
точечные преобразования; формулы этих
преобразований содержат только координаты
(«старые» и «новые»), но не содержат
явным образом временной переменной.
Последнее означает, что обе системы
координат описывают движение точки в
одной и той же (неподвижной) системе
отсчета. Области изменения цилиндрических
координат:
.
Координатные
поверхности в цилиндрической системе2:
— семейство
цилиндров кругового сечения радиуса
с осьюОz;
— семейство полуплоскостей, исходящих
из осиОz
, в которых лежат радиус-вектор точки
и осьОz;
—
семейство плоскостей, перпендикулярных
Oz. Линия
пересечения двух каких-либо координатных
поверхностей различных семейств
называется координатной линией. Так
как вдоль каждой координатной линии
меняется только одна координата, то ее
и называют соответствующей координатой.
Очевидно, координатные линии
— это концентрические окружности,
координатные линии— это полупрямые (лучи), исходящие из
начала координатО
(см. рис.
2.1), координатные линии
—
прямые, параллельные осиOz.
Так как
координатные линии
не являются прямыми, цилиндрические
координаты относятся к криволинейным.
Очевидно, что три координатные линии,
которые определяют точку пространства,
пересекают друг друга под прямыми
углами, т. е. цилиндрические координаты
являются ортогональными координатами.
Касательная,
проведенная к данной точке координатной
линии, называется координатной осью.
Все три оси цилиндрической системы
координат ортогональны друг другу.
Отложим по этим осям единичные векторы
в направлении возрастания координат и
разложим радиус-вектор точки по ортам
цилиндрических координат:
. (9.1)
Из рис. 2.1 видно,
что орты цилиндрических координат
связаны с ортами декартовых координат
соотношениями

Отсюда видно, что
при перемещении точки относительно S
положение ортов,
изменяется вследствие изменения угла.
Действительно, вычислим
и
(11.1)
Дифференцируя
(9.1) по t
и учитывая
(11.1), находим разложение вектора скорости
точки по ортам цилиндрической системы
координат:
. (12.1)
Аналогично,
дифференцируя
поt
и учитывая
(11.1), получим
. (13.1)
Таким образом,
проекции скорости и ускорения точки на
координатные оси
имеют вид

Приведем также
разложение вектора секторной скорости
точки по ортам цилиндрической системы
координат:

Из (14.1) и (15(1) следует,
что
. (16.1)
Рассмотрим далее
важный случай движения, при котором
секторная скорость точки остается
постоянной, т. е.
.
Введем цилиндрическую систему координат
с осью Оz,
направленной
по вектору
.
Так как,
то и радиус-вектор
и
скорость точки
в любой момент времени лежат в плоскости,
ортогональной вектору
.
В этом случае
проекции скоростейи ускорений
можно непосредственно выразить как
функциии
,
а неи
,
а также через производные пофункции
.
Действительно, в выбранной системе
координат имеем

. (18.1)
Значит,
. (19.1)
Далее из (16.1) имеем
,
а

Так что
.
(21.1)
Формулы (19.1) и
(21.1) называют первой и второй формулами
Бине соответственно. Они оказываются
полезными при исследовании различных
случаев движения материальной точки в
центрально-симметричном силовом поле.
Пример.
Траектории точек являются плоскими и
определяются уравнениями
а)
,
б),
—
параметр,
— эксцентриситет эллипса, секторная
скорость.
Начало цилиндрических координат помещено
в фокусе эллипса. Определить ускорения
точек.
Прежде всего,
заметим, что траектории точек различны.
Так, в случае а) точка движется по эллипсу
(рис. 3.l, а), в то время как в случае б)
траектория представляет собой розетку
и не обязательно является замкнутой
кривой (рис. 3.1, б).
По второй формуле
Бине, дважды дифференцируя
по
,
находим
и
в случае а),
а
и
в
случае б).
Отличие в ускорениях
точек согласно уравнениям движения
означает, что действующие на точки в
случаях а) и б)
силы имеют разные законы убывания с
расстоянием от центра силы до точки. В
частности, в случае б)
сила
~
.
Если речь идет о движении планет в
гравитационном поле Солнца, то мы видим,
что в случае б)
перигелий
планеты при каждом обороте смещается
на величину
.
Пример.
Определение
радиус-вектора
точки по скорости
Определить закон
движения, траекторию и ускорение точки,
движущейся по плоской траектории с
постоянной секторной скоростью, еcли
,
где— расстояние от точки до центра,
,
причем угол
между векторами
и
равен
.
Направим полярную
ось от центра к точке так, чтобы при
,
тогда,
а.
Отсюда,
так как если,
то.
Разделяя переменные
и интегрируя,
получим
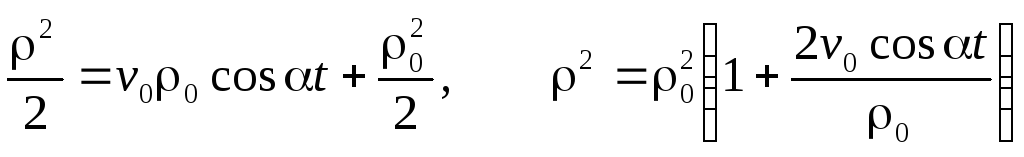
Далее найдем
:
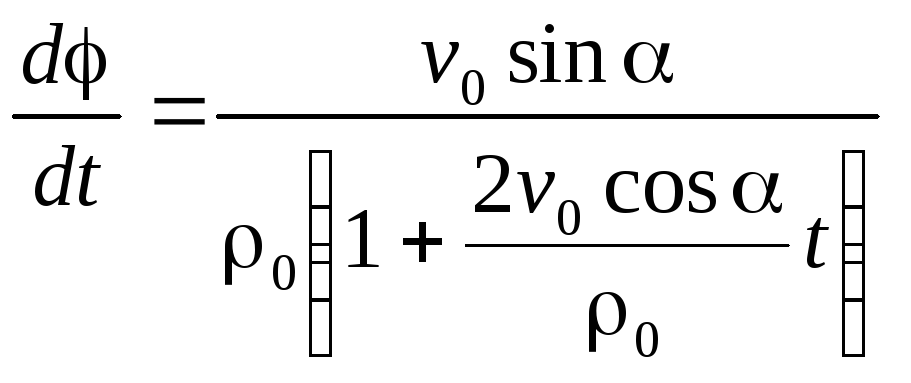
Отсюда
или
.
Ускорение точки
найдем по формуле Бине в виде:
.
Соседние файлы в папке teormeh
- #
- #
- #
- #
- #
- #
Цилиндрическая система координат (цилиндрические координаты)
Для введения цилиндрической системы координат в пространстве выбирается плоскость ( основная плоскость ) и на ней задается полярная система координат с полюсом и полярной осью . Через точку перпендикулярно основной плоскости проведем ось ( ось аппликат ) и выберем ее направление так, чтобы возрастание полярного угла, наблюдаемое со стороны положительного направления оси , происходило против часовой стрелки (рис.2.34,а).
В цилиндрической системе координат положение точки , не принадлежащей оси аппликат, характеризуется полярными координатами точки — ортогональной проекции точки на основную плоскость, и аппликатой — координатой точки — ортогональной проекции точки на ось аппликат. Таким образом, цилиндрические координаты точки — это упорядоченная тройка чисел — полярный радиус , полярный угол и аппликата . У точек, принадлежащих оси аппликат, не определен полярный угол, они задаются указанием нулевого полярного радиуса и аппликатой.
Переход от цилиндрических координат к декартовым (прямоугольным)
С цилиндрической системой координат можно связать прямоугольную систему координат (рис.2.34,б), у которой начало и базисные векторы совпадают с началом цилиндрической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).
Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим цилиндрическую систему координат ( связанную с данной прямоугольной ).
Поскольку аппликата точки в прямоугольной системе координат и аппликата в цилиндрической системе координат совпадают, то формулы, связывающие между собой прямоугольные координаты точки и ее цилиндрические координаты , имеют вид, следующий из
Эти формулы перехода позволяют найти прямоугольные координаты по известным цилиндрическим. Обратный переход выполняется по формулам
Главное значение полярного угла находится по формулам (см. рис.2.29).
Пример 2.12. В цилиндрической системе координат :
а) построить координатные поверхности ;
б) найти цилиндрические координаты точки , если известны ее прямоугольные координаты ;
в) найти прямоугольные координаты точки , если известны ее цилиндрические координаты: .
Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении полярного радиуса , является прямой круговой цилиндр, ось которого параллельна оси аппликат (рис.2.35). Этим объясняется название цилиндрической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении полярного угла , является полуплоскость, ограниченная осью аппликат (на рис.2.35 изображены полуплоскости и ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении аппликаты , является плоскость, перпендикулярная оси аппликат (на рис.2.35 изображены плоскости и ).
б) Найдем цилиндрические координаты точки . Аппликата , полярный радиус и полярный угол находим по формулам (2.20) (см. пример 2.11):
так как и ортогональная проекция точки на координатную плоскость (основную плоскость) лежит в IV четверти.
в) Найдем прямоугольные координаты точки . По формулам (2.19) вычисляем (см. пример 2.10):
Системы координат
Декартова система координат.
Фиксируем в пространстве точку (O) и рассмотрим произвольную точку (M). Радиус-вектором точки (M) по отношению к точке (O) называется вектор (overrightarrow). Если в пространстве кроме точки (O) выбран некоторый базис, то точке (M) сопоставляется упорядоченная тройка чисел — компоненты ее радиус-вектора.
Декартовой системой координат в пространстве называется совокупность точки и базиса.
Точка носит название начала координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат; первая — осью абсцисс, вторая — осью ординат, третья — осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.
Пусть дана декартова система координат (O), (boldsymbol>), (boldsymbol>), (boldsymbol>). Компоненты (x), (y), (z) радиус-вектора (overrightarrow) точки (M) называются координатами точки (M) в данной системе координат:
$$
overrightarrow = xboldsymbol> + yboldsymbol> + zboldsymbol>.nonumber
$$
Первая координата называется абсциссой, вторая — ординатой, а третья — аппликатой.
Аналогично определяются координаты на плоскости и на прямой линии. Разумеется, точка на плоскости имеет только две координаты, а на прямой линии — одну.
Координаты точки пишут в скобках после буквы, обозначающей точку. Например, запись (A(2, 1/2)) означает, что точка (A) имеет координаты 2 и 1/2 в ранее выбранной декартовой системе координат на плоскости (рис. 2.1).
Рис. 2.1
Координаты точки, как и компоненты вектора, — величины безразмерные. В частности, они не зависят от выбранной единицы измерения длин. В самом деле, раскладывая векторы в теореме о линейной зависимости систем векторов, мы сводили дело к разложению вектора по коллинеарному с ним ненулевому вектору. А в этом случае компонента равна отношению длин, взятому с определенным знаком.
Легко видеть, что при заданной системе координат координаты точки определены однозначно. С другой стороны, если задана система координат, то для каждой упорядоченной тройки чисел найдется единственная точка, имеющая эти числа в качестве координат. Система координат на плоскости определяет такое же соответствие между точками плоскости и парами чисел. Задание системы координат на прямой линии сопоставляет каждой точке вещественное число и каждому числу — точку.
Рис. 2.2
Рассмотрим две точки (A) и (B), координаты которых относительно некоторой декартовой системы координат (O), (boldsymbol>), (boldsymbol>), (boldsymbol>) соответственно (x_<1>), (y_<1>), (z_<1>) и (x_<2>), (y_<2>), (z_<2>). Поставим себе задачу найти компоненты вектора (overrightarrow). Очевидно, что (overrightarrow = overrightarrow-overrightarrow) (рис. 2.2). Компоненты радиус-векторов (overrightarrow) и (overrightarrow) равны ((x_<1>), (y_<1>), (z_<1>)) и ((x_<2>), (y_<2>), (z_<2>)) по определению координат. Из ранее доказанного предположения следует, что (overrightarrow) имеет компоненты ((x_<2>-x_<1>), (y_<2>-y_<1>), (z_<2>-z_<1>)). Этим доказано следующее утверждение.
Чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.
Деление отрезка в заданном отношении.
Найдем координаты точки (M) на отрезке (AB), которая делит этот отрезок в отношении (lambda/mu), то есть удовлетворяет условию
$$
frac<|AM|> <|MB|>= frac<lambda><mu>, lambda > 0, mu > 0nonumber
$$
(рис. 2.3). Это условие можно переписать в виде
$$
muoverrightarrow = lambdaoverrightarrow.label
$$
Рис. 2.3
Обозначив через ((x_<1>), (y_<1>), (z_<1>)) и ((x_<2>), (y_<2>), (z_<2>)) соответственно координаты точек (A) и (B), а через ((x), (y), (z)) координаты точки (M), разложим обе части равенства по базису, причем компоненты векторов (overrightarrow) и (overrightarrow) найдем по предложению 1. Тогда
$$
mu(x-x_<1>) = lambda(x_<2>-x), mu(y-y_<1>) = lambda(y_<2>-y), mu(z-z_<1>) = lambda(z_<2>-z).nonumber
$$
Из этих равенств можно найти (x), (y) и (z), поскольку (lambda + mu neq 0):
$$
x = frac <mu x_<1>+ lambda x_<2>><lambda + mu>, y = frac <mu y_<1>+ lambda y_<2>><lambda + mu>, z = frac <mu z_<1>+ lambda z_<2>><lambda + mu>label
$$
Если в формулах eqref мы будем считать одно из чисел (lambda) или (mu) отрицательным, то из равенства eqref увидим, что (M) находится на той же прямой вне отрезка (AB), деля его в отношении |(lambda/mu)|. Поэтому из формул eqref можно найти координаты точки, делящей отрезок в заданном отношении как внутренним, так и внешним образом.
На плоскости и на прямой линии задача о делении отрезка решается точно так же, только из трех равенств в eqref остается соответственно два и одно равенство.
Декартова прямоугольная система координат.
Общие декартовы системы координат используются реже, чем специальный класс таких систем — декартовы прямоугольные системы координат.
Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единице. Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.
Нетрудно проверить, что координаты точки относительно декартовой прямоугольной системы координат в пространстве по абсолютной величине равны расстояниям от этой точки до соответствующих координатных плоскостей. Они имеют знак плюс или минус в зависимости от того, лежит точка по ту же или по другую сторону от плоскости, что и конец базисного вектора, перпендикулярного этой плоскости.
Аналогично находят координаты точки относительно декартовой прямоугольной системы координат на плоскости.
Полярная система координат.
Декартовы системы координат не единственный способ определять при помощи чисел положение точки на плоскости. Для этого используются многие другие типы координатных систем. Здесь мы опишем некоторые из них.
На плоскости часто употребляется полярная система координат. Она определена, если задана точка (O), называемая полюсом, и исходящий из полюса луч (l), который называется полярной осью. Положение точки (M) фиксируется двумя числами: радиусом (r = overrightarrow) и углом (varphi) между полярной осью и вектором (overrightarrow). Этот угол называется полярным углом (рис. 2.4).
Рис. 2.4
Мы будем измерять полярный угол в радианах и отсчитывать от полярной оси против часовой стрелки. У полюса (r = 0), а (varphi) не определено. У остальных точек (r > 0), а (varphi) определяется с точностью до слагаемого, кратного 2(pi). Это означает, что пары чисел ((r, varphi)), ((r, varphi + 2pi)) и вообще ((r), (varphi + 2kpi)), где (k) — любое целое число, представляют собой полярные координаты одной и той же точки.
Иногда ограничивают изменение полярного угла какими-нибудь условиями, например, (0 leq varphi 0), то паре ((r, varphi)) ставим в соответствие точку, радиус-вектор которой имеет длину (r) и составляет с полярной осью угол (varphi). При этом парам чисел ((r, varphi)) и ((r_<1>, varphi_<1>)) сопоставляется одна и та же точка, если (r = r_<1>), а (varphi = varphi_ <1>= 2pi k), где (k) — целое число.
Выберем на плоскости декартову прямоугольную систему координат, поместив ее начало в полюс (O) и приняв за базис векторы (boldsymbol>) и (boldsymbol>) длины (l), направленные соответственно вдоль полярной оси и под углом (pi/2) к ней (угол отсчитывается против часовой стрелки). Как легко видеть из рис. 2.4, декартовы координаты точки выражаются через ее полярные координаты формулами
$$
x = r cos varphi, y = r sin varphi.label
$$
Цилиндрические и сферические координаты.
В пространстве обобщением полярных систем координат являются цилиндрические и сферические системы координат. И для тех, и для других фигура, относительно которой определяется положение точки, состоит из точки (O), луча (l), исходящего из (O), и вектора (boldsymbol), равного по длине 1 и перпендикулярного к (l). Через точку (O) проведем плоскость (Theta), перпендикулярную вектору (boldsymbol). Луч (l) лежит в этой плоскости.
Пусть дана точка (M). Опустим из нее перпендикуляр (MM’) на плоскость (Theta).
Цилиндрические координаты точки (M) — это три числа (r), (varphi), (h). Числа (r) и (varphi) — полярные координаты точки (M’) по отношению к полюсу (O) и полярной оси (l), a (h) — компонента вектора (overrightarrow) по вектору (boldsymbol). Она определена, так как эти векторы коллинеарны (рис. 2.5).
Рис. 2.5
Сферические координаты точки — три числа ((r), (varphi), (theta)). Они определяются так: (r = |overrightarrow|). Как и для цилиндрических координат, (varphi) — угол вектора (overrightarrow>) с лучом (l), а (theta) — угол вектора (overrightarrow) с плоскостью (Theta) (рис. 2.6).
Рис. 2.6
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Векторная алгебра.
- Высшая математика.
- Векторная алгебра.
- Полярная, цилиндрическая и сферическая системы координат. Формулы перехода.
Полярная, цилиндрическая и сферическая системы координат. Формулы перехода.
Полярные координаты.
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.
Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.
$$x=rho cosvarphi,; y=rhosinvarphi,quad (rhogeq 0,,,,0leqvarphileq 2pi)$$
Обобщённые полярные координаты.$$ x=arhocosvarphi,; y=brhosinvarphi,quad (rhogeq0, 0leqvarphileq 2pi)$$
Цилиндрические координаты:
Цилиндрической системой координат называют трёхмерную систему координат , являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой ), которая задаёт высоту точки над плоскостью.
$x=rhocosvarphi,;y=rhosinvarphi,z=h,$ $ (rhoge 0,, 0levarphile 2pi,, -infty
Сферические координаты.
Положение точки М в сферической системе координат задается тройкой чисел r , φ и θ, где r – расстояние от начала координат до точки M ( ); φ – угол, образованный проекцией радиус-вектора на плоскость О ху с положительным направлением оси О х ( ); θ – угол между положительным направлением оси O z и радиус-вектором точки М ( ).
$$left<begin x=rcosvarphicostheta,\ y=rsinvarphicostheta,\ z=rsintheta,endright.$$
$ (rgeq 0,;0leqvarphi leq 2pi,; -frac<pi><2>lethetalefrac<pi><2>).$
Обобщённые сферические координаты.
$$ left<begin x=arcos^alphavarphicos^betatheta,\ y=brsin^alphavarphicos^betatheta,\ z=crsin^betatheta, end right. $$
http://univerlib.com/analytic_geometry/vector_algebra/coordinate_systems/
http://mathportal.net/index.php/vektornaya-algebra/132-polyarnaya-tsilindricheskaya-i-sfericheskaya-sistemy-koordinat-formuly-perekhoda
From Wikipedia, the free encyclopedia
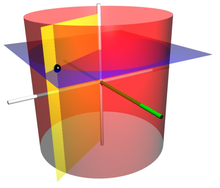
A cylindrical coordinate system with origin O, polar axis A, and longitudinal axis L. The dot is the point with radial distance ρ = 4, angular coordinate φ = 130°, and height z = 4.
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis (axis L in the image opposite), the direction from the axis relative to a chosen reference direction (axis A), and the distance from a chosen reference plane perpendicular to the axis (plane containing the purple section). The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.
The origin of the system is the point where all three coordinates can be given as zero. This is the intersection between the reference plane and the axis.
The axis is variously called the cylindrical or longitudinal axis, to differentiate it from the polar axis, which is the ray that lies in the reference plane, starting at the origin and pointing in the reference direction.
Other directions perpendicular to the longitudinal axis are called radial lines.
The distance from the axis may be called the radial distance or radius, while the angular coordinate is sometimes referred to as the angular position or as the azimuth. The radius and the azimuth are together called the polar coordinates, as they correspond to a two-dimensional polar coordinate system in the plane through the point, parallel to the reference plane. The third coordinate may be called the height or altitude (if the reference plane is considered horizontal), longitudinal position,[1] or axial position.[2]
Cylindrical coordinates are useful in connection with objects and phenomena that have some rotational symmetry about the longitudinal axis, such as water flow in a straight pipe with round cross-section, heat distribution in a metal cylinder, electromagnetic fields produced by an electric current in a long, straight wire, accretion disks in astronomy, and so on.
They are sometimes called «cylindrical polar coordinates»[3] and «polar cylindrical coordinates»,[4] and are sometimes used to specify the position of stars in a galaxy («galactocentric cylindrical polar coordinates»).[5]
Definition[edit]
The three coordinates (ρ, φ, z) of a point P are defined as:
- The axial distance or radial distance ρ is the Euclidean distance from the z-axis to the point P.
- The azimuth φ is the angle between the reference direction on the chosen plane and the line from the origin to the projection of P on the plane.
- The axial coordinate or height z is the signed distance from the chosen plane to the point P.
Unique cylindrical coordinates[edit]
As in polar coordinates, the same point with cylindrical coordinates (ρ, φ, z) has infinitely many equivalent coordinates, namely (ρ, φ ± n×360°, z) and (−ρ, φ ± (2n + 1)×180°, z), where n is any integer. Moreover, if the radius ρ is zero, the azimuth is arbitrary.
In situations where someone wants a unique set of coordinates for each point, one may restrict the radius to be non-negative (ρ ≥ 0) and the azimuth φ to lie in a specific interval spanning 360°, such as [−180°,+180°] or [0,360°].
Conventions[edit]
The notation for cylindrical coordinates is not uniform. The ISO standard 31-11 recommends (ρ, φ, z), where ρ is the radial coordinate, φ the azimuth, and z the height. However, the radius is also often denoted r or s, the azimuth by θ or t, and the third coordinate by h or (if the cylindrical axis is considered horizontal) x, or any context-specific letter.
The coordinate surfaces of the cylindrical coordinates (ρ, φ, z). The red cylinder shows the points with ρ = 2, the blue plane shows the points with z = 1, and the yellow half-plane shows the points with φ = −60°. The z-axis is vertical and the x-axis is highlighted in green. The three surfaces intersect at the point P with those coordinates (shown as a black sphere); the Cartesian coordinates of P are roughly (1.0, −1.732, 1.0).
Cylindrical coordinate surfaces. The three orthogonal components, ρ (green), φ (red), and z (blue), each increasing at a constant rate. The point is at the intersection between the three colored surfaces.
In concrete situations, and in many mathematical illustrations, a positive angular coordinate is measured counterclockwise as seen from any point with positive height.
Coordinate system conversions[edit]
The cylindrical coordinate system is one of many three-dimensional coordinate systems. The following formulae may be used to convert between them.
Cartesian coordinates[edit]
For the conversion between cylindrical and Cartesian coordinates, it is convenient to assume that the reference plane of the former is the Cartesian xy-plane (with equation z = 0), and the cylindrical axis is the Cartesian z-axis. Then the z-coordinate is the same in both systems, and the correspondence between cylindrical (ρ, φ, z) and Cartesian (x, y, z) are the same as for polar coordinates, namely
in one direction, and
in the other. The arcsine function is the inverse of the sine function, and is assumed to return an angle in the range [−π/2, +π/2] = [−90°, +90°]. These formulas yield an azimuth φ in the range [−90°, +270°].
By using the arctangent function that returns also an angle in the range [−π/2, +π/2] = [−90°, +90°], one may also compute 

For other formulas, see the article Polar coordinate system.
Many modern programming languages provide a function that will compute the correct azimuth φ, in the range (−π, π), given x and y, without the need to perform a case analysis as above. For example, this function is called by atan2(y, x) in the C programming language, and (atan y x) in Common Lisp.
Spherical coordinates[edit]
Spherical coordinates (radius r, elevation or inclination θ, azimuth φ), may be converted into cylindrical coordinates by:
Cylindrical coordinates may be converted into spherical coordinates by:
Line and volume elements[edit]
- See multiple integral for details of volume integration in cylindrical coordinates, and Del in cylindrical and spherical coordinates for vector calculus formulae.
In many problems involving cylindrical polar coordinates, it is useful to know the line and volume elements; these are used in integration to solve problems involving paths and volumes.
The line element is
The volume element is
The surface element in a surface of constant radius ρ (a vertical cylinder) is
The surface element in a surface of constant azimuth φ (a vertical half-plane) is
The surface element in a surface of constant height z (a horizontal plane) is
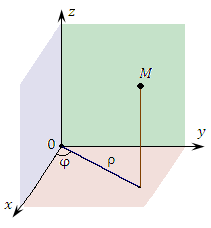
The del operator in this system leads to the following expressions for gradient, divergence, curl and Laplacian:
Cylindrical harmonics[edit]
The solutions to the Laplace equation in a system with cylindrical symmetry are called cylindrical harmonics.
Kinematics[edit]
In a cylindrical coordinate system, the position of a particle can be written as[6]
The velocity of the particle is the time derivative of its position,
where the term 

See also[edit]
- List of canonical coordinate transformations
- Vector fields in cylindrical and spherical coordinates
- Del in cylindrical and spherical coordinates
References[edit]
- ^ Krafft, C.; Volokitin, A. S. (1 January 2002). «Resonant electron beam interaction with several lower hybrid waves». Physics of Plasmas. 9 (6): 2786–2797. Bibcode:2002PhPl….9.2786K. doi:10.1063/1.1465420. ISSN 1089-7674. Archived from the original on 14 April 2013. Retrieved 9 February 2013.
…in cylindrical coordinates (r,θ,z) … and Z = vbzt is the longitudinal position…
- ^ Groisman, Alexander; Steinberg, Victor (1997). «Solitary Vortex Pairs in Viscoelastic Couette Flow». Physical Review Letters. 78 (8): 1460–1463. arXiv:patt-sol/9610008. Bibcode:1997PhRvL..78.1460G. doi:10.1103/PhysRevLett.78.1460. S2CID 54814721.
…where r, θ, and z are cylindrical coordinates … as a function of axial position…
- ^ Szymanski, J. E. (1989). Basic Mathematics for Electronic Engineers: models and applications. Tutorial Guides in Electronic Engineering (no. 16). Taylor & Francis. p. 170. ISBN 978-0-278-00068-1.
- ^ Nunn, Robert H. (1989). Intermediate Fluid Mechanics. Taylor & Francis. p. 3. ISBN 978-0-89116-647-4.
- ^ Sparke, Linda Siobhan; Gallagher, John Sill (2007). Galaxies in the Universe: An Introduction (2nd ed.). Cambridge University Press. p. 37. ISBN 978-0-521-85593-8.
- ^ a b Taylor, John R. (2005). Classical Mechanics. Sausalito, California: University Science Books. p. 29.
Further reading[edit]
- Morse, Philip M.; Feshbach, Herman (1953). Methods of Theoretical Physics, Part I. New York City: McGraw-Hill. pp. 656–657. ISBN 0-07-043316-X. LCCN 52011515.
- Margenau, Henry; Murphy, George M. (1956). The Mathematics of Physics and Chemistry. New York City: D. van Nostrand. p. 178. ISBN 9780882754239. LCCN 55010911. OCLC 3017486.
- Korn, Granino A.; Korn, Theresa M. (1961). Mathematical Handbook for Scientists and Engineers. New York City: McGraw-Hill. pp. 174–175. LCCN 59014456. ASIN B0000CKZX7.
- Sauer, Robert; Szabó, István (1967). Mathematische Hilfsmittel des Ingenieurs. New York City: Springer-Verlag. p. 95. LCCN 67025285.
- Zwillinger, Daniel (1992). Handbook of Integration. Boston: Jones and Bartlett Publishers. p. 113. ISBN 0-86720-293-9. OCLC 25710023.
- Moon, P.; Spencer, D. E. (1988). «Circular-Cylinder Coordinates (r, ψ, z)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed.). New York City: Springer-Verlag. pp. 12–17, Table 1.02. ISBN 978-0-387-18430-2.
External links[edit]
- «Cylinder coordinates», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- MathWorld description of cylindrical coordinates
- Cylindrical Coordinates Animations illustrating cylindrical coordinates by Frank Wattenberg

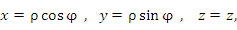

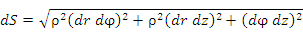
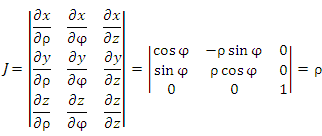
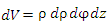










![{displaystyle {begin{aligned}nabla f&={frac {partial f}{partial rho }}{boldsymbol {hat {rho }}}+{frac {1}{rho }}{frac {partial f}{partial varphi }}{boldsymbol {hat {varphi }}}+{frac {partial f}{partial z}}{boldsymbol {hat {z}}}\[8px]nabla cdot {boldsymbol {A}}&={frac {1}{rho }}{frac {partial }{partial rho }}left(rho A_{rho }right)+{frac {1}{rho }}{frac {partial A_{varphi }}{partial varphi }}+{frac {partial A_{z}}{partial z}}\[8px]nabla times {boldsymbol {A}}&=left({frac {1}{rho }}{frac {partial A_{z}}{partial varphi }}-{frac {partial A_{varphi }}{partial z}}right){boldsymbol {hat {rho }}}+left({frac {partial A_{rho }}{partial z}}-{frac {partial A_{z}}{partial rho }}right){boldsymbol {hat {varphi }}}+{frac {1}{rho }}left({frac {partial }{partial rho }}left(rho A_{varphi }right)-{frac {partial A_{rho }}{partial varphi }}right){boldsymbol {hat {z}}}\[8px]nabla ^{2}f&={frac {1}{rho }}{frac {partial }{partial rho }}left(rho {frac {partial f}{partial rho }}right)+{frac {1}{rho ^{2}}}{frac {partial ^{2}f}{partial varphi ^{2}}}+{frac {partial ^{2}f}{partial z^{2}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f83defb6183acc79213d062ed3734d4c6f691bbf)


