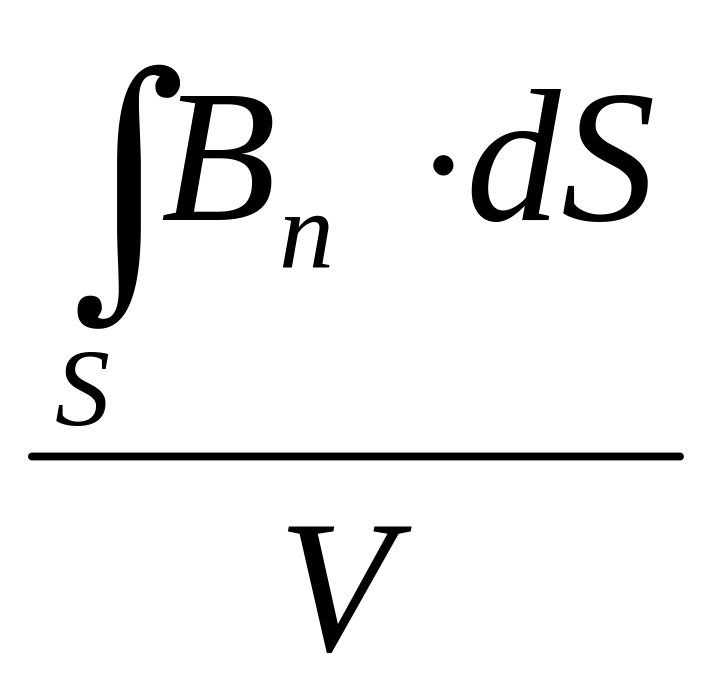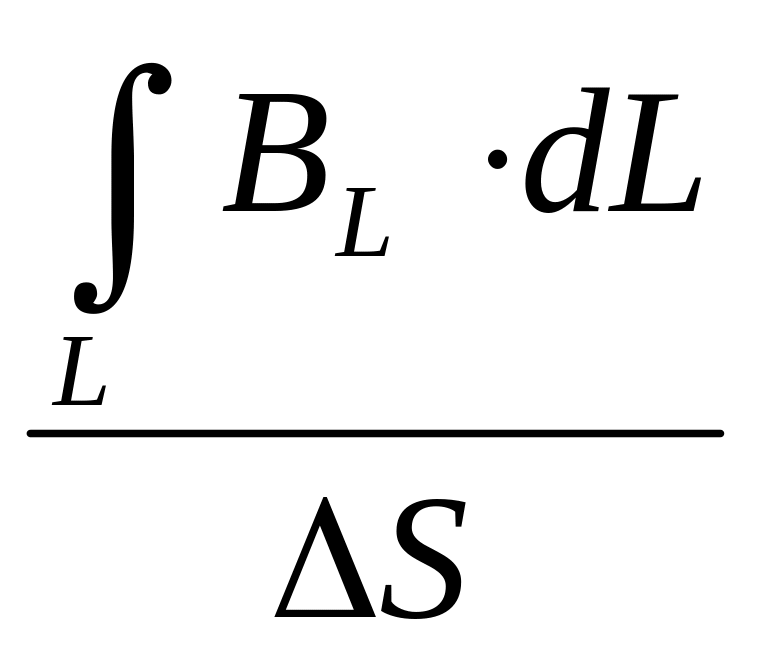Теорема
Остроградского – Гаусса для магнитного
поля свидетельствует о непрерывности
и замкнутости магнитных силовых линий,
и об отсутствии в природе магнитных
зарядов.
Магнитный
поток.
Поток
dФм
вектора магнитной индукции В
через малую поверхность с вектором
элементарной площади dS
= n·dS,
в пределах которой вектор В
можно считать неизменным, выражается,
по определению (см. разд. 1.7), произведением
величины площади поверхности dS
и проекции Вn
вектора индукции на нормаль n
к этой поверхности (рис. 31):
dФм
=
(В,
dS)
= В·dS·cosα
= Вn·dS,
где
α
– угол между векторами В
и n.
Магнитный поток Фм
через конечную поверхность S
определяется интегрированием по всей
поверхности:
Фм
=
dФм
=
Вn·dS.
Магнитный
поток Фм
– скалярная величина, определяющая
число силовых линий вектора В,
пересекающих данную поверхность. При
этом, в месте выхода силовых линий из
объема V,
ограниченного замкнутой поверхностью
S,
нормальная составляющая вектора Вn
к данному участку поверхности dS
считается положительной, то есть Вn>0,
и элементарный поток вектора индукции
через поверхность dS
также положительный dФм>0,
а в месте входа магнитных силовых линий
в объем, соответственно, Вn<0
и dФм<0.
Интегральная
форма теоремы Остроградского — Гауссадля
магнитного поля
показывает, что поток Фм
вектора магнитной индукции В
через любую замкнутую поверхность S,
охватывающую объем V,
всегда равен нулю:
Фм
=
Вn·dS
= 0.
Равенство
нулю интеграла по замкнутой поверхности
означает (по аналогии со случаем в
электростатике, когда замкнутая
поверхность не охватывает электрический
заряд), что число магнитных силовых
линий, выходящих из ограниченного этой
поверхностью объема, равно числу
магнитных силовых линий, входящих в
этот объем.
Из
вышесказанного можно сделать вывод,
что силовые линии магнитного поля (линии
вектора В)
всюду непрерывны
и замкнуты.
Магнитный
поток в СИ измеряется в веберах (Вб).
Теперь
устремим объем V
к нулю, стягивая ограничивающую его
поверхность S
к интересующей нас точке магнитного
поля. По аналогии с электростатикой
дифференциальная
форма теоремы Остроградского – Гаусса
для магнитного поля
имеет вид:
div
B
=
lim
= 0.
Таким
образом, дивергенция В
магнитного поля всюду равна нулю. Это
означает, что магнитное поле не
имеет магнитных источников и магнитных
зарядов в природе не существует.
Теорема
о циркуляции.
Из закона Био-Савара-Лапласа можно
вывести утверждение, что циркуляция
вектора индукции В
магнитного
поля в вакууме, создаваемого проводниками
любой формы с токами i,
вдоль любого замкнутого контура L,
охватывающего эти проводники с токами,
определяется алгебраической суммой
токов ∑i,
охватываемых этим контуром (то есть
суммарным током
=
∑i,
проходящим через натянутую на контур
поверхность S):
(В,
dL)
=
В·dL·cosα
=
ВL·dL
= μ0∑i,
где
α
– угол между векторами В
и
dL,
dL
–
вектор элементарной длины контура,
направленный по току, который считается
положительным, если его направление
связано с направлением обхода контура
правилом правого буравчика, а ток
противоположного направления считается
отрицательным.
Если
ток непрерывно распределен по поверхности
проводников, охватываемых контуром, с
некоторой плотностью j,
то:
ВL·dL
= μ0
d
=
μ0
jn·dS.
В
векторном виде интегральная
форма теоремы о циркуляции вектора В
записывается выражением:
(В,
dL)
= μ0
(j,
dS),
где
положительное направление нормали n
к
поверхности S
определяется движением правого буравчика
при его вращении в направлении обхода
контура L,
dS
=
n·dS
— вектор элементарной площади dS.
Тот
факт, что циркуляция вектора В
не
равна нулю, означает, что магнитное поле
не
потенциально.
Ему нельзя приписать скалярный потенциал,
поскольку он был бы неоднозначным.
Представим
данную теорему в дифференциальной
форме. Рассмотрим отношение циркуляции
вектора В
к
площади ∆S,
ограниченной плоским контуром L.
При стягивании контура в точку, площадь
плоской поверхности стремится к нулю
∆S→0,
а искомое отношение стремится к пределу,
величина которого равна вектору,
называемому ротором поля вектора В
и
обозначаемому rot
В,
на направление нормали к плоскости
контура в данной точке. Направление
нормали n
согласуется
с направлением обхода контура по правилу
буравчика:
lim
= (rot
В)n
Дифференциальная
форма теоремы о циркуляции вектора В
в векторном виде записывается соотношением:
rot
В
=
μ0
·j,
где
j
– плотность тока в данной точке. Таким
образом, векторное поле, ротор которого
равен нулю, является потенциальным
(электростатическое поле), в противном
случае – вихревым (магнитное поле).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Циркуляция вектора индукции магнитного поля
Содержание:
- Теорема о циркуляции вектора индукции магнитного поля
- Чему равна циркуляция, закон Био–Савара
- Дифференциальная форма теоремы о циркуляции
Теорема о циркуляции вектора индукции магнитного поля
Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур.
В виде формулы теорема записывается следующим образом:
(ointlimits_L;overrightarrow Bdoverrightarrow l;=;M_0sum_{k=1}^n;=;M_0I)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В данном случае I будет означать полный ток.
Теорема используется для того, чтобы облегчить вычисление индукции магнитного поля, созданного совокупностью токов, текущих по проводам. Упрощение достигается с учетом симметрии и конфигурации токов. К примеру, с применением этой теоремы возможен расчет магнитной индукции для проводников с высокой степенью симметрии.
Взглянем на циркуляцию вектора (overrightarrow B). Предположим, что условный замкнутый контур находится в пространстве с магнитным полем, а также предположим направление его обхода. В таком случае, касательная составляющая (B_l) вектора (overrightarrow B) определяется на каждом отдельно взятом маленьком участке (triangle l ) этого контура. Иными словами определяется проекция вектора (overrightarrow B) на направление касательной к определенному участку контура.
Циркуляцией вектора (overrightarrow B) является сумма произведений (B_l) и (triangle l), которая взята по целому контуру L: (overrightarrow B = textstylesum_{(L)} B_l triangle l.)
Исходя из этого, можно сформулировать следующее: принимая во внимание теорему о циркуляции, циркуляция вектора (overrightarrow B) магнитного поля постоянных токов по каждому из контуров L в любой момент времени рассчитывается как произведение магнитной постоянной (mu_0) на сумму всех токов:
({textstylesum_{(L)}};B_l;triangle l;=;mu_0;{textstylesum_{}};l_i)
Вывод из теоремы: так как циркуляция индукции магнитного поля не равняется нулю, магнитное поле прямолинейного тока не будет являться потенциальным.
(ointlimits_L;(overrightarrow Bdoverrightarrow l);neq0) , где (overrightarrow B) обозначает вектор магнитной индукции, а dl является элементом произвольного контура L.
Чему равна циркуляция, закон Био–Савара
Циркуляция вектора ( overrightarrow B) прямолинейного тока вдоль замкнутого контура, который не охватывает этот проводник, равняется нулю. В случае, когда несколько токов оказываются охваченными контуром, циркуляция вектора (overrightarrow B) равняется их алгебраической сумме:
(ointlimits_l;(overrightarrow Bdoverrightarrow l);=;mu_0sum_i;l_i)
Закон Био-Савара определяет вклад (triangleoverrightarrow B) в магнитную индукцию (overrightarrow B) результативного магнитного поля, образуемого маленьким участком (triangle l ) проводника с током I.
(triangle B;=;frac{mu_0;I;triangle l;sinleft(alpharight)}{4pi r^2})
В данном случае r является расстоянием от заданного участка (triangle l) до точки наблюдения, (alpha) обозначает угол между направлением на точку наблюдение и направлением тока на определенном участке, а (mu_0) является магнитной постоянной.
Благодаря закону Био-Савара можно определить магнитные поля током с различными конфигурациями и вычислить магнитное поле в центре кругового витка с током.
Дифференциальная форма теоремы о циркуляции
Предположим, что S — это поверхность, охватываемая контуром L. Правило правого винта будет связывать проложенную к поверхности нормаль и направление обхода контура L. В таком случае определить силу тока, текущего через поверхность S, можно с помощью следующей формулы:
(I;=;intlimits_S;overrightarrow jdoverrightarrow S)
В этой формуле (overrightarrow j) будет обозначать объемную плотность тока.
Исходя из этого, используем следующее написание формулы:
(ointlimits_L;overrightarrow Bdoverrightarrow l;=;mu_0intlimits_S;overrightarrow jdoverrightarrow S)
Теперь образуем ротор вектора (rotoverrightarrow B), основываясь на теореме Стокса, уточним, что:
(rotoverrightarrow B;=;begin{vmatrix}i&j&k\fracpartial{partial x}&fracpartial{partial y}&fracpartial{partial z}\B_x&B_y&B_zend{vmatrix} = 0)
Тогда формула примет вид:
(ointlimits_L;overrightarrow Bdoverrightarrow l;=;intlimits_Srotoverrightarrow Bdoverrightarrow S)
Теперь можно записать теорему о циркуляции в дифференциальной форме:
(rotoverrightarrow B;=;frac{4pi}coverrightarrow j)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Наталья Николаевна Пушкина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Интегральная форма теоремы о циркуляции
Линии индукции магнитного поля, которое возникает вокруг постоянного тока, который течет по прямолинейному длинному проводнику — концентрические окружности с центрами на линии тока. Интеграл вида $ointlimits_L{overrightarrow{B}doverrightarrow{l}} $- циркуляция вектора $overrightarrow{B}$ по замкнутому контуру L. Найдем $ointlimits_L{overrightarrow{B}doverrightarrow{l}}$ по некоторому замкнутому контуру вокруг тока I (рис. 1).
Рис. 1
Линии магнитной индукции лежат в плоскостях перпендикулярных линии тока I, контур L выбираем в плоскости одной из линий $overrightarrow{B}.$ Используем рис.1, получим:
Обозначим $left(widehat{overrightarrow{B}doverrightarrow{l}}right)=alpha $, тогда имеем:
По условию магнитное поле создает бесконечно длинный прямой проводник с током, индукцию поля которого мы знаем, и запишем в точке на расстоянии r от проводника как:
Подставим (3) и (2) в формулу (1), получим:
Теперь найдем циркуляцию вектора магнитной индукции, используя (4), получим:
где использовано то, что для замкнутого контура, который окружает начало координат:
Из полученного результата в (5) видим, что циркуляция вектора магнитной индукции по замкнутому контуру вокруг тока не зависит от вида контура и определена только силой тока. В том случае если контур ток не охватывает, то циркуляция вектора индукции равна нулю.
Тогда теорема о циркуляции для нескольких токов формулируется следующим образом:
Теорема
Циркуляция индукции магнитного поля постоянных токов по произвольному замкнутому контуру равна алгебраической сумме токов, которые пронизывают этот контур.
«Теорема о циркуляции вектора индукции магнитного поля» 👇
В математическом виде данная формулировка выглядит как уравнение:
[ointlimits_L{overrightarrow{B}doverrightarrow{l}}=м_0sumlimits^n_{k=1}{I_k=м_0Ileft(7right),}]
где через I — обозначают полный ток (алгебраическая сумма всех токов, охватываемых контуром). Теорема о циркуляции еще называется законом полного тока. Надо иметь в виду, что циркуляция вектора $overrightarrow{B}$ по замкнутому контуру равна нулю не только в случае отсутствия токов, которые пронизывают заданный контур, но и если токи текут в противоположных направлениях и в сумме дают ноль. В формуле (7) знак тока учитывается по правилу правого винта. Этот закон мы получили для прямого бесконечного проводника, но он справедлив и для произвольного тока.
Дифференциальная форма теоремы о циркуляции
Пусть S — поверхность, которую охватывает контур L. Положительная нормаль к поверхности связана с направлением обхода контура L правилом правого винта. Силу полного тока, который течет через поверхность S можно записать как:
[I=intlimits_S{overrightarrow{j}doverrightarrow{S}(8)},]
где $overrightarrow{j}$ — объёмная плотность тока. В таком случае теорему о циркуляции запишем как:
[ointlimits_L{overrightarrow{B}doverrightarrow{l}}={mu }_0intlimits_S{overrightarrow{j}doverrightarrow{S}left(9right).}]
По теореме Стокса можно записать, что:
[ointlimits_L{overrightarrow{B}doverrightarrow{l}}=intlimits_S{rotoverrightarrow{B}doverrightarrow{S}}left(10right).]
Следовательно, запишем:
[intlimits_S{(rotoverrightarrow{B}-{mu }_0overrightarrow{j})doverrightarrow{S}}=0left(11right).]
Равенство (11) выполняется для любой поверхности, следовательно, подынтегральное выражение также равно нулю:
[rotoverrightarrow{B}-{mu }_0overrightarrow{j}=0to rotoverrightarrow{B}={mu }_0overrightarrow{j} left(12right).]
Равенство (12) дифференциальная форма теоремы о циркуляции. Она справедлива для произвольного поля в каждой точке.
Напомним, что теорема о циркуляции в виде (7) и (12) записана для поля в вакууме и стационарных токов.
Пример 1
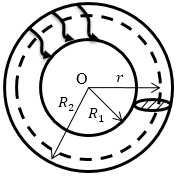
Задание: Тороид имеет каркас в виде тора и на него намотан проводник, по которому течет ток. Магнитное поле данной конфигурации токов сосредоточено в основном внутри тороида. Поле имеет осевую симметрию. Силовые линии магнитного поля тороида представляют собой окружности с центром на оси тороида. Используя теорему о циркуляции, найдите магнитное поле внутри тороида (рис.2) (B(r)). Если сила тока в нем равна I. N — число витков тороида.
Рис. 2
Решение:
В качестве контура циркуляции выберем силовую линию в виде окружности радиуса r (рис.2). Запишем, что циркуляция вектора индукции магнитного поля вдоль выбранной окружности равна:
[ointlimits_L{overrightarrow{B}doverrightarrow{l}}=B2pi r left(1.1right).]
Тогда теорема о циркуляции предстанет в виде:
[B2pi r={mu }_0NIleft(2.1right),]
где $N$ — число витков с током. Выразим модуль вектора индукции, получим:
[B=frac{{mu }_0NI}{2pi r}.]
Ответ: $B=frac{{mu }_0NI}{2pi r}.$
Пример 2
Задание: Какова циркуляция вектора индукции вдоль контура, который охватывает токи $I_1=5 A, I_2=6 A$, $I_3=10 A$, если первые два тока текут в одном направлении, третий в противоположном.
Решение:
По теореме о циркуляции:
[ointlimits_L{overrightarrow{B}doverrightarrow{l}}=sum{I_kleft(2.1right).}]
Для нашего случая имеем:
[ointlimits_L{overrightarrow{B}doverrightarrow{l}}=I_1+ I_2-I_3left(2.2right).]
Проведем вычисление, получим:
[ointlimits_L{overrightarrow{B}doverrightarrow{l}}=5+6-10=1 left(Тлcdot мright).]
Ответ: $ointlimits_L{overrightarrow{B}doverrightarrow{l}}=1Тл•м.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
ВИХРЕВОЙ ХАРАКТЕР МАГНИТНОГО ПОЛЯ.
Теорема о циркуляции вектора магнитной индукции поля постоянных токов в вакууме может быть доказана на основе закона Био-Савара, что, в общем случае, достаточно сложно.
— циркуляция вектора магнитной индукции по любому замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов охватываемых этим контуром.
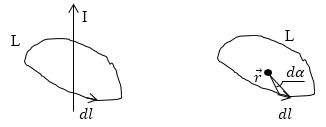
Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта (рис.75).
РИС.75 РИС.76 РИС.77
Если ток распределен по объему, в котором расположен контур, то полный ток охваченный контуром 
, где интеграл берется по произвольной поверхности натянутой на контур, плотность тока соответствует токе расположения площадки . В этом случае теорема о циркуляции:
Покажем справедливость теоремы на примерах.
ПРИМЕР 1. Контур охватывает прямолинейный бесконечно длинный провод с током, причем контур расположен в плоскости перпендикулярной проводу (рис.76). Найдем циркуляцию вектора магнитного поля, используя формулу для расчета индукции поля, полученную методом суперпозиции 
. Скалярное произведение под интегралом можно представить (рис.77):
РИС.78 РИС.79
Если замкнутый контур L` не охватывает ток (рис.78),
То 
и циркуляция также равна нулю.
ПРИМЕР 2. Контур лежит не в плоскости перпендикулярной проводу (рис.79). Разложим вектор 
на составляющие вектора, один из которых лежит в плоскости перпендикулярной проводу, а второй перпендикулярен этой плоскости:
Циркуляция вектора магнитной индукции определяется только «проекцией» контура на плоскость перпендикулярную проводу.
ПРИМЕР 3. Если контур охватывает несколько токов, то вектор индукции результирующего поля: 
ПРИМЕР 4. Если ток непрерывно распределен в объеме, в котором расположен контур, то полный ток, охватываемый контуром 
, где интеграл берется по произвольной поверхности натянутой на контур.
Тогда : 
РИС.80 РИС.81 РИС.82 РИС.83
Теорема о циркуляции позволяет достаточно просто рассчитать индукцию магнитного по известному распределению токов, если можно выбрать контур, вдоль которого модуль вектора магнитной индукции и направление постоянно.
В простейшем варианте можно выбрать контур полностью совпадающий с линией магнитной индукции как в поле прямого тока (рис.80), тороида (рис.81).
Поле внутри соленоида (рис.82) тем более однородно, чем больше длина соленоида по сравнению с его диаметром. Для «бесконечного» соленоида снаружи вблизи его поверхности магнитного поля нет и можно выбрать контур, лишь часть которого совпадает с линией магнитной индукции (рис.83).
Ток охватываемый контуром 
, где N – число витков с током, охваченных контуром. Тогда:
Следовательно, индукцию магнитного поля внутри «бесконечного» соленоида можно рассчитать по формуле
, где n – число витков соленоида на единицу длины.
Факт, что циркуляция вектора магнитной индукции по замкнутому контуру не равна нулю, означает, что, в отличие от электростатического, магнитное поле – не потенциально.
Используем теорему Стокса 
и сравним это выражение с записью теоремы о циркуляции вектора магнитной индукции в случае непрерывного распределения тока в некотором объеме.
— дифференциальная (локальная) форма теоремы о циркуляции. Математическая констатация того факта, что линии вектора магнитной индукции замкнуты вокруг вектора плотности тока по правилу правого буравчика и поэтому магнитное поле называют вихревым или соленоидальным.
Используем, что 
или с помощью определителя:
, .