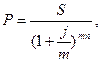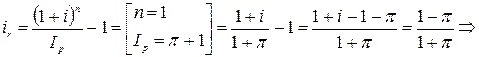Глава 3 УРАВНЕНИЯ ЭКВИВАЛЕНТНОСТИ
3.1 ДАТИРОВАННЫЕ СУММЫ
Использование значений денежных сумм без указания даты, когда они
|
должны использоваться, является |
бессмысленным. Очевидно, |
что 1000 |
||
|
рб наличными в |
настоящее |
время предпочтительнее, чем 1500 рб, |
||
|
обещанные через 50 лет. Сумма платежа вместе с |
датой погашения |
|||
|
называется датированной суммой. Например, 10000 |
рб, полагающиеся |
|||
|
7 июля 1995 г., являются датированной суммой. |
||||
|
Когда необходимо |
сравнивать датированные |
суммы, |
нужно |
обязательно знать норму процента. Если человек имеет возможность в
|
течение некоторого |
времени инвестировать свои деньги, получая 8% |
||
|
годовых, говорят, что |
его деньги стоят j1 = 8% . При |
такой |
норме 1000 |
|
рб, полагающиеся через три года, и |
1360,49 рб ( = |
1000 |
× (1,08) 4 ), |
|
полагающиеся через |
7 лет, могут |
рассматриваться |
как эквивалентные, |
так как после получения через три года 1000 рб можно в течение следующих четырех лет при норме 8% годовых накопить 1360,49 рб. Точно также 793,83 рб, ( = 1000 × (1,08) -3 ), имеющиеся в настоящее время, эквивалентны 1000 рб через три года.
В общем случае датированные суммы сравниваются по следующему правилу эквивалентности: сумма P , полагающаяся на данную дату, эквивалентна при данной норме сложного процента i сумме S , полагающейся на n периодов конверсии позже, если является справедливым хотя бы одно из следующих равенств:
S = P(1 + i) п или P = S(1 + i) —п .
Таким образом, накопление или дисконтирование могут рассматриваться как простое преобразование заданной датированной суммы к другой дате. Преобразование делается в соответствии со следующей временной диаграммой:
|
Прошлая дата |
Настоящая дата |
Будущая дата |
|
D(1 + i) —п |
D |
D(1 + i) п |
27

Прошлая и будущая суммы эквивалентны датированной сумме D.
Важным и полезным свойством эквивалентных датированных сумм является следующее свойство 1 : при данной норме сложного процента если A эквивалентно B и B эквивалентно C , то A эквивалентно C.
Для доказательства этого утверждения мы расположим данные на временной диаграмме следующим образом :
|
0 |
a |
b |
c |
|
P |
A |
B |
C |
|
где 0 означает настоящее время |
и |
a , b, c представляют числа |
|
|
периодов конверсии от |
настоящего |
времени до соответствующих дат |
|
|
погашения. |
Если A эквивалентно B , то B = A(1 + i) b-a . Если B эквивалентно C , то C = B(1 + i) c-a .
Исключая из этих равенств сумму B , получим, что
C = A(1 + i) b-a(1 + i) c-b = A(1 + i) c-a .
Полученный результат является условием эквивалентности датированных сумм A и C.
Это свойство не имеет места для норм простого процента и норм простого дисконта. Поэтому понятие эквивалентности для этих норм не применяется.
ПРИМЕР 1 Долг 10000 рб следует выплатить через 10 лет. Если деньги стоят j1 = 5% , найти эквивалентный долг через a) 1 год , b) 15 лет.
РЕШЕНИЕ Построим временную диаграмму
Согласно правилу эквивалентности
X = 10000 × (1,05) -9 = 6446,1 полагается через 1 год
28

Y = 10000 × (1,05) 5 = 12762,8 полагается через 15 лет
|
Иллюстрацией эквивалентности |
X |
и Y |
может |
служить применение |
|||||
|
свойства 1, так как (6446,1)(1,05) 14 = 12762,8. |
|||||||||
|
ПРИМЕР 2 |
Вексель |
на 10000 рб со |
сложным процентом при j4 = 6% |
||||||
|
за три |
года |
должен |
быть |
погашен |
через |
три |
года. Какая сумма, |
||
|
полагающаяся через 8 лет, эквивалентна этой сумме при j2 = 4% ? |
|||||||||
|
РЕШЕНИЕ |
Данная |
сумма, |
датированная |
на |
конец третьего года, |
||||
|
равна |
10000 |
× (1,015) 12 |
= |
11956,2 |
рб. |
Расположим данные на |
|||
|
временной диаграмме соответствующим образом |
|||||||||
|
0 |
6 |
16 |
11956,2 X
Здесь 6 и 16 представляют количества полугодовых периодов начисления, начиная с начального момента. Искомая сумма получается путем накопления основной суммы 11956,2 рб за 10 периодов начисления при норме 2% за период, то есть X = 11956,2 × (1,02) 10 = 14574,5 полагается через 8 лет.
3.2 СЕРИИ ДАТИРОВАННЫХ СУММ
Сумма двух или большего числа датированных сумм, погашаемых в различные даты, практически не имеет смысла. Например, предположим, что 20000 рб погашается через два года, а 30000 рб погашается через пять лет. Сумма 20000 + 30000 = 50000 рб не связана с какой либо датой и поэтому мало о чем говорит. Однако, если все рассматриваемые суммы преобразовать в эквивалентные датированные суммы с одной и той же датой погашения, то сумма таких эквивалентных сумм приобретает смысл и называется датированной суммой серии. Она будет изменяться в
|
зависимости |
от даты, к которой преобразованы |
эквивалентные |
|
суммы. Для |
различных датированных сумм одной |
и той же серии |
|
справедливо следующее свойство 2 |
: датированные суммы одной и |
той |
|||
|
же серии, |
определенные |
для |
различных |
дат, |
являются |
|
эквивалентными. |
|||||
|
Доказательство дадим для серии из двух датированных сумм. Пусть |
A и |
B будут двумя датированными суммами, погашаемыми через a и b периодов начисления от настоящего времени. Пусть также U и V
29

будут двумя датированными суммами этой серии, определенными для дат u и v ( за единицу времени принимается период начисления ). Представим эти данные на временной диаграмме
|
Время: |
0 |
a |
b |
u |
v |
|
Суммы: |
A |
B |
U |
V |
Преобразовывая значения A и B ко времени u согласно правилу эквивалентности и суммируя результаты, получим датированную сумму серии, погашаемую через u периодов
U = A(1 + i) u-a + B(1 + i) u-b
Умножая обе части этого равенства на (1 + i) v-u и производя очевидные упрощения, получим другую датированную сумму серии, погашаемую уже через v периодов начисления,
U(1 + i) v-u = A(1 + i) v-a + B(1 + i) v-b .
Но правая часть этого равенства в точности равна V, так что U(1 + i) v-u = V, и условие эквивалентности U и V выполняется, что и доказывает справедливость свойства 2.
ПРИМЕР Если деньги стоят j4 = 4% , найти одноразовую выплату, эквивалентную серии из 10000 рб, погашаемых через два года, и 15000 рб, погашаемых через 5 лет, для трех случаев погашения : a) в настоящее время; b) через 2 года; c) через пять лет.
РЕШЕНИЕ Представим серию на временной диаграмме
10000 15000
Вычислим эквивалентные значения обоих сумм для трех требуемых временных сроков и сведем их в таблицу
|
Настоящее |
Через |
Через |
|
|
время |
2 года |
5 лет |
|
|
Первая сумма |
9234,83 |
10000,00 |
11268,25 |
|
Вторая сумма |
12293,17 |
13311,74 |
15000,00 |
30

|
Сумма серии |
21528,00 |
23311,74 26268,25 |
В соответствии со свойством 2 все три датированные суммы серии должны быть эквивалентными. Это можно проверить следующим образом. Представим суммы серии на временной диаграмме
|
0 |
8 |
20 |
||
|
21528,00 |
23311,74 |
26268,25 |
||
|
Поскольку |
21528,00 × (1,1) 8 |
= 23311,74 , датированная сумма серии на |
||
|
настоящее |
время эквивалентна |
датированной сумме серии на конец |
второго года (8 периодов начисления). Подобным образом, 23311,74 × (1,1) 12 = 26268,25
означает, что вторая датированная сумма серии эквивалентна третьей и все три датированные суммы серии являются эквивалентными.
Как уже было выше сказано , для сравнения двух итоговых сумм, погашаемых в различные даты, необходимо заменить их эквивалентными суммами, пересчитанными на одну и ту же дату. Величина разности полученных эквивалентных сумм будет различной в зависимости от использованной для сравнения даты. Также как и в случае сумм серий, разности, рассчитанные на различные даты, будут эквивалентными. Доказательство этого повторяет те же рассуждения, которые были использованы выше при анализе сумм серий на различные даты при рассмотрении свойства 2.
ПРИМЕР Сравнить два обязательства: выплатить 20000 рб со сложным процентом на 2 года при норме j4 = 5% через два года, и 10000 рб через 6 лет, если деньги стоят j2 = 6% , рассматривая их стоимость в три различные момента времени: a) настоящее время; b) через два года; c) через 6 лет.
РЕШЕНИЕ Датированная сумма первого обязательства в момент погашения равна 20000 × (1,0125) = 22089,72. Построим временную диаграмму ( время измеряется полугодиями ) :
22089,72 10000
31
Соседние файлы в папке ФИНАНСОВАЯ МАТЕМАТИКА
- #
- #
- #
- #
- #
20.04.2015215.97 Кб33Сбербанк России Поволжский банк Пример расчета платежей за пользование кредитом.mht
- #
4. Деньги стоят j2 = 5%. Найти
датированную сумму по окончании трех лет для платежей: 5 тыс. руб. через пять
лет и 8 тыс. руб. через 8 лет.
Решение:
Сначала определим первоначальную сумму для срока 5 лет:
Где: m –
количество начислений процентов в году,
n – количество
лет,
S – наращенная сумма,
P – первоначальная
сумма,
j – процентная
ставка.
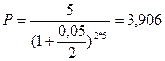
Теперь найдем датированную сумму по окончании трех лет для платежа 5 тыс.
руб. через пять лет:
тыс. руб.
Далее определим первоначальную сумму для срока 8 лет:
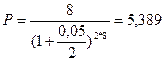
Теперь найдем датированную сумму по окончании трех лет для платежа 8 тыс.
руб. через восемь лет:
тыс. руб.
5. Найти эффективную ставку,
при которой 10 тыс. руб. теперь эквивалентны 20 тыс. руб. через 14 лет.
Решение:
Для определения эффективной ставки воспользуемся следующей формулой:
или 5,07%.
6. При данной процентной
ставке j2 10
млн. руб. прирастают до 25 млн. руб. через двадцать лет. Какой является сумма в
конце 10 лет?
Решение:
Сначала определим процентную ставку по данной операции:
или 4,62%
Теперь определим сумму в конце 10 лет:
млн. руб.
7. В рассматриваемый год
ожидаемая инфляция составляет 20%. Какую номинальную годовую процентную ставку
следует установить по вкладам в банке, чтобы реальная годовая ставка равнялась
3%?
Решение:
Вывод формулы для процентной ставки:
8. Судостроительная фирма
желает вносить в банк ежеквартально равные суммы. Банк выплачивает сложные
проценты по ставке j6
= 8%. Какую сумму должна вносить ежеквартально фирма, чтобы за 15 лет накопить
3 млн. руб.?
Решение:
млн. руб.
9. Предприятие создает фонд
для постройки нового здания, вкладывая в него каждые 4 года 15 млн. руб. Деньги
кладутся в банк, выплачивающий 5% годовых (сложных). Какая сумма будет в фонде
через 16 лет?
Решение:
Для решения воспользуемся следующей формулой ренты:
млн. руб.
10. Покупатель приобретает
дом, который стоит 50000 руб. Он уплатил сразу 20000 руб., а на остальную сумму
получил кредит на 1 год 6 месяцев под 4% годовых (простых), который должен
погасить ежемесячными равными уплатами. Чему равна каждая уплата?
Решение:
Сумма кредита составляет: 50000 – 20000 = 30000 руб.
Сумма долга с процентами составит:
S = P*(1 + n*i),
Где: S –
наращенная сумма по сертификату,
P –
первоначальная сумма,
n – количество лет,
i – процентная
ставка.
S = 30000*(1 + 1,5*0,04)
= 31800 руб.
Ежемесячная сумма составит: 31800 / 18 = 1766,67 руб.
| 🎓 Заказ №: 22497 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Экономика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 249 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Найти датированную сумму по окончании 3 лет при 6 % годовых, эквивалентную 10 000 000 руб. вместе с процентами за 10 лет при ставке 5% годовых с полугодовым начислением процентов.
Решение: 1. Сначала определим первоначальную сумму, используя следующую формулу: P = nm m j S 1 , где S – наращенная сумма; P – первоначальная сумма; j – номинальная ставка;
Готовые задачи по экономике которые сегодня купили:
- Необходимо заменить 2 платежа в 30 000 руб. и 55 000 руб. со сроками уплаты через 3,2 и 4,5 года, соответственно, новым платежом, при условии, что срок уплаты нового платежа равен 4 года.
- Определить размер ежегодных платежей по сложной ставке 20 % годовых для погашения кредита размером 300 000 руб. в течение 5 лет.
- Оборотные активы компании равны 3 млн. Коэффициент текущей ликвидности 1,5, а коэффициент быстрой ликвидности 1,0.
- Определить точку безразличия и обосновать выбор источника финансирования бизнеса
- Облигация федерального займа с переменным купоном была приобретена юридическим лицом за 77 дней до своего погашения по цене 103% (с учетом накопленного купонного дохода) от номинала. Доходность облигации к погашению в этот момент составляла 36% годовых.
- Фермер взял в банке кредит на сумму 5 000 000 руб. под 8 % годовых (сложных).
- Участок земли стоит 500 тыс. Добавив еще 800 тыс. Вы можете выстроить на этом участке пансионат. Через год это имущество должно стоить 1,5 млн.
- ГКО со сроком обращения один год продается на аукционе по цепе 72%.
- Определить граничную точку сфер реализации идентичных товаров, производимых двумя предприятиями (А и Б, расстояние между которыми L= 2000 км. ЗА = 450, ЗБ = 850
- В контракте предусматривается погашение обязательства через 1,67 года в размере 53000 руб., при учете, что наращение процентов происходило по простой процентной ставке в 14% годовых.
Преобразовывая значения А и Б ко времени и, согласно правилу эквивалентности и суммируя результаты, получим датированную сумму серии, погашаемую через и периодов [c.43]
Умножая обе части этого равенства на (1 + i)» u и произведя очевидные упрощения, получим другую датированную сумму серии, погашаемую уже через v периодов начисления [c.43]
Поскольку 21 528,00 х (1,1)8 = 23 311,74, да тированная сумма серии на настоящее время эквивалентна датированной сумме серии на конец второго года (восемь периодов начисления), Подобным же образом [c.44]
Ранее мы рассматривали датированную сумму серии платежей или обязательств. При этом было видно, что сумма серии зависела от используемой нормы процента и даты, на которую вычислялась сумма. На основе правила эквивалентности для таких серий можно сформулировать следующее утверждение при данной норме сложного процента две серии платежей являются эквивалентными, если датированные суммы этих серий на любую общую дату равны. Таким образом, если стоимость холодильника равна 3 млн руб., то любая серия платежей, использованная при его покупке, должна иметь стоимость на настоящий момент (текущую стоимость) 3 млн руб. Равенство, устанавливающее, что датированные суммы двух серий на общую дату равны, называется уравнением эквивалентности, или равенством стоимостей. Дата, используемая в этом равенстве, называется датой сравнения. Из свойства 1 следует, что в качестве даты сравнения может быть использована любая дата. [c.46]
Теперь нужно выбрать дату сравнения. Может быть использована любая дата (обычно выбирается самая поздняя). В нашем примере это восемь лет (шестнадцать полугодовых периодов). Равенство эквивалентности получается преобразованием всех сумм к дате сравнения и приравниванием датированных сумм серий. Это дает [c.47]
Выберем конец четвертого года в качестве дать сравнения, хотя любая другая дата была бы также возможна. Все суммы преобразовываются к дате сравнения, и датированные суммы серий приравниваются, образуя уравнение эквивалентности [c.48]
Деньги стоят у 4 = 3 %. Найти датированную сумму по окончании пяти лет для серии платежей 10 млн руб. через шесть лет и 20 млн руб. через десять лет. [c.53]
Деньги стоят 2 = 5 %. Найти датированную сумму по окончании трех лет для серии платежей 5 млн руб. через пять лет и 8 млн руб. через восемь лет. [c.53]
Деньги стоят jz = 4 %. Найти датированную сумму по окончании шести лет для серии платежей 10 млн руб. через три года и 15 млн руб. через восемь лет. [c.53]
Деньги стоят Д = 6 %. Найти датированную сумму по окончании семи лет для серии платежей 6 млн руб. через два года и 9 млн руб. через десять лет. [c.53]
Настоящая стоимость аннуитета определяется как датированная сумма, эквивалентная всей серии платежей на начало срока аннуитета. Итоговая сумма аннуитета определяется как датированная сумма, эквивалентная всей серии платежей аннуитета на конец срока. Таким образом, настоящая стоимость обыкновенного аннуитета является эквивалентной суммой, выплачиваемой за один период платежа до даты первой вьь платы. Итоговая сумма обыкновенного аннуитета является эквивалентной суммой на момент [c.58]
Заметим, что для получения настоящей стоимости А этого аннуитета А и S являются датированными суммами одной и той же серии платежей. Следовательно, они эквивалентны. Отсюда следует, что [c.61]
Сумма двух или более датированных сумм, по шаемых в различные даты, практически не им( смысла. Предположим, например, что 20 000 р погашаются через два года, а 30 000 руб. — че пять лет. Сумма 20 000 + 30 000 = 50 000 руб. связана с какой-либо датой и поэтому мало о ч говорит. Однако если все рассматриваемые су мы преобразовать в эквивалентные датировг ные суммы с одной и той же датой погашения, сумма таких эквивалентных сумм приобрети смысл и называется датированной суммой epi Она будет изменяться в зависимости от даты, которой преобразованы эквивалентные сумм Для различных датированных сумм одной и т же серии справедливо следующее свойство датированные суммы одной и той же epi определенные для различных дат, являют эквивалентными. [c.42]