Как найти давление газа химия - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

В химии «парциальным давлением» называют давление, которое оказывает отдельно взятый компонент из газовой смеси внешней среды, например, на колбу, баллон или границу атмосферы. Вы можете подсчитать давление каждого газа, если знаете его количество, какой объем он занимает и какова его температура. Затем вы можете сложить парциальные давления и найти общее парциальное давление смеси газов, или найдите вначале общее давление, а затем — парциальное.

1
Примите каждый газ как «идеальный». В химии «идеальный газ» — тот, который взаимодействует с другими веществами, не вступая с ними в соединение. Отдельные молекулы могут сталкиваться друг с другом и отталкиваться, как шары для бильярда, не деформируясь при этом.^[1]
- Давление идеального газа возрастает, если его поместить в меньший объем, и уменьшается, если газ находится в большем объеме. Это отношение называется законом Бойля-Мариотта, по имени ученых Роберта Бойля и Эдма Мариотта. Математическая запись закона: k = P x V или, упрощенно, k = PV, где k представляет константу соотношения, P — давление, а V — объем.^[2]
- Давление может быть указано в нескольких различных единицах. Одна из них, Паскаль (Па), определяется как сила в 1 ньютон, приложенная к площади в 1 квадратный метр. Другой вариант представления давления — в атмосферах (атм). Эта единица определяется как давление земной атмосферы на уровне моря. Давление в 1 атмосферу равно 101,325 Па.^[3]
- Температура идеального газа возрастает при увеличении его объема и снижается при уменьшении объема. Это отношение называют законом Чарльза, по имени Жака Чарльза. Математическая запись закона: k = V / T, где k — константа соотношения между объемом и температурой, V вновь представляет объем газа, а T — его температуру.^[4]^[5]
- Температура газов в этих уравнениях приведена в градусах Кельвина, ее можно найти, прибавив 273 к числу градусов Цельсия в температуре газа.
- Эти два отношения можно объединить в одно уравнение: k = PV / T, которое также можно записать как PV = kT.
2
Определите количество газов. У газов есть и масса, и объем. Объем обычно измеряют в литрах (л), но есть два варианта подсчета массы.
- Обычно массу измеряют в граммах или, если она достаточно велика, в килограммах.
- Поскольку газы обычно весят очень мало, их масса также вычисляется в отдельной единице измерения, называемой молекулярной массой, или молярной массой. Молярная масса определяется как сумма атомарных весов всех атомов в газообразном веществе, каждый атом сравнивается с массой карбона (12)^[6]
- Поскольку атомы и молекулы слишком малы, чтобы работать с ними непосредственно, количество газа определяется в молях. Количество молей в данном газе можно найти, разделив массу на молярную массу, значение отмечается буквой n.
- Мы можем заменить постоянную k константу в уравнении газа числом n, количеством молей (mol), и ввести новую константу R. Тогда уравнение будет записано в виде nR = PV/T или PV = nRT.^[7]
- Значение R зависит от единиц, в которых измеряются давление газа, объемы и температура. Для объема в литрах, температуры в Кельвинах и давления в атмосферах, значение равно 0,0821 л атм/K мол. Это можно записать в виде 0,0821 л атм K^-1 мол ^-1, чтобы избежать использования разделительной черты при указании единиц измерения.^[8]
3
Понимание закона Дальтона о парциальном давлении. Закон, открытый химиком и физиком Джоном Дальтоном, который первым предположил, что химические элементы состоят из отдельных атомов,^[9] гласит: общее давление смеси газов равняется сумме давлений каждого газа в смеси.
- Закон Дальтона можно записать в таком виде: P_общее = P₁ + P₂ + P₃ … с таким количеством слагаемых после знака равенства, каково количество газов в смеси.
- Уравнение закона Дальтона можно расширить при работе с газами, чье индивидуальное давление неизвестно, но для которых известны температура и объем. Парциальное давление газа — такое же, как и для равного объема газа, полностью занимающего отведенный объем.
- Для каждого парциального давления мы можем переписать уравнение идеального газа. Вместо PV = nRT мы может оставить только P в левой части перед знаком равенства. Чтобы сделать это, обе части уравнения нужно разделить на V: PV/V = nRT/V. Две V слева сокращаются, остается P = nRT/V.
- Затем для каждого P справа мы можем выполнить замену, вписав уравнение парциального давления: P_общее =(nRT/V) ₁ + (nRT/V) ₂ + (nRT/V) ₃ …
Реклама

1
Определите уравнение парциального давления для газов, с которыми вы работаете. Для вычислительных целей возьмем пример: в колбе объемом 2 литра содержится 2 газа, нитроген (N₂), оксиген (O₂) и карбон диоксид, углекислый газ (CO₂). Каждого газа — по 10 г, температура каждого газа в колбе равна 37 градусам Цельсия. Нужно найти парциальное давление каждого газа и общее давление смеси газов на емкость.
- Наше уравнение парциального давления будет выглядеть следующим образом: P_total = P_{нитроген} + P_{оксиген} + P_{карбон диоксид}.
- Поскольку мы пытаемся найти давление, которое оказывает каждый из газов, знаем объем и температуру и можем найти количество молей каждого газа, основываясь на массе вещества, мы можем переписать уравнение в следующей форме: P_общее =(nRT/V) _{нитроген} + (nRT/V) _{оксиген} + (nRT/V) _{карбон диоксид}
2

Переведите температуру в градусы Кельвина. Температура по Цельсию равна 37 градусам, потому мы добавим 273 к 37 и получим 310 градусов K.
3
Найдите количество молей каждого газа в образце. Число молей газа равно массе газа, деленной на его молярную массу,^[10] которая, как уже говорилось, равна сумме весов всех атомов в составе.
- Для нашего первого газа, нитрогена (N₂), каждый атом обладает атомарной массой 14. Поскольку нитроген содержит два атома (состоит из двухатомных молекул), мы должны умножить 14 на 2, чтобы найти молярную массу нитрогена, она равна 28. Затем мы делим массу в граммах, 10 г, на 28, чтобы получить количество молей, которое приблизительно равно 0,4 моль.
- У второго газа, оксигена (O₂), масса каждого атома равна 16. Оксиген также двухатомный газ, потому мы умножаем 16 на 2 и получаем молярную массу, равную 32. Разделив 10 г на 32, мы получим примерно 0,3 моль оксигена в составе образца смеси газов.
- Третий газ, карбон диоксид (CO₂), состоит из 3 атомов: одного атома карбона с атомарной массой 12 и двух атомов оксигена, каждый с атомарной массой 16. Мы складываем все три веса: 12 + 16 + 16 = 44 составляет молярную массу. Разделив 10 г на 44, мы получим примерно 0,2 моля карбон диоксида.
4
Подставьте значения для молей, объема и температуры. Наше уравнение будет выглядеть так: P_общее =(0,4 * R * 310/2) _{нитроген} + (0,3 *R * 310/2) _{оксиген} + (0,2 * R *310/2) _{карбон диоксид}.
- Для простоты мы оставили текущие значения единиц измерения. Эти единицы уйдут после математических вычислений, и останутся только те, которые участвуют в определении давления.
5

Подставьте значение константы R. Мы будем указывать парциальное и общее давление в атмосферах, потому используем значение R, равное 0,0821 л атм/K моль. Подстановка этого значения в уравнение дает нам P_общее =(0,4 * 0,0821 * 310/2) _{нитроген} + (0,3 *0,0821 * 310/2) _{оксиген} + (0,2 * 0,0821 * 310/2) _{карбон диоксид}.
6
Подсчитайте парциальное давление каждого газа. Сейчас все значения на месте, пора перейти к математическим вычислениям.
- Чтобы найти парциальное давление нитрогена, умножим 0,4 моль на нашу константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,4 * 0,0821 * 310/2 = 5,09 атм, приблизительно.
- Для получения парциального давления оксигена умножим 0,3 моль на константу 0,0821 и температуру 310 градусов K, затем разделим на 2 литра: 0,3 *0,0821 * 310/2 = 3,82 атм, приблизительно.
- Чтобы найти парциальное давление карбон диоксида, умножаем 0,2 моль на константу 0,0821 и температуру 310 градусов K, затем делим на 2 литра: 0,2 * 0,0821 * 310/2 = 2,54 атм, приблизительно.
- Теперь сложим полученные значения давлений и найдем общее давление: P_общее = 5,09 + 3,82 + 2,54, или 11,45 атм, приблизительно.
Реклама

1
Определите парциальное давление, как и раньше. Вновь, возьмем в пример колбу на 2 литра с тремя газами: нитрогеном (N₂), оксигеном (O₂) и карбон диоксидом (CO₂). У нас по 10 г каждого газа, температура каждого газа в колбе равна 37 °C.
- Температура по Кельвину будет такой же, 310 градусов, как и раньше, у нас будет примерно 0,4 моль нитрогена, 0,3 моль оксигена и 0,2 моль карбон диоксида.
- Мы также будем указывать давление в атмосферах, потому будем использовать значение 0,0821 л атм/K моль для константы R.
- Таким образом, наше уравнение парциального давления на текущий момент выглядит так же, как раньше: P_общее =(0,4 * 0,0821 * 310/2) _{нитроген} + (0,3 *0,0821 * 310/2) _{оксиген} + (0,2 * 0,0821 * 310/2) _{карбон диоксид}.
2
Сложите количество молей каждого газа в образце, чтобы найти общее количество молей в смеси газов. Поскольку объем и температура одинаковы для всех газов, не говоря о том, что каждая молярная масса умножается на одну и ту же константу, мы можем использовать распределительное свойство умножения и переписать уравнение в следующем виде: P_общее = (0,4 + 0,3 + 0,2) * 0,0821 * 310/2.
- Складываем 0,4 + 0,3 + 0,2 = 0,9 моль смеси газов. Это упростит наше выражение до P_общее = 0,9 * 0,0821 * 310/2.
3

Найдите общее давление смеси газов. Умножаем 0,9 * 0,0821 * 310/2 = 11,45 моль, приблизительно.
4
Найдите пропорцию каждого газа в смеси. Для этого разделите количество молей каждого газа на общее количество молей в смеси.
- У нас 0,4 моль нитрогена, потому 0,4/0,9 = 0,44 (44 процента) в образце, приблизительно.
- У нас 0,3 моль оксигена, потому 0,3/0,9 = 0,33 (33 процента) в образце, приблизительно.
- У нас 0,2 моль карбон диоксида, потому 0,2/0,9 = 0,22 (22 процента) в образце, приблизительно.
- Хотя в вычислениях выше сумма приблизительных значений в процентах дает всего 0,99, точные значения являются периодическими, так что сумма на самом деле будет равна повторяющимся девяткам после запятой. По определению это то же самое, что 1 или 100 процентов.
5
Умножим пропорциональное количество каждого газа на общее давление, чтобы найти парциальное давление.
- Умножаем 0,44 * 11,45 = 5,04 атм, приблизительно.
- Умножаем 0,33 * 11,45 = 3,78 атм, приблизительно.
- Умножаем 0,22 * 11,45 = 2,52 атм, приблизительно.
Реклама

Советы

Вы заметите небольшую разницу в значениях при вычислении сначала парциального давления, а затем общего, и при подсчете вначале общего, а затем парциального давления. Помните, что приведенные значения даны приблизительно, поскольку они округлены до 1 или 2 знаков после запятой для простоты подсчетов и понимания. Если вы выполняете вычисления самостоятельно без округления, вы заметите или меньшую разницу между значениями или не заметите ее вовсе.

Предупреждения

Знание парциального давления газов может стать вопросом жизни и смерти для дайверов. Слишком низкое парциальное давление кислорода может привести к бессознательному состоянию или смерти, но слишком высокое парциальное давление азота или кислорода также может привести к отравлению.^[11]^[12]

Вам потребуются

Калькулятор
Справочник атомарных весов / молярных масс

Об этой статье

Эту страницу просматривали 82 671 раз.

Была ли эта статья полезной?

Источник

В уроке 24 «Давление газа» из курса «Химия для чайников» рассмотрим устройство и принцип действия ртутного барометра, а также дадим определение давлению и рассмотрим его единицы измерения. Не пройдите мимо вводного урока в главу «Законы газового состояния», если вы его еще не читали.

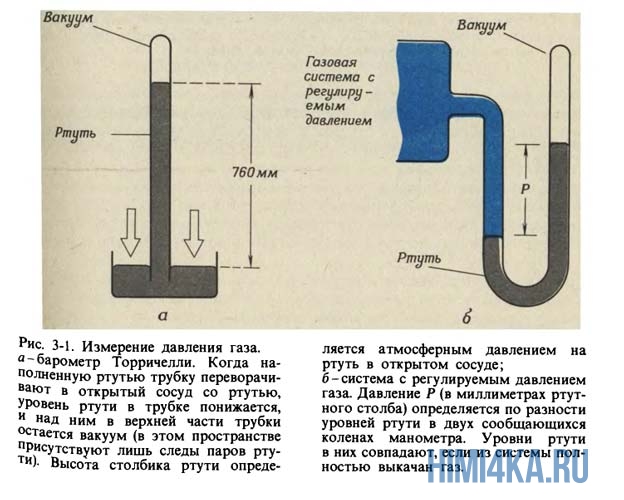
Ртутный барометр

Если стеклянную трубку, закрытую с одного конца, наполнить ртутью (Hg), а затем перевернуть открытым концом в сосуд с ртутью, как показано на рисунке 3-1 (а), уровень ртути в трубке будет опускаться до тех пор, пока высота ртутного столбика над поверхностью ртути в сосуде не достигнет приблизительно 760 миллиметров (мм).

Давление, оказываемое на поверхность ртути в сосуде весом ртутного столбика в трубке, в точности уравновешивается давлением окружающей атмосферы. Вследствие равенства этих давлений, действующих в противоположных направлениях, ртуть больше не выливается из трубки. Подобное устройство называется ртутным барометром. Его изобрел и впервые протестировал итальянский математик и физик Эванджелиста Торричелли для измерения атмосферного давления. Торричелли показал, что высота столбика ртути в барометрической трубке НЕ зависит от формы и размеров трубки, а потому, определяется не весом ртутного столбика, а давлением у его основания. Атмосферное давление на уровне моря поддерживает столбик ртути высотой 760 мм (в среднем). Поскольку в старину для измерения давления пользовались именно ртутными барометрами, то в качестве единицы измерения давления применялся «миллиметр ртутного столба«.

Единицы измерения давления

Давление определяется как сила, действующая на единицу площади (P = F/A), и поэтому в системе СИ единицей давления является паскаль (Па), определяемый как сила в 1 ньютон, действующая на площадь в 1 квадратный метр (Н/м²). Для тех, кто плохо учил физику, напоминаю, что ньютон представляет собой силу, которая придает телу массой 1 кг ускорение 1 м/c².

Пример 1. Плотность жидкой ртути равна 13,596 г/см³. Чему будет равен 1 мм ртутного столба (1 мм Hg) в паскалях?

Решение

Представим себе разлитый на столе слой ртути площадью 1 м² и толщиной 1 мм. Переведем сначала все размеры этого слоя в сантиметры; тогда его объем выразится как:

0,100 см × 100 см × 100 см = 1000 см³

Плотность жидкой ртути равна 13,596 г/см³, т.е масса 1 кубического сантиметра ртути составляет 13,596 г, а зная это, нетрудно установить, что масса слоя равна:

1000 см³ × 13,596 г/см³ = 13 596 г =13,596 кг

Вес этого слоя можно найти как произведение его массы на ускорение силы тяжести, которое равно g = 9,8 м/c²; таким образом, сила, с которой рассматриваемый слой ртути давит на стол, равна:

F = m·g = 13,596 кг × 9,806 м/c² = 133,32 кг·м·с² = 133,32 Н

Поскольку площадь слоя ртути равна равна 1 м², оказываемое им на стол давление определяется как :

P = F/A = 133,32 Н / 1 м² = 133,32 Н/м² = 133,32 паскаля (Па)

Пример 2. Стандартное давление на уровне моря считается равным точно 760 мм Hg. Выразите это давление в паскалях.

Решение:

Из примера 1 мы уже знаем, что давление 1 мм Hg эквивалентно 133,32 Па. Следовательно:

760 мм Hg × 133,32 Па/мм = 101 323 Па

Паскаль — слишком маленькая единица для измерения давлений газов, подобно тому как кубический метр — слишком неудобная единица для измерения объемов жидкостей в лабораторных условиях. Поэтому обычно давление газов измеряют в стандртных атмосферах:

1 атмосфера (атм) = 101 325 Па = 760 мм Hg

Пример 3. В горах, высота которых составляет около 2500 м над уровнем моря, атмосферное давление приблизительно равно 3/4 давления на уровне моря. Выразите это давление в стандартных атмофсерах, паскалях и миллиметрах ртутного столба.

Ответ: давление равно 0,750 атм, 76 000 Па или 570 мм Hg

Надеюсь урок 24 «Давление газа» помог создать некоторое представление о понятии давления и его единицах измерения. Если у вас возникли вопросы, пишите их в комментарии. Если вопросов нет, то переходите к следующему уроку.

Источник

Формулы для определения давления газа применимы только для так называемого идеального газа. Это такой газ, когда пренебрегается взаимодействием между молекулами. Для этого газ должен быть достаточно разряженным. Газ с хорошей точностью можно считать идеальным вплоть до давлений 20 – 30 атмосфер. Так что атмосферу Земли можно считать идеальной даже у самой поверхности Земли. Давление газа на какую-либо поверхность определяется ударами молекул об эту поверхность. Естественно, что тогда давление газа должно зависеть от скоростей движения молекул. Вот формула для определения давления газа р

p = (Nmv^2)/3V (1)

Естественно, что давление зависит от числа молекул N, от массы молекулы m, от средней скорости движения молекул v и от объема сосуда V, где находятся молекулы. Средняя кинетическая энергия молекулы равна Е = mv^2/2. Тогда получим следующую формулу для расчета давления газа через среднюю энергию молекул

р = 2NЕ/3V (2)

Больцман рассчитал, что средняя кинетическая энергия молекул пропорциональна абсолютной температуре Т. Е = (3/2)kT, где k – постоянная Больцмана и T – абсолютная температура. Тогда получим для давления идеального газа формулу р = (NkT)/V. Перепишем эту формулу в следующем виде

рV = NkT (3)

Концентрация молекул в газе равна n = N/V. Тогда формула (3) примет такой вид

pV = NkT (4)

Концентрацию молекул можно выразить через произведение числа молей ν на число частиц в моле N = νNa. Произведение Na*k = R. Где R – газовая постоянная. Тогда (4) запишется в виде

pV = νRT (5)

Число молей газа ν = M/μ, где М – масса газа и μ – масса одного моля (молярная масса). Тогда уравнение (5) примет вид

pV = (M/μ)RT (6)

Уравнение состояния идеального газа в таком виде называют уравнением Клапейрона – Менделеева. При постоянных температуре и массе из (6) следует, что

pV = const (7)

То есть давление будет обратно пропорционально объему газа. Такой закон получил название закона Бойля – Мариотта. Если же постоянным является давление, то

V = (MR/Vμ)T (8)

Давление пропорционально абсолютной температуре. Этот закон получил название закон Шарля.

Вот и используйте любую из этих формул для расчета давления газа.

Источник

Объединенный
газовый закон — объединение
трех независимых частных газовых
законов: Гей-Люссака, Шарля, Бойля-Мариотта,
уравнение, которое можно записать так:
P₁V₁
/ T₁
= P₂V₂
/ T₂

И, наоборот, из
объединенного газового закона при P =
const (P₁
= P₂)
можно получить Уравнение
Клайперона-Менделеева: Если
записать объединенный газовый закон
для любой массы любого газа, то получается
уравнение Клайперона-Менделеева:
pV= (m / M) RT

где m — масса газа,
г;

M — молекулярная
масса г/моль;

p – давление,
Па;

V – объем, м³;

T — абсолютная
температура, К;

R — универсальная
газовая постоянная (8,314 Дж/(моль • К) или
0,082 л атм/(моль • К)).

Пример. Какой
объем займет при температуре 17°C и
давлении 250 кПа оксид углерода (II) массой
84 г?

Решение.
Количество
моль CO равно:
n(CO)
= m(CO)
/ M(CO)
= 84 / 28 = 3 моль,

Объем CO при н.у.
составляет 3
• 22,4 л = 67,2 л

Из объединенного
газового закона Бойля-Мариотта и
Гей-Люссака:

(P • V) / T = (P₀
• V0) / T₀

Следует: V(CO)
= (P0 • T • V0) / (P • T0) = (101,3 • (273 + 17) • 67,2) /
(250 • 273) = 28,93 л

Относительная
плотность газов показывает, во сколько
раз 1 моль одного газа тяжелее (или легче)
1 моля другого газа.

Средняя молекулярная
масса смеси газов равна общей массе
смеси, деленной на общее число молей:

Пример 1.
Плотность некоторого газообразного
вещества по водороду равна 17. Чему равна
его плотность по воздуху (Мср.=29).

Решение. DH₂
= Mв-ва / MH₂
= Мв-ва / 2; Мв-ва= 2DH₂
= 34; Dвозд = Mв-ва / Mвозд. ср = 34 / 29 = 1,17

Пример2.Определите
плотность по воздуху смеси азота, аргона
и углекислого газа, если массовые доли
компонентов составляли 15, 50 и 35%
соответственно.

Решение.
Dсмеси(по
воздуху) = Mсмеси / Mвозд. = Мсмеси / 29

Mсмеси = (15 • 28 + 50
• 40 + 35 • 44) / 100 = (420 + 2000 + 1540) / 100 = 39,6

Dсмеси(по воздуху)
= Mсмеси / 29 = 39,6 / 29 = 1,37

Закон Авогадро
и следствие из него

Среди веществ с
различным агрегатным состоянием
необходимо выделить газы, которые играют
огромную роль не только в нашей жизни,
но в различных технологических процессах.
Необходимо помнить, что для количественной
характеристики любого газа используют
давление, температуру и занимаемый
объем. Наиболее часто применяют так
называемые нормальные условия (н.у.),
которые соответствуют давлению Р=105 Па
и температуре Т=273 К.

Согласно закону
Авогадро: одинаковые объемы различных
газов при одинаковых условиях (давлении
и температуре) содержат одинаковое
число молекул.

Большое практическое
значение имеет следствие из закона
Авогадро: при нормальных условиях (н.у.)
один моль любого газа занимает объем,
равный 22,4 л.

Объем 22,4 л называют
молярным (мольным) объемом газа и
обозначают соответственно V_M
= 22,4 л/моль.

Пример: углекислый
газ CO₂.
Имеем М(CO₂)
= 44 г/моль. Значит, один моль CO₂
имеет массу 44 г и занимает объем (при
н.у.), равный 22,4 л, а также содержит в этом
объеме 6,02·10²³
молекул газа.

Связь между массой
m и объемом V конкретного газа при н.у.
определяется формулой:

Если условия, в
которых находится газ отличается от
нормальных, то используют уравнение
Менделеева-Клапейрона, которое связывает
все основные параметры идеального
газа:

Закон Дальтона

Объемы реагирующих
газов и продуктов их реакций относятся
друг к другу как небольшие целые числа
(коэффициенты уравнения реакции).

Закон парциальных
давлений

Общее давление
газовой смеси равно сумме парциальных
давлений отдельных газов, составляющих
данную смесь, то есть Р_общ
= Р₁
+ Р₂
+ .. + Р_п

Из формулировки
закона следует, что парциальное
давление
представляет собой частичное давление,
создаваемое отдельным газом. ТО есть,
парциальное давление — это такое давление,
которое бы создавал данный газ, если бы
он один занимал весь объем.

Пример:
определить
давление газовой смеси, если в объеме
11,2 л при н.у. содержится 4 г Н₂,
14 г СО и 56 г N₂.

Решение: Определим
с помощью уравнения Менделеева-Клапейрона
парциальные давления каждого из газов,
составляющих данную газовую смесь:

Р(Н₂)
= (m/M)RT/V = (4г/2г/моль)·8,31·273К/0,0112мз = 4·105 Па,

Р(СО) =
(14г/28г/моль)·8,31·273К/0,0112мз = 105 Па,

Р(N₂)
= (56г/28г/моль)·8,31·273К/0,0112мз = 4·105 Па.

Общее давление
газовой смеси равно: Р_общ
= Р(Н₂)
+ Р(СО) + Р(N₂)
= 9·105 Па

Величина парциального
давления определяется несколькими
способами, но наиболее часто встречающийся
практически способ основан на использовании
формулы:

Парциальным
давлением газа в смеси называют давление,
которое оказывал бы газ, если бы занимал
объем, предоставленный всей смеси, при
отсутствии всех других компонентов.

Если смесь
представляет собой идеальную смесь
идеальных газов, то парциальное давление
каждого газа (Pi) можно вычислить из
соотношений:

где А — содержание
данного газа в газовой смеси в объемных
%.

Пример:
определить массу кислорода О₂,
содержащегося в 1 м³
воздуха при нормальных условиях, если
процентное содержание кислорода в
воздухе составляет 21% об.

Решение:

Парциальное
давление О₂
в воздухе определяем по формуле Р(О₂)
= 105Па·21%/100% = 0,21·105Па. Отсюда, согласно
уравнения Менделеева — Клапейрона:
m(O₂)
= PV_M/RT
= (0,21·105Па·1м³·32г/моль)/8,31·273К
= 297 г

Ответ: 297 г.

Рассмотрим
возможность учета изменения объема или
давления при протекании химической
реакции, в которой участвуют или
образуются газообразные продукты. Для
учета этого необходимо вспомнить, что
коэффициенты в уравнении химической
реакции прямо пропорциональны числу
молей реагирующих и образующихся
веществ.

Применительно к
газам необходимо учесть также, что: 1
моль любого газа при н.у. занимает объем,
равный 22,4 л;

объем 1 моля любого
газа значительно превышает объем 1 моля
жидкого или твердого вещества (сравните:
1 моль жидкой воды — 18 смз(0,018 л), 1 моль
водяного пара — 22,4 л) и в общем объеме
системы объемом жидких и твердых веществ
можно пренебречь.

Таким образом,
сравнивая коэффициенты исходных веществ
и продуктов реакции, можно сделать вывод
об изменении объема (давления) в ходе
химической реакции.

Например, в
химической реакции 2СО + О₂
= 2СО₂
все вещества являются газами, Видно,
что до реакции имелось 3 моля газа (2 моля
СО и 1 моль О2), а после реакции осталось
2 моля СО2. Ясно, что объем 3 молей газа
(22,4·3=67,2л) больше объема 2 молей
(22,4·2=44,8л), то есть Vнач> Vкон. Значит,
данная реакция протекает либо с
уменьшением объема (изобарный процесс),
либо с уменьшение давления (изохорный
процесс).

В случае химической
реакции СО₂
+ С = 2СО имеем газообразные вещества
СО₂
и СО и твердое вещество С. Сравниваем
коэффициенты только для газообразных
веществ и имеем для исходных веществ 1
и конечных веществ 2. Так как 1 < 2, то
объем системы в ходе химической реакции
увеличивается (либо увеличивается
давление при изохорном процессе).

Пример 1. Приведение
объема газа к нормальным условиям.

Какой объем
(н.у.) займут 0,4·10^-3
м³
газа, находящиеся при 50 ⁰С
и давлении 0,954·10⁵
Па?

Решение. Для
приведения объема газа к нормальным
условиям пользуются общей формулой,
объединяющей законы Бойля-Мариотта и
Гей-Люссака:

Объем газа (н.у.)
равен
,
гдеТ₀=273
К;
P₀=1,013·10⁵
Па;
Т=273+50=323
К.

Пример 2. Определение
средней молекулярной массы смеси газов
по относительной плотности.

Вычислите
среднюю молекулярную массу смеси газов,
состоящей на 80% из метана и 20% кислорода
(по объему), используя значения
относительной плотности этих газов по
водороду.

Решение. Часто
вычисления производят по правилу
смешения, которое заключается в том,
что отношение объемов газов в
двухкомпонентной газовой смеси обратно
пропорционально разностям между
плотностью смеси и плотностями газов,
составляющих эту смесь. Обозначим
относительную плотность газов через
.
Она будет больше плотности метана, но
меньше плотности кислорода:

Плотность этой
газовой смеси по водороду равна 9,6.
средняя молекулярная масса газовой
смесиравна
удвоенной ее плотности по водороду:

Пример 3. Определение
давления газовой смеси.

В сосуде объемом
0,05 м³
при 25 ⁰С
содержится смесь из 0,020 м³
этилена под давлением 83950 Па и 0,015 м³
метана под давлением 95940 Па. Найдите
общее давление газов в сосуде.

Решение. Сначала
определяем парциальное давление каждого
из газов:

Общее давление
газовой смеси равно сумме парциальных
давлений ее компонентов:

Пример 4. Вычисление
химических эквивалентов.

На восстановление
7,09 г оксида двухвалентного металла
требуется 2,24 л водорода, измеренного
при (н.у.). Вычислить молярные массы
металла и оксида. Чему равна относительная
масса металла?

Решение. По закону
эквивалентов массы веществ m₁
и m₂,
вступающих в реакцию, пропорциональны
молярным массам их эквивалентов