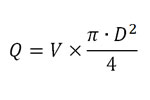2016-11-22
Калькулятор доступен на полной версии сайта, с помощью него вы можете узнать давление жидкости на глубине 1, 5, 10, 20, 50, 100, 500, 1000 метров.
Вычисления осуществляются по избыточной шкале давления, в которой за 0 принято давление атмосферы.
Результат расчета давления на глубине
Вычислить давление на другой глубине
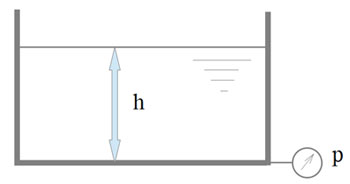
Расчет давления на глубине
Расчетная схема показана на рисунке:
Для расчета используется формула:
P=ρ × g × h
- ρ — плотность жидкость
- h — глубина погружения
- g — ускорение свободного падения
- P — величина давления на глубине h
Пример расчета давления воды на глубине 10 метров
Для расчета давления воды на глубине 10 м, введите в графу глубина (h) — 10, выберите жидкость — вода, нажмите кнопку рассчитать.
Каждые 10 метров воды создают давление в 1 атмосферу
Полученное значение давления воды на 10 метрах равно 98,1 кПа, что примерно равно атмосферному давлению 101 кПа. Поэтому в приблизительных расчетах принимают давление в воде на глубине 10 метров равным 1 атмосфере про избыточной шкале.
Администрация сайта за результаты онлайн вычислений ответственности не несет.
Читайте также:
Все новости
Глубина оказывает прямое воздействие на давление воды. Между ними прямая зависимость. Данное значение рассчитывается по специальной формуле. На различных участках глубоководья указанная величина заметно отличается.
Рассмотрим в статье особенности расчет и составляющие формулы, а также отличается ли давление на участках с разной глубиной.
Содержание
- Влияние глубины
- Зависимость двух физических показателей
- Формула для расчета
- Сколько составляет на различных глубоководных участках?
- Заключение
Влияние глубины
Чем глубже происходит погружение в водную толщу, тем больше становится ее сила. Глубина прямо влияет на увеличение давление. Это значение возрастает пропорционально.
Чем глубже, тем больше плотность водной толщи. С каждым последующим опусканием тела возникает все большая разница между внешним и внутренним водным давлением.
На поверхности действует атмосферное давление. При опускании в воду помимо него тела начинают испытывать еще и гидростатическое сдавливание.
Даже на мелководье на тело оказывается суммарное влияние, состоящее из атмосферного и гидростатического. При нырянии внешнее воздействие на тело возрастает. Возникает разница из-за увеличения плотности среды.
Верхние слои давят на нижние. За счет этого возникает сдавливающая сила на глубоководье. При этом ее показатель на одной глубине один и тот же по всем направлениям.
Зависимость двух физических показателей
С каждым последующим опусканием на 10 м воздействие становится больше на 1 атмосферу. Уже при погружении на 100 метров тела испытывают давление, соизмеримое с тем, что создается в паровом котле.
С погружением общее давление как на человека, так и на любой другой объект, возрастает. На 10 м оно становится больше вдвое.
Прирост давления на глубоководье неодинаков:
- На 10 м прирост составляет 100%.
- На 20 м он уже уменьшается вдвое (50%).
- На 40 он падает до 25%.
- На 60 он уже меньше 20% и составляет 17%.
В воде помимо атмосферного давления возникает еще гидростатический прессинг. Он также называется избыточным. При нахождении в воде любой объект будет испытывать уже сумму двух давлений: атмосферного и избыточного.
Зависимость двух величин напрямую прослеживается при изучении состояния человека, находящегося в условиях глубоководья. Если поместить человека в глубоководную среду, то он не сможет сделать полноценный вдох.
Возникшая разница между двумя давлениями, одно из которых оказывается на грудную клетку водой, а второе воздухом, что создается в легких, не позволит человеку нормально дышать. При большем погружении грудная клетка разорвется.
Формула для расчета
Данный показатель повышается пропорционально погружению. Он рассчитывается по специальной формуле:
P = p * g * h, где
- p — плотность среды. Примерно равна 1000 кг/м2.
- g — это ускорение, которое придается телу силой тяжести. Это значение называется ускорением силы тяжести или свободного падения. На Земле данная величина примерно равняется 9,81 м/с2.
- h — глубина, на которую погружается какой-либо объект. Высчитывается в метрах.
Формула является выражением закона Паскаля. По ней высчитывается значение гидростатического прессинга. Он напрямую зависит от высоты водного столба.
Произведение плотности (p) и ускорения (g) приблизительно равняется 0,1 атм. С каждым метром опускания на дно воздействие в водной среде повышается на 0,1 атм. Данное правило подтверждает тот факт, что чем глубже происходит опускание в толщу, тем выше становится показатель воздействия.
Сколько составляет на различных глубоководных участках?
Если какой-либо объект поместить в воду на один метр, то он будет испытывать на себе силу, равную 0,1 атм.
Предмет, погруженный на 2 м, уже станет испытывать прессинг величиной около 0,2.
С каждым последующим метром показатель будет возрастать на 0,1 атм. При 5 м значение равняется 0,5. При 10 оно будет уже равняться 1. Более точное число равняется 0,97 атмосферы.
На глубоководье водная толща становится сжатой. Ее плотность увеличивается. Уже на 100 м сила будет практически равняться 10. Более точное число составляет 9,7.
На глубинном участке в 1 км водная среда будет сдавливать находящиеся в ней объекты примерно со значением в 97 атм. Поскольку при 100 м величина равна 9,7, то на 1000 м она увеличивается в 10 раз.
Изменение показателя на разных глубоководных участках представлено в таблице.
| Глубина, на которую объект погружается в воду, в метрах | Давление в атмосферах. |
| 1 | 0,10 |
| 2 | 0,19 |
| 3 | 0,29 |
| 4 | 0,39 |
| 5 | 0,49 |
| 10 | 0,97 |
| 15 | 1,46 |
| 25 | 2,43 |
| 50 | 4,85 |
| 100 | 9,70 |
| 200 | 19,40 |
| 250 | 24,25 |
| 500 | 48,50 |
| 1000 | 97 |
При первых 10 метрах прирост невысокий и составляет 0,1 атмосферы. Дальше его показатель увеличивается.
Заключение
Глубина влияет на давление воды. С каждым метром движения объекта вглубь его показатель увеличивается на 0,1 атм. Уже на 10 м сдавливающая сила воды составляет почти 1 атмосферу. Зависимость обеих величин обусловлена плотностью воды, которая возрастает по мере движения тела в ней на дно.
Также на глубоководье происходит увеличение внешнего силового воздействия на объект. Если на поверхности тела испытывают воздействие только атмосферного давления, то в воде помимо него на них еще оказывается и гидростатическое.
При этом прирост воздействия на разных глубинных участках неодинаков. Особенно он высок при первых 10 м погружения. Дальше он начинает довольно быстро снижаться.
Давление жидкости .
(h) это глубина.
(rho) это плотность жидкости
1. Определить давление воды на глубине 7 м.Плотность воды: (rho=1000dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
2. Найти давление на дно цистерны с нефтью, если ее глубина (h=5м), а плотность нефти (rho=800dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
3. На какой глубине давление воды (p= 250 кПа) ? Плотность воды (rho=1000dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
4. Определить глубину озера, если давление воды на дне (p=900 кПа). Плотность воды (rho=1000dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
5. Давление жидкости на глубине (h=2м) равно 16 кПа. Найти плотность этой жидкости. Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
6. Определить силу, действующую снаружи на иллюминатор подводной лодки, если она находится на глубине (h=) 20 м, а его площадь (s=500 см^2) .Плотность воды (rho=1000dfrac{кг}{м^3}). Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
7. Определить силу, действующую на дно аквариума, если его глубина (h=40 см ) , а площадь дна (S= 3600 см^2) . Плотность воды (rho=1000dfrac{кг}{м^3}). Атмосферное давление не учитывать.
Показать ответ
Показать решение
Видеорешение
Перейти к контенту
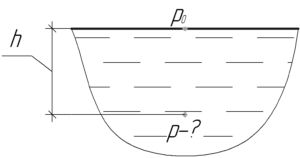
Условие задачи:
Найти давление в озере на глубине 4,5 м. Атмосферное давление 100 кПа.
Задача №3.2.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(h=4,5) м, (p_{атм}=100) кПа, (p-?)
Решение задачи:
Давление в озере на глубине (h) складывается из атмосферного давления (p_{атм}) и давления воды (p_{в}).
[p = {p_{атм}} + {p_в}]
Давление столба воды (p_{в}) высотой (h) определим по формуле:
[{p_в} = rho gh]
Здесь (rho) – плотность воды, равная 1000 кг/м3. Значит:
[p = {p_{атм}} + rho gh]
Численное значение искомого давления равно:
[p = 100 cdot {10^3} + 1000 cdot 10 cdot 4,5 = 145000;Па = 145;кПа]
Ответ: 145 кПа.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.2.7 На сколько отличается давление столбика ртути высотой 10 мм от давления столбика
3.2.9 Чему равно давление воды на глубине 2 м?
3.2.10 С какой силой действует вода на прямоугольную плотину высотой 75 м и шириной 120 м
( 5 оценок, среднее 5 из 5 )