Как найти давление манометра формула

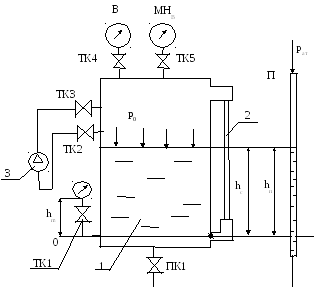
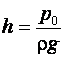Приборы для измерения давления, создаваемого жидкостями и газами, называют манометрами (от греч. манос – «редкий», «неплотный»). Рассмотрим устройство некоторых видов манометров.

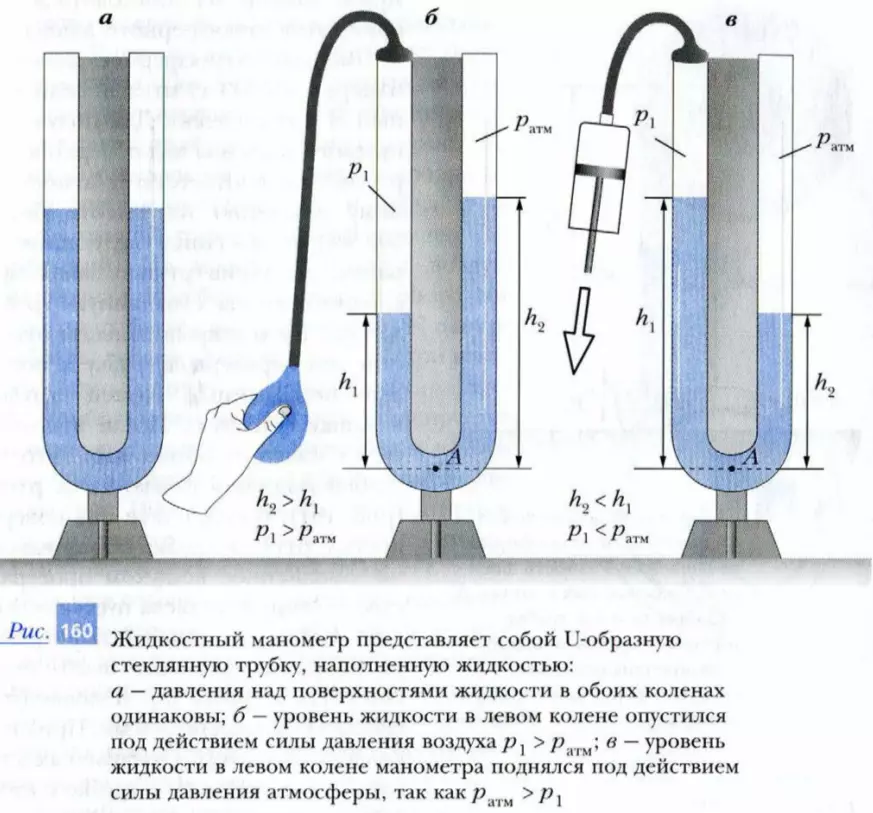
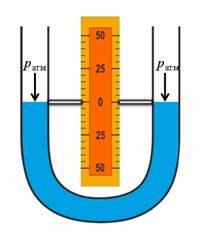
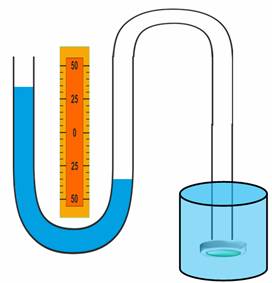
На рис. 160 показан жидкостный манометр. Он представляет собой U-образную стеклянную трубку, частично наполненную жидкостью. Если давления над поверхностями жидкости в обоих коленах одинаковы, например равны атмосферному давлению pатм, то поверхности жидкостей установятся на одном уровне. Если же давление над поверхностью жидкости в левом колене увеличить (см. рис. 160, б), то ситуации изменится: уровень жидкости в левом колене опустится под действием давления воздуха p1 > p_атм, а в правом колене – поднимется. При этом чем больше увеличится давление в левом колене, тем большей станет разность уровней жидкости в коленах манометра.

Пусть давление над поверхностью жидкости в левом колене равно p₁, а в правом – p_атм. Высота левого столба жидкости – h₁, а правого – h₂. Применим формулу для расчета гидростатического давления в нижней точке A трубки манометра. Это давление можно вычислить двумя способами. Рассматривая жидкость в левом колене, получим: p_A = p₁ + ρ · g · h₁; соответственно для правого колена: p_A = p_атм + ρ · g · h₂.

Приравнивая эти выражения, получим:

p₁ = p_атм + ρ · g · (h₂ — h₁) = p_атм + ρ · g · Δh

Таким образом, если известна плотность ρ жидкости, то, измеряя разность Δh высот столбов жидкости в коленах манометра, можно определить, на какую величину неизвестное давление p₁ отличается от атмосферного. Из полученной формулы следует, что если Δh > 0, т. е. h₂ > h₁, то измеряемое давление в левом колене больше атмосферного. Наоборот, если Δh < 0, т. е. h₂ < h₁, то измеряемое давление p₁ меньше атмосферного (см. рис. 160, в).

Продолжим анализ полученной формулы. Измеряемая разность давлений p₁ — pатм = ρ · g · Δh. Поэтому если перепад давлений достаточно большой, то для его измерения необходимо либо использовать трубку большой длины (для больших значений Δh), либо использовать жидкость с большой плотностью ρ. На практике в жидкостных манометрах обычно используют ртуть, плотность которой равна 13,6 г/см³. Поэтому давление часто измеряют в несистемных единицах – миллиметрах ртутного столба (мм рт. ст.). Давление столба ртути высотой 1 мм равно p = ρgh = 133,3 Па. (Нормальное атмосферное давление на уровне моря равно 101,325 кПа, что соответствует 760 мм рт. ст.)

Теперь представим себе, что давление в левом колене манометра над поверхностью жидкости равно нулю. Тогда полученная формула примет вид: p₁ = 0 = p_атм + ρg(h₂ — h₁). Следовательно, pатм = ρg(h₁ — h₂). Этой формулой можно воспользоваться для измерения атмосферного давления.

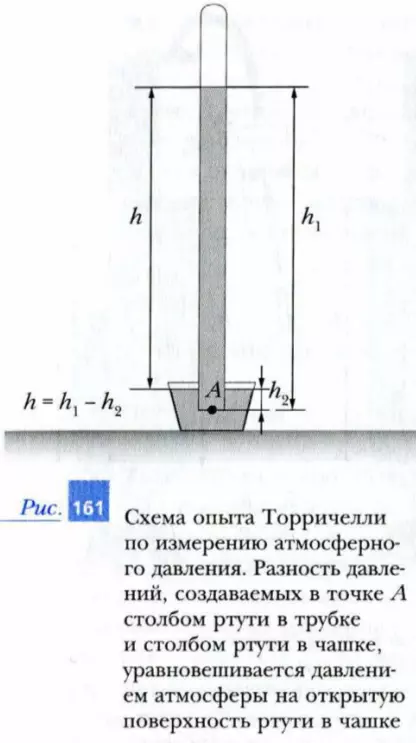
Впервые атмосферное давление измерил в 1643 г. итальянский ученый Э. Торричелли. Для получения нулевого давления над поверхностью ртути (что соответствует атмосферному давлению на высоте более 100 км) он поступил следующим образом. Заполнив ртутью запаянную с одного конца стеклянную трубку длиной 1 м и закрыв пальцем отверстие, он перевернул трубку и погрузил незапаянный конец трубки в чашку с ртутью. После этого он убрал палец и обнаружил, что из трубки вылилась только часть ртути (рис. 161). В результате над поверхностью ртути в трубке образовалось не заполненное воздухом пространство – «торричеллиева пустота». Высота h столба оставшейся в трубке ртути, равная разности высот столбов ртути в трубке (h₁) и чашке (h₂), составила примерно 760 мм. При этом разность давлений, создаваемых в точке A столбом ртути в трубке и столбом ртути в чашке, уравновешивается давлением атмосферы на открытую поверхность ртути в чашке:

0 + ρgh₁ = p_атм + ρgh₂

Следовательно,

p_атм = ρg(h₁ — h₂) = ρgh

Если к такой трубке с ртутью прикрепить шкалу с нанесенными на ней делениями в миллиметрах, то получится ртутный барометр – прибор для измерения атмосферного давления в миллиметрах ртутного столба.

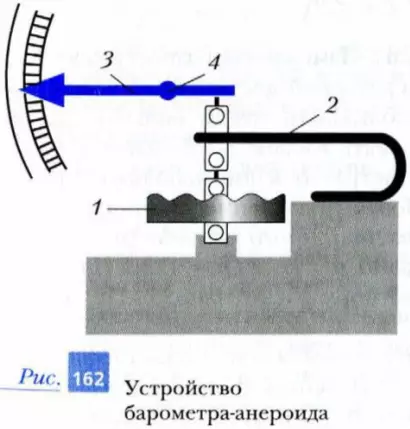
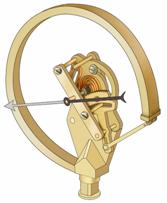
В настоящее время для измерения атмосферного давления используют безжидкостные приборы, получившие название барометров-анероидов. (Анероид в переводе с греческого – «безжидкостный».) Устройство одного из таких приборов показано на рис. 162. Основным элементом барометра-анероида является круглая металлическая коробка 1, закрытая тонкой гофрированной крышкой – мембраной. Из коробки откачан воздух, и мембрана под действием атмосферного давления прогибается внутрь коробки. К центру мембраны прикреплена пружина 2. При изменении атмосферного давления величина прогиба мембраны изменяется, что фиксируется с помощью стрелки 3, закрепленной на оси вращения 4. Такой прибор обычно имеет две шкалы (рис. 16З). Одна шкала проградуирована в миллиметрах ртутного столба (мм рт. ст.), другая – в гектопаскалях (гПа).

Как уже отмечалось, с увеличением высоты над поверхностью Земли атмосферное давление уменьшается. Поэтому по измерениям атмосферного давления на различных высотах можно судить о высоте подъема над поверхностью Земли. В барометрах, применяемых в авиации, шкалу градуируют в метрах, а прибор называют высотомером.

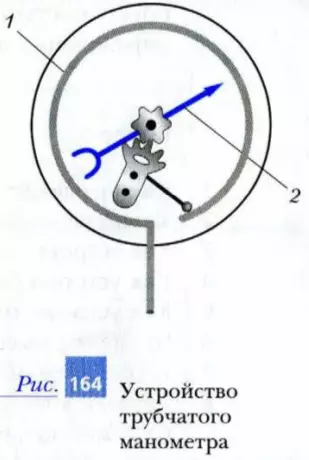
На практике для измерения давления часто используют трубчатые манометры. Устройство подобного прибора показано на рис. 164. Основным его элементом является изогнутая в дугу упругая металлическая трубка 1. Один жестко закрепленный конец этой трубки подсоединяется к системе, в которой необходимо измерить давление. Другой конец трубки запаян и находится в свободном положении. При увеличении давления внутри трубки она начинает разгибаться. В результате ее свободный конец перемещается относительно корпуса прибора. Это смещение вызывает поворот стрелки 2.

Подобные манометры позволяют измерять давление от сотен паскалей до нескольких гигапаскалей (10⁹ Па) и поэтому широко используются на практике. В частности, их применяют для измерения давления в шинах автомобилей, давления в водопроводных и газовых трубах и т. п.

Итоги

Приборы для измерения давления, создаваемого жидкостями и газами, называют манометрами.

Жидкостные манометры основаны на измерении разности высот столбов однородной жидкости в сообщающихся сосудах, один из которых находится под действием атмосферного давления. Измеряемая разность давлений равна

p₁ — p_атм = ρgΔh

Приборы для измерения атмосферного давления называют барометрами. Существуют ртутные барометры и барометры-анероиды (безжидкостные барометры).

Изменение (уменьшение) давления с увеличением высоты над поверхностью Земли позволяет использовать барометры для определения высоты полета летательных аппаратов.

Вопросы

1. Как называют приборы для измерения давления?
2. Какие виды приборов для измерения давления вы знаете?
3. Как устроен жидкостный манометр?
4. Как устроен барометр-анероид?
5. Как устроен трубчатый манометр?
6. Что такое высотомер?
7. Расскажите об опыте Торричелли.
8. Являются ли чашка и трубка в опыте Торричелли (см. рис. 161) сообщающимися сосудами?

Упражнения

1. Определите высоту столба воды, действие которого уравновесит атмосферное давление.
2. В течение суток барометр показывал давление: 740; 746; 752 мм рт. ст. Пересчитайте эти показания в Па.
3. Опустите стакан полностью в тазик с водой. Затем переверните стакан под водой вверх донышком и медленно поднимайте его. Объясните, почему вода из стакана не будет выливаться, пока края стакана не поднимутся выше уровня воды в тазике.
4. Как изменится показание барометра-анероида при его подъеме на высоту 300 м над поверхностью Земли?

Содержание

• Формулы и уравнения
• Изменение давления с глубиной
• Решение дифференциального уравнения
• Примеры
• Принцип Паскаля
• Гидростатический парадокс Стевина
• Упражнения
• Упражнение 1
• Контейнер 1
• Контейнер 2
• Упражнение 2.
• Решение
• Ссылки

В манометрическое давление п_м — это то, что измеряется по отношению к эталонному давлению, которое в большинстве случаев выбирается как атмосферное давление P_{банкомат} на уровне моря. Тогда это относительное давление, еще один термин, под которым он также известен.

Другой способ измерения давления — это сравнение его с абсолютным вакуумом, давление в котором всегда равно нулю. В таком случае мы говорим о абсолютное давление, который мы обозначим P_к.

Математическая связь между этими тремя величинами такова:

п_к = P_{банкомат} + P_м

Таким образом:

п_м = P_к — П_{банкомат}

Рисунок 1 наглядно иллюстрирует эту взаимосвязь. Поскольку давление вакуума равно 0, абсолютное давление всегда положительно, то же самое происходит с атмосферным давлением P_{банкомат}.

Манометрическое давление обычно используется для обозначения давлений выше атмосферного, например давления в шинах, давления на дне моря или бассейна, которое создается за счет веса водяного столба. . В этих случаях P_м > 0, поскольку P_к > P_{банкомат}.

Однако есть абсолютные давления ниже P_{банкомат}. В этих случаях P_м <0 и называется Давление из пустой и не следует путать с давлением из уже описан вакуум, то есть отсутствие частиц, способных оказывать давление.

Формулы и уравнения

Давление в жидкости — жидкости или газе — является одной из наиболее важных переменных в его исследовании.В неподвижной жидкости давление одинаково во всех точках на одной и той же глубине независимо от ориентации, в то время как движение жидкости в трубах вызывается изменениями давления.

Среднее давление определяется как отношение силы, перпендикулярной к поверхности. F_⊥и площадь указанной поверхности A, которая математически выражается следующим образом:

P = F_⊥ / TO

Давление — это скалярная величина, размеры которой представляют собой силу на единицу площади. Единицы его измерения в Международной системе единиц (СИ) — ньютон / м.², названный Паскалем и сокращенно Па, в честь Блеза Паскаля (1623–1662).

Кратно как килограмм (10³) Y мега (10⁶) часто используются, поскольку атмосферное давление обычно находится в диапазоне 90 000 — 102 000 Па, что равно: 90 — 102 кПа. Давление порядка мегапаскалей не редкость, поэтому важно ознакомиться с префиксами.

В англосаксонских единицах давление измеряется в фунтах на фут.²однако обычно это делается в фунтах на дюйм.² или psi (фунт-сила на квадратный дюйм).

Изменение давления с глубиной

Чем больше мы ныряем в воду в бассейне или в море, тем большее давление мы испытываем. Напротив, с увеличением высоты атмосферное давление падает.

Среднее атмосферное давление на уровне моря установлено на уровне 101300 Па или 101,3 кПа, в то время как в Марианской впадине в западной части Тихого океана — на самой большой известной глубине — оно примерно в 1000 раз больше, а на вершине Эвереста оно составляет всего 34 кПа.

Понятно, что давление и глубина (или высота) связаны. Чтобы выяснить это, в случае покоящейся жидкости (статическое равновесие) рассматривается дискообразная часть жидкости, заключенная в контейнер (см. Рисунок 2). Диск имеет площадь поперечного сечения К, вес dW и высота dy.

Мы позвоним п к давлению, которое существует на глубине «Y«Y P + dP давлению, которое существует на глубине (y + dy). Поскольку плотность жидкости ρ — это отношение ее массы дм и его объем dV, ты должен:

 ρ = dm / dV ⇒ dm = ρ.dV

Следовательно, вес dW элемента:

dW = г. dm = ρ.g.dV

И теперь действует второй закон Ньютона:

Σ F_Y = F₂ — F₁ — dW = 0

(P + dP) .A — P.A — ρ.g.dV = 0

(P + dP) .A — P.A — ρ.грамм. А. dy = 0

dP = ρ.g.dy

Решение дифференциального уравнения

Интегрируя обе стороны и учитывая, что плотность ρа также гравитация грамм постоянны, искомое выражение найдено:

п₂ — П₁ =ΔP = ρ.g. (и₂ — Y₁)

 ΔP = ρ.грамм. ΔY

Если в предыдущем выражении вы выбрали п₁ как атмосферное давление и Y₁ как поверхность жидкости, то Y₂ находится на глубине час Y ΔP = P₂ — П_{банкомат} — манометрическое давление как функция глубины:

п_м = ρ.g.h

Если вам нужно значение абсолютного давления, просто добавьте атмосферное давление к предыдущему результату..

Примеры

Для измерения манометрического давления устройство называется манометр, которые обычно предлагают разницу давлений. В конце будет описан принцип работы U-образного манометра, а теперь давайте рассмотрим некоторые важные примеры и следствия ранее выведенного уравнения.

Принцип Паскаля

Уравнение ΔP = ρ.g. (и₂ — Y₁) можно записать как P = Po + ρ.g.h, где п давление на глубине час, пока п_илидавление на поверхности жидкости, обычно п_{банкомат}.

Очевидно, каждый раз, когда он увеличивается По, увеличивает п в том же количестве, если это жидкость с постоянной плотностью. Это именно то, что предполагалось при рассмотрении ρ константу и поместите ее за пределы интеграла, решенного в предыдущем разделе.

Принцип Паскаля гласит, что любое увеличение давления удерживаемой жидкости в состоянии равновесия передается без каких-либо изменений во все точки указанной жидкости. Благодаря этому свойству можно умножить силу F₁ приложите к маленькому поршню слева, и получите F₂ справа.

Автомобильные тормоза работают по этому принципу: на педаль прикладывается относительно небольшое усилие, которое преобразуется в большее усилие на тормозной цилиндр на каждом колесе благодаря жидкости, используемой в системе.

Гидростатический парадокс Стевина

Гидростатический парадокс гласит, что сила, создаваемая давлением жидкости на дне контейнера, может быть равной, большей или меньшей, чем вес самой жидкости. Но когда вы ставите емкость на весы, она обычно регистрирует вес жидкости (плюс, конечно, вес емкости). Как объяснить этот парадокс?

Начнем с того, что давление на дне емкости зависит исключительно от глубины и не зависит от формы, как это было показано в предыдущем разделе.

Давайте посмотрим на несколько разных контейнеров. При общении, когда они наполняются жидкостью, все они достигают одинаковой высоты. час. Основные моменты находятся под одинаковым давлением, поскольку находятся на одной глубине. Однако сила давления в каждой точке может отличаться от веса (см. Пример 1 ниже).

Упражнения

Упражнение 1

Сравните силу давления на дно каждой из емкостей с весом жидкости и объясните, почему существуют различия, если таковые имеются.

Контейнер 1

В этом контейнере площадь основания равна A, поэтому:

Вес жидкости: мг = ρ.V.g = ρ . A .h. грамм

Давление на дно: ρ. грамм. час

Сила от давления: F = P.A = ρ. грамм. час К

Вес и сила давления равны.

Контейнер 2

Контейнер имеет узкую часть и широкую часть. На диаграмме справа он разделен на две части, и геометрия будет использоваться для определения общего объема. Площадь А₂ это внешний в контейнер, ч₂ высота узкой части, h₁ высота широкой части (основания).

Полный объем — это объем основания + объем узкой части. С этими данными мы имеем:

Вес жидкости: м. g = ρ . грамм. V = ρ . грамм. [TO₁ .час₁+ (А₁ -ТО₂) .h₂]=

= ρ . г (А₁.у него есть₂час₂)= ρ . грамм. К₁.h — ρ . грамм. ТО._. час₂ (Было использовано ч = ч₁ + ч₂)

Давление на дно: P = ρ. грамм. час

Сила на дно из-за давления: F = P. A₁ =ρ. грамм. час К₁

Сравнение веса жидкости с силой давления показывает, что она больше веса.

Что происходит, так это то, что жидкость также оказывает силу на часть ступеньки в контейнере (см. Красные стрелки на рисунке), которые включены в вышеприведенный расчет. Эта направленная вверх сила противодействует действию вниз, и вес, регистрируемый весами, является результатом этого. Согласно этому, величина веса составляет:

W = Сила на дно — Сила на ступенчатую часть = ρ . грамм. К₁.h — ρ . грамм. ТО._. час₂

Упражнение 2.

На рисунке показан манометр с открытой трубкой. Он состоит из U-образной трубки, один конец которой находится под атмосферным давлением, а другой подсоединен к S — системе, давление которой необходимо измерить.

Жидкость в трубке (показана на рисунке желтым цветом) может быть водой, хотя ртуть предпочтительно используется для уменьшения размера устройства. (Разница в 1 атмосферу или 101,3 кПа требует 10,3 метра водяного столба, ничего портативного).

Просит найти манометрическое давление п_м в системе S как функция высоты H столба жидкости.

Решение

Давление внизу для обоих ответвлений трубки одинаковое, так как они находятся на одинаковой глубине. Пусть P_К давление в точке A, расположенной в y₁ И п_B те точки B, которые находятся на высоте и₂. Поскольку точка B находится на границе раздела жидкости и воздуха, давление там равно P_или. В этой ветви манометра давление внизу составляет:

Po + ρ.g.y₂

Со своей стороны, давление внизу для ветви слева составляет:

P + ρ.g.y₁

Где P — абсолютное давление в системе, а ρ — плотность жидкости. Уравнивание обоих давлений:

Po + ρ.g.y₂ = P + ρ.g.y₁

Клиринг п:

 P = Po + ρ.g.y₂ — ρ.g.y₁ = Po + ρ.g (и₂ — Y₁) = Po + ρ.g. ЧАС

Следовательно, манометрическое давление п_м дан кем-то П — П_или = ρ.g. ЧАС и чтобы получить его значение, достаточно измерить высоту, на которую поднимается манометрическая жидкость, и умножить ее на значение грамм и плотность жидкости.

Ссылки

1. Цимбала, C. 2006. Механика жидкости, основы и приложения. Mc. Гроу Хилл. 66-74.
2. Фигероа, Д. 2005. Серия: Физика для науки и техники. Том 4. Жидкости и термодинамика. Отредактировал Дуглас Фигероа (USB). 3-25.
3. Мотт, Р. 2006. Механика жидкости. 4-й. Издание. Pearson Education. 53-70.
4. Shaugnessy, E. 2005. Введение в механику жидкости, Oxford University Press. 51 — 60.
5. Стилианос, В. 2016. Простое объяснение классического гидростатического парадокса. Получено с: haimgaifman.files.wordpress.com

h=p/ρg,
(3)

Отсюда 1 кг/см²=10
м водяного столба = 735 мм ртутного
столба.

Кроме
понятия “абсолютное давление” в технике
пользуются понятием “избыточное
давление”:

р_из=р-р_ат
(4)

и “вакуумметрическое
давление” или “вакуум”

р_вак=р_ат-р,
(5)

где р_ат—
атмосферное давление.

Понятием
“вакуумметрическое давление” пользуются,
если абсолютное давление в точке
измерения р меньше атмосферного
давления. Соотношение между различными
видами давления показано на рис. 3.

В

Рис.

Рис. 3

жидкости, находящейся в поле силы
тяжести, давление в любой точке
жидкости и положение этой точки,
определяемое относительно произвольно
взятой горизонтальной плоскости
(плоскости сравнения), связаны уравнением

z_i+p_i/
ρg=const,

т.е. сумма нивелирной
(z)
и пьезометрических высот (p/ρg),
называемая гидростатическим напором,
постоянна для всех точек покоящейся
жидкости.

Сравнив
гидростатические напоры произвольной
точки А с нивелирной высотой z
(погруженной под поверхность жидкости
на глубину h)
и точки В на свободной поверхности
жидкости с нивелирной высотой Z₀
(рис.4), получим основное уравнение
гидростатики

Рис. 4

р=p₀+
ρg(z₀-z)=p₀+
ρgh,
(6)

где
ρ-плотность
жидкости; g-ускорение
силы тяжести; р₀-давление
на свободной поверхности жидкости.

Рис. 5

В технике для измерения давления
применяются различные приборы. Простейшим
из них является пьезометр. Пьезометром
(рис.5) называется вертикальная стеклянная
трубка, верхний конец которой открыт
(сообщается с атмосферой), а нижний —
подсоединен к точке измерения давления.
Пьезометр показывает избыточное давление
в точке присоединения.

Для доказательства
этого рассмотрим абсолютное давление
в точке А. Слева оно равно измеряемому
абсолютному давлению в сосуде на уровне
расположения точки А:

р_а^л=р;

справа это давление
равно абсолютному давлению со стороны
пьезометра:

р_а^п=р_ат+
ρgh_п.

В соответствии
со вторым свойством гидростатического
давления

р^л=
р^п
, т. е.

р= р_ат+
ρgh_п
,

следовательно,

h_п=(р-р_ат)/
ρg=р_из/ρg
или

р_из=
ρgh_п
. (7)

Более универсальным
прибором является U
– образный (или дифференциальный)
манометр. По его показаниям можно
рассчитать разность давлений в двух
различных точках, определить избыточное
давление или вакуум в точке присоединения
манометра. Определим, например, давление
в точке А по показаниям дифманометра,
изображенного на рис. 6.

Пусть
в сосуде находится вода с плотностью
ρ_в,
а в U-образном
манометре – манометрическая жидкость
(ртуть) тяжелее воды и не смешивающаяся
с ней плотностью ρ_р.
Рассчитываем давление в точке А,
постепенно переходя от точки к точке,
начиная с точки Н.

Абсолютное давление
в точке Н равно р_ат
(избыточное давление в точке Н равно
нулю). В точке Е абсолютное давление
составляет

р_Е=р_ат+
ρ_вgh_в

(

Рис. 6

над ртутью, чтобы не испарялась,
налит столб воды высотой h_В
).

На точку D
жидкости будет давить атмосферное
давление, столб воды высотой h_В
и столб ртути высотой Δh,
следовательно, абсолютное давление в
точке D
равно

р_D=р_ат+
ρ_вgh_в+
ρ_рgΔh.

Давление в точках
В, С и D
одинаковы (точки С и D
лежат на одном уровне в ртути, а точки
В и С лежат на одном уровне в воде),
поэтому

p_В=р_C=р_D=
р_ат+
ρ_вgh_в+
ρ_рgΔh.

На точку А жидкости
действует давление р_В
и давление
столба воды высотой h_m^:

р_А=р_В+
ρ_вgh_m=
р_ат+
ρ_вgh_в+
ρ_рgΔh+
ρ_вgh_m=
р_ат+ρ_вg(h_в+h_m)+
ρ_рgΔh
. (8)

Избыточное давление
в точке А будет равно

р_из^А=р_а—
р_ат=
ρ_вg(h_в+h_m)+
ρ_рgΔh
. (9)

Если в сосуде над
поверхностью жидкости будет достаточно
большой вакуум, уровень ртути в левом
колене дифманометра будет выше, чем в
правом. Тогда абсолютное давление в
точке А составит

р_А=
р_ат+ρ_вg(h_в+h_m)-
ρ_рgΔh
. (10)

А вакуум в точке
А

р_вак^А=
р_ат-р_А=
ρ_рgΔh-
ρ_вg(h_в+h_m).
(11)

Рис. 7

Описанные приборы удобно использовать
в лабораторных условиях. В промышленности
широко используются пружинные манометры.
Пружинный манометр (рис. 7) представляет
собой изогнутую пустотелую трубку
овального сечения (трубка Бурдона),
запаянную с одного конца, а другим концом
присоединенную к точке замера давления.
Под действием давления р трубка Бурдона
распрямляется. Деформация трубки с
помощью рычажно–зубчатого механизма
трансформируется в поворот стрелки,
показывающей давление на шкале манометра.

Так как корпус
манометра, как правило, не герметизирован,
на трубку Бурдона снаружи действует
атмосферное давление р_ат.
Следовательно, трубка деформируется
под влиянием разности давлений р-р_ат,
т.е. пружинные манометры показывают
избыточное давление. Часто поэтому
избыточное давление называют
манометрическим.

В соответствии с
основным уравнением гидростатики (см.
рис. 7)

р_А=р+
ρ_вgh_н
,

т.е. избыточное
давление в точке А будет равно

р_из=р_а—
р_ат=М+
ρ_вgh_н
, (12)

где М – показание
манометра (М= р- р_ат).

Если шкала манометра
«немая», то на ней должно быть обозначено
предельное давление р_пр
, на которое рассчитан манометр. Такими
немыми шкалами обычно снабжают образцовые
манометры. Цена деления такого манометра
может быть определена по формуле

Ц= р_пр/m,
(13)

где m
– количество делений, соответствующее
предельному давлению.

Следовательно,
избыточное давление, показываемое
манометром, будет равно

М=Цn=
nр_пр/m,
(14)

где n
— показание манометра в делениях.

Формула (12)
показывает, что при расчете измеряемого
давления по показаниям пружинного
манометра следует учитывать положение
манометра относительно точки измерения
(h_н),
так как от этого положения зависит
показание манометра.

Принцип действия
пружинных вакуумметров и мановакуумметров
аналогичен принципу действия пружинных
манометров.

2.1. Ознакомиться
с приборами для измерения давления:
пьезометром, манометром, дифманометром,
вакуумметром.

2.2.
Научиться
определять по показаниям приборов
давление в заданной точке.

2.3.
Установить
связь между показаниями различных
приборов.

3.Описание опытной установки

Установка состоит
из герметического сосуда (1), заполненного
водой до определенной высоты, водомерного
стекла (2), по которому замеряется уровень
воды в сосуде. Сосуд имеет штуцера с
кранами ПК1, ТК1, ТК4, ТК5 для присоединения
приборов давления, ТК2, ТК3-для присоединения
воздушного насоса. В комплект установки
входит пьезометр П, вакуумметр В, нижний
МН_н
и верхний МН_в
манометры, а также воздушный насос (3),
с помощью которого изменяют давление
над свободной поверхностью жидкости в
сосуде 1.

4.Порядок проведения работы

Перед проведением
опытов следует убедиться в совпадении
показаний пьезометра и водомерного
стекла. При их несовпадении нужно,
отпустив гайку крепления шкалы пьезометра,
сместить шкалу по вертикали до совпадения
показаний. После этого необходимо,
затянув гайку, зафиксировать новое
положение шкалы.

Рис. 8

4.1. Подготовить
установку для снятия показаний приборов
при атмосферном давлении на свободной
поверхности (опыт №1):

-закрыть все краны
кроме кранов ПК1, ТК1, ТК2, ТК5. Кран ТК1
должен соединять манометр МН_н
с сосудом, а кран ТК2 должен соединять
сосуд с атмосферой;

-снять показания
приборов и занести их в табл.1.

4.2. Подготовить
систему к созданию в сосуде избыточного
давления (опыт №2):

-краны ТК1 и ТК5
должны соединять манометры только с
сосудом; кран ПК1 открыт, кран ТК2 должен
быть повернут так, чтобы соединить
воздушный насос с атмосферой и одновременно
перекрывать сосуд; кран ТК3 должен
соединять сосуд только с насосом;

— привести в действие
воздушный насос; по мере увеличения
давления в сосуде следить за повышением
уровня в пьезометре; по достижении
намеченного уровня (не доходя 10-15 см до
верхнего конца пьезометра) остановить
насос и быстро повернуть кран ТК3 так,
чтобы перекрыть сосуд;

— по команде
одновременно снять показания приборов
и занести их в табл. 2.

4.3. Подготовить
систему к созданию вакуума в сосуде
(опыт №3):

— краны ТК1 и ТК5
повернуть так, чтобы отсечь манометры
от сосуда и сосуд от атмосферы; краны
ПК1 и ТК4 открыть; кран ТК2 повернуть так,
чтобы воздушный насос соединить только
с сосудом, кран ТК3 – только с атмосферой
(сосуд должен быть перекрыт);

— привести в действие
воздушный насос; создать в сосуде
необходимое разряжение; по достижении
намеченного разряжения (уровень жидкости
в пьезометре должен быть на 30-40 см ниже
нуля) быстро повернуть кран ТК2 и отсечь
сосуд от насоса и атмосферы; остановить
насос;

-по команде
одновременно снять показания приборов
и занести их в табл. 3

5.Расчетные формулы

5.1. Пересчитать
показания приборов из ат. в см. вод.
столба по формуле (3):

h
= р_изб/_в.g_.

5.2. Определить
избыточное давление в точке А по
показаниям:

а) манометра МН_Н—
по формулам (12) и (14);

б) манометра МН_В
– по формуле (6) .

5.3. Определить
вакуум в точке измерения А по показаниям:

вакуумметра
В – по формуле (6).

5.4. Определить
погрешность измерения давления различными
приборами, считая правильными показания
пьезометра:

₁
= ((h_изб. ^МНн
– h_изб.ⁿ
)100%)/h_изб.ⁿ
(15)

₂
= ((h_изб. ^МНв
– h_изб.ⁿ
)100%)/h_изб.ⁿ
(16)

₃
= ((h_вак ^В
– h_вак.ⁿ
)100%)/h_вак.ⁿ
(17)

Таблица
1

Показания приборов
при атмосферном давлении

Показания	Избыточное давление в точке измерения А	Погреш- ность мано-метра МНн
водомерного стекла	пьезометра	манометра МНн Рпр= кгс/см2 m= hн=12 см	по пьезо-метру П	по мано-метру МНн
hc	hn	n	рMН 1	hM Нн	hизб	hизб МНн	δ
см	см	дел	ат	см.вод.ст	см.вод.ст	см.вод.ст.	%

Таблица 2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Манометры

«Искусство быть мудрым состоит

в умении знать, на что следует обращать внимание»

У. Джемс

В данной теме познакомимся с манометром.

В прошлых темах разговор шёл о сообщающихся сосудах. Сообщающиеся сосуды – это сосуды, имеющие соединяющую их часть и заполненные покоящейся жидкостью.

Вывели закон сообщающихся сосудов, согласно которому, в открытых сообщающихся сосудах уровень поверхностей однородной жидкости устанавливается на одинаковом уровне (при условии, что давление воздуха над поверхностью жидкости одинаково) и не зависит от формы сосудов.

Было установлено, что газы обладают массой и весом. Кроме того, земная атмосфера также обладает весом вследствие действия на нее притяжения Земли, а, следовательно, производит давление, которое называется атмосферным давлением. Для измерения атмосферного давления существуют приборы, называемые барометрами.

Однако одним измерением атмосферного давления человек ограничится не может. Ведь любые газы имеют вес и, следовательно, способны создавать давления. При этом это давление может быть как больше, так и меньше атмосферного. Так вот, для измерения таких давлений существует прибор, который называется манометр. В переводе с греческого «манос» означаете редкий, неплотный, а «метрео» — измеряю.

Все манометры делятся на два вида — это жидкостный и металлический манометры.

Чаще всего жидкостный манометр используется для измерения разности давлений в сосуде и атмосферного. Он представляет собой U‑образную стеклянную трубку, заполненную какой-либо жидкостью. Согласно закону сообщающихся сосудов, поверхности жидкости в такой трубке устанавливаются на одинаковом уровне, так как на них действует только атмосферное давление.

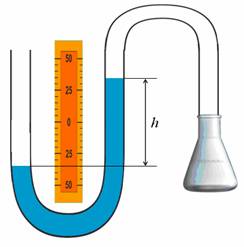
Чтобы разобраться как работает манометр, соединим одно колено трубки к сосуду с газом, давление которого необходимо измерить, а другое колено оставляют открытым. Если уровень поверхности жидкости в колене, соединенном с сосудом, выше, чем в открытом, значит давление газа в сосуде меньше атмосферного давления на величину давления столба жидкости высотой h.

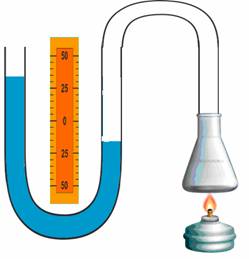
Если же нагревать этот сосуд с газом, то скорость его молекул возрастет, а значит, они чаще будут сталкиваться со стенками сосуда и тем самым создавать большее давление. Вследствие чего газ будет оказывать большее давление на жидкость в манометре, вытесняя её в открытое колено.

Таким образом, с помощью жидкостного манометра по высоте избыточного столба жидкости мы можем судить об изменении давления.

С помощью жидкостного манометра можно измерять и давление в жидкостях на небольших глубинах. Для примера возьмем небольшую коробочку, одна сторона которой затянута пленкой, и соединим ее с манометром при помощи резиновой трубочки. Будем постепенно погружать нашу коробочку в сосуд с водой. Чем глубже она погружается, тем больше становится разность высот в коленах манометра и, следовательно, тем большее давление производит жидкость на коробочку.

Ранее рассматривалось гидростатическое давление, где говорилось о том, что на одном и том же уровне давление внутри жидкости по всем направлениям неизменно. Проверим это утверждение с помощью жидкостного манометра и коробочки. Для этого установим коробочку на любой глубине внутри жидкости и будем ее поворачивать. И действительно, показания манометра не меняются, что говорит о том, что утверждение было верным.

У жидкостных манометров есть один серьезный недостаток — ими можно измерять давление, отличающееся от атмосферного лишь незначительно. Так, например, если давление газа в сосуде будет больше атмосферного в два раза, то согласно формуле высота столба жидкости в манометре будет определяться как отношение атмосферного давления к произведению плотности жидкости и коэффициента g.

Если в качестве жидкости в манометре использовать воду, то высота ее столба составит более 10 м. Таким образом, прибор получается очень больших размеров.

Можно сказать, что вместо воды можно использовать ртуть. Действительно, при использовании ртути размеры уменьшаются в 13,6 раза, но возникает новая проблема —  пары ртути ядовиты.

А если давление газа в несколько раз больше атмосферного? Для измерения высоких давлений применяется металлический манометр. Его основным элементом является полая тонкостенная металлическая трубка, согнутая в дугу. Один конец этой трубки закрыт, а другой присоединяется к сосуду с исследуемым газом.

       

Закрытый конец трубки через зубчатый механизм соединен со стрелкой, двигающейся относительно шкалы. Чем больше будет давление в трубке, тем больше будет отклонятся стрелка. Ноль на такой шкале соответствует атмосферному давлению. Если стрелка стоит на цифре 4, то давление в сосуде в 5 раз больше атмосферного.

Упражнения.

Задача 1. Определите давление в сосуде, изображенного на рисунке, если в манометре использована ртуть.

Задача 2. Чему равно давление ртути в точках А, Б и В, манометра, представленного на рисунке, если атмосферное давление можно считать нормальным?

Основные выводы:

– Манометр – прибор, используемый для измерения разности давлений.

– Все манометры делятся на два вида — это жидкостный и металлический.

– Жидкостный манометр используется для измерения разности давлений в сосуде и атмосферного.

– Для измерения высоких давлений применяется металлический манометр. Его основным элементом является полая тонкостенная металлическая трубка, согнутая в дугу. Один конец этой трубки закрыт, а другой присоединяется к сосуду с исследуемым газом. Закрытый конец трубки через зубчатый механизм соединен со стрелкой, двигающейся относительно шкалы.

– Ноль на шкале металлического манометра соответствует атмосферному давлению.

Пройдите тест