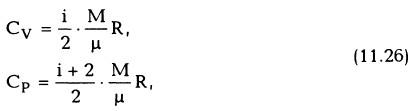Агрегатное состояние вещества, которое не способно сохранять свой объем и форму в открытом пространстве при воздействии малых внешних сил, называется газом. Существует четыре макроскопических параметра газа, которые можно измерить и вычислить. Одним из них является давление. В приведенной ниже статье изучим вопрос, с помощью каких формул давление газа можно вычислить.
Что такое давление?
В физике под давлением понимают величину, равную отношению механической силы F, которая перпендикулярно воздействует на поверхность некоторой площади S, то есть:
P = F / S.
Из равенства следует, что измеряться величина P должна в ньютонах на квадратный метр (Н/м2). В СИ эта единица называется паскалем (1 Па = 1 Н/м2).
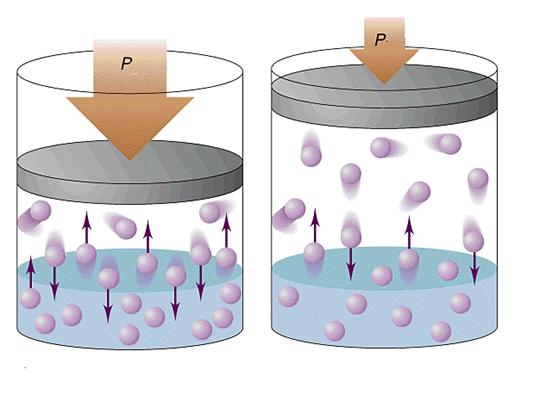
В случае газов давление возникает за счет столкновений со стенками сосудов газовых частиц. Последние могут быть атомами или сложными молекулами. В любом газе частицы хаотично движутся в разных направлениях. Их столкновение со стенкой сосуда приводит к передаче последней некоторого количества движения, что создает эффект воздействующей силы. Так как число сталкивающихся со стенкой частиц является огромным, то в среднем они создают некоторое постоянное давление, которое может быть измерено на практике при помощи барометра или манометра.
Идеальные и реальные газы
Каждому школьнику известно свойство газа, согласно которому он может занимать любой предоставленный ему объем. Если проверить это свойство на практике, то окажется, что оно практически никогда не выполняется: наступает момент, когда газ перестает расширяться, хотя возможность для этого присутствует. Связан этот факт с наличием межмолекулярных взаимодействий в газах.
Концепция идеального газа базируется на двух важных условиях:
- Газ будет идеальным, если потенциальная энергия его частиц на несколько порядков меньше средней кинетической энергии. В этом случае межмолекулярными взаимодействиями пренебрегают.
- Газ называют идеальным, если размеры частиц намного меньше расстояний между ними. В противном случае увеличивается вероятность столкновения частиц, а значит, вероятность их химического взаимодействия.
Изложенное выше можно резюмировать следующим образом: газовое состояние можно считать идеальным только при низких давлениях (плотностях), высоких температурах и высокой химической инертности составляющих частиц.
Если указанные условия не выполняются, то математическое описание поведения газов отличается от идеального.
Формулы давления газа (идеального)
В 1834 году в результате анализа экспериментальных данных относительно поведения газовых систем при различных условиях (законы Бойля-Мариотта, Гей-Люссака, Шарля, принцип Авогадро) французский инженер и ученый Эмиль Клапейрон вывел универсальное уравнение идеального газа. Впоследствии оно было несколько модифицировано русским химиком Менделеевым. В настоящее время его записывают так:
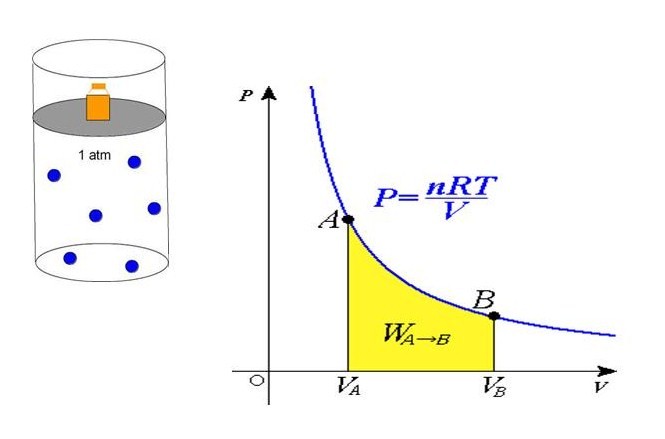
P * V = n * R * T.
Здесь n, T и V — количество вещества, абсолютная температура и объем газа. Постоянная R равна 8,314 Дж/(К*моль).
Это уравнение позволяет записать формулу абсолютного давления газа в следующем виде:
P = n * R * T / V.
Из этой формулы следует, что если происходит изотермический процесс в закрытой системе, то давление будет меняться обратно пропорционально величине V (закон Бойля-Мариотта). Если же объем в закрытой системе зафиксировать, то P будет линейно расти с увеличением абсолютной температуры (закон Гей-Люссака).
Помимо записанного выражения, можно привести еще одну формулу давления газа, объем которого изменяется. Эта формула следует из молекулярно-кинетической теории. Запишем ее:
P = N * m * v2 / (3 * V).
Где N, m — число частиц и масса одной частицы, v2 — квадрат средней скорости.
Обе формулы легко переводятся друг в друга, если использовать следующее выражение связи кинетической энергии частицы и абсолютной температуры:
m * v2 / 2 = 3 / 2 *kB * T.
Здесь постоянная Больцмана обозначена kB.
Давление смеси идеальных газов
Ярким примером такой смеси является воздух. Для определения давления смеси применяют на практике закон Дальтона, который гласит, что создаваемые каждым компонентом смеси давления парциальные в сумме дают абсолютное давление. В свою очередь парциальное давление компонента прямо пропорционально его атомной доли в смеси. Формула абсолютного давления газа из j компонент принимает вид:
P = R * T / V * ∑i=1j(ni).
Заметим, что в газовой смеси все компоненты находятся при одинаковой температуре и занимают один и тот же объем.
Давление в реальных газах
Как выше было сказано, давление легко измерить, используя соответствующий прибор. Однако для газов, поведение которых значительно отклоняется от идеального (алканы с длинными углеродными цепями, водяной пар), можно с высокой точностью рассчитать давление, если использовать уравнение состояния Ван-дер-Ваальса. Оно имеет форму:
(P + α * n2 / V2) * (V — n * β) = n * R * T.
Нетрудно увидеть, что это уравнение является модифицированным вариантом закона Клапейрона-Менделеева. Здесь α и β представляют собой некоторые числа, которые зависят от природы газа и определяются экспериментально. Соответствующая формула давления газа примет вид:
P = n * R * T / (V — n * β) — α * n2 / V2.
В реальных газах зависимость давления от объема является более сложной, чем в идеальных.
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
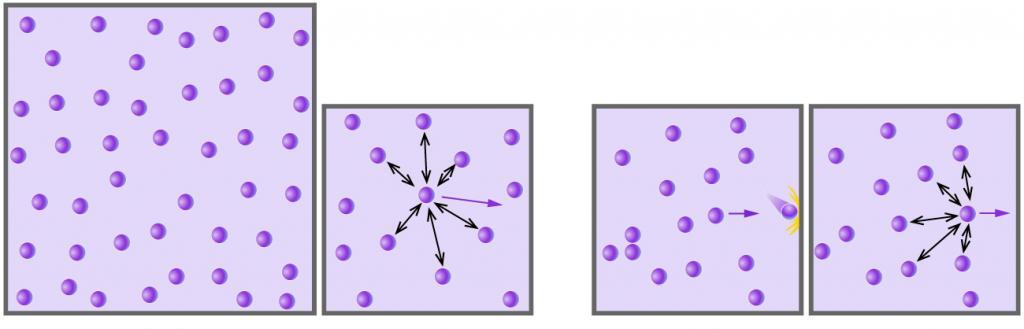
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния
В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Полученное
в предыдущей лекции уравнение состояния
идеального газа не является универсальным.
Оно оказывается справедливым при
достаточно малых давлениях (и плотностях)
и выполняется тем точнее, чем меньше
давление. По мере
же увеличения давления газа его свойства
все
более отклоняются от свойств идеального
газа и, в конце концов, наступает его
конденсация в жидкость.
В этом
нет ничего удивительного, если
вспомнить
те допущения, которые были сделаны
при
выводе уравнения состояния идеального
газа.
В
самом деле, идеальный газ мы определили
как
газ, состоящий из молекул, не
взаимодействующих
между собой, а сами молекулы
при этом считали материальными точками,
т.е. мы пренебрегали их размерами и
объемом.
Однако оба эти допущения являются
приближенными.
Так,
например, если при атмосферном давлении
среднее расстояние между молекулами
в 10
раз превосходит их собственные размеры,
то при
давлении в 100 атм молекулы газа в среднем
удалены
друг от друга на расстояние, которое
только
вдвое больше их размеров. В этих условиях
объемом
молекул нельзя пренебречь, а силы
взаимодействия
должны уже сказываться не только
в моменты столкновений.
Начнем
с того, что учтем в уравнении состояния
(которое мы будем писать для одного
моля
газа) ограниченную сжимаемость газа.
Для этого
надо в уравнении идеального газа Р =
RT/V
заменить
объем V
разностью (V-b),
где b
—
некоторая положительная постоянная,
учитывающая размеры молекул. Уравнение
показывает,
что объем не может быть сделан меньшим,
чем Ь, поскольку при V
-» b
давление Р обращается
в бесконечность.
Учтем
теперь притяжение молекул. Это притяжение
должно приводить к уменьшению давления
газа, поскольку на каждую молекулу,
находящуюся
вблизи стенки сосуда, будет действовать
со стороны остальных молекул сила,
направленная
внутрь сосуда. В грубом приближении
эта сила будет пропорциональна числу
молекул в единице объема, то есть
концентрации
газа.
С другой
стороны, давление само пропорционально
этому же числу. Поэтому общее уменьшение
давления, связанное с взаимным
или, иначе,
Это —
так называемое уравнение
Ван-дер-Ваальса,
или
уравнение состояния реального газа,
записанное
для одного моля. Для произвольного
притяжением
молекул, будет обратно пропорционально
квадрату его объема. В соответствии
с этим вычтем из (11.1) выражение
При
большом разрежении газа (большие объемы
V)
величинами а и b
можно пренебречь, и мы
возвращаемся к уравнению Менделеева
— Клапейрона.
Ниже мы увидим, что уравнение (11.3)
правильно описывает характер явлений
и в обратном
предельном случае больших сжатий.
Для
исследования поведения реального газа,
описываемого
уравнением Ван-дер-Ваальса, рассмотрим
определяемые этим уравнением изотермы
— кривые зависимости Р от V
при заданных
значениях Т. С этой целью перепишем
лтавнение
М1.2) (лля олного моля) в виде
При
заданных значениях Р и Т — это уравнение
третьей степени относительно неизвестного
V.
Как
известно, уравнение третьей степени
имеет
три корня, из которых вещественными
могут
быть либо все три, либо один (в последнем
случае
уравнение имеет также два комплексно
сопряженных
корня). Физическим смыслом объема
могут обладать, разумеется, лишь
вещественные
(причем положительные) корни. Поэтому
заданным значениям Р и Т по уравнению
Ван-дер-Ваальса
соответствуют либо три различных,
либо одно значение объема.
Второй
случай всегда имеет место
при
достаточно высоких температурах.
Соответствующие изотермы мало отличаются
от
45
изотерм
идеального газа и являются монотонно
спадающими
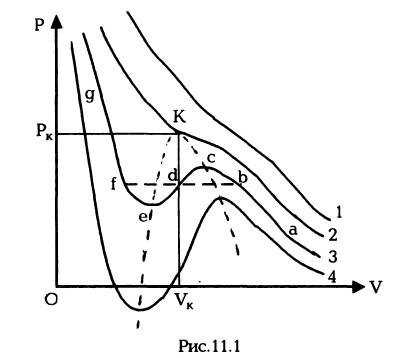
кривыми (кривая 1 на рис.11.1; увеличение
номера кривых соответствует убыванию
температуры). При более же низких
температурах
изотермы имеют максимум и минимум
(кривые 3, 4Г),
так что для каждой из них существуют
такие интервалы давлений, в которых
кривая определяет три различных значения
V
(три точки
пересечения изотермы с горизонтальной
прямой).
Рассмотрим
изотерму 3 и выясним, какой смысл
имеют различные ее участки. На участках
де
и са зависимость давления от объема
имеет нормальный
характер — давление уменьшается при
увеличении объема.
Участок
же ее соответствовал бы неестественному
положению, когда сжатие вещества
приводило бы к уменьшению давления.
Наличие
заведомо неосуществимого участка ее
изотермы
означает, что при постепенном изменении
объема вещество не может оставаться
все
время в виде однородной среды; в некоторый
момент
должно наступить скачкообразное
изменение
состояния и распадение вещества на две
фазы.
Другими
словами, истинная изотерма будет иметь
вид ломаной линии abfg.
Часть
ее ab
отвечает
газообразному состоянию вещества, а
часть
fg
—
жидкому состоянию. Горизонтальный же
прямолинейный отрезок bf
соответствует двухфазным
состояниям — переходу газа в жидкость,
происходящему (при заданной температуре)
при определенном постоянном давлении.
Можно показать, что отрезок bf
должен быть
расположен так, чтобы были одинаковы
площади bed
и def.
При
повышении температуры прямолинейный
участок
изотермы уменьшается и обращается в
нуль
(на изотерме 2) при температуре, которая
называется критической.
Проходящая
через эту точку изотерма 2 разделяет
изотермы двух типов: монотонные изотермы
вида 1 и изотермы 3, 4 с минимумами
и максимумами, на которых неизбежно
распадение вещества на две фазы (жидкость
и газ). При критической температуре
плотность
пара (газа) становится равной плотности
жидкости, и пар становится неотличим
от жидкости.
Используя уравнение (11.4),
нетрудно доказать, что
2.
Первое начало термодинамики
Обратимся теперь к энергетической
стороне процесса изменения состояния
какого-либо тела.
Любое
тело (твердое, жидкое, газообразное),
находящееся
в определенном состоянии,
которое
характеризуется его макроскопическими
параметрами
Р, V
и Т, обладает определенным запасом
внутренней
энергии U.
Внутренняя энергия
тела складывается из кинетической
энергии
поступательного движения молекул,
кинетической
энергии вращения молекул, кинетической
энергии движения атомов внутри молекулы
(если молекула не одноатомная),
потенциальной энергии взаимодействия
между атомами
и потенциальной энергии взаимодействия
молекул между собой. В нее, однако, не
входит кинетическая
энергия движения тела как целого и
потенциальная
энергия внешних сил, действующих
на тело.
помощью какого процесса
произошел этот переход,
и
Внутренняя
энергия тела является функцией
его
состояния. Это
означает, что при переходе
начальном
и конечном состояниях. Если над телом
совершается
циклический процесс, в результате
которого
тело возвращается в исходное состояние,
то
изменение внутренней энергии
за цикл
означает,
что бесконечно малое изменение внутренней
энергии dU
при любом процессе является
полным дифференциалом.
Внутреннюю энергию тела можно
изменить двумя способами:
если оно ее отдает. В
этом случае изменение внутренней
энергии
2) Наше тело можно теплоизолировать
и
предоставить
телу возможность совершить работу 6А
над окружающими телами. В первом случае
б А
— положительной
случае изменение внутренней энергии
Если же тело может получать (или
отдавать)
1) Привести тело в
контакт с более нагретым или менее
нагретым телом. При этом наше тело может
получать или отдавать
энергию, которая
46
Это важное
соотношение выражает закон сохранения
энергии при тепловых процессах. Его
называют первым
началом термодинамики.
Для конечного процесса
Наконец, при
изотермическом процессе (Т
= const)
Нетрудно
доказать, что при циклическом процессе
работа А числено равна площади петли
цикла
на диаграмме Р —V
и положительна, если процесс
происходит по часовой стрелке (рис.11.3).
процесса,
с помощью которого тело переводится
из
состояния 1 в состояние 2. Поэтому
говорят,
процесса
(а
не состояния, как внутренняя энергия
U).
Из (11.10) следует, что при циклическом
3.
Работа при изменении объема
Рассмотрим теперь каждое
из слагаемых, вхоляших
в пепвое начало тепмолинамики (11.9).
При изменении объема от
производит
над окружающими его телами механическую
работу. Если объем тела увеличивается
на dV,
то тело совершает бесконечно
малую или элементарную
работу
4.
Теплоемкость
Определим
теперь количество теплоты, которое
необходимо сообщить телу для его
нагревания
или отнять от тела для его охлаждения.
Конечно, это количество теплоты зависит
от массы тела и от того, на сколько
градусов
должна быть изменена его температура.
Поэтому
для характеристики тепловых свойств
тела
пользуются особой величиной —
теплоемкостью.
По
определению теплоемкостью тела С
называется
количество тепла, которое нужно подвести
или отнять у тела для изменения его
температуры
на 1 К.
Теплоемкость, отнесенная к единице
массы
тела М
называется удельной теплоемкостью
и численно равна площади
(см. рис.11.2) под кривой
процесса на диаграмме зависимости
Следует
отметить, что формулы (11.12) и (11.13) верны
для любых тел. Найдем работу, которую
совершает
идеальный газ при различных процессах.
Теплоемкость,
отнесенная к одному молю вещества,
называется молярной
теплоемкостью
Обе эти
теплоемкости уже характеризуют не само
тело, а вещество, из которого тело
состоит. Из определения теплоемкости
тела следует, что
Пусть
нагревание происходит при постоянном
объеме (V
= const).
Соответствующая теплоемкость называется
теплоемкостью
при постоянном
47
Следовательно,
подводимое к телу тепло SQ
расходуется на
изменение температуры dT
(изменение внутренней
энергии) и изменение объема
dV
(с этим связана механическая работа).
или на основании (11.19):
Если
при нагревании постоянным остается
давление,
то теплоемкость называется теплоемкостью
при постоянном давлении СР:
и показатель адиабаты
что хорошо согласуется с экспериментом.
Нетрудно показать, что
выражение (11.22) можно
записать через у:
Для идеального газа
следовательно,
5.
Внутренняя энергия газа
Начнем
с нахождения внутренней энергии
идеального
газа, которая, как мы знаем, состоит из
кинетической энергии поступательного
движения
молекул газа, кинетической энергии
вращения
молекул и из энергии колеблющихся
внутри
молекулы атомов. Каждый из этих трех
видов
движения вносит определенный вклад и
в теплоемкость
газа.
Легче
всего определить внутреннюю энергию
одноатомного
идеального газа (таковы благородные
газы Не, Ne,
Аг), которая представляет
собой просто сумму кинетических энергий
поступательного движения его частиц.
Поскольку
по определению температуры средняя
Попытаемся
теперь найти внутреннюю энергию
идеального газа, состоящего из
многоатомных
молекул. Как мы знаем из предыдущей
лекции, на каждую из трех поступательных
степеней свободы приходится кТ/2
кинетической энергии. Согласно
классической
механике такой результат получился бы
для всех вообще степеней свободы
молекулы, связанных
как с поступательным движением, так и
с ее вращением и с колебаниями атомов
в ней.
Действительно,
в классической (в отличие от квантовой)
физике доказывается так называемая
теорема
о равномерном распределении кинетической
энергии по всем
степеням свободы молекул.
Эту теорему можно сформулировать так:
если
система молекул находится в состоянии
теплового
равновесия при температуре Т, то средняя
кинетическая энергия равномерно
распределена
между всеми степенями свободы молекулы
и для каждой степени свободы молекулы
она равна
кТ/2.
Мы знаем
также, что при колебательном движении
(см. лекцию 5) среднее значение потенциальной
энергии равно среднему значению
кинетической
энергии, поэтому можно сделать вывод,
что на одну колебательную степень
свободы приходится
энергия кТ (кТ/2
кинетической
и кТ/2 потенциальной). В дальнейшем
мы будем считать, что на колебательную
(как на поступательную и вращательную)
степень свободы приходится энергия
кТ/2, но число колебательных степеней
будем удваивать.
Если
обозначить полное число степеней
свободы
молекулы буквой i
(с удвоенным количеством
колебательных степеней), то внутренняя
энергия газа из N таких молекул
то внутренняя энергия
газа, состоящего из N одноатомных
молекул
Поэтому его теплоемкости
(на основании (11.17)
и
(11.21))
Его теплоемкости
48
Выражение
для внутренней энергии (11.24) через
у остается в силе.
В
качестве примера рассмотрим газ,
состоящий из
двухатомных молекул. Полное число
степеней свободы
такой молекулы равно шести (шесть
координат
двух атомов). Поступательных степеней
—
три (три координаты центра масс молекулы),
вращательных
— две (вращение молекулы вокруг двух
взаимно перпендикулярных осей, проходящих
через центр масс и лежащих в плоскости,
ортогональной оси молекулы). Остается
одна колебательная степень свободы.
Согласно
(11.28)
сказывается
на теплоемкости газа лишь при достаточно
высоких температурах. При обычных
температурах колебательные степени
свободы как бы
«заморожены» и не дают вклада в
теплоемкость.
В области комнатных температур
теплоемкости двухатомных газов связаны
лишь с поступательным
и вращательными движениями молекул
и очень близки к своим теоретическим
значениям
(i
= 5)~
Найдем
теперь внутреннюю энергию реального
газа, подчиняющегося уравнению
Ван-дер-Ваальса.
Она включает в себя дополнительно к
энергии идеального газа потенциальную
энергию
взаимодействия молекул между собой.
Можно
доказать, что внутренняя энергия моля
реального газа
что
не согласуется с опытом при
обычных температурах.
Дело в том, что, как показывает
квантовая теория, колебательное
движение атомов
где
а — постоянная, входящая в уравнение
Ван-дер-Ваальса.
49
Лекция
12. ПРЕОБРАЗОВАНИЕ ТЕПЛОТЫ В РАБОТУ
Адиабатический
процесс; необратимость тепловых
процессов; преобразование
теплоты в механическую работу; цикл
Карно; энтропия; второе
начало термодинамики, сформулированное
с помощью энтропии; физический
смысл энтропии.

Адиабатический процесс
Займемся
теперь изучением некоторых
простейших
тепловых процессов
(кроме
изохорического, изобарического и
изотермического).
Очень
простым процессом является расширение
газа в пустоту: газ
вначале находится
в части сосуда, отделенной от другой
части
перегородкой, а после открывания
отверстия
в перегородке заполняет весь сосуд.
Так как
при таком расширении газ не совершает
никакой работы, то его энергия U
остается постоянной.
У идеального газа энергия зависит, как
мы уже знаем, только от температуры;
поэтому
из постоянства энергии следует также
и постоянство температуры идеального
газа при его расширении в пустоту.
Температура же реальных газов
при расширении в пустоту изменяется.
Очень
сильно отличается от расширения в
пустоту
другой процесс расширения газа,
называемый
адиабатическим.
Для
адиабатического процесса характерно,
что газ все время остается под внешним
давлением, равным
давлению самого газа. Другое условие
адиабатичности состоит в том, что в
течение всего процесса
газ остается теплоизолированным от
внешней среды, т.е. никуда не отдает и
ниоткуда не получает
тепла.
Наиболее
просто представить себе
адиабатическое
расширение (или сжатие)
газа,
находящегося в теплоизолированном
цилиндрическом
сосуде, снабженном поршнем. Для
выполнения первого условия адиабатичности
поршень должен двигаться достаточно
медленно, чтобы
газ, следующий за поршнем, успевал
перейти
в состояние теплового равновесия, (
соответствующего мгновенному положению
поршня.
При
слишком быстром вдвигании поршня газ
не
успевал бы следовать за ним и под поршнем
возникала
бы область пониженного давления, в
которую бы и расширялся остальной газ;
такой процесс
не был бы адиабатическим. Анализ
показывает,
что условие адиабатичности выполняется,
если скорость поршня мала по сравнению
со скоростью звука в газе.
Для
выполнения второго условия требуется,
с другой
стороны, достаточная быстрота процесса,
так
как за время его протекания газ не
должен успеть
обменяться теплом с окружающей средой.
При
адиабатическом процессе уже нельзя
утверждать,
что остается постоянной внутренняя
энергия
газа, поскольку газ при расширении
совершает
работу (или, при сжатии, над ним совершается
работа). Общее уравнение
адиабатического
процесса мы получим, если в первом
начале термодинамики положим
в
соответствии с условием теплоизолированности.
Таким
образом, при адиабатическом процессе
откуда
Выражение
(12.3) показывает, что газ совершает
работу за счет убыли своей внутренней
энергии.
Вспомнив, что для идеального
газа
Применим теперь уравнение
(12.2) к
Интегрируя (12.5), получим
после несложных преобразований,
что при адиабатическом процессе
расширение
сопровождается охлаждением, а
сжатие
— нагреванием газа.
Комбинируя уравнение (12.6) с
формулой
соотношение, связывающее изменение
температуры
и давления при адиабатическом
процессе
50
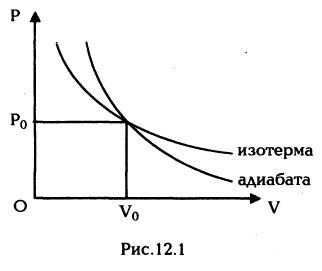
связывающее
давление и объем (последнее равенство
называют уравнением адиабаты
Пуассона).
При изотермическом расширении газа
его
Соседние файлы в папке Хороший учебник
- #
- #
Давление газа
Содержание:
- Давление газа — что это за параметр
- Причина возникновения давления в газах
- Формула давления идеального газа из молекулярно-кинетической теории
- Второй способ записи основного уравнения МКТ
Давление газа — что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
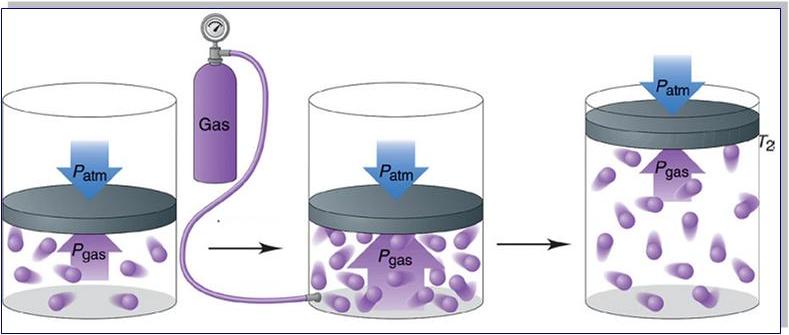
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.
Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
(P=frac{F}{S})
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
(F*Δt = Δp)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.
Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения. При этом можно наблюдать небольшой процент частиц со скоростями, приближенными к нулю, и малую долю частиц, обладающих огромной скоростью. Средняя квадратичная скорость в этом случае будет соответствовать некоторой величине, не изменяющейся с течением времени.
Средняя квадратичная скорость частиц однозначно характеризует температуру газа. Используя приближения молекулярно-кинетической теории в виде невзаимодействующих безразмерных и хаотично движущихся частиц, получают формулу для расчета давления газа в сосуде:
(P=frac{N*m*v^{2}}{3*V})
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
(P*V = n*R*T )
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
(P=frac{n*R*T}{V})
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.
Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.
Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
- Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример
Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.
Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:
(P=frac{N*m*v^{2}}{3*V})
Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:
(m=frac{M}{NA})
(n=frac{N}{NA})
(m*N= M*n)
(P=frac{M*n*v^{2}}{3*V})
Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.