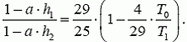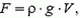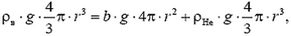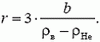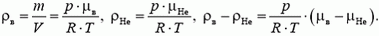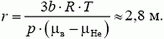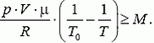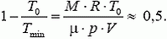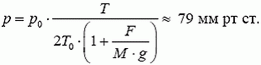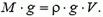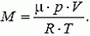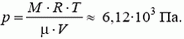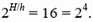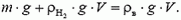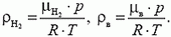2017-06-03
Однородный шар имеет массу $M$ и радиус $R$. Найти давление $p$ внутри шара, обусловленное гравитационным сжатием, как функцию расстояния $r$ от его центра. Оценить $p$ в центре Земли, считая, что Земля является однородным шаром.
Решение:
Разделим сплошную сферу на тонкие сферические слои и рассмотрим слой толщины $dr$, лежащий на расстоянии $r$ от центра шара. Каждый сферический слой надавливает на слои внутри него. Рассматриваемый слой притягивается к части лежащей внутри него сферы (внешняя часть не действует на слой). Следовательно, для рассматриваемого слоя
$dp 4 pi r^{2} = dF$
Или, $dP 4 pi r^{2} = frac{ gamma left ( frac{4}{3} pi r^{3} rho right ) (4 pi r^{2} dr rho)}{r^{2}}$
(Где $rho$ — средняя плотность сферы) или, $dp = frac{4}{3} pi gamma rho^{2} rdr$
Таким образом, $p = int_{r}^{R} dp = frac{2 pi}{3} gamma rho^{2} (R^{2} — r^{2})$
(При $r = R$ давление будет равным нулю)
Или, $p = frac{3}{8} (1 — (r^{2} / R^{2}2)) gamma M^{2} / pi R^{4}$, Полагая $rho = M / (4/3) pi R^{3}$
Полагая $r = 0$, получаем давление в центре сферы, и, рассматриваем его как Землю, где средняя плотность равна $rho = 5,5 cdot 10^{3} кг / м^{3}$ и $R = 64 cdot 10^{2} км$,
Получаем, $p = 1,73 cdot 10^{11} Па$ или $1,72 cdot 10^{6} атм$.
Давление внутри и снаружи воздушного шара одинаково. Так же как и давление снаружи и внутри человека, поэтому мы и не чувствуем на себе давление атмосферы. А на уровне моря нормальное давление равно 760 мм рт ст, или 100000 Па (паскаль), или 1 кг на квадратный сантиметр. С увеличением высоты давление атмосферы уменьшается. Поэтому воздушный шар раздувается (увеличивается его объем) до тех пор, пока давление газа (обычно гелия) внутри шара не станет равно давлению атмосферы снаружи шара. Для того чтобы определить давление внутри шара, достаточно определить давление снаружи (в гондоле шара). Для этого используются обычные барометры или альтиметр. Точно также измеряется давление и в самолете альтиметром на разной высоте. Но в физике есть формула, которая позволяет вычислить давление атмосферы, если известна высота над уровнем моря. Или если известно (измерено) давление, можно вычислить высоту. Но альтиметры в отличие от барометров имеют шкалу не в мм рт ст, а сразу показывают высоту полета самолета.
Давление атмосферы на любой высоте определяется формулой Больцмана p = p(0)exp[-Mgh/RT], где p(0) – давление на уровне моря, М – молярная масса газа (воздуха), равна 0,029, g – ускорение свободного падения равное 9,81, h – высота над уровнем моря, R – универсальная газовая постоянная равная 8,31, и T – абсолютная температура. Т = t + 273, t – температура в градусах Цельсия.
Представим, что земля — шар массой M и радиусом R. Выделим внешний слой на шаре, который давит на ядро.
Ускорение свободного падения на расстоянии r от ядра:
(g (r) = gamma {M over R^2 }cdot {r over R}),
где (gamma) — гравитационная постоянная.
Давление внешнего слоя на шар:
(p(r) = int_{R}^{r} rho g(r) dr), подставим g(r) :
(p(r) = int_{R}^{r} rho gamma {Mcdot r over R^3 } dr) (= rho gamma {M over R^3 } cdot ({R^2 — r^2 over 2});)
(p(r) = gamma {M over 2R} rho (1-{r^2 over R^2})) (1) ,
где (rho) — плотность несжимаемой земли.
(rho = {M over V} = {M over 4/3 pi R^3} ) (2).
Подставив (2) в (1) получим:
(p(r) = {3 over 8 pi}{gamma M^2 over R^4} (1- {r^2 over R^2})) — Зависимость давления в зависимости от расстояния до центра в модели несжимаемой жидкости.
В центре r = 0
(p = {3 over 8 pi}{gamma M^2 over R^4} )
Из справочников берем:
R = 6371 км = 6371000 м
M = 5,9726 * 1024 кг
(gamma) = 6,67 * 10-11 ({м^3 over с^{-2} кг })
Подставляя получаем:
(p = {3 over 8 cdot 3,14}{6,67 cdot 10^{-11} cdot 5,97^2 cdot 10^26 over 6371^4 cdot 10^7} ) (= 1,752 cdot 10^{11} [{кг over с^2 cdot м^2}])( = 1,752 cdot 10^{11} Па)
Ответ: гравитационное давление внутри земного шара в модели однородной несжимаемой жидкости. будет равно 1,752 * 1011 Па
Пример 1:
Внутри однородного шара с плотностью ρρ имеется сферическая полость, центр которой находится на расстоянии l от центра шара. Найти напряженность G поля тяготения внутри полости.
Решение от преподавателя:
Решение:
Рассмотрим полость как отрицательную массу плотности −ρ в однородной сфере плотностью +ρ с использованием принципа суперпозиции, искомая напряженность поля:
(Где r+ и r− — векторы положения орбитальной точки P внутри полости относительно центра сферы и полости соответственно.)
Пример 2:
Однородный шар имеет массу M и радиус R. Найти давление p внутри шара, обусловленное гравитационным сжатием, как функцию расстояния r от его центра. Оценить p в центре Земли, считая, что Земля является однородным шаром.
Решение от преподавателя:
Решение:
Разделим сплошную сферу на тонкие сферические слои и рассмотрим слой толщины dr, лежащий на расстоянии r от центра шара. Каждый сферический слой надавливает на слои внутри него. Рассматриваемый слой притягивается к части лежащей внутри него сферы (внешняя часть не действует на слой). Следовательно, для рассматриваемого слоя
(Где ρ — средняя плотность сферы) или,
Таким образом,
(При r=R давление будет равным нулю)
полагая, что
Полагая r=0, получаем давление в центре сферы, и, рассматриваем его как Землю, где средняя плотность равна
Пример 3:
Тонкий однородный стержень АВ массы m=1,0кг движется поступательно с ускорением w=2,0м/с2 под действием двух антипараллельных сил F1 и F2 (рис.). Расстояние между точками приложения этих сил a=20см. Кроме того, известно, что F2=5,0Н. Найти длину стержня.
Решение от преподавателя:
Решение:
Поскольку движение стержня является чисто поступательным, крутящим моментом вокруг центра масс стержня должны быть равны нулю.
Для поступательного движения стержня.
Из (1) и (2)
Пример 4:
К точке, радиус-вектор которой относительно начала координат О равен r = ai + bj, приложена сила F = Ai + Bj, где a, b, A, B — постоянные, i и j — орты осей х и у. Найти момент N и плечо l силы F относительно точки О.
Решение от преподавателя:
Решение:
Найденный момент
И плечо силы
Пример 5:
К точке с радиус-вектором r1=ai приложена сила F1=Aj , а к точке с r2=bj — сила F2=Bi. Здесь оба радиус-вектора определены относительно начала координат О, i и j — орты осей x и y, a, b, A и B — постоянные. Найти плечо l равнодействующей силы относительно точки О.
Решение от преподавателя:
Решение:
Относительно точки О, общий момент силы:
Результирующая внешняя сила
Пример 6:
К квадратной пластинке приложены три силы, как показано на рис. Найти модуль, направление и точку приложения равнодействующей силы, если эту точку взять на стороне ВС.
Решение от преподавателя:
Решение:
Относительно компланарных сил, в любой точке одной плоскости,
результирующая сила)
или
Таким образом, длина плеча,
Здесь, очевидно,
и он направлен вправо вдоль AC. Возьмем начало координат в C. Тогда,
Направленный нормально в плоскость фигуры. (Здесь a = сторона квадрата.)
Таким образом,
направленное в плоскость фигуры. Следовательно,
Таким образом, точка приложения силы находится в средней точке стороны ВС.
Пример 7:
Найти момент инерции:
а) тонкого однородного стержня относительно оси, перпендикулярной к стержню и проходящей через его конец, если масса стержня mm и его длина l;
б) тонкой однородной прямоугольной пластинки относительно оси, проходящей перпендикулярно к плоскости пластинки через одну из ее вершин, если стороны пластинки a и b, а ее масса m.
Решение от преподавателя:
Решение:
(a) Рассмотрим полосу длины dx на перпендикулярном расстоянии xx от оси, вокруг которой мы должны найти момент инерции стержня. Элементарная масса стержня равна
Момент инерции этого элемента вокруг оси
Таким образом, момент инерции стержня в целом вокруг данной оси
(б) Представим себе плоскость пластинки как плоскость ху, взяв начало координат в точке пересечения ребер пластины (рис.). очевидно
Аналогично,
Отсюда из теоремы о перпендикулярной оси
Который является искомым моментом инерции.
Пример 8:
Вычислить момент инерции:
а) медного однородного диска относительно оси симметрии, перпендикулярной к плоскости диска, если его толщина b = 2,0мм и радиус R = 100мм;
б) однородного сплошного конуса относительно его оси симметрии, если масса конуса m и радиус его основания R.
Решение от преподавателя:
Решение:
(а) Рассмотрим элементарный диск толщиной dx. Момент инерции этого элемента вокруг оси zz, проходящей через его центр масс.
где ρ = плотность материала пластины и S = площадь поперечного сечения пластины. Таким образом, искомый момент инерции
(б) Рассмотрим диск элемента радиуса rr и толщину dx на расстоянии xx от точки 0. Тогда r=xtgα и объем диска =πx2tg2αdx
Следовательно, его масса dm=πx2tgαdx⋅ρ (где ρ = Плотность конуса = m/(13πR2h) )
Момент инерции этого элемента, вокруг оси OA,
Таким образом, искомый момент инерции
следовательно,
Пример 9:
Показать, что для тонкой пластинки произвольной формы имеется следующая связь между моментами инерции: I1 + I2 = I3, где 1, 2, 3 — три взаимно перпендикулярные оси, проходящие через одну точку, причем оси 1 и 2 лежат в плоскости пластинки. Используя эту связь, найти момент инерции тонкого круглого однородного диска радиуса R и массы m относительно оси, совпадающей с одним из его диаметров.
Решение от преподавателя:
Решение:
(a) Рассмотрим пластинку произвольной формы и обозначим через 1,2 и 3 три оси, совпадающие с осью x, y и z, а плоскость пластинки — плоскостью x — y. Теперь момент инерции точечной массы около х — ось,
Таким образом, момент инерции пластинки вокруг этой оси
Аналогично,
Таким образом,
(б) Возьмем плоскость диска как плоскость x-y и начало координат в центре диска (рис.). Из симметрии Ix=Iy. Рассмотрим кольцевой элемент радиуса rr и толщину dr, тогда момент инерции кольцевого элемента вокруг оси y.
Таким образом, момент инерции диска вокруг оси z
Но, имея, Iz=Ix+Iy=2Ix
Таким образом,
Пример 10:
Однородный диск радиуса R=20см имеет круглый вырез, как показано на рис. Масса оставшейся (заштрихованной) части диска m=7,3кг. Найти момент инерции такого диска относительно оси, проходящей через его. центр инерции и перпендикулярной к плоскости диска.
Решение от преподавателя:
Решение:
Для простоты воспользуемся математическим трюком. Мы рассматриваем часть данного диска как наложение двух полных дисков (без отверстий), одну из положительной плотности и радиуса R и другую отрицательную плотность, но с одинаковыми величинами и радиусами R/2.
Поскольку (площадь) α (масса), соответствующие массы рассматриваемых дисков равны (4m/3) и (−m/3) соответственно, и эти массы можно представить, как расположенные в их соответствующих центрах масс. Возьмем точку O как начало координат, а ось x — вправо. Очевидно, центр масс заштрихованного положения данной формы лежит на оси х. Следовательно, центр масс (C) заштрихованной части дается формулой
Таким образом, центр масс фигуры находится на расстоянии R/6 от точки O к оси x Используя теорему о параллельной оси и учитывая, что момент инерции полного однородного круга радиуса m0 и радиуса r0 равен 12m0r02. Момент инерции небольшого диска массы (−m/3) и радиус R/2 вокруг оси, проходящей через точку C и перпендикулярной плоскости диска
По аналогии
Таким образом, искомый момент инерции,
Пример 11:
Исходя из формулы для момента инерции однородного шара, найти момент инерции тонкого сферического слоя массы mm и радиуса R относительно оси, проходящей через его центр.
Решение от преподавателя:
Решение:
Момент инерции заштрихованной части, вокруг оси, проходящей через его центр,
Тогда, если R=r+dr, заштрихованная часть становится оболочкой, которая является необходимой формой для вычисления момента инерции.
Пренебрежение более высокими степенями.
Пример 12:
На однородный сплошной цилиндр массы M и радиуса R намотана легкая нить, к концу которой прикреплено тело массы m (рис.). В момент t=0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени:
а) угловой скорости цилиндра;
б) кинетической энергии всей системы.
Решение от преподавателя:
Решение:
(a) Результирующая сила, действующая на систему (цилиндр M + тело m), представляет собой массу тела m в однородном гравитационном поле, которое является постоянным. Таким образом, начальное ускорение тела mm также является постоянным.
Из сохранения механической энергии указанной системы в однородном поле силы тяжести в момент времени
Следовательно, используя его в уравнении (1), получаем
Из кинематического соотношения,
Таким образом, искомая угловая скорость цилиндра
(б) Искомая кинетическая энергия.
Пример 13:
Концы тонких нитей, плотно намотанных на ось радиуса rr диска Максвелла, прикреплены к горизонтальной штанге. Когда диск раскручивается, штангу поднимают так, что диск остается неизменно на одной и той же высоте. Масса диска с осью mm, момент инерции прибора относительно его оси l. Найти натяжение каждой нити и ускорение штанги.
Решение от преподавателя:
Решение:
Для равновесия диска и оси
Когда диск разматывается, он имеет угловое ускорение β, заданное формулой
Соответствующее линейное ускорение
Поскольку диск остается неподвижным при совместном действии этого ускорения и ускорения (−w) стержня, который передается на ось, мы получаем
Пример 14:
Горизонтальный тонкий однородный стержень АВ массы m и длины l может свободно вращаться вокруг вертикальной оси, проходящей через его конец А. В некоторый момент на конец В начала действовать постоянная сила F, которая все время перпендикулярна к первоначальному положению покоившегося стержня и направлена в горизонтальной плоскости. Найти угловую скорость стержня как функцию его угла поворота ϕ из начального положения.
Решение от преподавателя:
Решение:
Пусть стержень отклоняется на угол ϕ из своего исходного положения в произвольный момент времени, измеренный относительно исходного положения в положительном направлении. Из уравнения приращения механической энергии системы.
Пример 15:
В установке (рис.) известны масса однородного сплошного цилиндра mm, его радиус R и массы тел m1 и m2. Скольжения нити и трения в оси цилиндра нет. Найти угловое ускорение цилиндра и отношение натяжений T1/T2 вертикальных участков нити в процессе движения.
Решение от преподавателя:
Решение:
Прежде всего, построим все силы, действующие на каждое тело. Поскольку цилиндр вращается и массивный, натяжение будет различным в обеих секциях нити. Из закона Ньютона в проекционной форме для тел m1 и m2 и отмечая, что w1=w2=w=βR, (без проскальзывания нити), имеем (m1>m2)
Теперь из уравнения вращательной динамики твердого тела относительно неподвижной оси вращения, т. е. Nz=Iβz, для цилиндра.
Одновременное решение вышеприведенных уравнений дает
Пример 16:
В системе (рис.) известны массы тел m1 и m2, коэффициент трения k между телом m1 и горизонтальной плоскостью, а также масса блока mm, который можно считать однородным диском. Скольжения нити по блоку нет. В момент t=0 тело m2 начинает опускаться. Пренебрегая массой нити и трением в оси блока, найти работу силы трения, действующей на тело m1, за первые t секунд после начала движения.
Решение от преподавателя:
Решение:
Поскольку система (m+m1+m2) находится под постоянными силами, ускорение тела m1 и m2 постоянное. Кроме того, скорости и ускорения тел m1 и m2 равны по величине (например, v и w), поскольку длина нити постоянна.
Из уравнения прироста механической энергии, т.е. ΔT+ΔU=Afr, в момент времени t, блок m1 на расстоянии h ниже от исходного положения, соответствующего t=0,
(угловая скорость ω=v/R для не проскальзывающей нити). Но
Поэтому, используя его в (1), получаем
Таким образом, работа, выполняемая силой трения на m1
Пример 17:
Однородный цилиндр радиуса R раскрутили вокруг его оси до угловой скорости ω0 и поместили затем в угол (рис.). Коэффициент трения между стенками угла и цилиндром равен k. Сколько оборотов сделает цилиндр до остановки?
Решение от преподавателя:
Решение:
твердое тело не перемещается, но есть угловое перемещение. Нарисуем все силы действующие на цилиндр. Очевидно, силы трения, действующие на цилиндр, являются кинетической.
Для вращения цилиндра вокруг его оси вращения,
Теперь, из кинематического уравнения,
Следовательно, искомое число оборотов,
Пример 18:
Однородный диск радиуса R раскрутили до угловой скорости ωω и осторожно положили на горизонтальную поверхность. Сколько времени диск будет вращаться на поверхности, если коэффициент трения равен k? Давление диска на поверхность считать равномерным.
Решение от преподавателя:
Решение:
Сила трения прикладывается к каждой части диска, и поскольку эти сечения лежат на разных расстояниях от оси, моменты сил трения отличаются от сечения к сечению.
Чтобы найти Nz, где z — ось вращения диска, разделим диск на тонкие кольца (рис.). Сила трения, действующая на рассматриваемый элемент dfr=k(2πrdrσ)g (где σ — плотность диска). Момент этой силы трения равен
Интегрируя по r от нуля до R, получим
Для вращения диска вокруг неподвижной оси z из уравнения
Таким образом, из углового кинематического уравнения
Пример 19:
Однородный сплошной цилиндр радиуса R и массы M может свободно вращаться вокруг неподвижной горизонтальной оси О (рис.). На цилиндр в один ряд намотан тонкий шнур длины l и массы m. Найти угловое ускорение цилиндра в зависимости от длины xx свешивающейся части шнура. Считать, что центр тяжести намотанной части шнура находится на оси цилиндра.
Решение от преподавателя:
Решение:
Воспользуемся уравнением
Относительно оси через O (1)
Для этого найдем угловой момент системы Mz вокруг данной оси вращения и соответствующего момента Nz. Угловой момент равен
Силы тяжести, нависающей части шнура, является единственной внешней силой, которая проявляет крутящий момент вокруг оси z, проходящий через O и дает,
Отсюда из уравнения
Таким образом,
Пример 20:
Однородный шар массы m и радиуса R скатывается без скольжения по наклонной плоскости, составляющей угол α с горизонтом. Найти:
а) значения коэффициента трения, при которых скольжения не будет;
б) кинетическую энергию шара через t секунд после начала движения.
Решение от преподавателя:
Решение:
(а) Укажем силы, действующие на сферу и точки их приложения. Выберем положительное направление x и ϕ (угол поворота) вдоль уклона в направлении вниз и ω (для ненаправленного вращения) соответственно. Теперь из уравнений динамики твердого тела, т.е
получаем,
Кроме того, отсутствие проскальзывания обеспечивает кинематическую связь между ускорениями:
Одновременное решение всех четырех уравнений дают:
(б) Решая уравнения (1) и (2) [части (а)], получаем
Поскольку сфера начинает двигаться при t=0 вдоль положительной оси x, для скатывания
Следовательно, искомая кинетическая энергия
Пример 21:
Однородный цилиндр массы m=8,0кг и радиуса R=1,3см(рис.) в момент t=0 начинает опускаться под действием силы тяжести. Пренебрегая массой нити, найти:
а) натяжение каждой нити и угловое ускорение цилиндра;
б) зависимость от времени мгновенной мощности, которую развивает сила тяжести.
Решение от преподавателя:
Решение:
(a) Укажем силы и точки их приложения для цилиндра. Выбирая положительное направление для x и ϕ, как показано на рисунке, запишем уравнение движения оси цилиндра и уравнение моментов в центре масс относительно системы отсчета этой оси, то есть из уравнения
Как нет скольжения нити на цилиндре
Из этих трех уравнений
(б) имеем
Пример 22:
онкие нити плотно намотаны на концах однородного сплошного цилиндра массы m. Свободные концы нитей прикреплены к потолку кабины лифта. Кабина начала подниматься с ускорением w0. Найти ускорение w′ цилиндра относительно кабины и силу F, с которой цилиндр действует (через нити) на потолок.
Решение от преподавателя:
Решение:
Опишем силы и точки их приложения, соответствующие цилиндру, прикрепленному к лифту. Второй закон Ньютона для твердого тела в векторной форме в системе отсчета лифта дает:
Уравнение моментов в центре масс системы относительно оси цилиндра,
Пример 23:
На гладкой наклонной плоскости, составляющей угол α=30∘ с горизонтом, находится катушка с ниткой, свободный конец которой укреплен, как показано на рис. Масса катушки m=200г, ее момент инерции относительно собственной оси I=0,45г⋅м2, радиус намотанного слоя ниток r=3,0см. Найти ускорение оси катушки.
Решение от преподавателя:
Решение:
Опишем силы и их точки приложения для катушки. Выбирая положительное направление для x и ϕ, как показано на рис., Применяем Fx=mwcx и Ncz=Icβz и получаем
Отметим, что если точка твердого тела в плоском движении связана с нитью, то проекция вектора скорости точки контакта твердого тела вдоль длины нити равна скорости другого конца нити ( Если она не ослаблена) Таким образом, в нашей задаче vp=v0, но v0=0, следовательно, точка P является мгновенным центром вращения для катушки. Поэтому vc=ωr
и впоследствии wc=βr. Решая уравнения одновременно, получим
Пример 24:
Однородный сплошной цилиндр массы mm лежит на двух горизонтальных брусьях. На цилиндр намотана нить, за свешивающийся конец которой тянут с постоянной вертикально направленной силой F (рис.). Найти максимальное значение силы F, при котором цилиндр будет катиться еще без скольжения, если коэффициент трения между ним и брусьями равен k. С каким ускорением wmaxwmax будет перемещаться ось цилиндра?
Решение от преподавателя:
Решение:
Нарисуем силы, действующие на цилиндр, и применим второй закон Ньютона в проекционной форме вдоль осей х и у (рис.):
берем положительное направление ϕ, как показано на рисунке и используя Ncz=Icβz, мы получаем
Решая уравнения, получим
Пример 25:
Установка (рис.) состоит из двух одинаковых сплошных однородных цилиндров каждый массы m, на которые симметрично намотаны две легкие нити. Найти натяжение каждой нити в процессе движения. Трения в оси верхнего цилиндра нет.
Решение от преподавателя:
Решение:
Для цилиндра из уравнения Nz=Iβz о его стационарной оси вращения.
Для вращения нижнего цилиндра из уравнения
Для поступательного движения нижнего цилиндра из уравнения
Поскольку на цилиндрах нет скольжения нитей:
Одновременное решение (1), (2) и (3) дает
Пример 26:
В системе (рис.) известны масса m груза А, масса M блока В, момент инерции I последнего относительно его оси и радиусы блока R и 2R. Масса нитей пренебрежимо мала. Найти ускорение груза А после того, как систему предоставили самой себе.

Решение от преподавателя:
Решение:
Нарисуем силы, действующие на шкив и вес A, и укажем положительное направление для x и ϕ, как показано на рисунке. Для цилиндра из уравнения
получаем
Для веса A из уравнения
Поскольку нет скольжения нитей на шкивах.
Одновременные решение четырех уравнений дают:
Пример 27:
Сплошной однородный цилиндр А массы m1 может свободно вращаться вокруг горизонтальной оси, которая укреплена на подставке В массы m2 (рис.). На цилиндр плотно намотана легкая нить, к концу К которой приложили постоянную горизонтальную силу F. Трения между подставкой и опорной горизонтальной плоскостью нет. Найти:
а) ускорение точки К;
б) кинетическую энергию этой системы через t секунд после начала движения.
Решение от преподавателя:
Решение:
(a) Для поступательного движения системы (m1+m2), из уравнения:
Для вращательного движения цилиндра из уравнения:
(б) Из уравнения приращения механической энергии:
Здесь ΔT=T(t), поэтому T(t)=Aext
Поскольку сила F постоянна и направлен вдоль оси х, искомая работа выполнена. (Где x — смещение точки приложения силы F в течение временного интервала t)
Альтернативный вариант:
Пример 28:
На гладкой горизонтальной плоскости лежит доска массы m1 и на ней однородный шар массы m2. К доске приложили постоянную горизонтальную силу F. С какими ускорениями будут двигаться доска и центр шара в отсутствие скольжения между ними?
Решение от преподавателя:
Решение:
Выбирая положительное направление для x и ϕ, как показано на рис., Запишем уравнение движения для сферы
(w2 — ускорение центра масс сферы). Для доски из уравнения
Кроме того, условие отсутствия скольжения сферы дает кинематическую связь между ускорениями:
Одновременное решение четырех уравнений дает
Пример 29:
Однородный шар радиуса r скатывается без скольжения с вершины сферы радиуса R. Найти угловую скорость шара после отрыва от сферы. Начальная скорость шара пренебрежимо мала.
Решение от преподавателя:
Решение:
Запишем уравнение движения для центра сферы в момент отрыва:
где v — скорость центра сферы в этот момент, а θ — соответствующий угол (рис.). Скорость v можно найти из закона сохранения энергии:
Где I — момент инерции сферы относительно оси, проходящей через центр сферы, то есть
К тому же,
Из этих четырех уравнений получаем
Пример 30:
Сплошной однородный цилиндр радиуса R=15см катится по горизонтальной плоскости, которая переходит в наклонную плоскость, составляющую угол α=30∘ с горизонтом (рис.). Найти максимальное значение скорости v0, при котором цилиндр перейдет на наклонную плоскость еще без скачка. Считать, что скольжения нет.
Решение от преподавателя:
Решение:
Поскольку цилиндр движется без скольжения, центр цилиндра вращается вокруг точки O, проходя через общий край плоскостей. Другими словами, точка O становится опорой мгновенной оси вращения цилиндра. В любой момент времени, движение скорости центра масс v1, когда угол (показанный на рисунке) равен β, имеем
В любой момент времени, движение скорости центра масс v1, когда угол (показанный на рисунке) равен β, имеем
Где N — нормальная реакция края или,
Из закона сохранения энергии
(Из теоремы о параллельной оси) Таким образом,
Из (1) и (2)
Где N0 — соответствующая реакция. Заметим, что N≥N0. Во время этого поворота не происходит прыжка, если N0>0. Следовательно, v0 должно быть меньше
Пример 31:
На внутренней стороне тонкого жесткого обруча радиуса R прикреплено небольшое тело А, масса которого равна массе обруча. Последний катится без скольжения по горизонтальной плоскости так, что в моменты, когда тело А оказывается в нижнем положении, скорость центра обруча равна v0 (рис.). При каких значениях v0 обруч не будет подпрыгивать?
Решение от преподавателя:
Решение:
Очевидно, что обруч будет подскакивать, когда небольшое тело А будет находиться на самой высокой точке обруча во время его движения. Пусть скорость центра масс обруча равно vv в этом положении. Трения нет, поэтому из закона сохранения механической энергии; E1=E2
Из уравнения Fn=mwn для тела A в конечном положении 2
Поскольку обруч не имеет ускорения в вертикальном направлении, поэтому,
Из уравнений (2) и (3),
Поскольку обруч не отскакивает, N≥0 (5)
Итак, из уравнений (1), (4) и (5),
Пример 32:
Найти кинетическую энергию гусеницы трактора, движущегося со скоростью vv, если масса гусеницы равна m(рис. ).
Решение от преподавателя:
Решение:
Поскольку нижняя часть ремня находится в контакте с жестким полом, скорость этой части становится равной нулю. Гусеница движется со скоростью v, поэтому скорость верхней части пояса становится равной 2v2v условие вращения и кинетической энергией верхней части =12(m2)(2v)2=mv2, так что кинетическая энергия гусеницы намного больше радиуса колес.
Пример 33:
Однородный шар массы m и радиуса r катится без скольжения по горизонтальной плоскости, вращаясь вокруг горизонтальной оси ОА (рис.). При этом центр шара движется со скоростью v по окружности радиуса R. Найти кинетическую энергию шара.
Решение от преподавателя:
Решение:
Сфера имеет два типа движения, одно — вращение вокруг своей оси, а другое — движение в круге радиуса R. Следовательно, искомая кинетическая энергия
Где I1 — момент инерции вокруг собственной оси, I2 — момент инерции относительно вертикальной оси, проходящий через O,
Но,
(с использованием теоремы о параллельной оси) (2)
Кроме того
Используя (2) и (3) в (1), получим
Пример 34:
Середина однородного тонкого стержня АВ массы m и длины l жестко скреплена с осью вращения OO′, как показано на рис. Стержень привели во вращение с постоянной угловой скоростью ω. Найти результирующий момент центробежных сил инерции относительно точки С — в системе отсчета, связанной с осью OO′ и стержнем.
Решение от преподавателя:
Решение:
Рассмотрим небольшой элемент длины dx на расстоянии x от точки C, вращающейся в круге радиуса r=xsinθ
Масса элемента равна
Итак, центробежная сила, действующая на этот элемент
момент этой силы относительно C,
И, следовательно, полный момент
Пример 35:
Конический маятник — тонкий однородный стержень длины l и массы m — вращается равномерно вокруг вертикальной оси с угловой скоростью ω (верхний конец стержня укреплен шарнирно). Найти угол θ между стержнем и вертикалью.
Решение от преподавателя:
Решение:
Рассмотрим систему в системе отсчета, вращающейся со стержнем. В этом системе стержень находится в состоянии покоя и испытывает не только гравитационную силу mg и силу реакции R, но и центробежную силу Fcf.
В рассматриваемой системе из условия равновесия, т.е. N0z=0 или,
где Ncf — момент центробежной силы вокруг O. Для вычисления Ncf рассмотрим элемент длины dx, расположенный на расстоянии xx от точки O. Этот элемент подвергается действию горизонтальной псевдосилы
Момент этой псевдосилы вокруг оси вращения через точку O равен
Из уравнений (1) и (2), что,
Пример 36:
Однородный кубик со стороной a находится на горизонтальной плоскости с коэффициентом трения k. Кубику сообщили начальную скорость, после чего он прошел некоторое расстояние по плоскости и остановился. Объяснить исчезновение момента импульса кубика относительно оси, лежащей на плоскости и перпендикулярной к направлению движения кубика. Найти расстояние между равнодействующими сил тяжести и нормального давления со стороны опорной плоскости.
Решение от преподавателя:
Решение:
Когда кубу задана начальная скорость на столе в некотором направлении (как показано), он приобретает угловой момент вокруг оси на столе, перпендикулярной начальной скорости и, скажем, чуть ниже CG. Этот угловой момент исчезнет, когда куб останавливается, и это может быть только из-за крутящего момента. Фрикционные силы не могут сделать это сами по себе, потому что они действуют в плоскости, содержащей ось. Но если сила нормальной реакции действует эксцентрично (как показано), их крутящий момент может привести к исчезновению момента количества движения. Мы можем рассчитать расстояние Δx между точкой приложения нормальной реакции и C.G. куба следующим образом. Возьмите момент относительно C.G. всех сил. Он должен исчезнуть, потому что куб не поворачивается и не падает на стол. Тогда, если сила трения равна fr
Пример 37:
Гладкий однородный стержень АВ массы M и длины l свободно вращается с угловой скоростью ω0 в горизонтальной плоскости вокруг неподвижной вертикальной оси, проходящей через его конец А. Из точки А начинает скользить по стержню небольшая муфта массы m. Найти скорость v′ муфты относительно стержня в тот момент, когда она достигнет его конца В.
Решение от преподавателя:
Решение:
В процессе движения данной системы кинетическая энергия и угловой момент относительно оси вращения не меняются. Отсюда следует, что
(ω — конечная угловая скорость стержня) и
Из этих уравнений получаем
Пример 38:
На гладкой горизонтальной поверхности лежит однородный стержень массы m=5,0кг и длины l=90см. По одному из концов стержня произвели удар в горизонтальном направлении, перпендикулярном к стержню, в результате которого стержню был передан импульс p=3,0 Н⋅с. Найти силу, с которой одна половина стержня будет действовать на другую в процессе движения.
Решение от преподавателя:
Решение:
Из-за удара угловой импульс, получаемый стержнем вокруг центра масс равен p2. Если ω — угловая скорость, приобретаемая стержнем, имеем
В системе отсчета центра масс, стержень вращается вокруг оси, проходящей через ее среднюю точку с угловой скоростью ω. Следовательно, сила, оказываемая одной половиной на другую = половины массы × ускорения центра масс этой части, в системе отсчета центра масс.
Пример 39:
Однородная тонкая квадратная пластинка со стороной l и массы M может свободно вращаться вокруг неподвижной вертикальной оси, совпадающей с одной из ее сторон. В центр пластинки по нормали к ней упруго ударяется шарик массы mm, летевший со скоростью v. Найти:
а) скорость шарика v′ после удара;
б) горизонтальную составляющую результирующей силы, с которой ось будет действовать на пластинку после удара.
Решение от преподавателя:
Решение:
(а) В процессе движения данной системы кинетическая энергия и угловой момент относительно оси вращения не меняются. Отсюда следует, что
Из этих уравнений получаем
Поскольку v’↑↑v, то векторная форма
(б) Очевидно, что искомая сила обеспечивает центростремительное ускорение центра масс стержня и является
Пример 40:
Горизонтально расположенный однородный диск массы M и радиуса R свободно вращается вокруг неподвижной вертикальной оси, проходящей через его центр. Диск имеет радиальную направляющую, вдоль которой может скользить без трения небольшое тело массы m. К телу привязана легкая нить, пропущенная через полую ось диска вниз. Первоначально тело находилось на краю диска и вся система вращалась с угловой скоростью ω0. Затем к нижнему концу нити приложили силу F, с помощью которой тело медленно подтянули к оси вращения. Найти:
а) угловую скорость системы в конечном состоянии;
б) работу, которую совершила сила F.
Решение от преподавателя:
Решение:
(a) Поскольку сила F на теле радиальная, поэтому ее угловой момент вокруг оси обращается в нуль и сохраняется угловой момент системы относительно данной оси. Таким образом
(б) Из уравнения приращения механической энергии системы
Подставляя значение ω из части (а) и решая, получим
Пример 41:
Два горизонтальных диска свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны I1 и I2, а угловые скорости — ω1 и ω2. После падения верхнего диска на нижний оба диска благодаря трению между ними начали через некоторое время вращаться как единое целое. Найти:
а) установившуюся угловую скорость вращения дисков;
б) работу, которую совершили при этом силы трения.
Решение от преподавателя:
Решение:
(a) Из закона сохранения момента количества движения системы относительно вертикальной оси z следует, что:
Следовательно,
НО для ωz>0, соответствующий вектор ω совпадает с положительным направлением по оси z и наоборот. Поскольку оба диска вращаются вокруг одной и той же вертикальной оси z, таким образом, в векторной форме.
Однако проблема имеет смысл только в том случае, если
(б) Из уравнения приращения механической энергии системы:
Используя уравнение (1)
Пример 42:
Горизонтально расположенный однородный стержень АВ массы m=1,40кг и длины l0=100см вращается свободно вокруг неподвижной вертикальной оси OO′, проходящей через его конец A. Точка A находится посередине оси OO′, длина которой l=55см. При каком значении угловой скорости стержня горизонтальная составляющая силы, действующей на нижний конец оси OO′, будет равна нулю? Какова при этом горизонтальная составляющая силы, действующей на верхний конец оси?
Решение от преподавателя:
Решение:
Общая центробежная сила может быть рассчитана,
Тогда для равновесия,
Таким образом, T1 обращается в нуль, когда
Пример 43:
Середина однородного стержня массы m и длины l жестко соединена с вертикальной осью OO′ так, что угол между стержнем и осью равен θ (см. рис.). Концы оси OO′ укреплены в подшипниках. Система вращается без трения с угловой скоростью ω. Найти:
а) модуль и направление момента импульса M стержня относительно точки С ,а также его момент импульса относительно оси вращения;
б) модуль приращения вектора M относительно точки С за полоборота;
в) момент внешних сил N, действующих на ось OO′′ при вращении.
Решение от преподавателя:
Решение:
(a) Угловая скорость ω относительно OO′ может быть разложена на части, параллельные стержню, и ωsinθ, перпендикулярные стержню через C. Часть, параллельная стержню, не вносит вклад, так что угловой момент
(б) Модуль M не изменяется, но модуль изменения M равен
Пример 44:
На полу кабины лифта, которая начинает подниматься с постоянным ускорением w=2,0м/с2, установлен гироскоп — однородный диск радиуса R=5,0см на конце стержня длины l=10см (рис.). Другой конец стержня укреплен в шарнире О. Гироскоп прецессирует с угловой скоростью n=0,5об/с. Пренебрегая трением и массой стержня, найти собственную угловую скорость диска.
Решение от преподавателя:
Решение:
Момент инерции диска вокруг оси симметрии —
Если угловая скорость диска равна ωω, тогда момент импульса равен
Частота прецессии 2πn, имеем
Получаем, m(g+w)l, эффективные гравитационные моменты (g заменяется на g+w в лифте). Таким образом,
Пример 45:
Однородный шар массы m=5,0кг и радиуса R=6,0см вращается с угловой скоростью ω=1250рад/с вокруг горизонтальной оси, проходящей через его центр и укрепленной в подшипниках подставки. Расстояние между подшипниками l=15см. Подставку поворачивают вокруг вертикальной оси с угловой скоростью ω′=5,0рад/с. Найти модуль и направление гироскопических сил.
Решение от преподавателя:
Решение:
Момент инерции сферы
и, следовательно, значение момента количества движения
Поскольку он прецессирует со скоростью ω′, требуемый крутящий момент равен
(Сила F′ должна быть вертикальной.)
Пример 46:
Корабль движется со скоростью v=36км/ч по дуге окружности радиуса R=200м. Найти момент гироскопических сил, действующих на подшипники со стороны вала с маховиком; которые имеют момент инерции относительно оси вращения I=3,8⋅103кг⋅м2 и делают n=300об/мин. Ось вращения расположена вдоль корабля.
Решение от преподавателя:
Решение:
Число оборотов в минуту маховика, равное n, угловой момент маховика l×2πn. Скорость прецессии равна vR.
Таким образом,
Баканина Л.П. Задачи о воздушных шарах // Квант. — 1975. — № 1. — С. 60-63.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В наш век самолетов и ракет, для которых доступны любые высоты над поверхностью Земли, воздушные шары, громоздкие, ненадежные и неуправляемые, уже отошли в прошлое, хотя когда-то именно они дали человеку возможность подняться в воздух. Впрочем, в некоторых случаях воздушные шары очень удобны, они используются и сейчас. Например, с аэростата удобно обучать прыжкам с. парашютом, а метеорологи исследуют давление, температуру и воздушные потоки в атмосфере с помощью шаров-зондов.
Задачи о воздушных шарах даются иногда на вступительных экзаменах. Обычно их можно разделить на два типа:
1) задачи, в которых нужно найти связь между габаритами и наполнением шара и подъемной силой, действующей на шар у поверхности Земли;
2) задачи, в которых нужно определить максимальную высоту подъема шара; при этом задается какая-нибудь модель атмосферы, то есть закон изменения давления и температуры с высотой.
По существу, задачи обоих типов – это задачи на статику. Для их решения нужно уметь применять уравнение состояния газов и найти условие равновесия шара, на который действует сила притяжения Земли и выталкивающая сила со стороны окружающего шар воздуха. Если выталкивающая сила больше силы притяжения (разность этих сил называют подъемной силой), шар поднимается вверх. Но по мере подъема уменьшается плотность окружающего воздуха, а, следовательно, уменьшается и выталкивающая сила, по закону Архимеда равная
где ρ — плотность воздуха, а V — объем шара. На некоторой высоте выталкивающая сила окажется равной силе притяжения – это и будет максимальной высотой подъема шара.
Разберем теперь несколько конкретных задач, которые в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт.
Задача 1. Сферическая оболочка воздушного шара сделана из материала, квадратный метр которого имеет массу b = 1 кг/м2. Шар наполнен гелием при нормальном атмосферном давлении. При каком минимальном радиусе шар поднимает сам себя? Температура гелия и температура окружающего воздуха одинаковы и равны 0 ºС. Молекулярная масса воздуха 29 кг/кмоль, молекулярная масса гелия 4 кг/кмоль.
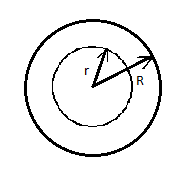
При увеличении радиуса шара выталкивающая сила растет пропорционально кубу радиуса, а вес оболочки – пропорционально квадрату радиуса. Следовательно, выталкивающая сила растет быстрее и, начиная с какого-то значения радиуса, станет больше, чем вес оболочки. Тогда шар начнет подниматься. Обозначим этот радиус оболочки через r. При этом
откуда
Плотности воздуха ρв и гелия ρНе при данных условиях найдем с помощью закона Менделеева–Клапейрона 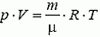
Окончательно получаем
Задача 2. Объем воздушного шара равен V = 230 м3, масса оболочки М = 145 кг. Шар наполнен горячим воздухом при нормальном атмосферном давлении. Какую температуру должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Температура наружного воздуха t0 = 0 оС.
При нагревании воздуха его плотность уменьшается, так как 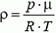
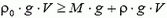
Отсюда
значит,
Tmin » 2T0 = 546 ºK = 273 ºC.
Задача 3. Для удержания на поверхности Земли метеорологического шара-зонда с массой М = 20 кг необходимо приложить силу F = 1000 Н. Шар поднимается до такой высоты, где его объем увеличивается в два раза. Температура воздуха, измеренная на этой высоте с помощью зонда, оказалась равной t = –43 ºС. Вычислить давление воздуха на этой высоте, если на поверхности Земли давление р0 = 754 мм рт. ст., а температура t0= +17 °С.
Условие равновесия шара у поверхности Земли записывается так:
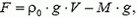
где V — объем шара у поверхности Земли, а 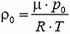
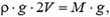
где 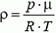
Задача 4. Шар-зонд, наполненный водородом, имеет герметичную оболочку постоянного объема V = 50 м3. Масса шара вместе с водородом М = 5 кг. Определить, на какую максимальную высоту он сможет подняться, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура в стратосфере t = –60 ºС. Молекулярная масса воздуха 29 кг/кмоль. Давление у поверхности Земли р0 = 1 атм.
На максимальной высоте выталкивающая сила равна весу шара- зонда:
Выразив плотность окружающего воздуха через давление и температуру, получим
Таким образом, давление воздуха на этой высоте равно
Посмотрим теперь, во сколько раз давление р меньше давления у поверхности Земли р0: 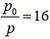
Из условия известно, что давление падает в два раза через каждые 5 км подъема, то есть 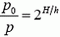
Отсюда
H = 4h = 20 км.
Задача 5. Нерастяжимая оболочка шара-зонда объема V = 75 м3 имеет в нижней части небольшое отверстие. Масса оболочки t = 7 кг. Шар наполнен водородом. Определить, на какую максимальную высоту сможет подняться этот шар-зонд, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура воздуха в стратосфере t = –60 °С, температура водорода равна температуре окружающего воздуха. Давление у поверхности Земли р0 = 1 атм.
Эта задача отличается от предыдущей тем, что оболочка шара не герметична, а имеет отверстие. Следовательно, давление внутри шара все время равно давлению в атмосфере, и по мере увеличения высоты подъема шара водород вытекает из отверстия. Будем, считать, что подъем происходит достаточно быстро и можно пренебречь диффузией воздуха внутрь оболочки, тогда условие равновесия шара на максимальной высоте
Плотности водорода и воздуха можно найти из уравнения Менделеева-Клапейрона:
Таким образом, давление на максимальной высоте
Отношение 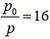
Высота подъема в задаче 5 получилась такая же, как для герметичного шара в задаче 4, но не следует забывать, что мы рассматривали разные шары, с разными объемами и массами. А если оба шара совершенно одинаковы и отличаются только тем, что у одного оболочка герметичная, а у другого имеет отверстие, — какой из шаров поднимется выше в этом случае?
Выталкивающая сила будет одинакова для обоих шаров, так как их объемы равны. Если начальные массы шаров были одинаковы, то после подъема шар с отверстием окажется легче, так как часть наполняющего его газа вытечет при подъёме. Следовательно, шар с отверстием сможет подняться на большую высоту.
Обычно человеку, впервые задумавшемуся над этим вопросом, такой результат кажется странным. Часто задают вопрос: «Как вообще в шаре с отверстием возникает подъемная сила? Ведь снизу, там, где отверстие, воздух и газ внутри шара находятся в равновесии».
Давайте рассмотрим верхнюю точку шара. Если в нижней точке шара давление воздуха и газа равно р0, в верхней точке давление воздуха 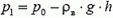
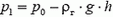
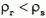
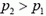
то, так как h мало — всего несколько метров, 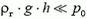
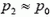
то здесь оба члена одинаковы по порядку величины, и учитывать их надо оба. Кстати сказать, то, что мы считаем ρв и ρг постоянными, — тоже приближение, на самом деле они уменьшаются с высотой по мере уменьшения давления. Но учет этого обстоятельства дал бы значительно меньшую поправку к выталкивающей силе, этой поправкой можно пренебречь.
Упражнения
1. Определить подъемную силу воздушного шара, в котором находится t г водорода. Оболочка шара герметичная и сделана из легкого неупругого материала, который может свободно растягиваться.
2. На сколько градусов надо нагреть воздух внутри сообщающегося с атмосферой воздушного шара, сферическая оболочка которого имеет диаметр 10 м и весит 10 кг, для того чтобы шар взлетел? Атмосферное давление 735 мм. рт. ст., температура окружающего воздуха +27 °С.
3. Воздушный шар представляет собой баллон постоянного объема, наполненный гелием. Через отверстие в нижней части шар сообщается с атмосферой. Как изменится максимальная высота подъема шара, если гелий нагреть до температуры t1? Температуру атмосферы считать постоянной и равной t0, а давление изменяющимся по закону 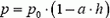
Ответы.
1. 13,5m·g.
2. Не менее чем на 5º.
3.