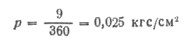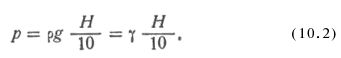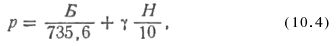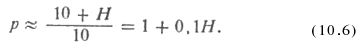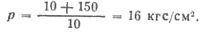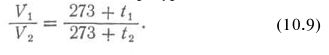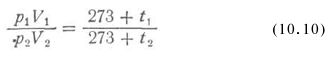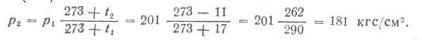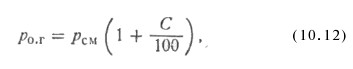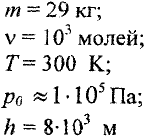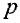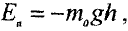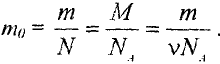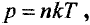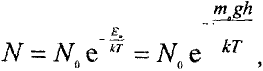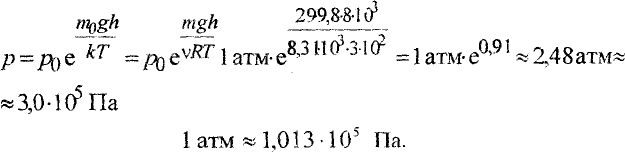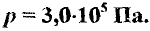Перейти к контенту
Условие задачи:
Найти давление в озере на глубине 4,5 м. Атмосферное давление 100 кПа.
Задача №3.2.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(h=4,5) м, (p_{атм}=100) кПа, (p-?)
Решение задачи:
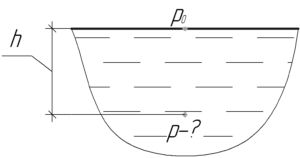
[p = {p_{атм}} + {p_в}]
Давление столба воды (p_{в}) высотой (h) определим по формуле:
[{p_в} = rho gh]
Здесь (rho) – плотность воды, равная 1000 кг/м3. Значит:
[p = {p_{атм}} + rho gh]
Численное значение искомого давления равно:
[p = 100 cdot {10^3} + 1000 cdot 10 cdot 4,5 = 145000;Па = 145;кПа]
Ответ: 145 кПа.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.2.7 На сколько отличается давление столбика ртути высотой 10 мм от давления столбика
3.2.9 Чему равно давление воды на глубине 2 м?
3.2.10 С какой силой действует вода на прямоугольную плотину высотой 75 м и шириной 120 м
( 5 оценок, среднее 5 из 5 )
2018-04-16
Пусть на поверхности Земли воздух находится при нормальных условиях. Считая, что температура и молярная масса воздуха не зависят от высоты, найти его давление на высоте 5,0 км над поверхностью Земли и в шахте на глубине 5,0 км.
Решение:
Имеем, $dp = — rho g dh$ из закона Менделеева $rho = frac{M}{RT} p$ (1)
таким образом $frac{dp}{p} = — frac{Mg}{RT} dh$
Интегрируя, получаем
или, $int_{p_{0} }^{p} frac{dp}{p} = — frac{- Mg}{RT} int_{0}^{h} dh$ или, $ln frac{p}{p_{0} } = — frac{Mg}{RT}h$,
(где $p_{0}$ — давление на поверхности Земли).
$p = p_{0} e^{ — Mgh/RT}$,
При стандартных условиях, $p_{0} = 1 атм, T = 273 К$
Давление на высоте $5 атм = 1 cdot e^{ — 28 cdot 9,81 cdot 5000/8314 cdot 273} = 0,5 атм$.
Давление в шахте на глубине $5 км = 1 cdot e^{ -28 cdot 9,81 cdot ( -5000) /8314 cdot 273 } = 2 атм$.
2016-11-22
Калькулятор доступен на полной версии сайта, с помощью него вы можете узнать давление жидкости на глубине 1, 5, 10, 20, 50, 100, 500, 1000 метров.
Вычисления осуществляются по избыточной шкале давления, в которой за 0 принято давление атмосферы.
Результат расчета давления на глубине
Вычислить давление на другой глубине
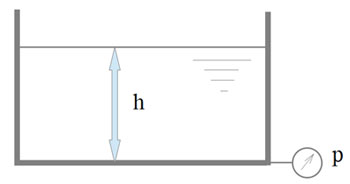
Расчет давления на глубине
Расчетная схема показана на рисунке:
Для расчета используется формула:
P=ρ × g × h
- ρ — плотность жидкость
- h — глубина погружения
- g — ускорение свободного падения
- P — величина давления на глубине h
Пример расчета давления воды на глубине 10 метров
Для расчета давления воды на глубине 10 м, введите в графу глубина (h) — 10, выберите жидкость — вода, нажмите кнопку рассчитать.
Каждые 10 метров воды создают давление в 1 атмосферу
Полученное значение давления воды на 10 метрах равно 98,1 кПа, что примерно равно атмосферному давлению 101 кПа. Поэтому в приблизительных расчетах принимают давление в воде на глубине 10 метров равным 1 атмосфере про избыточной шкале.
Администрация сайта за результаты онлайн вычислений ответственности не несет.
Читайте также:
Все новости
10. Типовые расчеты
10.1. Вычисление давления
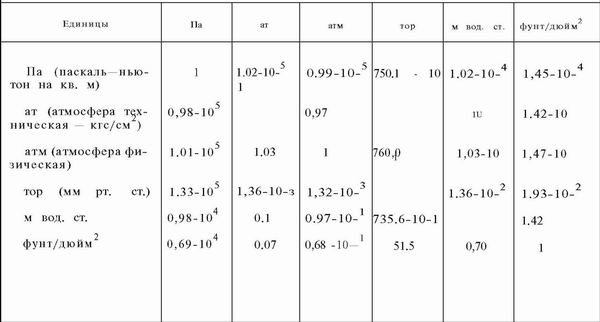
В водолазной практике часто приходится встречаться с вычислением механического, гидростатического и газового давления широкого диапазона величин. В зависимости от значения измеряемого давления применяют различные единицы.
В системах СИ и МКС единицей давления служит паскаль (Па), в системе МКГСС – кгс/см2 (техническая атмосфера – ат). В качестве внесистемных единиц давления применяются тор (мм рт. ст.), атм (физическая атмосфера),м вод. ст., а в английских мерах – фунт/дюйм2. Соотношения между различными единицами давления приведены в табл, 10.1.
Механическое давление измеряется силой, действующей перпендикулярно на единицу площади поверхности тела:
где р – давление, кгс/см2;
F – сила, кгс;
S – площадь, см2.
Пример 10.1. Определить давление, которое водолаз оказывает на палубу судна и на грунт под водой, когда он делает шаг (т. е. стоит на одной ноге). Вес водолаза в снаряжении на воздухе 180 кгс, а под водой 9 кгс. Площадь подошвы водолазной галоши принять 360 см2. Решение. 1) Давление, передаваемое водолазной галошей на палубу судна, по (10.1):
р = 180/360 = 0.5 кгс/см
или в единицах СИ
р = 0,5 * 0,98.10 5 = 49000 Па = 49 кПа.
Таблица 10.1. Соотношения между различными единицами давления
2) Давление, передаваемое водолазной галошей на грунт под водой:
или в единицах СИ
р = 0,025*0,98*10 5 = 2460 Па = 2,46 кПа.
Гидростатическое давление жидкости везде перпендикулярно к поверхности, на которую оно действует, и возрастает с глубиной, но остается постоянным в любой горизонтальной плоскости.
Если поверхность жидкости не испытывает внешнего давления (например, давления воздуха) или его не учитывают, то давление внутри жидкости называют избыточным давлением
где p – давление жидкости, кгс/см2;
р – плотность жидкости, гс» с4/см2;
g – ускорение свободного падения, см/с2;
Y – удельный вес жидкости, кг/см3, кгс/л;
Н – глубина, м.
Если поверхность жидкости испытывает внешнее давление пп. то давление внутри жидкости
Если на поверхность жидкости действует атмосферное давление воздуха, то давление внутри жидкости называют абсолютным давлением (т. е. давлением, измеряемым от нуля – полного вакуума):
где Б – атмосферное (барометрическое) давление, мм рт. ст.
В практических расчетах для пресной воды принимают
Y = l кгс/л и атмосферное давление p0 = 1 кгс/см2 = = 10 м вод. ст., тогда избыточное давление воды в кгс/см2
а абсолютное давление воды
Пример 10.2. Найти абсолютное давление морской воды действующее на водолаза на глубине 150 м, если барометрическое давление равно 765 мм рт. ст., а удельный вес морской воды 1,024 кгс/л.
Решение. Абсолютное давление волы по (10/4)
приолиженное значение абсолютного давления по (10.6)
В данном примере использование для расчета приближенной формулы (10.6) вполне оправданно, так как ошибка вычисления не превышает 3%.
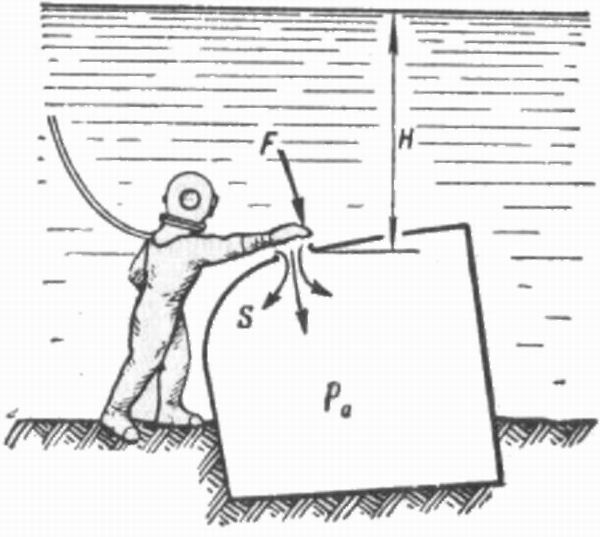
Пример 10.3. В полой конструкции, содержащей воздух под атмосферным давлением рa = 1 кгс/см2, находящейся под водой, образовалось отверстие, через которое стала поступать вода (рис. 10.1). Какую силу давления будет испытывать водолаз, если он попытается это отверстие закрыть рукой? Площадь «У сечения отверстия равна 10X10 см2, высота столба воды Н над отверстием 50 м.
Рис. 9.20. Наблюдательная камера «Галеацци»: 1 – рым; 2 – устройство отдачи троса и среза кабеля; 3 – штуцер для телефонного ввода; 4 – крышка люка; 5 – верхний иллюминатор; 6 – резиновое привальное кольцо; 7 – нижний иллюминатор; 8 – корпус камеры; 9 – баллон кислородный с манометром; 10 – устройство отдачи аварийного балласта; 11 – аварийный балласт; 12 – кабель светильника; 13 – светильник; 14 – электровентилятор; 15-телефон- микрофон; 16 – аккумуляторная батарея; 17 – коробка регенеративная рабочая; 18 – иллюминатор крышки люка
Решение. Избыточное давление воды у отверстия по (10.5)
P = 0,1-50 = 5 кгс/см 2 .
Сила давления на руку водолаза из (10.1)
F = Sp = 10*10*5 = 500 кгс =0,5 тс.
Давление газа, заключенного в сосуд, распределяется равномерно, если не принимать во внимание его весомость, которая при размерах сосудов, применяемых в водолазной практике, оказывает ничтожное влияние. Величина давления неизменной массы газа зависит от объема, который он занимает, и температуры.
Зависимость между давлением газа и его объемом при неизменной температуре устанавливается выражением
P1 V1 = p 2 V 2 (10.7)
где р1 и р2 – первоначальное и конечное абсолютное давление, кгс/см2;
V1 и V2 – первоначальный и конечный объем газа, л. Зависимость между давлением газа и его температурой при неизменном объеме устанавливается выражением
где t1 и t2 – начальная и конечная температура газа, °С.
При неизменном давлении аналогичная зависимость существует между объемом и температурой газа
Зависимость между давлением, объемом и температурой газа устанавливается объединенным законом газового состояния
Пример 10.4. Емкость баллона 40 л, давление воздуха в нем по манометру 150 кгс/см2. Определить объем свободного воздуха в баллоне, т. е. объем, приведенный к 1 кгс/см2.
Решение. Начальное абсолютное давление р = 150+1 = 151 кгс/см2, конечное р2 = 1 кгс/см2, начальный объем V1 =40 л. Объем свободного воздуха из (10.7)
Пример 10.5. Манометр на баллоне с кислородом в помещении с температурой 17° С показывал давление 200 кгс/см2. Этот баллон перенесли на палубу, где на другой день при температуре -11° С его показания снизились до 180 кгс/см2. Возникло подозрение на утечку кислорода. Проверить правильность подозрения.
Решение. Начальное абсолютное давление p2 =200 + 1 = =201 кгс/см2, конечное р2 = 180 + 1 = 181 кгс/см2, начальная температура t1 = 17°С, конечная t2 =-11° С. Расчетное конечное давление из (10.8)
Подозрения лишены оснований, так как фактическое и расчетное давления равны.
Пример 10.6. Водолаз под водой расходует 100 л/мин воздуха, сжатого до давления глубины погружения 40 м. Определить расход свободного воздуха (т. е. при давлении 1 кгс/см2).
Решение. Начальное абсолютное давление на глубине погружения по (10.6)
Р1 = 0,1*40 =5 кгс/см2 .
Конечное абсолютное давление Р2 = 1 кгс/см2
Начальный расход воздуха V1 = l00 л/мин.
Расход свободного воздуха по (10.7)
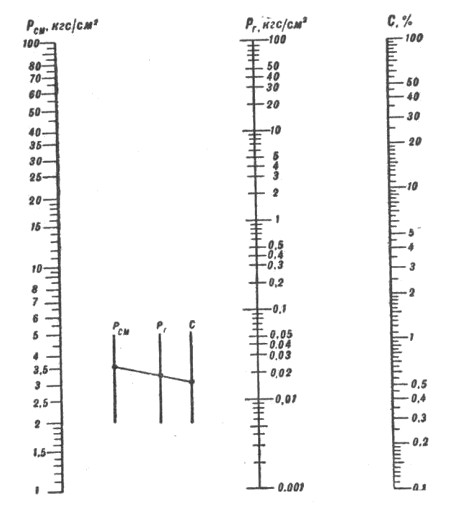
Парциальное давление газа, входящего в состав воздуха (искусственной дыхательной смеси), определяется по номо- грамме рис. 10.2 или из выражения
где рсм – парциальное давление газа в смеси, кгс/см2; Рсм – абсолютное давление газовой смеси, кгс/см2; С – объемное содержание газа в смеси, %.
Пример 10.7. Определить парциальное давление газов, входя щих в состав воздуха, подаваемого в скафандр водолаза на поверхности и на глубине 40 м, если анализ показал содержание азота 79%, кислорода 20% и углекислого газа 1%.
Решение. Абсолютное давление воздуха на поверхности Рсм -1 кгс/см2.
Рис. 10.2. Номограмма для определения парциального давления газа р г в зависимости от процентного содержания газа С и абсолютного давления газовой смеси Р СМ
Парциальное давление газов на поверхности по (10.11):
Приближенно эти же результаты можно получить и по номограмме рис. 10.2.
Остаточное давление газа в баллонах. Для получения газовых смесей способом перепуска (см. схему а рис. 8.15) часто необходимо знать остаточное давление газа (кислорода) в баллоне подачи газа (баллон К), которое равно
где po.r -остаточное абсолютное давление газа (кислорода) в баллоне подачи, кгс/см2; Рсм – абсолютное давление газовой смеси в смесительном баллоне, кгс/см2; С – содержание газа (кислорода) в газовой смеси по объему, %.
Задача №28
Каким должно быть давление воздуха на дне скважины глубиной 8 км, если считать, что масса одного киломоля воздуха 29 кг, температура по всей высоте постоянна и равна 27 °C, а давление воздуха у поверхности Земли равно 1 атм.
Дано:
Найти:
Решение:
Определим потенциальную энергию молекулы воздуха, находящегося на дне скважины, относительно поверхности Земли
где 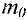
Из основного уравнения молекулярно — кинетической теории
следует, что давление газа при постоянной температуре прямо пропорционально концентрации его молекул. Распределение молекул в поле сил тяжести (распределение Больцмана) имеет вид
где 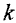
С учетом (10.3), из (10.2) получаем, что давление газа на глубине 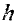
Ответ.
Эта задача взята со страницы задач по физике с решением:
Решение задач по физике
Возможно эти задачи вам будут полезны: