Как найти дебаевскую температуру

2018-07-04   

Вычислить дебаевскую температуру для железа, у которого скорости распространения продольных и поперечных колебаний равны соответственно 5,85 и 3,23 км/с.

Решение:

Мы действуем так же, как и в задаче 8635. Общее число мод должно быть $3 n_{0}v$ (общее поперечное и одно продольное на атом). С другой стороны, число поперечных мод на единицу частотного интервала дается выражением

$dN^{ perp} = frac{V omega^{2} }{ pi^{2} v_{ perp}^{3} } d omega$

а число продольных мод не имеет единичной частоты в интервале,

$dN^{ parallel} = frac{V omega^{2} }{2 pi^{2} v_{ parallel}^{3} } d omega$

Общее число на единицу частотного интервала равно

$dN = frac{V omega^{2} }{2 pi^{2} } left ( frac{2}{v_{ perp}^{3} } + frac{1}{v_{ parallel}^{3} } right ) d omega$

Если отрезок высокой частоты находится в точке $omega_{0} = frac{k Theta}{ hbar}$, общее число мод будет

$3n_{0} V = frac{V}{6 pi^{2} } left ( frac{2}{v_{ perp}^{3} } + frac{1}{v_{ parallel}^{3} } right ) left ( frac{k Theta}{ hbar} right )^{3}$

Здесь $n_{0}$ — число атомов железа на единицу объема. Таким образом

$Theta = frac{ hbar}{k} sqrt[3]{ frac{18 pi^{2} n_{0} }{ frac{2}{v_{ perp}^{3}} + frac{1}{v_{ parallel}^{3} } } }$

Для железа

$n_{0} = frac{N_{A} }{ frac{M}{ rho} } = frac{ rho N_{A} }{M}$

($rho$ — плотность, $M$ — атомный вес железа $N_{A}$ — число Авогадро).

$n_{0} = 8,389 cdot 10^{22} $за куб.см

Подставляя полученные данные

$Theta = 469,1 К$

In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat (Heat capacity) in a solid.^[1] It treats the vibrations of the atomic lattice (heat) as phonons in a box, in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to – the Debye T ³ law. Similarly to the Einstein photoelectron model, it recovers the Dulong–Petit law at high temperatures. Due to simplifying assumptions, its accuracy suffers at intermediate temperatures.

Derivation[edit]

The Debye model is a solid-state equivalent of Planck’s law of black body radiation, where one treats electromagnetic radiation as a photon gas. The Debye model treats atomic vibrations as phonons in a box (the box being the solid). Most of the calculation steps are identical as both are examples of a massless Bose gas with linear dispersion relation.

Consider a cube of side . From the particle in a box article, the resonating modes of the sonic disturbances inside the box (considering for now only those aligned with one axis) have wavelengths given by

where is an integer. The energy of a phonon is

where is the Planck constant and is the frequency of the phonon. Making the approximation that the frequency is inversely proportional to the wavelength, we have

in which is the speed of sound inside the solid. In three dimensions we will use

in which is the magnitude of the three-dimensional momentum of the phonon.

The approximation that the frequency is inversely proportional to the wavelength (giving a constant speed of sound) is good for low-energy phonons but not for high-energy phonons (see the article on phonons). This disagreement is one of the limitations of the Debye model. It produces incorrect results at intermediate temperatures, whereas the results are exact at the low and high temperatures limits.

Let’s now compute the total energy in the box,

where is the number of phonons in the box with energy . In other words, the total energy is equal to the sum of energy multiplied by the number of phonons with that energy (in one dimension). In 3 dimensions we have:

Here, the Debye model and Planck’s law of black body radiation differ. Unlike electromagnetic photon radiation in a box, there is a finite number of phonon energy states because a phonon cannot have arbitrarily high frequencies. Its frequency is bounded by the medium of its propagation—the atomic lattice of the solid. Consider an illustration of a transverse phonon below.

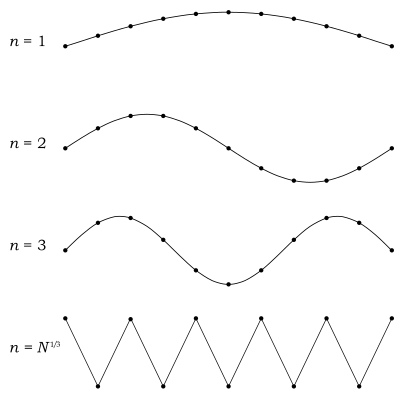
It is reasonable to assume that the minimum wavelength of a phonon is twice the atom separation, as shown in the lower figure. There are atoms in a solid. Our solid is a cube, which means there are atoms per edge. Atom separation is then given by , and the minimum wavelength is

making the maximum mode number (infinite for photons)

This number bounds the upper limit of the triple energy sum

For slowly varying, well-behaved functions, a sum can be replaced with an integral (also known as Thomas–Fermi approximation)

So far, there has been no mention of , the number of phonons with energy Phonons obey Bose–Einstein statistics. Their distribution is given by the famous Bose–Einstein statistics formula

Because a phonon has three possible polarization states (one longitudinal, and two transverse which approximately do not affect its
energy) the formula above must be multiplied by 3,

Actually one uses an effective sonic velocity , i.e. the Debye temperature (see below) is proportional to , more precisely , where one distinguishes longitudinal and transversal sound-wave velocities (contributions 1/3 and 2/3, respectively). The Debye temperature or the effective sonic velocity is a measure of the hardness of the crystal.

Substituting into the energy integral yields

The ease with which these integrals are evaluated for photons is due to the fact that light’s frequency, at least semi-classically, is unbound. As the figure above illustrates, this is not true for phonons. In order to approximate this triple integral, Debye used spherical coordinates.

and approximated the cube by an eighth of a sphere

where is the radius of this sphere, which is found by conserving the number of particles in the cube and in the eighth of a sphere. The volume of the cube is unit-cell volumes,

so we get

The substitution of integration over a sphere for the correct integral introduces another source of inaccuracy into the model.

The energy integral becomes

.

Changing the integration variable to ,

To simplify the appearance
of this expression, define the Debye temperature

where is the volume of the cubic box of side .

Many references^[2][3] describe the Debye temperature as merely shorthand for some constants and material-dependent variables. However, as shown below, is roughly equal to the phonon energy of the minimum wavelength mode, and so we can interpret the Debye temperature as the temperature at which the highest-frequency mode (and hence every mode) is excited.

Continuing, we then have the specific internal energy:

where is the (third) Debye function.

Differentiating with respect to we get the dimensionless heat capacity:

These formulae treat the Debye model at all temperatures. The more elementary formulae given further down give the asymptotic behavior in the limit of low and high temperatures. As already mentioned, this behavior is exact, in contrast to the intermediate behavior. The essential reason for the exactness at low and high energies, respectively, is that the Debye model gives (i) the exact dispersion relation at low frequencies, and (ii) corresponds to the exact density of states , concerning the number of vibrations per frequency interval.

Debye’s derivation[edit]

Debye derived his equation somewhat differently and more simply. Using continuum mechanics, he found that the number of vibrational states with a frequency less than a particular value was asymptotic to

in which is the volume and is a factor which he calculated from elasticity coefficients and density. Combining this formula with the expected energy of a harmonic oscillator at temperature T (already used by Einstein in his model) would give an energy of

if the vibrational frequencies continued to infinity. This form gives the behaviour which is correct at low temperatures. But Debye realized that there could not be more than vibrational states for N atoms. He made the assumption that in an atomic solid, the spectrum of frequencies of the vibrational states would continue to follow the above rule, up to a maximum frequency chosen so that the total number of states is

Debye knew that this assumption was not really correct (the higher frequencies are more closely spaced than assumed), but it guarantees the proper behaviour at high temperature (the Dulong–Petit law). The energy is then given by

Substituting for ,

where is the function later given the name of third-order Debye function.

Another derivation[edit]

First we derive the vibrational frequency distribution; the following derivation is based on Appendix VI from.^[4] Consider a three-dimensional isotropic elastic solid with N atoms in the shape of a rectangular parallelepiped with side-lengths . The elastic wave will obey the wave equation and will be plane waves; consider the wave vector and define . Note that we have

(1)

Solutions to the wave equation are

and with the boundary conditions at , we have

(2)

where are positive integers. Substituting (2) into (1) and also using the dispersion relation , we have

The above equation, for fixed frequency , describes an eighth of an ellipse in «mode space» (an eighth because are positive). The number of modes with frequency less than is thus the number of integral points inside the ellipse, which, in the limit of (i.e. for a very large parallelepiped) can be approximated to the volume of the ellipse. Hence, the number of modes with frequency in the range is

(3)

where is the volume of the parallelepiped. Note that the wave speed in the longitudinal direction is different from the transverse direction and that the waves can be polarised one way in the longitudinal direction and two ways in the transverse direction; thus we define .

Following the derivation from,^[5] we define an upper limit to the frequency of vibration ; since there are N atoms in the solid, there are 3N quantum harmonic oscillators (3 for each x-, y-, z- direction) oscillating over the range of frequencies . Hence we can determine using

.

(4)

By defining , where k is the Boltzmann constant and h is the Planck constant, and substituting (4) into (3), we get

(5)

this definition is more standard. We can find the energy contribution for all oscillators oscillating at frequency . Quantum harmonic oscillators can have energies where and using Maxwell-Boltzmann statistics, the number of particles with energy is

The energy contribution for oscillators with frequency is then

.

(6)

By noting that (because there are modes oscillating with frequency ), we have

From above, we can get an expression for 1/A; substituting it into (6), we have

Integrating with respect to ν yields

Low-temperature limit[edit]

The temperature of a Debye solid is said to be low if , leading to

This definite integral can be evaluated exactly:

In the low-temperature limit, the limitations of the Debye model mentioned above do not apply, and it gives a correct relationship between (phononic) heat capacity, temperature, the elastic coefficients, and the volume per atom (the latter quantities being contained in the Debye temperature).

High-temperature limit[edit]

The temperature of a Debye solid is said to be high if . Using if leads to

where

This is the Dulong–Petit law, and is fairly accurate although it does not take into account anharmonicity, which causes the heat capacity to rise further. The total heat capacity of the solid, if it is a conductor or semiconductor, may also contain a non-negligible contribution from the electrons.

Debye versus Einstein[edit]

The Debye and Einstein models correspond closely to experimental data, but the Debye model is correct at low temperatures whereas the Einstein model is not. To visualize the difference between the models, one would naturally plot the two on the same set of axes, but this is not immediately possible as both the Einstein model and the Debye model provide a functional form for the heat capacity. As models, they require scales to relate them to their real-world counterparts. One can see that the scale of the Einstein model is given by :

The scale of the Debye model is , the Debye temperature. Both are usually found by fitting the models to the experimental data. (The Debye temperature can theoretically be calculated from the speed of sound and crystal dimensions.) Because the two methods approach the problem from different directions and different geometries, Einstein and Debye scales are not the same, that is to say

which means that plotting them on the same set of axes makes no sense. They are two models of the same thing, but of different scales. If one defines the Einstein condensation temperature as

then one can say

and, to relate the two, we must seek the ratio

The Einstein solid is composed of single-frequency quantum harmonic oscillators, . That frequency, if it indeed existed, would be related to the speed of sound in the solid. If one imagines the propagation of sound as a sequence of atoms hitting one another, then it becomes obvious that the frequency of oscillation must correspond to the minimum wavelength sustainable by the atomic lattice, , where

,

which makes the Einstein temperature

and the sought ratio is therefore

Using the ratio, both models can be plotted on the same graph. This ratio is the cube root of the ratio of the volume of one octant of a 3-dimensional sphere to the volume of the cube that contains it, which is just the correction factor used by Debye when approximating the energy integral above. Alternatively, the ratio of the two temperatures can be seen to be the ratio of Einstein’s single frequency at which all oscillators oscillate and Debye’s maximum frequency. Einstein’s single frequency can then be seen to be a mean of the frequencies available to the Debye model.

Debye temperature table[edit]

Even though the Debye model is not completely correct, it gives a good approximation for the low temperature heat capacity of insulating, crystalline solids where other contributions (such as highly mobile conduction electrons) are negligible. For metals, the electron contribution to the heat is proportional to , which at low temperatures dominates the Debye result for lattice vibrations. In this case, the Debye model can only be said to approximate the lattice contribution to the specific heat. The following table lists Debye temperatures for several pure elements^[2] and sapphire:

The Debye model’s fit to experimental data is often phenomenologically improved by allowing the Debye temperature to become temperature dependent;^[6] for example, the value for water ice increases from about 222 K^[7] to 300 K^[8] as the temperature goes from absolute zero to about 100 K.

Extension to other quasi-particles[edit]

For other bosonic quasi-particles, e.g., for magnons (quantized spin waves) in ferromagnets instead of the phonons (quantized sound waves) one can derive analogous results. In this case at low frequencies one has different dispersion relations of momentum and energy, e.g., in the case of magnons, instead of for phonons (with ). One also has different density of states (e.g., ). As a consequence, in ferromagnets one gets a magnon contribution to the heat capacity, , which dominates at sufficiently low temperatures the phonon contribution, . In metals, in contrast, the main low-temperature contribution to the heat capacity, , comes from the electrons. It is fermionic, and is calculated by different methods going back to Sommerfeld’s free electron model.

Extension to liquids[edit]

It was long thought that phonon theory is not able to explain the heat capacity of liquids, since liquids only sustain longitudinal, but not transverse phonons, which in solids are responsible for 2/3 of the heat capacity. However, Brillouin scattering experiments with neutrons and with X-rays, confirming an intuition of Yakov Frenkel,^[9] have shown that transverse phonons do exist in liquids, albeit restricted to frequencies above a threshold called the Frenkel frequency. Since most energy is contained in these high-frequency modes, a simple modification of the Debye model is sufficient to yield a good approximation to experimental heat capacities of simple liquids.^[10]

Debye frequency[edit]

The Debye frequency (Symbol: or ) is a parameter in the Debye model. It refers to a cut-off angular frequency for waves of a harmonic chain of masses, used to describe the movement of ions in a crystal lattice and more specifically, to correctly predict the heat capacity in such crystals to be constant for high temperatures (Dulong–Petit law). The term was first introduced by Peter Debye in 1912.^[11]

Throughout this whole article periodic boundary conditions are assumed.

Definition[edit]

Assuming the dispersion relation is

with the speed of sound in the crystal; and k the wave vector, the value of the Debye frequency is as follows:

For a one dimensional monatomic chain the Debye frequency is equal to^[12]

with the distance between two neighbouring atoms in the chain when the system is in its ground state of energy (in this case that means that none of the atoms are moving with respect to each other); the total number of atoms in the chain; and the size (volume) of the system (length of the chain); and is the linear number density. Where the following relation holds: .

For a two dimensional monatomic square lattice the Debye frequency is equal to

where and are the same as before; is the size (area) of the surface; and the surface number density.

For a three dimensional monatomic primitive cubic crystal, the Debye frequency is equal to^[13]

where and are the same as before; the size of the system; and the volume number density.

The speed of sound in the crystal could depend on (among others) the mass of the atoms, the strength of their interaction, the pressure on the system, and/or the polarization of the spin wave (longitudinal or transverse), but in the following we will first assume the speed of sound to be the same for any polarization (this assumption however does not render far-reaching implications).^[14]

The assumed dispersion relation is easily proven wrong for a one-dimensional chain of masses, but in Debye’s model this did not prove to be problematic.

Relation to Debye’s temperature[edit]

The Debye temperature , another parameter in Debye model, is related to the Debye frequency by the relation

where is the reduced Planck constant and is the Boltzmann constant.

Debye’s derivation[edit]

Three dimensional crystal[edit]

In Debye’s derivation of the heat capacity he sums over all possible modes of the system. That is: including different directions and polarizations. He assumed the total number of modes per polarization to be (with the amount of masses in the system), or in mathematical language^[14]

where the on both sides is because of the three polarizations, so the sum runs over all modes for one specific polarization. Debye made this assumption because he knew from classical mechanics that the number of modes per polarization in a chain of masses should always be equal to the amount of masses in the chain.

The left hand side is now to be made explicit to show how it depends on the Debye frequency (here simply introduced as a cut-off frequency, that is: higher frequencies than the Debye frequency cannot exist), so that an expression for it could be found.

First of all, by assuming to be very large ( ≫ 1, with the size of the system in any of the three directions) the smallest wave vector in any direction could be approximated by: , with . Smaller wave vectors cannot exist because of the periodic boundary conditions. Thus the summation would become 4

where ; is the size of the system; and the integral is (as the summation) over all possible modes, which is assumed to be a finite region (bounded by the cut-off frequency).

The triple integral could be rewritten as a single integral over all possible values of the absolute value of (see: Jacobian for spherical coordinates). The result is

with the absolute value of the wave vector corresponding with the Debye frequency, so .

Since we know the dispersion relation to be , this can be written as an integral over all possible

After solving the integral it is again equated to to find

Conclusion:

One dimensional chain in 3D space[edit]

The same derivation could be done for a one dimensional chain of atoms. The number of modes remains unchanged, because there are still three polarizations. So

The rest of the derivation is analogous to the previous, so again the left hand side is rewritten;

In the last step the multiplication by two is because the integrand in the first integral is even and the bounds of integration are symmetric about the origin, so the integral can be rewritten as from 0 to after scaling by a factor of 2. Applying a change a substitution of , our bounds are now 0 to , which gives us our rightmost integral.
We continue;

Conclusion:

Two-dimensional crystal[edit]

The same derivation could be done for a two dimensional crystal. Again, the number of modes remains unchanged, because there are still three polarizations. The derivation is analogous to the previous two. We start with the same equation,

And then the left hand side is rewritten and equated to

where is the size of the system.

Conclusion

Allowing polarization to make a difference[edit]

As mentioned in the introduction: in general, longitudinal waves have a different wave velocity than transverse waves. For clarity they were first assumed to be equal, but now we drop that assumption.

The dispersion relation becomes , where , which correspond to the three polarizations. The cut-off frequency (Debye frequency) however does not depend on . And we can write the total number of modes as , which is again equal to . Here the summation over the modes is (although not explicitly stated) dependent on .

One dimension[edit]

Once again the summation over the modes is rewritten

The result is

Thus the Debye frequency is found

Or by assuming the two transverse polarizations to be the same (to have the same phase speed and frequency)

One can check this relation is equivalent to the one found earlier (when polarization did not make a difference) by setting .

Two dimensions[edit]

The same derivation can be done for a two dimensional crystal to find (the derivation is analogous to previous derivations)

Or by assuming the two transverse polarizations are equal (although for two dimensions it would be more logical if all polarizations would be different):

Again, one can check this relation is equivalent to the one found earlier by setting .

Three dimensions[edit]

The same derivation can be done for a three dimensional crystal to find (the derivation is analogous to previous derivations)

Or by assuming the two transverse polarizations are equal (although for three dimensions it would be more logical when all polarizations would be the same):

Again, one can check this relation is equivalent to the one found earlier by setting .

Derivation with the actual dispersion relation[edit]

This problem could be made more insightful by making it more complex. Instead of using the dispersion relation , the correct dispersion relation is now going to be assumed. From classical mechanics it is known that for an equidistant chain of masses which interact harmonically with each other the dispersion relation reads as follows^[14]

After plotting this relation, it is clear that Debye’s estimation of the cut-off wavelength was right after all. Because for every wavenumber bigger than (that is: is smaller than ) a wavenumber that is smaller than could be found with the same angular frequency. This means the resulting physical manifestation for the mode with the larger wavenumber is indistinguishable from the one with the smaller wavenumber. Thereby, the study of the dispersion relation can be limited to the first brillouin zone^[15] i.e. for .This is possible because the system consists of discretized points, as is demonstrated in the animated picture. Dividing the dispersion relation by and inserting for , we find the speed of a wave with to be

By simply inserting in the original dispersion relation we find

Combining these results the same result is once again found

However, for diatomic chains (and more complex chains) the associated cut-off frequency (and wavelength) is not very accurate, since the cut-off wavelength is twice as big and the dispersion relation consists of two branches (for a diatomic chain). It is also not certain from this whether for more dimensional systems the cut-off frequency was accurately predicted by Debye.

Alternative derivation[edit]

For a one dimensional chain this result could also be reproduced using theory on aliasing. The Nyquist–Shannon sampling theorem is used in the following derivation; the main difference being that in the following derivation the discretization is not in time, but in space. If we use the correct dispersion relation from last paragraph, it will be clear in another insightful way why the cut-off frequency has the value previously (twice) derived. So again,

is assumed.

This derivation is completely equivalent to the previous one, that is: the same assumptions are made to retrieve the result. It is not more or less accurate, it is just a different approach.

To determine where the cut-off frequency should be, it is useful to first determine where the cut-off of the wavelength should be. From the dispersion relation we know that for every mode is repeated, so the cut-off wavelength would be at . From this and the periodic boundary conditions you can immediately see that the total number of modes per polarization would be . As seen in the gif of the previous paragraph this is because every wave with a wavelength shorter than could be replaced by a wave with a wavelength longer than to regain the same physical result.

However, the dispersion relation from previous paragraph (the correct one) is not even necessary in reasoning as to why the cut-off should be at . Because, as is depicted, only waves with a longer wavelength than could render the same physical result as another one. So this is another way to correctly predict the cut-off wavelength of phonons without using the correct dispersion relation (or even knowledge from classical mechanics as Debye did). However, using the wrong dispersion relation which Debye assumed, waves with a smaller wavelength would have a higher frequency, but the relative movement of the masses would be the same, so this does not render new modes.

This results again in , rendering

Also here it does not matter which dispersion relation is used (the correct one or the one Debye used), the same cut-off frequency would be found.

Unfortunately, the same method could not be used (as easily) for a two- or three-dimensional crystal, because diagonal waves would have a larger cut-off wavelength, which are also difficult to predict.

See also[edit]

• Bose gas
• Gas in a box
• Grüneisen parameter

References[edit]

Further reading[edit]

• CRC Handbook of Chemistry and Physics, 56th Edition (1975–1976)
• Schroeder, Daniel V. An Introduction to Thermal Physics. Addison-Wesley, San Francisco (2000). Section 7.5.

External links[edit]

• Experimental determination of specific heat, thermal and heat conductivity of quartz using a cryostat.
• Simon, Steven H. (2014) The Oxford Solid State Basics (most relevant ones: 1, 2 and 6)

Температура Дебая — температура, при которой возбуждаются все моды колебаний в данном твёрдом теле. Дальнейшее увеличение температуры не приводит к появлению новых мод колебаний, а лишь ведёт к увеличению амплитуд уже существующих, то есть средняя энергия колебаний с ростом температуры растёт.

Температура Дебая — физическая константа вещества, характеризующая многие свойства твёрдых тел — теплоёмкость, электропроводность, теплопроводность, уширение линий рентгеновских спектров, упругие свойства и т. п. Введена впервые П. Дебаем в его теории теплоёмкости.

Температура Дебая определяется следующей формулой:

где — постоянная Планка, — максимальная частота колебаний атомов твёрдого тела, — постоянная Больцмана.

Температура Дебая приближённо указывает температурную границу, ниже которой начинают сказываться квантовые эффекты.

Физическая интерпретация

При температурах ниже температуры Дебая теплоёмкость кристаллической решётки определяется в основном акустическими колебаниями и, согласно закону Дебая, пропорциональна кубу температуры.

При температурах намного выше температуры Дебая справедлив закон Дюлонга-Пти, согласно которому теплоёмкость постоянна и равна , где количество элементарных ячеек в теле,  — количество атомов в элементарной ячейке,  — постоянная Больцмана.

При промежуточных температурах теплоёмкость кристаллической решётки зависит от других факторов, таких как дисперсия акустических и оптических фононов, количества атомов в элементарной ячейке и т. д. Вклад акустических фононов, в частности, даётся формулой

,

где  — температура Дебая, а функция

называется функцией Дебая.

При температурах намного ниже температуры Дебая, как указывалось выше, теплоёмкость пропорциональна кубу температуры

.

Оценка температуры Дебая

При выводе формулы Дебая для определения теплоёмкости кристаллической решётки принимаются некоторые допущения, а именно принимают линейным закон дисперсии акустических фононов, пренебрегают наличием оптических фононов и заменяют зону Бриллюэна сферой такого же объёма. Если радиус такой сферы, то , где скорость звука, называется частотой Дебая. Температура Дебая определяется из соотношения

.

Значения температуры Дебая для некоторых веществ приведено в таблице.

См. также

• Модель Дебая
• Теплоёмкость твёрдого тела
• Теплоёмкость электронного газа

Примечания

Источники

• Большая советская энциклопедия

Метод в физике Питер Дебай

В термодинамике и физике твердого тела, модель Дебая — это метод, используйте Питером Дебаем в 1912 году для оценки вклада фононов в удельную теплоемкость (тепло емкость) в твердом теле. Он рассматривает колебания атомной решетки (тепло) как фононы в коробке, в отличие от модели Эйнштейна, которая рассматривает твердое тело как множество отдельных невзаимодействующих квантовых гармонических осцилляторов. Модель Дебая правильно предсказывает низкотемпературную зависимость теплоемкости, которая пропорциональна T 3 { displaystyle T ^ {3}}— закон Дебая T . Как и модель Эйнштейна, она также восстанавливает закон Дюлонга — Пети при высоких температурах. Его точность страдает при промежуточных температурах.

Содержание

• 1 Вывод
• 2 Вывод Дебая
• 3 Другой вывод
• 4 Предел низкой температуры
• 5 Предел высокой температуры
• 6 Дебая в сравнении с Эйнштейном
• 7 Таблица температур Дебая
• 8 Расширение на другие квазичастицы
• 9 Расширение на жидкости
• 10 Частота Дебая
  • 10.1 Определение
  • 10.2 Связь с температурой Дебая
  • 10.3 Вывод Дебая
    • 10.3.1 Трехмерный кристалл
    • 10.3.2 Одномерная цепочка в трехмерном пространстве
    • 10.3.3 Двумерный кристалл
  • 10.4.1 Возможность поляризации иметь значение
    • 10.4.1 Одно измерение
    • 10.4.2 Два измерения
    • 10.4.3 Три измерения
  • 10.5 Вывод с фактическим использованием дисперсии
  • 10.6 Альтернативный вывод
• 11 См. Также
• 12 Ссылки
• 13 Дополнительная литература
• 14 Внешние ссылки

Вывод

Модель Дебая является твердотельным эквивалентом закона излучения черного тела Планка, где электромагнитное излучение рассматривается как фотонный газ. Модель Дебая рассматривает атомные колебания как фононы в прямоугольнике (прямоугольник — твердое тело). Этапов идентичности, поскольку оба являются примерами безмассового бозе-газа с линейным распределением дисперсии.

Рассмотрим куб со стороной L { displaystyle L}. Из частиц в цилиндрах из ящика, которые имеют резонирующие частицы, которые выровнены по одной оси, имеют длину волн, равные

λ n = 2 L n, { displaystyle lambda _ {n} = {2L over n} ,,}

где n { displaystyle n}— целое число. Энергия фонона равна

E n = h ν n, { displaystyle E_ {n} = h nu _ {n} ,,}

где h { displaystyle h}— постоянная Планка, и ν n { displaystyle nu _ {n}}— частота фонона. Делая приближение, что частота обратно пропорциональна длине волны, мы имеем:

E n = h ν n = hcs λ n = hcsn 2 L, { displaystyle E_ {n} = h nu _ {n} = {hc _ { rm {s}} over lambda _ {n}} = {hc_ {s} n over 2L} ,,}

в котором cs { displaystyle c_ {s}}— скорость звука внутри твердого тела. В трех измерениях мы будем использовать:

E n 2 = pn 2 cs 2 = (hcs 2 L) 2 (nx 2 + ny 2 + nz 2), { displaystyle E_ {n} ^ {2} = {p_ {n} ^ {2} c _ { rm {s}} ^ {2}} = left ({hc _ { rm {s}} over 2L} right) ^ {2} left (n_ {x} ^ {2} + n_ {y} ^ {2} + n_ {z} ^ {2} right) ,,}

где pn { displaystyle p_ {n}}— величина трехмерного импульса фонона.

Приближение, согласно которой частота обратно пропорциональна длине волны (что дает постоянную скорость звука), подходит для фононов низкой энергии, но не для фононов высокой энергии (см. Статью о фононах.) несогласие является одним из ограничений модели Дебая и соответствует некорректности результатов при промежуточных температурах, тогда как при низких, так и при высоких температурах они точны.

Давайте теперь вычислим полную мощность в коробке,

E = ∑ n E n N ¯ (E n), { displaystyle E = sum _ {n} E_ {n} , { bar {N}} (E_ {n}) ,,}

где N ¯ (E n) { displaystyle { bar {N}} (E_ {n})}— количество фононов в коробке с энергией E n { displaystyle E_ {n}}. Другими словами, полная энергия равна сумме энергии, умноженной на фононов с этой энергией (в одном измерении). В трех измерениях мы имеем:

U = ∑ n x ∑ n y ∑ n z E n N ¯ (E n). { displaystyle U = sum _ {n_ {x}} sum _ {n_ {y}} sum _ {n_ {z}} E_ {n} , { bar {N}} (E_ {n}) ,.}

Здесь модель Дебая и закон Планка излучения черного тела различаются. В отличие от электромагнитного числа излучения в коробке существует конечное энергетическое состояние фонона, потому что фонон не может иметь произвольно высокие частоты. Его частота ограничена средой его распространения — атомной решеткой твердого тела. Рассмотрим иллюстрацию поперечного фонона ниже.

Разумно предположить, что минимальная длина волны фонона в два раза больше расстояния между атомами, как показано на нижнем рисунке. В твердом теле N { displaystyle N}элементы. Наше твердое тело представляет собой куб, а это означает, что на ребро приходится N 3 { displaystyle { sqrt [{3}] {N}}}элементов. Разделение элементов тогда дается выражением L / N 3 { displaystyle L / { sqrt [{3}] {N}}}, а минимальная длина волны составляет

λ min = 2 LN 3, { displaystyle lambda _ { rm {min}} = {2L over { sqrt [{3}] {N}}} ,,}

, что делает максимальное число режима n { displaystyle n}(бесконечно для фотонов )

nmax = N 3. { displaystyle n _ { rm {max}} = { sqrt [{3}] {N} } ,.}

Это число ограничивает верхний предел тройной суммы энергии

U = ∑ nx N 3 ∑ ny N 3 ∑ nz N 3 E n N ¯ (E n). { Displaystyle U = amount _ {n_ {x}} ^ { sqrt [{3}] {N}} sum _ {n_ {y}} ^ { sqrt [{3}] {N}} sum _ {n_ {z}} ^ { sqrt [{3}] {N}} E_ {n} , { bar {N}} (E_ {n}) ,.}

Для медленно изменяющихся функций с хорошим поведением, сумму можно заменить интегралом (также известное как приближение Томаса — Ферми )

U ≈ ∫ 0 N 3 ∫ 0 N 3 ∫ 0 N 3 E (n) N ¯ (E (n)) dnxdnydnz. { Displaystyle U приблизительно int _ {0} ^ { sqrt [{3}] {N}} в t _ {0} ^ { sqrt [{3}] {N}} int _ {0} ^ { sqrt [{3}] {N}} E (n) , { bar {N}} left (E (n) right) , dn_ {x} , dn_ {y} , dn_ {z} ,.}

До сих пор не упоминалось N ¯ (E) { displaystyle { bar {N}} (E)}, число фононов с энергией E. { displaystyle E ,.}Фононы подчиняются статистике Бозе — Эйнштейна. Их определение дается известной формулой Бозе — Эйнштейна

N⟩ BE = 1 e E / k T — 1. { displaystyle langle N rangle _ {BE} = {1 over e ^ {E / kT} -1 } ,.}

3D фонон имеет три состояния поляризации (одно продольное, и два поперечного, которые приблизительно влияют на его энергию) формулу выше необходимо умножить на 3,

N ¯ (E) = 3 e E / k T — 1. { displaystyle { bar {N}} (E) = {3 over e ^ {E / kT} -1} ,.}

(На самом деле используется эффективная скорость звука cs: = ceff { displaystyle c_ {s}: = c _ { rm {eff}}}, т.е. температура Дебая TD { displaystyle T _ { rm {D}}}(см.) Пропорционально ceff { displaystyle c _ { rm {eff}}}, точнее TD — 3 ∝ ceff — 3: = (1/3) clong — 3 + (2/3) ctrans — 3 { displaystyle T _ { rm {D}} ^ {- 3} propto c _ { rm {eff}} ^ {- 3}: = (1/3) c _ { rm {long}} ^ {- 3} + (2/3) c _ { rm {trans }} ^ {- 3}}, где разли чают продольные и поперечные скорости звуковых волн (вклад 1/3 и 2/3 соответственно. Температура Дебая или эффективная скорость звука являются мерой твердости кристалла.)

Подстановка в интеграл энергии дает

U = ∫ 0 N 3 ∫ 0 N 3 ∫ 0 N 3 E (n) 3 e E (n) / к Т — 1 днхдныднз. { Displaystyle U = int _ {0} ^ { sqrt [{3}] {N}} int _ {0} ^ { sqrt [{3}] {N}} int _ {0} ^ { sqrt [{3}] {N}} E (n) , {3 over e ^ {E (n) / kT} -1} , dn_ {x} , dn_ {y} , dn_ {z} ,.}

Легкость, с которой эти интегралы вычисляются для фотонов, обусловлена ​​тем фактом, что частота света, по крайней мере, полуклассически, не связана. Как показано на рисунке выше, это неверно для фононов. Чтобы аппроксимировать этот тройной интеграл, Дебай использовал сферические координаты

(nx, ny, nz) = (n sin ⁡ θ cos ⁡ ϕ, n sin ⁡ θ sin ⁡ ϕ, n cos ⁡ θ) { displaystyle (n_ {x}, n_ {y}, n_ {z}) = (n sin theta cos phi, n sin theta sin phi, n cos theta)}

и аппроксимировали куб восьмой части сферы

U ≈ ∫ 0 π / 2 ∫ 0 π / 2 ∫ 0 RE (n) 3 e E (n) / k T — 1 n 2 sin ⁡ θ dnd θ d ϕ, { Displaystyle U приблизительно int _ {0} ^ { pi / 2} int _ {0} ^ { pi / 2} int _ {0} ^ {R} E (п) , {3 над e ^ {E (n) / kT} -1} n ^ {2} sin theta , dn , d theta , d phi ,,}

где R { displaystyle R}— радиус этой сферы, который находится в пределах численности в кубе и в восьмой части сферы. Объем куба равен N { displaystyle N}объем элементарной ячейки,

N = 1 8 4 3 π R 3, { displaystyle N = {1 over 8} {4 over 3} pi R ^ {3} ,,}

, поэтому получаем:

R = 6 N π 3. { displaystyle R = { sqrt [{3}] {6N over pi} } ,.}

Замена правильного интеграла интегрированием по сфере вносит еще один источник неточности в модель.

Интеграл энергии принимает вид

U = 3 π 2 ∫ 0 R hcsn 2 L n 2 ehcsn / 2 L k T — 1 dn { displaystyle U = {3 pi over 2} int _ {0} ^ {R} , {hc_ {s} n over 2L} {n ^ {2} over e ^ {hc _ { rm {s}} n / 2LkT} -1} , dn }

Изменение модели интегрирования на x = hcsn 2 L k T { displaystyle x = {hc _ { rm {s}} n over 2LkT}},

U = 3 π 2 k T ( 2 L K T hcs) 3 ∫ 0 hcs R / 2 L K T x 3 ex — 1 dx { displaystyle U = {3 pi over 2} kT left ({2LkT over hc _ { rm {s }})} right) ^ {3} int _ {0} ^ {hc _ { rm {s}} R / 2LkT} {x ^ {3} over e ^ {x} -1} , dx}

Чтобы упростить внешний вид этого выражения, определите температуру Дебая TD { displaystyle T _ { rm {D}}}

TD = defhcs R 2 L k = hcs 2 L К 6 N π 3 знак равно hcs 2 К 6 π NV 3 { displaystyle T _ { rm {D}} { stackrel { mathrm {def}} {=}} {hc _ { rm {s}} R более 2Lk} = {hc _ { rm {s}} over 2Lk} { sqrt [{3}] {6N over pi}} = {hc _ { rm {s} } более 2k} { sqr t [{3}] {{6 over pi} {N over V}}}}

Где V { displaystyle V}— объемная кубическая рамка стороны L { displaystyle L}.

Во многих источников температуры Дебая описывается как сокращение для некоторых констант и число, зависящих от материала. Однако, как показано ниже, k TD { displaystyle kT _ { rm {D}}}примерно равно энергии фононов моды с минимальной длиной волны, и поэтому мы можем интерпретировать температуру Дебая как температура, при которой возбуждается самая высокочастотная мода (и, следовательно, каждая мода).

Продолжая, мы получаем удельную внутреннюю энергию:

UN k = 9 T (TTD) 3 ∫ 0 TD / T x 3 ex — 1 dx = 3 TD 3 (TDT), { displaystyle { frac {U} {Nk}} = 9T left ({T over T _ { rm {D}}} right) ^ {3} int _ {0} ^ {T _ { rm {D} } / T} {x ^ {3} over e ^ {x} -1} , dx = 3TD_ {3} left ({T _ { rm {D}} over T} right) ,,}

где D 3 (x) { displaystyle D_ {3} (x)}— это (третья) функция Дебая.

, дифференцирующая по T { displaystyle T}получаем безразмерную теплоемкость:

CVN k = 9 (TTD) 3 ∫ 0 TD / T x 4 ex (ex — 1) 2 dx. { displaystyle { frac {C_ {V}} {Nk}} = 9 left ({T over T _ { rm {D}}} right) ^ {3} int _ {0} ^ { T_ { rm {D}} / T} {x ^ {4} e ^ {x} over left (e ^ {x} -1 right) ^ {2}} , dx ,.}

Эти формулы относ к модели Дебая при всех температурах. Более элементарные формулы, приведенные ниже, дают асимптотику в пределе низких и высоких температур. Как уже указано, это поведение точное, в отличие от промежуточного поведения. Основная причина точности при низких и высоких энергиях, соответственно, заключается в том, что модель Дебая дает (i) точное дисперсионное соотношение E (ν) { displaystyle E ( nu)}на низких частотах, и (ii) соответствует точной плотности состояния (∫ g (ν) d ν ≡ 3 N) { displaystyle ( int g ( nu) , { rm {d nu}} Equiv 3N) ,}, относительно количества колебаний на частотный интервал.

Вывод Дебая

Дебай вывел свое уравнение несколько иначе и проще. Используя механику сплошной среды, он обнаружил, что колебательных состояний с выбором меньше определенного количества было асимптотически

n ∼ 1 3 ν 3 VF, { displaystyle n sim {1 over 3} nu ^ {3} VF ,,}

, в котором V { displaystyle V}— объем, а F { displaystyle F}— коэффициент, который он рассчитал из коэффициентов эластичности и плотности. Комбинируя эту формулу с ожидаемой энергией гармонического осциллятора при температуре T (уже использованной Эйнштейном в его модели), мы получим энергию

U = ∫ 0 ∞ h ν 3 VF eh ν / k T — 1 d ν, { Displaystyle U = int _ {0} ^ { infty} , {h nu ^ {3} VF over e ^ {h nu / kT} -1} , d nu ,, }

, если частоты колебания продолжаются до бесконечности. Эта форма дает поведение T 3 { displaystyle T ^ {3}}, которое является правильным при низких температурах. Но Дебай понял, что для N атомов не может быть более 3 N { displaystyle 3N}колебательных состояний. Он предположение, что в атомном твердом спектре частот колебательных состояний будет следовать указанным выше правилам до максимальной частоты ν m { displaystyle nu _ {m}}выбрано так, чтобы общее число состояний было 3 N { displaystyle 3N}:

3 N = 1 3 ν m 3 VF. { displaystyle 3N = {1 over 3} nu _ {m} ^ {3} VF ,.}

Дебай знал, что это предположение было неверным (более высокие частоты расположены друг к другу, чем предполагалось), но он гарантирует правильное поведение при высоких температурах (закон Дюлонга — Пети ). Тогда энергия определяется следующим образом:

U = ∫ 0 ν mh ν 3 VF а ν / k T — 1 d ν, { displaystyle U = int _ {0} ^ { nu _ {m}} , {h nu ^ {3} VF over e ^ {h nu / kT} -1} , d nu ,,}

= VF k T (k T / h) 3 ∫ 0 TD / T x 3 ex — 1 dx, { displaystyle = VFkT (kT / h) ^ {3} int _ {0} ^ {T _ { rm {D}} / T} , {x ^ {3} над e ^ {x} -1} , dx ,,}

где TD { displaystyle T _ { rm {D}}}равно h ν m / к { displaystyle h nu _ {m} / k}.

= 9 N k T (T / TD) 3 ∫ 0 TD / T x 3 ex — 1 dx, { displaystyle = 9NkT (T / T_ { rm {D}}) ^ {3} int _ {0} ^ {T _ { rm {D}} / T} , {x ^ {3} over e ^ {x} -1 } , dx ,,}

= 3 N k TD 3 (TD / T), { displaystyle = 3NkTD_ {3} (T _ { rm {D}} / T) ,,}

где D 3 { displaystyle D_ {3}}— функция, позже получившая название третьего порядка функция Дебая.

Другой вывод

Сначала мы выводим колебательный Распределение частоты; следующий вывод основан на Приложении VI от. Рассмотрим трехмерное изотропное тело в форме прямоугольного параллелепипеда со стороны L x, L y, L z { displaystyle L_ {x}, L_ {y}, L_ {z}}. Упругая волна будет подчиняться волновому уравнению и будет плоскими волнами ; рассмотрим волновой вектор k = (kx, ky, kz) { displaystyle mathbf {k} = (k_ {x}, k_ {y}, k_ {z})}и определите lx = kx | k |, l y = k y | k |, l z = k z | k | { displaystyle l_ {x} = { frac {k_ {x}} {| mathbf {k} |}}, l_ {y} = { frac {k_ {y}} {| mathbf {k} | }}, l_ {z} = { frac {k_ {z}} {| mathbf {k} |}}}. Обратите внимание, что у нас есть

lx 2 + ly 2 + lz 2 = 1. { displaystyle l_ {x} ^ {2} + l_ {y} ^ {2} + l_ {z} ^ {2} = 1.}

(1)

Решения волнового уравнения :

u (x, y, z, t) = sin ⁡ (2 π ν t) sin ⁡ (2 π lxx λ) грех ⁡ (2 π lyy λ) грех ⁡ (2 π lzz λ) { displaystyle u (x, y, z, t) = sin (2 pi nu t) sin left ({ frac {2 pi l_ {x} x} { lambda}} right) sin left ({ frac {2 pi l_ {y} y} { lambda}} right) sin left ( { frac {2 pi l_ {z} z} { lambda}} right)}

и с граничными условиями u = 0 { displaystyle u = 0}при x, y, z = 0, x = L x, y = L y, z = L z { displaystyle x, y, z = 0, x = L_ {x}, y = L_ {y}, z = L_ {z}}, имеем

2 лк L x λ = nx; 2 l y L y λ = n y; 2 lz L z λ знак равно nz { displaystyle { frac {2l_ {x} L_ {x}} { lambda}} = n_ {x}; { frac {2l_ {y} L_ {y}} { lambda}} = n_ {y}; { frac {2l_ {z} L_ {z}} { lambda}} = n_ {z}}

(2)

где nx, ny, nz { displaystyle n_ {x}, n_ {y}, n_ {z}}— целые положительные числа. Подставляя (2) в (1), а также используя соотношение дисперсии cs = λ ν { displaystyle c_ {s} = lambda nu}, имеем

nx 2 (2 ν L x / cs) 2 + ny 2 (2 ν L y / cs) 2 + nz 2 (2 ν L z / cs) 2 = 1. { displaystyle { frac { n_ {x} ^ {2}} {(2 nu L_ {x} / c_ {s}) ^ {2}}} + { frac {n_ {y} ^ {2}} {(2 nu L_ {y} / c_ {s}) ^ {2}}} + { frac {n_ {z} ^ {2}} {(2 nu L_ {z} / c_ {s}) ^ {2}}} = 1.}

Вышеприведенное уравнение для фиксированной частоты ν { displaystyle nu}появление восьмой части эллипса в «визу мод» (восьмую, потому что nx, ny, nz { displaystyle n_ {x}, n_ {y}, n_ {z}}положительны). Таким образом, количество режимов с меньше ν { displaystyle nu}— это количество целых точек внутри эллипса, которое в пределах L x, L y, L z → ∞ { displaystyle L_ {x}, L_ {y}, L_ {z} to infty}(т.е. для очень большого параллелепипеда) может быть аппроксимировано объемом эллипса. Следовательно, количество способов N (ν) { displaystyle N ( nu)}с диапазоном в диапазоне [0, ν] { displaystyle [0, nu]}равно

N (ν) = 1 8 4 π 3 (2 ν cs) 3 L x L y L z = 4 π ν 3 V 3 CS 3, { displaystyle N ( nu) = { frac {1} {8}} { frac {4 pi} {3}} left ({ frac {2 nu} {c _ { mathrm {s}}}} right) ^ {3 } L_ {x} L_ {y} L_ {z} = { frac {4 pi nu ^ {3} V} {3c _ { mathrm {s}} ^ {3}}},}

(3)

где V = L x L y L z { displaystyle V = L_ {x} L_ {y} L_ {z}}— объем параллелепипеда. Обратите внимание, что скорость волны в продольном направлении отличается от поперечного направления, и что волна может быть поляризована в одной стороне в продольном направлении и двумя способами в поперечном направлении; таким образом, мы определяем 3 cs 3 = 1 c long 3 + 2 c trans 3 { displaystyle { frac {3} {c_ {s} ^ {3}}} = { frac {1} {c _ { text {long}} ^ {3}}} + { frac {2} {c _ { text {trans}} ^ {3}}}}.

Следуя производным от, мы определяем верхний предел частоты вибрации ν D { displaystyle nu _ {D}}; Поскольку в твердом теле N элементов имеется 3N квантовых гармонических осцилляторов (по 3 для каждого направления x, y, z), колеблющихся в диапазоне частот [0, ν D] { displaystyle [0, nu _ {D} ]}. Следовательно, мы можем определить ν D { displaystyle nu _ {D}}так:

3 N = N (ν D) = 4 π ν D 3 V 3 cs 3 { Displaystyle 3N = N ( nu _ { rm {D}}) = { frac {4 pi nu _ { rm {D}} ^ {3} V} {3c _ { rm {s} } ^ {3}}}}.

(4)

Определив ν D = k TD h { displaystyle nu _ { rm {D}} = { frac {kT _ { rm {D}}} {h}}}, где k — постоянная Больцмана, а h — постоянная Планка, и замена (4) на ( 3), получаем

N (ν) = 3 N час 3 ν 3 k 3 TD 3, { displaystyle N ( nu) = { frac {3Nh ^ {3} nu ^ {3}} {k ^ {3} T _ { rm {D}} ^ {3}}},}

(5)

это определение более стандартное. Мы можем найти вкладчики энергии для всех осцилляторов, колеблющихся начастоту ν { displaystyle nu}. Квантовые гармонические осцилляторы могут иметь энергию E i = (i + 1/2) h ν { displaystyle E_ {i} = (i + 1/2) h nu}где i = 0, 1, 2,… { displaystyle i = 0,1,2, dotsc}и используя статистику Максвелла-Больцмана, количество частиц с энергией E я { displaystyle E_ {i}}равно

ni = 1 A e — E i / (k T) = 1 A e — (i + 1/2) h ν / (к T) { displaystyle n_ {i} = { frac {1} {A}} e ^ {- E_ {i} / (kT)} = { frac {1} {A}} e ^ {- (i + 1/2) h nu / (kT)}}.

Вклад энергии для осцилляторов с выбором ν { displaystyle nu}тогда равенство

d U (ν) Знак равно ∑ я знак равно 0 ∞ E я 1 A е — E я / (К T) { Displaystyle dU ( nu) = sum _ {я = 0} ^ { infty} E_ {i} { frac {1 } {A}} e ^ {- E_ {i} / (kT)}}.

(6)

Отметил, что ∑ i = 0 ∞ ni = d N (ν) { displaystyle сумма _ {я = 0} ^ { infty} n_ {i} = dN ( nu)}(потому что есть d N (ν) { displaystyle dN ( nu)}моды, колеблющи е ся с указанием ν { displaystyle nu}), мы имеем

1 A e — 1/2 h ν / (k T) ∑ i = 0 ∞ e — ih ν / (К T) знак равно 1 A e — 1/2 час ν / (k T) 1 1 — e — h ν / (К T) знак равно d N (ν) { Displaystyle { frac {1} { A}} e ^ {- 1 / 2h nu / (kT)} sum _ {i = 0} ^ { infty} e ^ {- ih nu / (kT)} = { frac {1} { A}} e ^ {- 1 / 2h nu / (kT)} { frac {1} {1-e ^ {- h nu / (kT)}}} = dN ( nu)}

Из вышесказанного мы можем получить выражение для 1 / A; подставляя его в (6), получаем

d U = d N (ν) e 1/2 h ν / (k T) (1 — e — h ν / (k T)) ∑ i = 0 ∞ час ν (я + 1/2) е — час ν (я + 1/2) / (к T) = { displaystyle dU = dN ( nu) e ^ {1/2h nu / (kT)} ( 1-e ^ {- h nu / (kT)}) sum _ {i = 0} ^ { infty} h nu (i + 1/2) e ^ {- h nu (i + 1 / 2) / (kT)} =}

= d N (ν) (1 — e — h ν / (k T)) ∑ i = 0 ∞ h ν (i + 1/2) e — h ν i / (k T) = d N (ν) h ν (1 2 + (1 — e — h ν / (k T)) ∑ i = 0 ∞, т.е. — h ν i / (k T)) знак равно { Displaystyle = dN ( Nu) (1-е ^ {- ч nu / (kT)}) сумма _ {я = 0} ^ { infty} ч nu (я + 1/2) е ^ {- h nu i / (kT)} = dN ( nu) h nu left ({ frac {1} {2}} + (1-e ^ {- h nu / (kT) })) sum _ {i = 0} ^ { infty} ie ^ {- h nu i / (kT)} right) =}

d N (ν) h ν (1 2 + 1 eh ν / (к T) — 1) { displaystyle dN ( nu) h nu left ({ frac {1} {2}} + { frac {1} {e ^ {h nu / (kT)} — 1}} right)}

Интегрирование по ν дает

U = 9 N h 4 k 3 TD 3 ∫ 0 ν D (1 2 + 1 eh ν / (k T) — 1) ν 3 d ν { displaystyle U = { frac {9Nh ^ {4}} {k ^ {3} T _ { rm {D}} ^ {3}}} int _ {0} ^ { nu _ {D}} left ({ f rac {1} {2}} + { frac {1} {e ^ {h nu / (kT)} — 1}} right) nu ^ {3} d nu}

Нижний предел температуры

Температура твердого тела Дебая считается низкой, если T ≪ TD { displaystyle T ll T _ { rm {D}}}, что к

CVN k ∼ 9 (TTD) 3 ∫ 0 ∞ x 4 ex (ex — 1) 2 dx { displaystyle { frac {C_ {V}} {Nk}} sim 9 left ({T над T_ { rm {D}}} right) ^ {3} int _ {0} ^ { infty} {x ^ {4} e ^ {x} over left (e ^ {x} — 1 right) ^ {2}} , dx}

Этот определенный интеграл можно вычислить точно:

CVN k ∼ 12 π 4 5 (TTD) 3 { displaystyle { frac {C_ {V}} { Nk}} sim {12 pi ^ {4} over 5} left ({T over T _ { rm {D}}} right) ^ {3}}

В пределе низкой температуры ограничения упомянутой выше модели Дебая не применяются, и она дает правильное соотношение между (фононной) теплоемкостью, температурой, коэффициентами упругости ости и объем ом на атом (последние значения в температуре Дебая).

Предел высокой температуры

Температура твердого тела Дебая считается высокой, если T ≫ TD { displaystyle T gg T _ { rm {D}}}. Использование e x — 1 ≈ x { displaystyle e ^ {x} -1 приблизительно x}if | х | ≪ 1 { displaystyle | х | ll 1}приводит к

CVN k ∼ 9 (TTD) 3 ∫ 0 TD / T x 4 x 2 dx { displaystyle { frac {C_ {V}} {Nk}} sim 9 left ({T over T _ { rm {D}}} right) ^ {3} int _ {0} ^ {T _ { rm {D}} / T} {x ^ { 4} over x ^ {2}} , dx}

CVN k ∼ 3. { displaystyle { frac {C_ {V}} {Nk}} sim 3 ,.}

Это закон Дюлонга — Пети, и он довольно точен, хотя и не учитывает учет ангармонизма, который вызывает дальнейшее повышение теплоемкости. Общая теплоемкость твердого тела, если это проводник или полупроводник, также может содержать значительный вклад от электронов.

Дебай против Эйнштейна

Дебай против Эйнштейна . Прогнозируемая теплоемкость как функция температуры.

Итак, насколько точно модели Дебая и Эйнштейна соответствуют эксперименту? Удивительно близко, но Дебай верен при низких температурах, а Эйнштейн — нет.

Чем отличаются модели? Чтобы ответить на этот вопрос, структура построить их на одном наборе осей… за исключением одной. И модель Эйнштейна, и модель Дебая установите функциональную форму теплоемкости. Это модели, и ни одна модель не обходится без масштаба. Масштаб соотносит модель с ее реальным аналогом. Можно видеть, что масштаб модели Эйнштейна, который определяется как

CV = 3 N k (ϵ k T) 2 e ϵ / k T (e ϵ / k T — 1) 2 { displaystyle C_ {V} = 3Nk left ({ epsilon over kT} right) ^ {2} {e ^ { epsilon / kT} over left (e ^ { epsilon / kT} -1 right) ^ {2}}}

равно ϵ / k { displaystyle epsilon / k}. А масштаб модели Дебая — T D { displaystyle T _ { rm {D}}}, температура Дебая. И то и другое обычно находят путем подгонки моделей к экспериментальным данным. (Температуру теоретически можно рассчитать, исходя из скорости звука и размеров кристалла.) При использовании этих двух методов подходят к проблеме с разными ориентациями и разной геометрии, шкалы Эйнштейна и Дебая не одинаковы, то есть скажем

ϵ k ≠ TD, { displaystyle { epsilon over k} neq T _ { rm {D}} ,,}

, что означает их построение на одном наборе осей не имеет смысла. Это две модели одного и того же, но разного масштаба. Если определить температуру Эйнштейна как

TE = def ϵ k, { displaystyle T _ { rm {E}} { stackrel { mathrm {def}} {=}} { epsilon over k} ,,}

, тогда можно сказать

TE ≠ TD, { displaystyle T _ { rm {E}} neq T _ { rm {D}} ,,}

и, чтобы связать эти два, мы должны найти соотношение

TETD =? { displaystyle { frac {T _ { rm {E}}} {T _ { rm {D}}}} =?}

твердое тело Эйнштейна состоит из одиночного -частотные квантовые гармонические осцилляторы, ϵ = ℏ ω = h ν { displaystyle epsilon = hbar omega = h nu}. Эта частота, если бы она действительно существовала, была бы со скоростью звука в твердом теле. Если представить себе распространение звука как последовательность ударов атомов друг о друга, то становится очевидным, что частота колебаний должна соответствовать минимальной длине волны, поддерживаемой атомной решеткой, λ min { displaystyle lambda _ {min}}.

ν = CS λ = CS N 3 2 L = CS 2 NV 3 { Displaystyle Nu = {c _ { rm {s}} over lambda} = {c _ { rm {s}} { sqrt [{ 3}] {N}} over 2L} = {c _ { rm {s}} over 2} { sqrt [{3}] {N over V}}}

который делает температура Эйнштейна

TE = ϵ k = h ν k = hcs 2 k NV 3, { displaystyle T _ { rm {E}} = { epsilon over k} = {h nu над k} = {hc _ { rm {s}} над 2k} { sqrt [{3}] {N over V}} ,,}

, поэтому искомое отношение составляет

TETD = π 6 3 = 0.805995977… { displaystyle {T _ { rm {E}} over T _ { rm {D}}} = { sqrt [{3}] { pi over 6}} = 0.805995977…}

Теперь обе модели могут быть построены на одном графике. Обратите внимание, что это соотношение является одним из поправочных коэффициентов, используемым при аппроксимации интеграла энергии, приведенным выше.

С другой стороны, соотношение двух температур можно рассматривать как отношение одной частоты Эйнштейна, на которой колеблются все осцилляторы, и максимальная частота Дебая. Тогда единственная частота Эйнштейна может рассматривать как среднее значение частот, доступных для модели Дебая.

Таблица температур Дебая

Несмотря на то, что модель Дебая не полностью верна, она дает хорошее приближение для низкотемпературной теплоемкости изолирующих твердых тел, где другие факторы (например, высокая подвижная проводимость) электронов) незначительны. Для металлов вклад электронов в тепло пропорционален T { displaystyle T}, который при низких температурах доминирует над дебаевским T 3 { displaystyle T ^ {3}}результат для решетки. В этом случае можно сказать, что модель Дебая приближает только решеточный вклад в теплоемкость. В следующей таблице приведены температуры Дебая для нескольких чистых элементов и сапфира:

Модель Дебая часто соответствует экспериментальным данным. феноменологически улучшено, позволив температуре Дебая стать зависимой от температуры; например, для водяного льда увеличивается примерно с 222 K до 300 K при изменении температуры от абсолютного нуля до примерно 100 K.

Распространение на другие квазичастицы

Для других бозонных квазичастиц, например, для магнонов (квантованные спиновые волны) в ферромагнетиках вместо фононов (квантованные звуковые волны) легко получить аналогичные результаты. В этом случае на низких частотах используются другие дисперсионные соотношения, например, E (ν) ∝ k 2 { displaystyle E ( nu) propto k ^ {2}}для магнонов, вместо E (ν) ∝ k { displaystyle E ( nu) propto k}для фононов (с k = 2 π / λ { displaystyle k = 2 pi / lambda}). Один имеет другую плотность (например, ∫ g (ν) d ν ≡ N { displaystyle int g ( nu) { rm {d}} nu Equiv N ,}). Как следствие, в ферромагнетиках появляется магнонный вкладыш вемкость Δ C V | магнон ∝ T 3/2 { displaystyle Delta C _ {, { rm {V | , magnon}}} , propto T ^ {3/2}}, который доминирует при достаточно при низких температурах фононный вклад, Δ CV | п ч о н о N ∝ T 3 { displaystyle , Delta C _ {, { rm {V | , phonon}}} propto T ^ {3}}. В металлах, напротив, основной вклад в теплоемкость при низких температурах, ∝ T { displaystyle propto T}, вносит электроны. Это фермионный, и он использует различные методы, восходящими к модели свободных электронов Зоммерфельда .

Распространение на жидкости

Долгое время считалось эта теория фононов не может Благодаря этому есть только продольные, но не поперечные фононы, которые в твердых телах обеспечивают 2/3 теплоемкости. эксперименты по рассеянию Бриллюэна с нейтронами и с рентгеновскими лучами, подтверждающие интуицию Якова Френкеля, показали, что поперечные фононы действительно существуют в жидкостях, хотя и ограничены частотами выше порогового значения, называемого. Поскольку большая часть энергии содержится в этих высокочастотных модах, простой модификации модели Дебая достаточно для получения хорошего приближения к экспериментальной теплоемкости простых жидкостей.

Частота Дебая

частота Дебая (Символ: ω D ebye { displaystyle omega _ { rm {Debye}}}или ω D { displaystyle omega _ { rm {D}}}) — параметр в модели Дебая. Это относится к отсечке угловой частоты для волн гармонической цепочки масс, используемой для описания движения ионов в кристаллической решетке . и более конкретно, чтобы правильно спрогнозировать теплоемкость в таких кристаллах, чтобы она была постоянной при высоких температурах (закон Дюлонга – Пети ). Термин был впервые введен Питером Дебаем в 1912 году.

На протяжении всей этой статьи предполагаются периодические граничные условия.

Определение

Предполагая, что дисперсионное соотношение равно

ω = v s | k | { displaystyle omega = v _ { rm {s}} | mathbf {k} |},

с vs { displaystyle v _ { rm {s}}}скорость звука в кристалле; и k волновой вектор, значение частоты Дебая выглядит следующим образом:

Для одномерной одноатомной цепочки частота Дебая равна

ω D = vs π / a знак равно против π N / L = против π λ { displaystyle omega _ { rm {D}} = v _ { rm {s}} pi / a = v _ { rm {s}} pi N / L = v _ { rm {s}} pi lambda},

с a { displaystyle a}расстоянием между двумя соседними атомами в цепочке, когда система находится в ее основное состояние (в данном случае это означает, что ни один из атомов не движется относительно друг друга); N { displaystyle N}общее количество атомов в цепочке; и L { displaystyle L}размер (объем) системы (длина цепочки); и λ { displaystyle lambda}— линейная числовая плотность. Если выполняется следующее соотношение: L = N a { displaystyle L = Na}.

Для двумерной одноатомной квадратной решетки частота Дебая равна

ω D 2 = 4 π a 2 vs 2 = 4 π NA против 2 ≡ 4 π σ против 2 { displaystyle omega _ { rm {D}} ^ {2} = { frac {4 pi} {a ^ {2}}} v _ { rm { s}} ^ {2} = { frac {4 pi N} {A}} v _ { rm {s}} ^ {2} Equiv 4 pi sigma v _ { rm {s}} ^ { 2}},

где a { displaystyle a}и N { displaystyle N}такие же, как и раньше; A ≡ L 2 = N a 2 { displaystyle A Equiv L ^ {2} {=} Na ^ {2}}— размер (площадь) поверхности; и σ { displaystyle sigma}поверхностная числовая плотность.

Для трехмерного одноатомного примитивного кубического кристалла частота Дебая равна

ω D 3 знак равно 6 π 2 a 3 vs 3 = 6 π 2 NV vs 3 ≡ 6 π 2 ρ vs 3 { displaystyle omega _ { rm {D}} ^ {3} = { frac {6 pi ^ {2}} {a ^ {3}}} v _ { rm {s}} ^ {3} = { frac {6 pi ^ {2} N} {V}} v _ { rm { s}} ^ {3} Equiv 6 pi ^ {2} rho v _ { rm {s}} ^ {3}},

где a { displaystyle a}и N { displaystyle N}такие же, как и раньше; V ≡ L 3 = N a 3 { displaystyle V Equiv L ^ {3} = Na ^ {3}}размер системы; и ρ { displaystyle rho}объемная числовая плотность.

Скорость звука в кристалле может зависеть (среди прочего) от массы элементов, силы их взаимодействия, давление в системе и / или поляризация волны (продольная или поперечная), но в дальнейшем мы сначала примем скорость звука как то же самое для любой поляризации (однако это предположение не имеет далеко идущих последствий).

Предполагаемое дисперсионное соотношение легко доказано неверным для одномерной цепочки масс, но в моделях Дебая это не оказалось проблемой.

Отношение к температуре Дебая

Температура Дебая θ D { displaystyle theta _ { rm {D}}}, еще один параметр в модели Дебая, соответствует с выбором Дебая движение

θ D = ℏ KB ω D, { displaystyle theta _ { rm {D}} = { frac { hbar} {k _ { rm {B}}}} omega _ { rm {D}},}

где ℏ { displaystyle hbar}— это уменьшенная постоянная Планка и k B { displaystyle k _ { rm {B}}}— постоянная Больцмана.

вывод Дебая

Трехмерный кристалл

В теории Дебая при выводе теплоемкости он суммирует все возможные режимы работы системы. То есть: включая разные направления и поляризации. Он предположил, что общее количество мод на поляризацию составляет 3 N { displaystyle 3N}(с N { displaystyle N}количество масс в системе), или на математическом языке

∑ режимы 3 = 3 N { displaystyle sum _ { rm {Mode}} 3 = 3N},

, где 3 { displaystyle 3}с Другая сумма сторон из-за трех поляризаций проходит по всем модам для одной настройки. Дебай сделал это предположение, потому что он знал из классической механики, что количество мод на поляризацию в цепочке всегда должно быть равно количеству масс в цепочке.

Левая часть теперь должна быть явной, чтобы она зависела от частоты Дебая (здесь просто введена как частота среза, то есть более высокие частоты, чем частота Дебая, не может существовать), поэтому это выражение для него можно найти.

Прежде всего, предположив, что L { displaystyle L}очень большой (L { displaystyle L}>>1, с L { displaystyle L}размером системы в любом из трех направлений) наименьший волновой вектор в любом направлении можно аппроксимировать следующим образом: dki = 2 π / L { displaystyle dk_ {i} = 2 pi / L}, где i = x, y, z { displaystyle i = x, y, z}. Волновые меньшего размера не могут существовать из-за периодических граничных условий. Таким образом, суммирование будет следующим образом: 4

∑ режимы 3 = 3 V (2 π) 3 ∭ dk { displaystyle sum _ { rm {mode}} 3 = { frac {3V} {(2 pi) ^ {3}}} iiint d mathbf {k}},

где k ≡ (kx, ky, kz) { displaystyle mathbf {k} Equiv (k_ {x}, k_ { y}, k_ {z})}; V ≡ L 3 { displaystyle V Equiv L ^ {3}}— размер системы; и интеграл (как суммирование) по всем возможным режимам, обязательной конечной областью.

Тройной интеграл можно переписать как единый интеграл по всем возможным значениям k { displaystyle mathbf {k}}(см.: Якобиан для сферических координат ). Результат:

3 V (2 π) 3 ∭ d k = 3 V 2 π 2 ∫ 0 k D | k | 2 dk { displaystyle { frac {3V} {(2 pi) ^ {3}}} iiint d mathbf {k} = { frac {3V} {2 pi ^ {2}}} int _ {0} ^ {k _ { rm {D}}} | mathbf {k} | ^ {2} d mathb {k}},

с k D { displaystyle k _ { rm {D}}}абсолютное значение волнового облака, форма дебаевской формы, поэтому К D = ω D / vs { displaystyle k _ { rm {D}} = omega _ { rm {D}} / v _ { rm {s}}}.

Мы знаем, что соотношение дисперсии ω = vs | k | { displaystyle omega = v _ { rm {s}} | mathbf {k} |}, это можно записать как интеграл по всем возможным ω { displaystyle omega}

3 V 2 π 2 ∫ 0 k D | k | 2 dk знак равно 3 V 2 π 2 vs 3 ∫ 0 ω D ω 2 d ω { displaystyle { frac {3V} {2 pi ^ {2}}} int _ {0} ^ {k _ { rm {D}}} | mathbf {k} | ^ {2} d mathbf {k} = { frac {3V} {2 pi ^ {2} v _ { rm {s}} ^ {3}}} int _ {0} ^ { omega _ { rm {D}}} omega ^ {2} d omega},

После решения интеграла он снова приравнивается к 3 N { displaystyle 3N}, чтобы найти

V 2 π 2 против 3 ω D 3 = 3 N { displaystyle { frac {V} {2 pi ^ {2} v _ { rm {s}} ^ {3}}} omega _ { rm {D}} ^ {3} = 3N}.

Заключение:

ω D 3 = 6 π 2 NV против 3 { displaystyle omega _ { rm {D}} ^ {3} = { frac {6 pi ^ {2} N} {V}} v _ { rm {s}} ^ {3}}.

Одномерная цепочка в трехмерном пространстве

То же самое можно сделать для одномерного цепочки атомов. Количество мод остается неизменным, поскольку по-прежнему три. Итак,

∑ м о d е s 3 = 3 N { displaystyle sum _ { rm {mode}} 3 = 3N}.

Остальная часть вывода аналогична предыдущему, поэтому снова переписывается левая часть;

∑ режимы 3 = 3 L 2 π ∫ — К D К D dk = 3 L π vs ∫ 0 ω D d ω { displaystyle sum _ { rm {mode}} 3 = { frac {3L} {2 pi}} int _ {- k _ { rm {D}}} ^ {k _ { rm {D}}} dk = { frac {3L} { pi v _ { rm { s}}}} int _ {0} ^ { omega _ { rm {D}}} d omega}.

На последнем этапе умножения на два происходит потому, что k { displaystyle k}имеет отрицательное значение, а ω { displaystyle omega}— нет. Мы продолжим;

3 L π vs ∫ 0 ω D d ω знак равно 3 L π vs ω D = 3 N { displaystyle { frac {3L} { pi v _ { rm {s}}}} int _ {0} ^ { omega _ { rm {D}}} d omega = { frac {3L} { pi v _ { rm {s}}}} omega _ { rm {D}} = 3N}.

Заключение:

ω D = π vs NL { displaystyle omega _ { rm {D}} = { frac { pi v _ { rm {s}} N} {L }}}.

Двумерный кристалл

То же самое можно сделать и для двумерного кристалла. Опять же, количество мод остается неизменным, потому что есть еще три поляризации. Вывод аналогичен двум предыдущим. Начнем с того же уравнения:

∑ mode 3 = 3 N { displaystyle sum _ { rm {mode}} 3 = 3N}.

А переписываем левую часть и приравниваем к 3 N { displaystyle 3N}

∑ режимы 3 = 3 A (2 π) 2 ∬ dk = 3 A 2 π vs 2 ∫ 0 ω D ω d ω = 3 A ω D 2 4 π vs 2 = 3 N { displaystyle sum _ { rm {mode}} 3 = { frac {3A} {(2 pi) ^ {2}}} iint d mathbf {k} = { frac {3A} {2 pi v _ { rm {s}} ^ {2}}} int _ {0} ^ { omega _ { rm {D}}} omega d omega = { frac {3A omega _ { rm { D}} ^ {2}} {4 pi v _ { rm {s}} ^ {2}}} = 3N},

где A ≡ L 2 { displaystyle A Equiv L ^ { 2}}— размер системы.

Заключение

ω D 2 = 4 π NA vs 2 { displaystyle omega _ { rm {D}} ^ {2} = { frac {4 pi N} {A}} v _ { rm {s}} ^ {2}}.

Разрешение поляризации имеет значение

Как упоминалось во введении: в общем, продольные волны имеют другую скорость волны, чем поперечные волны. Для ясности сначала предполагалось, что они равны, но теперь мы отказываемся от этого предположения.

Дисперсионное соотношение принимает вид ω i = v s, i | k | { displaystyle omega _ {i} = v_ {s, i} | mathbf {k} |}, где i = 1, 2, 3 { displaystyle i = 1,2, 3}, которые соответствуют трем поляризации. Однако частота среза (частота Дебая) не зависит от i { displaystyle i}. И мы можем записать общее количество режимов как ∑ i ∑ mode 1 { displaystyle sum _ {i} sum _ { rm {mode}} 1}, что снова равно к 3 N { Displaystyle 3N}. Здесь суммирование по режимам (хотя явно не указано) зависит от i { displaystyle i}.

Одно измерение

Еще раз суммирование по режимам переписывается

∑ i ∑ режимы 1 знак равно ∑ я L π vs, я ∫ 0 ω D d ω я знак равно 3 N { displaystyle sum _ {i} sum _ { rm {mode}} 1 = sum _ {i} { frac {L} { pi v_ {s, i}}} int _ {0} ^ { omega _ { rm {D}}} d omega _ {i} = 3N}.

Результат:

L ω D π (1 против, 1 + 1 против, 2 + 1 против, 3) = 3 N { displaystyle { frac {L omega _ { rm {D}}} { pi}} ({ frac {1 } {v_ {s, 1}}} + { frac {1} {v_ {s, 2}}} + { frac {1} {v_ {s, 3}}}) = 3N}.

Таким образом образом, частота Дебая находится

ω D = 3 π NL vs, 1 vs, 2 vs, 3 vs, 2 vs, 3 + vs, 1 vs, 3 + vs, 1 vs, 2 { displaystyle omega _ { rm {D}} = { frac {3 pi N} {L}} { frac {v_ {s, 1} v_ {s, 2} v_ {s, 3}} {v_ {s, 2} v_ {s, 3} + v_ {s, 1} v_ {s, 3} + v_ {s, 1} v_ {s, 2}}}}.

Или предполагая две поперечные поляризации быть одинаковыми (иметь одинаковую фазовую скорость) и частоту)

ω D = 3 π NL vs, t 2 vs, l 2 vs, tvs, l + vs, t 2 { displaystyle omega _ { rm {D}} = { frac {3 pi N} {L}} { frac {v_ {s, t} ^ {2} v_ {s, l}} {2v_ {s, t} v_ {s, l} + v_ {s, t} ^ {2 }}}}.

Можно проверить, что это соотношение эквивалентно найденному ранее (когда поляризация не имеет значения), задав vs, t = vs, l { displaystyle v_ {s, t} = v_ {s, l }}.

Два измерения

Тот же вывод может быть выполнен для двумерного кристалла, чтобы найти (аналогичный предыдущим выводам)

ω D 2 = 12 π NA (vs, 1 vs, 2 vs, 3) 2 (vs, 2 vs, 3) 2 + (vs, 1 vs, 3) 2 + (vs, 1 vs, 2) 2 { displaystyle omega _ { rm {D}} ^ {2} = { frac {12 pi N} {A}} { frac {(v_ {s, 1} v_ {s, 2} v_ {s, 3}) ^ {2}} {(v_ {s, 2} v_ {s, 3}) ^ {2} + (v_ {s, 1} v_ {s, 3}) ^ {2} + (v_ {s, 1} v_ {s, 2}) ^ {2}} }}.

Или, предполагая, что две поперечные поля измерения равны (хотя для двух измерений было бы логичнее, если бы все поляризации были разными):

ω D 2 = 12 π NA (vs, t 2 vs, l) 2 2 (vs, tvs, l) 2 + vs, т 4 { Displaystyle omega _ { rm {D}} ^ {2} = { frac {12 pi N} {A} } { frac {(v_ {s, t} ^ {2} v_ {s, l}) ^ {2}} {2 (v_ {s, t} v_ {s, l}) ^ {2} + v_ {s, t} ^ {4}}}}.

Опять же, можно проверить, что это соотношение эквивалентен найденному ранее, установив vs, t = vs, l { displaystyle v_ {s, t} = v_ {s, l}}.

Три измерения

Тот же вывод может выполнить трехмерный кристалл, чтобы найти (вывод предыдущим выводам)

ω D 3 = 18 π 2 NV (vs, 1 vs, 2 vs, 3) 3 (vs, 2 vs, 3) 3 + (vs, 1 vs, 3) 3 + (vs, 1 vs, 2) 3 { displaystyle omega _ { rm {D}} ^ {3} = { frac {18 pi ^ {2} N} {V}} { frac {(v_ {s, 1} v_ {s, 2} v_ {s, 3}) ^ {3}} {(v_ {s, 2} v_ {s, 3}) ^ {3} + (v_ {s, 1} v_ {s, 3}) ^ {3} + (v_ {s, 1} v_ {s, 2}) ^ {3}}}}.

Предполагаемая две поперечные поляризации равны (хотя для трех измерений было бы логичнее, если бы все поляризации были одинаковыми):

ω D 3 = 18 π 2 NV (vs, т 2 вс, л) 3 2 (vs телеведущая изоры, l) 3 + vs, t 6 { displaystyle omega _ { rm {D}} ^ {3} = { frac {18 pi ^ {2} N} {V}} { frac {( v_ {s, t} ^ {2} v_ {s, l}) ^ {3}} {2 (v_ {s, t} v_ {s, l}) ^ {3} + v_ {s, t} ^ {6}}}}.

Опять же, можно проверить, что это отношение эквивалентно найденному ранее, установив vs, t = vs, l { displaystyle v_ {s, t} = v_ {s, l}}.

Вывод с фактическим использованием дисперсии

имеют значение только дискретизированные точки, две волны могут отображать одинаковые физическое проявление (см. Phonon ).

Эту проблему можно было бы сделать более проницательной, сделав ее более сложной. Вместо использования дисперсионного соотношения ω = v s k { displaystyle omega = v _ { rm {s}} k}теперь правильное дисперсионное соотношение. Из классической механики известно, что для эквидистантной цепочки масс, гармонически взаимодействующих друг с другом, дисперсионное соотношение имеет вид:

ω (k) = 2 κ m | sin ⁡ (k a 2) | { displaystyle omega (k) = 2 { sqrt { frac { kappa} {m}}} left | sin left ({ frac {ka} {2}} right) right |}.

После построения этой зависимости ясно, что оценка Дебая длины волныечки в конце концов была верной. Для каждого волнового числа больше π / a { displaystyle pi / a}(то есть: λ { displaystyle lambda}меньше, чем 2 a { displaystyle 2a}) волновое число меньше π / a { displaystyle pi / a}может быть найдено с той же угловой границей. Это означает, что это означает, что физическое проявление моды с большим волновым числом неотличимо от моды с большим волновым числом. Таким образом, исследование дисперсионного соотношения может быть ограничено первой зоной бриллюэна, т.е. для k ∈ [- π a, π a] { displaystyle k in [- { frac { pi} {a}}, { frac { pi} {a}}]}. Это возможно, потому что система состоит из дискретизированных точек, как показано на анимированном изображении. Разделив соотношение дисперсии на k { displaystyle k}и вставив π / a { displaystyle pi / a}для k { displaystyle k }, мы находимся скоростью волны с k = π / a { displaystyle k = pi / a}как

vs (k = π / a) знак равно 2 a π κ м { Displaystyle v _ { rm {s}} (k = pi / a) = { frac {2a} { pi}} { sqrt { frac { kappa} {м }}}}.

Просто вставив k = π / a { displaystyle k = pi / a}в исходное дисперсионное соотношение, мы находим

ω (k знак равно π / а) знак равно 2 κ м = ω D { displaystyle omega (к = pi / a) = 2 { sqrt { frac { kappa} {m}}} = omega _ { rm {D} }}.

Объединяя эти результаты, мы снова получаем тот же результат

ω D = π vsa { displaystyle omega _ { rm {D}} = { frac { pi v _ { rm {s }}} {a}}}.

Однако для двухатомных цепей соответствующая частота отсечки (и длина волны) не очень точны, поскольку длина волны отсечки вдвое больше, соотношение дисперсии состоит из двух ветвей (для объявления яатомная цепочка). Из этого также неясно, была ли частота отсечки точно предсказана Дебаем для более размерных систем.

.

Альтернативное происхождение

Физический результат двух волн может быть идентичным, если одна из них имеет длину волны, превышающую вдвое исходное расстояние между массами (взято из теоремы выборки Найквиста — Шеннона ).

Теорема выборки Найквиста — Шеннона используется в следующем выводе; главное отличие состоит в том, что в следующем выводе дискретизация не времени, но в пространстве. Таким образом, снова,

ω (k) Знак равно 2 κ м | грех ⁡ (ка 2) | {, дисперсии из последнего абзаца, станет ясно проницательным способом, почему частота среза имеет значение, полученное ранее (дважды). displaystyle omega (k) = 2 { sqrt { frac { kappa} {m}}} left | sin left ({ frac {ka} {2}} right) right |} <940

Этот вывод полностью эквивалентен предыдущему, а именно: те же пр едположения сделаны для получения результат. Это не более-точно менее, это просто другой подход.

Чтобы определить, где должна быть граничная частота, сначала нужно определить, где должна быть граница длины волны. Из дисперсионного соотношения мы знаем, что для k>π / a { displaystyle k> pi / a}повторяется каждый режим, поэтому длина волны отсечки будет на уровне λ D = 2 a { displaystyle lambda _ { rm {D}} = 2a}. Из этих периодических граничных условий вы можете сразу увидеть, что общее количество мод на поляризацию будет N { displaystyle N}. Как видно на gif-изображении в предыдущем абзаце, это связано с тем, что каждая волна с длиной волны меньше 2 a { displaystyle 2a}может быть заменена на волна с длиной волны больше, чем 2 a { displaystyle 2a}, чтобы восстановить тот же физический результат.

Однако дисперсионное соотношение из предыдущего абзаца (правильное) не нужно даже при рассуждении о том, почему граница должна быть на λ Знак равно 2 a { displaystyle lamb da = 2a}. Если показано, как показано, только волна с большей длиной волны, чем 2, { displaystyle 2a}может дать тот же физический результат, что и другой. Таким образом, это еще один способ правильно предсказать длину волны отсечки без использования правильного дисперсионного соотношения. Однако, используя неправильное соотношение дисперсии, предположение, что это не приведет к появлению новых мод.

Это снова приводит к k D = π / a { displaystyle k _ { rm {D}} = pi / a}, рендеринг

ω D = π vsa { displaystyle omega _ { rm {D}} = { frac { pi v _ { rm {s}}} {a}}}.

Также здесь не имеет значения, какое соотношение дисперсии используется такая или правильный тот, который использовал Дебай), будет найдена же частота среза.

К сожалению, тот же метод нельзя использовать для двух- или трехмерного кристалла, потому что диагональные волны имеют большую длину волны волны, что также трудно предсказать.

См. Также

Ссылки

1. ^Дебай, Питер (1912). «Zur Theorie der spezifischen Waerme». Annalen der Physik (на немецком языке). 39 (4): 789–839. Bibcode : 1912AnP… 344..789D. doi : 10.1002 / andp.19123441404.
2. ^ Киттель, Чарльз (2004). Введение в физику твердого тела (8-е изд.). Джон Вили и сыновья. ISBN 978-0471415268.
3. ^Шредер, Дэниел В. «Введение в теплофизику» Аддисон-Уэсли, Сан-Франциско (2000). Раздел 7.5.
4. ^Хилл, Террелл Л. (1960). Введение в статистическую механику. Ридинг, Массачусетс, США: Addison-Wesley Publishing Company, Inc. ISBN 9780486652429.
5. ^Обераи, М.М.; Srikantiah, G (1974). Первый курс термодинамики. Нью-Дели, Индия: Prentice-Hall of India Private Limited. ISBN 9780876920183.
6. ^Паттерсон, Джеймс Д.; Бейли, Бернард С. (2007). Физика твердого тела: Введение в теорию. Springer. С. 96–97. ISBN 978-3-540-34933-4.
7. ^Шульман, Л. М. (2004). «Теплоемкость водяного льда в межзвездных или межпланетных условиях». Астрономия и астрофизика. 416 : 187–190. Bibcode : 2004AA… 416..187S. doi : 10.1051 / 0004-6361: 20031746.
8. ^Флубачер, П.; Leadbetter, A.J.; Моррисон, Дж. А. (1960). «Теплоемкость льда при низких температурах». Журнал химической физики. 33 (6): 1751. Bibcode : 1960JChPh..33.1751F. doi : 10.1063 / 1.1731497.
9. ^В учебнике «Кинетическая теория жидкостей» (англ. 1947)
10. ^Болматив, Бражин, Траченко, Фононная теория термодинамики жидкости, Sci Rep. 2 : 421 (2012)
11. ^Дебай, П. (1912). «Zur Theorie der spezifischen Wärmen». Annalen der Physik. 344 (14): 789–839. doi : 10.1002 / andp.19123441404. ISSN 1521-3889.
12. ^«Одномерное одноатомное твердое тело» (PDF). Проверено 27 апреля 2018 г.
13. ^Фитцпатрик, Ричард (2006). «Удельная теплота твердого тел». Ричард Фицпатрик Техасский университет в Остине. Проверено 27 апреля 2018 г.
14. ^ Саймон, Стивен Х. (20 июня 2013 г.). Основы Оксфордского твердого тела (первое издание). Оксфорд: Издательство Оксфордского университета. ISBN 9780199680764. OCLC 859577633.
15. ^Шривастава Г.П. (16.07.2019). Физика фононов. Рутледж. ISBN 978-1-351-40955-1.

Дополнительная литература

• Справочник CRC по химии и физике, 56-е издание (1975–1976)
• Шредер, Дэниел В. Введение в теплофизику. Аддисон-Уэсли, Сан-Франциско (2000). Раздел 7.5.

Внешние ссылки

Задача: Вычислить дебаевскую температуру некоторого металла, если скорость распространения звука в нем равна 5850 м/с.

Насколько знаю, справедливы формулы

и

где — характеристическая температура, — скорость звука, — параметр решётки. Отсюда дебаевская температура и скорость звука в кристалле связаны соотношением

Но в условии задачи конкретный металл не указан, и, значит, параметр решётки неизвестен. Как быть?

— 20.04.2014, 17:35 —

Хм, что-то я напутал в формулах, похоже. Но всё равно в формулу связи и входит постоянная решётки. А здесь она не дана. Ошибка в условии, или я чего-то не понял?