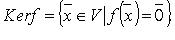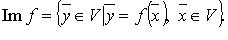Задача №1. В арифметическом пространстве [math]mathbb{R}^4[/math] линейный оператор [math]displaystyle varphi[/math] задан матрицей
[math]A= left(!!begin{array}{rrrr} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{array}!!right)[/math]
Найти базисы ядра и образа, ранг и дефект линейного оператора. Найти операторы, индуцированныe в ядре и образе.
Решение.
1) По определению ядро линейного оператора [math]displaystyle varphi[/math] ([math]displaystyle ker varphi[/math]) есть множество всех векторов [math]displaystyle x[/math], которые [math]displaystyle varphi[/math] переводит в нулевой вектор. Это означает, что [math]displaystyle ker varphi[/math] состоит из векторов, координаты которыx [math]displaystyle x_1, x_2, x_3, x_4[/math] (в некотором базисе [math]displaystyle { e_1, e_2, e_3, e_4 }[/math]) удовлетворяет условию:
[math]begin{pmatrix} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{pmatrix}!!! begin{pmatrix} x_1\ x_2 \ x_3 \ x_4 end{pmatrix}!=! begin{pmatrix} 0\ 0 \ 0 \ 0 end{pmatrix}[/math]. То есть, [math]kervarphi[/math] cooтветствует пространству [math]L[/math] решений системы [math]begin{cases}x_1-2x_2+x_3+3x_4=0,\ -2x_1+5x_2+6x_3-12x_4=0,\ 5x_1+9x_2+13x_3+9x_4=0,\ -x_1+3x_2+7x_3-9x_4=0.end{cases}[/math]
Общим решением системы является семейство векторов [math]left(-frac{15}{4}C , 0, frac{3}{4}C, C right)[/math]. Полагая [math]C=4[/math], находим базис [math]ker varphi[/math]: [math](-15,,0,,3,,4)[/math].
2) Дефектом линейного оператора называется размерность его ядра ([math]dim ker varphi[/math]). Здесь [math]dim ker varphi=1[/math], т.к. в ядре существует лишь один линейно независимый вектор.
Верны ли мои рассуждения?
3) Не знаю, как найти образ линейного отображения [math]varphi[/math] ([math]im varphi[/math]). Подскажите идею.
4) Рангом линейного отображения [math]varphi[/math] называется размерность его образа ([math]dim im varphi[/math]). Здесь всё ясно.
5) Что такое операторы, индуцированные в ядре и образе?
Задача №2. Найти матрицу, область значений и ядро оператора [math]A[/math] проектирования на плоскость [math]x-z=0[/math]. Если [math]x={x_1, x_2, x_3 }[/math], то [math]Ax={x_1-x_2-x_3, -2x_1+3x_2, x_2- x_3 }[/math].
1) Cовершенно не знаю, как найти матрицу. И что означает проектирование на плоскость?
2) Если найду матрицу, то можно найти ядро.
3) Область значений — это синоним образа или что-то другое?
И ещё один вопрос общего характера. Существует ли какое-то обозначение для базиса линейного пространства (как, например, для ядра или размерности)?
Пусть — линейный оператор действующий в линейном пространстве V (комплексном или вещественном)
Определение: Совокупность всевозможных векторов вида называется образом оператора A и обозначается ImA. Таким образом
.
Определение: Совокупность всевозможных векторов для которых
называется ядром оператора A и обозначается KerA. Таким образом
.
Утверждение: образ и ядро линейного оператора А являются подпространствами линейного пространства V.
Доказательство: В самом деле в силу линейности оператора А имеем:
1) тогда
и т. к
то
и т. к.
, то
является подпространством пространства V.
2) отсюда
.
является подпространством пространства V. #
Пример:
Пусть V – n мерное комплексное или вещественное линейное пространство.
1) Тождественный оператор , при этом Ax = Ix = X, тогда ImA=ImI=V, KerA=KerI={θ}
/ ядро состоит из единственного нулевого элемента /
2) Нулевой оператор, тогда
3) Рассмотрим оператор дифференцирования на пространстве
многочленов степени не выше N, тогда
отсюда
. Видно, что во всех приведенных примерах справедливо:
, что не является случайным.
Теорема (о сумме размерностей образа и ядра линейного оператора) :
Пусть A — линейный оператор, действующий в линейном пространстве V. Тогда сумма размерностей образа и ядра оператора равна размерности данного линейного пространства, т. е.
Доказательство:
Пусть , причем
Выберем в пространстве V произвольный базис . Поскольку по определению
, то можно записать, что
линейная оболочка, порождаемая совокупностью образов базисных векторов
, причем
, где R – максимальное число л. н.з. векторов в системе
. Но координаты именно этих векторов стоят в столбцах матрицы
линейного оператора А в базисе
, поэтому
.
Рассмотрим ядро оператора А: .
В выбранном базисе равенству соответствует однородная СЛАУ:
, которая, как известно, имеет (N—R) л. н.з. решений, образующих ФСР. Поскольку неизвестными данной системы являются координаты векторов, составляющих KerA, то отсюда заключаем, что dim(KerA)=N—R. В результате получаем, что
Определение: Размерность образа оператора называется рангом оператора, размерность ядра оператора называется дефектом оператора.
Определение: Линейный оператор называется невырожденным, если в произвольном базисе (E) данного линейного пространства V Оператор А имеет невырожденную матрицу
.
Следствие: Если А – невырожденный линейный оператор, то его образ совпадает со всем пространством, в котором этот оператор действует.
Доказательство: Если , то по предыдущей теореме запишем
. По Свойству 40 невырожденных операторов (докажем позже в параграфе 12 главе 7) равенство
возможно только при
отсюда
откуда
. Т. к.
, то отсюда следует, что
.
Определение: Подпространство L пространства V называется инвариантным относительно линейного оператора А, если .
Теорема (об инвариантности образа и ядра линейного оператора):
Образ и ядро линейного оператора А являются подпространствами инвариантными относительно оператора А.
Доказательство:
1) Пусть , т. к.
то
и поэтому
, т. е. подпространство ImA является инвариантным относительно оператора А.
2) Пусть . Тогда
, т. у.
а значит подпространство KerA инвариантно относительно оператора А.
| Следующая > |
|---|
Линейный
оператор ,
действующий из пространства
в пространство ,
ставит в соответствие каждому вектору
определенный вектор
из .
При этом вектор
называется образом
вектора
,
а вектор
— прообразом
вектора
при отображении .
Пусть
и
— некоторые базисы линейных пространств
и
соответственно. Тогда ,
и координаты вектора — образа
связаны с координатами вектора — прообраза
соотношением

(7.2.1)
в
котором
— матрица линейного оператора
в паре базисов
и .
В
случае, когда пространства
и
совпадают, базисы
и
также совпадают, и формула (7.2.1) принимает
вид

(7.2.2)
Образом
(областью
значений)
линейного
оператора
называется
множество всех элементов
вида .
Образ линейного оператора является
подпространством пространства
и обозначается .
Размерность образа называется рангом
оператора
и обозначается .
Ядром
линейного оператора
называется
множество всех векторов пространства
,
которые переводятся оператором
в нулевой вектор пространства .
Ядро линейного оператора является
подпространством пространства
и обозначается .
Размерность ядра называется дефектом
оператора
и обозначается .
Сумма
ранга и дефекта оператора
равна размерности пространства
.
Ранг
линейного оператора равен рангу матрицы
этого оператора.
Базис
системы векторов — столбцов матрицы
линейного оператора
образует систему координатных столбцов
базиса образа .
Базис подпространства решений однородной
системы линейных алгебраических
уравнений с матрицей оператора
образует базис ядра .
Пример
1.
Из пространства
с базисом
в пространство
с базисом
действует линейный оператор ,
имеющий в данной паре базисов матрицу

Найдите столбец координат в базисе
образа вектора
и столбец координат в базисе
прообраза вектора .
Решение.
Столбец координат образа вектора
в базисе находим
непосредственно по формуле (7.2.1):

Для
определения прообраза вектора
по той же формуле (7.2.1) имеем

или,
что то же самое,
Отсюда
находим все прообразы
вектора ,
где
— свободная переменная, принимающая
произвольные значения.
Пример
2.
В пространстве с
базисом линейный
оператор
переводит векторы ,
в
векторы ,
соответственно. Найдите матрицу оператора
в
базисе .
Решение.
Пусть 
матрица оператора в
базисе .
Тогда из условий ,
по формуле (7.2.2) имеем 
или,
в подробной записи,
Отсюда
получаем
Следовательно,
.
Пример
3.
Найдите базис ядра и базис образа
линейного оператора пространства ,
если этот оператор задан матрицей 
Решение.
При помощи элементарных преобразований
над строками матрицы
приведём её к ступенчатому виду:

Отсюда
следует, что .
Базис составляют,
например, векторы
и .
Дефект
оператора найдём по формуле
,
т.е.
фундаментальная система решений
однородной системы линейных алгебраических
уравнений с матрицей
будет состоять из одного вектора. Общее
решение однородной системы можно
записать в виде .
Полагая
получаем базисный вектор .
7.2.1.
Линейный оператор переводит
вектор
в вектор.
Найдите образ вектора
и прообраз вектора ,
если
,
,
;
,
,
;
,
,
.
7.2.2.
Линейный оператор в
паре базисов и
имеет матрицу .
Найдите прообраз вектора ,
если

;
б)
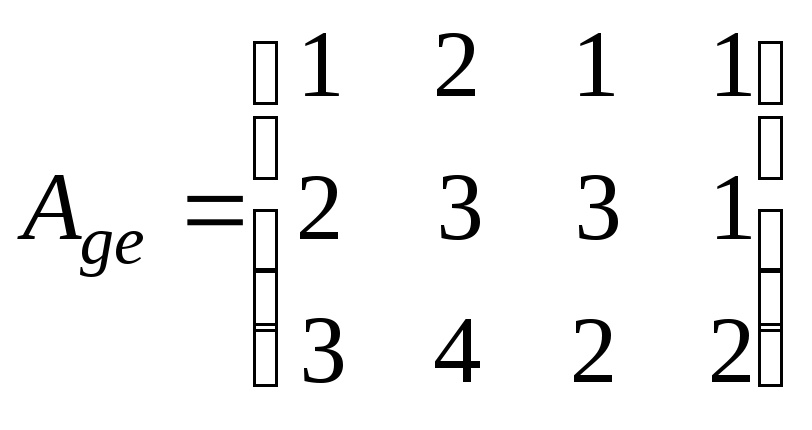
;
в)

.
7.2.3.
Выясните, существует ли линейный оператор
двумерного пространства, переводящий
векторы ,
соответственно в векторы ,
,
и найдите матрицу этого оператора в
базисе ,
:
а)
б)
в)
7.2.4.
Выясните, существует ли линейный оператор
трехмерного пространства, переводящий
векторы ,
,
соответственно в векторы ,
,
,
и найдите матрицу этого оператора в том
же базисе, в котором даны координаты
всех векторов:
а)
б)
7.2.5.
Для указанных линейных операторов
пространства
найдите дефект и ранг, а также постройте
базисы ядра и образа. Каждый оператор
описывается своим действием на
произвольный вектор :
а)
б)
в)
7.2.6.
Найдите образ и ядро оператора
дифференцирования в пространстве .
7.2.7.
В пространстве
рассмотрите разностный
оператор
где
— фиксированное
число, отличное от нуля. Найдите его
образ и ядро.
7.2.8.
Найдите образ и ядро оператора
проектирования (см. задачу 7.1.2) на
параллельно
и оператора отражения (см. задачу 7.1.3) в
параллельно .
7.2.9.
Найдите базис ядра и базис образа
линейного
оператора из ,
заданного в некотором базисе матрицей
:
а)
;
б)
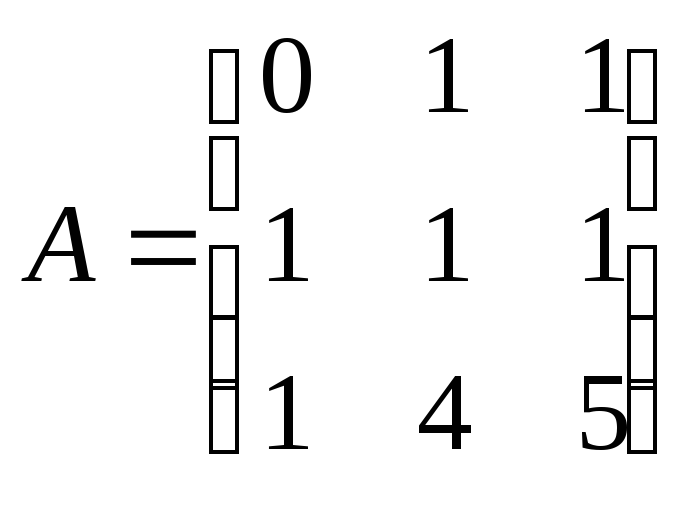
в)
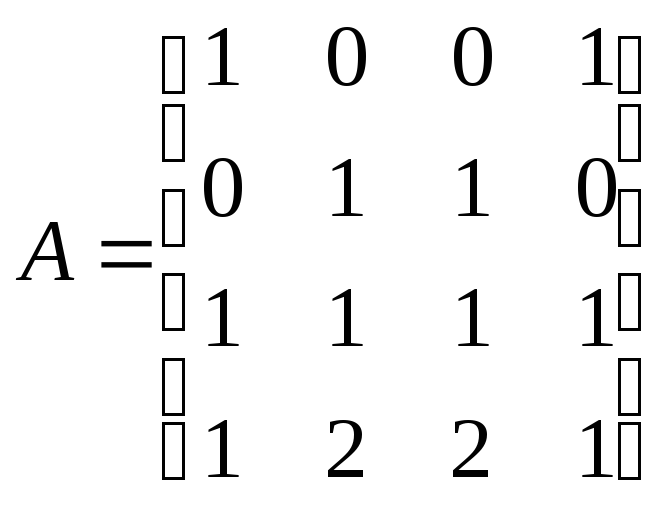
7.2.10.
Найдите размерность линейного пространства
всех линейных операторов, действующих
в
— мерном линейном пространстве
и постройте базис пространства .
Соседние файлы в папке Задачник-2
- #
- #
- #
- #
- #
- #
01.Образ и ядро линейного оператора. Ранг и дефект линейного оператора
Определение: Совокупность всевозможных векторов вида называется образом оператора A и обозначается ImA. Таким образом .
Определение: Совокупность всевозможных векторов для которых называется ядром оператора A и обозначается KerA. Таким образом .
Утверждение: образ и ядро линейного оператора А являются подпространствами линейного пространства V.
Доказательство: В самом деле в силу линейности оператора А имеем:
1) тогда и т. к то
и т. к. , то является подпространством пространства V.
является подпространством пространства V. #
Пусть V – n мерное комплексное или вещественное линейное пространство.
1) Тождественный оператор , при этом Ax = Ix = X, тогда ImA=ImI=V, KerA=KerI=θ>
/ ядро состоит из единственного нулевого элемента /
2) Нулевой оператор, тогда
3) Рассмотрим оператор дифференцирования на пространстве многочленов степени не выше N, тогда отсюда. Видно, что во всех приведенных примерах справедливо:
, что не является случайным.
Теорема (о сумме размерностей образа и ядра линейного оператора) :
Пусть A — линейный оператор, действующий в линейном пространстве V. Тогда сумма размерностей образа и ядра оператора равна размерности данного линейного пространства, т. е.
Доказательство:
Выберем в пространстве V произвольный базис . Поскольку по определению , то можно записать, что линейная оболочка, порождаемая совокупностью образов базисных векторов , причем , где R – максимальное число л. н.з. векторов в системе. Но координаты именно этих векторов стоят в столбцах матрицы линейного оператора А в базисе, поэтому .
Рассмотрим ядро оператора А: .
В выбранном базисе равенству соответствует однородная СЛАУ:, которая, как известно, имеет (N—R) л. н.з. решений, образующих ФСР. Поскольку неизвестными данной системы являются координаты векторов, составляющих KerA, то отсюда заключаем, что dim(KerA)=N—R. В результате получаем, что
Определение: Размерность образа оператора называется рангом оператора, размерность ядра оператора называется дефектом оператора.
Определение: Линейный оператор называется невырожденным, если в произвольном базисе (E) данного линейного пространства V Оператор А имеет невырожденную матрицу .
Следствие: Если А – невырожденный линейный оператор, то его образ совпадает со всем пространством, в котором этот оператор действует.
Доказательство: Если , то по предыдущей теореме запишем . По Свойству 40 невырожденных операторов (докажем позже в параграфе 12 главе 7) равенство возможно только при отсюда откуда . Т. к. , то отсюда следует, что .
Определение: Подпространство L пространства V называется инвариантным относительно линейного оператора А, если .
Теорема (об инвариантности образа и ядра линейного оператора):
Образ и ядро линейного оператора А являются подпространствами инвариантными относительно оператора А.
Доказательство:
1) Пусть , т. к. то и поэтому , т. е. подпространство ImA является инвариантным относительно оператора А.
2) Пусть . Тогда, т. у. а значит подпространство KerA инвариантно относительно оператора А.
Как найти дефект матрицы
Определение 2. Пусть — линейный оператор, действующий в пространстве Совокупность всевозможных векторов вида где называется областью значений оператора или образом пространства при преобразовании а множество всевозможных векторов х, для которых — ядром оператора
Покажем, что область значений и ядро линейного оператора являются подпространствами в
Действительно, для области значений это вытекает из теоремы 1, если рассматриваемое в ней подпространство совпадает со всем пространством
С другой стороны, если т. е. если то и и значит, — подпространство.
Размерность области значений оператора совпадает с рангом матрицы А (и называется рангом оператора Действительно, подпространство порождается векторами
где — любой базис пространства и значит, размерность равна максимальному числу линейно независимых векторов в системе (6), т. е. равна максимальному числу линейно независимых столбцов матрицы
Размерность ядра называется дефектом линейного оператора
Теорема 4. Сумма ранга и дефекта линейного оператора равна размерности пространства.
Доказательство. Если ранг линейного оператора равен то среди векторов найдется линейно независимых, через которые линейно выражаются все остальные. Пусть, для определенности, это будут
Обозначим через подпространство, порожденное в векторами и покажем, что (r-мерное) подпространство и ядро пересекаются только по нулевому вектору. Действительно, если то Но так как векторы линейно независимы, то
Покажем теперь, что подпространства и порождают все (т. е. что их сумма совпадает с Пусть х — произвольный вектор из Тогда , следовательно, Вектор принадлежит, очевидно, а разность так как Мы нашли, что где
Таким образом, пространство равно прямой сумме подпространств и а значит, его размерность равна сумме размерностей этих подпространств.
В дальнейшем нам понадобится еще такое
Определение 2. Пусть — линейный оператор, отображающий пространство в пространство (вообще говоря, другой размерности). Тогда множество всех векторов у из вида где называется областью значений оператора (или образом пространства при отображении а множество всех векторов х из таких, что его ядром.
Нетрудно видеть, что область значений оператора заявляется подпространством в а его ядро — подпространством в (докажите это),
Линейное пространство
Пусть L- это некоторое множество, элементы которого мы удем называть «векторами», P- некоторое(числовое поле). Пусть так же выполняются следующие условия.
1. В L определена операция сложения элементов.
2. В Lопределена операция умножения элемента на число из P.
3. Эти операции удовлетворяют законам дистрибутивности.
Тогда говорим, что L образует линейное пространство над полем P относительно операций сложений и умножней.
Произведение линейных операторов: определение и свойства.
Критерии невырожденности линейного оператора.
Ядро, образ, ранг и дефект линейного оператора. Связь ранга и дефекта
ВНИМАНИЕ, ДЛЯ ПОЛНОГО ОЗНАКОМЛЕНИЕ ПРОСМОТРИТЕ ВОПРОС 33!
Ядро и область значений линейного оператора
Ядро оператора: 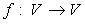
Область значений (образ) оператора 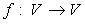
Множества Ker f и Im f являются подпространствами пространства V.
Ранг оператора 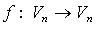
dim Im f = rank A.
Дефектом оператора 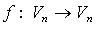
dim Im f + dim Ker f = n.
Матрица линейного оператора. Теорема о координатах образа вектора при линейном преобразовании
-Матрица линейного оператора.
Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y .
В этих пространствах определены базисы e = 1, . en> и f = 1, . fm>.
Пусть A(ei ) = a1i·f1 + a2i·f2 + . + ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2, . n.
Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = aij>= A(ej )i>:
Координаты образа y = A(x) и прообраза x связаны соотношеннием:
y =A· x,
-Теорема о координатах образа вектора при линейном преобразовании.
Образ вектора х равен произведению матрицы линейного оператора на столбец его координат: если у = А(х), то
Решение.
Множество 

То есть 
Найдем ядро оператора.
Определение. Ядром (или нуль-пространством) линейного оператора 
В соответствии с определением ядра
Итак, ядром оператора A является точка 
Найдем собственные вектора заданного линейного оператора.
Число 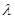
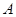
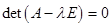
Решая его, имеем
Таким образом, получаем собственные числа оператора:
Для каждого из полученных собственных значений найдем собственные векторы.
Их можно найти их системы 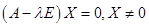
А)
Решим однородную систему уравнений.
Матрица коэффициентов 


Таким образом, общее решение системы

Из общего решения находим фундаментальную систему решений:

С использованием фундаментальной системы решений, общее решение может быть записано в виде 
Б)

Решим однородную систему уравнений.

Матрица коэффициентов 


Таким образом, общее решение системы 
Из общего решения находим фундаментальную систему решений: 
С использованием фундаментальной системы решений, общее решение может быть записано в виде 
Ответ:

Собственные числа оператора: 
Собственные векторы: