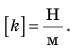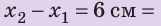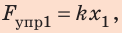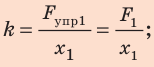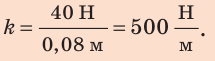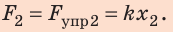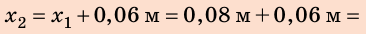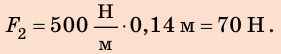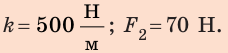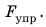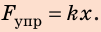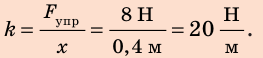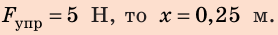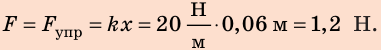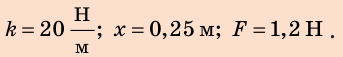Содержание:
Деформация тела:
Вспомните ненастный день: дует порывистый ветер, гнутся деревья. Чем сильнее ветер, тем больше гнутся деревья. А вот физики говорят, что деревья деформируются. Когда ветер стихает, деревья возвращаются в свое первоначальное положение — деформация исчезает. Но если ветер достаточно сильный, то ветви деревьев и даже их стволы могут сломаться.
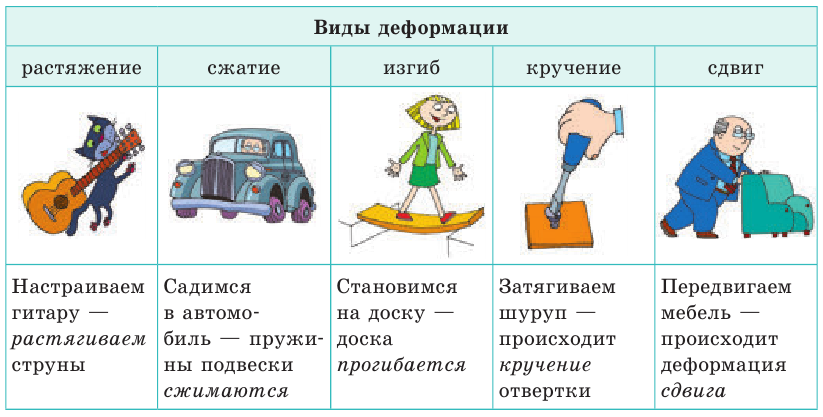
Виды деформации
Уже отмечалось, что результатом действия силы на тело может быть как изменение скорости движения тела, так и его деформация. Например, если толкнуть мячик, то он придет в движение, а некоторые его части при толчке сместятся относительно друг друга — мячик деформируется.
Деформация — изменение формы и (или) размеров тела. В зависимости от того, как именно части тела смещаются относительно друг друга, различают деформации растяжения, сжатия, изгиба, кручения, сдвига (см. таблицу).
Различия упругих и пластических деформаций
Возьмите эспандер (или ластик) и сожмите его — эспандер согнется. Но если прекратить сжимать эспандер, он полностью восстановит свою форму — деформация исчезнет (рис. 19.1). Деформации, которые полностью исчезают после прекращения действия на тело внешних сил, называют упругими.
Делая глиняную фигурку, мастер мнет руками комок глины, и глина сохранит форму, которую придаст ей мастер (рис. 19.2). Тяжелый пресс на монетном дворе чеканит монеты из металлических заготовок, — после прекращения действия пресса монета не восстановит свою прежнюю форму куска металла. И глина, и металл «не помнят» своей формы до деформации и не восстанавливают ее. Деформации, которые сохраняются после прекращения действия на тело внешних сил, называют пластическими. Попробуйте привести другие примеры упругих и пластических деформаций.
Определение силы упругости
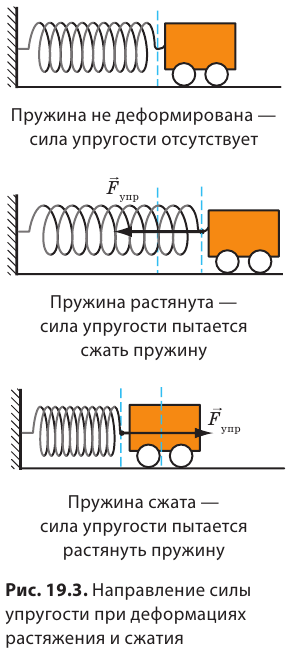
При деформации всегда возникает сила, стремящаяся восстановить то состояние тела, в котором оно находилось до деформации. Эту силу называют силой упругости (рис. 19.3).
Сила упругости — это сила, которая возникает во время деформации тела и направлена в сторону, противоположную направлению смещения частей этого тела при деформации. Обычно силу упругости обозначают символом 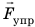
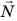
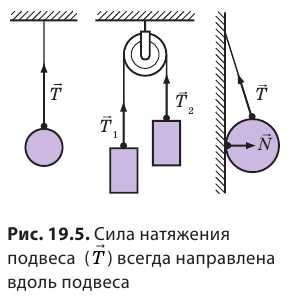
Если тело растягивает подвес (нить, жгут, шнур), то возникает сила упругости, направленная вдоль подвеса. Эту силу называют силой натяжения подвеса и обозначают символом 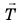
Закон Гука
Научное исследование процессов растяжения и сжатия тел начал Роберт Гук (рис. 19.6) в XVII в. Результатом работы ученого стал закон, который позже получил название закон Гука: При малых упругих деформациях растяжения или сжатия сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: 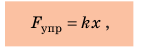
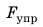
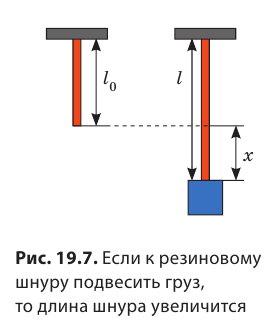
Удлинение — это физическая величина, которая характеризует деформации растяжения и сжатия и равна изменению длины тела в результате деформации. Удлинение х определяется по формуле: 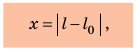
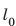
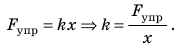
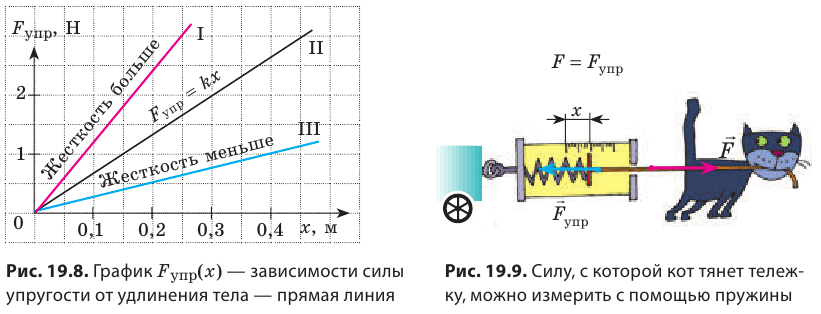
Жесткость — это характеристика тела, поэтому она не зависит ни от силы упругости, ни от удлинения. Жесткость зависит от формы и размеров тела, а также от материала, из которого тело изготовлено. Сила упругости прямо пропорциональна удлинению тела, поэтому график зависимости 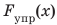
- Заказать решение задач по физике
Почему возникает сила упругости
Вы хорошо знаете, что все тела состоят из частиц (атомов, молекул, ионов). В твердых телах частицы колеблются около положений равновесия и взаимодействуют межмолекулярными силами притяжения и отталкивания. В положениях равновесия данные силы уравновешены. При деформации тела во взаимном расположении его частиц происходят изменения. Если расстояние между частицами увеличивается, то межмолекулярные силы притяжения становятся больше сил отталкивания. Если же частицы сближаются, то больше становятся межмолекулярные силы отталкивания. Другими словами: при деформации частицы «стремятся» вернуться в положение равновесия. Силы, возникающие при изменении положения одной частицы, очень малы. Но когда тело деформируется, изменяется взаимное расположение огромного количества частиц. В результате сложение сил дает заметную равнодействующую, которая противостоит деформации тела. Это и есть сила упругости. Итак, сила упругости — проявление действия межмолекулярных сил.
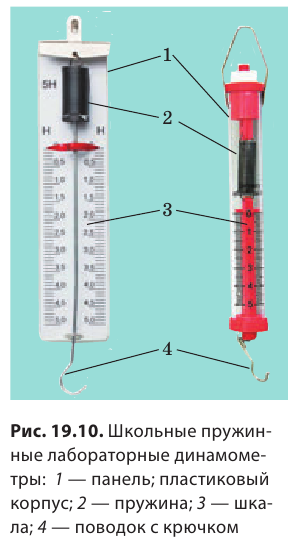
Приборы для измерения силы
Сила — это физическая величина, поэтому ее можно измерить. Приборы для измерения силы называют динамометрами. Основная составляющая простейших динамометров — пружина. Рассмотрим принцип действия таких динамометров на простом примере. Чтобы с помощью пружины, жесткость k которой известна, измерить силу F, с которой кот тянет тележку (рис. 19.9), необходимо:
1) измерить удлинение x пружины; 2) воспользовавшись законом Гука, определить силу упругости 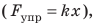
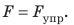
Пример №1
Действуя на пружину силой 40 Н, мальчик растянул ее на 8 см. Определите жесткость пружины. Какую силу нужно приложить мальчику, чтобы растянуть эту пружину еще на 6 см? Деформацию пружины считайте малой упругой. Анализ физической проблемы. Сила, которую прикладывает мальчик, по значению равна силе упругости, возникающей при растяжении пружины: F= уFпр (рис. 19.12). Деформация является малой упругой, поэтому воспользуемся законом Гука. Задачу будем решать в единицах СИ.
Дано:
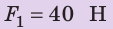
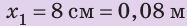
Найти:

Решение:
1. Вычислим жесткость пружины:
поэтому
2. Найдем силу, которую нужно приложить мальчику, чтобы дополнительно растянуть пружину:
По условию 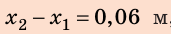
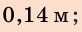
Анализ результатов. Для удлинения пружины на 8 см мальчик прикладывал силу 40 Н; для удлинения пружины еще на 6 см ему нужно увеличить силу на 30 Н — это правдоподобный результат.
Ответ:
Пример №2
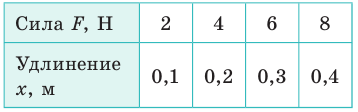
Выполняя экпериментальное задание, девочка увеличивала нагрузку на резиновый шнур. Каждый раз она измеряла силу, действующую на шнур, и соответствующее удлинение шнура. Воспользовавшись таблицей, составленной девочкой, постройте график уFпр(x). С помощью графика определите: 1) жесткость шнура; 2) удлинение шнура, когда к нему приложена сила 5 Н; 3) силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 6 см.
Анализ физической проблемы. При растяжении шнура возникает сила упругости, которая по значению равна силе, действующей на шнур: 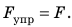
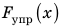
Решение:
Построив указанные в таблице точки (см. рисунок), увидим, что все они принадлежат одной прямой, значит, для любой точки графика имеем:
1) Выбрав точку А графика, найдем жесткость шнура:
2) Удлинение шнура в результате действия силы 5 Н найдем по графику: если
3) Силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 0,06 м, найдем по закону Гука:
Ответ:
Итоги:
Деформацией называют изменение формы и (или) размеров тела. Если после прекращения действия на тело внешних сил деформация полностью исчезает, то это упругая деформация; если деформация сохраняется, то это пластическая деформация.
Сила упругости 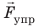
Сила упругости — проявление действия межмолекулярных сил. При малых упругих деформациях растяжения и сжатия выполняется закон Гука: сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: 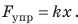
- Плотность вещества в физике
- Сила трения в физике
- Вес тела в физике
- Закон всемирного тяготения
- Сила в физике
- Силы в механике
- Сила тяжести в физике
- Сила упругости в физике и закон Гука
Деформация
Определение деформации
Деформация появляется в том случае, если разные части тела совершают разные перемещения. Так, например, если резиновый шнур тянуть за концы, то разные его части сместятся относительно друг друга, и шнур окажется деформированным (растянется, удлинится). При деформации изменяются расстояния между атомами или молекулами тел, поэтому появляются силы упругости.
Виды деформации твердого тела
Деформации можно разделить на упругие и неупругие. Упругой называют деформацию, которая исчезает при прекращении действия деформирующего воздействия. При таком виде деформации происходит возврат частиц из новых положений равновесия в кристаллической решетке в старые.
Неупругие деформации твердого тела называют пластическими. При пластической деформации происходит необратимая перестройка кристаллической решетки.
Кроме этого выделяют следующие виды деформации: растяжение (сжатие); сдвиг, кручение.
Одностороннее растяжение заключается в увеличении длины тела, при воздействии силы растяжения. Мерой такого вида деформации служит величина относительного удлинения ().
Деформация всестороннего растяжения (сжатия) проявляется в изменении (увеличении или уменьшении) объема тела. При этом форма тела не изменяется. Растягивающие (сжимающие) силы равномерно распределяются по всей поверхности тела. Характеристикой, такого вида деформации, является относительное изменение объема тела ().
Сдвиг – это вид деформации, при которой плоские слои твердого тела смещены параллельно друг другу. При этом виде деформации слои не изменяют свою форму и размер. Мерой данной деформации служит угол сдвига.
Деформация кручения состоит в относительном повороте параллельных друг другу сечений, перпендикулярных оси образца.
В теории упругости доказано, что все виды упругой деформации могут сводиться к деформациям растяжения или сжатия, которые происходят в один момент времени.
Закон Гука
Рассмотрим однородный стержень, имеющий длину l и площадь сечения S. К концам стержня приложены две силы равные по величине F, направленные по оси стержня, но в противоположные стороны. При этом длина стержня изменилась на величину .
Английским ученым Р. Гуком эмпирически было установлено, что для небольших деформаций относительное удлинение () прямо пропорционально напряжению (
):
где E – модуль Юнга; – сила, которая действует на единичную площадь поперечного сечения проводника. Иначе закон Гука записывают как:
где k – коэффициент упругости. Для силы упругости, возникающей в стержне закон Гука имеет вид:
Линейная зависимость между и
выполняется в узких пределах, при небольших нагрузках. При увеличении нагрузки зависимость
становится нелинейной, а далее упругая деформация переходит в пластическую деформацию.
Примеры решения задач
Известно, что на все тела, находящиеся на Земле, действует сила тяжести, обусловленная гравитацией.
Какие ещё силы могут возникнуть? Рассмотрим несколько примеров.
(1). На яблоко в тарелке действует сила притяжения Земли. Фрукт не проваливается сквозь тарелку, а находится в покое.
Значит, существует сила, которая уравновешивает силу тяжести.
(2). Рассмотрим тело, подвешенное на нити. Сила тяжести будет направлена вниз.
Тело не может упасть, потому что силу тяжести компенсирует сила натяжения нити.
(3). Проведём опыт.
Позволим гире опуститься на середину доски на опорах.
Рис. (1). Гиря
Вес гири воздействует на доску и оказывает деформацию изгиба — заставляет сгибаться. Свойство упругости доски вызывает противоположную силу — силу реакции опоры — для того, чтобы вернуться в исходное, недеформированное состояние. Обе силы направлены вдоль одной прямой через центр масс гири, но направления противоположны, поэтому сумма сил равна нулю.
Под весом гири доска прогнулась — изменила свою форму.
Деформацией тела называют изменение размера или формы тела под воздействием внешних сил.
При изменении формы и размера под воздействием деформирующих сил каждое упругое тело пытается вернуться в начальное состояние.
Сила упругости — сила, которая возникает при деформации тела и стремится вернуть его в исходное состояние.
Сила упругости — векторная величина, обозначается (vec{F})(_{упр}).
Чем сильнее давит тело на опору, тем больше деформация и возникающая в ответ на деформацию сила упругости. Деформация опоры прекращается в тот момент, когда действующие по вертикали силы уравновесят друг друга (сила упругости станет равной силе тяжести).
Если исчезнет деформирующая сила, то исчезнет и сила упругости.
В зависимости от приложенных сил различают виды деформации:
-
деформация растяжения и сжатия;
-
деформация сдвига;
-
деформация изгиба;
-
деформация кручения.
Деформация называется упругой в случае, если тело полностью восстанавливает свою форму и объём после прекращения действия деформирующей силы.
(4). Рассмотрим силы, действующие в опыте с гирей, подвешенной на нити.
Рис. (2). Гиря на штативе
Синей стрелкой обозначен вектор силы тяжести (vec{F_2}), направленной к центру Земли (вертикально вниз). Силе тяжести противодействует сила упругости нити (vec{F_1}), называемая силой натяжения нити. Она обозначена красной стрелкой, направленной вверх.
Гиря не движется, значит, силы компенсируют друг друга, сила тяжести равна силе упругости: (vec{F_1}+vec{F_2}=0), но направлена противоположно.
Подвесом называют нить, на которую подвешивается тело. Обычно имеют в виду нерастяжимую прочную нить.
Подвесом может быть упругое тело: пружина, резина. Значит, оно может растягиваться (деформироваться) под действием силы тяжести тела. При растяжении длина подвеса изменяется на некоторую величину, которую называют удлинением: (Delta l=l-l_0), где (l_0) — начальная длина нити, а (l) — конечная длина.
Закон Гука: изменение длины тела при растяжении (или сжатии) прямо пропорционально модулю силы упругости
(Δl) — удлинение тела (изменение его длины),
(k) — коэффициент пропорциональности, называющийся жёсткостью (пружины), которая зависит от материала.
Закон Гука работает только в случае, если деформация была упругая.
Источники:
Рис. 1. Гиря. © ЯКласс.
Рис. 2. Гиря на штативе. © ЯКласс.
The deformation of a thin straight rod into a closed loop. The length of the rod remains almost unchanged during the deformation, which indicates that the strain is small. In this particular case of bending, displacements associated with rigid translations and rotations of material elements in the rod are much greater than displacements associated with straining.
In physics and continuum mechanics, deformation is the transformation of a body from a reference configuration to a current configuration.[1] A configuration is a set containing the positions of all particles of the body.
A deformation can occur because of external loads,[2] intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc.
Strain is related to deformation in terms of relative displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered.
In a continuous body, a deformation field results from a stress field due to applied forces or because of some changes in the temperature field of the body. The relation between stress and strain is expressed by constitutive equations, e.g., Hooke’s law for linear elastic materials. Deformations which cease to exist after the stress field is removed are termed as elastic deformation. In this case, the continuum completely recovers its original configuration. On the other hand, irreversible deformations remain. They exist even after stresses have been removed. One type of irreversible deformation is plastic deformation, which occurs in material bodies after stresses have attained a certain threshold value known as the elastic limit or yield stress, and are the result of slip, or dislocation mechanisms at the atomic level. Another type of irreversible deformation is viscous deformation, which is the irreversible part of viscoelastic deformation.
In the case of elastic deformations, the response function linking strain to the deforming stress is the compliance tensor of the material.
Strain[edit]
Strain represents the displacement between particles in the body relative to a reference length.
Deformation of a body is expressed in the form x = F(X) where X is the reference position of material points of the body. Such a measure does not distinguish between rigid body motions (translations and rotations) and changes in shape (and size) of the body. A deformation has units of length.
We could, for example, define strain to be
where I is the identity tensor.
Hence strains are dimensionless and are usually expressed as a decimal fraction, a percentage or in parts-per notation. Strains measure how much a given deformation differs locally from a rigid-body deformation.[3]
A strain is in general a tensor quantity. Physical insight into strains can be gained by observing that a given strain can be decomposed into normal and shear components. The amount of stretch or compression along material line elements or fibers is the normal strain, and the amount of distortion associated with the sliding of plane layers over each other is the shear strain, within a deforming body.[4] This could be applied by elongation, shortening, or volume changes, or angular distortion.[5]
The state of strain at a material point of a continuum body is defined as the totality of all the changes in length of material lines or fibers, the normal strain, which pass through that point and also the totality of all the changes in the angle between pairs of lines initially perpendicular to each other, the shear strain, radiating from this point. However, it is sufficient to know the normal and shear components of strain on a set of three mutually perpendicular directions.
If there is an increase in length of the material line, the normal strain is called tensile strain, otherwise, if there is reduction or compression in the length of the material line, it is called compressive strain.
Strain measures[edit]
Depending on the amount of strain, or local deformation, the analysis of deformation is subdivided into three deformation theories:
- Finite strain theory, also called large strain theory, large deformation theory, deals with deformations in which both rotations and strains are arbitrarily large. In this case, the undeformed and deformed configurations of the continuum are significantly different and a clear distinction has to be made between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.
- Infinitesimal strain theory, also called small strain theory, small deformation theory, small displacement theory, or small displacement-gradient theory where strains and rotations are both small. In this case, the undeformed and deformed configurations of the body can be assumed identical. The infinitesimal strain theory is used in the analysis of deformations of materials exhibiting elastic behavior, such as materials found in mechanical and civil engineering applications, e.g. concrete and steel.
- Large-displacement or large-rotation theory, which assumes small strains but large rotations and displacements.
In each of these theories the strain is then defined differently. The engineering strain is the most common definition applied to materials used in mechanical and structural engineering, which are subjected to very small deformations. On the other hand, for some materials, e.g., elastomers and polymers, subjected to large deformations, the engineering definition of strain is not applicable, e.g. typical engineering strains greater than 1%,[6] thus other more complex definitions of strain are required, such as stretch, logarithmic strain, Green strain, and Almansi strain.
Engineering strain[edit]
Engineering strain, also known as Cauchy strain, is expressed as the ratio of total deformation to the initial dimension of the material body on which forces are applied. The engineering normal strain or engineering extensional strain or nominal strain e of a material line element or fiber axially loaded is expressed as the change in length ΔL per unit of the original length L of the line element or fibers. The normal strain is positive if the material fibers are stretched and negative if they are compressed. Thus, we have
where e is the engineering normal strain, L is the original length of the fiber and l is the final length of the fiber. Measures of strain are often expressed in parts per million or microstrains.
The true shear strain is defined as the change in the angle (in radians) between two material line elements initially perpendicular to each other in the undeformed or initial configuration. The engineering shear strain is defined as the tangent of that angle, and is equal to the length of deformation at its maximum divided by the perpendicular length in the plane of force application which sometimes makes it easier to calculate.
Stretch ratio[edit]
The stretch ratio or extension ratio is a measure of the extensional or normal strain of a differential line element, which can be defined at either the undeformed configuration or the deformed configuration. It is defined as the ratio between the final length l and the initial length L of the material line.
The extension ratio is approximately related to the engineering strain by
This equation implies that the normal strain is zero, so that there is no deformation when the stretch is equal to unity.
The stretch ratio is used in the analysis of materials that exhibit large deformations, such as elastomers, which can sustain stretch ratios of 3 or 4 before they fail. On the other hand, traditional engineering materials, such as concrete or steel, fail at much lower stretch ratios.
True strain[edit]
The logarithmic strain ε, also called, true strain or Hencky strain.[7] Considering an incremental strain (Ludwik)
the logarithmic strain is obtained by integrating this incremental strain:
where e is the engineering strain. The logarithmic strain provides the correct measure of the final strain when deformation takes place in a series of increments, taking into account the influence of the strain path.[4]
Green strain[edit]
The Green strain is defined as:
Almansi strain[edit]
The Euler-Almansi strain is defined as
Normal and shear strain[edit]
Two-dimensional geometric deformation of an infinitesimal material element.
Strains are classified as either normal or shear. A normal strain is perpendicular to the face of an element, and a shear strain is parallel to it. These definitions are consistent with those of normal stress and shear stress.
Normal strain[edit]
For an isotropic material that obeys Hooke’s law, a normal stress will cause a normal strain. Normal strains produce dilations.
Consider a two-dimensional, infinitesimal, rectangular material element with dimensions dx × dy, which, after deformation, takes the form of a rhombus. The deformation is described by the displacement field u. From the geometry of the adjacent figure we have
and
For very small displacement gradients the squares of the derivative of 

The normal strain in the x-direction of the rectangular element is defined by
Similarly, the normal strain in the y— and z-directions becomes
Shear strain[edit]
| Shear strain | |
|---|---|
|
Common symbols |
γ or ε |
| SI unit | 1, or radian |
|
Derivations from |
γ = τ/G |
The engineering shear strain (γxy) is defined as the change in angle between lines AC and AB. Therefore,
From the geometry of the figure, we have
For small displacement gradients we have
For small rotations, i.e. α and β are ≪ 1 we have tan α ≈ α, tan β ≈ β. Therefore,
thus
By interchanging x and y and ux and uy, it can be shown that γxy = γyx.
Similarly, for the yz— and xz-planes, we have
The tensorial shear strain components of the infinitesimal strain tensor can then be expressed using the engineering strain definition, γ, as
Metric tensor[edit]
A strain field associated with a displacement is defined, at any point, by the change in length of the tangent vectors representing the speeds of arbitrarily parametrized curves passing through that point. A basic geometric result, due to Fréchet, von Neumann and Jordan, states that, if the lengths of the tangent vectors fulfil the axioms of a norm and the parallelogram law, then the length of a vector is the square root of the value of the quadratic form associated, by the polarization formula, with a positive definite bilinear map called the metric tensor.
Description of deformation[edit]
Deformation is the change in the metric properties of a continuous body, meaning that a curve drawn in the initial body placement changes its length when displaced to a curve in the final placement. If none of the curves changes length, it is said that a rigid body displacement occurred.
It is convenient to identify a reference configuration or initial geometric state of the continuum body which all subsequent configurations are referenced from. The reference configuration need not be one the body actually will ever occupy. Often, the configuration at t = 0 is considered the reference configuration, κ0(B). The configuration at the current time t is the current configuration.
For deformation analysis, the reference configuration is identified as undeformed configuration, and the current configuration as deformed configuration. Additionally, time is not considered when analyzing deformation, thus the sequence of configurations between the undeformed and deformed configurations are of no interest.
The components Xi of the position vector X of a particle in the reference configuration, taken with respect to the reference coordinate system, are called the material or reference coordinates. On the other hand, the components xi of the position vector x of a particle in the deformed configuration, taken with respect to the spatial coordinate system of reference, are called the spatial coordinates
There are two methods for analysing the deformation of a continuum. One description is made in terms of the material or referential coordinates, called material description or Lagrangian description. A second description of deformation is made in terms of the spatial coordinates it is called the spatial description or Eulerian description.
There is continuity during deformation of a continuum body in the sense that:
- The material points forming a closed curve at any instant will always form a closed curve at any subsequent time.
- The material points forming a closed surface at any instant will always form a closed surface at any subsequent time and the matter within the closed surface will always remain within.
Affine deformation[edit]
A deformation is called an affine deformation if it can be described by an affine transformation. Such a transformation is composed of a linear transformation (such as rotation, shear, extension and compression) and a rigid body translation. Affine deformations are also called homogeneous deformations.[8]
Therefore, an affine deformation has the form
where x is the position of a point in the deformed configuration, X is the position in a reference configuration, t is a time-like parameter, F is the linear transformer and c is the translation. In matrix form, where the components are with respect to an orthonormal basis,
The above deformation becomes non-affine or inhomogeneous if F = F(X,t) or c = c(X,t).
Rigid body motion[edit]
A rigid body motion is a special affine deformation that does not involve any shear, extension or compression. The transformation matrix F is proper orthogonal in order to allow rotations but no reflections.
A rigid body motion can be described by
where
In matrix form,
Displacement[edit]
Figure 1. Motion of a continuum body.
A change in the configuration of a continuum body results in a displacement. The displacement of a body has two components: a rigid-body displacement and a deformation. A rigid-body displacement consists of a simultaneous translation and rotation of the body without changing its shape or size. Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration κ0(B) to a current or deformed configuration κt(B) (Figure 1).
If after a displacement of the continuum there is a relative displacement between particles, a deformation has occurred. On the other hand, if after displacement of the continuum the relative displacement between particles in the current configuration is zero, then there is no deformation and a rigid-body displacement is said to have occurred.
The vector joining the positions of a particle P in the undeformed configuration and deformed configuration is called the displacement vector u(X,t) = uiei in the Lagrangian description, or U(x,t) = UJEJ in the Eulerian description.
A displacement field is a vector field of all displacement vectors for all particles in the body, which relates the deformed configuration with the undeformed configuration. It is convenient to do the analysis of deformation or motion of a continuum body in terms of the displacement field. In general, the displacement field is expressed in terms of the material coordinates as
or in terms of the spatial coordinates as
where αJi are the direction cosines between the material and spatial coordinate systems with unit vectors EJ and ei, respectively. Thus
and the relationship between ui and UJ is then given by
Knowing that
then
It is common to superimpose the coordinate systems for the undeformed and deformed configurations, which results in b = 0, and the direction cosines become Kronecker deltas:
Thus, we have
or in terms of the spatial coordinates as
Displacement gradient tensor[edit]
The partial differentiation of the displacement vector with respect to the material coordinates yields the material displacement gradient tensor ∇Xu. Thus we have:
or
where F is the deformation gradient tensor.
Similarly, the partial differentiation of the displacement vector with respect to the spatial coordinates yields the spatial displacement gradient tensor ∇xU. Thus we have,
or
Examples of deformations[edit]
Homogeneous (or affine) deformations are useful in elucidating the behavior of materials. Some homogeneous deformations of interest are
- uniform extension
- pure dilation
- equibiaxial tension
- simple shear
- pure shear
Plane deformations are also of interest, particularly in the experimental context.
Plane deformation[edit]
A plane deformation, also called plane strain, is one where the deformation is restricted to one of the planes in the reference configuration. If the deformation is restricted to the plane described by the basis vectors e1, e2, the deformation gradient has the form
In matrix form,
From the polar decomposition theorem, the deformation gradient, up to a change of coordinates, can be decomposed into a stretch and a rotation. Since all the deformation is in a plane, we can write[8]
where θ is the angle of rotation and λ1, λ2 are the principal stretches.
Isochoric plane deformation[edit]
If the deformation is isochoric (volume preserving) then det(F) = 1 and we have
Alternatively,
Simple shear[edit]
A simple shear deformation is defined as an isochoric plane deformation in which there is a set of line elements with a given reference orientation that do not change length and orientation during the deformation.[8]
If e1 is the fixed reference orientation in which line elements do not deform during the deformation then λ1 = 1 and F·e1 = e1.
Therefore,
Since the deformation is isochoric,
Define
Then, the deformation gradient in simple shear can be expressed as
Now,
Since
we can also write the deformation gradient as
See also[edit]
- The deformation of long elements such as beams or studs due to bending forces is known as deflection.
- Euler–Bernoulli beam theory
- Deformation (engineering)
- Finite strain theory
- Infinitesimal strain theory
- Moiré pattern
- Shear modulus
- Shear stress
- Shear strength
- Stress (mechanics)
- Stress measures
References[edit]
- ^ Truesdell, C.; Noll, W. (2004). The non-linear field theories of mechanics (3rd ed.). Springer. p. 48.
- ^ Wu, H.-C. (2005). Continuum Mechanics and Plasticity. CRC Press. ISBN 1-58488-363-4.
- ^ Lubliner, Jacob (2008). Plasticity Theory (PDF) (Revised ed.). Dover Publications. ISBN 978-0-486-46290-5. Archived from the original (PDF) on 2010-03-31.
- ^ a b Rees, David (2006). Basic Engineering Plasticity: An Introduction with Engineering and Manufacturing Applications. Butterworth-Heinemann. ISBN 0-7506-8025-3. Archived from the original on 2017-12-22.
- ^ «Earth.»Encyclopædia Britannica from Encyclopædia Britannica 2006 Ultimate Reference Suite DVD .[2009].
- ^ Rees, David (2006). Basic Engineering Plasticity: An Introduction with Engineering and Manufacturing Applications. Butterworth-Heinemann. p. 41. ISBN 0-7506-8025-3. Archived from the original on 2017-12-22.
- ^ Hencky, H. (1928). «Über die Form des Elastizitätsgesetzes bei ideal elastischen Stoffen». Zeitschrift für technische Physik. 9: 215–220.
- ^ a b c Ogden, R. W. (1984). Non-linear Elastic Deformations. Dover.
Further reading[edit]
- Bazant, Zdenek P.; Cedolin, Luigi (2010). Three-Dimensional Continuum Instabilities and Effects of Finite Strain Tensor, chapter 11 in «Stability of Structures», 3rd ed. Singapore, New Jersey, London: World Scientific Publishing. ISBN 978-9814317030.
- Dill, Ellis Harold (2006). Continuum Mechanics: Elasticity, Plasticity, Viscoelasticity. Germany: CRC Press. ISBN 0-8493-9779-0.
- Hutter, Kolumban; Jöhnk, Klaus (2004). Continuum Methods of Physical Modeling. Germany: Springer. ISBN 3-540-20619-1.
- Jirasek, M; Bazant, Z.P. (2002). Inelastic Analysis of Structures. London and New York: J. Wiley & Sons. ISBN 0471987166.
- Lubarda, Vlado A. (2001). Elastoplasticity Theory. CRC Press. ISBN 0-8493-1138-1.
- Macosko, C. W. (1994). Rheology: principles, measurement and applications. VCH Publishers. ISBN 1-56081-579-5.
- Mase, George E. (1970). Continuum Mechanics. McGraw-Hill Professional. ISBN 0-07-040663-4.
- Mase, G. Thomas; Mase, George E. (1999). Continuum Mechanics for Engineers (2nd ed.). CRC Press. ISBN 0-8493-1855-6.
- Nemat-Nasser, Sia (2006). Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials. Cambridge: Cambridge University Press. ISBN 0-521-83979-3.
- Prager, William (1961). Introduction to Mechanics of Continua. Boston: Ginn and Co. ISBN 0486438090.
Деформация тела
Код классификатора ОГЭ 1.12.
Деформация тела. Упругие и неупругие деформации. Закон упругой деформации (закон Гука).
Под нагрузкой материалы деформируются. Это связано с тем, что нагрузка вызывает перемещение частиц тела относительно друг друга. Деформация сопровождается изменением величин межатомных сил, мерой которого является механическое напряжение.
Определение деформации
Деформация тела – изменение формы или объёма тела под действием внешних сил.
Изменение длины тела Δl = l – l0, где l0 – начальная длина недеформированного тела, l – длина деформированного тела, принято называть величиной деформации.
Величина деформации – это скалярная физическая величина, которая может быть и положительной (тело растягивается), и отрицательной (тело сжимается).
Сила упругости направлена против смещения частей тела при деформации, возникает в деформируемом теле, но приложена к тому объекту, действием которого вызвана деформация.
Виды и типы деформации
Деформации разделяются на два типа:
- обратимые или упругие – исчезают после окончания действия приложенных сил;
- необратимые или неупругие (пластические, ползучести) – остаются после окончания действия приложенных сил.
Пластические деформации – это необратимые деформации, вызванные изменением напряжений. Пластичностью называется способность
вещества получать большие остаточные деформации без разрушения.
Деформации ползучести – это деформации, возникающие под действием длительного воздействия на тело постоянного напряжения.
Ползучесть и пластичность внешне схожи, но механизм ползучести имеет преимущественно диффузионную природу, а пластичность связана
с быстрым скольжением вдоль атомных плоскостей. При температурах, близких к температуре плавления, различие между этими видами деформации исчезает.
Наиболее простые виды деформации: 1) растяжение / сжатие, 2) сдвиг, 3) изгиб, 4) кручение. Практически любую деформацию можно представить одновременным наложением нескольких из указанных видов простой деформации, которые, в конечном счете, могут быть сведены к двум первым видам.
Упругие и неупругие деформации
Упругая деформация – деформация, при которой после прекращения действия силы размеры и форма тела полностью восстанавливаются. Деформация перестает быть упругой, если внешняя сила становится больше определенной величины, которая носит название предела упругости. При таком виде деформации происходит возврат частиц из новых положений равновесия в кристаллической решетке в старые. Тело полностью восстанавливает свои размеры и форму после снятия нагрузки.
Неупругая деформация — деформация, при которой происходит необратимая перестройка кристаллической решетки.
Упругие деформации весьма малы, и их измерение требует высокой точности. Измерение деформаций называется тензометрией.
Закон упругой деформации (закон Гука)
Закон Гука: Для тонкого растяжимого стержня модуль силы упругости прямо пропорционален величине деформации: Fупр = k |Δl|, где
k — коэффициент пропорциональности (коэффициент упругости), называемый жёсткостью;
Δl — абсолютное удлинение (сжатие) стержня.
Единица измерения жёсткости в системе СИ: Н/м. Коэффициент упругости зависит от материала, формы и размеров деформируемого тела. Можно выделить зависимость от размеров стержня (площади поперечного сечения — S и длины — L) явно, записав коэффициент упругости как k = ES/L.
Величина E называется модулем Юнга. Если ввести относительное удлинение ε = Δl/l и нормальное напряжение в поперечном сечении σ = F/S, то закон закон Гука для относительных величин запишется как σ = Eε. В такой форме он справедлив для любых малых объёмов материала. Также при расчёте прямых стержней применяют запись закона Гука в относительной форме Δl = Fl/ES.
Внимание! Если тело отсчёта выбранной ИСО расположить у свободного конца деформируемого тела, то при его деформации координата этого конца тела равна величине деформации. Тогда формула закона Гука, записанного для проекции силы упругости, принимает вид: Fупр.x = –kх. Знак «минус» в этом случае указывает на то, что сила упругости направлена в сторону, противоположную смещению частей тела при деформации.
Величины деформаций, для которых справедлив закон Гука, определяются экспериментально для каждого деформируемого тела.
Внимание! Линейная зависимость между модулем силы упругости и удлинением пружины (закон Гука) лежит в основе способа измерения силы с помощью динамометра.
При этом модуль измеряемой силы равен силе упругости пружины, которая, в свою очередь, рассчитывается по величине деформации. Для правильного измерения силы, растягивающей пружину динамометра, необходимо, чтобы во время измерения динамометр находился в покое или двигался прямолинейно и равномерно! Только в этом случае модуль измеряемой силы и модуль силы упругости равны друг другу.
Закон Гука — описывает поведение деформируемого твердого тела в зоне упругости. Закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между силой и деформацией становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Частные случаи силы упругости:
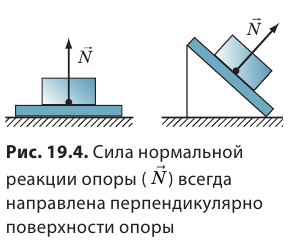
- Сила реакции опоры N: возникает при деформации опоры, приложена к телу, деформирующему опору, и направлена перпендикулярно поверхности опоры.
- Сила натяжения (нити, сцепки) Т: возникает в нити, приложена к телу, действие которого вызывает деформацию нити, и направлена вдоль нити в сторону, противоположную деформации.
Внимание! При решении задач часто используется физическая модель «невесомая нерастяжимая нить». Если нить невесома, то она не рассматривается в качестве отдельного тела, для неё не пишется уравнение движения. Условие невесомости приводит также к тому, что силы упругости, возникающие в нити и приложенные к двум связанным телам, равны по модулю (исключение могут составлять задачи, в которых нить перекинута через весомый блок). Нерастяжимость нити приводит к тому, что связанные ею тела движутся с одинаковым по модулю ускорением.
Конспект урока по физике «Деформация тела». Следующая тема: «Всемирное тяготение».
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике