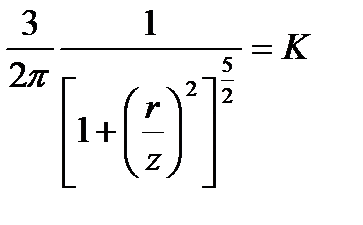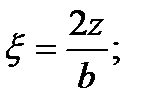Содержание:
- Сосредоточенные силы и распределенные нагрузки
- Плоская система параллельных сил
- Равновесие системы тел
- Статически обозначенные и статически неопределенные задачи
- Методика решения задач на равновесие системы тел
Такие силы называются сосредоточенными. Однако в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы прежде всего характеризуются интенсивностью q, т.е. величиной силы, приходящейся на единицу поверхности или линии.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Сосредоточенные силы и распределенные нагрузки
Мы рассматривали силы, которые были представлены в виде вектора, приложенного к точке. Однако в природе существует большое количество взаимодействий тел, осуществляются не в точке и которые нельзя представить в виде вектора, приложенного к точке.
Такими силовыми факторами являются силы давления жидкости или газа в поверхность твердых тел, силы тяжести, как массовые силы, электромагнитные силы тому подобное. Поэтому в теоретической механике вводится понятие о распределенных силах, которые делятся на поверхностные и объемные.
Поверхностные силы действуют на некоторую поверхность тела. Объемные силы действуют на каждый элемент объема тела, рассматривается. Примером последних сил является сила притяжения.
В теоретической механике рассматривается воздействие на тело только сосредоточенных сил, приложенных к абсолютно твердым телам. А потому
распределенную нагрузку необходимо заменить его равнодействующей, то есть
сосредоточенной силой. Введем несколько общих положений.
Распределенная нагрузка характеризуется его интенсивностью 
силовых схемах оно изображается в виде эпюры элементарных сил, то есть графика интенсивности нагрузки, приложенная к линейному элементу тела.
В общем случае распределенная нагрузка изображается в виде определенной кривой, отражающей данный закон изменения интенсивности нагрузки на участке тела (рис. 1.20). Направление действия нагрузки показывается стрелками.
Сначала рассмотрим равномерно распределенную нагрузку и нагрузку, распределенную по линейному закону. Заменяем распределенную нагрузку сосредоточенной силой.
Рассмотрим эти два случая:
— равномерно распределенная нагрузка (или нагрузка, распределенная по закону прямоугольника) изображается на схемах в виде прямоугольника, размеры которого таковы: высота — это интенсивность нагрузки 

Q = q · l,
где q — интенсивность нагрузки, Н/м; l — длина участка тела, на которой приложенная нагрузка, м.
Точка C приложения равнодействующей силы 

— нагрузка распределена по линейному закону (то есть по закону треугольника). В этом случае (рис. 1.22) интенсивность распределенной нагрузки на участке l меняется от 0 до максимального значения qmax. Равнодействующая сила 
Точка C приложения равнодействующей 


Плоская система параллельных сил
Когда линии действия всех сил параллельны, то всегда в плоскости можно так
расположить оси координат, одна из них будет обязательно параллельной заданным силам, а вторая — перпендикулярной. А потому, чтобы тело под действием плоской системы параллельных сил находилось в равновесии, необходимо приравнять к нулю алгебраическую сумму проекций всех сил на параллельную ось и алгебраическую сумму моментов всех сил относительно произвольной точки. В данном случае система условий равновесия (1.54) упрощается и будет иметь такой вид
Для равновесия тела, находящегося под действием системы параллельных сил
на плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил
на ось, параллельная силам, и алгебраическая сумма моментов всех сил относительно произвольной точки А плоскости равны нулю.
Для системы параллельных сил на плоскости можно использовать и такие условия равновесия
Для равновесия тела, находящегося под действием системы параллельных сил на плоскости, необходимо и достаточно, чтобы алгебраические суммы моментов всех
сил относительно любых двух точек плоскости равны нулю.
Однако для этих условиях существует ограничение: линия АВ, которой можно соединить
центры моментов, не должна быть параллельной силам.
Данные условия наиболее пригодны при расчетах двухопорных балок. Используя эти условия, составляют алгебраические суммы моментов всех сил относительно точек A и B, в которых установлены опоры балки.
Рассмотрим примеры задач на равновесие тела под действием плоской системы произвольных сил.
Пример:
Однородная балка АВ прямоугольного сечения весом 400 Н имеет один конец А, который закреплен шарнирно, и опирается на точечную опору O (рис. 1.23). Ко второму концу балки В подвешен груз весом 200 Н. Длина балки 4 м, точечная опора расположена на расстоянии ¾ длины балки от шарнирной опоры. Угол наклона балки к горизонту составляет α = 30º.
Определить реакции опор балки.
Краткое условие задачи:
G = 400 H ;
Q = 200 H ;
AB = 4 м;
AO = 3/4 AB = 3 м ;
α = 30º.
RA = ?
Rо = ?
Решение.
Составляем расчетно–силовую схему задачи. Приложим к оси балки заданные активные силы: силу тяжести 



Далее условно освобождаем балку от связей и заменяем их соответствующими реакциями связей. В точке A размещена неподвижная шарнирная опора, она имеет
две составляющие реакции 

координат. В точке O — точечная опора, которая имеет одну реакцию 
Таким образом, балка находится в равновесии под действием плоской системы произвольных сил. Для решения этой задачи используем условия равновесия (1.54),
Поскольку оси координат x и y заданные по условию задачи, то составим соответствующие уравнения равновесия
Если подставить значения известных величин в эти уравнения равновесия, то получим
С третьего уравнения вычислим реакцию Ro:
Ro = 
и подставим ее значение в первые два уравнения. Будем иметь
ХА = 
YА = 400 + 200 – 0,866 · 461,86 = 160,04 Н.
Поскольку определены две составляющие реакции, приложенные в точке A, — ХА и YА, то геометрическим добавлением можно вычислить модуль полной реакции RA. А именно:
Таким образом определении все искомые реакции.
Ответ: RA = 280,97 Н;
Rо = 461,86 Н.
Пример.
Определить реакции опоры однородной балки АВ прямоугольного сечения, один конец которого A жестко закреплен в стене и находящийся под действием сосредоточенной силы P = 4,0 kH, пары сил с моментом m = 2,0 kH · м и равномерно распределенной нагрузки интенсивностью q = 1,5 
нагрузка действует на участке 3 м от точки A. Угол наклона сосредоточенной силы 
Краткое условие задачи:
P = 4,0 kH;
m = 2,0 kH · м;
q = 1,5 
АВ = 5 м;
AС = 3 м;
α = 30º
RA = ?
МA = ?
Решение.
Составляем расчетно-силовую схему. Покажем все силы, приложенные к балке АВ. Прежде всего, это заданные активные силы — сила 


Сила 
Далее условно освобождаем балку от вязи и заменяем ее соответствующими реакциями вязи. В точке A — жесткое закрепление балки в стене, а потому оно имеет две составляющие реакции: 

координат, и реактивный момент MA. Направление этого неизвестного момента
показываем на силовой схеме произвольно, например, — против направления стрелки
часов. Если же при окончательном определении момента MA получим отрицательный знак, то получим, что действительное направление момента — противоположно. Покажем на силовой схеме линейные и угловые размеры. Оси координат показаны на схеме.
Как видно из построенной расчетно–силовой схемы, балка находится под действием плоской системы произвольных сил. Используем условия равновесия (1.54). А именно = 0.
Составим соответствующие уравнения равновесия
Если подставить значения известных величин в эти уравнения равновесия, то получаем
Из первого уравнения вычислим XA:
XA = 4,0

Из второго уравнения вычислим YA:
YA = 4,5 + 4,0 · 
С третьего уравнения вычислим MA:
MA = 2,0 + 4,5 

Поскольку составляющие реакций XA и YA, приложенных в точке A, вычислены, то можно найти модуль RA полной реакции в точке A. Будем иметь
Таким образом, определены все искомые реакции.
Ответ: RA = 4,30 kH; MA = 18,75 kH.
Равновесие системы тел
Системой тел называется совокупность нескольких тел, или которые опираются друг на друга, или соединены шарнирами, которые дают возможность относительного движения тел.
При решении задач на систему тел различают силы внешние и внутренние.
Внешние силы — это силы взаимодействия тел данной системы с другими телами, которые не входят в состав системы.
Внутренние силы — это силы взаимодействия между отдельными телами, которые входят в состав данной системы. Внутренние силы существуют попарно, как действие и
противодействие.
Статически обозначенные и статически неопределенные задачи
Задача является статически обозначенной, если для нее можно составить такое
количество уравнений равновесия материальной системы, не меньше, чем число
неизвестных.
Задача, является статически неопределенной, если число уравнений равновесия
системы меньше, чем число неизвестных.
В теоретической механике рассматриваются только статически обозначенные
материальные системы.
Методика решения задач на равновесие системы тел
Равновесие системы тел можно рассматривать в целом под действием только
внешних сил. Но может так случиться, что количество уравнений равновесия будет
меньше, чем количество неизвестных. Тогда необходимо рассматривать равновесие
отдельных тел системы, условно разделяя ее обязательно по внутренним связям. Причем необходимо учитывать, что внутренние силы реакций входят попарно, как действие и противодействие.
Рассмотрим пример решения задач на равновесие системы тел.
Пример.
На трех-шарнирную арку А В С (рис. 1.25) действует вертикальная сила Р = 10 kH. Вес каждой части балки Q1 = Q2 = 6 kH. Определить реакции шарниров А, В, С арки, размеры которой данные на рисунке.
Решение.
Как видно из схемы, заданная система тел состоит из двух пиварок I и II, которые соединены шарниром в точке С. Составим расчетно–силовую схему, где покажем заданные активные силы Q1, Q2, 












Покажем оси прямоугольной декартовой системы координат Axy.
Условно разделяем систему тел на два отдельных тела по шарниру С. Действие отброшенной части заменяем двумя реакциями 

Теперь рассмотрим отдельно равновесие каждого тела, для чего составим две системы уравнений равновесия. Используем условия равновесия.
Для первого тела (левая половина арки):



Для второго тела (правая половина арки):



Как видно из полученных шести уравнений равновесия, в них содержатся шесть неизвестных: ХА, ХB, ХС, YA, YB, YC .
Определим эти неизвестные величины. С третьего уравнения второй системы определим Y´C . Перепишем это уравнение следующим образом:
5Y´C = 4Х´С — Q2,
откуда находим реакцию Y´C :
Поскольку численно Y´C = YC , а ХС = Х´С, то подставив значения этих реакций в третье уравнение первой системы, получаем
или
8ХС = Q1 + Q2 + 4P,
откуда
Теперь есть возможность определить неизвестную реакцию Y´C . Подставив значение XC в третье уравнение второй системы, будем иметь
Из первого уравнения первой системы имеем XA = XC = 6,5 kH. А с первого уравнения второй системы должны XB = – X´C = – 6,5 kH. Направление этой реакции противоположно показанному на силовой схеме. Из второго уравнения первой системы получаем
YA = Q1 + P – YC = 6,0 + 10,0 – 4,0 = 12,0 kH.
Из второго уравнения второй системы вычислим последнюю неизвестную реакцию YB. Она будет равняться YB = Y´C + Q2 = 4,0 + 6,0 = 10,0 kH.
Таким образом вычислено все искомые величины.
Ответ:
XA = 6,5 kH; YA = 12,0 kH; XB = — 6,5 kH; YB = 10,0 kH; XC = 6,5 kH; YC = 4,0 kH.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Определение напряжений от действия нескольких сосредоточенных сил. Способ элементарного суммирования
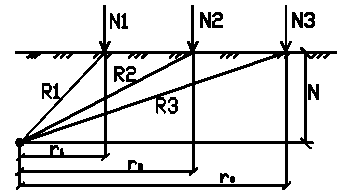
При действии нескольких сосредоточенных сил(рис.1) напряжения определяют на основе принципа (суперпозиции) независимости действия сил простым суммированием напряжений от каждой силы.
Рис1. Схема к определению напряжений от действия нескольких сил
Значение по σz определяется по следующей формуле:
Значение Кi определяется в зависимости от отношения r1/z, r2/z, r3/z по графику или таблицам.
40. Определение напряжений в грунте от действия произвольной в плане и по величине распределенной нагрузки
Пусть к поверхности изотропного линейно-деформируемого полупространства в пределах площади приложено распределенное давление. Загруженную площадь можно разбить на небольшие прямоугольники со сторонами b и l и более сложные фигуры по контуру. С некоторым приближением давление, распределенное в пределах i-го прямоугольника , можно заменить равнодействующей Ni, приложенной в центре тяжести этого давления. Вертикальное сжимающее напряжение от действия силы Ni составит σzi= KiNi/z².
Определив величину σzi от нагрузки каждой из небольших фигур , на которые разбита площадь А, и произведя суммирование этих напряжений , определим напряжение σz от действия распределенной местной нагрузки :
Точность расчета увеличивается с уменьшением b и l
Источник
Определение напряжений от действия сосредоточенной силы


Рис. 11. Схема к определению напряжений
от действия сосредоточенной силы
В строительной практике наибольший интерес представляет закономерность распределения нормальных вертикальных напряжений σZ.
В грунтовом массиве возьмем т. М, положение которой определяется полярными координатами R и β, в системе координат с началом в точке О приложения силы N.
Для упрощения вывода примем как постулат, что напряжение σR пропорционально Сosβ и обратно пропорционально квадрату расстояния R 2 от точки приложения сосредоточенной силы до т. М:
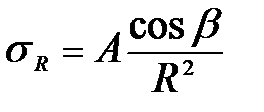
где А — коэффициент пропорциональности, определяемый из условия равновесия:

Подставив значение А из формулы (35) в формулу (34), получим
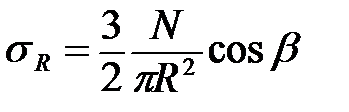
Отнесем величину радиальных напряжений не к площадке, перпендикулярной к радиусу, а к площадке, параллельной ограничивающей плоскости и составляющей с ней угол 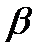
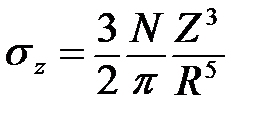
Положение точки М определяется двумя координатами z и r, тогда
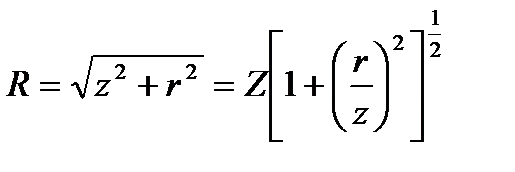
где z — глубина рассматриваемой точки от ограничивающей полупространство плоскости;
r — расстояние по горизонтали от т. М до оси Z, проходящей через точку О приложения сосредоточенной силы (рис. 11).
Подставив значение R из формулы (38) в формулу (37), получим

где коэффициент К табулирован в зависимости от соотношения r/z (табл. 6).
Определение напряжений от действия нескольких
Сосредоточенных сил
Рис. 12. Схема к расчету действия нескольких сосредоточенных сил
Если к поверхности линейно деформируемого полупространства приложить несколько сосредоточенных сил N1, N2, N3. Nn (рис. 12), то вертикальное сжимающее напряжение 

Значения коэффициентов К определяют из табл. 6 в зависимости от соотношения r/z.
Определение напряжений от действия равномерно распределенной нагрузки по прямоугольной площади
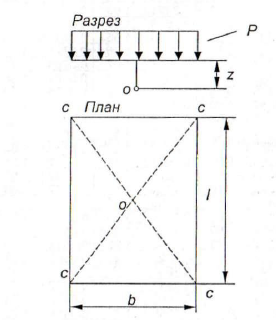
Практический интерес для строителей представляет задача об упругом полупространстве, загруженном вертикальной равномерно распределенной нагрузкой интенсивностью Р на прямоугольной площади размером Ixb (рис.13).
Эта задача используется в механике грунтов для определения напряжений в основаниях прямоугольных фундаментов.
Значение коэффициента К для вычисления сжимающих напряжений от действия сосредоточенной силы в зависимости от отношения r/z
| r/z | К | r/z | К | r/z | К | r/z | К |
| 0.00 | 0.4775 | 0.50 | 0.2733 | 0.0844 | 1.50 | 0.0251 | |
| 0.01 | 0 4773 | 0.51 | 0.2679 | 1,01 | 0.0823 | 1.51 | 0.0245 |
| 0.02 | 0 4770 | 0 52 | 0.2625 | 1,02 | 0.0803 | 1.52 | 0.0240 |
| 0.03 | 0.4764 | 0.53 | 0.2571 | 1,03 | 0.0783 | 1.53 | 0.0234 |
| 0.04 | 0.4756 | 0.54 | 0.2518 | 1,04 | 0.0764 | 1.54 | 0.0229 |
| 0.05 | 0.4745 | 0.55 | 0.2466 | 1,05 | 0.0744 | 1.55 | 0.0224 |
| 0.06 | 0.4732 | 0.56 | 0.2414 | 1,06 | 0.0727 | 1.56 | 0.0219J |
| 0 07 | 0.4717 | 0.57 | 0.2363 | 1,07 | 0.0709 | 1.57 | 0.0214 |
| 0.08 | 0.4699 | 0.58 | 0.2313 | 1,08 | 0.0691 | 1.58 | 0.0209 |
| 0.09 | 0.4679 | 0.59 | 0 2263 | 1,09 | 0.0674 | 1.59 | 0.0204 |
| 0.10 | 0.4657 | 0.60 | 0.2214 | 1,1 | 0.0658 | 1.60 | 0.0200 |
| 0.11 | 0.4633 | 0.61 | 0.2165 | 1,11 | 0.0641 | 1.61 | 0.0195 |
| 0.12 | 0.4607 | 0.62 | 0.2117 | 1,12 | 0 0626 | 1.62 | 0.0191 |
| 0.13 | 0.4579 | 0.63 | 0.2070 | 1,13 | 0.0610 | 1.63 | 0.0187 |
| 0.14 | 0.4548 | 0.64 | 0 2024 | 1,14 | 0.0595 | 1.64 | 0.0183 |
| 0.15 | 0.4516 | 0.65 | 0 1978 | 1,15 | 0.0581 | 1.65 | 0.0179 |
| 0.16 | 0.4482 | 0.66 | 0.1934 | 1,16 | 0.0567 | 1.66 | 0.0175 |
| 0.17 | 0.4446 | 0.67 | 0.1889 | 1,17 | 0.0553 | 1.67 | 0.0171 |
| 0.18 | 0.4409 | 0.68 | 0.1846 | 1,18 | 0.0539 | 1.68 | 0.0167 |
| 0.19 | 0.4370 | 0.69 | 0.1804 | 1,19 | 0.0526 | 1.69 | 0.0163 |
| 0.20 | 0.4329 | 0.70 | 0.1762 | 1,2 | 0.0513 | 1.70 | 0.0160 |
| 0.21 | 0.4286 | 0.71 | 0.1721 | 1,21 | 0.0501 | 1.71 | 0.0153 |
| 0.22 | 0.4242 | 0.72 | 0.1681 | 1,22 | 0.0489 | 1.72 | 0.0147 |
| 0.23 | 0.4197 | 0.73 | 0.1641 | 1,23 | 0.0477 | 1.73 | 0.0141 |
| 0.24 | 0.4151 | 0.74 | 0.1603 | 1,24 | 0.0466 | 1.74 | 0.0135 |
| 0.25 | 0.4103 | 0.75 | 0.1565 | 1,25 | 0.0454 | 1.75 | 0.0129 |
| 0.26 | 0.4054 | 0.76 | 0.1527 | 1,26 | 0.0443 | 1.76 | 0.0124 |
| 0.27 | 0.4004 | 0.77 | 0.1491 | 1,27 | 0.0433 | 1.77 | 0.0119 |
| 0.28 | 0.3954 | 0.78 | 0.1455 | 1,28 | 0.0422 | 1.78 | 0.0114 |
| 0.29 | 0.3902 | 0.79 | 0.1420 | 1,29 | 0.0412 | 1.79 | 0.0109 |
| 0.30 | 0.3849 | 0.80 | 0 1386 | 1,3 | 0.0402 | 1.80 | 0.0105 |
| 0.31 | 0.3796 | 0.81 | 0.1353 | 1,31 | 0.0393 | 1.81 | 0.0101 |
| 0.32 | 0.3742 | 0 82 | 0.1320 | 1,32 | 0.0384 | 1.82 | 0.0097 |
| 0.33 | 0.3687 | 0.83 | 0.1288 | 1,33 | 0.0374 | 1.83 | 0.0093 |
| 0.34 | 0.3632 | 0.84 | 0.1257 | 1,34 | 0.0365 | 1.84 | 0.0089 |
| 0.35 | 0.3577 | 0.85 | 0.1226 | 1,35 | 0.0357 | 1.85 | 0.0085 |
| 0.36 | 0.3521 | 0.86 | 0.1196 | 1,36 | 0.0348 | 1.86 | 0.0070 |
| 0.37 | 0.3465 | 0 87 | 0.1166 | 1,37 | 0.0340 | 1.87 | 0.0058 |
| 0.38 | 0.3408 | 0.88 | 0 1138 | 1,38 | 0.0332 | 1.88 | 0.0048 |
| 0.39 | 0.3351 | 0 89 | 0.1110 | 1,39 | 0.0324 | 1.89 | 0.0040 |
| 0.40 | 0.3294 | 0 90 | 0.1083 | 1,4 | 0.0317 | 1.90 | 0.0034 |
| 0.41 | 0.3238 | 0.91 | 0 1057 | 1,41 | 0.0309 | 1.91 | 0.0029 |
| 0.42 | 0.3181 | 0.92 | 0.1031 | 1,42 | 0.0302 | 1.92 | 0.0024 |
| 0.43 | 0.3124 | 0.93 | 0 1005 | 1,43 | 0.0295 | 1.93 | 0.0021 |
| 0.44 | 0.3068 | 0.94 | 0.0981 | 1,44 | 0.0288 | 1.94 | 0.0017 |
| 0.45 | 0.3011 | 0.95 | 0.0956 | 1,45 | 0.0282 | 1.95 | 0.0015 |
| 0.46 | 0.2955 | 0.96 | 0 0933 | 1,46 | 0.0275 | 1.96 | 0.0007 |
| 0.47 | 0.2899 | 0.97 | 0.0910 | 1,47 | 0.0269 | 1.97 | 0.0004 |
| 0.48 | 0.2843 | 0.98 | 0.0887 | 1,48 | 0 0263 | 1.98 | 0.0002 |
| 0.49 | 0.2788 | 0.99 | 0.0865 | 1,49 | 0.0257 | 1.99 | 0.0001 |
Рис. 13. Схема к расчету действия равномерно распределенной
Вертикальная составляющая напряжений σZ0 в точках, расположенных на различной глубине под центром прямоугольной площади, определяется по формуле:

где
b — ширина прямоугольной площадки загружения;
z — глубина рассматриваемой точки.
Тогда формула (41) примет вид

Для точек, расположенных под углами загруженной площади, вертикальная составляющая напряжений определится по формуле
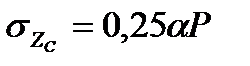
где α — коэффициент рассеивания напряжений с глубиной, принимается в зависимости от формы подошвы фундамента, соотношения сторон прямоугольного фундамента 

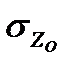

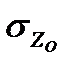
Источник
Примеры расчетов при действии сосредоточенных сил
- Пример расчета Под действием концентрированной силы Рассмотрим некоторые проблемы, связанные с растяжением и сжатием. 1. Определите диаметр стержня с постоянной длиной поперечного сечения I=60 см(рис. 130). Материал стержня-сталь СТЗ, модуль упругости Е=2-106кгф/см2. Давайте также построим график X-смещения сечения стержня и определим изменение его общей длины. Этот стержень от продольных сил участка только 120преще. В крайних случаях наблюдается сила тяги A7=N / H=P-1200 КГС, в среднем сила сжатия L/n=2P=2400 кгс. Поскольку выступающий стержень должен иметь определенное поперечное сечение,
то последнее должно быть выбрано так, чтобы абсолютная величина силы, действующей на центральную часть, была больше. Представление напряжения в разделе этого раздела описывается следующим образом: «=F-F’P^1t2ic п*. 1___________ л ___ _ 1/3 1/3 — * X в SP X ППК Д Икс Или Откуда 2Р Ф Условия интенсивности просмотра Et Я p2R ^=0g0078cm СТЗ −0.0078 см рисунок. Сто тридцать. f> / oj * сталь [допустимое напряжение / SG] растяжение и сжатие одинаковы. Статическая нагрузка может быть под 10). Если подставить число, то получится площадь поперечного сечения стержня: Ф, ч. я…
я ж г г? Принимают равным 1600 кгс / см2(см. В- F>2 1S0 cm2=1>5cm2 И его
Людмила Фирмаль
диаметр: д= Диаметр должен быть увеличен до ближайшего большого, принятого по ГОСТу. Вы должны взять D=14 мм (F=1.54cm2). Следует отметить, что расчет прочности на сжатие достаточен только для коротких стержней, особенно стальных круглых стержней менее 20. При сжатии же длинного стержня может произойти потеря сопротивления1. В нашем случае вышеуказанные условия для сжатой части маршрута выполняются. Давайте определим движение секции стержня. Например, мы условно фиксируем начало координат левого конца стержня (разрез а). Напомним, что смещение любого
поперечного сечения 1 отсчет сжатого стержня лампы указывается на CH, J9, 121 к исходной точке равно изменению длины стержневого участка между неподвижным и рассматриваемым участками. В первой секции переместите секцию, расположенную на расстоянии x от левого края стержня А-О; ОВ К(ч) — Когда Х= * О Я Когда X= — y На втором сайте Р4 — Она-3.2 • 106 • 1,54 см~0.0078 см. Я Икс= XW= п — =0,0078 см; Когда x= ~ g2~ / 1 С-1 К с=~эф Два. В третьем разделе-g-1<x< /, Схема перемещения показана на рисунке. 130 в этом случае длина
- всего стержня не изменяется. 2. Создайте график вертикальной силы, вертикального напряжения, относительной деформации и смещения ступенчатого сердечника (рис. 131). Стержень состоит из трех частей. В первом из них, на расстоянии x от неподвижного конца (0<x</), продольные силы, вертикальные напряжения и удлинение зависят не от координаты x, то есть положения сечения.: Рис сто тридцать один Перемещение сечения х от закрепленного конца стержня, Х(х) = ех== 4 пикселя Таким образом, смещение изменяется по линейному закону. В начале и в конце графика, если x=0, у вас есть следующие значения ^л= = 0; Когда x=Z 3.’ Аналогично, в следующих разделах(/<x<3Z) o _ _ _ _ _ _ e her’ Перемещение сечения
х от закрепленного конца стержня, 7L W EP • В начале второго раздела, x-I,. 4Р/ «3EF» L В конце раздела, x-31, Знак минус указывает, что рассматриваемый участок движется в направлении участка в начале координат. Третий сайт (31<x<4/) уу=р; о= Переместите участок, расположенный на расстоянии x от конуса D, P (x-31}ее В начале третьего раздела, В x-3/, В конце третьего раздела x=■41, Графики N, o, b и K показаны на рисунке. 131. График х позволяет определить изменение расстояния между любыми двумя
участками стержня, а следовательно, и изменение длины любой его части.
Людмила Фирмаль
Определим, например, изменение длины второй части стержня. Для этого переместите последний раздел(раздел с) Лучший Солнце= п п 60, 60, 60. В начале раздела (Раздел B) вам нужно вычесть движение раздела. Результат,- 2P1, 4P1. 3EF3EF Знак минус рис 112 указывает на то, что длина рассматриваемого участка уменьшилась. 3. Проверим прочность ступенчатых стержней круглого сечения(рис. 132). Материал стержня твердеет из высокоуглеродистой стали с временным сопротивлением ov=9000kgf / cm2. Стержень растягивается с усилием P=8000kgf. Из-за резких изменений поперечного сечения стержня возникает концентрация напряжений. Поскольку закаленная сталь чувствительна к нему, испытание
на прочность следует проводить при самых высоких локальных напряжениях. Чтобы найти эти напряжения, необходимо знать коэффициент концентрации напряжений. Последнее зависит от отношения радиуса скругления к меньшему диаметру чернил 124g5 PJ в нашем случае-y — =0,25. Согласно таблице. 11 теоретический коэффициент концентрации напряжений a=1,2. Номинальное напряжение рассчитывается из меньшей площади поперечного сечения стержня: he= — F— = ——-= 2550 кгс / см2. * I. 2! Четыре. Максимальное локальное напряжение определяется по формуле (4.37): Дополнением=О0″=1.2 * 2550kgs/см2=3060kgs / см2. Прибыль Или °М<Х Для хрупких материалов при статических нагрузках, как уже говорилось, возьмем коэффициент / безопасность? Б=2.5 3. Запас прочности рассматриваемого стержня находится
в заданных пределах*, то есть стержень при данной нагрузке имеет достаточный запас прочности. 4. Определите размеры поперечного сечения стержня AB и кронштейнов BC (рис. 133, а) для фиксации блока, С помощью которого груз весит Q-2000KGE, также поднимается поперечное сечение подвески блока BD. Стержни AB и подвески BD (выше) имеют круглое поперечное сечение. Материал-сталь СТЗ. Полюса Солнца сделаны из сосны и имеют квадратное сечение. Он также определяет вертикальное перемещение узлов в скобке. Конструкция кронштейна позволяет приблизительно рассчитать шарнирные их соединения друг с другом, учитывая стержни, закрепленные на стене. Конструктивная схема кронштейнов приведена на рисунке. 133, б. 125прежде просто определяет силу в узле подвески и равную ей силу, действующую на узел в — это
вторая ветвь троса, брошенная на блок. К узлу в кронштейне, и таким образом приложите усилие P=—4000kgs. Для стали СТЗ допустимое напряжение растяжения[о]= — 1600кгф/см2, для сосен допустимое напряжение сжатия fa_]=120кгф / см2. Модуль упругости для стали EO=2×10®кгс/см2,£d=10®кгс / см2 для сосны. Найти требуемую площадь поперечного сечения подвески BD. Нормальное напряжение подвески определяется по формуле Запишите условия прочности Где находится требуемая площадь поперечного сечения подвески п i_4000 м [о]1600′ =2. 5cm2. Определите диаметр подвески: dt=] L1,
13K2^=1,78 см=17,8 мм. Г Л Возьмем ближайший стандартный диаметр d=18 мм (F-2,5 4 см2). Поскольку предполагается, что стержни крепятся к стене, соединенной шарнирами, а нагрузка прикладывается к узлам (шарнирам), рассмотрим уравновешивание узлов (рис. 133, в), к которому приложены вертикальная нагрузка B и две неизвестные силы N2 11L^z, действующие соответственно на стороны стержней AB и BC и направленные вдоль их оси. При определении неизвестных сил в стержне обычно предполагается, что они растянуты и, соответственно, ведут вектор силы от узла. Знак плюс решения силы подтверждает правильность предположения о направлении силы, а знак минус должен заставить N2 и направить, как показано
на рисунке, предполагая, что на самом деле сила направлена в противоположную сторону и оба стержня сжимаются, а соответствующие стержни растягиваются. 133. Для равновесия узла B на плоскости сумма проекций всех сил, приложенных к узлам на координатных осях, достаточна, чтобы быть x 126II y был равен нулю. Направьте оси, как показано на рисунке. 133, ст. и далее… = — Az2-L’a cos a=0;= — P-JVgSin a-0. Следовательно, л^з=С-В — =- — — К Г с-5660kgf; Но У2 / 4000 • 2 / 2 п, п, п, п, п, п L; 2= — X3cosa=j кгс-4000 кгс, то есть стержень AB растягивается, а стержень BC сжимается. Из условий прочности стержня. о= — тг —
<Н G2 Определите необходимую площадь его поперечного сечения: P^9 4000 2O G. два. — 1600Х М» ■ S М • В этом случае она была равна площади поперечного сечения подвески. Так, диаметр стержня АВ должен быть равен диаметру подвески, то есть d=18 мм. Требуемая площадь поперечного сечения деревянных брусков. Г Г Ns5660 2 2Вт=[о_]=120С М=4 7С м • Квадратная сторона a-U с поперечным сечением 47 см=6,85 см. Округлите до ближайшего целого числа, возьмите== * 70 мм (F=49cm2). Определите вертикальное перемещение шарнира в кронштейне. Стержень AB удлиняется на величину ^2^2 ^С^2 4000 * 150 2 * 10E * 2.54 мм см=0,118 см. Бар сокращается на количество * 8/8 * Д * з 5660 • 1 5 0 /2 10 * * 49 см0. 245 сантиморганов
Смотрите также:
- Решение задач по сопротивлению материалов
СОСРЕДОТОЧЕННАЯ СИЛА, ДЕЙСТВУЮЩАЯ НА БАЛКУ [c.109]
Силы, действующие на балку, могут быть сосредоточенными (рис. 3.18), распределенными (рис. 3.19) или комбинированными (рис. 3.20). [c.111]
Определим внутренние силовые факторы в сечениях балки АВ (рис. 89, а), на которую действуют сосредоточенные силы / , перпендикулярные к ее оси. Эти силы вызывают вертикальные реакции и Яд опор балки. Горизонтальная составляющая реакции шарнирно-неподвижной опоры при действии только вертикальных сил, перпендикулярных к оси балки, очевидно, равна нулю. Опорные реакции и Яв могут быть определены из уравнений равновесия, составленных для всех сил, действующих на балку. Проведем мысленно произвольное поперечное сечение С на расстоянии г от левой опоры и рассмотрим условия равновесия левой и правой отсеченных частей балки (рис. 89, б и в). Левая часть должна находиться в равновесии под действием внешних сил Яа, 1, и внутренних сил, возникающих в сечении С. Правая часть должна находиться в равновесии под действием внешних сил Рд, и внутренних сил в проведенном сечении С. [c.93]
Предположим, что внешние силы, действующие на балку, смещают материальную точку вверх или вниз, смотря по направлению сил. В рассмотренном примере на левом конце балки приложена сила А. Она смещает точку вверх на величину Л =22,5 кн. Затем точка движется горизонтально до сечения С. Дальше идет равномерная нагрузка, которая смещает точку понемногу на каждом малом участке. Следовательно, точка спускается по наклонной прямой и до сечения балки О спустится на величину всей равномерной нагрузки 60 кн. Далее точка движется горизонтально до опоры В, где приложена реакция В. Она смещает точку вверх на величину В=67,5 кн. Затем движется горизонтально до сечения Е, где приложена сосредоточенная сила 30 кн, которая опускает точку на ось. [c.213]
Внешние силы, действующие на балку, сводятся к сосредоточенным силам Р, измеряемым в единицах веса (г, кг), парам сил тм, кгм) (рис. 7.2, а) и сплошным равномерно распределенным или неравномерно распределенным по длине балки нагрузкам (рис. 7.2, бив). [c.148]
Рассмотрим еще один пример решения Файлона — действие на балку-полосу трех сил, близких к сосредоточенным (рис. 4.28). Они соответствуют действию на балку силы Р и опорных реакций по PI2 (рис. 4.29). Сила считается равномерно распределенной ш длине [c.100]
Величина поперечной силы Qj. в каком-нибудь сечении балки равна алгебраической сумме проекций всех внешних сил (сосредоточенных и распределенных), действующих на балку по одну сторону от рассматриваемого сечения на одну из главных центральных осей инерции сечения. [c.93]
При действии на балку распределенной нагрузки ее разбивают на части линиями, перпендикулярными геометрической оси балки. Площадь каждой части представляют вектором, приложенным в ее центре тяжести, С помощью этих векторов, как векторов сосредоточенных сил, строят и план сил, и веревочный многоугольник. Полученную полигональную эпюру УИ уточняют путем проведения кривой, вписанной в полигон, а ступенчатую эпюру Q — путем проведения кривой или прямой (в зависимости от порядка распределенной нагрузки), проходящей через точки горизонтальных отрезков ступенчатой эпюры, находящиеся против начала и конца каждой части площади распределенной нагрузки. [c.107]
При действии на балку сосредоточенных пар сил моменты М этих пар сил откладывают на эпюре изгибающего момента в соответ- [c.107]
При статическом действии на балку сосредоточенной силы Q и распределенной силы Qo наибольшее нормальное напряжение Ста, и наибольший прогиб имеют значения [c.397]
При статическом действии на балку сосредоточенной силы Q прогиб 8 в произвольном сечении, находящемся на расстоянии [c.397]
Сосредоточенная сила может быть приложена внутри тела. В этом случае она представляет собой равнодействующую объемных сил, действующих на малый объем Д1/, а точка приложения совпадает с точкой, к которой стягивается объем АУ при предельном переходе. Примером такой силы может быть действие магнитного поля на малый магнит, помещенный внутри немагнитного тела. Внешние силы могут быть разделены на активные и реактивные по некоторому условному признаку. Например, нагруженная силами Fi балка АВ давит на опоры в точках А и В, в результате чего появляются опорные реакции Ra и Rg. В этом случае силы Fi — активные (первичные), а силы Ra и Rb — реактивные (вто- [c.20]
Действие на балку сосредоточенной силы [c.127]
ДЕЙСТВИЕ НА БАЛКУ СОСРЕДОТОЧЕННОЙ СИЛЫ [c.131]
При статическом действии на сооружение группы внешних сил работа этих сил равна половине суммы произведений каждой силы на величину соответствующего ей перемещения, вызванного действием всей группы сил. Так, например, при действии на балку (рис. 11.3) сосредоточенных сил Р , и сосредоточенных моментов ЗЛг работа внешних сил [c.426]
На основании (4.28) ясно, что функция 2 (т, х) есть прогиб в точке X при приложении сосредоточенной силы в точке т. Из (4.28) следует, что прогиб максимален при действии на балку сосредоточенной силы. [c.203]
Если массу опоры и поперечной связи присоединить к сосредоточенной массе на продольных балках, то силы, действующие на невесомую поперечную связь, будут удовлетворять следующим уравнениям равновесия [c.113]
На поперечную связь, кроме реакций ротора Q Ti Q, действуют реакции продольных балок. Если массу опоры и поперечной связи присоединить к сосредоточенной массе т на продольных балках, то силы, действующие на поперечную связь, будут удовлетворять следующим уравнениям равновесия [c.14]
Совершенство сечений по массе. В узлах конструкций применяют детали типа кронштейна, балок, цилиндрических осей и т. п., которые при передаче сосредоточенных сил работают на изгиб. За расчетную схему для таких деталей обычно принимается консольно защепленная или опертая на нескольких опорах балка, находящаяся под действием сосредоточенных сил. [c.330]
При вычислении моментов на последнем участке погонная сила, действующая на участке 3-5, разделена на две нагрузки, соответствующие участкам 3-4 и 4-5. Вычисление Qy и на левом и правом концах балки можно было бы и не проводить, так как их значения известны (см. (5.17) и (5.24)). Также можно было бы не находить значения внутренних силовых факторов на левых концах участков, начиная со второго, если там отсутствуют соответствующие сосредоточенные нагрузки. Однако эти операции удобно использовать для проверки. [c.127]
Для того чтобы пояснить содержание предыдущего параграфа, рассмотрим балку на упругом основании, подверженную действию только одной сосредоточенной силы, приложенной посредине балки. Весом балки пренебрегаем. Основное уравнение этой задачи (вне точки приложения силы) [c.285]
На свободно опертую балку действуют три сосредоточенные силы, расположенные на одинаковом расстоянии. Первая сила приложена на расстоянии 1/4 от левой опоры, вторая — в середине пролета, третья — на расстоянии L/4 от правой опоры. Найти прогиб O в середине пролета балки, если все силы имеют равную величину Р. [c.263]
Расчет на изгиб системы рама — платформа. Существующая методика расчета на изгиб рамы и платформы грузового автомобиля неудовлетворительно отражает их взаимодействие. Раму принято рассчитывать от сосредоточенных сил, действующих в опорах платформы. Значение этих сил определяется при расчете платформы как балки, находящейся под распределенной нагрузкой и лежащей на п жестких опорах. [c.129]
На правом конце балки (в сечении В) поперечная сила имеет скачок от (—2Т) до нуля, т. е. скачок, равный — -2Т, а изгибающий момент имеет скачок, равный (— 1 Тм). Следовательно, на правом конце балки к ней приложены сосредоточенная сила Рд = 2Т и сосредоточенный момент ЭЛв = —IT м. Действующая на балку нагрузка показана на рис. 29.7, в. [c.271]
Значительно сложнее определение предельных нагрузок при действии на балку сил, направленных не только сверху вниз, но также и снизу вверх, а также при действии сосредоточенных моментов. [c.713]
Таким образом, определение частот собственных колебаний балки с сосредоточенными массами сводится к решению системы однородных уравнений. Так как для каждого узла составляются два уравнения, (2. 58) и (2. 59), то для п узлов система будет состоять из 2п уравнений. Уравнение (2. 58) выражает равенство нулю суммы моментов, действующих на вырезанный узел (точка приложения сосредоточенной массы). Уравнение (2.59) выражает равенство нулю суммы проекций сил, действующих на этот узел. [c.59]
При одновременном действии на балку сосредоточенных пар сил и равномерно распределенной нагрузки получается сложная эпюра, которую необходимо предварительно расслоить , т. е. разбить ее на самостоятельные эпюры, полученные от действия сосредоточенных пар и от равномерно распределенной нагрузки. При этом часто оказывается более удобным строить эпюры с двух сторон относительно сечения, перемещение которого требуется определить. [c.161]
Балки очень часто одновременно работают на изгиб и сжатие (растяжение). Такая сложная деформация может возникнуть от совместного действия на балку осевых сил и сил, перпендикулярных ее оси, или любых сосредоточенных сил, направленных под углом, не равным 90°, к оси балки. Например, в случае торможения крана подкрановая балка подвергается одновременному действию изгиба от вертикальных сил Ру, передающихся от колес тележки, и сжатия от тормозной силы Рг, возникаю-щей при торможении (рис. 143, а). Лестничные косоуры рассчитывают на сплошную равномерно распределенную нагрузку от толпы людей, которая, действуя под углом к продольной оси косоура, вызывает в его сечениях продольную силу и изгибающий момент (рис. 143, б). [c.194]
Применяя принцип сложения действия, легко получить общие уравнения поперечной силы и изгибающего момента при действии на балку сплошной поперечной нагрузки системы сосредоточенных сил Р1 и сосредоточенных пар сил моментами ЖГ (рис. 101). Всю действующую на балку нагрузку можно расчленить на сплошную поперечную интен- [c.159]
Направления наибольших главных напряжений в различных точках сечения изображены на рис. 120, в. Эпюра шах по высоте сечения представлена на рис. 120, г. В заключение заметим, что наибольшее главное напряжение следует искать в том сечении, в котором одновременно возникают значительный изгибающий момент М и значительная поперечная сила Q, так как согласно формуле (9.21) в выражение входят Ох и т. Следовательно, для балки на двух опорах при действии сосредоточенной силы определяем у места приложения сосредоточенной силы, для заделанной балки — у защемления балки. [c.189]
Сосредоточенная сила, действующая на балку. Задача распределения напряжений в балке, подвергающейся действию сосредоточенной силы, имеет очень большое практическое значение. Ранее было показано (параграф 19), что в балках узкого прямоугольного сечения, нагруженных сплошной нагрузкой, распределение напряженийполучается с достаточной точностью на основании элементарной теории изгиба. [c.109]
Сосредоточенные силы. Если на балку действуют только ог-де-гьные силы Р , Р (фиг. 10), ю между двумя соседними силами поперечная сила не изменяется, а изгибающий момент следует закону прямой линии в зависимости от х. Линия такой балки имеет вид ступенчатой линии, а линия будет многоугольник. [c.18]
Задача 1.13. Консольная балка АО весом Р=4 Т лежит на двух опорах В к О, прйчем опора В расположена на катках. На конце А к балке приложена вертикальная сосредоточенная сила В =8 Т. На участке СО на балке находится равномерно распределенная нагрузка интенсивности = 0,5 Г/лг (интенсивностью называется величина силы, действующей на единицу длины). На участке АВ к балке приложена пара сил с моментом т = Тм. [c.47]
Решение этого уравнения в обш,ем случае представляет значительные трудности. Однако ряд важных для приложений выводов можно получить из приближенных решений. Рассмотрим задачу о действии на балку поперечной сосредоточенной возмущ,аюш,ей силы, изме-няюш,ейся периодически по закону синуса [c.286]
Дальнейшего прогресса в этой области достиг Лэмб ), который рассмотрел бесконечную балку, нагруженную через равные промежутки равными сосредоточенными силами, действующими попеременно вверх и вниз, и получил для нескольких случаев выражения кривой прогибов. Полученные результаты показывают, что элементарная теория изгиба Бернулли—Эйлера является весьма точной, если высота балки мала по сравнению с длиной. Было также показано, что уточнения для поперечной силы, даваемые элементарной теорией Ренкина и Грасхофа (см. стр. 67), являются несколько завышенными и должны быть уменьшены примерно на 25% = ). [c.130]
Рассмотрим теперь бесконечно длпную прямую балку высотою 26 и толщиною 2с, находящуюся под действием сосредоточенных сил, показанных на фиг. 5.07. [c.371]
Этот результат представляет собой случай изгиба пластинок, исиользоваиный впоследствии А. Надаи для экспериментального подтверждения приближенной теории изгиба ), предложенной Кирхгоффом. О другой интересной краевой задаче упоминается н Натуральной философии Томсона—Тэйта. Здесь сообщается по этому поводу До сих пор, к сожалению, математикам не удалось решить, а возможно, что они даже и не пытались решать, прекрасную задачу об изгибании широкой, весьма тонкой полосы (подобной, например, часовой пружине) в круговое кольцо ). Лэмб исследовал антикластический изгиб по краю тонкой полосы ) и достиг большого прогресса в решении задачи о балке ). Рассматривая бесконечно длинную балку узкого прямоугольного сечения, нагруженную через равные интервалы равными сосредоточенными силами, действующими поочередно вверх и вниз, он упростил решение двумерной задачи а для некоторых случаев получил уравнения кривых прогиба. Таким путем было показано, что элементарная теория изгиба Бернулли достаточно точна, если высота сечения балки мала в сравнении с ее длиной. При этом было также показано, что поправка на поперечную силу, даваемая элементарной теорией Рэнкина и Грасхофа, несколько преувеличена и должна быть снижена до 75% от рекомендуемого этой теорией значения. Надлежит упомянуть также и о труде Лэмба, посвященном теории колебаний упругих сфер ) и распространению упругих волн по поверхности полубесконечного тела ), а также в теле, ограниченном двумя плоскими гранями ). Он изложил также и теорию колебаний естественно искривленного стержня ). Особый интерес для инженеров представляет его и Р. В. Саусвелла трактовка колебаний круглого диска ). [c.407]