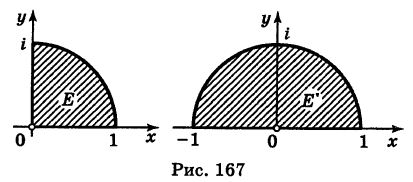
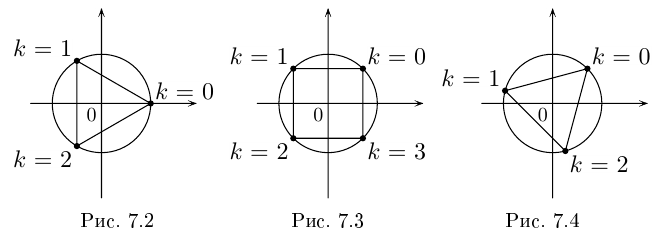
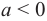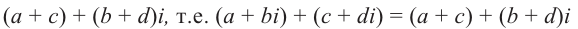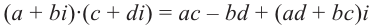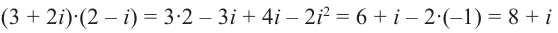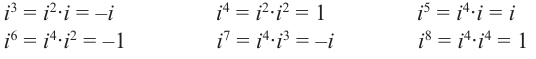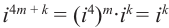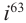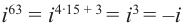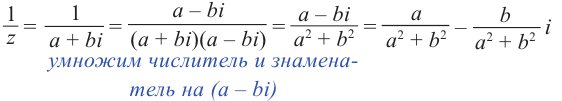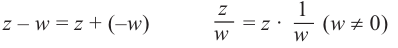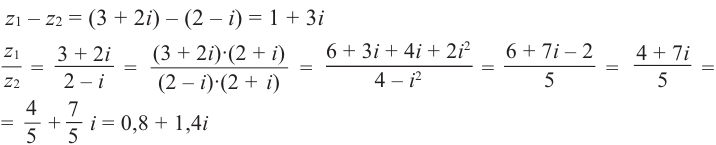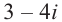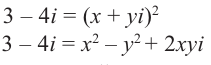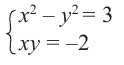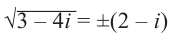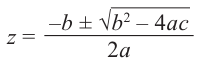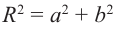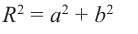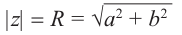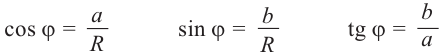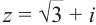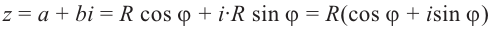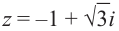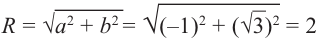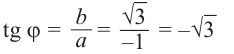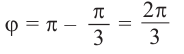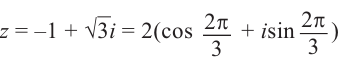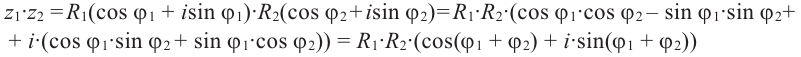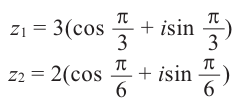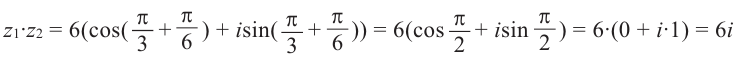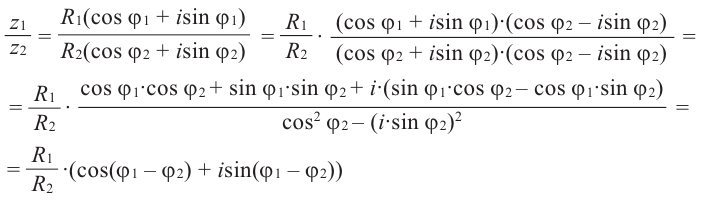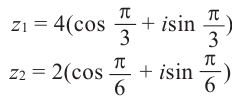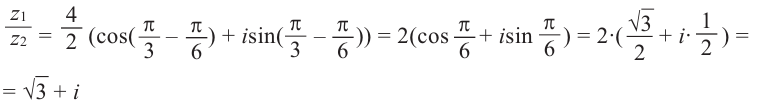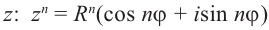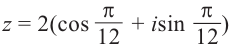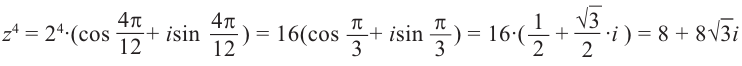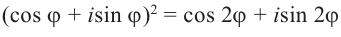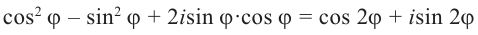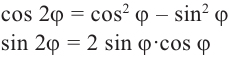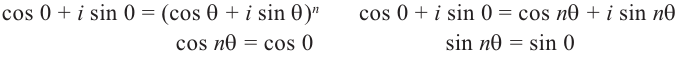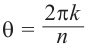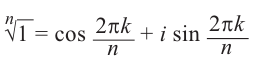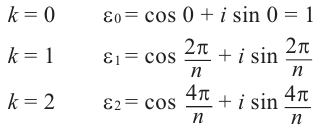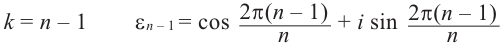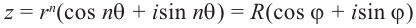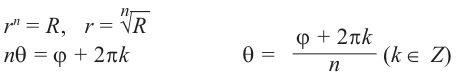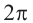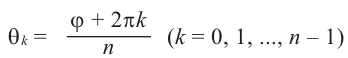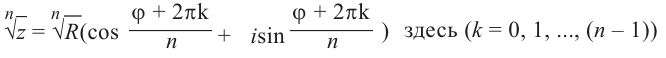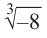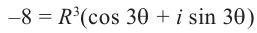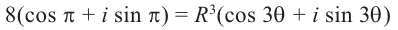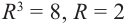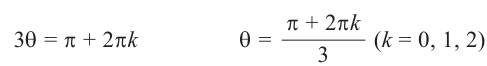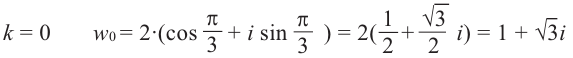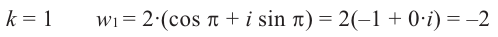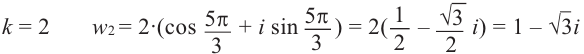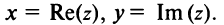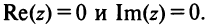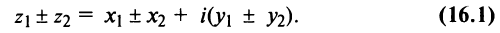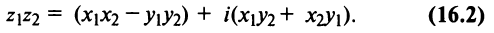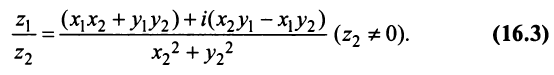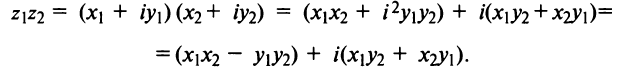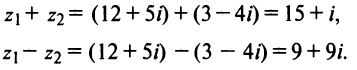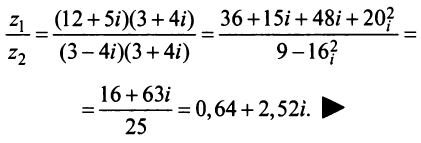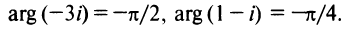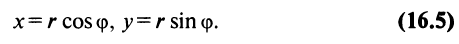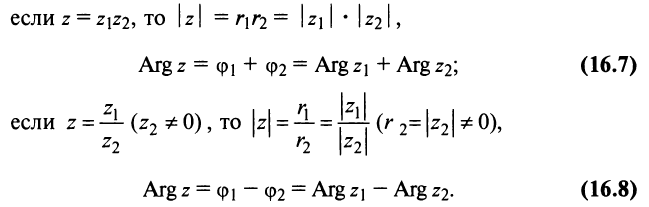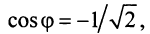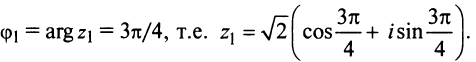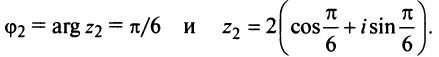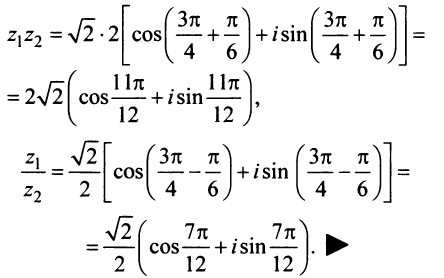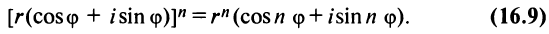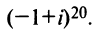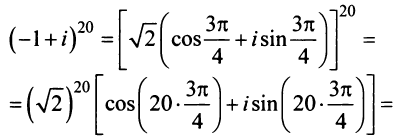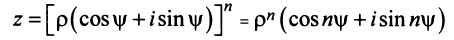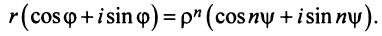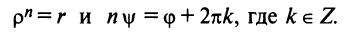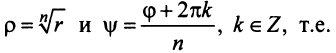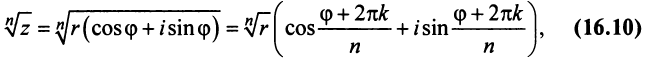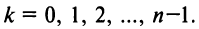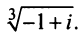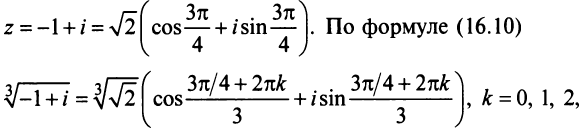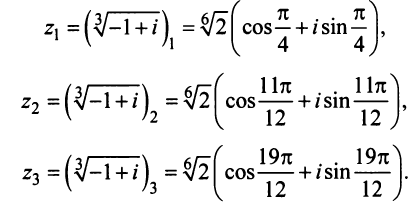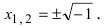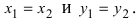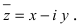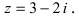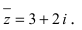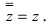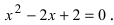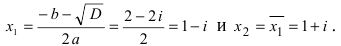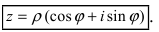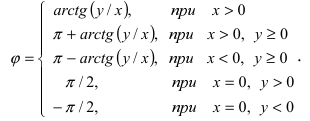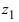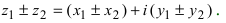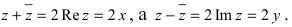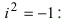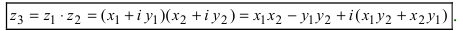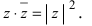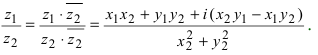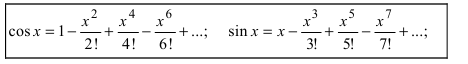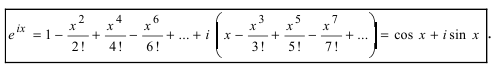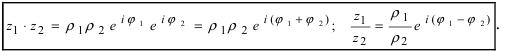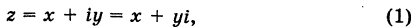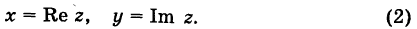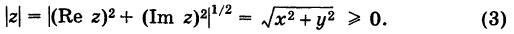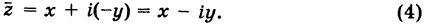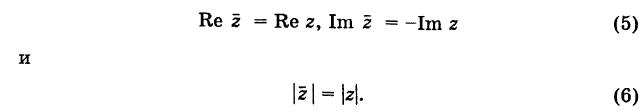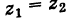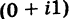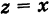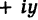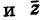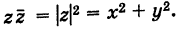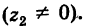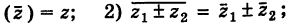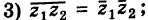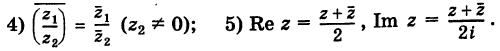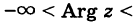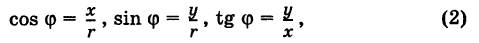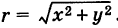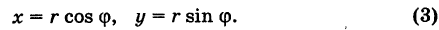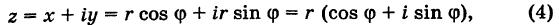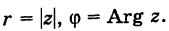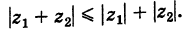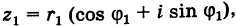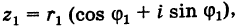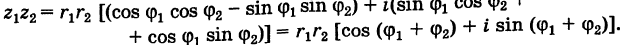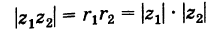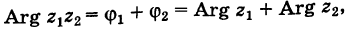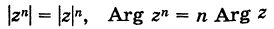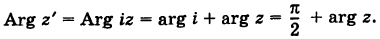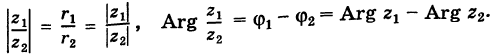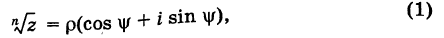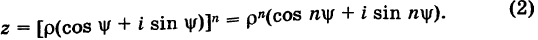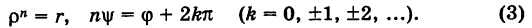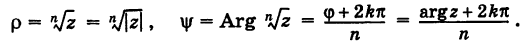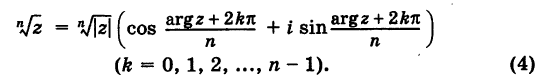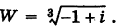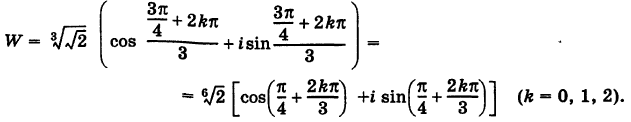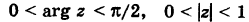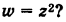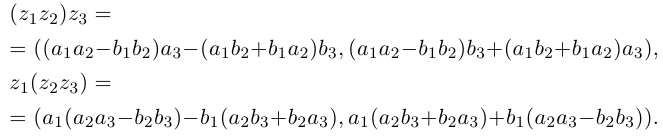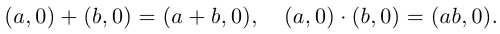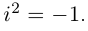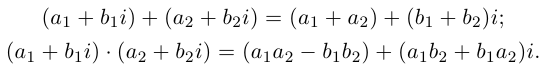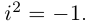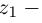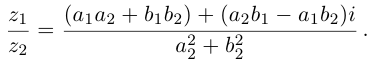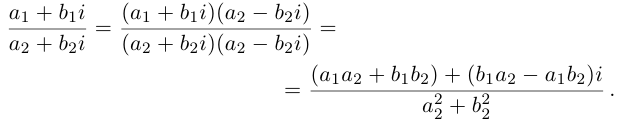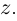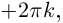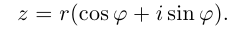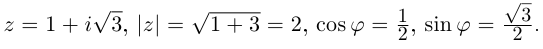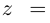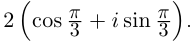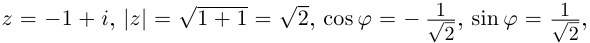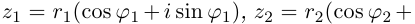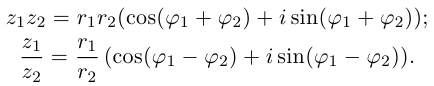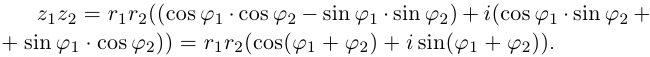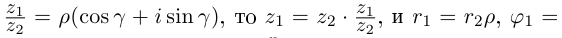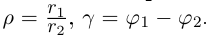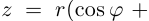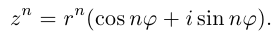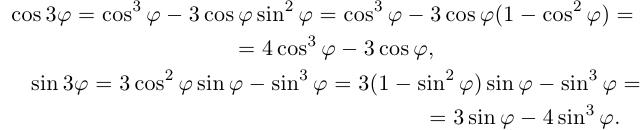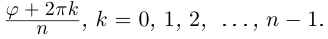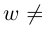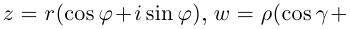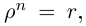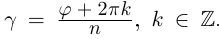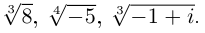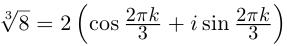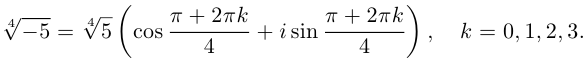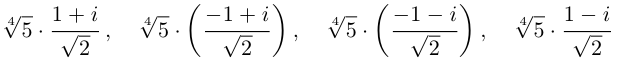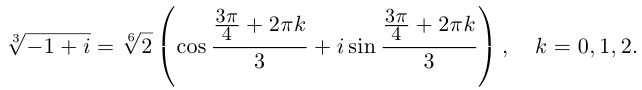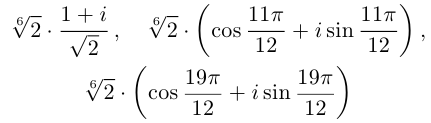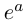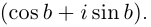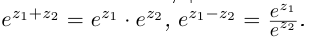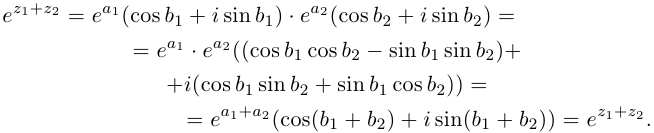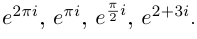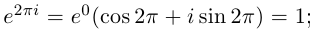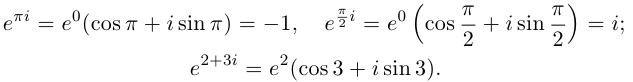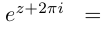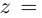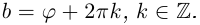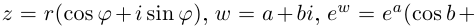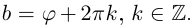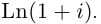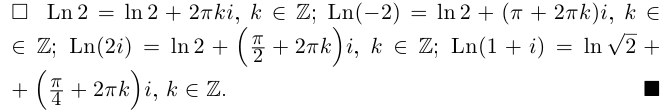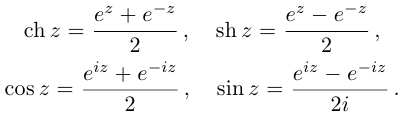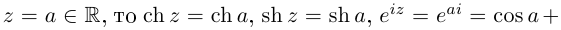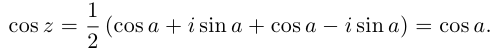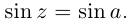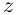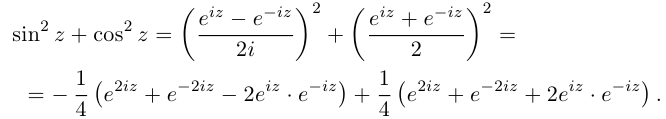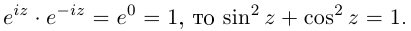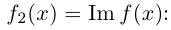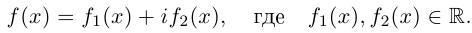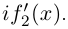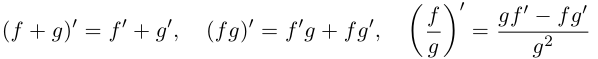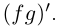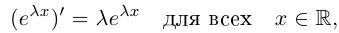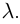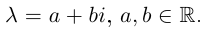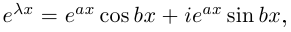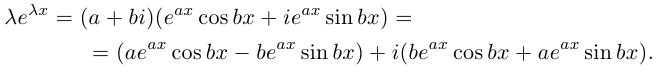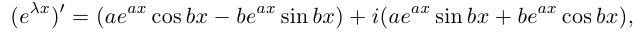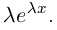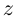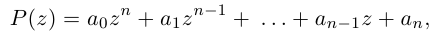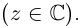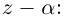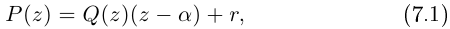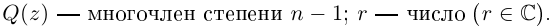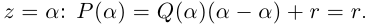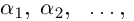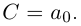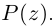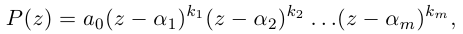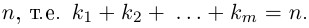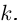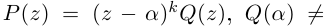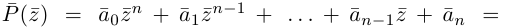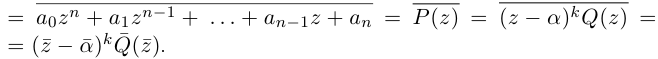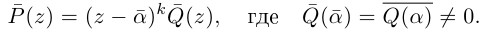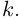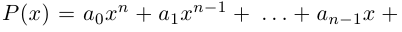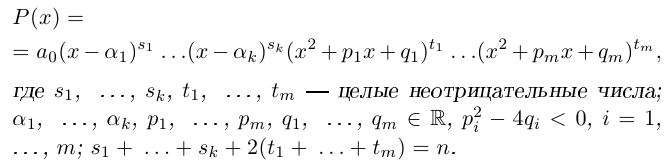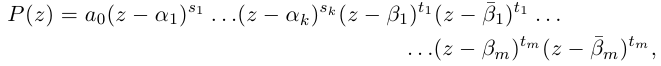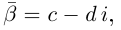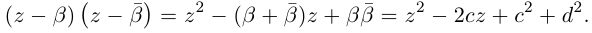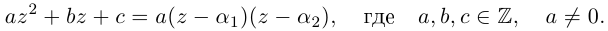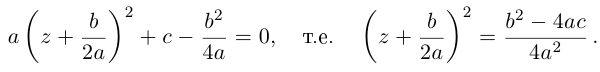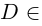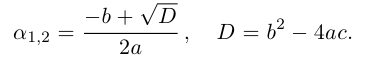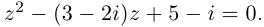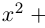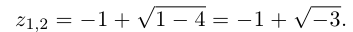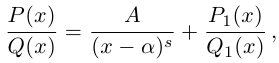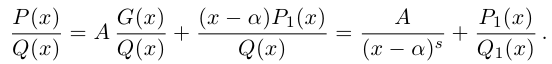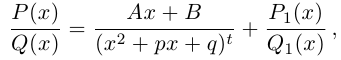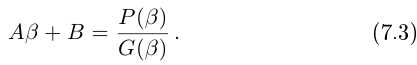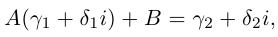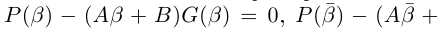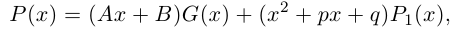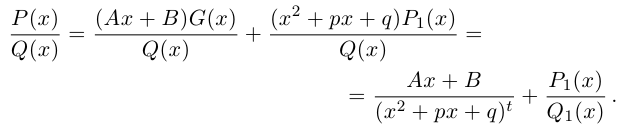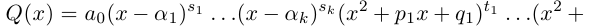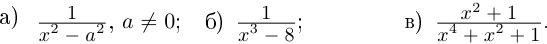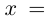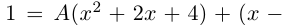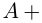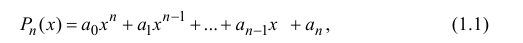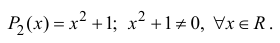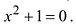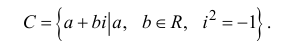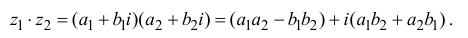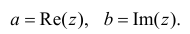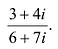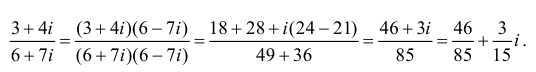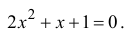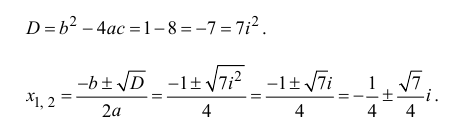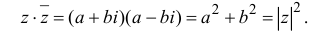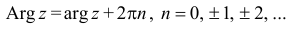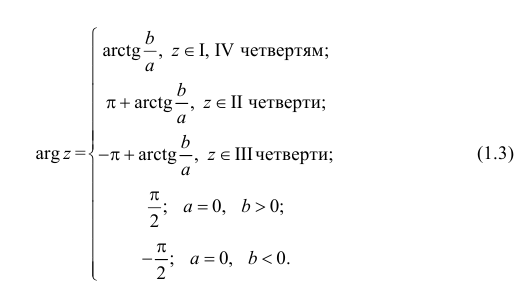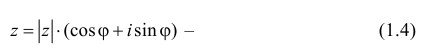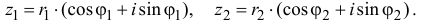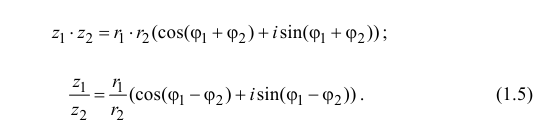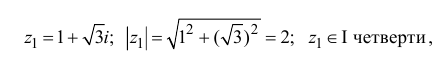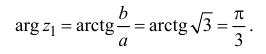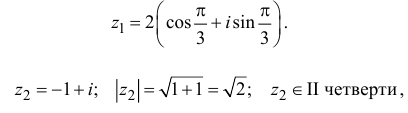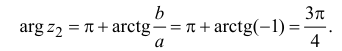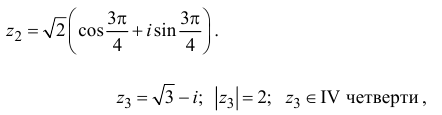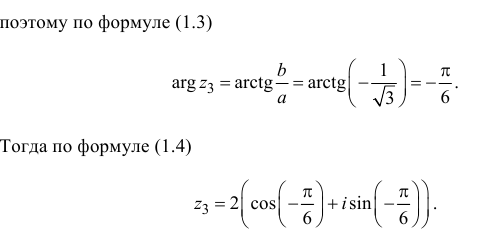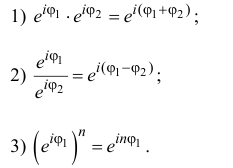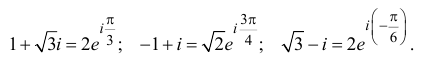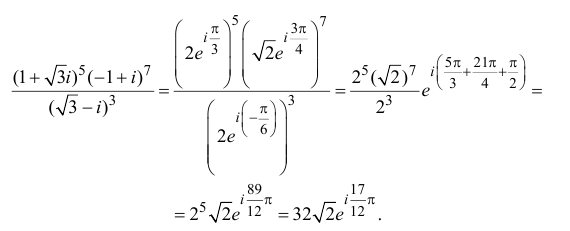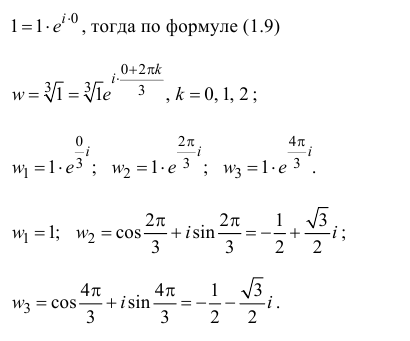8
Занятие 12.
Комплексные
числа.
12.1. Определение комплексных чисел в
алгебраической форме. Сравнение и
изображение комплексных чисел на
комплексной плоскости. Комплексное
сопряжение. Сложение, умножение, деление
комплексных чисел.
12.2. Модуль, аргумент комплексного числа.
12.3. Тригонометрическая и показательная
формы записи комплексного числа.
12.4. Возведение в целую степень и извлечение
корня из комплексного числа.
Определение комплексных чисел в
алгебраической форме. Сравнение и
изображение комплексных чисел на
комплексной плоскости. Комплексное
сопряжение. Сложение, умножение, деление
комплексных чисел.
Комплексным числом в алгебраической
форме называется число
,
(1)
где
называется мнимой единицей и
— действительные числа:
называется действительной (вещественной)
частью;
— мнимой частью комплексного числа
.
Комплексные числа вида
называются чисто мнимыми числами.
Множество всех комплексных чисел
обозначается буквой
.
По определению,
,
и т.д.
Множество всех действительных чисел
является частью множества
:
.
С другой стороны, существуют комплексные
числа, не принадлежащие множеству
.
Например,
и
,
т.к.
.
Комплексные числа в алгебраической
форме естественным образом возникают
при решении квадратных уравнений с
отрицательным дискриминантом.
Пример 1. Решить уравнение
.
Решение.
,
т.к.
.
Следовательно, заданное квадратное
уравнение имеет комплексные корни
,
.
Пример 2. Найти действительную и
мнимую части комплексных чисел
,
,
.
Решение.
— соответственно вещественная и мнимая
части числа
,
.
.
.
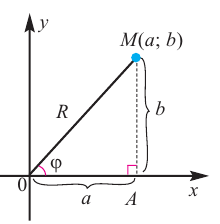
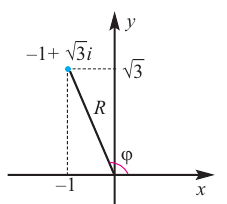
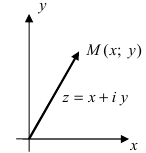
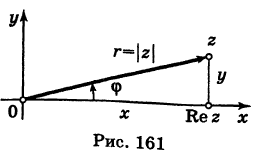
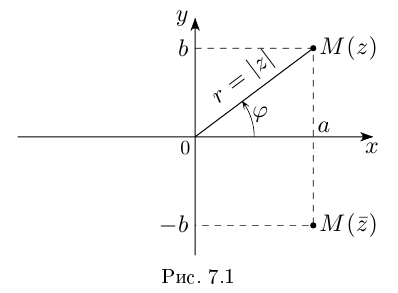
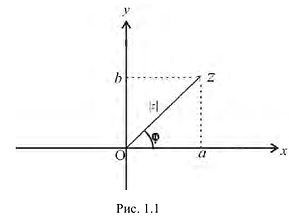
Любое комплексное число
изображается вектором на комплексной
плоскости
,
представляющей плоскость с декартовой
системой координат
.
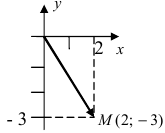
Начало вектора лежит в точке
,
а конец — в точке с координатами
(рис
1.) Ось
называется
вещественной осью, а ось
— мнимой осью комплексной плоскости
.
Рис. 1.
Комплексные числа
сравниваются между собой только знаками
.
.
Если же хотя бы одно из равенств:
нарушено, то
.
Записи типа
не имеют смысла.
По определению, комплексное число
называется комплексно сопряженным
числу
.
В этом случае пишут
.
Очевидно, что
.
Везде далее черта сверху над комплексным
числом будет означать комплексное
сопряжение.
Например,
.
Над комплексными числами можно выполнять
такие операции, как сложение (вычитание),
умножение, деление.
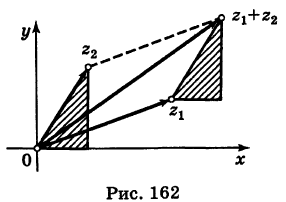
1. Сложение комплексных чисел
производится так:
.
Свойства операции сложения:
— свойство коммутативности;
— свойство ассоциативности.
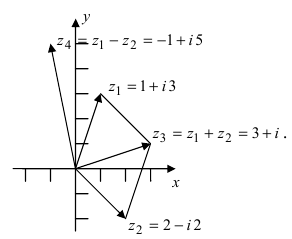
Нетрудно видеть, что геометрически
сложение комплексных чисел
означает сложение отвечающих им на
плоскости
векторов по правилу параллелограмма.
Операция вычитание числа
из числа
производится так:
.
2. Умножение комплексных чисел
производится так:
.
Свойства операции умножения:
— свойство коммутативности;
— свойство ассоциативности;
— закон дистрибутивности.
3. Деление комплексных чисел
выполнимо только при
и производится так:
.
Пример 3. Найти
,
если
.
Решение.
1)
.(ош!)
2)
.(ош!)
3)
.(ош!)
4)
.
5)
.
Пример 4. Вычислить
,
если
.
Решение.
.
z, т.к.
.
.(ош!)
Нетрудно проверить (предлагается это
сделать самостоятельно) справедливость
следующих утверждений:
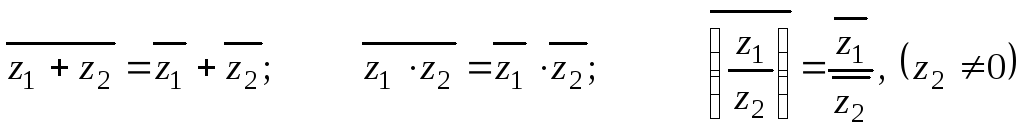
Модуль, аргумент комплексного числа.
Модуль комплексного числа
(модуль
обозначается
)
это — неотрицательное число
,
т.е.
.
Геометрический смысл
— длина вектора, представляющего число
на комплексной плоскости
.
Уравнение
определяет множество всех чисел
(векторов на
),
концы которых лежат на единичной
окружности
.
Аргумент комплексного числа
(аргумент
обозначается
)
это – угол
в радианах между вещественной осью
и числом
на комплексной плоскости
,
причем
положителен, если он отсчитывается от
до
против часовой стрелки, и
отрицателен, если
отсчитывается от оси
до
по часовой стрелке.
Таким образом, аргумент числа
определяется неоднозначно, с точностью
до слагаемого
,
где
.
Однозначно аргумент числа
определяется в пределах одного обхода
единичной окружности
на плоскости
.
Обычно требуется найти
в пределах интервала
,
такое значение называется главным
значением аргумента числа
и обозначается
.
и
числа
можно найти из уравнения
,
при этом обязательно нужно
учитывать, в какой четверти плоскости
лежит конец вектора
— точка
:
если
(1-я четверть плоскости
),
то
;
если
(2-я четверть плоскости
),
то;
если
(3-я четверть плоскости
),
то
;
если
(4-я четверть плоскости
),
то
.
Фактически, модуль и аргумент числа
,
это полярные координаты
точки
— конца вектора
на плоскости
.
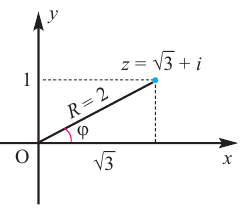
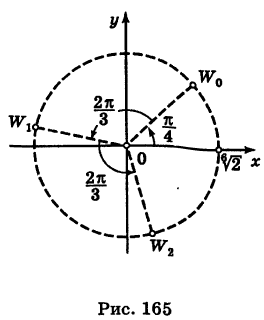
Пример 5. Найти модуль и главное
значение аргумента чисел:
.
Решение.
1)
.
2)
.
3)
.
4)
.
5)
.
6)
.
7)
.

.
Аргументы чисел
,
лежащих осях
,
разделяющих четверти 1,2,3,4 комплексной
плоскости
,
находятся сразу же по графическим
изображениям этих чисел на плоскости
.
Тригонометрическая и показательная
формы записи комплексного числа.
Умножение и деление комплексных чисел
в тригонометрической и показательной
формах записи.
Тригонометрическая форма записи
комплексного числа
имеет вид:
,
(2)
где
—
модуль,
—
аргумент комплексного числа
.
Такое представление комплексных чисел
вытекает из равенств
.
Показательная (экспоненциальная)
форма записи комплексного числа
имеет вид:
,
(3)
где
—
модуль,
—
аргумент числа
.
Возможность представления комплексных
чисел в показательной форме (3) вытекает
из тригонометрической формы (2) и формулы
Эйлера:
.
(4)
Эта формула доказывается в курсе ТФКП
(Теория функций комплексного переменного).
Пример 6. Найти тригонометрическую
и экспоненциальную формы записи
комплексных чисел:
из примера 5.
Решение. Воспользуемся результатами
примера 5, в котором найдены модули и
аргументы всех указанных чисел.
1)
— тригонометрическая форма записи числа
,
— показательная (экспоненциальная)
форма записи числа
.
2)
— тригонометрическая форма записи числа
,
— показательная (экспоненциальная)
форма записи числа
.
3)
— тригонометрическая форма записи числа
,
— показательная (экспоненциальная)
форма записи числа
.
4)
— тригонометрическая форма записи числа
,
— показательная (экспоненциальная)
форма записи числа
.
5)
— тригонометрическая форма записи числа
,
— показательная (экспоненциальная)
форма записи числа
.
6)
— тригонометрическая форма числа
,
— показательная (экспоненциальная)
форма числа
.
7)
— тригонометрическая форма записи числа
,
— показательная (экспоненциальная)
форма числа
.

— тригонометрическая форма записи числа
,
— показательная (экспоненциальная)
форма записи числа
.
Показательная форма записи комплексных
чисел приводит к следующей геометрической
трактовке операций умножения и деления
комплексных чисел. Пусть
— показательные формы чисел
.
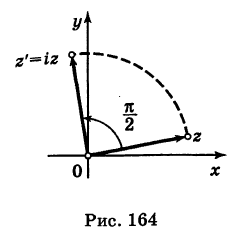
1.
При перемножении комплексных чисел
их модули перемножаются, а аргументы
складываются.
2.
При делении комплексного числа
на число
получается комплексное число
,
модуль
которого равен отношению модулей
,
а аргумент
— разности
аргументов чисел
.
Возведение в целую степень и извлечение
корня из комплексного числа.
По определению,
.
При возведении в целую степень
комплексного
числа
,
следует действовать так: сначала найти
модуль
и аргумент
этого числа; представить
в показательной форме
;
найти
,
выполнив следующую последовательность
действий
,
где
.
(5)
Замечание. Аргумент
числа
может не принадлежать интервалу
.
В этом случае следует по полученному
значению
найти главное значение
аргумента
числа
,
прибавляя (или вычитая) число
с таким значением
,
чтобы
принадлежало интервалу
.
После этого, нужно заменить в формулах
(5)
на
.
Пример 7. Найти
и
,
если
.
Решение.
1)
=
(см. число
из примера 6).
2)
,
где
.
.
.
Следовательно,
можно заменить на
и, значит,
,
где
.
3)
,
где
.
.
Заменим
на
.
Следовательно,
.
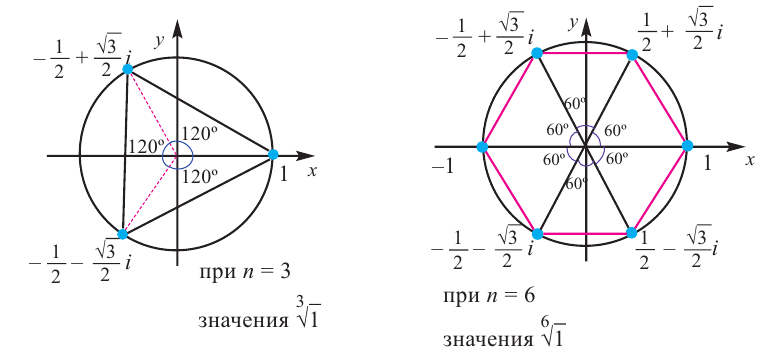
Извлечение корня
-й
степени
из комплексного числа
проводится по формуле Муавра-Лапласа
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Развитие понятия числа является
важнейшей сквозной методико-содержательной
линией школьного курса математики, проходящий в
той или иной степени через все классы средней
школы. В приложении «Математика» неоднократно
публиковались статьи о методике изучения
различных числовых систем в школе. В частности, в
1995–96 гг. были опубликованы три лекции академика
РАО, профессора Г. Глейзера:
Лекция 1. Натуральные числа,
1995, № 47.
Лекция 2. Рациональные числа, 1995, № 48.
Лекция 3. Действительные числа, 1996, № 3.
Публикуемая ниже статья завершает цикл этих
лекций.
Введение
Начнем с нескольких
напоминаний.
Одна из причин введения
рациональных чисел обусловлена требованием,
чтобы всякое линейное уравнение ax = b (где a № 0) было
разрешимо. В области целых чисел линейное
уравнение разрешимо лишь в том случае, когда b
делится нацело на a.
Одна из причин расширения
множества рациональных чисел до множества
действительных чисел была связана с
разрешимостью квадратных уравнений, например,
уравнения вида x2 = 2. На множестве
рациональных чисел это уравнение не разрешимо,
так как среди рациональных нет числа, квадрат
которого равен двум. Как известно, – число иррациональное. На
множестве же действительных чисел уравнение x2
= 2 разрешимо, оно имеет два решения x1 = и x2 = –
.
И все же нельзя считать, что на
множестве действительных чисел разрешимы все
квадратные уравнения. Например, квадратное
уравнение x2 = – 1 на множестве
действительных чисел решений не имеет, так как
среди действительных чисел нет такого числа,
квадрат которого отрицателен.
Таким образом, действительных
чисел явно недостаточно, чтобы построить такую
теорию квадратных уравнений, в рамках которой
каждое квадратное уравнение было бы разрешимо.
Это соображение приводит к необходимости
вводить новые числа и расширять множество
действительных чисел до множества комплексных
чисел, в котором было бы разрешимо любое
квадратное уравнение.
Вспомним о едином принципе
расширения числовых систем и поступим в
соответствии с этим принципом.
Если множество А расширяется
до множества В, то должны быть выполнены
следующие условия:
1. Множество А есть
подмножество В.
2. Отношения элементов множества А (в частности,
операции над ними) определяются также и для
элементов множества В; смысл этих отношений для
элементов множества А, рассматриваемых уже как
элементы множества В, должен совпадать с тем,
какой они имели в А до расширения.
3. В множестве В должна выполняться операция,
которая в А была невыполнима или не всегда
выполнима.
4. Расширение В должно быть минимальным из всех
расширений данного множества А, обладающих
первыми тремя свойствами, причем это расширение
В должно определяться множеством А однозначно (с
точностью до изоморфизма).
Итак, расширяя множество
действительных чисел до множества новых чисел,
названных комплексными, необходимо, чтобы:
а) комплексные числа
подчинялись основным свойствам действительных
чисел, в частности, коммутативному,
ассоциативному и дистрибутивному законам;
б) в новом числовом множестве были разрешимы
любые квадратные уравнения.
Множество действительных
чисел недостаточно обширно, чтобы в нем были бы
разрешимы все квадратные уравнения. Поэтому,
расширяя множество действительных чисел до
множества комплексных чисел, мы потребуем, чтобы
в нем можно было бы построить полную и
законченную теорию квадратных уравнений.
Другими словами, мы расширим множество
действительных чисел до такого множества, в
котором можно будет решить любое квадратное
уравнение. Так, уравнение x2 = – 1 не имеет
решений во множестве действительных чисел
потому, что квадрат действительного числа не
может быть отрицательным. В новом числовом
множестве оно должно иметь решение. Для этого
вводится такой специальный символ i, называемый
мнимой единицей, квадрат которого равен – 1.
Ниже будет показано, что
введение этого символа позволит осуществить
расширение множества действительных чисел,
пополнив его мнимыми числами вида bi (где b –
действительное число) таким образом, чтобы в
новом числовом множестве (множестве комплексных
чисел) при сохранении основных законов
действительных чисел были разрешимы любые
квадратные уравнения.
Основные
определения. Операции над комплексными числами
1. Существует элемент i (мнимая
единица) такой, что i2 = – 1.
2. Символ a + bi называют
комплексным числом с действительной частью a и
мнимой частью bi, где a и b – действительные числа, b
– коэффициент мнимой части.
Комплексное число a + 0i
отождествляется с действительным числом a, т.е. a +
0i = a, в частности, 0 + 0i = 0. Числа вида bi (b № 0) называют чисто
мнимыми.
Например, комплексное число 2 +
3i имеет действительную часть – действительное
число 2 и мнимую часть 3i, действительное число 3 –
коэффициент мнимой части.
Комплексное число 2 – 3i имеет
действительную часть число 2, мнимую часть – 3i,
число – 3 – коэффициент при мнимой части.
3. Правило равенства. Два
комплексных числа равны тогда и только тогда,
когда равны их действительные части и равны
коэффициенты мнимых частей.
Т.е., если a + bi = c +di, то a = c, b = d: и,
обратно, если a = c, b = d, то a + bi = c +di.
4. Правило сложения и
вычитания комплексных чисел.
(a + bi) + (c + di) = (a + c) + (b +
d)i.
Например:
(2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i
= 7 + 4i;
(– 2 + 3i) + (1 – 8i) = (– 2 + 1)
+ (3 + (– 8))i = – 1 – 5i;
(– 2 + 3i) + (1 – 3i) = (– 2 + 1)
+ (3 + (– 3))i =
= – 1 + 0i = – 1.
Вычитание комплексных чисел
определяется как операция, обратная сложению, и
выполняется по формуле:
(a + bi) – (c + di) = (a – c) + (b
– d)i.
Например:
(5 – 8i) – (2 + 3i) = (3 – 2) +
(– 8 – 3)i = 1 – 11i;
(3 – 2i) – (1 – 2i) = (3 – 1) +
((– 2) – (– 2))i = 2 + 0i = 2.
5. Правило умножения
комплексных чисел.
(a + bi)(c + di) = (aс + bd) + (ad +
bc)i.
Из определений 4 и 5 следует,
что операции сложения, вычитания и умножения над
комплексными числами осуществляются так, как
будто мы выполняем операции над многочленами,
однако с условием, что i2 = – 1.
Действительно: (a + bi)(c + di) = ac + adi
+ bdi2 = (ac – bd) + (ad + bc)i.
Например, (– 1 + 3i)(2 + 5i) = – 2 – 5i +
6i + 15i2 = – 2 – 5i + 6i – 15 = – 17 + i; (2 + 3i)(2 – 3i) = 4
– 6i + 6i – 9i2 = 4 + 9 = 13.
Из второго примера следует,
что результатом сложения, вычитания,
произведения двух комплексных чисел может быть
число действительное. В частности, при умножении
двух комплексных чисел a + bi и a – bi, называемых
сопряженными комплексными числами, в результате
получается действительное число, равное сумме
квадратов действительной части и коэффициента
при мнимой части. Действительно:
(a + bi)(a – bi) = a2 –
abi + abi – b2i2 = a2 + b2.
Произведение двух чисто
мнимых чисел – действительное число.
Например: 5i•3i = 15i2 = –
15; – 2i•3i = – 6i2 = 6, и вообще bi•di = bdi2
= – bd.
6. Деление комплексного числа a
+ bi на комплексное число c + di № 0 определяется как операция
обратная умножению и выполняется по формуле:
.
Формула теряет смысл, если c + di
= 0, так как тогда c2 + d2 = 0, т. е. деление
на нуль и во множестве комплексных чисел
исключается.
Обычно деление комплексных
чисел выполняют путем умножения делимого и
делителя на число, сопряженное делителю.
Например,
Опираясь на введенные
определения нетрудно проверить, что для
комплексных чисел справедливы коммутативный,
ассоциативный и дистрибудивный законы. Кроме
того, применение операций сложения, умножения,
вычитания и деления к двум комплексным числам
снова приводит к комплексным числам. Тем самым
можно утверждать, что множество комплексных
чисел образует поле. При этом, так как
комплексное число a + bi при b = 0 отождествляется с
действительным числом a = a + 0i, то поле комплексных
чисел включает поле действительных чисел в
качестве подмножества.
Приведем классификацию
комплексных чисел:
Решение квадратных
уравнений
Одна из причин введения
комплексных чисел состояла в том, чтобы добиться
разрешимости любого квадратного уравнения, в
частности уравнения
x2 = – 1.
Покажем, что расширив поле
действительных чисел до поля комплексных чисел,
мы получили поле, в котором каждое квадратное
уравнение разрешимо, т.е. имеет решение. Так,
уравнение x2 = – 1 имеет два решения: x1
= i, x2 = – i.
Это нетрудно установить
проверкой: i•i = i2 = – 1, (– i)•(– i) = i2
= – 1.
Перейдем теперь к вопросу о
решении полного квадратного уравнения.
Квадратным уравнением называют уравнение вида:
ax2 + bx + c = 0 (a № 0),
где x – неизвестная, a, b, c –
действительные числа, соответственно первый,
второй коэффициенты и свободный член, причем a № 0. Решим это
уравнение, выполнив над ним ряд несложных
преобразований.
· Разделим все члены
уравнения на a № 0 и перенесем свободный член в
правую часть уравнения:
Теперь можно исследовать
полученное решение. Оно зависит от значения
подкоренного выражения, называемого
дискриминантом квадратного уравнения. Если b2
– 4ac > 0, то
есть действительное число и квадратное
уравнение имеет действительные корни. Если же – мнимое число,
квадратное уравнение имеет мнимые корни.
Результаты
исследования представлены ниже в таблице:
Итак, введение комплексных
чисел позволяет разработать полную теорию
квадратных уравнений. В поле комплексных чисел
разрешимо любое квадратное уравнение.
Примеры.
1. Решите уравнение x2 – 2x
– 8 = 0.
Решение. Найдем
дискриминант D = b2 – 4ac = (– 2)2 –
4•1•(– 
Уравнение имеет два
действительных корня:
2. Решите уравнение x2 + 6x +
9 = 0.
Решение. D = 62 – 4•1•9 = 0,
уравнение имеет два равных действительных корня:
3. Решите уравнение x2 – 4x
+ 5 = 0.
Решение. D = 16 – 4•1•5 = – 4 < 0,
уравнение имеет мнимые корни:
Геометрическая
интерпретация комплексных чисел
Известно, что отрицательные
числа были введены в связи с решением линейных
уравнений с одной переменной. В конкретных
задачах отрицательный ответ истолковывался как
значение направленной величины (положительные и
отрицательные температуры, передвижения в
противоположных направлениях, прибыль и долг и
т.п.). Однако еще в ХVI веке многие математики не
признавали отрицательных чисел. Только с
введением координатной прямой и координатной
плоскости отчетливо проявился смысл
отрицательных чисел, и они стали такими же
«равноправными» и понятными, как и натуральные
числа. Аналогично обстоит дело с комплексными
числами. Смысл их отчетливо проявляется при
введении их геометрической интерпретации.
интерпретация комплексных чисел состоит в том,
что каждому комплексному числу z = x + yi ставится в
соответствие точка (x, y) координатной плоскости
таким образом, что действительная часть
комплексного числа представляет собой абсциссу,
а коэффициент при мнимой части – ординату точки.
Таким образом,
устанавливается взаимно однозначное
соответствие между множеством комплексных чисел
и множеством точек координатной плоскости.
Подобным образом было установлено соответствие
между множеством действительных чисел и
множеством точек числовой прямой.
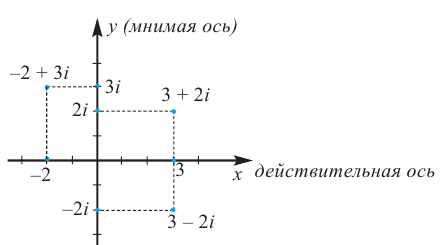
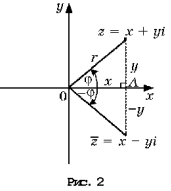
На рисунке 1 изображена
координатная плоскость. Числу 2 + 3i соответствует
точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3);
числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка
D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а
числу – 3i – точка F(0, – 3). Итак, каждому
комплексному числу соответствует единственная
точка координатной плоскости и, обратно, каждой
точке координатной плоскости соответствует
единственное комплексное число, при этом двум
различным комплексным числам соответствуют две
различные точки координатной плоскости. Ясно,
что действительным числам x + 0i соответствуют
точки оси абсцисс, а чисто мнимым числам 0 + yi, где y
№ 0 –
точки оси ординат. Поэтому ось Oy называют мнимой,
а ось Ox – действительной. Сопряженным
комплексным числам соответствуют точки, симметричные
относительно оси абсцисс (рис. 2).
Тригонометрическая
форма комплексного числа
Точка координатной плоскости,
соответствующая комплексному числу z = x + yi, может
быть указана по-другому: ее координатами могут
быть расстояние r от начала координат и величина
угла j между положительной полуосью Ox и лучом Oz
(рис. 3).
Расстояние r от начала системы
координат до точки, соответствующей
комплексному числу z, называют модулем этого
числа. Тогда по теореме Пифагора (рис. 2)
имеем: r2 = x2 + y2 = (x + yi)(x – yi)
= z•z.
Отсюда найдем модуль
комплексного числа как арифметическое
(неотрицательное) значение корня:
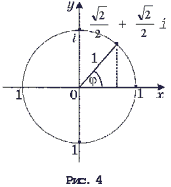
Если комплексное число z
изображается точкой оси абсцисс (т.е. является
действительным числом), то его модуль совпадает с
абсолютным значением. Все комплексные числа,
имеющие модуль 1, изображаются точками единичной
окружности – окружности с центром в начале
системы координат, радиуса 1 (рис. 4).
лучом Oz называют аргументом комплексного числа z
= x + yi (рис. 3).
Сопряженные комплексные
числа имеют
один и тот же модуль и аргументы, отличающиеся знаком: j = – j.
В отличие от модуля аргумент
комплексного числа определяется неоднозначно.
Аргумент одного и того же комплексного числа
может иметь бесконечно много значений,
отличающихся друг от друга на число, кратное 360°.
Например, число z (рис. 3) имеет модуль r, аргумент
же этого числа может принимать значения j; j + 360°; j + 720°; j + 1080°; … или
значения j – 360°; j –720°; j – 1080°; … Данное значение модуля r и любое из
приведенных выше значений аргумента определяют
одну и ту же точку плоскости, соответствующую
числу z.
Пусть точке с координатами (x;
y) соответствует комплексное число z = x + yi. Запишем
это комплексное число через его модуль и
аргумент. Воспользуемся определением
тригонометрических функций синуса и косинуса
(рис. 3):
x = r cos j; y = r sin j.
Тогда число z выражается через
модуль и аргумент следующим образом: z = x + yi =
r(cos j + i sin
j).
Выражение z = r(cos j + i sin j) называют
тригонометрической формой комплексного числа, в
отличии от выражения z = x + yi, называемого
алгебраической формой комплексного числа.
Приведем примеры обращения
комплексных чисел из алгебраической формы в
тригонометрическую:
Для числа i имеем r = 1, j = 90°, поэтому
i = 1(cos 90° + i sin 90°);
Для числа – 1 имеем r = 1, j = 180°,
поэтому – 1 = 1(cos 180° + i sin 180°);
Для числа 1 + i имеем поэтому
Для числа имеем r = 1, j = 45°, поэтому
Для числа имеем r = 2, j = 120°, поэтому
Справедливость приведенных
равенств нетрудно проверить путем подстановки в
их правой части числовых значений
тригонометрических функций. Итак, для того, чтобы
комплексное число, заданное в алгебраической
форме, обратить в тригонометрическую форму,
необходимо найти его модуль r и аргумент j,
пользуясь формулами:
Комплексные числа и
векторы
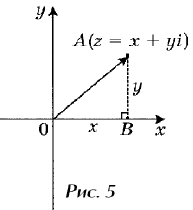
геометрической интерпретации комплексных чисел.
Каждой точке (x , y) координатной плоскости,
изображающей комплексное число
z = x + yi, соответствует единственный вектор,
отложенный от начала системы координат и обратно
(рис. 5). При этом двум различным точкам
координатной плоскости будут соответствовать
два таких различных вектора.
Таким образом, может быть
установлено взаимно однозначное соответствие
между множеством точек координатной плоскости
(комплексными числами) и множеством векторов,
отложенных от начала системы координат.
Если z = x + yi (рис. 5), то вектор , отложенный от
начала системы координат до точки, изображающей
число z, будет иметь координаты (x; y). Известно, что
равные векторы имеют равные координаты.
Итак, мы рассмотрели два
способа интерпретации комплексных чисел: их
можно изображать либо точками координатной
плоскости, либо векторами, отложенными от начала
системы координат. При этом любые два равных
вектора (имеющих одно и то же направление и
равные длины) изображают одно и то же комплексное
число, а векторы, отличные либо длиной, либо
направлением, изображают разные числа. На
рисунке 6 с помощью векторов изображены
различные комплексные числа: изображает число 2 + 0i;
– число – 3 + 0i;
– число 0 + i;
– число 0 + 2i;
– число 0 – 3i;
– число 3 + 2i;
– число – 1 – 2i.
Ясно, что любой ненулевой
вектор, лежащий на оси Oy (или параллельный ей),
изображает чисто мнимое число yi, причем y > 0,
если направление вектора совпадает с
направлением оси, y < 0, если направление вектора
противоположно направлению оси. Вследствие
этого ось Oy называют мнимой. Все векторы, лежащие
на оси Ox (или параллельные ей) изображают
действительные числа, поэтому ее называют
действительной осью.
Векторная интерпретация
комплексных чисел позволяет уяснить
геометрический смысл операций над комплексными
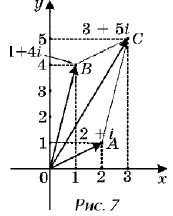
числами. Например, сумма двух комплексных чисел 2
+ i и 1 + 4i равна 3 + 5i. Каждое из слагаемых изображает
соответствующий вектор, отложенный от начала O
координат (рис. 7):
= 2 + i;
= 1 + 4i.
Сумма этих векторов – вектор = 3 + 5i, изображается
диагональю параллелограмма, построенного на
векторах и .
себе геометрический смысл умножения двух
комплексных чисел, воспользуемся их
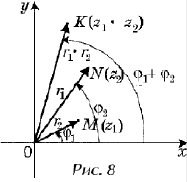
тригонометрической формой. Пусть векторы изображают
соответственно комплексные числа:
соответственно модули этих
чисел, а j1
и j2
– их аргументы. Найдем произведение этих чисел:
z1z2 = r1r2(cosj1 + i sin j1)(cos j2 + i sin j2) = r1r2(cos
j1cos
j2
– sin j1
sin j2)
+ i = (cos j1sin
j2 +
sin j1cos
j2).
школы теоремами сложения синуса и косинуса:
cos j1cos j2 – sin j1 sin j2 = cos(j1 + j2);
cos j1sin j2 + sin j1cos j2 = sin(j1 + j2).
Тогда произведение данных
комплексных чисел равно комплексному числу:
z1z2 = r1r2(cos(j1 + j2) + isin(j1 + j2)).
Последнее соотношение
позволяет сформулировать правило умножения
комплексных чисел: при умножении двух
комплексных чисел их модули перемножаются, а их
аргументы складываются. Это проиллюстрировано
на рисунке 8.
комплексных чисел связано с поворотом
(вращением). Так, произведение z1z2
изображается вектором представляющим собой образ вектора
, повернутого на
угол j2
(или образ вектора , повернутого на угол j1), при этом модуль вектора
равен произведению модулей данных векторов.
Связь произведения
комплексных чисел с вращением становится более
наглядной, если рассматривать произведение
различных комплексных чисел (векторов) на
комплексное число i, у которого модуль равен 1, а
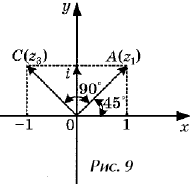
аргумент 90°. Например, найдем произведение
комплексных чисел z1 = 1 + i и z2 = i.
z = z1z2 = (1 +
i)i = i + i2 = – 1 + i.
Числа z1 и z2
соответственно изображают векторы и (рис.9). Мы
видим, что модуль комплексного числа z равен
модулю числа z1:
Аргумент же комплексного
числа z равен 45° + 90° = 135°, в то время, как аргумент
комплексного числа z1 равен 45°. Т.е. вектор ,
изображающий число z, есть образ вектора ,
изображающего число z1 при повороте на 90°.
Введение в комлексные числа
Время на прочтение
2 мин
Количество просмотров 28K
Привет!
Выяснив, что многие знакомые программисты не помнят комплексные числа или помнят их очень плохо, я решил сделать небольшую шпаргалку по формулам.
А школьники могут что-то новое узнать 
// Всех кого заинтересовал прошу под кат.
Итак, комплексные числа эта такие числа, которые можно записать как
Где x, y вещественные числа(т.е привычные всем числа), а i — число, для которого
выполняется равенство
Кстати, -i в квадрате тоже дает -1.
Так что утверждение, что если дискрименант отрицательный, то корней нет это вранье.
А точнее оно выполняется на множестве вещественных чисел.
Т.е можем записать:
x называется действительной частью, y — мнимой.
Это алгебраическая форма записи комплексного числа.
Существует также тригонометрическая форма записи комплексного числа z:
С введением, пожалуй, все.
Переходим к самому интересному — операциям над комплексными числами!
Для начала рассмотрим сложение.
У нас есть два таких комплексных числа:
Как же их сложить?
Очень просто: сложить действительную и мнимую части.
Получим число:
Все просто, не так ли?
Вычитание выполняется аналогично сложению.
Нужно просто вычесть из действительной части 1 числа действительную часть 2 числа,
а потом проделать тоже с мнимой частью.
Получим число
Умножение выполняется вот так:
Напомню, x это действительная часть, y — мнимая.
Деление выполняется вот так:
Кстати, поддержка комплексных чисел есть в стандартной библиотеке Python:
z1=1+2j
z2=3+5j
z3=z1+z2
print(z3) #4+7i
Вместо i используется j.
Кстати, это потому что Python принял конвенцию инженеров-электриков, у которых
буква i обозначает электрический ток.
Задавайте свой вопросы, если они есть, в комментариях.
Надеюсь, вы узнали для себя что-то новое.
UPD: В комментариях просили рассказать о практическом применении.
Так вот комплексные числа нашли широкое практическое применение в авиации
(подъемная сила крыла) и в электричестве.
Как видете, очень нужная вещь 
Журнал Потенциал
Какие числа бывают[править]

Прежде, чем изучать новые, комплексные числа, давайте вспомним числа,
которые мы знаем.
Самые простые числа — это натуральные, они обозначаются буквой 
1, 2, 3, 4, 5, 6, …
С помощью этих чисел мы считаем разные объекты.
Натуральные числа мы можем складывать и умножать.
Целые числа, обозначаемые 
чисел — добавляют нуль и отрицательные числа. Наличие
отрицательных чисел позволяет нам вычитать любое число из
любого, тогда как «живя» в натуральных числах, при вычитании мы
должны были всегда следить, чтобы из большего вычиталось меньшее.
Вот примеры целых чисел:

Чтобы рассматривать части целого (например, три восьмых от пирога), были придуманы
дробные числа 
Кроме сложения, вычитания, умножения рациональные числа можно делить друг на друга
и снова получать рациональное число (конечно, на ноль делить при этом нельзя).
Следующее множество чисел, расширяющее множество рациональных чисел — это
действительные (вещественные) числа 
Задача 1[8] Задача Архимеда[править]
Докажите, что существуют иррациональные числа.

Рисунок 1. Длина диагонали единичного квадрата иррациональна
Решение.
Замечание: этот подход не является строгим в современном смысле. Нужно дать определение вещественных чисел и доказать, что среди них вообще существуют иррациональные числа. Например, в Фихтенгольце это делается с помощью Дедекиндового сечения, а уж потом доказывается, что корень из двух является примером такого числа.
Точнее эта задача звучит так: докажите, что есть отрезки, длина которых не является рациональным
числом. Рассмотрим диагональ единичного квадрата. По теореме Пифагора, квадрат её длины есть
то есть
Докажем, что это число не рационально. Пусть это не так (применяем метод доказательства от противного).
Тогда есть такие натуральные
числа 

— несократимая дробь. Возведем равенство в квадрат и умножим на

Отсюда следует, что 


натуральное число. Получаем:
Из последнего уравнения следует, что 
Итак, мы получили, что 

что 
А значит, наше предположение, что существуют натуральные 

неверно.
Конец решения.
Действительные числа очень обширны, с их помощью можно описывать любое количество вещества,
любой объём жидкости, длину любого отрезка. Действительные числа можно складывать,
вычитать, умножать, делить (только на ноль делить нельзя). Кроме того, можно брать корни
из неотрицательных чисел и вычислять самые разные функции, например, синус, косинус, экспоненту и др.
Действительные числа можно представлять в виде направленной прямой с выделенной точкой 
Точке 

Такое представление называется «числовой осью»:

Задача 2[8][править]
а) Может ли сумма двух иррациональных чисел быть рациональна?
Если да, то приведите пример двух иррациональных чисел, сумма которых рациональна.
б) Приведите пример двух иррациональных чисел, сумма которых иррациональна.
Докажите, что сумма действительно иррациональна.
Решение
а) 
б) 
Задача 3[9][править]
Докажите, что следующие числа не рациональны
а) 


г) 
![,!{sqrt[ {3}]{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b4ef5e4e11581dcc1d84fd8afebc02a0333776b)
![,!{sqrt[ {3}]{2}}+{sqrt {3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9677facd50123506b2ae4356d440d1b6e081e1bd)
Решение:
а) если 

б) так же, как и в а);
в) возведите число в квадрат, и докажите, что результат не рационален.
г) аналогично доказательству иррациональности 
из 



Кроме корней натуральных чисел и, вообще, корней различных многочленов
с целочисленными коэффициентами действительные числа содержат бесконечное множество
трансцендентных чисел.
Например, число 
Число 
Трансцендентные числа — это числа, которые
не являются корнями никакого многочлена с целыми коэффициентами.
Доказательство того, что есть трансцендентные числа, довольно сложное
и мы углубляться в эту тему не будем.
Суть в том, что действительные числа содержат все возможные длины —
какой бы кусочек веревки вы не отрезали, длина его всегда будет действительным числом.
Действительные числа представляют собой полноценный набор чисел,
которого, кажется, должно хватить для любых нужд. Но это не так.
Существует ещё одно расширение чисел — комплексные числа.
В комплексных числах можно брать корни из отрицательных чисел.
Комплексные числа хороши ещё тем,
что любой многочлен имеет среди этих чисел корень. Например, уравнения
не имеют корней в действительных числах, зато в комплексных числах имеют.
Что такое комплексные числа?[править]
Знакомство с мнимой единицей  [править]
[править]
Число 


Рисунок 2. Комплексная плоскость. Каждая точка на плоскости соответствует
комплексному числу. Координаты 
соответствуют действительной и мнимой части комплексного числа.
Примеры вычислений с мнимой единицей:
Задача 4[8][править]
Вычислите следующие выражения:
а) 
б) 
в) 
г) 
д) 
е) 
Решение
а) 
б) 
в) 
г) 
д) 
е) 
Определение 1
Таким образом, комплексное число задается двумя действительными числами.
Если понимать эти числа как декартовы координаты, то
получим естественное соответствие комплексных чисел и точек на плоскости
(рис. 2).
Если в случае действительных чисел мы имели числовую прямую, то в случае комплексных чисел
получаем числовую плоскость, которая называется комплексной плоскостью.
Задача 5[8][править]
Вычислите:
а) 
б) 
в) 
г) 
д) 
е) 
Решение
а) 
б) 
в) 
г) 
д) 
е) 
Задача 6[9][править]
Вычислите:
а) 
б) 
в) 
г) 
д) 
Решение:
а) 
б) 
в) 
г) 
д) 
Операции сложения и умножения комплексных чисел осуществляются так,
как если бы мнимая единица 
при этом 
Задача 7[9][править]
Докажите, что любой многочлен от 

Задача 8[8][править]
Вычислите:
а) 
б) 
в) 
Решение
а) 
б) 
в) 
Задача 9[8][править]
Найдите комплексное число 
а) 
б) 
в) 
г) 
Подсказка
Пусть

следует
Задача 10[9][править]
Найдите два комплексных числа, сумма и произведение которых равны 2.
Задача 11[9][править]
Найдите сумму 
Решение: 
Подсказка:
Чему равны частичные суммы 



Задача 12[9][править]
Найдите 
Решение: 
Подсказка:
Чему равно 
Задача 13[9][править]
Найдите все 

Решение:



Подсказка:

Задача 14[8][править]
Проверьте правильность следующих утверждений:
а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.
б) Произведение двух чисто мнимых чисел равно действительному числу.
в) Квадрат чисто мнимого числа равен действительному отрицательному числу.
г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.
Задача 15[8][править]
Найдите число 
Решение


Задача 16[8][править]
Найдите число 



Решение


Задача 17[9][править]
Найдите число, отличное от 

Решение


Задача 18[10][править]
Найдите (отметьте) на комплексной плоскости все числа 
квадрат которых равен
a) чисто мнимому числу;
б) действительному числу;
в) действительному положительному числу.
Решение:
а) 


б) 





Cопряженные числа. Модуль. Деление[править]
Cопряженные числа[править]
Определение 3
Пусть
Тогда число
называется комплексно-сопряженным или просто сопряженным к числу 
Комплексное число 
отличаются знаком мнимой части, действительная часть у них одинаковая:
Задача 19[7][править]
Докажите, что 
Задача 20[8][править]
Найдите, чему равны выражения
а) 
б) 
в)
для 
Решение
а) 


Задача 21[9][править]
Докажите тождества:

Задача 22[9][править]
Докажите, что
Подсказка Используйте задачу 21 и метод математической индукции.
Задача 23[9][править]
Пусть 

Задача 24[8][править]
Докажите, что числа 

Задача 25[9][править]
Докажите, что многочлен от 

где 
(если раскрыть скобки и привести подобные).
Задача 26[9][править]
Докажите, что если комплексное число 


— действительные числа, то 
Задача 27[9][править]
Вычислите число 
Решение

Задача 28[9][править]
Найдите целые 

а) 
б) 
Как отличаются ответы для а) и б)?
Задача 29[9][править]
Найдите целые 

а) 
б) 
Как отличаются ответы для а) и б)?
Задача 30[9][править]
Даны числа 

Докажите, что 



Найдите 
Решение

Подсказка При решении можно использовать формулу
Чему равно 
Задача 31[9][править]
Число 
Решение

Задача 32[9][править]
Число 
Решение

Задача 33[9][править]
Даны два действительных числа 



Докажите, что 

Задача 34[9][править]
Даны два комплексных числа 



Докажите, что 

Задача 35[8][править]
Покажите, что
Модуль[править]
Определение 4
Пусть 
Модулем комплексного числа 
— длина отрезка 
Посмотрите на рисунок 2. Модуль числа 
отрезка 

Модуль комплексного числа есть неотрицательное действительное число.
Модуль равен нулю тогда и только тогда, когда само число равно нулю.
Задача 36[8][править]
Домножьте на сопряженные следующие числа
а) 
б) 
в) 
г) 
д) 
е) 
Задача 37[9][править]
Докажите тождество 
Подсказка Пусть 

Запишите равенство
которое соответствует равенству
Таким образом, утверждение последней задачи равносильно следующему утверждению:
Модуль произведения комплексных чисел равен произведению их модулей.
Деление[править]
Идея домножения на сопряженное помогает нам определить операцию деления
комплексных чисел. Рассмотрим деление на примере:
Умножим и числитель и знаменатель на одно и то же число
(это число, сопряженное знаменателю). Получим:
В знаменателе стоит 
Разделить комплексное число на действительное не сложно: нужно просто действительную и комплексную
часть разделить на это число. Получаем:
Алгоритм деления на комплексное число аналогичен алгоритму избавления
от иррациональности в знаменателе. Например:
Абстрактный подход[править]
Комплексные числа можно рассматривать как множество пар 
на котором специальным образом определены операция сложения, умножения и деления.
Паре 

Операция сложения на этих парах определяется очевидным образом — надо просто
сложить соответствующие элементы пар:
Найдем, как определяется умножение для этих пар:
Таким образом, мы можем дать такое определение комплексным числам:
Определение 5
Задача 38[9][править]
Покажите, что
а) 
б) 
в) 
г) 
д) 
Такой подход к определению комплексных чисел требует доказательства
многих фактов, которые в предыдущей части (когда мы 
для которой выполнено 
Задача 39[10][править]
Пусть 





Вычитание определяется очевидным образом:
Определить операцию деления несколько сложнее.
Деление — это операция обратная к умножению. Следующая теорема
утверждает корректность операции деления.
Теорема 1 (О существовании деления)
Пусть даны два комплексных числа 

Тогда уравнение
[1]
относительно 
Это решение обозначим как частное:
В принципе, мы уже научились делить в предыдущей части — нужно
просто числитель и знаменатель умножить на сопряженное, после
чего в знаменателе будет действительное положительное число, равное квадрату модуля знаменателя.
Это значит, что хотя бы одно решение у уравнения [1] точно есть.
Чтобы показать единственность решения, применим метод доказательства от противного.
Пусть у нас есть два решения уравнения [1]:
где 
Но мы знаем, что модуль произведения равен произведению модулей.
Оба множителя, 

значит их произведение не может быть равно нулю, так как модуль произведения равен произведению модулей.
Поэтому последнее равенство не может быть верным,
и не может быть два разных решения у уравнения [1].
Есть другой подход к доказательству этой теоремы.
Пусть
Распишем 
Последняя строчка соответствует системе из двух уравнений:
Когда эта система имеет решение? Умножим первое уравнение на 

И сложим их:
Задача 40[10][править]
Покажите, что
Как видите, 


когда комплексное число 
можно делить на любое другое, не равное 
Геометрическая интерпретация[править]
В этой части мы будем изучать различные геометрические свойства комплексных чисел:
преобразования комплексной плоскости, множества на комплексной плоскости,
геометрическую интерпретацию сложения и умножения.
Итак, комплексные числа образуют плоскость. Координатные оси на
этой плоскости соответствуют действительной и мнимой части
комплексного числа. Два числа — действительная часть 



на комплексной плоскости.
Преобразования комплексной плоскости[править]
Поговорим о том, какие преобразования
плоскости соответствуют различным операциям с комплексными числами.
Задача 41[8][править]
Какое преобразование плоскости переводит 

Решение
При этом преобразовании и действительная, и мнимая части увеличиваются в два раза.
Число 



Все числа удаляются от точки 
но при этом остаются в том же направлении, что и до преобразования.
Комплексная плоскость как бы растягивается в два раза относительно точки 
Смотрите рисунки 3 и 4.
Примечание Это преобразование называется гомотетией относительно точки 

Гомотетия с коэффициентом 
Задача 42[9][править]
Какое преобразование плоскости
а) переводит 

б) переводит 

в) переводит 

г) переводит 

д) переводит 

е) переводит 

ж) переводит 

Используйте рисунки 3—8.
Задача 43[9][править]
На плоскости задано две системы координат: 

Система координат 



определить её координаты 

Подсказка
Заметьте, что если мы точку 
координат 


и координаты 

где 



Осталось подобрать их. Рассмотрим точки с координатами
равными 



им соответствуют?
Примечание
Эту задачу можно интерпретировать по-другому:
У нас есть одна единственная система координат.
Мы осуществляем поворот всей плоскости против часовой стрелки на 45° относительно точки 

Все точки плоскости, кроме точки 
переместилась в точку с координатами 
от 
Задача 44[9][править]
Какое преобразование плоскости переводит 
а) 
б) 
в) 
Подсказка
Докажите, что модуль 


не меняется. Эти преобразования — повороты. Какие именно?
Задача 45[9][править]
Запишите формулу 
а) мнимой оси;
б) прямой 
Задача 46[9][править]
Запишите формулу 

Решение
Подсказка Докажите, что искомое преобразование имеет вид 
где 

Задача 47[10][править]
Запишите формулу симметрии относительно прямой,
проходящей через 

Решение
Обозначим 
на это число соответствует повороту. Симметрию относительно
прямой, направленной под углом 
представить как последовательность поворота на 
симметрии относительно действительной оси, а потом поворота на 

Множества на комплексной плоскости и уравнения[править]
Задача 48[9][править]
Найдите (нарисуйте) множество точек (комплексных чисел)
на комплексной плоскости, для которых верно равенство
Задача 49[9][править]
Чему равно расстояние на комплексной плоскости между числами 
(запишите это число как функцию от 



Решение

Задача 50[9][править]
Запишите уравнение на комплексное число 
решением которого является круг на комплексной плоскости
с центром 

Задача 51[9][править]
Где находятся комплексные числа 
а) 
б) 
в) 
г) 
д) 
е) 
Задача 52[9][править]
Параметр 
Какое множество на комплексной плоскости пробежит число 
а) 
б) 
д) 
е) 
ж) 
з) 
и) 
к) 
Решение
Пусть 
а) прямая 
б) парабола;
в) парабола — то же самое что и в предыдущем пункте, только нужно домножить
на 

г) прямая 
Подсказка Попробуйте подставить различные значения 
и отметить их на комплексной плоскости. Затем нужно соединить их гладкой кривой.
Задача 53[10][править]
Параметр 
Какое множество на комплексной плоскости пробежит число 
а) 
б) 
Решение
Пусть 
а) луч, направленный вниз от точки 

б) «худая» парабола, направленная вниз.
Задача 54[9][править]
Докажите, что треугольник с вершинами 


с вершинами 


Задача 55[9][править]
Докажите, что отношение двух комплексных чисел равно действительному числу
тогда и только тогда, когда они лежат на одной прямой с 
Задача 56[9][править]
Опишите множество комплексных чисел 

а) чисто мнимым;
б) действительным.
Подсказка
а) Алгебраический подход: положите 

выразите 







Геометрический подход: найдите множество чисел 
плоскости, для которых треугольник




б) Алгебраический подход: положите 
где 


Геометрический подход: найдите множество чисел 
плоскости, для которых точки 


Тригонометрическое представление[править]
Посмотрите на рисунок 9.
Комплексное число однозначно определяется своим модулем (расстоянием до точки 
и углом между 
комплексного числа и обозначается так:

Рис.9 Комплексное число однозначно определяется своим модулем 

Определение 6
Комплексное число с модулем 

мы будем обозначать как

Задача 57[9][править]
Докажите, что действительная и мнимая части числа 
и

Задача 58[9][править]
Запишите в виде 
а) 
б) 
в) 
г) 
д) 
е) 
Задача 59[9][править]
Запишите в виде 


а) 
б) 
в) 
г) 
д) 
е) 
Теорема 2
При умножении двух комплексных чисел их модули умножаются а аргументы складываются:

Доказательство теоремы отложим на потом.
Посмотрите на рисунок 10, где пояснено содержание теоремы.
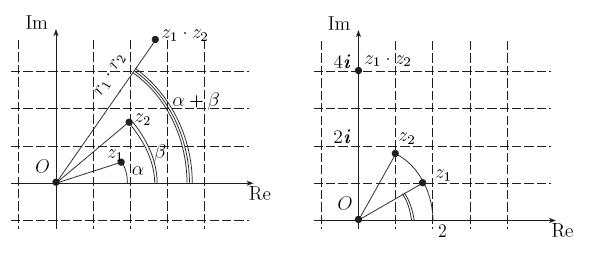
Рис. 10. При умножении чисел их модули умножаютcя, a аргументы складываются: 

Приведем несколько примеров того, как работает эта теорема:
Пример 1.
Пример 2.
Величину 
и в то же время
Как видите, оба метода приводят к одному и тому же результату.
Пример 3.
Величину 
и в то же время
в итоге снова получаем 
Доказательство теоремы 2.
Для доказательства теоремы достаточно показать, что
Это действительно так. Раскрывая левую часть, получим:
В скобках стоят формулы для косинуса суммы и синуса суммы.
Примечание Интересна следующая интерпретация комплексных чисел: каждое комплексное число 
это преобразование комплексной плоскости, а именно, гомотетия относительно центра 
и поворот против часовой стрелки на угол 
композиции соответствующих преобразований.
Задача 60[10][править]
Найдите чему равно 
Решение

Задача 61[10][править]
Рассмотрите два уравнения:
Выразите из них 

Задача 62[10][править]
Найдите значение 
Покажите, что это действительное число, большее 
Задача 63[10][править]
Найдите
а) 

б) 
в) 
Решение
а)
б) 
в) 
Извлечение корней[править]
Возвести число в 

на 
Это правило следует непосредственно из теоремы 2 предыдущего параграфа.
Задача обратная возведению в 

Задача 64[9][править]
Дано уравнение относительно 

где 

удовлетворяющие этому уравнению.
Рис. 11. Корни уравнений: а) 


Прежде, чем решать это общее уравнение, рассмотрим частный случай 

Один из корней равен 

корни? Так как 
единичный модуль 
Комплексные числа, лежащие на единичной окружности, имеют вид:
После возведения в степень имеем:
Осталось найти такие 
Последнее равенство верно, когда аргумент 

Получили, что все комплексные числа вида
являются корнями уравнения 


Для 
Задача 65[9][править]
Найдите все корни уравнения 
Задача 66[9][править]
Найдите все корни уравнения 
Теперь нетрудно записать общее решение для уравнения [3].
Если 

можно записать как
Числа 

Поэтому
Кроме того, аргументы правой и левой части должны совпадать с точностью до 
Из первого уравнения 
![r={sqrt[ {n}]{rho }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d558017488f75a5a4a8d110c1100b4c928476793)
Аргумент 






Теорема 3.
Докажите эту теорему самостоятельно.
Как видите, чтобы найти все корни уравнения 

а остальные корни получатся умножением его на 



Задача 67 [9][править]
Найдите все корни уравнений
а) 
б) 
в) 
г) 
д) 
е) 
Задача 68 [9][править]
Решите уравнения
а) 
б) 
Подсказка Домножьте уравнения на 
Многочлены[править]
Многочлены от 
с помощью умножения (в узком смысле без деления), сложения и вычитания.
Многочлены можно умножать, складывать и вычитать, получая снова многочлены.
Рассмотрим многочлены с действительными коэффициентами от переменной 
Примеры многочленов:
Все многочлены, если раскрыть скобки и привести подобные слагаемые, имеют вид
Числа 
Коэффициент 

а число 
Задача 69 [8][править]
Найдите степени многочленов, приведенных выше.
Задача 70 [9][править]
Докажите, что при умножении многочленов их степени складываются, а
старшие (младшие) коэффициенты умножаются, то есть степень
многочлена, равного произведению двух других, равна сумме их
степеней, а старший (младший) коэффициент равен произведению их
старших (младших) коэффициентов.
Задача 71 [9][править]
Раскройте скобки и приведите подобные:
а) 
б) 
в) 
г) 
д) 
е) 
ж) 
Деление многочленов[править]
Умножать и складывать многочлены просто. Оказывается, их можно ещё и делить.
Рассмотрим деление многочленов на примере:
Cтепень числителя равна 

Давайте вычтем и добавим к числителю 
Теперь старшая степень числителя равна 
нужно прибавить к знаменателю 

Дальше этот процесс продолжать нельзя, поскольку степень числителя стала меньше, чем степень
знаменателя. Таким образом, результат деления можно записать так:
Здесь 

Примеры деления многочленов:
Когда остаток при делении равен нулю, то значит
первый многочлен делится на второй.
Определение 7.
Задача 72[9][править]
Разделите один многочлен на другой с остатком:
а) 
б) 
в) 
г) 
д) 
е) 
Решение
а)
б) 
в) 
г) 
д) 
е) 
Задача 73[9][править]
Известно, что 

Ответ: 

Подсказка Разделите 

Задача 74[9][править]
Известно, что 

Ответ: 


Задача 75[9][править]
Найдите все корни уравнения 
Ответ: 



Подсказка Один из корней равен 
Задача 76[12] Исследовательская задача[править]
Пусть 
При каких 


на 
Например:
многочлен 



многочлены 


на 



не делятся на 
Подсказка Заметьте, что 

Но это не достаточное условие.
Докажите, что 
при нечетном 
Мы умеем делить многочлены друг на друга с
остатком, и значит можно говорить о наибольшем общем делителе
двух многочленов.
Пусть 

степени. Тогда
НОД(

есть многочлен максимальной степени с коэффициентом 
который делятся 

Задача 77[10][править]
Найдите
а) НОД(

б) НОД(

в) НОД(

г) НОД(

д) НОД(

е) НОД(

Задача 78[10][править]
Докажите, что НОД двух многочленов, есть многочлен, корни которого являются
корнями как первого, так и второго многочлена.
Задача 79[10][править]
Найдите общие корни многочленов
Решение
НОД(




Основная теорема алгебры[править]
Мы уже с вами отмечали, что некоторые многочлены не имеют действительных корней, зато имеют
комплексные корни. Например, уравнения
не имеют действительных корней, так как их правая часть положительна при любых действительных 
Но, в то же время, комплексное число 
Верна следующая теорема:
Теорема 4 (Основная теорема алгебры)
Любой многочлен имеет комплексный корень.
Пояснения:
Коэффициенты многочлена могут быть как действительными, так и
комплексными.
Многочлен может иметь только действительные корни, но
это не противоречит теореме, так как действительные числа являются подмножеством
комплексных.
Степень многочлена больше либо равна 
Более того, многочлен степени 

А именно, верно следующее следствие из основной теоремы алгебры:
Следствие 1
Любой многочлен степени 

с комплексными коэффициентами.
Многочлены степени 
Например, многочлен
раскладывается в произведение линейных многочленов с действительными коэффициентами:
А многочлен
не может быть разложен в произведение действительных линейных многочленов —
для его разложения нужны комплексные числа:
Задача 80[9][править]
Проверьте последнее равенство.
В комплексных числах любой многочлен (даже с комплексными коэффициентами)
раскладывается в произведение линейных многочленов.
Каждый множитель — линейный многочлен — дает один корень многочлена.
Задача 81[9][править]
Почему многочлен степени 
линейных множителей?
Доказательство основной теоремы алгебры довольно сложно. В конце
этой части мы рассмотрим схему одного очень популярного
интуитивного доказательства. А сейчас давайте поверим, что это
теорема действительно имеет место. Для этого вспомните задачи
1,2 и 3.
Задача 82[10][править]
Докажите, что если комплексное число 
то и сопряженное число 
Решение
Если многочлен 

и если 

Задача 83[10][править]
Найдите многочлен с действительными коэффициентами, имеющий комплексный корень 
Решение:
Можно вспомнить про формулу квадратного уравнения и понять,
что второй корень будет сопряжен первому. Остается по двум корням,


Для этого раскройте скобки 
Подсказка: Среди квадратных трехчленов есть подходящий.
Задача 84[10][править]
Найдите многочлен с действительными коэффициентами, имеющий комплексные
корни 

Решение

Задача 85[10][править]
Используя основную теорему алгебры, докажите, что любой
многочлен с действительными коэффициентами разлагается
в произведение многочленов первой или второй степени с действительными
коэффициентами.
Решение
Можно доказывать методом математической индукции по степени
многочлена. Идея доказательства: у любого многочлена 
корень (основная теорема алгебры). Если это действительный корень


многочлен степени на 
Если корень комплексный 




действительными коэффициентами. После деления получаем многочлен
на степени на 
Задача 86[10][править]
Укажите разложение на линейные множители для многочленов
а) 
б) 
в) 
г) 
Решение
а)
б) 
в) 
г) 
Схема доказательства основной теоремы алгебры[править]
Непрерывность — отображение кривых[править]
Пусть 
Тогда если мы будем медленно менять 

будет меняться медленно. Если 

двигаться по некоторой непрерывной кривой.
Например, пусть 
Тогда 
кривой в комплексной плоскости — малое изменение 
малое смещение 
Таким образом, мы можем говорить об отображении кривых —
под действием многочлена 
На рисунке 12 изображена кривая, в которую
отобразится окружность 



Рис. 12 Образ окружности 


Доминирование старшей степени[править]
Как будет двигаться 



Другими словами, как выглядит образ окружности 

Заметьте, что 
только в то время, как 


Если 






Свойство доминирования старшей степени заключается в том,
что при очень больших по модулю значениях 


Например, если 

После того, как мы вынесли за скобку 
которое не содержит 

совсем маленькими и не значительными.
На рисунке 13 изображены образы трех окружностей радиусов



вокруг центра.
Непрерывность — движение кривых[править]

Рис. 13 Образ окружностей 




А теперь представьте, что мы начали непрерывно менять 


Тогда образ окружности 


постепенно будет деформироваться.
- Сначала, при
это будет просто точка
.
- Потом, при маленьком
, например
, вокруг точки
появится некоторая замкнутая кривая (рис. 13).
- Потом, при некоторых средних значениях
, например
,будем иметь нечто необычное (рис. 12 справа).
- Потом, постепенно увеличивая
до
, получим три ярко выраженных оборота (рис. 13}).
- При больших
, например
, обороты все больше будут сближаться друг к другу и выглядеть почти как
окружностей.
(рис. 13).
Во время этой деформации кривая в какой-то момент пройдёт через
точку 

находится снаружи замкнутой кривой, а при больших 
замкнутой кривой, которая, более того, делает вокруг
несколько оборотов. Это означает, что при некотором 
некотором 

следовательно, 
многочлена.
Таким образом, наш многочлен 
Конец схемы доказательства
Алгебра многочленов по модулю многочлена[править]
Очень часто в практике находит применение следующая конструкция.
Рассматриваются многочлены от переменной 

от 
Например, верно равенство
Заметьте, что из этого равенства можно заключить, что
а также, после умножения на 

…
— то есть все степени 

через многочлены меньшей степени. А значит, любой многочлен
степени больше 
Задача 87[9][править]
Докажите, что если 
от 

Подсказка Попробуйте упростить многочлен 
совпадает с остатком при делении 

Задача 88[9][править]
Докажите, что если дан многочлен 

и многочлен 



быть упрощен до многочлена степени меньше 
при этом, единственным образом.
Подсказка Результат упрощения равен остатку при делении
на 
существуют единственные 

где степень 

Определение 8
Задача 89[9][править]
Найдите, чему равны следующие многочлены по модулю 
Определение 9
Выражение
означает остаток при делении 

Задача 90[9][править]
Найдите, чему равно
Задача 91[10][править]
Для многочлена 

Для каждого ли многочлена 

Решение



Задача 92[10][править]
Докажите, что алгебра многочленов по модулю 
В каком смысле они совпадают?
Задача 93[10][править]
Рассмотрите алгебру многочленов по модулю 
Верно ли что, для каждого многочлена 
на 

Задача 94[10][править]
Рассмотрите алгебру многочленов по модулю 
Верно ли что, для каждого многочлена 
на 

Определение 10
Многочлен называется неприводимым, если он не может быть разложен в произведение
многочленов степени больше 
Задача 95[11][править]
а) Докажите, что в алгебре многочленов над комплексными числами не существует неприводимых многочленов степени
больше 
б) Докажите, что в алгебре многочленов над действительными числами не существует неприводимых многочленов степени
больше 
Задача 96[12][править]
Многочлены с действительными коэффициентами
по модулю любого неприводимого многочлена 
Примечание
Изоморфность означает одинаковость с точностью до переобозначения.
Два множества элементов 

изоморфны если между их элементами существует взаимооднозначное соответствие,
которое сохраняет операции сложения и умножения.
Например, пусть элементу 





Пусть 


Заметьте, что операции сложения и умножения слева от знака «равно» — это операции на множестве 
а операции сложения и умножения справа — операции на множестве 
Подсказка Это соответствие строится следующим образом. Любой неприводимый
квадратный трехчлен можно линейной заменой переменной
превратить в 

найти многочлен 
соответствуют мнимой и действительной части соответствующего 
Действительные и комплексные числа называются числовыми полями.
Есть ещё другие числовые поля.
Если в каком-то числовом поле нет неприводимых многочленов степени больше 
оно называется алгебраически замкнутым.
Комплексные числа — единственное алгебраически замкнутое числовое поле,
где бесконечное (точнее несчетное) число элементов.
Матрицы[править]
Матрицы — это ещё одно обобщение чисел. Мы с вами изучим матрицы 
Определение 11
Матрицы 

на которых определены операции сложения и умножения. А именно, пусть
Тогда

Примечание
Первый индекс соответствует номеру строчки, второй — номеру столбца.
Правила сложения и умножения можно коротко обозначить так:
Если бы мы рассматривали матрицы 
Чтобы получить элемент матрицы 


столбце, нужно взять 



перемножить соответствующие элементы и сложить.
Задача 97[8][править]
Пусть
Вычислите:
а) 
б) 
в) 
г) 
д) 
е) 
Определение 12.
Матрица
называется единичной матрицей.
Задача 98[9][править]
Докажите, что
для любой матрицы 
Таким образом, единичная матрица обладает такими же свойствами,
как и число 

Определение 13
Введем обозначение:

Задача 99[9][править]
Докажите, что
то есть произведение матрицы 
Определение 14
Матрицы можно умножать на число, при этом каждый элемент матрицы умножается на это число.
Например:

Задача 100[9][править]
Покажите, что
а) 
б) 
в) 
Задача 101[9][править]
Раскройте скобки
Введем обозначение
Задача 102[9][править]
Найдите результат умножения матриц 
Подсказка Обратите внимание на то, что получится снова матрица вида

угол — нижний правый) стоят одинаковые числа, а два числа на
другой диагонали противоположны.
Задача 103[9][править]
Найдите результат умножения матриц 
Задача 104[9][править]
Покажите, что матрицы вида
с операциями сложения и умножения матриц
соответствуют комплексным числам с операциями сложения и умножения комплексных чисел.
Задача 105[11][править]
На основе предыдущей задачи предположите, чему равно
Решение

Подсказка Чему равно 
Определение 15
Задача 106[9][править]
Найдите матрицу, обратную к матрице 
Задача 107[10][править]
Система линейных уравнений
может быть записана как
Покажите, что решение этой системы может быть записано как
Рекомендуемая литература[править]
- «Теорема Абеля в задачах», В. Б. Алексеев, — М.:МЦНМО, 2001.
Содержание:
Хроника возникновения комплексных чисел:
Исследование.
1) Подтвердите примерами справедливость следующих высказываний. Если высказывание ложно, то сделайте так, чтобы оно стало истинным.
- а) Если а и b — натуральные числа, то корень уравнения х + а = b также является натуральным числом.
- б) Если а и b -целые числа, то корень уравнения ах = b также является целым числом
- в) Если а неотрицательное рациональное число, то корень уравнения х1 = а также является рациональным числом.
- г) Если а неотрицательное действительное число, то корень уравнения х2 = а также является действительным числом.
2) Существует ли действительное число квадрат которого равен -1?
3)
- а) Существуют ли действительные корни уравнения х2 = а при
- б) Можно ли решить эту задачу расширив множество действительных чисел?
4) Существует ли однозначное соответствие между множеством действительных чисел и множеством точек на числовой оси? А какие числа соответствуют точкам на координатной плоскости?
На множестве действительных чисел уравнение х2 = -1 не имеет решений. Значит, мы должны расширить множество действительных чисел так, чтобы корни этого уравнения входили в него. Для этого введём новое число и примем, что оно является корнем уравнения х2 + 1 = 0, т.е. 
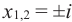
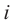
Расширим множество действительных чисел так, чтобы в него входили все действительные числа и число 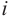
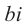
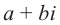
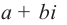
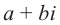
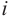
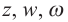
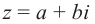
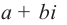
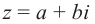
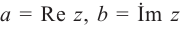


Следствие: для комплексных чисел а + 

а + 

Пример. Из равенства 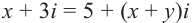
Решение: Из равенства действительных и мнимых частей получаем: х = 5
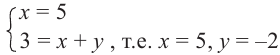
Суммой комплексных чисел 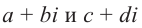
Действия над комплексными числами
Произведением комплексных чисел 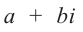
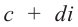
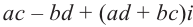
Значит, два комплексных числа умножаются по правилу умножения многочленов при условии, что 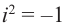
Пример №1
Рассмотрим частные случаи степеней мнимых единиц:
Как видно, натуральные степени мнимой единицы 
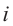
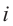
Пример №2
Вычислите: а) 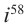
Решение: а) 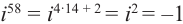
Число 

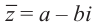




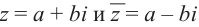
Произведение взаимно сопряжённых комплексных чисел является действительным числом: 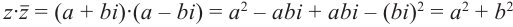
В частном случае, сопряжённым для действительного числа является само число, для мнимого — произведение числа и (-1).
Для каждого комплексного числа 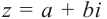
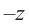
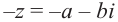
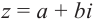
Вычитание и частное комплексных чисел определяется равенствами:
Для нахождения отношения комплексных чисел, удобнее числитель и знаменатель умножить на число, сопряжённое для знаменателя .
Пример №3
Найдём разность и отношение чисел 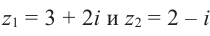
Решение:
Все свойства арифметических операций для действительных чисел, справедливы для комплексных чисел. Как следствие, получаем, что любые алгебраические тождества справедливы для множества комплексных чисел. Например, для комплексных чисел 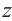
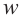
Квадратный корень комплексного числа
Число, квадрат которого равен 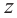
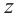
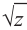
Пример №4
Найдём квадратный корень комплексного числа
Решение: Пусть 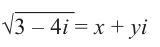
Из равенства действительных и мнимых частей имеем:
Отсюда получаем решение (2; -1) и (-2; 1). Значит,
Примечание: В отличии от действительных чисел, говоря о квадратном корне комплексного числа, имеется в виду каждое из двух значений, различающихся знаками. Корни квадратного уравнения 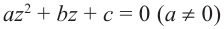
Пример №5
Решим уравнение 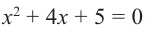
Решение:
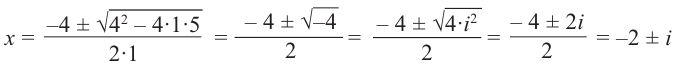
Легко можно проверить, что также в силе остаётся и теорема Виета. Для квадратного уравнения с действительными коэффициентами комплексные корни являются сопряжёнными числами. Комплексное число 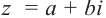
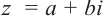
Пример:
Точки, соответствующие комплексно сопряжённым числам располагаются симметрично оси абсцисс.
Модуль и аргумент комплексного числа
Тригонометрическая форма комплексного числа
Пусть на комплексной плоскости комплексному числу 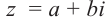

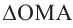
Отсюда:
Расстояние, от начала координат до точки соответствующей комплексному числу, называется модулем комплексного числа и обозначается как: 
Угол, образованный конечной стороной угла поворота луча ОМ,
называется аргументом 
Из 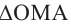
Модуль числа 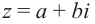


Для аргумента комплексного числа, обычно берётся угол принадлежащий промежутку [0; 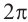
Пример №6
Найдём модуль и аргумент комплексного числа
Решение: Из того, что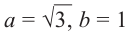
и принимая внимание, что угол 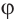
получим:
Из формул 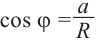
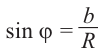
Тогда
Для комплексного числа 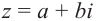
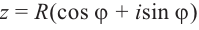
В частном случае для модуля и аргумента числа 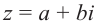
Пример №7
Запишем комплексное число
в тригонометрической форме.
Решение:
Так как угол 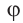
Действия над комплексными числами, заданными в тригонометрической форме
Найдём произведение комплексных чисел, заданных в тригонометрической форме 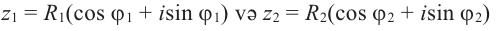
Чтобы найти произведение комплексных чисел, заданных в тригонометрической форме, надо перемножить их модули и сложить их аргументы.
Пример:
Теперь найдём отношение
Модуль отношение равен отношению модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.
Пример:
Возвести число 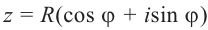
Модуль степени комплексного числа с натуральным показателем равен степени модуля основания, а аргумент равен аргументу основания умноженному на показатель степени n.
Пример:
Формулу 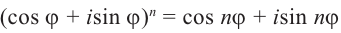
Отсюда
Из равенства двух комплексных чисел имеем:
Аналогичным образом можно написать формулы для 
Корень n-ой степени комплексного числа
Найдём значение выражения 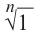
Запишем в виде 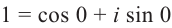
виде 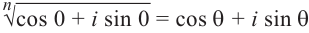
Возведём каждую из двух сторон в n-ую степень:
Если два комплексных числа, заданных в тригонометрической форме равны, то их модули равны, а аргументы отличаются на 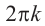
Это значит,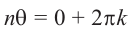
Таким образом,
Отсюда при 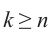
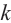

Обозначим корни 
Как видно, модули корней 
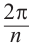

Корнем 
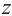
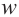
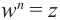
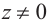


Запишем 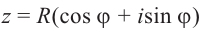
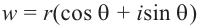
Для 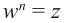
Из равенства двух комплексных чисел получим:
Значения при 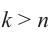

Поэтому, должно соблюдаться следующее:
Формула корни n-ой степени комплексного числа
Если 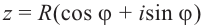
Пример №8
Найдём все значения
Решение: пусть 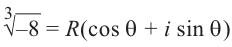
Отсюда
При
При
При
Для чего нужны комплексные числа
Комплексные числа возникают в связи с задачей решения квадратных уравнений. Так, оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Арифметические операции над комплексными числами
Комплексным числом называется выражение вида 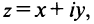
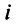
Число 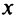
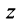
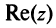
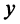
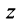
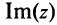
Действительное число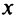
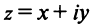
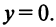
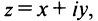
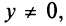
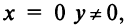
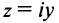
Числа 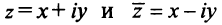
Два комплексных числа 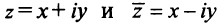
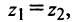
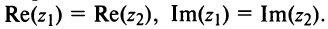
Арифметические операции на множестве комплексных чисел определяются следующим образом.
1.Сложение (вычитание) комплексных чисел
2. Умножение комплексных чисел
В частности,
т.е. мнимая единица есть число, квадрат которого равен — 1.
3. Деление двух комплексных чисел
Нетрудно убедиться в том, что все арифметические операции (16.1)-(16.3) над комплексными числами определяются естественным образом из правил сложения и умножения многочленов 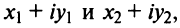
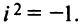
Пример №9
Даны комплексные числа
Найти
Решение:
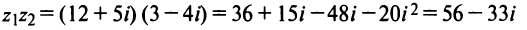
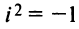
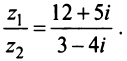
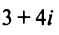
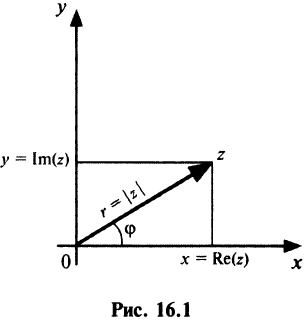
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости
Плоскость называется комплексной, если каждому комплексному числу 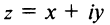
Оси 
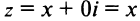
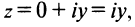
Тригонометрическая и показательная формы комплексного числа
С каждой точкой 
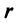
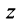
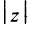
Угол 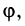
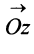
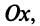
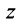
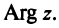
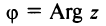
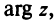
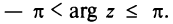
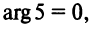
Очевидно (см. рис. 16.1), что
Следовательно, комплексное число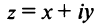
Представление комплексного числа в виде (16.6), где 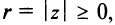
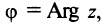
Сформулируем некоторые свойства арифметических операций над комплексными числами.
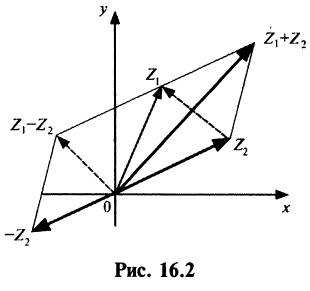
1. При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
На рис. 16.2 показаны радиусы-векторы комплексных чисел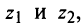
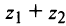
2. Модуль произведения (частного) двух комплексных чисел равен произ ведению (частному) модулей этих чисел, а его аргумент — сумме (разности) аргументов этих чисел, т.е.
Геометрически умножение числа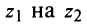
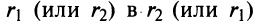
Пример №10
Комплексные числа 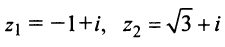
Решение:
По формуле (16.4) найдем модуль комплексного числа 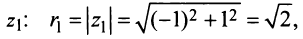
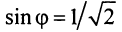
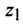
Аналогично 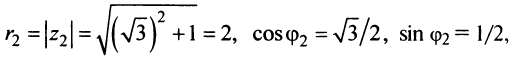
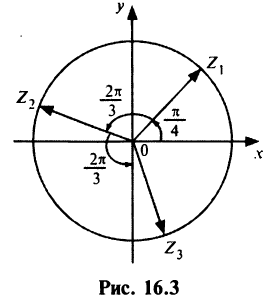
Теперь по формулам (16.7) и (16.8)
Так как в соответствии с формулами (16.7) и (16.8) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень 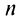
Пример №11
Найти
Решение:
По формуле Муавра (16.9)
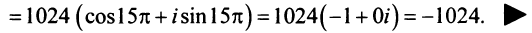
Пусть
Тогда, используя определение корня и формулу Муавра (16.9), получим
или
Отсюда следует, что
Итак,
где
При 
Таким образом, корень 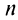
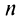
Пример №12
Найти
Решение:
В примере 16.2 было получено
откуда получаем три значения корня
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки 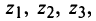
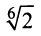
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера.
Отсюда следует показательная форма комплексного числа.
где
В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.
Формы записи комплексного числа
Решение простейшего квадратного уравнения 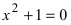
Определение: Выражение 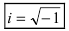
Определение: Комплексным числом называется выражение вида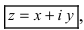
Определение: Приведенная форма записи комплексного числа называется алгебраической.
Определение: Два комплексных числа 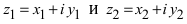
Определение: Комплексное число называется нулевым, если вещественная и мнимая части равны нулю.
Определение: Комплексно-сопряженным к комплексному числу 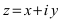
Пример №13
Записать комплексно-сопряженное число к комплексному числу
Решение:
Согласно определению комплексно-сопряженного числа получаем
Замечание: Двойное комплексное сопряжение приводит к исходному комплекс- ному числу, т.е.
Решение квадратных уравнений с отрицательным дискриминантом невозможно в области вещественных чисел, так как нельзя извлекать корень четной степени из отрицательного числа на множестве действительных чисел. Однако это ограничение снимается в области комплексных чисел.
Пример №14
Решить квадратное уравнение
Решение:
Вычислим дискриминант уравнения 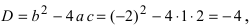
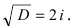
Замечание: Решение квадратного уравнения с отрицательным дискриминантом всегда состоит из комплексно-сопряженных корней.
Комплексное число 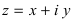
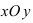
Рис. 2. Изображение комплексного числа на комплексной плоскости.
Пример №15
Изобразить на комплексной плоскости число z = 2-3i (Рис. 3).
Решение:
Рис. 3. Изображение комплексного 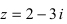
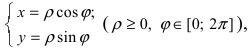
Определение: Полученная форма записи комплексного числа называется тригонометрической.
Обратный переход от полярной системы отсчета к декартовой системе координат осуществляется по формулам: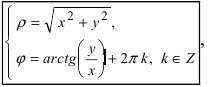
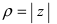
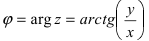
Замечание: Аргумент комплексного числа 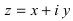
Действия с комплексными числами
1. Для того чтобы сложить (найти разность) два комплексных числа 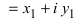
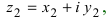
Пример №16
Найти сумму и разность чисел 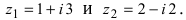
Решение:
Найдем сумму заданных комплексных чисел 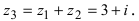
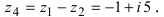
Рис. 4. Изображение комплексных чисел на комплексной плоскости.
Замечание: Отметим, что
2. Для того чтобы найти произведение двух комплексных чисел 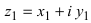
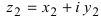
Замечание: Отметим, что
Замечание: Произведение комплексных чисел в тригонометрической форме записи имеет вид 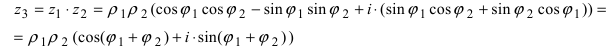
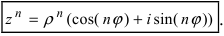
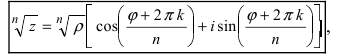
3. Деление комплексного числа 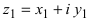
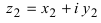
Замечание: Деление этих чисел в тригонометрической форме записи имеет вид: 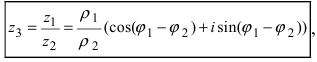
Показательная форма записи комплексного числа
Известно, что любую дифференцируемую функцию можно представить по формуле Тейлора-Маклорена (см. Лекцию № 22, Первый семестр), например,
Последняя формула называется формулой Эйлера. Используя эту формулу,
запишем комплексное число 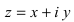
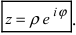
Комплексные числа и арифметические операции
Как известно, под комплексным числом понимается выражение вида
где х и у — действительные числа, a i — мнимая единица.
Числа вида 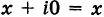
Действительные числа х и у называются соответственно действительной и мнимой частями числа z и обозначаются следующим образом:
Под модулем комплексного числа z понимается неотрицательное число
Сопряженным числом 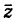
Таким образом,
На множестве комплексных чисел следующим образом определено отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
I. Пусть z1=x1+iy1 и z2=x2+iy2.Тогда
В частности, z = 0 
II. z1±z2= (x1± x2) + i(y1 ± y2)-
Отсюда следует, что
Re (z1 ± z2) — Re z1 ± Re z2,
Im (z1 ± z2) — Imz1 ± 1mz2
III. z1z2 = (x1x2 — y1y2) + i(x1y2+x2y1).
Отсюда, в частности, получаем важное соотношение
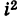
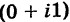
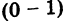
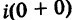
Заметим, что правило умножения III получается формально путем умножения двучленов 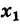
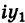
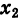
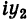
Очевидно также, что для 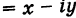
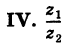
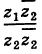
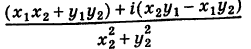
Легко проверить следующие свойства:
1)
- Заказать решение задач по высшей математике
Комплексная плоскость
Рассмотрим плоскость с прямоугольной системой координат Оху. Каждому комплексному числу z = х + iy может быть поставлена в соответствие точка плоскости z(x, у) (рис. 161), причем это соответствие взаимно однозначно. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
На оси Ох расположены действительные числа: z =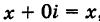
Заметим, что г = |z| представляет собой расстояние точки г от начала координат.
С каждой точкой z связан радиус-вектор этой точки Oz; угол, образованный радиусом-вектором точки z с осью Ох, называется аргументом ф = Arg z этой точки. Здесь 
Для аргумента ср имеем (рис. 161)
где
Примеры: 1) arg 2 = 0; 2) arg (-1) = 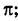
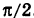
Модуль г и аргумент ф комплексного числа z можно рассматривать (рис. 161) как полярные координаты точки z. Отсюда получаем
Таким образом, имеем тригонометрическую форму комплексного числа
где
Теорема: При сложении комплексных чисел их радиусы-векторы складываются (по правилу параллелограмма).
Действительно, если число 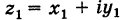
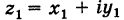
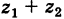
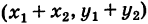
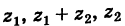
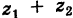
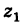
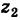
Следствие. Так как 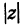
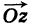
Теорема: При вычитании комплексных чисел их радиусы-векторы вычитаются. Так как 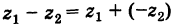

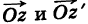
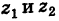
Следствие. Расстояние между двумя точками 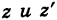
Теоремы о модуле и аргументе
Теорема: Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей. Действительно, если
то имеем
Отсюда
и
где значения многозначной функции Arg, стоящие в левой и правой частях равенства (1), следует подбирать соответствующим образом. Это замечание надо иметь в виду и для дальнейшего.
Следствие. Модуль целой положительной степени комплексного числа равен такой же степени модуля этого числа, а аргумент степени равен аргументу числа, умноженному на показатель степени, т. е.
(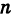
Доказательство непосредственно вытекает из рассмотрения произведения равных сомножителей.
Пример №17
Построить точку 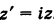
Решение:
Имеем
Следовательно, при умножении на i вектор 
Теорема: Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя. Пусть
Так как
то на основании теоремы 1 имеем
Отсюда
Извлечение корня из комплексного числа
Пусть
где 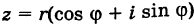
Отсюда получаем
Таким образом,
Заметим, что здесь под 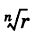
Здесь в качестве числа k достаточно брать лишь значения 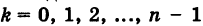
Из формулы (4) следует, что корень 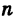
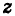
Пример №18
Найти
Решение:
Так как 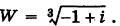
Отсюда
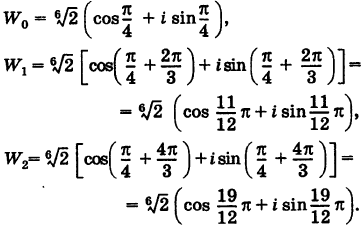
Точки 
Понятие функции комплексной переменной
Пусть даны две комплексные плоскости Оху (плоскость г) и O’uv (плоскость w).
Определение: Если каждой точке z 
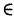
с областью определения Е, значения которой принадлежат множеству Е’ (рис. 166). Если множество значений функции f(z) исчерпывает все множество Е то Е’ называется множеством значений (областью изменения) функции f(z). В этом случае пишут
Множества Е и Е’ можно изображать на одной комплексной плоскости.
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).
Раздел математики, изучающий свойства комплексных функций, носит название теории функций комплексной переменной.
Пример:
Во что переходит сектор Е
(рис. 167, а) при отображении
Решение:
Имеем
Поэтому отображенная область E’ представляет собой полукруг (рис. 167, б).
Определение комплексных чисел
Определение комплексного числа и основные функции комплексной переменной
Определение 7.1. Множеством комплексных чисел 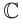
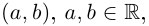
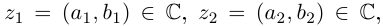
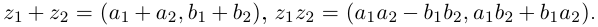
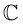
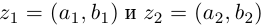
Операции сложения и умножения на множестве 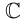
Лемма 7.1. Для любых комплексных чисел 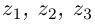
□ Докажем, например, свойство 4 (свойство 5 доказывается аналогично, свойства 1, 2, 3 очевидны).
Пусть 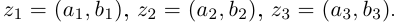
Два последних комплексных числа совпадают. После раскрытия скобок оказывается, что оба они равны
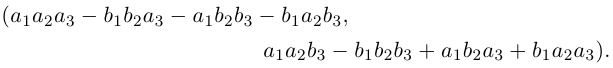
Определение 7.2. Комплексное число 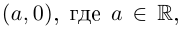
Это определение оправдывается тем, что установлено взаимно однозначное соответствие между множеством пар 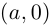
Такое соответствие в высшей алгебре называется изоморфизмом.
Определение 7.3. Комплексное число (0,1) обозначается буквой
Легко видеть, что 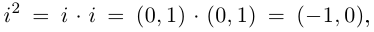
Далее, так как 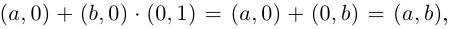
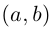
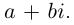
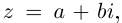
Иными словами, комплексные числа можно складывать и умножать, пользуясь известными законами сложения и умножения (лемма 7.1), имея в виду, что
Определение 7.4. Разностью двух комплексных чисел 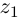
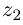
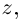
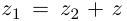
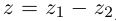
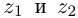
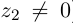
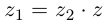
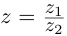
Проверим, что эти операции однозначно определены.
□ Пусть 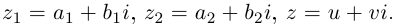
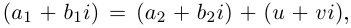
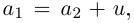
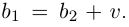
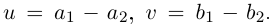
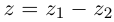
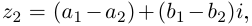
Для частного имеем: 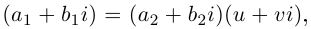
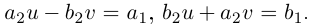
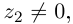
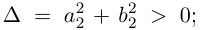
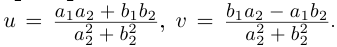
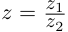
Такое деление можно осуществлять непосредственно:
Комплексное число 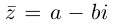
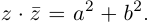
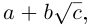
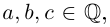

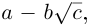
Определение 7.5. Пусть 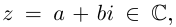
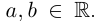
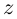
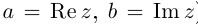
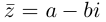
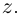
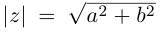
Лемма 7.2. Для любых комплексных чисел 
Доказать эти утверждения будет предложено самостоятельно в качестве упражнения.
Множество комплексных чисел 
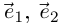
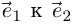
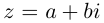
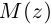
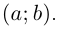
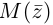
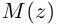
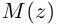
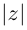
Аргументом числа 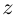
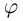
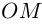
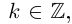
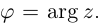
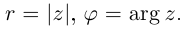
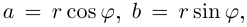
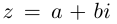
Пример:
Записать в тригонометрической форме числа
□ 1)
При записи комплексного числа в тригонометрической форме обычно берут одно фиксированное («наиболее простое») значение аргумента. Возьмём 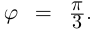
2) 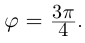
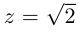
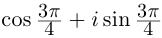
Комплексные числа, записанные в тригонометрической форме, удобно умножать и делить. При умножении модули чисел перемножаются, аргументы складываются. При делении модули делятся, аргументы вычитаются.
Лемма 7.3. Пусть 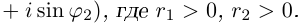
Если
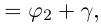
Степень с целым показателем для комплексных чисел определяется так же, как и для действительных. Поэтому мы можем сформулировать
Следствие (формула Муавра). Если 
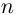
Иными словами, при возведении комплексного числа в целую степень модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Пример:
Применяя формулу Муавра, получить известные формулы тригонометрии для
□ Имеем: 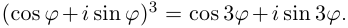
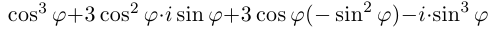
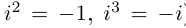
Определение 7.6. Пусть 
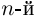
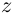
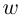
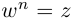
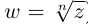
Лемма 7.4. Если 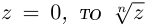
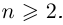
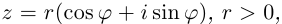
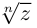
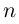
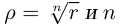
□ Правая часть леммы очевидна, так как 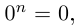
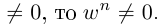
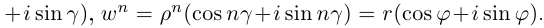
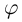
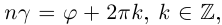
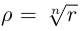
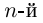
При замене 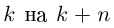
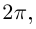
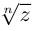
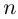
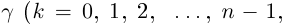
Замечание. 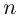
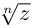
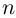
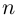
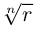
Пример №19
Найти все значения
□ 1) 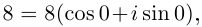
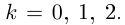
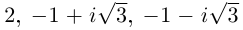
Первое из них — арифметическое значение кубического корня из положительного числа 8.
2) 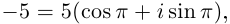
Получим 4 значения:
(см. рис. 7.3). 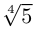
3) 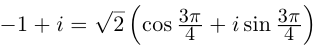
Получим 3 значения:
(см. рис. 7.4). ■
Определение 7.7. Пусть 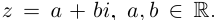
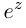
Если 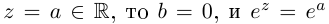
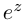
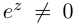
Лемма 7.5. Для любых 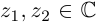
□ Пусть 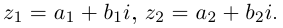
Далее, так как 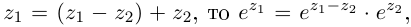
Пример №20
Вычислить
□ Имеем:
Так как при всех 
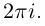
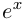
Определение 7.8. Логарифмом комплексного числа 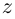
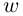
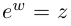
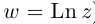
Лемма 7.6. Если 
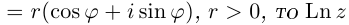
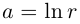
□ Первая часть леммы следует из того, что 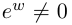
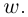
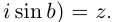
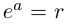
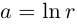
Таким образом, множество значений функции 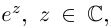
Пример №21
Найти все значения 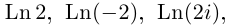
Определение 7.9. Для любых 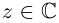
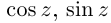
Если
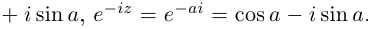
Аналогично,
Отметим также, что все известные формулы тригонометрии сохраняются для комплексных значений аргументов (при этом 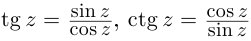
Так как
Легко видеть, что 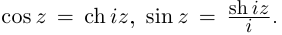
Комплекснозначные функции действительной переменной
Рассмотрим функцию 
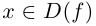
Так как 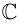
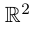
Определение 7.10. Комплекснозначная функция действительной переменной 
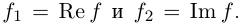
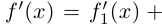
Для комплекснозначных функций сохраняются формулы производной суммы, произведения и частного.
Лемма 7.7. Если комплекснозначные функции действительной переменной 
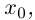
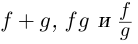
в точке 
□ Докажем лемму для случая производной произведения. Утверждение для производной суммы доказывается проще, а для производной частного — несколько сложнее, но, по сути дела, аналогично.
Пусть 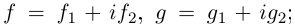
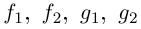
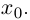
Функция 
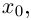
Легко видеть, что это выражение совпадает с
Пример №22
Доказать, что при любом 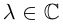
т.е. привычная для действительных 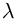
□ Пусть
Тогда
С другой стороны,
что совпадает с
Отметим, что производная комплекснозначной функции берётся по действительной переменной. Принципиально иная ситуация возникает при рассмотрении комплекснозначных функций комплексной переменной и при дифференцировании их по комплексной переменной. Здесь имеют место совершенно неожиданные эффекты (например, если функция дифференцируема в окрестности точки, то она имеет производные всех порядков в этой окрестности), которые студенты обычно изучают на III курсе (курс ТФКП — теория функций комплексной переменной).
Многочлены
Функция комплексной переменной
где 
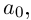
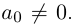
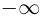
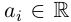
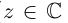
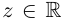
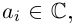
Если 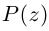
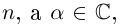
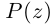
где
Теорема 7.1 (Безу). Остаток от деления многочлена 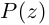
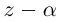
□ Из (7.1) имеем при
Следствие. Многочлен 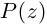

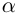
□ Утверждение немедленно следует из теоремы Безу.
Таким образом, число 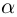
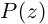
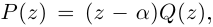
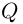
Теорема 7.2 (основная теорема алгебры). Любой многочлен степени 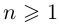
В настоящее время мы не располагаем математическим аппаратом для доказательства этой теоремы, поэтому примем её без доказательства. Доказана она будет очень просто в курсе ТФКП (и даже двумя способами — как простое следствие из теоремы Лиувилля или теоремы Руше).
Теорема 7.3. Многочлен с комплексными коэффициентами
раскладывается в произведение линейных множителей
где 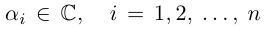
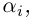
□ По основной теореме алгебры 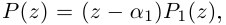
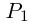
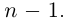
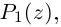
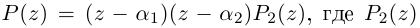
где 
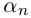
Если раскрыть скобки в правой части (7.2), то коэффициент при 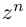
Определение 7.11. Комплексное число 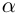
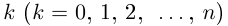
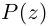
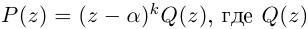
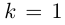
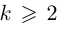
Если 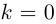
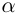
В общем случае, учитывая кратность корней, многочлен 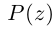
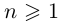
где все комплексные числа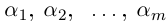
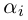
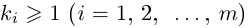
Лемма 7.8. Пусть 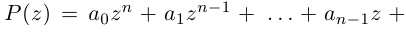
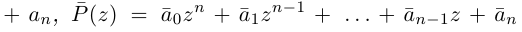
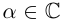
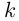
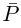
□ Так как 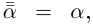
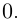
Так как 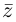
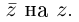
Это и означает, что 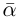
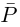
Следствие. Если 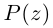
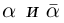
□ Это очевидно из леммы 7.8, так как 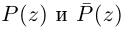
Теорема 7.4. Многочлен степени 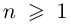
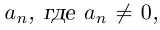
□ По теореме 7.3 и лемме 7.8
где 
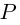


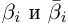

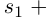
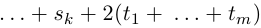
Пусть 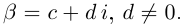
Получили квадратный трёхчлен с действительными коэффициентами 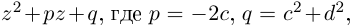
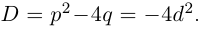
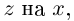
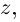
Теорема 7.4 является примером утверждения, в формулировке которого отсутствуют комплексные числа (чисто действительное утверждение), а естественное доказательство его получается с выходом во множество комплексных чисел. Таких утверждений можно встретить немало в различных математических курсах и прикладных науках.
Кстати, квадратный трехчлен с комплексными коэффициентами имеет такой же вид разложения на линейные множители, как и квадратный трёхчлен с действительными корнями в элементарной алгебре:
Корни 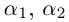
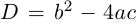
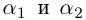
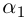
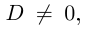
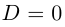
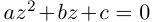
Если 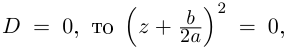
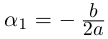
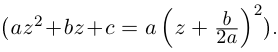
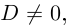
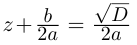
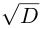
Пример №23
Решить уравнение
□ 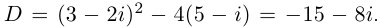
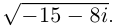
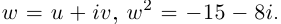
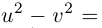
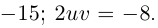
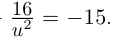
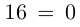
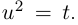
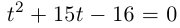
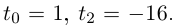
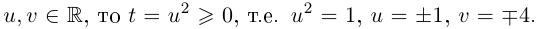
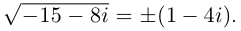
Пример №24
Найти все значения 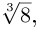
□ Левая часть раскладывается на множители:
Поэтому один из корней равен 2. Квадратный трёхчлен 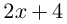
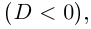
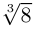
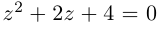
Во множестве комплексных чисел 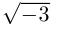
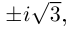
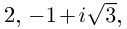
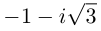
Разложение правильной дроби в сумму простейших дробей
Мы будем рассматривать действительные дробно-рациональные функции 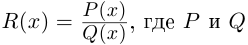
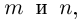
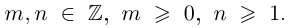
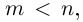
Лемма 7.9. Если 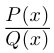
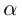
где 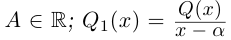
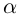
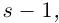
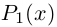
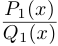
□ Так как 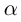
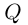
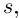
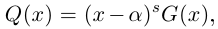
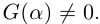
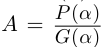
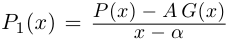
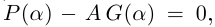
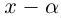
Так как степень G меньше степени Q и степень Р меньше степени Q, то степень числителя последней дроби меньше степени Q; значит, степень 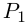
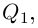
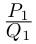
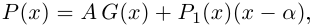
Утверждение леммы, очевидно, сохраняется, если все числа и многочлены считать комплексными.
Лемма 7.10. Пусть
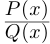
где 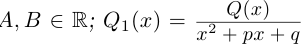
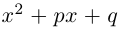
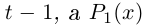
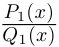
□ Пусть 
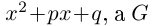
Такие числа А и В определены единственным образом, так как если 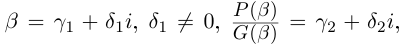
и числа А, В находятся из системы 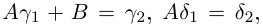
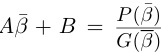
Рассмотрим многочлен 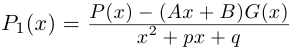
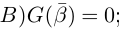
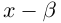
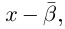
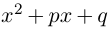
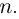
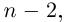
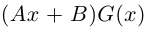
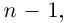
Значит, степень 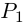
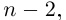
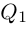
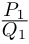
откуда
Последовательно выделяя из многочлена 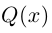
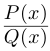
(здесь
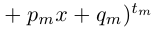
Все слагаемые последней суммы называются простейшими дробями. Все коэффициенты, обозначенные символом 
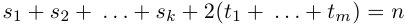
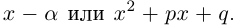
Теорема 7.5. Любая правильная рациональная дробь с действительными коэффициентами раскладывается в сумму простейших дробей.
Пример №25
Разложить в сумму простейших дробей:
а) 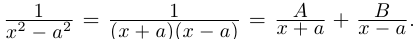
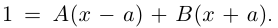
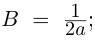
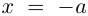
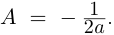
б)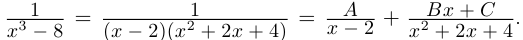
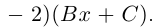
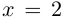
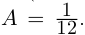
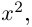
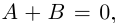
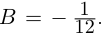
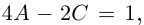
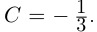
в)
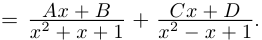
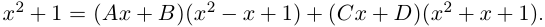
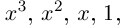
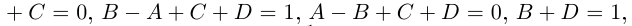
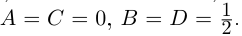
Вычисление комплексного числа
Определение 1.1. Многочленом (полиномом) степени n с действительными коэффициентами называется любое выражение вида
где
х – переменная.
Корнем многочлена (1.1) называется любое число 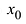
Нетрудно заметить, что некоторые многочлены вообще не имеют
действительных корней, например:
Расширим множество действительных чисел. Добавим к этому
множеству символ i , такой что 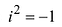
Тогда ±i – два корня уравнения
Определение 1.2. Множеством комплексных чисел называется множество
Суммой двух комплексных чисел 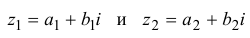
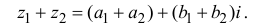
Произведением двух комплексных чисел 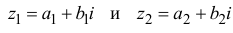
Для числа z= a +bi число а называется действительной частью,
число b – мнимой частью. Обозначения:
Относительно операций «+» и « · » комплексные числа С обладают
такими же свойствами, как и действительные числа. Эти операции
коммутативны и ассоциативны; для них существуют обратные операции:
вычитание и деление (кроме деления на 0).
Пример №26
Найти
Решение:
Теорема 1.1 (основная теорема алгебры). Любое уравнение вида (1.2)
имеет решение во множестве С.
Пример №27
Решить уравнение
Решение:
Определение 1.3. Для комплексного числа z =a +bi число z =a -bi называется комплексно-сопряженным, число 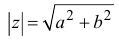
Если рассмотреть плоскость с декартовой системой координат ( O,x,y ) и на оси Ох отложить а – действительную часть z, а на оси Oy – b – мнимую часть z, то получим взаимно однозначное соответствие между множеством С всех
комплексных чисел и множеством точек плоскости.
Такая плоскость называется комплексной плоскостью, рис. 1.1.
При этом 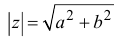
Определение 1.4. Аргументом комплексного числа z =a +bi называется
угол 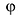
направлением оси Ох Аргумент будем обозначать Argz . Аргумент
определен с точностью до 2 πn. При этом значение 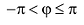
главным и обозначается argz.
Замечание.
При этом
Если 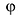
тригонометрическая форма комплексного числа.
Теорема 1.2. Пусть
Доказательство
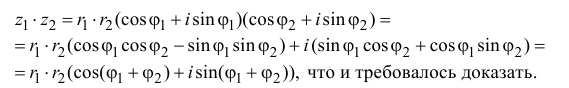
Из формул (1.5) следует, в частности, что 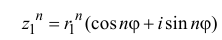
Пример №28
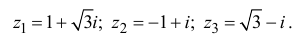
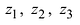
Решение:
поэтому по формуле (1.3)
Тогда по формуле (1.4)
поэтому по формуле (1.3)
Тогда
Из формул (1.5), (1.6) видно, что аргумент 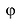
умножении, делении, возведении в степень ведет себя как показатель
степени. Обозначим 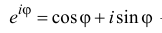
Тогда из теоремы 1.2 следует, что
Учитывая (1.7), формулу (1.4) для z можно переписать в виде 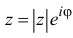
Пример №29
Вычислить
Решение:
Согласно примеру 1.3
Поэтому
Определение 1.5. Корнем n-й степени из числа z 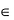
число 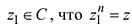
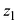
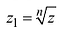
Из формулы (1.8) видно что 
если 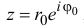
Пример №30
Найти
Решение:
- Координаты на прямой
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных




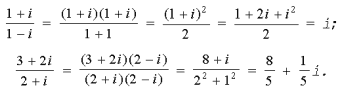
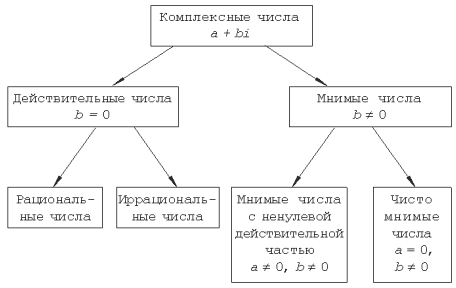

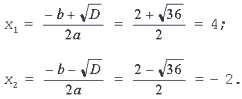
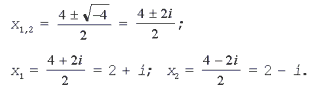
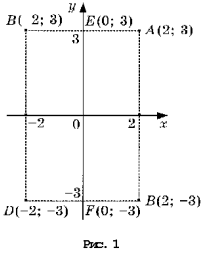
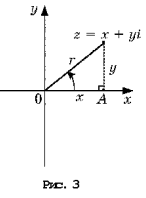
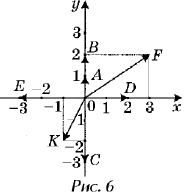
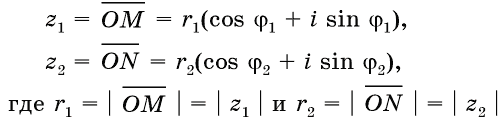





































































































![z=Rcdot e^{{icdot phi }},quad phi in [0,,2pi ].](https://wikimedia.org/api/rest_v1/media/math/render/svg/a63e42930bb0f8a32786df275adb66b4f973a950)