СОДЕРЖАНИЕ
1.Введение
2. История
Глава 1. Решение уравнений высших степеней методом разложения на
множители.
1.1.
Разложение на множители
методом группировки.
1.2.
Теорема Безу, теорема
Виета и следствия из них, схема Горнера.
Глава 2. Уравнения высших степеней, решение которых
приводится
к решению квадратных уравнений.
2.1. Биквадратные уравнения.
2.2. Уравнения, содержащие взаимно обратные выражения.
2.3. Уравнения четвертой степени, решение которых приводится к решению
квадратных уравнений путем выделения полного квадрата.
2.4. Возвратные уравнения.
2.5. Уравнения вида .
2.6. Уравнения вида .
Глава 3. Решение уравнений высших степеней методом введения новой
переменной.
Глава 4. Нестандартные способы решения уравнений высших
степеней.
Литература.
Цели и задачи:
Цель работы:
рассмотреть различные способы решения
алгебраических уравнений;
проанализировать существующие способы решения
уравнений высших
степеней.
Задачи работы:
изучить
алгоритм решения алгебраических уравнений высших степеней, используя:
·
Общий способ,
·
Формулу Кардано,
·
Схему Горнера;
рассмотреть
различные способы и методы решения уравнений высших степеней:
·
Разложение на множители. Способ
группировки;
·
Замена переменной;
·
Метод деления на
многочлен, содержащий переменную;
·
Метод выделения полного
квадрата.
ü
показать некоторые
нетрадиционные способы решений уравнений
Глава
1. Решение уравнений высших степеней
методом разложения на множители.
Один из способов решения уравнения состоит
в разложении многочлена на множители, что
позволяет свести решение исходного уравнения к решению нескольких уравнений
более низких степеней.
1.1.
Разложение на
множители методом группировки.
Решение уравнений высших степеней является трудной задачей, и
нельзя указать универсального способа нахождения корней. Рассмотрим некоторые
из них на примерах.
Пример 1. Решите уравнение (х +1)(х+2) + (х +2)(х
+1) = 2
Решение. Раскроем скобки и приведем подобные слагаемые.
;
;
;
;
;
;
; или
;
х = -1. D = 1 – 16 = -15, D < 0,
значит квадратное уравнение
действительных корней не
имеет.
Ответ: х = -1.
Пример 2. Решите уравнение
Методом группировки левую часть уравнения разложим на множители.
;
;
;
; или
;
х₁ = 2; х₂
= -2.
Ответ: х₁ = 2; х₂ = -2; .
Пример 3. Решите уравнение
Методом группировки левую часть уравнения разложим на множители.
;
;
;
;
2х — 1 = 0; х – 1 = 0; х + 1 = 0;
х₁ = 0,5. х₂ =
1. х ₃ = -1.
Ответ: х₁ = 0,5; х₂ =
1; х ₃ = -1.
Пример 4. Решите уравнение
Методом группировки левую часть уравнения разложим на множители.
;
;
;
; или
;
х₁ = ; Сумма
коэффициентов квадратного уравнения равна нулю,
х₂ = —.
следовательно, корни уравнения х₃ = 1; х₄ = 3.
Ответ: х₁ = ; х₂
= —; х₃ = 1;
х₄ = 3.
Пример 5. Решите уравнение
Так как х = 1 не является корнем, поэтому домножим обе части уравнения
на (х – 1). Получаем:
;
Тогда ;
;
;
;
; x = 0; х = 1 —
не является корнем. Ответ: х = 0.
Пример 6. Решите уравнение
Так как х = 1 не является корнем, поэтому домножим обе части
уравнения на (х – 1). Получаем:
(х – 1)∙
∙ (х – 1)
;
;
;
;
;
;
Х₁ = 0; или
х ₂ = -1; х₃ = 1
— не является корнем.
Ответ: Х₁ = 0; х ₂ = -1.
Пример 7. Решите уравнение
Решение. Используя формулы сокращенного умножения
, представив левую часть уравнения в
виде произведения, а правую часть перенести влево. Получим: 
Данное уравнение равносильно совокупности двух уравнений:
1)

Ответ:
1.2 . Теорема Безу, теорема Виета и следствия из них,
схема Горнера.
Для изучения уравнений высших
степеней
(1)
первостепенное значение имеет теорема Безу и
ее следствия.
Теорема Безу:
Остаток от деления многочлена относительно x на
двучлен х – а равен значению этого многочлена при х , равном а.
Следствие:
1)Для того чтобы многочлен f(x) делился на х
– а необходимо и достаточно, чтобы f(a) = 0.
2) Для того чтобы многочлен f(x)
делился на х + а необходимо и достаточно, чтобы f(-a)=0.
3) Таким образом, если число — корень уравнения, то левую часть
уравнения (1) можно записать в виде: , где
многочлен степени n-1.
Как же найти корень ?
Вспомним теорема Виета.
Теорема Виета:
Корни уравнения ,
с его коэффициентами связаны следующими соотношениями:
1)
Таким образом, для того
чтобы несократимая дробь была корнем уравнения
с целыми коэффициентами ,
Необходимо и достаточно, чтобы p было
делителем свободного члена
, а
q – делителем коэффициента .
2)
Если
уравнение имеет целые коэффициенты и коэффициент при
равен 1, то рациональными
корнями могут быть только целыми числами.
3)
Целые
корни уравнения с целыми коэффициентами
являются делителями свободного
члена. (Это свойство позволяет легко найти корни уравнения с целыми
коэффициентами.)
4)
Число 1
является корнем уравнения с целыми
коэффициентами, если сумма всех коэффициентов равна нулю.
5)
Число -1
является корнем уравнения с целыми коэффициентами, если
суммы коэффициентов при слагаемых с четными показателями степени равна сумме
коэффициентов слагаемых с нечетными показателями степени.
Пример 1. Решите уравнение .
Решение. Так как уравнение имеет
целые коэффициенты и коэффициент при равен 1 , то целыми корнями могут быть только
делители свободного члена, то есть 1, 2, 3, 6, -1, -2, -3, -6.
Число 1 является ли корнем уравнения,
так как сумму коэффициентов: 1 – 6 +11 — 6 = 0. Тогда на основании теоремы Безу
многочлен, стоящий в левой части уравнения делится на двучлен х – 1. Используя
схему Горнера разделим левую часть на х – 1:
|
1 |
-6 |
11 |
-6 |
|
|
1 |
1 |
-5 |
6 |
0 |
Квадратный трехчлен легко разложит на
множители, используя теорему Виета: корни
Таким образом, левую часть уравнения
мы разложили на множители:
Ответ:
Пример 2. Решите уравнение .
Решение. Делителями числа 18 будут
числа 1, 2, 3, 6, 9, а делителями числа 3 – числа 1 и 3. Среди чисел ±1, ±2, ±3, ±6, ±9, ±
Число 1 не является корнем уравнения,
так как сумма 3 – 4 + 5 — 18 ≠ 0.
Число -1 не является корнем уравнения
, так как сумма 3 + 5 ≠ -4 – 18.
По схеме Горнера найдем среди этих
чисел корень уравнения.
|
3 |
-4 |
5 |
-18 |
|
|
2 |
3 |
2 |
9 |
0 |
Используя следствие из теоремы Безу,
запишем уравнение в виде:.
Уравнение корней
не имеет, так как D = 4 – 108 = -104, D<0.
Ответ : х = 2
Пример 3. Решите уравнение .
Решение . Делителями числа 3 будут
числа 1, 3, а делителями числа 8 – числа 1 ,2, 4, 8. Среди чисел ±1, ±.
Число 1 не является корнем уравнения,
так как сумма 8 – 13 + 6 – 1 + 3 ≠ 0.
Число -1 не является корнем уравнения
, так как сумма 8 – 13 + 3 ≠ 6 – 1.
По схеме Горнера найдем среди этих
чисел корень уравнения.
|
8 |
6 |
-13 |
-1 |
3 |
|
|
|
8 |
-4+6=2 |
-1-13=-14 |
7-1=6 |
-3+3=0 |
Число -0,5 является корнем
уравнения, используя следствие из теоремы Безу исходное уравнение можно
записать в виде:
Найдем корни уравнения ,
среди чисел ±1, ±2, ±3,±6,
Число 1 не является корнем уравнения,
так как сумма 8 – 14 + 6 +2 ≠ 0.
Число -1 не является корнем уравнения
, так как сумма 8 – 14 ≠ 6 + 2.
По схеме Горнера найдем среди этих
чисел корень уравнения.
|
8 |
2 |
-14 |
6 |
|
|
|
8 |
6+2=8 |
6-14=-8 |
-6+6=0 |
Число является
корнем уравнения,
используя следствие из теоремы Безу исходное уравнение можно записать в виде:

уравнение равносильно совокупности уравнений: 1) 

Ответ :
Пример 4. Решите уравнение
Решение. Среди делителей числа 3 — ±1, ±3 будем искать корни уравнения. Число 1 не является
корнем уравнения, так как сумма
1+ 4 +6 + 3 ≠ 0. Число -1
является корнем уравнения , так как сумма
6 + 1 = 4 + 3. По схеме Горнера
найдем частное от деления левой части уравнения на двучлен х + 1.
|
1 |
4 |
6 |
3 |
|
|
-1 |
1 |
-1 |
-3 |
-3 + 3 = 0 |
Число -1 является корнем уравнения, используя следствие из
теоремы Безу исходное уравнение можно записать в виде:
Данное уравнение равносильно
совокупности уравнений:
1)
и 2)
Ответ: х₁ = -1.
Пример 5. Решите уравнение .
Решение. Среди чисел ±1, ±2, ±5, ± найдем корень уравнения .
Число 1 является корнем уравнения,
так как сумма
2 – 1 — 9 + 13 — 5 = 0. По схеме
Горнера найдем частное от деления левой части уравнения на двучлен х — 1.
|
2 |
-1 |
-9 |
13 |
-5 |
|
|
1 |
2 |
1 |
-8 |
5 |
0 |
Число 1 является корнем уравнения, используя следствие из
теоремы Безу исходное уравнение можно записать в виде:
.
Найдем корни уравнения среди чисел ±1, ±5,
Число 1 является корнем уравнения,
так как сумма
2 + 1 — 8 + 5 = 0. По схеме
Горнера найдем частное от деления левой части уравнения на двучлен х — 1.
|
2 |
1 |
-8 |
5 |
|
|
1 |
2 |
3 |
-5 |
0 |
Число 1 является корнем уравнения, используя следствие из
теоремы Безу исходное уравнение можно записать в виде: . Данное
уравнение равносильно совокупности уравнений:
1)
2)

как сумма коэффициентов равна
нулю.
Ответ:
Пример 6. Решите уравнения .
Решение. Корни уравнения будем
искать среди делителей числа -120.
Число 1 не является корнем
уравнения, так как сумма
1 – 4 – 19 + 106 — 120 ≠ 0. Число
-1 является корнем уравнения , так как сумма 1 — 19 — 120 ≠ — 4 + 106.
По схеме Горнера найдем корни
уравнения.
|
1 |
-4 |
-19 |
106 |
-120 |
|
|
2 |
1 |
-2 |
-4-19=-23 |
-46+106=60 |
120-120=0 |
Число 2 является корнем уравнения, используя следствие из
теоремы Безу исходное уравнение можно записать в виде:
Найдем корни уравнения среди делителей числа 60.
По схеме Горнера найдем корни
уравнения.
|
1 |
-2 |
-23 |
60 |
|
|
4 |
1 |
2 |
8-23=-15 |
-60+60=0 |
Число 4 является корнем уравнения, используя следствие из
теоремы Безу исходное уравнение можно записать в виде:
Данное уравнение равносильно
совокупности уравнений:
1)
2)
3)
Ответ:
Глава 2. Уравнения
высших степеней, решение которых приводится к решению квадратных уравнений.
Рассмотрим
частные случаи, в которых решение уравнений высших степеней приводится к
решению квадратных уравнений.
2.1
Биквадратные уравнения;
2.2.
Сравнения, содержащие взаимно обратные выражения;
2.3.
Уравнения
четвертой степени, решение которых приводится к решению квадратных уравнений путем
выделения полного
квадрата.
Уравнения
четвертой степени, решение которых приводится к решению квадратных уравнений
путем выделения полного квадрата, рассмотрим на следующих примерах.
Пример 1. Решить уравнение
Решение. В левой части уравнения выделим полный квадрат; получим
или
Обозначим ; тогда уравнение примет вид
, так как сумма коэффициентов равна нулю,
то и
Так
как , то
или
D=b —
4ac; D=9 + 4 = 13. D=b —
4ac; D= 9 + 12 = 21.
Ответ: ;
.
Пример 2. Решите уравнение .
Решение. В левой части уравнения выделим полный квадрат; получим
или
Раскладывая левую часть уравнения на множители, как разность
квадратов, получаем 
Произведение двух действительных чисел равно нулю тогда и только тогда,
когда хотя бы одно из них равно нулю. Из последнего уравнения получаем два
уравнения:
1)
D=b — 4ac;
D=1 – 4 = -3 — уравнение действительных корней не
имеет,
и уравнение
2)
D=b — 4ac; D=9 + 4 = 13 – два действительных корня,
;
Ответ: ;
2.4.
Возвратные уравнения.
Целое алгебраическое уравнение
называется возвратным, если совпадают коэффициенты при слагаемых,
сумма степеней которых равна степени многочлена, т.е. ….
Алгебраическое уравнение четвертой степени вида ,
е ≠ 0, называется возвратным, если коэффициенты связаны равенствами
—
некоторое число.
Легко показать, что если — корень возвратного
уравнения, то и — также корень этого
уравнения.
Для решения этих уравнений используют метод замены переменной
или
.
Пример 1. Решите уравнение
Решение. Разделив обе части уравнения на х≠
0, получим
, или
Обозначим , тогда
или
, тогда уравнение примет вид
, или
D=b — 4ac; D=9 + 160 = 169 – два действительных корня
,
.
Так как , получим два уравнения.
1)
Умножим уравнение на 2х , получим квадратные уравнения
D=b — 4ac; D = (-5)
— 16 =
9 – два действительных корня.
;
.
2)
Умножим уравнение на х , получим уравнение
k = b : 2 , k=2
D₁
= k — ac; D₁ = 2
— 1 =
3 – два действительных корня
,
.
Ответ: , х₂ = 0,5,
,
.
Пример 2. Решите уравнение
Решение. Сгруппируем слагаемые:
Сделаем подстановку , тогда
. Отсюда
.
В результате приходим к уравнению:
Исходное уравнение равносильно совокупности уравнений.
1)

Ответ:
Пример 3. Решите уравнение
Решение. Обозначим , тогда
, тогда
.
Запишем исходное уравнение в новых обозначениях

Так как , то получим 2 уравнения:
1)


Ответ: 
Пример 4. Решите уравнение
Решение. Обозначим , тогда
, тогда
.
Запишем исходное уравнение в новых обозначениях

Так как , то получим 2 уравнения:
1)


Ответ: 
2.5. Решение уравнений вида
Решение уравнений вида (
)
приводится к решению квадратного уравнения делением на х (как возвратного), если
. Поэтому такое уравнение иногда
называют возвратным.
Пример. Решите уравнение .
Решение. Так как условие выполняется, т.е.
или 25 = 25,
то обе части уравнения делим на х; получим
,
или
Обозначим ; тогда
, тогда уравнение примет вид
или
D=b — 4ac; D = (-21)
— 432
= 441- 432 = 9 – два действительных корня.
,
.
Так как получим два уравнения:
1)

теореме Виета 2)
Ответ: ;
;
;
2.6. Решение уравнения вида .
Уравнения вида приводится к биквадратному уравнению заменой
заменим
Вычитая, получим или
, тогда
Или
Относительно t уравнение примет вид:
или, после
упрощений, .
Заметим, что решение
будет аналогичным, если степень двучленов будет и другой. В работе
рассмотрены примеры с показателем степени 3; 4; 5.
Пример 1. Решите уравнение (7 — х)
+ (9 — х
)
= 16.
Решение. Введем новую переменную у = 8 – х.
После замены выражения х на 8 – у , исходное
уравнение приводим к виду
(у — 1) + (у + 1)
= 16.
Раскроем скобки и приведем подобные слагаемые.
;
;
;
Пусть , тогда получим квадратное
уравнение .
Сумма коэффициентов этого квадратного уравнения равна нулю,
значит t₁ = 1; t₂
= -7.
= 1; или
= -7 — данное уравнение корней не
имеет.
y₁
= 1; y₂ =
-1.
Так как у = 8 — х, то 8 — х
= 1; или 8 — х
= -1;
х = 7; х
= 9;
х₁ = ; х₂ = —
. х₃ = 3;
х₄ = -3.
Ответ: х₁ = ; х₂ =
— ; х₃ = 3; х₄ =
-3.
Пример 2. Решите уравнение (х +3) — (х +1)
= 56 .
Решение. Введем новую переменную у = х +2.
После замены переменной х на выражение у — 2 , исходное уравнение
приводим к виду (у +1) — (у — 1)
= 56. Раскроем скобки и приведем
подобные слагаемые.
;
2 ∙ (;
2 ∙ (3;
;
;
; y₁
= 3; y₂ = -3.
Так как у = х +2 , то х +2 =3; или х +2 = -3;
х₁ = 1
; х₂ = -5. Ответ: х₁ = 1 ; х₂ = -5.
Пример 3. Решите уравнение
Решение. Введем
новую переменную у = х + 1. После замены переменной х на выражение у — 1
, исходное уравнение приводим к виду
(у — 2) + (у + 2)
= 242 ∙ у Раскроем
скобки и приведем подобные слагаемые.
;
;
;
;
у = 0; или —
это биквадратное уравнение.
Пусть t = , тогда получим квадратное уравнение
,
сумма коэффициентов этого уравнения
равна нулю, следовательно ;
.
Так как t = , то
=
1; или = — 41
y₁
= 1; y₂ =
-1. Уравнение корней не имеет.
Так как у = х + 1, то х + 1 = 1; х + 1 =
-1; х + 1 = 0;
х₁ =
0. х₂ = -2. х₃
= -1.
Ответ: х₁ = 0; х₂ = -2;
х₃ = -1.
2.7. Решение уравнения вида .
Уравнение вида приводится к решению квадратного
уравнения, если a + b = c + d или a + c = b + d или
a + d = b + c.
Пример 1. Решите уравнение .
Решение. Раскроем скобки, группируя их следующим образом, получим
Сделаем замену у = . Тогда получаем:
Исходное уравнение равносильно совокупности уравнений:
=41 и
= — 41
По теореме Виета: D=25 –
184 = -159, D < 0

уравнение действительных корней не имеет.
Ответ : х₁ =-9; х₂ = 4.
Пример 2. Решите уравнение
Решение. С группируем скобки следующим образом:
раскроем скобки и приведем подобные слагаемые
Сделаем замену . Тогда получим:
или
Исходное уравнение равносильно совокупности
уравнений:
1)

Ответ:
Пример 3. Решите уравнение
Решение. Сгруппируем множители следующим
образом:
Обозначим .
Тогда получим :
Исходное уравнение равносильно совокупности
уравнений.
1) 
Ответ:
Пример
4. Решите
уравнение
Решение.
Так как 2 + 1 =-3 + 6, то можно сгруппировать множители левой части уравнения
так: ,
или
Обозначим, тогда относительно
получим:

Исходное уравнение равносильно совокупности
уравнений.
1)

теореме Виета. 2)
Ответ:
Глава 3.
Решение уравнений методом замены неизвестного.
Решение многих уравнений заключается в сведении
их к уравнениям видов рассмотренных в главе 2, способом введения
вспомогательной неизвестной.
Пример 1. Решите
уравнение
Решение. Введем новую
переменную , получим:
или разделив на
,
Решением данного уравнения является число -1, так как сумма
коэффициентов слагаемых с четными показателями степеней равна сумме
коэффициентов слагаемых с нечетными показателями степеней. (2+1=3)
Используя схему Горнера , получим:
|
х |
2 |
0 |
1 |
3 |
|
-1 |
2 |
-2 |
3 |
0 |
Левую часть уравнения можно разложить на множители:
Произведение двух действительных чисел равно нулю тогда и только тогда,
когда хотя бы одно из них равно нулю. Из последнего уравнения получаем два
уравнения:

не имеет.
у + 2 = 0,
у = -2.
Ответ: у = — 2.
Пример2. Решите уравнение
Введем новую переменную , тогда уравнение
примет вид: Пусть
,
получим уравнение:
Сумма коэффициентов квадратного уравнения равна нулю, значит
t₁
= 1, t₂ =32. Таким образом: или
Так как , получим два уравнения:

Ответ: х₁ = 1; х₂ =4.
Пример 3. Решите уравнение
Решение. Введем новую переменную , тогда
уравнение примет вид:
По теореме Виета: 
Так как , то получим два уравнения:
1)


Ответ: х₁ =-3;
х₂ = -2; х₃ =1; х₄ =2.
Глава 4. Нестандартные способы решения уравнений высших
степеней.
Пример 1. Найдите действительные корни уравнения
Решение. Поскольку в левой части уравнения стоит выражение все
слагаемые, которого неотрицательные, а по условию их сумма равна нулю, то это
возможно лишь при условии, что каждое слагаемое равно нулю: 
Ответ: х = 1,8.
Пример 2. Решите уравнение .
Рассмотрим два способа решения данного уравнения
. Решение. 1
способ. Заметим, что х = 1 не является корнем данного уравнение, поэтому
разделим левую и правую части уравнения на выражение (х – 1), получим

Далее заменим и уравнение примет вид
. Сумма коэффициентов данного уравнения
равна нулю ( 1 — 5 + 4 = 0), значит корни уравнения ;
Так как , то получим два уравнения:
1)

D < 0
– данное уравнение х = 2.
корней не
имеет. Ответ: х = 2.
2 способ. Раскроем скобки и приведем
подобные слагаемые. Получим уравнение четвертой степени:
1. Используя схему Горнера, находим, среди
делителей свободного члена
±1; ≠2; ± 4, целые корни
уравнения.
Заметим, что сумма коэффициентов не
равна нулю, то х=1 не является корнем
уравнения. (1 – 5 + 9 – 8 + 4 ≠ 0)
Число -1 так же не является корнем, так
как сумма коэффициентов слагаемых с четными показателями степени не равна
сумме коэффициентов слагаемых с не четными показателями степени.
(1+ 9 +4≠ — 5 – 8). Составим
таблицу:
|
х |
1 |
— |
9 |
— |
4 |
|
2 |
1 |
— |
3 |
— |
0 |
Из таблицы видно, что х = 2 корень уравнения,
и уравнение можно записать в виде: .
Решим уравнение
Используя схему Горнера, находим, среди
делителей свободного члена
±1;
≠2, целые корни уравнения.
Заметим, что сумма коэффициентов не
равна нулю, то х=1 не является корнем
уравнения. (1 – 3 + 3 – 2 ≠ 0)
Число -1 так же не является корнем, так
как сумма коэффициентов слагаемых с четными показателями степени не равна
сумме коэффициентов слагаемых с не четными показателями степени.
(1+ 3 ≠ — 3 – 2). Составим
таблицу:
|
х |
1 |
-3 |
3 |
-2 |
|
2 |
1 |
— |
1 |
0 |
Из таблицы видно, что х = 2 корень уравнения,
и уравнение можно записать в виде: .
Таким образом, левую часть уравнения
можно разложить на множители следующим
образом: Произведение двух действительных чисел
равно нулю тогда и только тогда, когда хотя бы одно из них равно нулю. Из
последнего уравнения получаем два уравнения:
1)
2)
данное уравнение
действительных корней не
имеет.
Ответ: х = 2.
Я привела два способа решения
уравнения ,
чтобы показать, насколько первый способ проще
и необходимость поиска рациональных способов решения.
Пример 3. Решим уравнение .
Решение. Заметим, что х = 1 не является
корнем данного уравнение, поэтому умножим левую и правую части уравнения на
выражение (х – 1), получим
,
Так как х≠1, то
уравнение имеет один корень х = 0.
Ответ: х = 0.
Пример 4. Решите уравнение .
Решение. Запишем уравнение в виде
или
откуда
Решим два уравнения:
1)
2)
D= 6 —
4(3 + )= — 6 — 4
D = 6 – 4 (3 —
)= — 6 + 4
D <
0, действительных корней нет.
.
Ответ: .
Пример 5. Решите уравнение
Решение. Заметим, что х = -1 не является
корнем данного уравнение, поэтому умножим левую и правую части уравнения на
выражение (х +1), получим:

или
Пусть
,
,
Сумма чисел равна 4, а произведение 3 — это
числа 1 и 3. Проверим:
х₁ = 1, получим и
х ₂= 3, получим и
Ответ: х₁ = 1, х
₂= 3.
2 способ: Раскроем скобки и приведем
подобные слагаемые, получим:
Сумма коэффициентов многочлена стоящего в
левой части уравнения равна нулю (1 — 7 + 19 — 25 +12 = 0), значит х =1
корень уравнения.
По теореме Безу многочлен делится на х – 1. Выполним деление и
получим:
: (х – 1) =
.
Найдем корни уравнения =0 среди делителей свободного члена, ±1;
±2; ±3; ±4; ±6; ±12.
Сумма коэффициентов 1 – 6 + 13 – 12 ≠ 0,
значит, число 1 не является корнем уравнения.
Так же число -1 так же не является корнем,
так как сумма коэффициентов слагаемых с четными показателями степени не
равна сумме коэффициентов слагаемых с не четными показателями степени (1 + 13
≠ -6 – 12)
Составим таблицу и проверим по схеме
Горнера:
|
|
1 |
-6 |
13 |
-12 |
|
2 |
1 |
-4 |
5 |
-2 |
|
3 |
1 |
-3 |
4 |
0 |
Число 3 является корнем уравнения, значит,
многочлен делится на х – 3. Запишем многочлен в
виде :
= (х – 3)(
.
Учитывая предыдущие рассуждения, запишем
уравнение в виде
Произведение действительных чисел равно нулю
тогда и только тогда, когда хотя бы одно из них равно нулю. Из последнего
уравнения получаем три уравнения: х – 1 = 0, или х – 3 =
0, или ,
х₁
=1. х₂ =
3. D = 9 – 16 = -7
D < 0 , корней нет.
Ответ: х₁ =1, х₂
= 3.
Пример 6. Решите уравнение
Решение. Разделим обе части уравнения на 4, получим:
;
;
;
;
.
Произведение действительных чисел равно нулю
тогда и только тогда, когда хотя бы одно из них равно нулю. Из последнего
уравнения получаем два уравнения:
1)

Произведение действительных чисел равно нулю
тогда и только тогда, когда хотя бы одно из них равно нулю. Из последнего
уравнения получаем два уравнения:

или
Ответ: ;
;
;
.
Пример 7. Решите уравнение
Решение. Используя, равенство преобразуем уравнение
.
Раскроем скобки и преобразуем выражение:
Произведение действительных чисел равно нулю тогда
и только тогда, когда хотя бы одно из них равно нулю. Из последнего уравнения
получаем два уравнения:
1)
,
D=1 — 4= -3, D < 0, действительных корней
нет.
2)
Ответ:
Пример 8. Решите уравнение
Решение. Сумма коэффициентов не равна нулю 1
— 1 + 1 – 1+1 ≠0, число 1 не является корнем уравнения.
Число -1 так же не является корнем, так как сумма коэффициентов слагаемых с
четными показателями степени не равна сумме коэффициентов слагаемых с не
четными показателями степени
(1 + 1 + 1 ≠ — 1 –
1)
Умножим обе части уравнения на
(х + 1), получим:
Уравнение ,
является следствием исходного уравнения , имеет
единственный корень х = -1, который не является корнем исходного, значит,
уравнение корней не имеет.
Ответ: корней нет.
Пример 9. Решите уравнение
Решение. Перепишем уравнение в виде

х имеем и
, то
данное уравнение равносильно уравнению Решением
этого уравнения х =-1, а следовательно и решение исходного.
Ответ: х = -1
2 способ. Раскроем скобки и приведем подобные
слагаемые.
Число -1 является корнем, так как сумма
коэффициентов слагаемых с четными показателями степени равна сумме
коэффициентов слагаемых с не четными показателями степени (2 + 2 – 9 + 7 =
4 – 8 + 6)
По теореме Безу многочлен, стоящий в левой
части уравнения делится на
(х + 1). Выполним деление по схеме Горнера:
|
2 |
4 |
2 |
-8 |
-9 |
6 |
7 |
|
|
-1 |
2 |
2 |
0 |
-8 |
-1 |
7 |
0 |
=0
Рассмотрим уравнение
Так как сумма коэффициентов уравнения не равна
нулю, то число 1 не является корнем уравнения, число -1 является корнем, так
как сумма коэффициентов слагаемых с четными показателями степени равна
сумме коэффициентов слагаемых с не четными показателями степени
(2 — 1 = 2 – 8 + 7). Выполним деление по
схеме Горнера:
|
2 |
2 |
0 |
-8 |
-1 |
7 |
|
|
-1 |
2 |
0 |
0 |
-8 |
7 |
0 |
=0,
Рассмотрим уравнение .
Среди чисел ±7 , ±1,
нет корней уравнения , значит корнем
уравнения является только число -1.
Ответ: х = -1.
Литература
1. Э.Н. Балаян «750 лучших олимпиадных и
занимательных задач
по математике» Ростов-на-Дону
«Феникс», 2014
2. «Сборник задач по математике для поступающих в
ВУЗы» под редакцией М.И.Сканави, М. «Высшая школа», 1982.
3. Довбыш Р.И., Потемкина Л.Л., Трегуб Н.Л.,
Лиманский В.В., Оридорога Л.Л., Кулеско Н.А. «Сборник материалов математических
олимпиад: 906 самых интересных задач и примеров с решениями» , Донецк: ООО ПКФ
«БАО», 2002.
4. А.М. Назаренко, Л.Д. Назаренко «Тысяча и
один пример. Равенства и неравенства», Сумы «Слобожанщина», 1994.
5. Ф.П. Яремчук, П.А. Рудченко «Алгебра и
элементарные функции» , Х. «Полиграфкнига», 1975.
Уравнение и его корни: определения, примеры
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня — 2 , 1 и 5 , то пишем — 2 , 1 , 5 или < — 2 , 1 , 5 >.
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Уравнение и его корни
Время чтения: 11 минут
Основные понятия уравнения
Уравнением называют равенство, в котором одна из переменных неизвестна, и её нужно найти. Значение этой неизвестной должно быть таким, чтобы равенство было верным.
К примеру: 3+4=7 это числовое равенство, при вычислении которого с левой стороны получается 7=7.
Уравнением же будет называться следующее равенство: 3+х=7, поскольку есть неизвестная переменная х, её значение можно найти.
Из этого уравнения следует, что переменная х=4, только при таком его значении равенство 3+х=7, будет верным.
Неизвестные переменные принято писать в виде маленьких латинских букв, можно любыми, но чаще используют x,y,z.
Получается, чтобы равенство сделать уравнением необходимо, чтобы в нем была буква, значение которой неизвестно.
Как мы понимаем существует множество примеров уравнений с разными арифметическими действиями.
Пример: х + 5 = 1= 9; z — 2 = 7; 9 * y = 18, 6 : f = 2
Помимо этого существуют уравнения со скобками. К таким уравнениям относится 8 : (х — 4) = 2 * (8 — х), неизвестных может быть несколько, они могут быть, как слева уравнения, так и справа или в обеих частях.
Помимо таких простых уравнений они могут быть с корнями, логарифмами, степенями и тд.
Уравнение может содержать несколько переменными, тогда их принято называть, соответственно уравнениями с двумя, тремя и более переменными.
3 * а = 15 : х — уравнение с двумя переменными:
8 — а = 5 * х — z — уравнение с тремя переменными.
Корень уравнения
Мы часто слышим фразу на уроках математики, «найдите корень уравнения», давайте разберёмся, что же это значит.
В примере 3+х=7, можно представить вместо буквы число, и уравнение тогда станет равенством, оно может быть либо верным, либо неверным, если поставить х=3, то первичное равенство примет вид 3+3 = 7 и станет неверным, а если х= 4 то равенство 3+4=7 будет верным, а значит х = 4 будет называться корнем или по другому решением уравнения 3+х=7.
Определение.
Отсюда можно выделить следующее определение: корень уравнения — это такое значение неизвестной переменной, при котором числовое равенство будет верным.
Стоит отметить, что корней может быть несколько или не быть вовсе.
Рассмотрим подробнее пример который не будет иметь корней. Таким примером станет 0 * х = 7, сколько бы чисел мы сюда не подставляли равенство не будет верным, так как умножая на ноль будет ноль, а не 7.
Но существуют и уравнения с множественным числом корней, к примеру, х — 3 = 6, в таком уравнении только один корень 9, а в уравнении квадратного вида х2 = 16, два корня 4 и -4, можно привести пример и с тремя корнями х * (х — 1) * (х — 2) = 0, в данном случае три решения ноль, два и один.
Для того чтобы верно записать результат уравнения мы пишем так:
- Если корня нет, пишем уравнение корней не имеет;
- Если есть и их несколько, они либо прописываются через запятые, либо в фигурных скобках, например, так: <-2, 3, 5>;
- Еще одним вариантом написания корней, считается запись в виде простого равенства, к примеру неизвестная х а корни 3,5 тогда результат прописывается так: х=3, х=5.
- или прибавляя индекс снизух1 =3 , х2 = 5. данным способом указывается номер корня;
- Если решений уравнения бесконечное множество, то запись будет либо в виде числового промежутка от и до, или общепринятыми обозначениями. множество натуральных чисел N, целых – Z, действительных — R.
Стоит отметить, что если уравнение имеет два и более корней, то чаще употребляется понятие решение уравнения. Рассмотрим определение уравнения с несколькими переменными.
Решение уравнения с двумя и более переменными, означает, что эти несколько значений превращают уравнение в верное равенство.
Представим, что мы имеем следующее уравнение х + а = 5, такое уравнение имеет две переменные. Если мы поставим вместо них числа 3 и 6 то равенство не будет верным, соответственно и данные числа не являются решением для данного примера. А если взять числа 2 и 3 то равенство превратится в верное, а числа 2 и 3 будут решением уравнения. Представленные уравнения с несколькими переменными, тоже могут или не иметь корня вообще или наоборот иметь множество решений.
Правила нахождения корней
Таких правил существует несколько рассмотрим их ниже.
Пример 1
Допустим мы имеем уравнение 4 + х = 10, чтобы найти корень уравнения или значение х в данном случае необходимо найти неизвестное слагаемое, для этого есть следующее правило или формула. Для нахождения неизвестного слагаемого, нужно из суммы вычесть известное значение.
Решение:
Чтобы проверить является ли 6 решением, мы ставим его на место неизвестной переменной х в исходное уравнение, получаем следующее равенство 4 + 6 = 10, такое равенство является верным, что означает число корня уравнения, равно 6.
Пример 2
Возьмём уравнение вида х — 5 = 3, в данном примере х это неизвестное уменьшаемое, для того чтобы его найти необходимо следовать следующему правилу:
Для нахождения уменьшаемого необходимо сложить разность и вычитаемое.
Решение:
Проверяем правильность нахождения корня уравнения, подставляем, вместо переменной неизвестной, найденное число 8, получаем равенство 8 — 5 = 3, так как оно верное, то и корень уравнения найден правильно.
Пример 3
Берём уравнение, в котором неизвестное х будет вычитаемое к примеру: 8 — х = 4. для того чтобы найти х необходимо воспользоваться правилом:
Для нахождения вычитаемого, нужно из уменьшаемого вычесть разность.
Решение:
Проверяем правильность нахождения корня уравнения, для этого полученное значение ставим вместо неизвестного вычитаемого в исходный пример, и получаем следующее равенство 8 — 4 = 4, равенство верно, значит и корень найден правильно.
Уравнение — определение и вычисление с примерами решения
Содержание:
Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
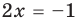
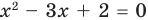
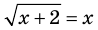
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
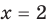
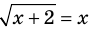
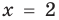
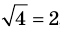
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 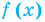
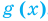
Для уравнения 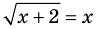
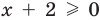
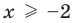
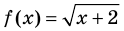

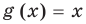
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 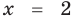
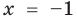
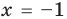
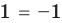
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
5. Схема поиска плана решения уравнений



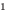
Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 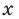
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 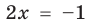
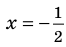
а уравнение 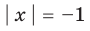
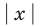
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 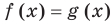
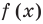
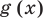
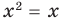
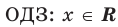
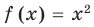
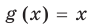
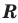
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 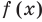
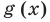
Например, в уравнении 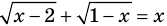
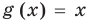
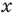
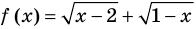
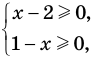
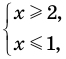
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 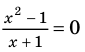
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 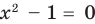
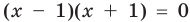
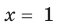
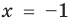
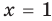
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
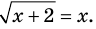
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
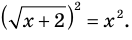
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 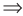
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 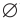
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 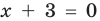
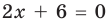
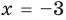
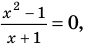
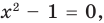
то, как было показано выше, уравнение (3) имеет единственный корень 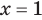
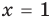
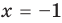
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 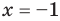
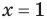
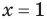
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 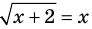
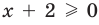

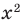
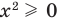
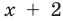


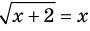
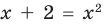
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 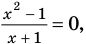
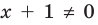
Запись решения в этом случае может быть такой:
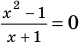
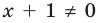
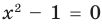
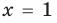
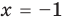
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Пример №423
Решите уравнение 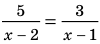
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 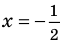
Ответ:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
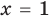
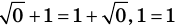
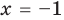
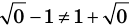
2. Оценка левой и правой частей уравнения
Если надо решить уравнение вида 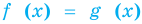


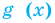
Пример:
►
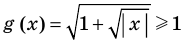
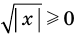
Итак, заданное уравнение равносильно системе
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 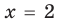
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 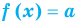
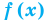
Пример:
Уравнение 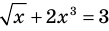
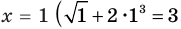
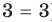
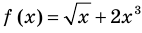
Если в уравнении 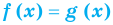
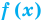
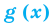
Пример:
Уравнение 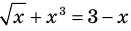
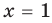
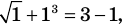
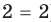
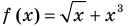

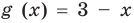
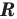
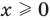
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 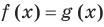
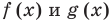
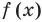
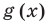
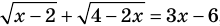
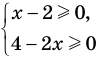
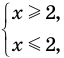


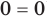


Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 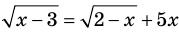
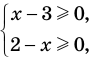
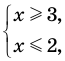
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 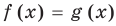
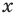
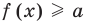
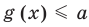
Рассмотрим два случая:
Если 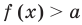
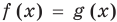
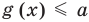
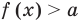
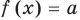
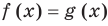
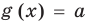
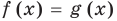
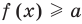
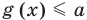
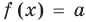
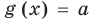
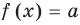
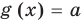
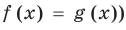
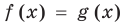
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 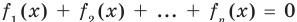
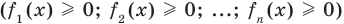
Если предположить, что 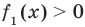

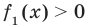
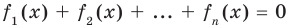
Например, чтобы решить уравнение 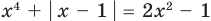
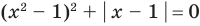
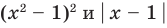
Из второго уравнения получаем 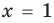
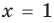
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
Теорема 1. Если в уравнении 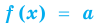
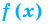
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 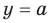
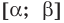
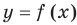
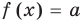
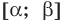
• Если на промежутке 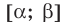
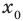
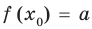
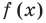
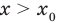
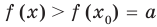
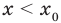
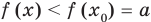
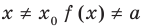
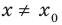
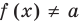
Теорема 2. Если в уравнении 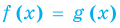
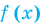
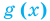
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 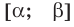
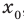
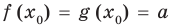
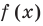
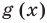
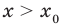
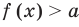
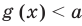
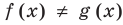
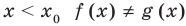
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 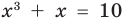
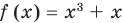

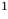
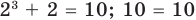
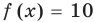
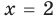
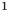

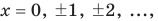
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 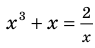
► Сначала следует учесть его ОДЗ: 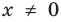
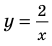
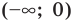
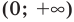
1) При 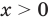
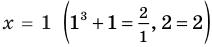
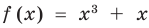

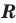
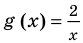

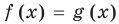
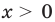
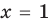
2) При 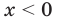
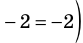
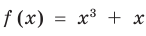
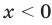
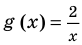
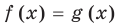
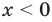
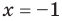
Примеры решения задач:
Пример №424
Решите уравнение 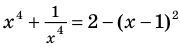
Решение:
► ОДЗ: 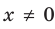
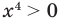
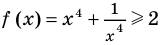
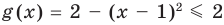
Таким образом, данное уравнение равносильно системе 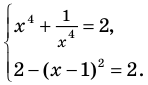
Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ , то в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. В правой части из 2 вычитается неотрицательное число . Таким образом, при всех значениях получаем значение, меньшее или равное 2. Равенство между левой и правой частями возможно тогда и только тогда, когда обе части равны 2.
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: Рассмотрим функцию . На своей области определения эта функция является возрастающей (как сумма двух возрастающих функций). Тогда первое уравнение заданной системы, которое имеет вид , равносильно уравнению . Таким образом, на ОДЗ заданная система равносильна системе
Подставляя во второе уравнение системы, имеем , . Учитывая, что на ОДЗ , получаем . Тогда .
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство для возрастающей функции возможно тогда и только тогда, когда , поскольку возрастающая функция может принимать одинаковые значения только при одном значении аргумента. (Заметим, что такое же свойство будет иметь место и для убывающей функции.)
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция является возрастающей (или убывающей) на определенном множестве, то на этом множестве
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://www.napishem.ru/spravochnik/matematika/uravnenie-i-ego-korni.html
http://www.evkova.org/uravnenie-opredelenie-i-vyichislenie-s-primerami-resheniya
Применение производной для решения нелинейных уравнений и неравенств
- Количество корней кубического уравнения
- Количество корней произвольного уравнения
- Решение неравенств с построением графиков
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin{gather*} f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end{gather*} Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_{1,2}=frac{-2bpmsqrt{D}}{6a}). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Уравнение (ax^3+bx^2+cx+d=0)
Имеет три корня, если ( begin{cases} b^2-3acgt 0\ f(x_1)cdot f(x_2)lt 0 end{cases} )
Имеет два корня, если ( begin{cases} b^2-3acgt 0\ f(x_1)cdot f(x_2)= 0 end{cases} )
В противном случае – один корень.
Пример 1. Сколько корней имеют уравнения:
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac{1}{x-1}+frac{1}{x-3})
б) Найдите число корней уравнения (frac 1x+frac{1}{x-1}+frac{1}{x-3}=k)
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac{1}{x-1}+frac{1}{x-3} $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft{0;1;3right})
Все три точки – точки разрыва 2-го рода. begin{gather*} lim_{xrightarrow -0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=-infty-1-frac13=-infty\ lim_{xrightarrow +0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=+infty-1-frac13=+infty\ lim_{xrightarrow 1-0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=1-infty-frac12=-infty\ lim_{xrightarrow 1+0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=1+infty-frac12=+infty\ lim_{xrightarrow 3-0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=frac13+frac12-infty=-infty\ lim_{xrightarrow 3+0}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=frac13+frac12+infty=+infty end{gather*} 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin{gather*} lim_{xrightarrow -infty}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=-0-0-0=-0\ lim_{xrightarrow +infty}left(frac1x+frac{1}{x-1}+frac{1}{x-3}right)=+0+0+0=+0\ end{gather*} Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac{1}{x^2}-frac{1}{(x-1)^2}-frac{1}{(x-3)^2}lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) — три корня
При (k=0) — два корня
При (kgt 0) — три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt{x-1}+sqrt{10-2x}=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt{x-1}+sqrt{10-2x})
ОДЗ: ( begin{cases} x-1geq 0\ 10-2xgeq 0 end{cases} Rightarrow begin{cases} xgeq 1\ xleq 5 end{cases} Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt{8}=2sqrt{2}, f(5)=sqrt{4}+0=2)
Первая производная: begin{gather*} f'(x)=frac{1}{2sqrt{x-1}}+frac{-2}{2sqrt{10-2x}}=frac{1}{2sqrt{x-1}}-frac{1}{sqrt{10-2x}}\ f'(x)=0 text{при} 2sqrt{x-1}=sqrt{10-2x}Rightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt{frac73-1}+sqrt{10-2cdot frac73}=sqrt{frac43}+sqrt{frac{16}{3}}=frac{6}{sqrt{3}}=2sqrt{3} end{gather*} Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | — | ∅ |
| (f(x)) | (2sqrt{2}) | (nearrow ) | max (2sqrt{3}) |
(searrow ) | 2 |
Можем строить график:
(y=a) — горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt{2} $$ | 1 решение |
| $$ 2sqrt{2}leq alt 2sqrt{3} $$ | 2 решения |
| $$ a=2sqrt{3} $$ | 1 решение |
| $$ agt 2sqrt{3} $$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt{3}).
Ответ: (ainleft[2;2sqrt{3}right])
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (frac{2+log_3 x}{x-1}gt frac{6}{2x-1})
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin{gather*} left[ begin{array}{l} begin{cases} xgt 1\ 2+log_3 xgtfrac{6(x-1)}{2x-1} end{cases} \ begin{cases} 0lt xlt 1\ 2+log_3 xltfrac{6(x-1)}{2x-1} end{cases} end{array} right. \ 2+log_3 xgt frac{6(x-1)}{2x-1}Rightarrow log_3 xgt frac{6(x-1)-2(2x-1)}{2x-1}Rightarrow log_3 xgt frac{2x-4}{2x-1}\ left[ begin{array}{l} begin{cases} xgt 1\ log_3 xgtfrac{2x-4}{2x-1} end{cases} \ begin{cases} 0lt xlt 1\ log_3 xltfrac{2x-4}{2x-1} end{cases} end{array} right. end{gather*} Исследуем функцию (f(x)=frac{2x-4}{2x-1}=frac{2x-1-3}{2x-1}=1-frac{3}{2x-1})
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin{gather*} lim_{xrightarrow frac12 -0}left(1-frac{3}{2x-1}right)=1-frac{3}{-0}=+infty\ lim_{xrightarrow frac12 +0}left(1-frac{3}{2x-1}right)=1-frac{3}{+0}=-infty end{gather*} Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin{gather*} lim_{xrightarrow -infty}left(1-frac{3}{2x-1}right)=1-frac{3}{-infty}=1+0\ lim_{xrightarrow +infty}left(1-frac{3}{2x-1}right)=1-frac{3}{+infty}=1-0 end{gather*} На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-frac{3}{2x-1}right)’=frac{3}{(2x-1)^2}gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-frac{6}{(2x-1)^3} $$ Одна критическая точка 2-го порядка (x=frac12)
| (x) | (left(0;frac12right)) | (frac12) | (left(frac12;+inftyright)) |
| (f»(x)) | >0 | ∅ | <0 |
| (f(x)) | (cup) | ∅ | (cap) |
Пересечения с осью OY: (f(0)=1-frac{3}{0-1}=4), точка (0;4)
Пересечение с осью OX: (1-frac{3}{2x-1}=0Rightarrow 2x-1=3 Rightarrow x=2), точка (2;0)
Строим графики (f(x)=frac{2x-4}{2x-1}) и (g(x)=log_3 x)
Первая система из совокупности ( begin{cases} xgt 1\ log_3 xgt frac{2x-4}{2x-1} end{cases} )
Логарифм при (xgt 1) все время выше, чем правая ветка гиперболы, т.е. система справедлива для всех (xgt 1).
Вторая система из совокупности ( begin{cases} 0lt xlt 1\ log_3 xlt frac{2x-4}{2x-1} end{cases} )
Логарифм попадает под левую ветку гиперболы на интервале (0lt xltfrac12), т.е. $$ begin{cases} 0lt xlt 1\ 0lt xltfrac12 end{cases} Rightarrow 0lt xltfrac12 $$ Решение совокупности – это объединение полученных решений систем: $$ 0lt xltfrac12cup xgt 1 $$ Ответ: (xinleft(0;frac12right)cup (1;+infty))
Содержание
- Как найти дискриминант квадратного уравнения
- Понятие квадратного уравнения
- Понятие дискриминанта
- Как решать квадратные уравнения через дискриминант
- Примеры решения квадратных уравнений с помощью дискриминанта
- Решение простых линейных уравнений
- Понятие уравнения
- Какие бывают виды уравнений
- Как решать простые уравнения
- Примеры линейных уравнений
- Как решать квадратные уравнения
- Понятие квадратного уравнения
- Приведенные и неприведенные квадратные уравнения
- Полные и неполные квадратные уравнения
- Решение неполных квадратных уравнений
- Как решить уравнение ax 2 = 0
- Как решить уравнение ax 2 + с = 0
- Как решить уравнение ax 2 + bx = 0
- Формула Виета
- Как разложить квадратное уравнение
- Дискриминант: формула корней квадратного уравнения
- Выводим формулу корней квадратного уравнения
- Алгоритм решения квадратных уравнений по формулам корней
- Примеры решения квадратных уравнений
- Формула корней для четных вторых коэффициентов
- Упрощаем вид квадратных уравнений
- Связь между корнями и коэффициентами
Как найти дискриминант квадратного уравнения
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие квадратного уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.
Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Есть три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Чаще всего для поиска дискриминанта используют формулу:
В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:
Эта формула подходит даже для неполных квадратных уравнений.
Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.
Как решать квадратные уравнения через дискриминант
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
- как найти дискрининант: D = b 2 − 4ac;
- если дискриминант отрицательный — зафиксировать, что действительных корней нет;
- если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b 2 /2a;
- если дискриминант положительный — найти два действительных корня квадратного уравнения по формуле корней
А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!
Примеры решения квадратных уравнений с помощью дискриминанта
Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.
- Определим коэффициенты: a = 3, b = -4, c = 2.
- Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.
Ответ: D 2 — 6x + 9 = 0.
- Определим коэффициенты: a = 1, b = -6, c = 9.
- Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.
- D = 0, значит уравнение имеет один корень:
Ответ: корень уравнения 3.
Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.
- Определим коэффициенты: a = 1, b = -4, c = -5.
- Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.
- D > 0, значит уравнение имеет два корня:

Ответ: два корня x1 = 5, x2 = -1.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.
Источник
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.
В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
- кубические
- уравнение четвёртой степени
- иррациональные и рациональные
- системы линейных алгебраических уравнений
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.
А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на общий множитель, то есть 6.
Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены.
5х — 3х — 2х = — 12 — 1 + 15 — 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Найти неизвестную переменную.
Пример 4. Решить: 4(х + 2) = 6 — 7х.
- 4х + 8 = 6 — 7х
- 4х + 7х = 6 — 8
- 11х = −2
- х = −2 : 11
- х = — 0, 18
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 — 7х..
- 2х + 6 = 5 — 7х
- 2х + 6х = 5 — 7
- 8х = −2
- х = −2 : 8
- х = — 0,25
Источник
Как решать квадратные уравнения
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие квадратного уравнения
Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Есть три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней. Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению ax 2 + c = 0, которое:
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Пифагора: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам: Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Выводим формулу корней квадратного уравненияПродолжим изучать формулу корней квадратного уравнения. Пусть перед нами есть задача решить квадратное уравнение ax 2 + bx + c = 0. Выполним ряд равносильных преобразований:
выделим полный квадрат левой части нового уравнения:
после чего уравнение примет вид перенесем два последних слагаемых в правую часть и сменим знак на противоположный: преобразуем выражение в правой части: Так, мы пришли к уравнению Отсюда выводы про корни уравнения И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D. По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников: Источник Читайте также: Что значит фамилия игнатьев Adblock |
Общие свойства алгебраических уравнений Определение числа действительных корней алгебраического уравнения.
Общие
свойства алгебраического уравнения:
В
общем виде алгебраическое уравнение
может быть записано в виде:
Pn(x)
= a0
+ a1x
+ a2x2
+ … + anxn
.
где
Pn(x)
— многочлен
n-ой
степени, n
— наивысшая
степень при неизвестном, a0,
a1,
… , an
— действительные
коэффициенты.
Всякое
число x,
обращающее многочлен в ноль, т.е. Pn(x)
= 0 называется
корнем
многочлена. Согласно основной теореме
алгебры, многочлен Pn(x)
степени
n (n ³
1)
с любыми числовыми коэффициентами,
имеет n
корней,
если каждый из корней считать столько
раз, какова его кратность.
Число
x
является корнем многочлена Pn(x)
тогда и только тогда, когда Pn(x)
делится
без остатка на х — x
. Если
при этом Pn(x)
делится
без остатка на (х-x)k
(k ³1),
но уже не делится на (х-x)k+1,
то x
называется k-кратным
корнем
(или корнем
кратности k)
многочлена
Pn(x).
Корни
кратности k=1
называются
простыми
корнями
многочлена.
Прежде
чем вычислять корни алгебраического
уравнения, сначала необходимо:
а)
определить число корней, которое имеет
данное уравнение;
б)
найти область существования корней
(установить верхнюю и нижнюю границу
расположения корней).
Определение
числа действительных корней алгебраических
уравнений.
Для
этого используют правило Декарта:
Количество
действительных положительных корней
алгебраического уравнения Pn(x)
= 0 с действительными коэффициентами
либо равно числу перемен знака в
последовательности коэффициентов
уравнения Pn(x)
= 0, либо на четное число меньше (равные
нулю коэффициенты не учитываются).
Количество
отрицательных корней уравнения равно
числу перемен знака в последовательности
коэффициентов Pn(-x)
= 0 или на четное число меньше.
Пример:
x5
— 17x4 +
12x3
+ 7x2
— x + 1 = 0 .
Это
уравнение имеет пять корней (из них хотя
бы один является действительным).
Уравнение
является полным, последовательность
знаков коэффициентов уравнения такова:
+ , — , + , + , — , + . Знак изменяется четыре
раза — значит, положительных корней
будет либо четыре, либо два, либо ни
одного.
Заменив
х
на -х,
получим:
-x5
— 17x4
— 12x3
+ 7x2
+ x + 1 = 0
число
постоянств знака равно одному,
следовательно, уравнение имеет один
отрицательный корень.
Пример:
x6
— 3x4
+ x3
+ x2
— 1 = 0 .
Данное
уравнение имеет шесть корней;
последовательность знаков: + , — , + , + , —
. Имеет место три перемены знака;
следовательно, положительных корней
либо 3 либо 1.
Для
многочлена
Pn(-x)
= x6
— 3x4
— x3
+ x2
— 1 = 0 .
последовательность
знаков: + , — , — , + , — . Здесь также три
перемены знака — поэтому число отрицательных
корней либо 3, либо 1.
Нахождение области существования корней алгебраического уравнения
Правило
кольца — пусть
дано алгебраическое уравнение
Pn(x)
= a0
+ a1x
+ a2x2
+ … + anxn
, где
a0,
a1,
… , an
— действительные
коэффициенты, и пусть
A = max {½a0½,
½a1½,
… , ½an-1½}
, B = max {½a1½,
½a2½,
… , ½an½}
.
Тогда
корни уравнения заключены в круговом
кольце r
< ½x½
< R , где


При
этом r
— нижняя,
а R
— верхняя
граница положительных корней
алгебраического уравнения Pn(x)
= 0, и
—R,
-r —
соответственно
нижняя и верхняя граница отрицательных
корней.
Пример.
Определить границы корней уравнения
5x3
— 20x + 3 =
0 .
Здесь
½an½
= 5, A =
20 , ½a0½
= 3, B = 20,
т.е.

Тогда,
если действительные корни уравнения
5x3
— 20x + 3 + 0
существуют (а они обязательно существуют,
так как уравнение нечетной степени), то
они расположены в интервале (-5, 5); при
этом отрицательные корни лежат в
интервале (-5, -0.013), а положительные — в
интервале (0.013, 5).
Метод
Ньютона —
если при х
= с
многочлен
Pn(x)
= a0
+ a1x
+ a2x2
+ … + anxn
и
его производные Pn‘(x),
Pn»(x),
… принимают
положительные значения, то с
является верхней границей положительных
корней уравнения Pn(х)
= 0 .
Пример.
Методом
Ньютона определить верхнюю границу
положительных корней уравнения 8x4
— 32x2
—
32х
+ 1
= 0 .
Находим
P(x) = 8x4
— 32x2
—
32х
+ 1
; P'(x) = 32x3
— 16x —
32
;
P»(x)
= 96x2
— 16 ; P»’(x)
= 192x ; PIV(x)
= 192 .
Проверке
подлежат только значения x
> 0.
При
x=c=1
имеем
P(1)<
0. Значит
проводить далее проверку для х=1 не
следует.
Проверка
x=c=2:
P(2) > 0 ; P‘(x)
> 0 ; P»(x)
> 0 ; P»’(2)
> 0 : PIV(x)
> 0 .
Таким
образом, верхней границей положительных
корней является число R
= 2.
В качестве нижней границы можно взять
число, обратное R,
т.е.
r = 1/2 =
0.5 .
Необходимо
добавить оценку скорости сходимости
методов
Соседние файлы в папке 2
- #
- #
- #
- #
- #
- #
- #
- #
- #































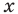
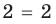
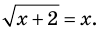
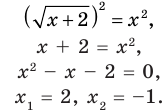
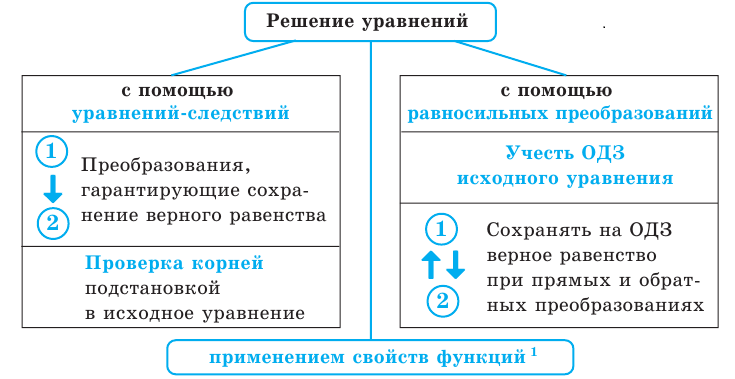
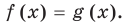
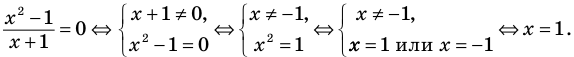
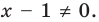
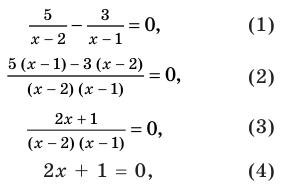
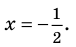
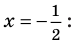
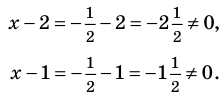
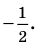




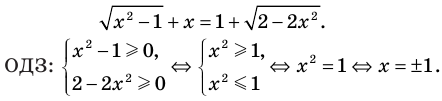

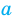
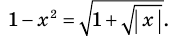
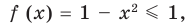
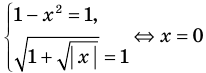
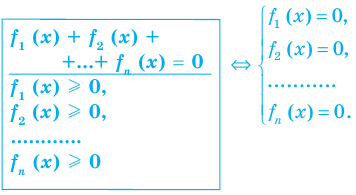
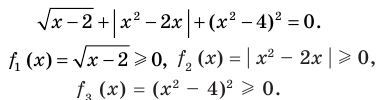
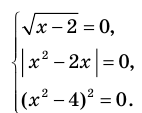
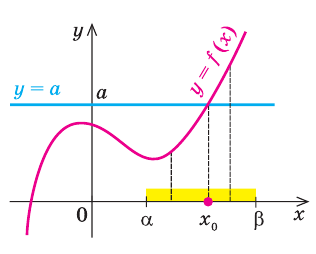
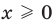
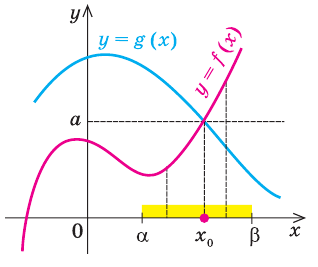
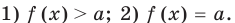
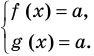
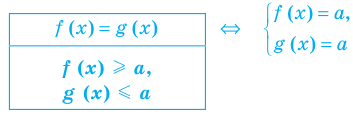
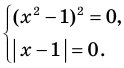
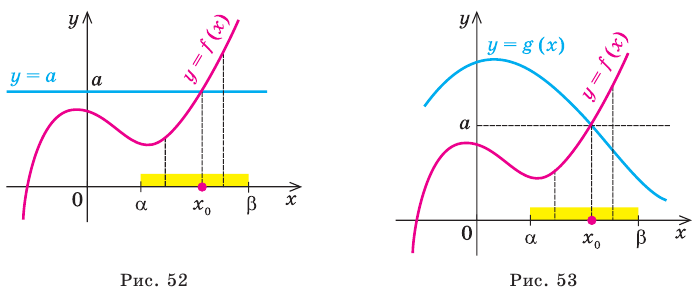
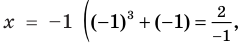





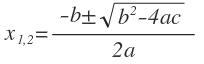

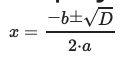

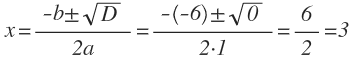









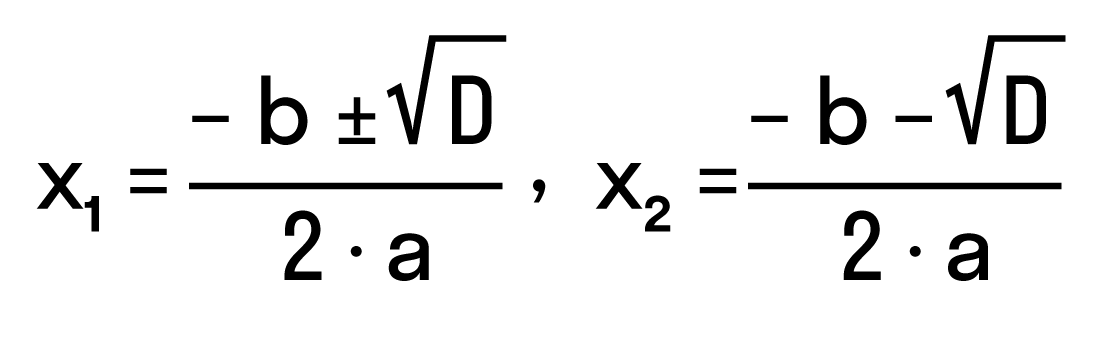
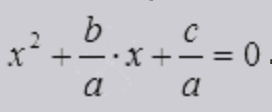
 ,
,
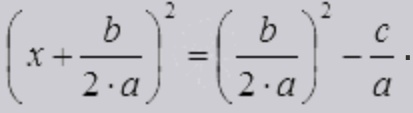

 , которое полностью равносильно исходному ax 2 + bx + c = 0.
, которое полностью равносильно исходному ax 2 + bx + c = 0.



