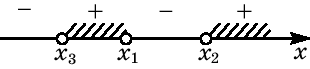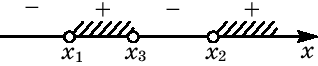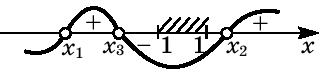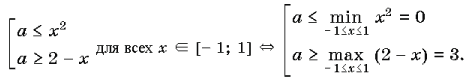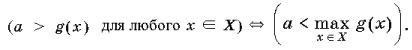Как найти действительные значения параметра

В. Голубев, А. Гольдман,
Москва

О задачах с параметром

Первоначальные сведения

I. Что такое параметр?

Если вы вспомните некоторые основные уравнения
(например, kx+l=0, ax²+bx+c=0),
то обратите внимание, что при поиске их корней
значения остальных переменных, входящих в
уравнения, считаются фиксированными и заданными.
Все разночтения в существующей литературе
связаны с толкованием того, какими
фиксированными и заданными могут быть эти
значения остальных переменных.

Например, в уравнениях |x|=a–1
и ax=1 при a=0
равенства не выполняются при любых значениях
переменной x, а в уравнения при a=0
их левые части не определены. Есть авторы,
допускающие рассмотрение значения a=0
во всех приведенных случаях, и есть авторы,
исключающие его в двух последних, вводя понятие
допустимых значений переменной a.

Поскольку в школьных учебниках нет определения
параметра, мы предлагаем взять за основу
следующий его простейший вариант.

Определение. Параметром называется
независимая переменная, значение которой в
задаче считается заданным фиксированным или
произвольным действительным числом, или числом,
принадлежащим заранее оговоренному множеству.

Комментарий. Независимость параметра
заключается в его «неподчинении» свойствам,
вытекающим из условия задачи. Например, из
неотрицательности левой части уравнения |x|=a–1
не следует неотрицательность значений выражения
a–1, и если a–1<0,
то мы обязаны констатировать, что уравнение не
имеет решений.

 II. Что означает «решить задачу с
параметром»?

Естественно, это зависит от вопроса в задаче.
Если, например, требуется решить уравнение,
неравенство, их систему или совокупность, то это
означает предъявить обоснованный ответ либо для
любого значения параметра, либо для значения
параметра, принадлежащего заранее оговоренному
множеству.

Если же требуется найти значения параметра, при
которых множество решений уравнения,
неравенства и т. д. удовлетворяет объявленному
условию, то, очевидно, решение задачи и состоит в
поиске указанных значений параметра.

Более прозрачное понимание того, что означает
решить задачу с параметром, у читателя
сформируется после ознакомления с примерами
решения задач на последующих страницах.

III. Какие основные типы задач с
параметрами?

Тип 1. Уравнения, неравенства, их
системы и совокупности, которые необходимо
решить либо для любого значения параметра
(параметров), либо для значений параметра,
принадлежащих заранее оговоренному множеству.

Этот тип задач является базовым при овладении
темой «Задачи с параметрами», поскольку
вложенный труд предопределяет успех и при
решении задач всех других основных типов.

Тип 2. Уравнения, неравенства, их
системы и совокупности, для которых требуется
определить количество решений в зависимости от
значения параметра (параметров).

Обращаем внимание на то, что при решении задач
данного типа нет необходимости ни решать
заданные уравнения, неравенства, их системы и
совокупности и т. д., ни приводить эти решения;
такая лишняя в большинстве случаев работа
является тактической ошибкой, приводящей к
неоправданным затратам времени. Однако не стоит
абсолютизировать сказанное, так как иногда
прямое решение в соответствии с типом 1 является
единственным разумным путем получения ответа
при решении задачи типа 2.

Тип 3. Уравнения, неравенства, их
системы и совокупности, для которых требуется
найти все те значения параметра, при которых
указанные уравнения, неравенства, их системы и
совокупности имеют заданное число решений (в
частности, не имеют или имеют бесконечное
множество решений).

Легко увидеть, что задачи типа 3 в каком-то
смысле обратны задачам типа 2.

Тип 4. Уравнения, неравенства, их
системы и совокупности, для которых при искомых
значениях параметра множество решений
удовлетворяет заданным условиям в области
определения.

Например, найти значения параметра, при
которых:

1) уравнение выполняется для любого значения
переменной из заданного промежутка;
2) множество решений первого уравнения
является подмножеством множества решений
второго уравнения и т. д.

Комментарий. Многообразие задач с
параметром охватывает весь курс школьной
математики (и алгебры, и геометрии), но
подавляющая часть из них на выпускных и
вступительных экзаменах относится к одному из
четырех перечисленных типов, которые по этой
причине названы основными.

Наиболее массовый класс задач с
параметром — задачи с одной неизвестной и
одним параметром. Следующий пункт указывает
основные способы решения задач именно этого
класса.

IV. Каковы основные способы (методы)
решения задач с параметром?

Способ I (аналитический). Это способ
так называемого прямого решения, повторяющего
стандартные процедуры нахождения ответа в
задачах без параметра. Иногда говорят, что это
способ силового, в хорошем смысле «наглого»
решения.

Комментарий. По мнению авторов,
аналитический способ решения задач с параметром
есть самый трудный способ, требующий высокой
грамотности и наибольших усилий по овладению им.

Способ II (графический). В
зависимости от задачи (с переменной x и
параметром a) рассматриваются графики или в
координатной плоскости (x; y), или в координатной
плоскости (x; a).

Комментарий. Исключительная наглядность и
красота графического способа решения задач с
параметром настолько увлекает изучающих тему
«Задачи с параметром», что они начинают
игнорировать другие способы решения, забывая
общеизвестный факт: для любого класса задач их
авторы могут сформулировать такую, которая
блестяще решается данным способом и с
колоссальными трудностями остальными способами.
Поэтому на начальной стадии изучения опасно
начинать с графических приемов решения задач с
параметром.

Способ III (решение относительно
параметра). При решении этим способом переменные
x и a принимаются равноправными и выбирается та
переменная, относительно которой аналитическое
решение признается более простым. После
естественных упрощений возвращаемся к исходному
смыслу переменных x и a и заканчиваем решение.

Перейдем теперь к демонстрации указанных
способов решения задач с параметром.

Задача 1. Для всех действительных
значений параметра a решите уравнение x³–(2–a)x²–ax–a(a–2)=0.

Решение. Исходное кубическое по x уравнение
является квадратным относительно a.
Поэтому, считая переменную x
параметром, перепишем это уравнение в виде
стандартного квадратного уравнения
относительно a, опуская промежуточные шаги по
раскрытию скобок и перегруппировке:

a²–(x²–x+2)a
– x³ + 2x² = 0.

Поскольку

x²–x+2=x²+(2–x) и –x³+2x²=x²(2–x),

то по обратной теореме Виета

a₁=x², a₂=2–x.

Поэтому исходное уравнение равносильно
совокупности уравнений

a=x² и a=2–x.

Первое уравнение преобразуется к виду x²=a,
откуда

(1): при a<0 решений нет;
(2): при a=0 единственное
решение x=0; при a>0
два решения
(3):

Второе уравнение совокупности имеет
единственное решение (5): x=2–a
для любого значения параметра a.

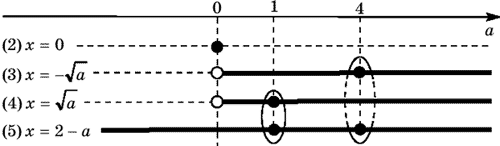
Комментарий 1. Многие учащиеся, доведя
решение до данного момента, испытывают трудности
в формировании общего ответа. Приведем удобный
прием представления полученных результатов для
дальнейшего продвижения в решении задачи. Будем
называть данный прием: «разверткой вдоль оси
параметра».

Изображаем ось параметра a
и отмечаем на ней граничные значения параметра,
которые фигурируют в ответах к каждому уравнению
совокупности. Все найденные решения уравнений
для тех значений параметра a,
при которых хотя бы одно решение существует,
выписываем в таблице слева (последовательно
сверху вниз). Сплошной линией, параллельной оси
параметра, указываем те промежутки значений
параметра, при которых полученное решение
существует. Заметим, что концы промежутков
изображаются «светлыми» точками в случае, когда
соответствующее решение не существует, а
«темными» точками — в противном случае.

Таблица 1

Данная развертка позволяет легко найти все
решения исходного уравнения для любого
действительного значения параметра: x=2–a
при a<0; x=0 или
x=2 при a=0; или или x=2–a
при a>0.

Комментарий 2. Возникает принципиальный
вопрос: является ли приведенный выше ответ
окончательным? С одной стороны, для поставленной
задачи ответ можно считать окончательным, если
допустить возможность повторения в ответе
одного и того же решения в различном виде.

Например, при a = 1 равенства и x = 2
– a определяют одно и то же значение переменной x=1,
а при a=4 равенства   и x=2–a
аналогично определяют одно значение x=–2.
Однако оставлять подобные повторения без
внимания обычно не принято, тем более, что при
других, особенно популярных в последнее время
постановках задач («Укажите количество
различных корней данного уравнения в
зависимости от параметра a» или «При каких
значениях параметра a уравнение имеет одно
решение?») игнорирование указанного
обстоятельства приводит к неверному ответу.

Полученные равенства (2)–(5) могут при некоторых
значениях параметра a
определять одно и то же значение переменной x.
Найдем указанные значения параметра. Поскольку
значения –
различны для всех a>0,
осталось выяснить, при каких значениях a
выполняются равенства Пусть  тогда первое уравнение приводится к виду t²+t–2=0,
откуда t=1 и t=–2
(не подходит, так как при a > 0), т. е.. Аналогично решая
второе уравнение, находим a=4.

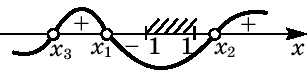
Таблица 2

Полученный результат в таблице 2
проиллюстрирован следующим образом: линии
равенства (4) и (5) «сливаются» при a=1,
линии (3) и (5) «сливаются» при a=4.

Замечания. 1. При практическом
использовании «развертки по параметру»
таблицу 2 рекомендуем не воспроизводить, а
полученные «слияния» изображать в таблице 1.

2. Для изолированных значений параметра
естественно приводить числовые значения корней.

Используя таблицу 2, легко сформулировать
окончательный ответ задачи.

Ответ: x=2–a при a<0;
x₁=0, x₂=2 при a=0;

Задача 2. Для всех действительных
значений параметра a найдите число различных
корней уравнения (a–x²)(a+x–2)=0.

Замечание. Очевидно, что решение предыдущего
примера позволяет, в частности, получить ответ и
на поставленный вопрос. Для этого в таблицу 2
удобно ввести еще одну строчку, соответствующую
количеству различных корней по переменной x при
данном значении параметра a (в дальнейшем будем
обозначать указанное число различных корней
через N(a)). В этом случае таблица 2
будет выглядеть следующим образом.

Таблица 3

Количество различных корней для каждого
значения a совпадает с числом
пересечений соответствующей вертикальной линии
с приведенными ранее сплошными горизонтальными
линиями (или «темными» точками) с учетом
совпадений решений при найденных значениях
параметра. Например, при a=2
соответствующая вертикальная линия пересекает
сплошные горизонтальные три раза, а при a=4
она хотя и пересекает те же линии, но две из них
«сливаются», поэтому при a=4
количество различных корней равно двум, а не
трем, т. е. N(2)=3 и N(4)=2.

Ответ: уравнение имеет один корень при a<0;
два корня — при a=0, a=1,
a=4; три корня — при 0<a<1,
1<a<4, a > 4.

Укажем иной (достаточно популярный и
эффективный) способ решения данной задачи,
который с успехом может быть использован и при
решении задач других типов (включая и задачи типа
1). Предлагаемый способ основан на рассмотрении
множества точек плоскости с координатами (x; a),
для которых выполняются соответствующие
уравнения. Это множество точек обычно называют
графиком уравнения.

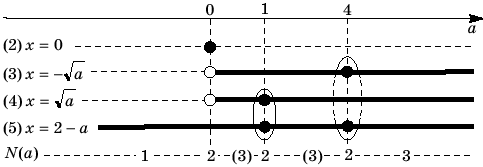
Решение. Исходное уравнение равносильно
совокупности a–x²=0 или a+x–2=0.
Поэтому построение искомого множества
точек — графика уравнения — сводится к
построению графиков a=x²
и a=2–x (рис. 1).

Рис. 1

Координаты точек пересечения графиков
определяются как решение системы уравнений 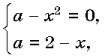решив которую
находим координаты (1; 1) точки A и (– 2; 4) —
точки B.

Понятно, что все точки параболы и прямой (и
только они) имеют координаты (x; a),
удовлетворяющие исходному уравнению. Поэтому
количество различных корней уравнения по
переменной x при каждом значении
параметра a=a₀ совпадает
с количеством точек пересечения прямой l,
задаваемой равенством a=a₀,
с построенным множеством точек.

Очевидно, что при a<0 прямая l
лежит в нижней полуплоскости и пересекает график
исходного уравнения (объединение точек параболы
и прямой) в одной точке, т. е. N(a)=1
при a<0. При a=0
прямая l касается параболы a=x²,
т. е. имеет с ней одну общую точку и пересекает
прямую a=2–x, поэтому N(0)=2.
При дальнейшем возрастании параметра a
от 0 до 1 (не включая значения 1) прямая l пересекает
график уравнения в трех точках, откуда N(a)=3
при 0<a<1. Аналогично
получаем N(1)=N(4)=2 и N(a)=3 при 1<a<4,
a>4.

Ответ: N(a)=1 при a<0;
N(a)=2 при a=0, a=1, a=4;
N(a)=3 при 0<a<1, 1<a<4,
a>4.

Комментарий. При решении рассмотренным
способом задач типа 1 при данном значении
параметра a₀ решениями
уравнения являются абсциссы точек пересечения
прямой a=a₀ с графиком
уравнения.

Задача 3. При каких значениях
параметра a уравнение |x+2|=ax
не имеет решений?

Решение 1. Для каждого значения параметра a
решим данное уравнение, после чего отберем те
значения параметра, при которых уравнение
решений не имеет.

На основании определения модуля заключаем, что
исходное уравнение равносильно совокупности
двух систем:

. 

или

Первая система имеет одно решение при т. е. при aЈ0
или a>1 и не имеет решений
при остальных значениях параметра. Вторая
система имеет одно решение т. е. при – 1<a<0
и не имеет решений при остальных значениях
параметра.

Объединяя решения систем, имеем: данное
уравнение имеет одно решение aЈ–1,
a=0, a>1; два решения Анализируя полученный
результат, определяем значения параметра a,
при которых уравнение не имеет решений.

Ответ: 0<aЈ1.

Замечание. Мы привели здесь решение задачи в
общем виде с целью повторной иллюстрации решения
задач типа 1 (рекомендуем для анализа полученных
решений составить таблицу «развертки вдоль оси
параметра», табл. 1–3).

Может показаться, что приведенное решение не
экономно и содержит много лишних ходов. Например,
кажется естественным после получения
совокупности двух систем сразу искать лишь те
значения параметра, при которых не имеет решений
каждая из систем, после чего найти значения
параметра, при которых обе системы не имеют
решений одновременно. Однако даже понимание
того, что требуется проделать в этом случае, уже
представляет собой определенную трудность для
ряда учащихся. Сказанное, разумеется, не
означает, что во всех аналогичных задачах
целесообразно выходить на более общую
постановку вопроса (выбор оптимального способа
решения зависит от конкретной задачи).

Решение 2. Приведем еще один вариант
использования графических представлений для
решения задач с параметрами.

Как известно, число решений уравнения f(х)=g(x)
совпадает с количеством точек пересечения
графиков функций y=f(x) и y=g(x),
построенных в одной системе координат.
Рассмотрим графики функций y=|x+2| и y=ax
(рис. 2). График первой функции не зависит от
параметра a; график второй
функции (правой части уравнения) принадлежит
семейству прямых, проходящих через начало
координат, — «подвижный» график. Поэтому
искомые значения параметра a
соответствуют тем прямым из указанного
семейства, которые не пересекают график функции y=|x+2|.

Рис. 2

При изменении параметра a от – Ґ до +Ґ
прямая y=ax поворачивается, начиная от
«вертикального» положения «слева» от оси
координат, против часовой стрелки вокруг начала
координат. Очевидно, что при aЈ0 прямая y=ax
пересекает по крайней мере один раз
«неподвижный» график y=|x+2|; при
дальнейшем возрастании параметра a
до момента a=1 (включительно)
прямая не имеет общих точек с «неподвижным»
графиком; при a>1 у графиков
снова появляется общая точка. Поэтому исходное
уравнение не имеет решений при 0<aЈ1.

Комментарий. В общем случае решение
уравнений предложенным способом состоит в
предварительном преобразовании уравнения к
одному из видов: f(x)=g(x; a) или f(x; a)=g(x;
a), после чего рассматриваются графики
обеих частей уравнения в одной системе
координат. При этом в первом случае изучается
взаимное расположение «неподвижного» графика
функции f и «подвижного» (в зависимости
от параметра) графика функции g, а во
втором случае оба графика «подвижны».

Выбор того или иного варианта предопределяется
как возможностью приведения исходного уравнения
к одному из видов, так и искусством работы с
графиками того, кто решает данное уравнение.

Для сравнения решите самостоятельно известную
задачу.

При каких значениях параметра a
уравнение x–a=2|2|x|– a²| имеет
ровно три различных корня?

Рассмотрите сначала графики функций f₁(x;
a)=x–a и g₁(x; a)=2|2|x|–a²|,
а затем графики функций f₂(x)=x
и g₂(x; a)=2| 2| x|–a²|+a.

Ответ: a=–2, a=–0,5.

Задача 4. Найдите все значения
параметра a, при каждом из
которых множество решений неравенства (a–x²)(a+x–2)<0
не содержит ни одного решения неравенства x²Ј1.

Замечание. Ниже приводятся три решения
данной задачи.

Первое из них традиционно для большинства
учащихся (обычно решение такого рода называют
прямым алгебраическим решением). Как правило,
попытки подобного решения характерны и для
начинающих овладевать методами решений задач с
параметрами, и для «опытных бойцов», которых не
смущает обилие технических трудностей.

Рекомендуем обратить самое пристальное
внимание на второе решение, поскольку приводимый
способ, во-первых, отличен от уже разобранных в
настоящей статье и, во-вторых, его можно
расценивать как достаточно самостоятельный и
эффективный метод решения широкого класса задач
с параметрами.

Третье решение проводится уже знакомым вам по
примерам 2 и 3 графическим способам.

Решение 1. Множитель (a–x²)
является квадратным трехчленом относительно x,
который не имеет корней при a<0,
имеет один корень при a=0 и
имеет два различных корня при a>0.
Второй множитель, линейный по переменной x,
имеет один корень при любом значении параметра a.
Поэтому в данной задаче целесообразно
рассмотреть три случая.

Случай 1. Пусть a<0; тогда
a–x²<0 при любом x,
а значит, исходное неравенство равносильно
неравенству a+x–2>0, т. е. x>2–a.

Комментарий. В этот момент возникает
основная логическая трудность, характерная для
данного способа решения задач типа 4: определение
тех значений параметра a<0, при которых
найденное множество решений, зависящее от
параметра, удовлетворяет условию задачи, т. е.
не содержит ни одного решения неравенства x²Ј1 (не содержит ни одного x
из отрезка [– 1; 1]).

Так как полученное множество решений
неравенства при a<0 есть
открытый луч (2–x; +Ґ),
то, очевидно, данный луч не содержит точек
отрезка [– 1; 1] тогда и только тогда, когда
начало луча лежит «правее» отрезка либо
совпадает с его правым концом, т. е.
выполняется условие 2–aі1,
которое, очевидно, истинно при всех
рассматриваемых значениях параметра a<0.

Таким образом показано, что все значения
параметра a<0 удовлетворяют
условию задачи, т. е. имеем «часть» общего
ответа: a<0.

Случай 2. Пусть a=0. В этом
случае исходное неравенство имеет вид (– x²)(x–2)<0,
решая которое получим x>2. Это
означает, что значение параметра a=0
удовлетворяет условию задачи: луч (2; + Ґ) не содержит точек отрезка
[– 1; 1], и мы имеем еще одну «часть» ответа:
a=0.

Комментарий. При разбиении решения задачи на
случаи в зависимости от параметра рекомендуем
все граничные значения параметра исследовать
непосредственной подстановкой в исходное
уравнение (неравенство, систему). Это полезно для
промежуточного контроля решения задачи.

Случай 3. Пусть a>0. Тогда
неравенство можно переписать в виде

   (A)

Комментарий. Ясно, что при фиксированном
значении a полученное неравенство легко решается
методом интервалов, однако в нашем случае (и это
характерно для задачи с параметрами!) процесс
упорядочения корней по возрастанию выделяется в
самостоятельный фрагмент решения.

Корень первого множителя при любом a>0
меньше корня второго множителя Корень третьего множителя
x₃=2–a в зависимости от a
может находиться как на промежутке от x₁
до x₂, так и вне его (слева
либо справа). Для определения возможных
вариантов сравним x₃ с x₁
и x₂.

Вариант 1. Пусть Полученное неравенство решаем как
квадратное относительно (t>0, так как в
рассматриваемом случае a>0): t²–t–2>0,
откуда t<–1 или t>2;
с учетом условия t>0 получаем, что
t>2. Возвращаясь к параметру a,
имеем неравенство т. е. a>4. Итак, для a>4
справедливо соотношение x₃<x₁<x₂,
следовательно, решая неравенство (A) методом
интервалов (рис. 3), находим решения

x₃<x<x₁, x>x₂, 
т. е.

Рис. 3.

Полученное множество решений не
содержит ни одной точки отрезка [– 1; 1] тогда и
только тогда, когда отрезок [– 1; 1] расположен
либо левее точки x₃=2–a,
либо между точками С учетом условия a>4
первая ситуация исключается, а вторая
определяется системой неравенств которая выполняется для
любого a>4. В итоге приходим
к выводу, что все значения параметра a>4
являются искомыми.

Вариант 2. Пусть x₃=x₁,
т. е. откуда a=4
и неравенство (A), принимая вид (x+2)²(x–2)>0,
имеет решение x>2, которое не
содержит точек отрезка [– 1; 1]. Следовательно,
значение a=4 — искомое.

Вариант 3. Пусть Решая соответствующую систему неравенств
получим, 1<t<2,
т. е. 1<a<4. При найденных
значениях параметра неравенство (A) имеет решение

x₁<x<x₃,  x>x₂,
т. е.

Рис. 4.

Следовательно, условию задачи удовлетворяют те
и только те значения параметра, при которых
отрезок [– 1; 1] расположен либо левее точки либо между
точками.
Поскольку первая ситуация, очевидно, невозможна то искомые
значения a определяются системой неравенств
aі3. С учетом того, что в данном
варианте рассматривались значения параметра a
от 1 до 4, получаем 3Јa<4.

Вариант 4. Пусть откуда a=1 и
неравенство (A) принимает вид (x+1)(x–1)²>0.
Решением последнего неравенства (рис. 4)
является объединение интервалов (–1;1)
и (1;+ Ґ), в котором
содержатся точки отрезка [– 1; 1]. Значит,
изучаемое значение параметра a=1
не удовлетворяет условию задачи.

Вариант 5. Пусть Решив полученное неравенство (квадратное
относительно ),
находим, что –2<t<1, т. е. 0<a<1
(напомним, что мы находимся в рамках
случая 3, определяемого условием a>0).
Неравенство (A) при полученных значениях
параметра (рис. 5) имеет решение

 

Найденное множество решений не содержит ни
одной точки отрезка [– 1; 1] тогда и только
тогда, когда этот отрезок расположен либо левее
точки либо
между точками
Ни та, ни другая ситуация невозможна ввиду
неотрицательности арифметического квадратного
корня. Следовательно, среди рассматриваемых
значений параметра 0<a<1
нет искомых.

Итак, после рассмотрения всех пяти возможных
вариантов получен ответ в случае 3: aі3.

Таким образом, окончательный ответ задачи
следующий: aЈ0, aі3.

Замечание к решению 1. При решении данным
способом практически всегда возникает
возможность продвигаться к поставленной цели с
существенно меньшими затратами времени, что
сопряжено, однако, с увеличением логических
трудностей. Например, в случаев 3 (a >
0) нашего решения можно было рассуждать
следующим образом.

Определив корни каждого множителя в неравенстве (A),
замечаем, что при значении параметра a<1
независимо от взаимного расположения корней в
окрестностях корней всегда найдется хотя бы одно решение
исходного неравенства из отрезка [– 1; 1]
(поскольку при переходе через корни x₁
и x₂ левая часть неравенства
(A) меняет знак), что не соответствует искомым
значениям параметра a.

Следовательно, осталось рассмотреть значения
параметра aі1.
Непосредственной проверкой легко убедиться, что
значение a=1 также не
удовлетворяет условию задачи. При a>1
корень корень а корень x₃=2–a<1.
Поэтому большим корнем левой части неравенства
(A) является x₂; значит, все
значения x из интервала (x₂;+ Ґ) не всегда являются
решениями неравенства (A). Поэтому неравенство (A)
не имеет ни одного решения из отрезка [– 1; 1]
тогда и только тогда, когда x₃Ј–1 (независимо (!) от
расположения корней x₁ и
x₃, (рис. 5, 6).

Рис. 5.

Рис. 6.

Итак, имеем 2–aЈ–1,
откуда aі3.

Решение 2. Основная идея решения: неравенство
(a – x²)(a+x–2)<0
будем рассматривать как неравенство
относительно параметра a и исследовать
полученный ответ (зависящий от x!) с целью
получения искомых значений параметра a.

Комментарий. Очевидно, сама идея
рассматриваемого метода предопределяет
ограничения по его использованию: во-первых,
далеко не всегда возможно решить уравнение
относительно параметра; во-вторых, в случае
возможности такого решения не всегда
целесообразно применение обсуждаемого способа в
силу возникновения в дальнейшем серьезных
технических и логических трудностей (оценка
подобных трудностей приходит, естественно, с
опытом решения такого рода задач).

Так как при любом x из отрезка [– 1;
1] справедливо соотношение x²Ј2–x, то при данных x исходное
неравенство как квадратное относительно a
равносильно неравенству a₁<a<a₂,
где a₁=x², a₂=2–x, т. е.
имеем x²<a<2–x для
любого xО[– 1; 1].     
(B)

Комментарий. Типичной трудностью при
решении задач предлагаемым способом является
осознание того, какому условию должны
удовлетворять искомые значения параметра для
вновь полученных уравнений (неравенств, систем).

В нашем случае задачу, равносильную исходной,
можно сформулировать следующим образом.

При каких значениях параметра a
двойное неравенство x²<a<2–x не
имеет ни одного решения из отрезка [–1;1]?

Чтобы понять, как действовать дальше, нужно для
конкретного значения параметра a=a₀
уметь ответить на вопрос: почему значение a₀
не является искомым? Очевидно, значение
параметра a₀ не
является искомым, если существует хотя бы одно
значение x₀ из отрезка [– 1;
1], при котором выполняется неравенство x₀²<a₀<2–x₀.
Следовательно, значение параметра a
является искомым тогда и только тогда, когда для
любого x из отрезка [– 1; 1] либо aЈx², либо aі2–x.

Найдем сначала все значения параметра a,
для которых при любом x из отрезка [– 1; 1]
имеет место неравенство aЈx².
Понятно, что если aЈx²
при любом x из отрезка [– 1; 1],
то это то же самое (!), что значение a
не больше наименьшего значения функции f(x)=x²
на этом отрезке. Поскольку наименьшее значение
функции f(x)=x² на отрезке [– 1;
1] равно 0, получаем aЈ0.

Теперь осталось найти все значения параметра a,
для которых при любом x из отрезка [– 1;
1] выполняется неравенство aі2–x. По аналогии с
предыдущими рассуждениями можно утверждать, что aі2–x для всех x из
отрезка [– 1; 1] тогда и только тогда,
когда a не меньше наибольшего
значения функции f(x)=2–x на отрезке
[–1;1]. Поскольку наибольшее значение
убывающей линейной функции f(x)=2–x
на отрезке [– 1; 1] равно ее значению в
точке x=–1, т. е. равно 3, то
искомые значения параметра aі3.

Объединяя полученные ответы, приходим к
окончательному ответу исходной задачи: aЈ0, aі3.

Комментарий. Обращаем особое внимание на
заключительный фрагмент решения задачи, который
характерен для многих задач с параметрами: мы
показали, что

Часто приходится иметь дело и с аналогичными
задачами: «Найти все значения параметра a,
при которых неравенство a<f(x) (или
неравенство a>g(x))
выполняется для любого x из заданного
множества X». Подобная постановка
вопроса у большинства учащихся вызывает
серьезные затруднения.

Приводим ответ на поставленный вопрос.

1. Неравенство a < f(x)
выполняется для любого x из множества X
тогда и только тогда, когда a меньше наименьшего
значения f(x) на множестве X
(если оно существует!), т. е.

2. Неравенство a>g(x)
выполняется для любого x из
множества X тогда и только тогда, когда a
больше наибольшего значения g(x) на
множестве X (если оно существует!),
т. е. 

На этом мы заканчиваем разбор отдельных
примеров и в заключение особо выделим важные, по
нашему мнению, соображения, которые необходимо
учитывать учащемуся при овладении темой «Задачи
с параметрами».

V. Заключительные рекомендации

1. Прежде чем приступить к решению задачи с
параметрами, советуем разобраться в ситуации для
конкретного числового значения параметра.
Например, возьмите значение параметра a=5
и ответьте на вопрос: является ли данное значение
a=5 искомым для задачи 4?
Неудачная попытка получения ответа на
поставленный вопрос, к сожалению, означает вашу
принципиальную неготовность решить задачу в
общем виде. В этом случае необходимо срочно
принять меры к овладению основными темами
школьного курса математики. Заметим, что
подстановка фиксированного значения параметра
позволяет во многих случаях нащупать путь
решения задачи.

2. Рекомендуем обратить ваше внимание на то,
что при решении задач с параметрами особую роль
играет обработка результатов, полученных на том
или ином этапе решения. Одной из удобных,
апробированных на практике форм организации
результатов, является представление их в
табличном виде (см. задачу 1). Советуем в первую
очередь обратить внимание на эту рекомендацию
тем, кто только начинает овладевать методами
решения задач с параметрами.

.

Рассмотрим два случая.

1) $%xge a$%. Здесь $%(a-2.5)x+1=4x-4a$%, откуда $%(a-6.5)x=-4a-1$%. При $%a=6.5$% решений в рамках данного случая нет. Если $%ane6.5$%, то $%x=-frac{4a+1}{a-6.5}$%. Далее надо выяснить, при каких $%a$% это решение подходит, то есть выполнено условие $%-frac{4a+1}{a-6.5}ge a$%. Упрощая, получаем $%a+frac{8a+2}{2a-13}=frac{2a^2-5a+2}{2a-13}le0$%, где в числителе находится произведение $%(2a-1)(a-2)$%. Метод интервалов даёт $%ain[-infty;0.5]cup[2;6.5)$%.

2) $%x < a$%. Здесь $%(a-2.5)x+1=4a-4x$%, и $%(a+1.5)x=4a-1$%. При $%a=-1.5$% решений нет. Если $%ane-1.5$%, то $%x=frac{4a-1}{a+1.5}$%. Здесь нам нужно, чтобы было $%frac{4a-1}{a+1.5} < a$%, то есть $%frac{2a^2-5a+2}{2a+3} > 0$%. Отсюда $%ain(-1.5;0.5)cup(2;+infty)$%.

Два решения получатся при тех $%a$%, которые дают решение в каждом из подслучаев. Поэтому надо взять пересечение двух множеств. Решений будет при этом ровно два, так как подслучаи взаимоисключающие. Ответом будет $%ain(-1.5;0.5)cup(2;6.5)$%.

Возможен также графический способ решения.

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

И заодно – стоит повторить темы «Квадратные уравнения» и «Квадратичные неравенства».

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

1)

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

2)

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Найдем дискриминант :

< 0.

< 0

< 0

Решив неравенство, получим

С учетом пункта 1, получим ответ: .

2. Найдите все значения a, при каждом из которых сумма квадратов действительных корней уравнения

минимальна.

Мы привыкли находить корни квадратного уравнения по известной формуле, с помощью дискриминанта. Однако для задач с параметрами такой способ подходит не всегда. А вот теорема Виета нам поможет.

В условии сказано: «Сумма квадратов действительных корней…» Это значит, во-первых, что корни есть, а во-вторых, их должно быть два. А это будет в случае, когда дискриминант положителен ( > 0).

Если и – корни квадратного уравнения
, то по теореме Виета:

В нашем случае:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

Ответ: 1

3) Найдите все значения , при каждом из которых все решения уравнения

положительны.

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

Решение системы: .

С учетом пункта 1 получим ответ

Ответ:

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Получим:

Сделаем замену 

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Его дискриминант

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

а)

Тогда

б)

Объединив все случаи, получим ответ.

Ответ:

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

1) отрезок

2) 2 луча

3) точка

4) ∅

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Решим систему

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого:

Единственное решение

Если , при этом система примет вид:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.

Ответ:

На этой странице вы узнаете

• Игра в прятки: как значение одной переменной может помочь найти другую?
• Парадокс: как стоять на месте и бежать с любой скоростью одновременно? 
• Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром? 

Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье. 

Что такое параметр 

Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов? 

Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно (frac{20}{5} = 4). А если было 10 градусов, то искомое число было бы равно (frac{20}{10} = 2). 

Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными. 

Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a”  называется параметр. 

Параметр — это условная буква, вместо которой можно подставить число. 

То есть параметр — это еще одна переменная, которая может принять несколько значений. 

Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.

Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 

Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.

Линейные уравнения с параметром

Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a. 

(x = frac{20}{a})

Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5 

Что, если a=0? Мы получаем уравнение (x = frac{20}{0}), у которого нет решения, поскольку на 0 делить нельзя. 

Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0. 

Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a (neq) 0 — x = 20a. 

Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев. 

1) b (neq) 0. 

Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b. 

Получаем уравнение ax = 15. Как найти начальную скорость Пети? (x = frac{15}{a}). 

Такое уравнение мы уже решали выше. Получаем два случая: 

• Если a = 0 — решений нет. 
• Если a (neq) 0, то изначальная скорость Пети была равна (x = frac{15}{a}). 

2) b = 0. 

Мы получаем уравнение ax = 0. Также разберем два случая значений параметра: 

• a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось? 

Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений. 

• a (neq) 0. Здесь получается, что равен 0 уже х: (x = frac{0}{a} = 0). 

Подведем итог. Как можно решить уравнение вида ax = b?

• Если a = 0, b = 0 — бесконечное множество решений. 
• Если a = 0, b (neq) 0 — решений нет. 
• Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 

Квадратные уравнения с параметром

Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции». 

Квадратное уравнение имеет вид ax² + bx + c = 0, а графиком функции y = ax² + bx + c будет парабола. 

Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.  

Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней: 

• При D > 0 уравнение имеет два корня. 
• При D = 0 уравнение имеет один корень. 
• При D < 0 уравнение не имеет корней. 

Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х. 

Рассмотрим три уравнения. 

1) x² — x — 2 = 0
Решим уравнение с помощью дискриминанта. 
D = 1² — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня. 

(x_1 = frac{1 + 3}{2} = 2)
(x_2 = frac{1 — 3}{2} = -1)

Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) . 

2) x² -4x + 4 = 0
Решим уравнение с помощью дискриминанта. 
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень. 

(x = frac{4}{2} = 2)

Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0). 

3) x² — 5x + 7 = 0
Решим уравнение с помощью дискриминанта. 
D = 25 — 4 * 1 * 7 = 25 — 28 = -3

Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет. 

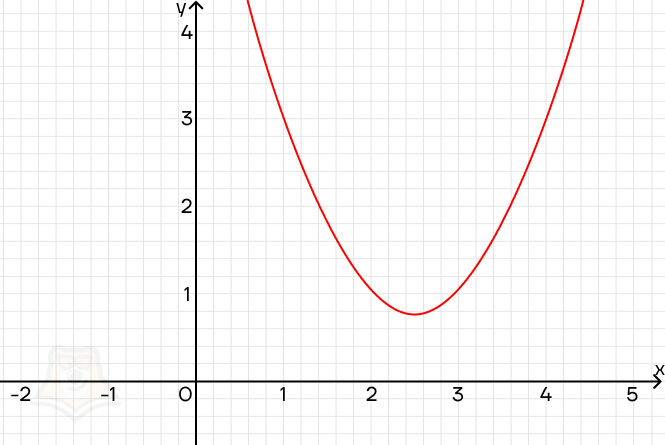
Где можно применить эти знания, решая параметры? 

Пример 1. Найдите все значения параметра a, при которых уравнение x² + (3a + 11)x + 18,25 + a = 0 имеет два различных решения. 

Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?

Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным. 

1. Для начала найдем сам дискриминант. 

D = (3a + 11)² — 4 * 1 * (a + 18,25) = 9a² + 66a + 121 — 4a — 73 = 9a² + 62a + 48

2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a² + 62a + 48 > 0

3. Решим его «Методом интервалов».

9a² + 62a + 48 = 0
D = 3844 — 1728 = 2116
(a_1 = frac{-62 + 46}{18} = -frac{16}{18} = -89)
(a_2 = frac{-62 — 46}{18} = -frac{108}{18} = -6)

4. Дискриминант будет положительным при (a in (-infty; -6) cup (-frac{8}{9}; +infty)). Это и будет ответ. 

Ответ: (a in (-infty; -6) cup (-frac{8}{9}; +infty)).

Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения. 

Пример 2. При каких значениях параметра a уравнение (2a + 1)x² — ax + 3a + 1 = 0 имеет два различных решения? 

Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0? 

Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи. 

1. Поскольку по условию должно быть 2 решения, мы получаем, что a (neq) -0,5. 

2. Найдем дискриминант уравнения. Он должен быть строго больше 0, чтобы у уравнения было два решения. 

D = a² — 4 * (2a + 1) * (3a + 1) = a² — 24a² — 20a -4 = -23a² — 20a — 4

3. Составим неравенство и решим его:

-23a² — 20a — 4 > 0
23a² + 20a + 4 < 0
23a² + 20a + 4 = 0
D = 400 — 4 * 23 * 4 = 400 — 368 = 32
(a_1 = frac{-20 + 4 sqrt{2}}{46} = frac{2sqrt{2} — 10}{23})
(a_2 = frac{-20 — 4sqrt{2}}{46} = frac{-2sqrt{2} — 10}{23})

4. Разложим уравнение на множители: 

(23a^2 + 20a + 4 = 23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23}))

5. Получаем неравенство:

(23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23} < 0)

6.Тогда  (a in (frac{-2sqrt{2} — 10}{23}; frac{2sqrt{2} — 10}{23})). Вспомним, что a (neq) -0,5, следовательно, мы получаем ответ (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23})).

Ответ: (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23}))

Теорема Виета 

Дискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax² + bx + c = 0, то его корни можно найти с помощью следующей системы: 

Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения. 

Пример 3. При каких значениях параметра a корни уравнения x² — 3ax — a(a — 1) = 0 удовлетворяют условию x₁ = 5x₂. 

Решение. 1. Корни уравнения — это два различных числа. Значит, дискриминант должен быть строго больше 0: 

D = 9a² — 4 * 1 * (-a² + a) = 9a² + 4a² — 4a = 13a² — 4a = a(13a — 4)

Получаем неравенство a(13a — 4) > 0, следовательно, (a in (-infty; 0) cup (frac{4}{13}; +infty)). 

2. По теореме Виета найдем корни уравнения: 

3. По условию x₁ = 5x₂, тогда 5x₂ + x2 = 6x₂ = 3a, откуда получаем:
(x_2 = frac{3a}{6} = frac{a}{2})
(x_1 = 5 * a_2 = frac{5a}{2})

4. Подставим во второе уравнение системы:
(frac{a}{2} * frac{5a}{2} = a — a^2)
(frac{5a^2}{4} = a — a^2 | * 4)
5a² = 4a — 4a²
(9a^2 — 4a = 0 rightarrow a(9a — 4) = 0 rightarrow a = 0, a = frac{4}{9})

5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня. 

a = 0 не подходит, поскольку ограничение (a in (-infty; 0) cup (frac{4}{13}; +infty)) не включает точку 0. 

(a = frac{4}{9}) подходит, поскольку (frac{4}{9} > frac{4}{13}). 

Ответ: (a = frac{4}{9})

Условия на корни квадратного трехчлена 

Однако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев. 

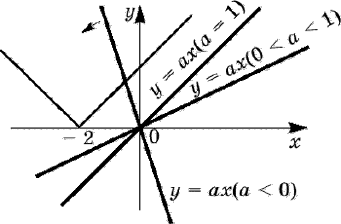
1. Корни квадратного трехчлена меньше, чем число N. 

Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз. 

Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N. 

Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту. 

Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка. 

Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа. 

Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы. 

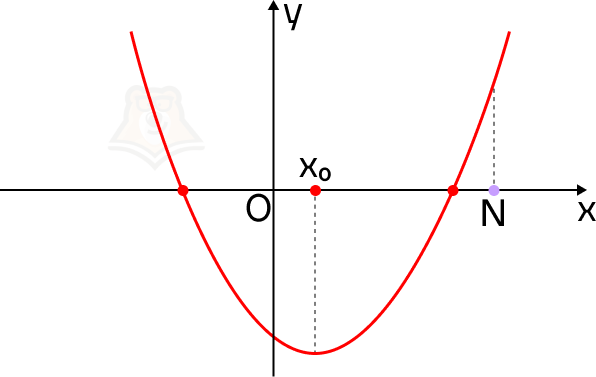
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N. 

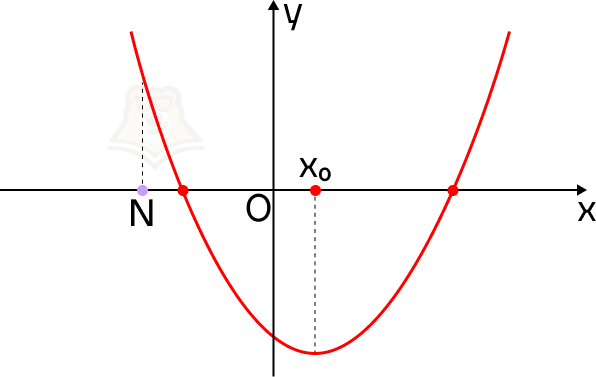
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов. 

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними. 

В этом случае смотровая площадка окажется между привалами. 

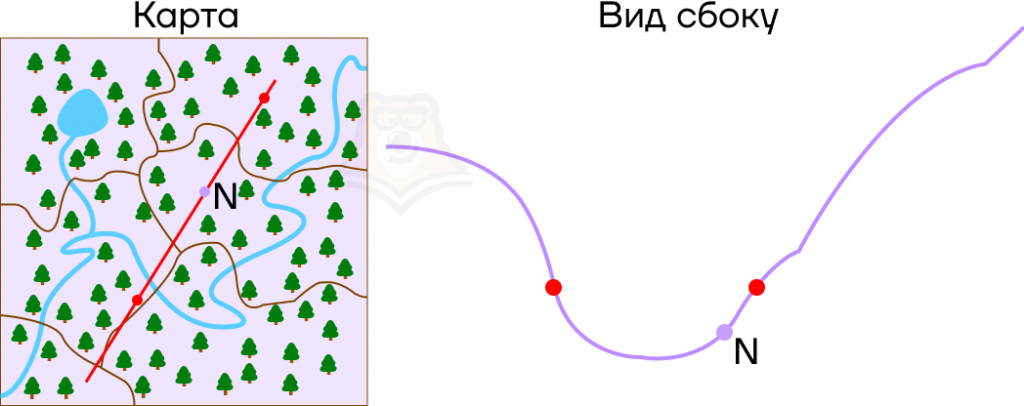
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг. 

Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы. 

Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

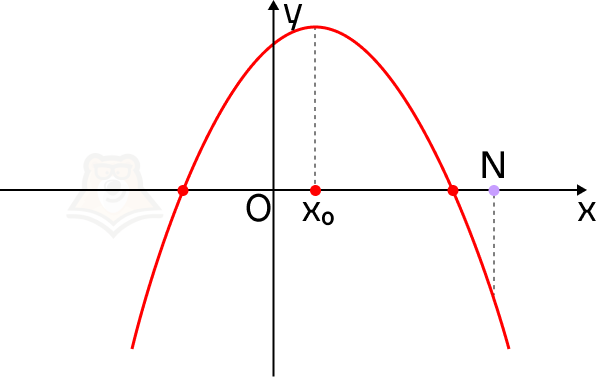
2. Корни квадратного трехчлена больше, чем число N. 

Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы. 

Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

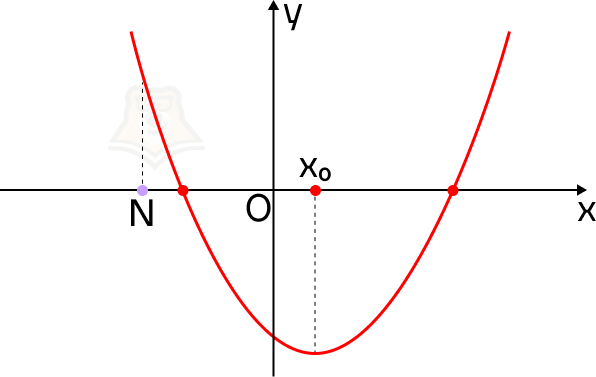
Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько. 

В итоге должна получиться система, с помощью которой можно решить задачу.

Фактчек

• Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 
• При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b (neq) 0 — решений нет. Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 
• При решении квадратного уравнения обязательно проверять коэффициент перед x². Если коэффициент будет равен 0, то уравнение станет линейным.
• При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней. 
• Решить квадратное уравнение можно и с помощью теоремы Виета. 
• Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций. 

Проверь себя

Задание 1. 
Что такое параметр?

1. Это буква a, вместо которой можно подставить число.
2. Это коэффициент перед x² в квадратном уравнении.
3. Это переменная х.
4. Это значение функции в определенной точке. 

Задание 2. 
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?

1. Решений нет.
2. Одно решение.
3. Бесконечное множество решений.
4. Невозможно определить количество решений. 

Задание 3. 
При каких значениях дискриминанта уравнение будет иметь корни?

1. D > 0
2. D = 0
3. D < 0
4. D (neq) 0

Задание 4. 
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?

1. Справа.
2. Слева.
3. Совпадать с точкой А.
4. Невозможно определить расположение вершины. 

Задание 5. 
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?

1. Значение функции в точке В будет меньше 0.
2. Значение функции в точке В будет равно 0.
3. Значение функции в точке В будет больше 0.
4. Невозможно определить значение функции. 

Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.

Для того чтобы наиболее полно
раскрыть возможности этого метода, будем рассматривать основные типы задач.

Образцы заданий при отработке знаний и умений
при решении задач с параметрами графическим методом (координатная плоскость )

Задание 1.

При каких значениях a уравнение  =  имеет
два корня?

Решение.

Переходим к равносильной системе:

Эта система на координатной плоскости (;)
задаёт кривую. Ясно, что все точки этой дуги параболы (и только они) имеют
координаты, удовлетворяющие исходному уравнению.
Поэтому число решений уравнения при каждом фиксированном значении параметра , равно количеству точек
пересечения кривой с горизонтальной прямой, соответствующей этому значению
параметра.

Очевидно при  указанные
 прямые пересекают график    в двух точках, что равносильно исходному уравнению
иметь два корня.

Ответ: при .

Задание 2.

Найти все значения а, при которых система    имеет     единственное решение.

Решение.

Перепишем исходную систему в таком виде:        

Все решения этой системы (пары вида ) образуют область, показанную на рисунке
штриховкой. Требование единственности решения данной системы на графический
язык переводится так: горизонтальные прямые должны иметь с полученной областью
только одну общую точку. Легко заметить, что лишь прямые  и удовлетворяют выдвинутому требованию.

Ответ: или .

Только что разобранные две задачи позволяют дать более
конкретные рекомендации по сравнению с приведёнными раннее:

· 
попытаться  выразить
параметр через переменную, т. е получить равенства вида  , затем

· 
на плоскости  строить график функции .

Задание 3.

При каких значениях а уравнение  имеет ровно три корня?

Решение.

Имеем

График этой совокупности – объединение «уголка» и
параболы. Очевидно, лишь прямая     пересекает полученное
объединение в трёх точках.

Ответ: .

Замечание: Параметр обычно рассматривается как
фиксированное, но неизвестное число. Между тем с формальной точки зрения
параметр – это переменная, причём «равноправная» с другими, присутствующими в
задаче. При таком взгляде на параметр формы задают
функции не с одной, а с двумя переменными.

    Задание 4.

Найти все значения параметра ,
при которых уравнение  имеет одно решение.

Решение.

Дробь равна нулю тогда и только тогда, когда числитель
дроби равен нулю, а знаменатель отличен от нуля.

Находим корни квадратного трёхчлена :

Данное уравнение равносильно системе:

С помощью полученной системы легко построить график
исходного уравнения. Именно наличие «проколов» в этом графике позволяет при и =  иметь  уравнению единственное решение.
Это определяющий фактор в решении.

Ответ:  и .

Задание 5.

При каких значениях параметра, а уравнение  имеет единственное решение.

Решение.

Запишем систему, равносильную исходному уравнению

Отсюда получаем

              

Строим график  и будем проводить прямые
перпендикулярные оси а.

Первые два неравенства системы задают множество точек,
показанное штриховкой, причём в это множество не входят гиперболы и .

Тогда отрезок и луч , отрезок и луч , лежащие соответственно на прямых и ,
являются графиком исходного уравнения. Одно решение будет, если 2 < < или  < или  = .

Ответ: 2 <  < или  <  или  = .

Задание 6.

Найти все значения параметра а, при которых
уравнение

 имеет
ровно два различных решения

Решение.

Рассмотрим совокупность двух систем

Если , то .

     

Если < , то .

     

Отсюда

  или  

Параболы и прямая   имеют
две общие точки: А (-2; — 2), В (-1; -1), причём,  В –
вершина первой параболы, D –
вершина второй. Итак, график исходного уравнения показан на рисунке.

 Должно быть ровно два различных решения. Это
выполняется при   или .

Ответ:  или .

Задание 7.

Найдите множество всех чисел ,
для каждого из которых уравнение

 имеет только два
различных корня.

Решение.

Перепишем данное уравнение в виде

.

Корни уравнения, ,  при
условии, что .

Строим график данного уравнения. В данном случае
график удобно строить, отнеся переменной  ось
ординат. Здесь ответ «считываем» вертикальными прямыми, получим, что данное
уравнение имеет только два различных корня при  = -1
или   или .

Пунктиры говорят о том, что .

Ответ: при  = -1 или   или .

Задание 8.

Для каких  в множестве решений
неравенства  содержится промежуток .

Решение.

Запишем совокупность двух систем, равносильную
исходному уравнению:

   или     

Поскольку в решение первой системы ни при каких
значениях параметра а не может входить  отрезок ,
то необходимые исследования проведём для второй системы.

Имеем    

Обозначим . Тогда второе
неравенство системы принимает вид < — и на координатной плоскости  задаёт множество, показанное на рисунке.

С помощью рисунка устанавливаем, что при  в полученном множестве содержатся все
точки, абсциссы в которых пробегают все значения промежутка  

Тогда , отсюда .

 Ответ: .

Задание 9.

Найти все неотрицательные числа , при которых существует единственное
число , удовлетворяющее системе

  

Решение.

Имеем,

Первое уравнение на координатной плоскости  задаёт семейство вертикальных прямых.
Прямые и  разбивают
плоскости на четыре области. Некоторые из них являются решениями неравенства
системы. Конкретно какие – можно установить, взяв из каждой области по пробной
точке. Та область, точка которой удовлетворяет неравенству, является его
решением (такой приём ассоциируется с методом интервалов при решении неравенств
с одной переменной). Строим прямые

 и .

Например, берём точку  и
подставляем в  Координаты точки удовлетворяют
неравенству.

Получаем две области (I) и (II), но,
учитывая, что по условию , мы берём только
область (I). Строим прямые , k.

Итак, исходной системе удовлетворяют все точки (и
только они), лежащие на лучах и выделенные на чертеже жирными линиями, (т. е.
строим точки  в заданной области).

Теперь надо найти единственное  при
фиксированном . Строим параллельные прямые,
пересекающие ось . и находим где будет одна точка
пересечения с прямой .

Находим по рисунку, что требование единственности
решение достигается, если  (при   уже 2 точки),

где  — ордината точки
пересечения прямых   и ,

где – ордината точки
пресечения прямых  и  .

Итак, получаем  < .

Ответ:  <
.

Задание 10.

При каких значениях параметра, а система  имеет решения?

Решение.

Разложим на множители левую часть неравенства системы,
имеем

Строим прямые   и . Показываем на рисунке штриховкой
множество точек плоскости, удовлетворяющее неравенству системы.

Строим гиперболу = .

Тогда абсциссы выделенных дуг гиперболы – решения
исходной системы. M, P, N, Q –
узловые точки. Найдём их абсциссы.

.

Для точек P, Q имеем

 

Остаётся записать ответ:   или .

Ответ:    или .

Задание 11.

Найти все значения , при которых любое решение неравенства                        по модулю не превосходит двух ().

Решение.

Перепишем данное неравенство в таком виде . Построим графики уравнений  и  =.

«Методом интервалов» устанавливаем, что решением
исходного неравенства будут заштрихованные области.

Теперь строим область   и смотрим, какая её часть попадает в
заштрихованную область.

Т.е. теперь, если при каком – то фиксированном
значении  прямая  в
пересечении с полученной областью даёт лишь точки, абсциссы которых
удовлетворяют условию  < 2, то  – одно из искомых значений параметра.

Итак, мы видим, что  .

Ответ: .

Задание 12.

При каких значениях параметра  множество
решений неравенства                                                        содержит не более четырёх целых значений ?

Решение.

Преобразуем данное неравенство к виду . Это неравенство равносильно совокупности
двух систем

  или

Изображаем с помощью этой совокупности решение
исходного неравенства.

Проведём прямые , где . Тогда значение ,
для которого прямая  пересекает прямые  не более чем в четырёх  точках из
отмеченного множества, будет искомым. Итак, мы видим, что  или или .

Ответ: или  или .

Задание 13.

При каких значениях параметра а имеет решения
система

Решение.

Корни квадратного трёхчлена  и
.

Тогда

Строим прямые  и .

Методом «интервалов» находим решение неравенства
системы (заштрихованная область).

Та часть окружности с центром в начале координат и
радиуса 2, которая попадает в заштрихованную область и будет решением данной
системы. .

Значения и находим из системы      

Значеня и – из системы  .

Ответ:

Задание 14.

В зависимости от значений параметра а решить
неравенство                  > .

Решение.

Перепишем данное неравенство в виде  и
рассмотрим функцию       , которую, раскрывая модули, запишем
так:      

Строим график. График разбивает координатную плоскость
на две области. Взяв т. (0;0) и подставив и  в 
исходное неравенство, получим, что 0 > 1, и поэтому исходное неравенство
выполняется в области лежащей выше графика.

Непосредственно из рисунка получаем:

при  решений
нет;

при      ;

при              .

Ответ:  при  решений
нет;

                при      ;

               при              .    

Задание 15.

Найдите все значения параметра ,
при котором система неравенств

 удовлетворяется лишь
при одном .

Решение.

Перепишем данную систему в таком виде:

Построим область, задаваемую данной системой.

1) , – вершина параболы.

=,

,

. 

  2) —
прямая, проходящая через точки и .

Требование единственности решения на графический язык
переводится так: горизонтальные прямые  с
полученной областью должны иметь только одну общую точку. Выдвинутому
требованию удовлетворяют прямые  и , где –
ордината точки пересечения параболы и прямой.

Найдём значение :

 =
(не подходит по смыслу задачи),

 =
. Находим ординату:

= .

Ответ: ,

Задание 16.

Найти все значения параметра а, при которых
система неравенств

 удовлетворяет лишь
при одном х.

Решение.

Построим параболы и штриховкой покажем решение последней
системы.

1)  ,   .

2)  ,   .     

Из рисунка видно, что условие задачи выполняется при или .

Ответ: или .

Задание 17.

При каких значениях  уравнение
 имеет ровно три корня.

Решение.

Данное уравнение равносильно совокупности

График совокупности  — объединение графиков параболы и
уголка.

Прямые  пересекают полученное
объединение в трёх точках.

Ответ:  при  .

Задание 18.

При каких значениях  уравнение
имеет ровно три решения.

Решение.

Преобразуем левую часть данного уравнения. Получим
квадратное уравнение относительно .

,

.

Получим уравнение

, которое равносильно
совокупности

Объединение графиков парабол есть решение
совокупности.

Находим ординату очки пересечения парабол:

Считываем нужную информацию с рисунка: данное
уравнение имеет три решения при  или

Ответ: при  или

Задание 19.

В зависимости от параметра  определить
число корней уравнения

Решение.

Рассмотрим данное уравнение как квадратное
относительно а.

   ,

.

Получаем совокупность

      

Строим графики уравнений совокупности  и отвечаем на
поставленный вопрос задачи.

Ответ:          : нет решений;

                       : одно
решение;

                        : два
решения;

                        или : три решения;

                       или : четыре решения.

Задание 20.

Сколько решений имеет система

Решение.

Ясно, что количество корней второго уравнения системы
равно числу решений самой системы.

Имеем, .

Рассмотрев это уравнение как квадратное относительно , получаем совокупность.

Теперь обращение к координатной плоскости  делает задачу простой.
Координаты точек пересечения находим, решив уравнение

Отсюда

Вершины парабол   и  .

Ответ:     :
четыре решения;

                : два решения;

              : одно решение;

             : нет решений.

Задание 21.

Найти все действительные значения параметра , для которых уравнение                      имеет только два
различных корня. Запишите эти корни.

Решение.

.

Найдём корни квадратного трёхчлена, стоящего в
скобках:

Изобразим множество решений данного уравнения в
координатной плоскости , построив графики    при условии, что

Считываем с рисунка нужную информацию. Итак, данное
уравнение имеет два различных корня при  ( и ) и при
 (и )

Ответ:  при  ( и ) и

             при  (и ).

Задание 22.

Решить систему неравенств:

Решение.

Строим в плоскости графики параболы и прямой  .  

Все точки закрашенной
области – решение системы. Разобьём построенную область на две части.

Если  и , то нет решений.

Если , то абсциссы  точек закрашенной области будут больше
абсцисс точек прямой , но меньше абсцисс (большего
корня уравнения ) параболы.

Выразим  через  из уравнения прямой :

 Найдём корни уравнения  :               

                                      ,

                                                ,

                                     .

Тогда .

Если же  , то .

Ответ: при 
и  1 нет решений;

               при       ;

               при        .

Задание 23.

Решить систему неравенств

Решение.

 – вершина параболы  .

 — вершина параболы  .

Находим абсциссы точек пересечения парабол:

Закрашенная область – решение системы. Разбиваем её на
две части.

В уравнениях парабол выражаем  через
:

  

Записываем ответ:

если  и , то нет решений;

если , то < ;

если ,
то .

Задание 24.

При каких значениях, а уравнение не имеет решений?

Решение.

Уравнение равносильно системе

 

   

Построим множество решений системы.

Три кусочка параболы решение данного уравнения.

Найдем  при котором  и исключим его.

.

Итак, при   нет
решений;

          при   нет решений;

(замечание: при остальных а есть одно или два решения).

Ответ:  ; 
.

Задание 25.

При каких действительных значениях параметра  существует хотя бы одно , удовлетворяющее условиям:

Решение.

Решим графически «методом интервалов» неравенство в и построим       график  . Посмотрим, какая часть графика попадает
в построенную область решения неравенства, и найдём соответствующие значения а.

 

Строим графики прямых   и 

Они разбивают координатную плоскость  на 4 области.

«Методом интервалов» решим графически последнее
неравенство.

Заштрихованная область является его решением. В эту 
область попадает часть графика параболы . На
интервале  ;  (по
условию неравенство системы строгое) существуют , удовлетворяющие
условиям данной системы.

Ответ:

Задание 26.

Найдите все значения параметра ,
при каждом из которых множество решений неравенства не
содержит ни одного решения неравенства .

Решение.

Построим множество решений неравенства («методом
интервалов»). Затем построим «полосу»  Искомые
значения параметра q те,
при которых ни одна из точек указанных областей не принадлежит «полосе»

Ответ:  или .

Задание 27.

При каких значениях параметра ,
уравнение  имеет единственное решение.

Решение.

Разложим на множители числитель дроби.

,

,

 Данное уравнение равносильно системе:

 

Построим график совокупности в координатной плоскости .

    или  

 – точка пересечения прямых  и .
График совокупности — объединение прямых.

    «Выкалываем» точки графика с абсциссами ,.

Проводим прямые  и 
смотрим, где существует одна  точка пересечения с графиком.

Очевидно, что только при  или  данное уравнение имеет единственное
решение.

Ответ:  или .

Задание 28.

При каких действительных значениях параметра  система неравенств  не имеет решений.

Решение.

Множество точек плоскости  заштрихованной
области удовлетворяет данной системе неравенств.

Строим прямые . По
рисунку определяем, что при (—
абсцисса точки пересечения гиперболы и прямой) прямые  не
пересекают  заштрихованную область.

Ответ:  при  .

Задание 29.

При каких значениях параметра а система  имеет единственное решение.

Решение.

Перейдём к системе, равносильной  данной.

В координатной плоскости  построим
графики парабол  и  Вершины
парабол соответственно точки   и  .

Вычислим абсциссы точек пересечения парабол, решив
уравнение

Заштрихованная область – решения системы неравенств.
Прямые  и   

имеет с закрашенной
областью одну общую точку.

Ответ: при    и  .

Задание 30.

Решите неравенство:

Решение.

В зависимости от параметра  найдём
значение .

Неравенство будем решать «методом интервалов».

Построим параболы

:      .

 :          .

Вычислим координаты 
точки пересечения парабол:

 

Точки   закрашенной области удовлетворяют данному
неравенству. Проведя прямую , разобьём эту область
на три части.

1) Если  ,
то нет решений.

        2)Если  ,
то в уравнении  выразим   через :

Таким образом,  в области I имеем  .

2)                                                                     
Если , то смотрим:

а) область II.

 Выразим в уравнении   через .

 ,

—
меньший корень,

—
больший корень.

Итак, в области II  имеем  .

б) область III:    .

Ответ:  при   нет
решений;

                 при        

                 при            ,  .

Литература:

1.                    
Галицкий
М. Л., Гольдман А. М., Звавич Л. И. Сборник задач по алгебре для 8 – 9 классов:
Учебное пособие для учащихся школ и классов с углубленным изучением математики
– 2-е изд. – М.: Просвещение, 1994.

2.                    
П. И.
Горнштейн, В. Б. Полонский, М. С. Якир. Задачи с параметрами. 3-е издание,
дополненное и переработанное. – М.: Илекса, Харьков: Гимназия, 2003.

3.                    
Фаддеев
Д. К. Алгебра 6 – 8. – М.: Просвещение, 1983 (б – ка учителя математики).

4.                    
А. Х.
Шахмейстер. Уравнения и неравенства с параметрами. Под редакцией Б. Г. Зива. С
– Петербург. Москва. 2004.

5.                    
В. В.
Амелькин, В. Л. Рабцевич. Задачи с параметрами Минск «Асар», 2002.

6.                    
А. Х.
Шахмейстер. Задачи с параметрами в ЕГЭ. Издательство Московского университета,
ЧеРо на Неве МЦНМО.
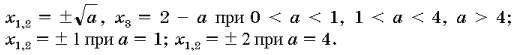
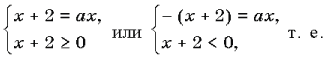