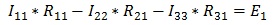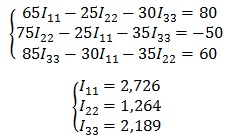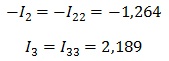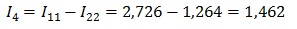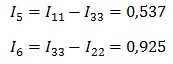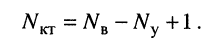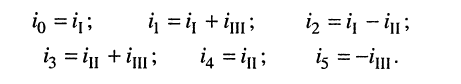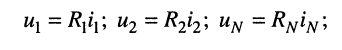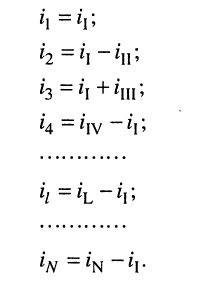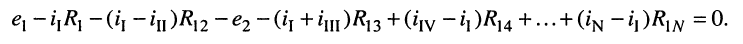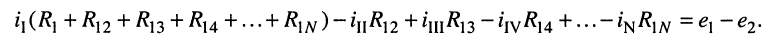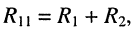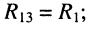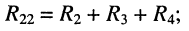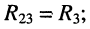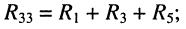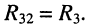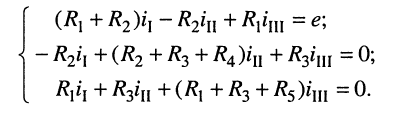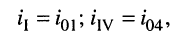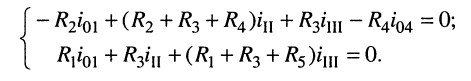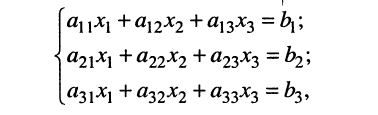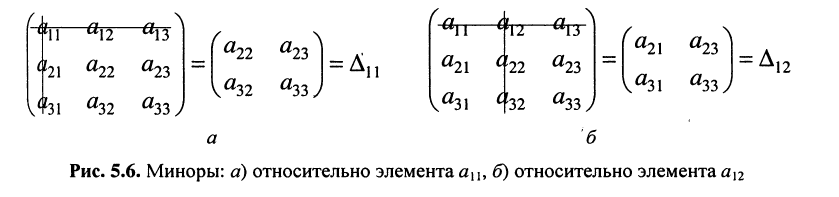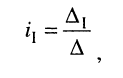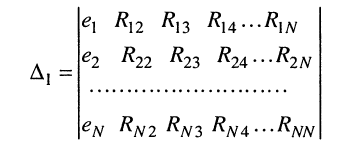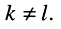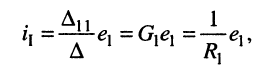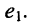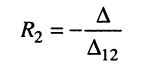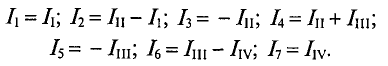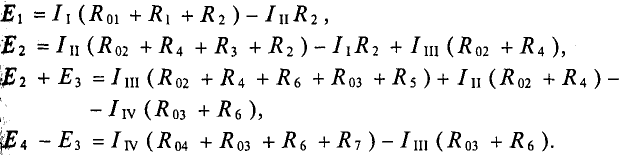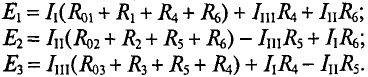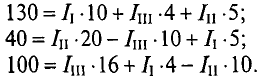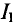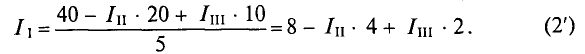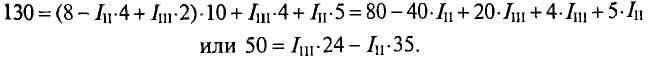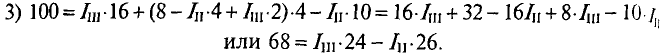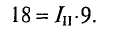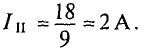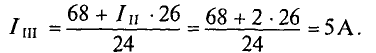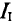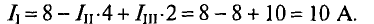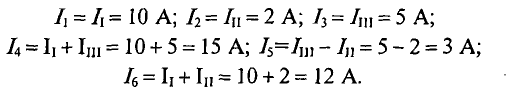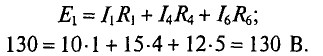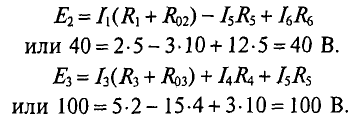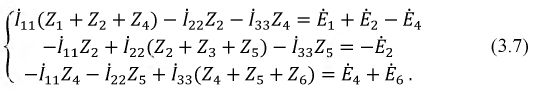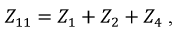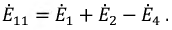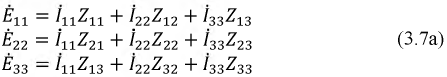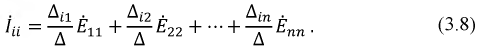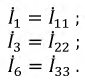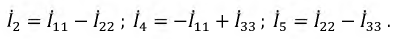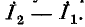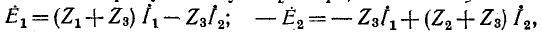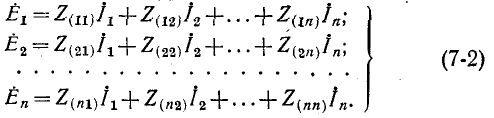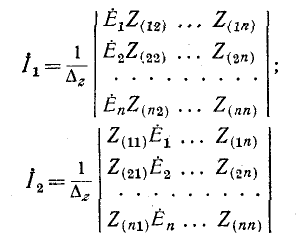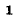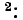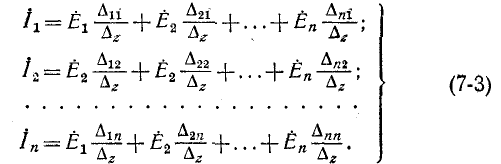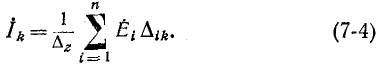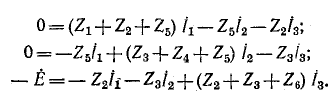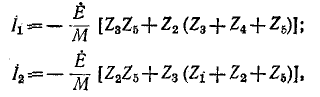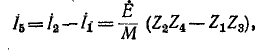Как найти действительный ток в цепи - Исправление недочетов и поиск решений вместе с Examum.ru

Метод контурных токов.Решение задач

Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m — количество ветвей, а n — количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.

Основные понятия

Контурный ток — это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I₁₁, I₂₂ и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС — это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

Выполняем все поэтапно.

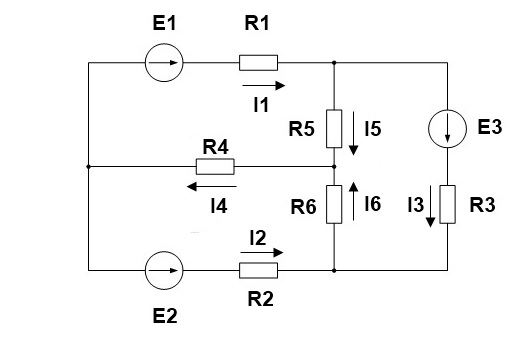
1. Произвольно выбираем направления действительных токов I₁-I₆.

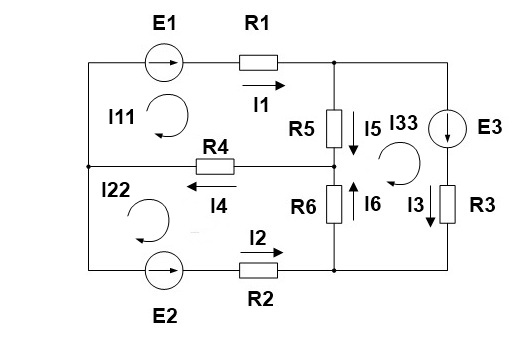
2. Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

R₁₁=R₁+R₄+R₅=10+25+30= 65 Ом

R₂₂=R₂+R₄+R₆=15+25+35 = 75 Ом

R₃₃=R₃+R₅+R₆=20+30+35= 85 Ом

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

R₁₂=R₂₁=R₄=25 Ом

R₂₃=R₃₂=R₆=35 Ом

R₃₁=R₁₃=R₅=30 Ом

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E₁ этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.

5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.

Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

А для остальных

Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!

Рекомендуем — Метод двух узлов

Источник

Изучаем метод контурных токов с примерами

Электрические схемы могут быть очень сложными. Чтобы рассчитать действующие в них токи, пользуются первым и вторым правилами Кирхгофа. В этом случае составляют систему уравнений, на основании которых можно узнать, какова сила электротока в каждом контуре. Метод контурных токов позволяет сократить объем проводимой работы. Решать уравнения можно самостоятельно или же используя онлайн калькулятор.

Суть метода

В составе любой электрической цепи имеются контуры и ветви. Действующие в них электротоки определяют при помощи правил Кирхгофа. При этом количество уравнений будет совпадать с количеством неизвестных величин.

Существуют способы упростить расчет цепей, сокращая количество необходимых для решения задачи уравнений. Один из наиболее известных основывается на таком понятии, как контурный ток. С его помощью процедура расчёта становится более эффективной, что особенно выгодно при рассмотрении наиболее сложных электрических цепей.

Иногда возникает вопрос, являются ли контурные токи реальными токами ветвей. В отдельных случаях это может быть так, но не всегда. Действительный ток равен контурному, если он протекает лишь в одном контуре.

При проведении расчётов онлайн или офлайн применяются особые, искусственно смоделированные электротоки. Одна из особенностей смоделированных электротоков заключается в том, что каждый проходит внутри элементарного контура. При этом рассматриваются только те из них, которые по сравнению друг с другом имеют новые ветви.

Расчет по методу контурных токов предполагает, что не все токи в рассматриваемой схеме являются независимыми. Поэтому этот способ позволяет сократить количество нужных для расчета уравнений. С его помощью можно определить действительные токи на каждом участке схемы.

Практическое применение

Чтобы лучше понять, как можно определить токи в ветвях цепи методом контурных токов, предлагаем рассмотреть такую схему.

Анализ схемы показывает, что есть и контурные, и реально протекающие электротоки. Первые имеют индекс из одной цифры, вторые — из двух. Нужно заметить, что каждая сторона треугольника является отдельным контуром. В каждом из них задано направление обхода. Оно выбирается произвольно, но определяет знаки токов проходящих в ветвях. В качестве нагрузки используются резисторы, но могут рассматриваться и более сложные элементы. Учитывая направление токов, составляем систему уравнений:

Чтобы рассчитать составленную систему, воспользуемся правилами Кирхгофа:

Расчет цепей методом контурных электротоков можно выполнить также с помощью специальных онлайн сервисов. Приведенная выше формула может быть представлена следующим равенством:

В этом выражении использованы следующие обозначения:

Равные индексы, относящиеся к сопротивлению, представляют собой суммарную величину для k-го контура электрической цепи.
Если для сопротивления использованы индексы k и m, то речь идёт об общем сопротивлении, которое входит одновременно в 2 контура с такими номерами.
Нужно обратить внимание, что в последней формуле присутствуют контурные токи в k-м контуре.
С правой стороны знака равенства указана суммарная электродвижущая сила для k-го контура.

При определении неизвестной величины слагаемое берётся с плюсом в тех ситуациях, когда направления электротоков в соседних контурах совпадают, и с минусом, когда они противоположные. ЭДС контура может быть положительной или отрицательной. Первый вариант применяется в тех случаях, когда направления электродвижущей силы и контурного электротока совпадают. В противном случае ЭДС берётся с минусом.

Уравнение составляется не для всех контуров. Исключением являются те, в которых присутствует источник электротока. В такой ситуации контурный ток совпадает с реальным. Количество уравнений в полученной системе равно количеству контуров, являющихся независимыми, то есть тех, у которых имеется хотя бы одна ветвь, отличающая их от всех других. Решение полученной системы уравнений позволит вычислить электротоки на каждом участке схемы.

Примеры решения задач

Необходимо решить задачу с исходными данными, представленными на рисунке ниже.

Исходя из заданной схемы, можно выделить три контура. Затем следует указать направление контурных и действительных электротоков.

Теперь следует рассчитать собственные сопротивления каждого контура.

Составляем систему уравнений для определения контурных токов. Поскольку есть три контура, то уравнений также будет три. При этом следует учитывать направление электротоков и ЭДС.

После подстановки известных значений сопротивлений в полученные уравнения находим величину интересующих нас токов.

На последнем этапе определяем значения действительных токов.

Так решаются задачи с помощью метода контурных электротоков. Главное преимущество данного метода заключается в сокращенном числе уравнений. Оно уменьшается до m – n + 1, где m — это количество ветвей, а n — узлов в электроцепи.

Видео по теме

Источник

Содержание:

Метод контурных токов:

Контурным током называют условный ток, протекающий внутри независимого контура.

Напомним, что контуры называются независимыми (подробнее см. разд. 2.1), если они отличаются друг от друга хотя бы одним элементом (ветвью). Направление отсчёта контурного тока выбирается произвольно и независимо от выбора направлений отсчётов контурных токов в других контурах. В отличие от метода токов ветвей, рассмотренного в лекции 4, данный метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной числу

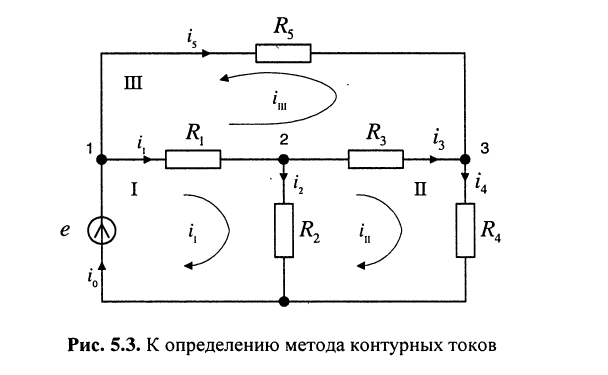
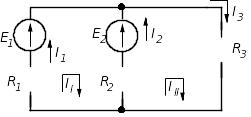
Предварительно покажем, что при известных контурных токах можно найти токи всех ветвей, а потому и напряжения на всех элементах цепи. Действительно, ток в любом элементе (ветви) определяется по первому закону Кирхгофа (ЗТК) как алгебраическая сумма контурных токов, протекающих в этом элементе. Например, при выбранных в удлинителе (рис. 5.3) направлениях отсчётов токов элементов и контурных токов имеем:

Зная токи, протекающие в элементах, можно по закону Ома определить напряжения на каждом из них.

Определение:

Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются контурные токи, называется методом контурных токов.

Составление контурных уравнений

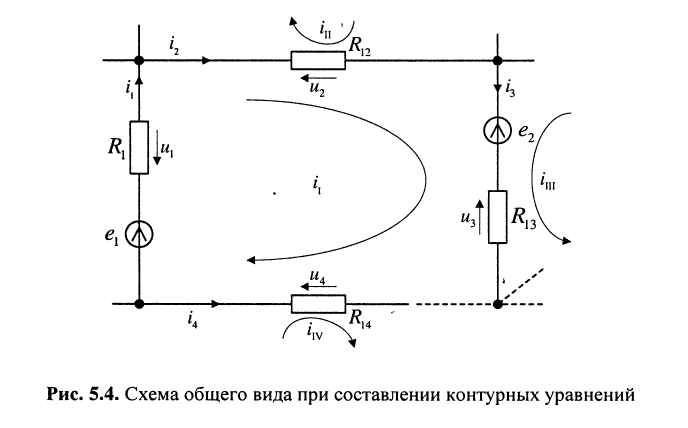
При составлении системы контурных уравнений воспользуемся вторым законом Кирхгофа и будем полагать, что (рис. 5.4):

При этих условиях, выбранных независимых контурах и заданных направлениях отсчётов контурных токов запишем уравнение для первого контура (см. рис. 5.4) согласно второму закону Кирхгофа:

(5.5)

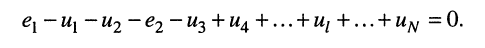
Выразим напряжения на элементах 1-го контура через токи ветвей по закону Ома:

или в общем виде:

(5.6)

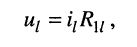
Подставим (5.6) в (5.5)

(5.7)

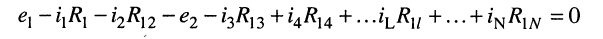
и выразим токи ветвей через контурные токи, нумерация которых осуществляется римскими цифрами и прямыми латинскими буквами. Из рис. 5.4 видно, что:

Произведём замену токов ветвей в выражении (5.7) через соотношения (5.8):

Умножим полученное уравнение на-1, раскроем скобки, приведём подобные члены и перенесём в правую часть известные значения напряжений источников; после выполнения этих действий контурное уравнение принимает вид

Подобное уравнение можно было бы составить и для любого другого контура, поэтому полученный результат позволяет сделать обобщающие выводы:

Аналогично записываются узловые уравнения для всех других контуров цепи, в результате чего образуется система контурных уравнений вида:

(5.9)

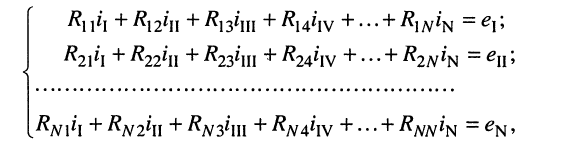
где:

Система контурных уравнений (5.9) составлена относительно неизвестных контурных токов и записана в канонической форме, а именно:

контурные ЭДС, как свободные члены, записываются в правых частях уравнений;
неизвестные контурные токи записываются в левых частях уравнений с последовательно возрастающими индексами;
уравнения располагаются в соответствии с порядковыми номерами контуров.

Пример 5.2.

Записать систему контурных уравнений для удлинителя (рис. 5.3).

Решение. Предварительно найдём собственные и взаимные сопротивления трёх контуров:

I контура:

• собственное сопротивление
• взаимные сопротивления: со вторым контуром 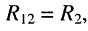с третьим контуром

II контура:

• собственное сопротивление
• взаимные сопротивления: с первым контуром с третьим контуром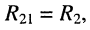

III контура:

• собственное сопротивление
• взаимные сопротивления: с первым контуром с третьим контуром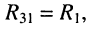

Заметим, что:

Теперь можно записать систему контурных уравнений, руководствуясь указанными ранее правилами:

Особенности составления контурных уравнений

Рассмотренные ранее цепи не содержали независимых источников тока, поэтому количество контурных уравнений согласно (5.4) равно количеству независимых контуров. Однако цепь может иметь несколько источников токов. В этом случае следует выбрать такое дерево цепи, при котором источники токов входили бы в число соединительных элементов. Тогда через каждый источник тока будет проходить ток только одного контура, который равен задающему току источника. Поэтому уменьшается как число неизвестных контурных токов, так и число контурных уравнений. 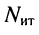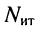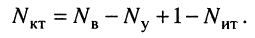Следовательно, если цепь содержит источников тока, то известно контурных токов, а число контурных уравнений оказывается равным

(5.10)

Пример 5.3.

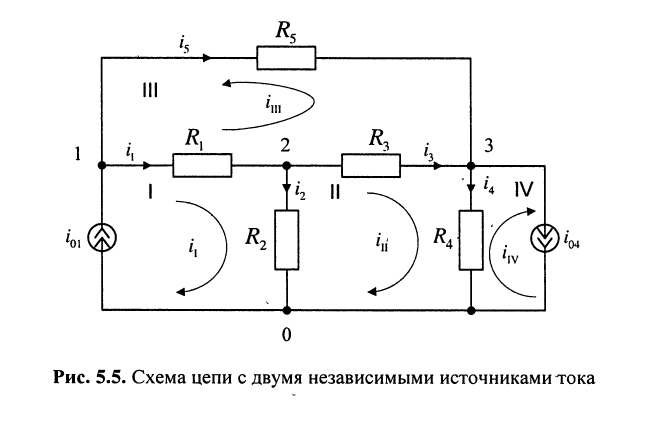
Записать систему контурных уравнений для цепи, схема которой изображена на рис. 5.5.

Решение. Цепь содержит два источника тока: в первом и четвёртом контурах, где контурные токи совпадают с токами источников:

поэтому достаточно записать только два контурных уравнения — для второго и третьего контуров.

В уравнении для третьего контура отсутствует слагаемое, содержащее ток 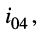поскольку взаимное сопротивление этого контура с четвёртым равно нулю, т. е. между этими контурами нет никакой связи.

Важно:
метод контурных токов применяют в тех случаях, когда число контурных уравнений меньше числа узловых уравнений, а также при анализе колебаний в линейных электрических цепях произвольной конфигурации, содержащих все виды элементов.

Решение системы контурных (узловых) уравнений

Решение системы контурных (узловых) уравнений состоит в нахождении неизвестных контурных токов (узловых напряжений) для последующего вычислением токов и напряжений на элементах цепи. Если параметры цепи (сопротивления, проводимости, токи источников токов, ЭДС источников напряжений) заданы численно, то решение систем осуществляется с помощью специальных пакетов программ математического моделирования, например, Matlab или Matcad.

Основные понятия теории определителей

При теоретическом анализе удобнее использовать методы теории определителей, позволяющие записать решения в компактной форме. Прежде чем обращаться к этим методам, дадим основные понятия теории определителей.

(5.11)

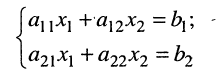
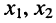
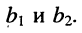
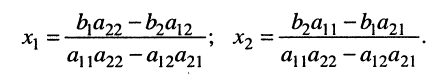
с неизвестными и свободными членами Решая эту систему, получаем:

(5.12)

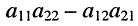
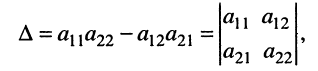
Стоящее в знаменателях полученных дробей выражение называется определителем (детерминантом) второго порядка и записывается в виде

(5.13)

где вертикальные чёрточки являются знаком определителя. С помощью этого обозначения формулы (5.13) можно записать в виде

(5.14)

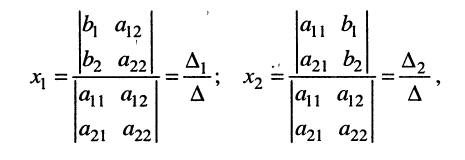
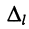
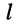
где — определитель, полученный из определителя системы заменой столбца коэффициентов при -ой неизвестной столбцом свободных членов.

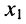
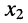
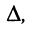
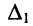
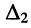
Из соотношений (5.14) следует: каждая из неизвестных и равна дроби, у которой в знаменателе стоит определитель системы а в числителе — определитель и соответственно, полученный из определителя системы подстановкой столбца свободных членов вместо столбца коэффициентов при данной неизвестной.

Подобным образом решается система уравнений любого порядка. Остаётся выяснить, как вычислять определители, если их порядок больше двух.

Рассмотрим вычисление определителя на примере системы третьего порядка:

решение которой приводит к дробям вида (5.12), где в знаменателе оказывается выражение

(5.15)

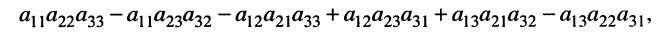
называемое определителем третьего порядка и обозначаемое

(5.16)

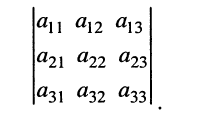
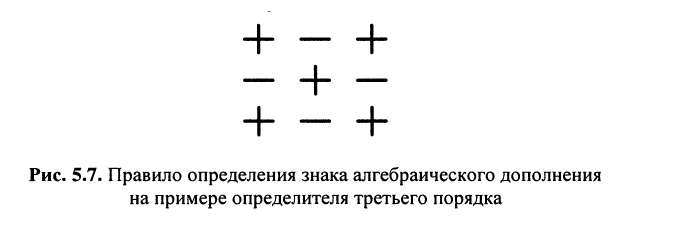
Применяя к (5.16) выражение (5.15), запишем определитель (5.16) в более удобной и наглядной форме:

(5.17)

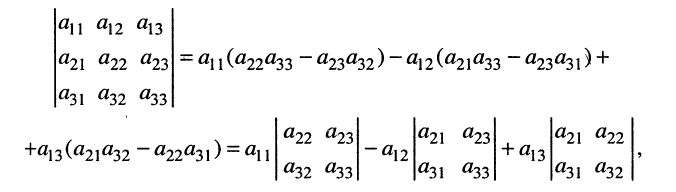
по которой можно вычислять значение определителя третьего порядка. Нетрудно видеть, что правая часть равенства состоит из суммы произведений коэффициентов (элементов) первой строки и определителей второго порядка с нужными знаками. Эти определители называются минорами и получаются из исходного определителя вычёркиванием первой строки и соответствующего данному элементу столбца. 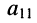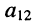Например, минор относительно элемента получается вычёркиванием первой строки и первого столбца (рис. 5.6, а), минор относительно элемента получается вычёркиванием первой строки и первого столбца (рис. 5.6, б). Таким образом, получено разложение определителя третьего порядка по элементам первой строки.

Подобные разложения можно произвести относительно элементов любой строки, предварительно записав соответствующие миноры.

Определение:

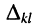
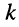
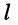
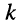
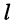
Минором относительно -ой строки и -ro столбца (относительно элемента аи) называется определитель, получаемый из исходного определителя, если в последнем вычеркнуть -ю строку и -ый столбец.

Знак минора определяется по формуле 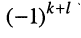или же по мнемоническому правилу: для левого верхнего элемента всегда берётся «+», а для других элементов — в шахматном порядке по схеме, представленной на рис. 5.7.

Определение:

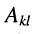
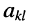
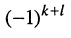
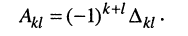
Алгебраическим дополнением относительно к-ой строки и 1-го столбца (относительно элемента ) называется минор, взятый с нужным знаком по правилу , т. е.

(5.18)

Из сказанного следует: определитель равен сумме произведений элементов какого-нибудь из рядов (строки или столбца) на алгебраические дополнения этих элементов.

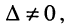
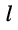
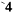
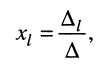
При вычислении определителей больших порядков их предварительно разлагают на алгебраические дополнения. Отметим также, что подобно (5.14) для любой системы, у которой имеет место формула для вычисления -ой неизвестной (формула, или правило Крамера)

(5.19)

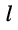
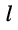
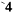
т. е. каждая -ая неизвестная равна дроби, у которой в знаменателе стоит определитель системы, а в числителе — определитель, полученный из определителя системы подстановкой столбца свободных членов вместо столбца коэффициентов при -ой неизвестной.

Габриэль Крамер (1704—1752) — швейцарский математик, заложивший в 1750 г. основы теории определителей.

Применение теории определителей для решения контурных (узловых) уравнений

Применяя методы теории определителей к системе контурных уравнений (5.9), по формуле Крамера находим решение для первого контурного тока

где

(5.20)

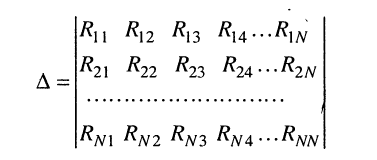
представляет собой определитель системы контурных уравнений (5.9), а

находится из определителя (5.20) при замене в нём первого столбца свободными членами. Заметим, что определитель (5.20) является симметричным относительно главной диагонали, поскольку 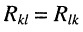при

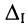
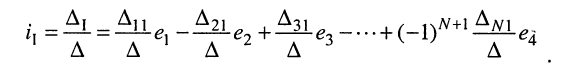
Разлагая определитель на алгебраические дополнения по элементам первого столбца, получаем выражение для первого контурного тока

(5.21)

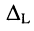
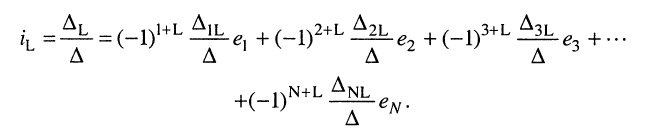
Аналогичное решение можно найти и для L-го контурного тока, разлагая определитель на алгебраические дополнения по элементам 1-го столбца:

(5.22)

Полученное общее решение (5.22) системы контурных уравнений (5.9) показывает, что реакция в виде токов в электрической цепи представляет собой сумму реакций, вызываемых каждым из воздействий 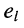в отдельности в предположении, что все другие источники отсутствуют. Этот факт является следствием линейности электрической цепи, описываемой системой линейных уравнений, и составляет содержание принципа наложения.

Аналогичным образом рассчитывается система узловых уравнений (5.2).

Примеры использования теории определителей

Задача 5.1.

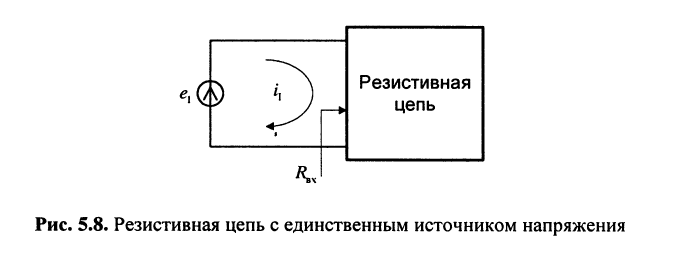
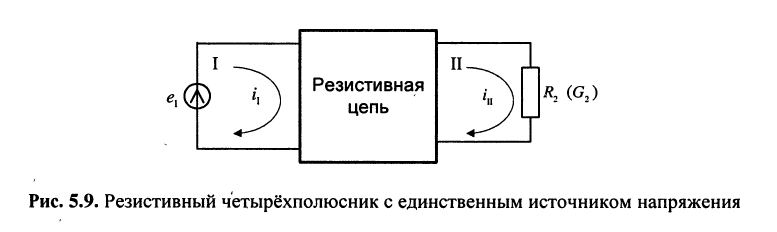
Цепь имеет единственный источник напряжения 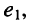по отношению к которому сама цепь представляет собой пассивный резистивный двухполюсник (рис. 5.8). Требуется найти входное сопротивление двухполюсника.

Решение. Для удобства назовём контур, замыкающийся через источник, первым. Тогда из (5.21) следует

(5.23)

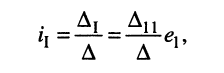
и согласно закону Ома имеем

откуда получаем соотношение

(5.24)

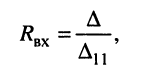
называемое входным сопротивлением двухполюсника. Оно представляет собой эквивалентное сопротивление пассивного резистивного двухполюсника.

Заметим, что в резистивном двухполюснике электрическая энергия может только рассеиваться, поэтому при выбранных на рис. 5.8 направлениях отсчёта тока и напряжения коэффициент 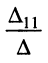в (5.23) представляет собой вещественное положительное число, что справедливо и для (5.24). Следовательно, любой резистивный двухполюсник ведёт себя подобно резистивному элементу, сопротивление которого равно входному сопротивлению двухполюсника.

Задача 5.2.

Найти ток в заданной ветви резистивной цепи (рис. 5.9), имеющей единственный источник напряжения в

Решение. Такую цепь можно рассматривать как резистивный четырёхполюсник, в котором вновь для удобства обозначим контур, содержащий источник напряжения, первым (I), а контур, содержащий интересующую нас ветвь, вторым (II).

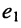
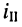
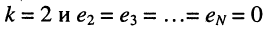
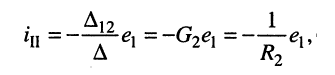
При выбранных направлениях отсчёта ЭДС источника и тока второго контура согласно (5.22) при получаем:

(5.25)

где

представляет собой собственное сопротивление второго контура и потому эквивалентное сопротивление четырёхполюсника.

Метод контурных токов

При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вычисления.

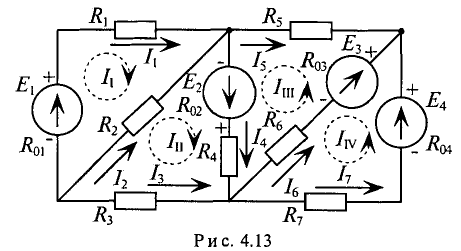
Так, для схемы рис. 4.13 необходимо составить и рассчитать систему из 7-ми уравнений

Ту же задачу можно решить, записав только 4 уравнения по второму закону Кирхгофа, если воспользоваться методом контурных токов.

Суть метода состоит в том, что в схеме выделяют т независимых контуров, в каждом из которых произвольно направлены (см. пунктирные стрелки) контурные токи 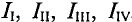. Контурный ток — это расчетная величина, измерить которую невозможно.

Как видно из рис. 4.13, отдельные ветви схемы входят в два смежных контура. Действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров.

Таким образом

Для определения контурных токов составляют т уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторону от знака равенства), и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).

Для данной схемы (рис. 4.13) необходимо составить 4 уравнений. Со знаком «плюс» записываются ЭДС и падения напряжено разные стороны знака равенства), действующие в направлении контурного тока, со знаком «минус» — направленные проконтурного тока.

Система уравнений для схемы (рис. 4.13):

Решением системы уравнений вычисляются значения контур-токов, которые и определяют действительные токи в каждой и схемы (рис. 4.13).

Пример 4.11

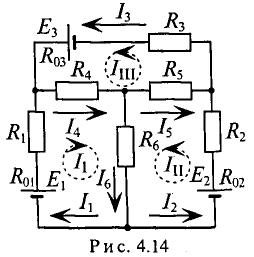
Определить токи во всех участках сложной цепи (рис. 4.14), если:

Решение

Необходимо составить 3 уравнения по второму закону для определения контурных токов 1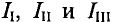 (направление урных токов выбрано произвольно указано пунктирными линиями).

Подставляются числовые значения величин

Из уравнения (2) определяется ток

Значение тока 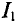(выражение (2′)) подставляется в уравнение (1):

То же значение тока 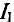подставляется в уравнение (3):

Из полученного уравнения (3) вычитается полученное уравнение (1). В результате получим

Откуда контурный ток

Из уравнения (3) определяется контурный ток

Из уравнения (2′) определяется ток

Вычисляются реальные токи в заданной цепи:

Проверяется правильность решения для 1 -го контура (рис. 4.14).

Решение правильное.

Такую же проверку можно произвести и для других контуров (2-го и 3-го):

Проверка показала правильность решения.

Определение метода контурных токов

Данный метод является фундаментальным и применим для расчета любых электрических цепей. Он базируется на уравнениях, составленных по второму закону Кирхгофа. В схеме выделяются независимые контуры, в каждом из них произвольно выбираются направления контурных токов и составляются уравнения по второму закону Кирхгофа. Для цепи по рис. 3.1 имеем:

Введем в полученную систему уравнений обобщенные параметры:

собственное сопротивление контура — сумма сопротивлений, входящих в состав контура, например, для первого контура:

смежные сопротивления — сопротивления на границах контуров, например, 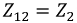сопротивление на границе первого и второго контуров, суммарная ЭДС, например, для первого контура:

Тогда система уравнений примет вид:

Используя матричный метод расчета, можем записать:

В уравнении (3.8) — главный определитель системы (3.7a), a — алгебраическое дополнение для соответствующей контурной ЭДС. В ветвях, которые не граничат с другими контурами, реальные токи будут:

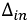
Токи ветвей, находящихся на границах контуров:

Справочный материал по методу контурных токов

Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурное токи, замыкающиеся в контурах.

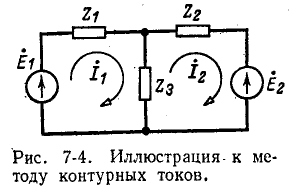
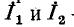
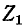
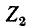
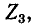
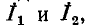
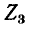
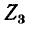
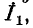
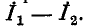
На рис. 7-4 в виде примера показана двухконтурная электрическая цепь, в которой — контурные токи. Токи в сопротивлениях и равны соответствующим контурным токам; ток в сопротивлении являющемся общим для обоих контуров, равен разности контурных токов так как эти токи направлены в ветви встречно*. При этом если положительное направление искомого тока в ветви принять совпадающим с направлением контурного тока то ток в ветви будет равен В противном случае он будет равен

Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, т. е. для электрической схемы с числом узлов q и числом ветвей р задача нахождения контурных токов сведется к решению системы р — q + I уравнений. Так, в схеме рис. 7-4 q = 2, р = 3; следовательно, число уравнений равно 3 — 2+1=2 (число независимых контуров).

Следует отметить, что если положительное направление одного из контурных токов изменить на обратное, то ток в ветви будет равен сумме этих токов.

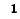
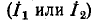
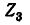
Условимся сумму комплексных сопротивлений, входящих в контур, называть собственным сопротивлением контура, а комплексное сопротивление, принадлежащее одновременно двум или нескольким контурам, — общим сопротивлением этих контуров.

Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от данного контурного тока в собственном сопротивлении контура берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис. 7-4, где направление обоих контурных токов выбрано по ходу часовой стрелки.

Для заданной электрической схемы с двумя независимыми контурами (рис. 7-4) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:,

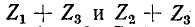
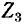
где — собственные сопротивления контуров 1 и 2; — общее сопротивление контуров 1 и 2 (знак минус в уравнениях обусловлен выбором положительных направлений контурных токов).

Если заданная электрическая схема содержит п независимых контуров, то на основании второго закона Кирхгофа получается система из п уравнений:

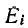
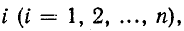
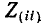
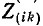
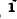
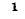
Здесь — контурная э. д. с. в контуре т. е. алгебраическая сумма э. д. с., действующих в данном контуре; э. д. с., совпадающие по направлению с направлением обхода, берутся со знаком плюс, а направленные встречно — со знаком минус;

— собственное сопротивление контура i;

— общее сопротивление контуров i и k.

Индексы собственных и общих сопротивлений контуров заключены в скобки для отличия их от входных и передаточных сопротивлений, приводимых в последующих разделах книги.

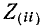
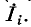
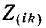
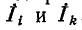
В соответствии со сказанным ранее собственные сопротивления войдут со знаком плюс, поскольку обход, контура принимается совпадающим с положительным направлением контурного тока Общие сопротивления войдут со знаком минус, когда токи направлены в них встречно.

Решение уравнений (7-2) относительно искомых контурных токов может быть найдено с помощью определителей:

ит. д., где определитель системы

Согласно правилу разложения определителя по элементам столбца определитель равен сумме произведений элементов столбца на их алгебраические дополнения. Поэтому решение уравнений запишется в виде

Определитель снабжен индексом z, так как его элементами являются комплексные сопротивления.

На практике во многих случаях решение системы уравнений (7-2) может быть выполнено более просто последовательным исключением неизвестных,

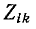
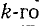
Здесь Дitl — алгебраическое дополнение элемента Z{lk) определителя системы, т. е. умноженный на (—1)‘+* минор элемента (минор образуется из определителя системы исключением из него i-й строки и столбца).

Сокращенно система уравнений (7-3) записывается в виде:

Первый индекс алгебраического дополнения i, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру контура, контурная э. д. с. которого умножается на данное алгебраическое дополнение. Второй индекс 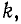обозначающий номер столбца, вычеркиваемого в определителе системы, соответствует номеру контура, для которого вычисляется контурный ток.

Уравнения (7-2), выражающие второй закон Кирхгофа, записаны в предположении, что источниками электрической энергии служат источники э. д. с. При наличии в электрической схеме источников тока они могут быть заменены эквивалентными источниками э. д. с.

Если проводимости источников тока равны нулю, то целесообразно выбрать заданные токи в качестве контурных; тогда число неизвестных контурных токов и соответственно число уравнений сократятся на число заданных токов.

Если в заданной электрической схеме имеются параллельные ветви, то замена их эквивалентным комплексным сопротивлением сокращает число контуров (за счет тех, которые образованы параллельными ветвями).

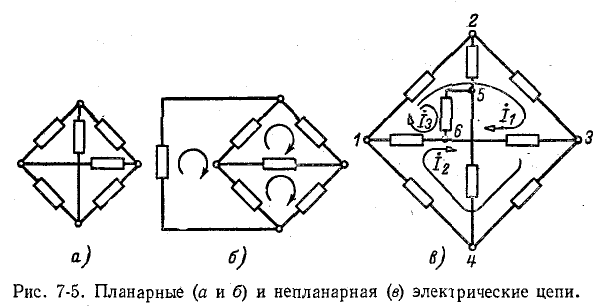
Электрические цепи могут быть планарными или непланарными.

Планарная, или плоская, электрическая цепь может быть вычерчена на плоскости в виде схемы с непере-крещивающимися ветвями. В некоторых случаях пересечение ветвей в электрической схеме, являющееся результатом Принятого способа начертания схемы, устраняется при другом способе изображения данной планарной электрической цепи, как это, например, представлено на рис. 7-5.

Электрическая цепь, приведенная на рис. 7-5, а, планарна, так как имеющееся пересечение ветвей устранимо в соответствии с рис. 7-5, б.

Не планарная электрическая цепь не может быть вычерчена на плоскости в виде схемы с неперекрещиваю-щимися ветвями. Примером такой электрической цепи служит приведенная на рис. 7-5, в непланарная цепь, пересечение ветвей в которой не может быть устранено.

Если направление контурных токов во всех контурах планарной электрической цепи одинаково, например совпадает с ходом часовой стрелки, то общие сопротивления смежных контуров входят в систему уравнений (7-2) со знаком минус, так как контурные токи смежных контуров

направлены в общих ветвях встречно. Направление контурных токов по ходу часовой стрелки принимается во всех контурах, кроме внешнего, охватывающего всю схему. В последнем контурный ток направляется против часовой стрелки'(см. пример 7-2). Это правило, однако, не является обязательным.

В случае непланарной электрической цепи не представляется возможным иметь в общих ветвях только разности контурных токов, как это, например, видно из схемы рис. 7-5, в.

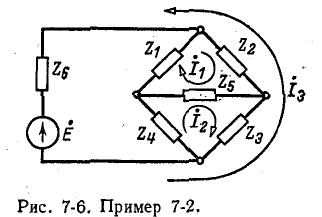
Пример 7-2.

Пользуясь методом контурных токов, определить ток в диагонали бюстовой схемы рис. 7-6.

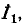
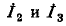
Выбранные положительные направления контурных токов указаны на схеме стрелками. Число уравнений, записываемых по второму закону Кирхгофа, равно трем (по числу независимых контуров):

Решение полученной системы уравнений относительно контурных токов 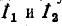дает:

где М имеет то же значение, что и в примере 7-1.

Искомый ток в диагонали мостовой схемы равен разности контурных токов:

что совпадает с полученным в примере 7-1 ответом.

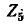
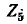
Следует заметить, что если в заданной схеме контуры выбрать так, чтобы через ветвь проходил только один контурный ток, то искомый ток в ветви будет равен именно Рис. 7-6. Пример 7-2. этому контурному току, т, е.

задача сведется к нахождению только одного контурного тока (вместо двух).

Метод свертывания электрической цепи
Метод преобразования схем электрических цепей
Параллельное соединение генераторов
Метод узловых и контурных уравнений
Метод узловых потенциалов
Принцип и метод наложения
Входные и взаимные проводимости
Преобразование треугольника сопротивлений в эквивалентную звезду

Источник

Применяется
для упрощения расчёта сложных схем.

Контурный
ток – это некоторая расчётная величина,
которая одинакова для ветвей данного
контура.

ис.
16.

Контурные
токи: I_I
и I_II

Контурный
ток равен действительному току ветви,
которая принадлежит только одному
контуру.

Рис. 16

сли ветвь относиться к 2-м смежным
контурам, то ток в них равен алгебраической
сумме контурных токов тех

контуров,
в которые эта ветвь входит.

Сопротивления
ветвей, входящих в данный контур,
называются собственными сопротивлениями
контуров.

Сопротивления
ветвей, входящих в два смежных контура,
называют общими сопротивлениями
контуров.

Алгоритм
расчёта:

1. В
заданной схеме выбираем произвольно
направление токов в ветвях.

2.
Намечаем независимые контура и для них
выбираем направление контурных токов,
например по часовой стрелке.

3.
Определяем контурные ЭДС, собственные
и общие сопротивления контуров, обходя
контуры в направлении контурных токов.
Выбираем действительные токи ветвей
через контурные (см. выше).

4.
Составляем уравнения по второму закону
Кирхгофа. В левой части их слагаемые с
собственными сопротивлениями контуров
берут со знаком плюс, а слагаемые с
общими сопротивлениями – со знаком
минус.

5.
Полученные уравнения объединяем в
систему и решаем любым способом, известным
из математики.

6. Затем
найдём действительные токи, выраженные
через контурные.

7.
Выполним проверку по первому закону
Кирхгофа для любого узла и составим
баланс мощностей.

ример.

Рис. 17.

Определить
токи во всех ветвях схемы рис. 17, если
Е₁=Е₃=120 В; Е₂=60 В;
R₁=R₂=R₃=10
Ом; R₄=R₅=10
Ом.

Решение:

1.
Разобьём схему на три контура: I₁,
I₂, I₃.

2. Получим
три контурных тока, направленных по
часовой стрелке: I₁,
I₂, I₃.

3. Выразим
действительные токи ветвей через
контурные:

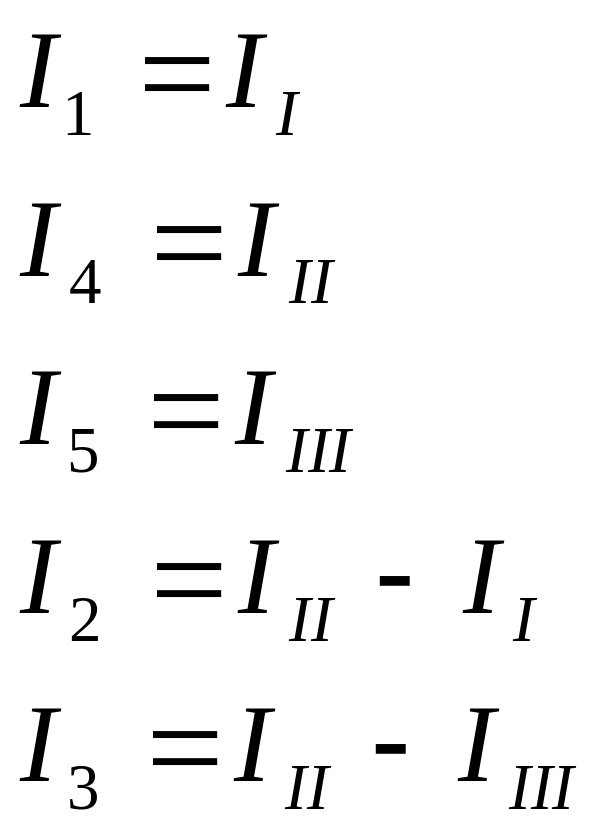
4.
Составим уравнение по второму закону
Кирхгофа.

Решив
полученную систему уравнений, определим
контурные токи:

5. В
схеме пять ветвей, следовательно пять
токов I₁, I₂,
I₃, I₄,
I₅.

6.
Определим действительные токи внешних
ветвей:

7. Токи
внутренних ветвей:

Знак
«–» означат, что действительный ток I₅
направлен обратно указанному на схеме.

2.3 Метод наложения (суперпозиция) токов

Этот
метод можно применять для определения
токов в цепи, в которой одновременно
действуют несколько ЭДС. Этот метод
основан на принципе наложения и применим
только для линейных цепей.

Сущность
принципа наложения заключается в том,
что ток в любой ветви цепи с постоянными
сопротивлениями равен алгебраической
сумме частичных токов, создаваемых в
этой ветви каждой из ЭДС в отдельности.

Алгоритм
расчёта:

1.
Определим количество токов в цепи.
Выбираем условно направление тока в
каждой ветви.

а)
Предложим, что в цепи действует только
одна какая–либо ЭДС.

б) Все
остальные ЭДС приравниваем к нулю.

в) Все
сопротивления оставляем неизменённым,
включая внутреннее сопротивления всех
источников.

г)
Получим цепь с последовательно–параллельным
соединением сопротивлений.

д) Для
такой схемы находим токораспределение.
Указываем на схеме направления токов,
вызванных действием только одной ЭДС.
Это так называемые частичные токи.
Обозначают их с одним штрихом: I’.

е) Зная
сопротивления участков и ЭДС источника,
используя закон Ома и соотношения
величин при последовательном и
параллельном соединении резисторов,
определим значение частичных токов от
одного источника ЭДС.

3.
Аналогично полагаем, что в цепи действует
вторая ЭДС, а все остальные не действуют.
Повторяем расчёт частичных токов от
действия второго источника, их обозначают
с двумя штрихами: I″.

4.
Аналогично производим расчёты поочерёдно
для всех ЭДС схемы.

5.
Определяем действительные значения
токов в каждой ветви по принципу наложения
токов, то есть, алгебраически сложив
частичные токи, определяем действительные
значения токов на каждом участке сложной
цепи, когда все ЭДС действуют одновременно.

Правило
алгебраического сложения токов:

Знак,
который ставится перед частичным током
при алгебраическом сложении, зависит
от того, совпадает ли направление этого
тока с выбранным направлением
действительного тока в ветви или
противоположно ему. Если совпадает, то
знак «+», если противоположно, то знак
«–».

Пример:

Дано:
(Рис18) R₁=R₃=2
Ом; R₂=1,6 Ом; E₁=3,6
В; E₂=4,8 В; r₀₁=r₀₂=0,5
Ом.

Найти:
все токи.

Решение
задачи:

1.
Применение метода наложения к цепи на
рис.18.

Разветвление
цепи с несколькими источниками энергии,
включенными в разные ветви, к числу
которых относится и цепь на рис. 18,
являются сложными цепями. Для таких
сложных электрических цепей существует
ряд методов, один из которых (метод
наложения) рассматривается в этом
параграфе, а другие методы в следующих
параграфах.

По
методу наложения ток в любом участке
цепи рассматривается как алгебраическая
сумма частичных токов, созданных каждой
ЭДС в отдельности. В нашем случае следует:

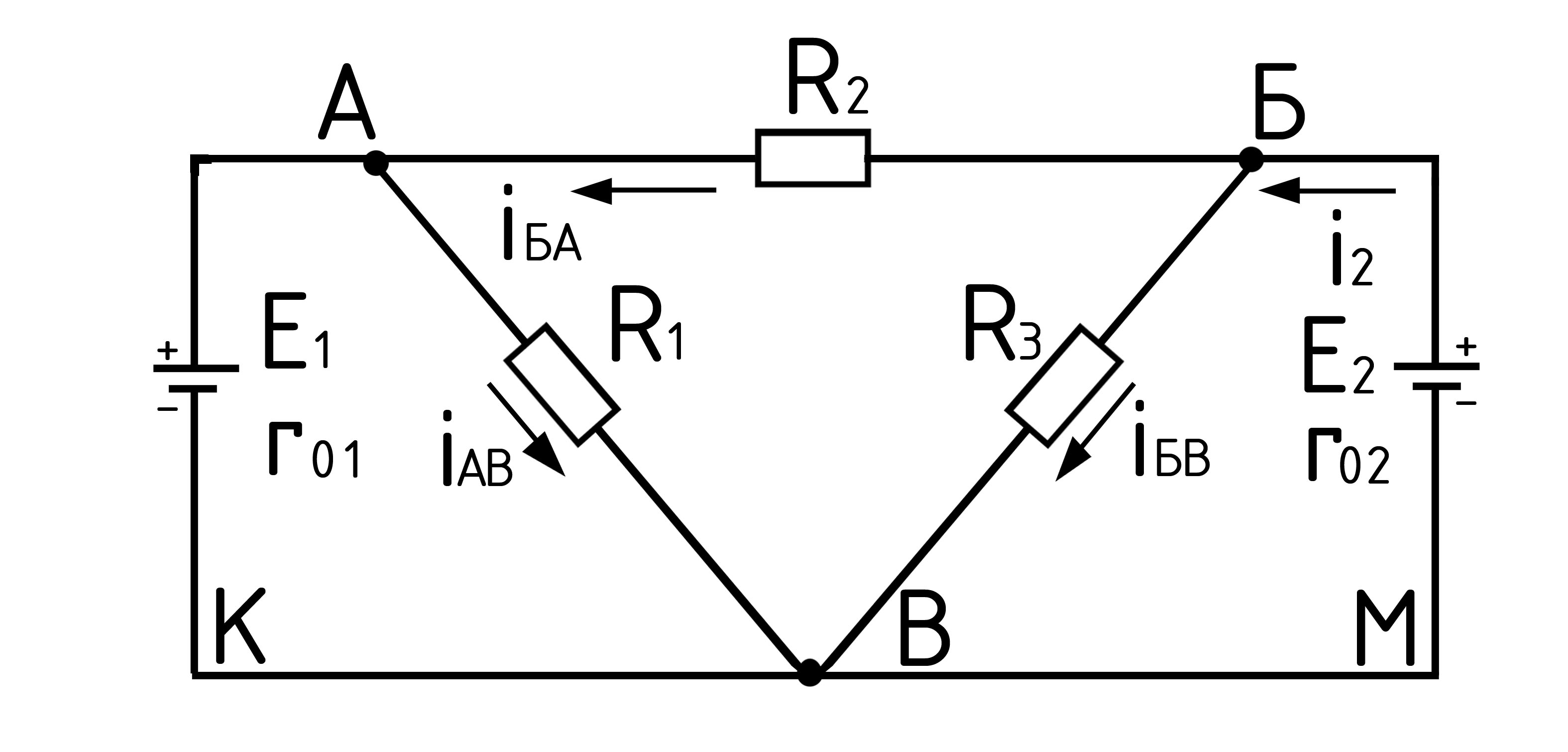
Рис. 18.

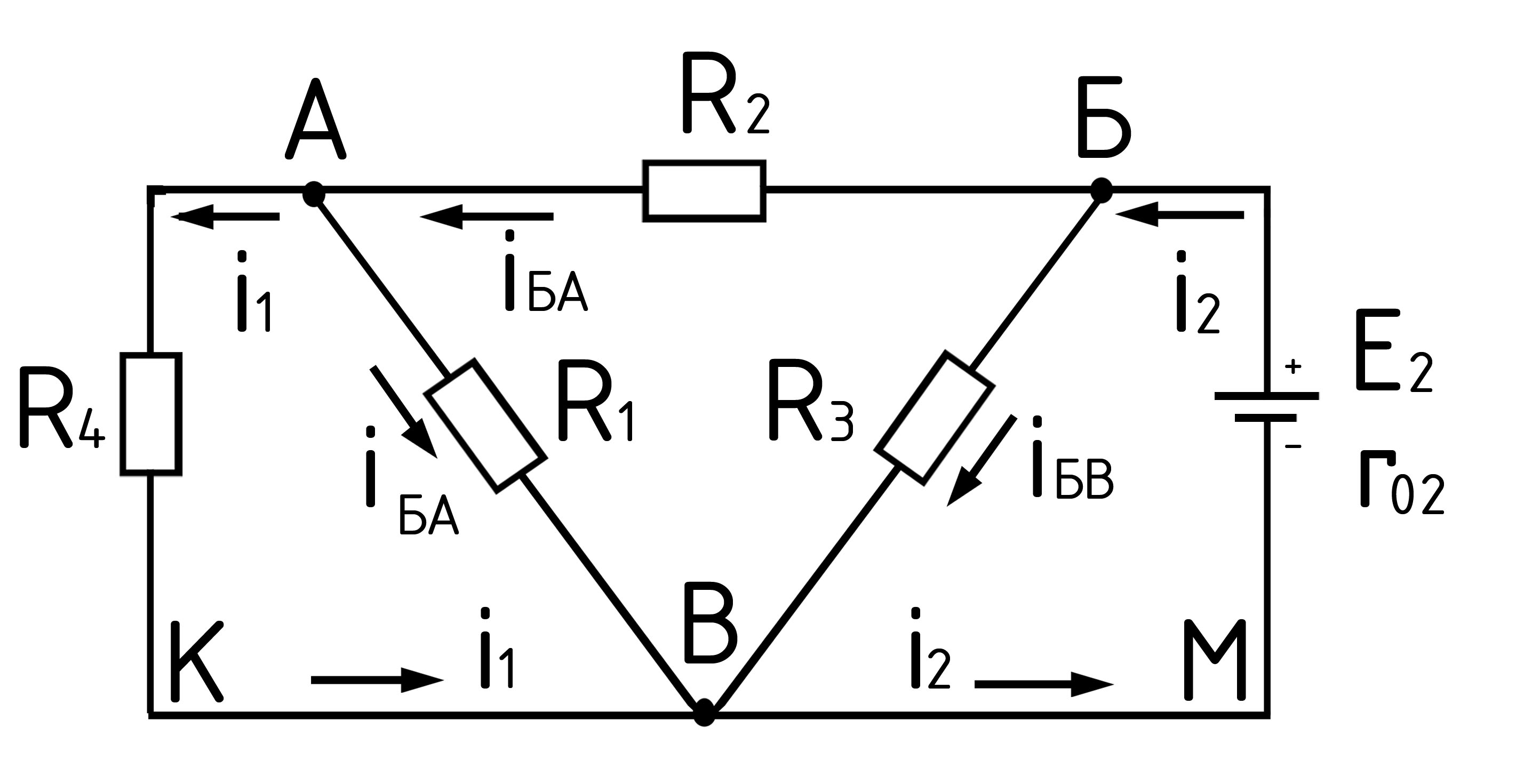
Рис. 19.

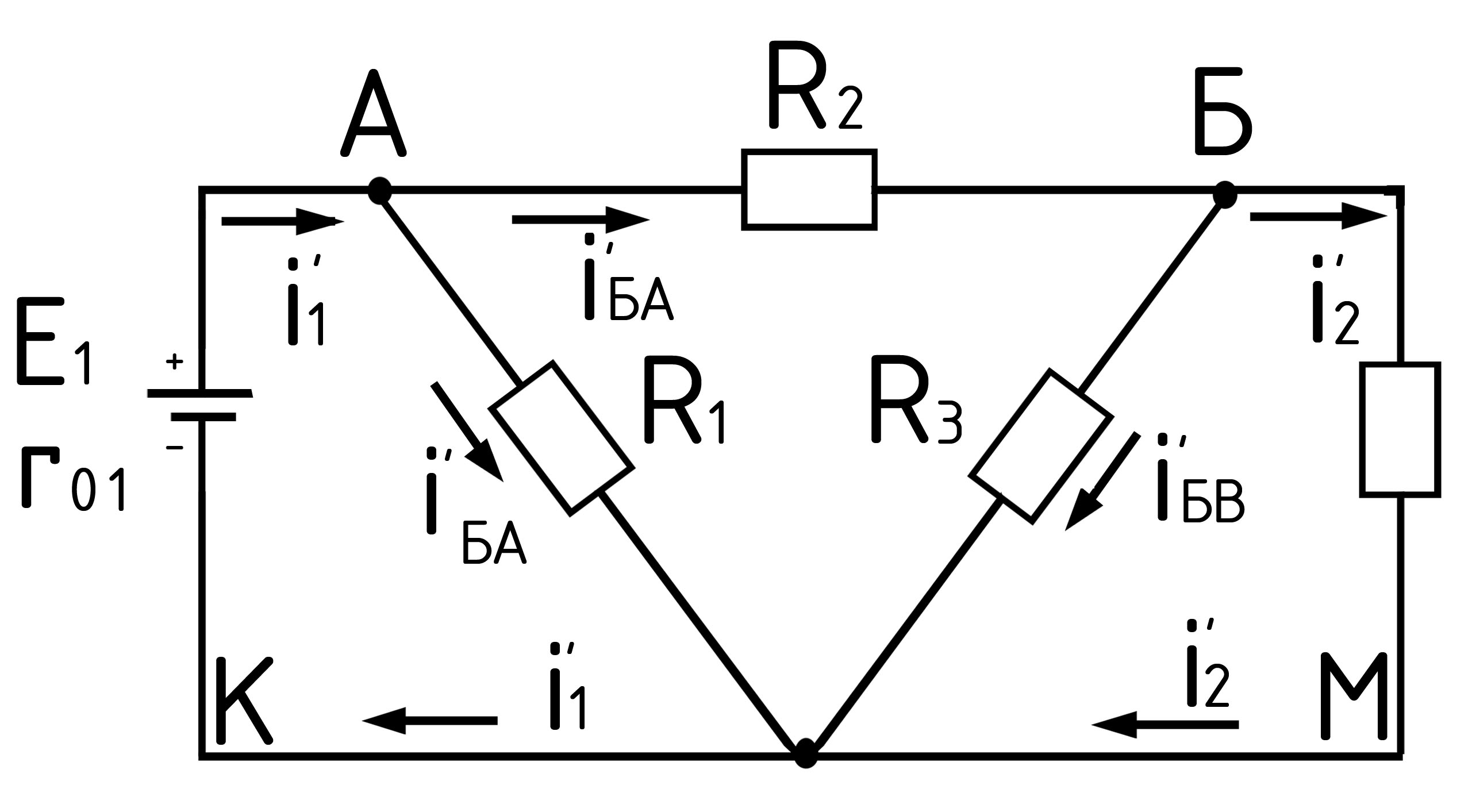
Рис. 20.

во-первых, определить частичные токи
от ЭДС Е₁при отсутствии
ЭДС Е₂, т.е. рассчитать простую
цепь по рис. 19; во-вторых найти частичные
токи от ЭДС Е₂ при отсутствии
ЭДС Е₁, т.е. рассчитать простую
цепь по рис. 20; в-третьих, алгебраически
сложить частичные токи двух последних
схем.

Итак,
метод наложения позволяет заменить
расчёт одной сложной цепи с несколькими
источниками энергии (рис. 18) расчётом
нескольких в данном случае двух) цепей
с одним источником энергии в каждой.

2.
Обозначение частичных токов. Все
частичные токи от ЭДС Е₁ (рис. 19.)
обозначим буквой I с одним
штрихом, а все частичные токи от ЭДС Е₂
(рис. 20.) – с двумя штрихами.

3.
Вычисление частичных токов. Для цепи с
ЭДС Е₁ (рис. 19.) рассчитаем сначала
общее сопротивление. Сопротивление
участка БВ

Ом.

Оно
соединено последовательно с сопротивлением
R₂, поэтому

Ом.

Два
одинаковых сопротивления R’_АБВ
R₁ соединены
параллельно, поэтому общее сопротивление
всей внешней цепи

Ток
источника

разветвляется
в узловой точке А на два одинаковых
тока:

Ток
I’_АБ разветвляется
в узловой точке Б на токи:

Для
цепи с ЭДС E₂ (рис.20
):

так как
R₃=R″_БАВ.

В ветви
источника с ЭДС E₂
ток

Поскольку
R″_БАВ=R₃=2,0
Ом, то ток

Токи в
параллельных ветвях участка АВ:

4.
Вычисление токов в цепи на рис. 20. Выполним
алгебраическое сложение частичных
токов.

На
участке ВКА частичный ток I’₁
(рис. 19 ) направлен от узла В к узлу А, а
частичный ток I″₁
(рис. 20 ) – от А к В, т.е. навстречу первому.
Поэтому суммарный ток

Направление
тока I₁ (рис. 19.)
совпадает с направлением большего
частичного тока, т.е. тока I’₁.

Аналогичным
образом определяем I_БА
и I₂:

Направления
токов I_БА и I₂
(рис.20 ) совпадают с направлениями токов
I″_БА и I″₂
соответственно.

В ветви
АВ оба частичных тока (I’_АБ
и I″_АБ) совпадают
по направлению, поэтому

Аналогично

5.
Вычисление напряжений. Напряжения между
узловыми точками:

6.
Проверка результатов вычислений. Для
проверки расчётов составим уравнение
по законам Кирхгофа.

Для
узла А:

; действительно, 1,52=1,12+0,4.

Для
узла Б:

; действительно, 2,24=0,4+1,84.

Для
контура АВБ:

;
действительно, +3,04-3,68+0,64=0 (обходим против
направления движения стрелки часов).

*Дополнительные
вопросы к задаче

1. Как
применяется метод наложения для расчёта
цепей. содержащих более двух источников?

если
сложная цепь содержит, например три
источника ЭДС Е₁, Е₂ и Е₃,
включенных в разные ветви, то следует
составить три схемы для расчёта частичных
токов: одна схема будет содержать только
ЭДС Е₂, а третья – только ЭДС Е₃.

Рассчитав
в трёх схемах частичные токи и алгебраически
сложив их, получим токи заданной цепи.

2. В
каких случаях для расчёта сложной цепи
целесообразно применять метод наложения?

Наиболее
трудоёмкой частью в расчётах по методу
наложения является вычисление частичных
токов. Поэтому его применяют при небольшом
числе источников – при двух, иногда
трёх.

Этот
метод удобен также в тех случаях, когда
не нужен полный расчёт цепи, а требуется
найти, например, только токи в участках
с источниками.

3. В
каких случаях расчёт токов методом
наложения может привести к большим
погрешностям в результатах?

Если
результирующий ток ветви выражается
разностью двух близких величин, то
незначительная относительная погрешность
в определении слагаемых (частичных
токов) может привести к весьма большой
относительной погрешности результата
(действительного тока ветви). В таких
случаях метод наложения применять
нецелесообразно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В каждой электрической цепи имеются так называемые Р – ребра (они же ветви, звенья, участки) и У – узлы. Для ее описания существует система уравнений, в которых используются два правила Кирхгофа. В них, в качестве независимых переменных, выступают токи ребер. Поэтому количество независимых переменных будет равно количеству уравнений, что дает возможность нормального разрешения данной системы. На практике используются методы, направленные на сокращение числа уравнений. Среди них очень часто используется метод контурных токов, позволяющий выполнять расчеты и получать точные результаты.

Основные понятия

Контурный ток — это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I11, I22 и тд.

Контурная ЭДС — это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Суть метода контурных токов

Основные принципы данного метода основываются на том факте, что протекающие в ребрах цепи токи, не все считаются независимыми. Присутствующие в системе У-1 уравнения для узлов, четко показывают зависимость от них У-1 токов. При выделении в электрической цепи независимого тока Р-У+1, вся система может быть сокращена до уравнений Р-У+1. Таким образом, метод контурных токов представляет собой очень простое и удобное выделение в цепи независимых токов Р-У+1.

Использование данного способа расчетов допускает, что в каждом независимом контуре Р-У+1 осуществляется циркуляция определенного виртуального контурного тока. Если какое-либо ребро относится лишь к одному конкретному контуру, то значение протекающего в нем реального тока будет равно контурному. В том случае, когда ребро входит в состав сразу нескольких контуров, ток, протекающий в нем, будет представлять собой сумму, включающую в себя соответствующие контурные токи. В этом случае обязательно учитывается направление обхода контуров. Независимыми контурами перекрывается практически вся схема, поэтому ток, протекающий в каком угодно ребре может быть выражен путем контурных токов, составляющих полную систему всех токов.

Закон Кирхгофа – расчет и применение

Для того чтобы построить систему независимых контуров, используется простой и наглядный метод создания планарных графов. На данной схеме ветви и узлы цепи размещаются на плоскости таким образом, что взаимное пересечение ребер полностью исключается. С помощью этого метода плоскость разбивается на области, ограниченные замкнутыми цепочками ребер. Именно они и составляют систему независимых контуров. Данный метод более всего подходит для ручных расчетов схем. Однако его применение может стать затруднительным или вовсе невозможным, если рассматриваемая схема не укладывается в рамки планарного графа.

Как определить токи в ветвях цепи

Решение

Рассчитать токи во всех участках цепи легче всего методом постепенного свертывания цепи,

т.е. упрощения электрической цепи.

Резисторы R2 и R3 соединены параллельно: R23 =

Резисторы R1, R23, R4 cоединены последовательно. Эквивалентное сопротивление всей

цепи равно сумме этих сопротивлений:

Ток в неразветвленных участках цепи :

I = I1 = U / RЭ = 120 / 80 =1,5 A

4. Напряжение между узлами сопротивлений R2 и R3 :

U23 = I × R23 = 1,5 × 12 = 18 B

5. Ток в цепи с резистором R2 :

6. Ток в цепи с резистором R3 :

7. Ток в цепи с резистором R4 равен току в неразветвленной части цепи, т.к. R1 , R23 и R4

соединены последовательно: I4 = I1 = 1,5 A.

8. Напряжение на резисторе сопротивлением R1:

Напряжение на резисторе цепи сопротивлением R4 :

По закону сохранению энергии мощность, отдаваемая источниками, должна равняться мощности, рассеиваемой на всех сопротивлениях цепи.

Выражение баланса мощностей имеет вид : Σ РИ = Σ РН, где Σ РИ – алгебраическая сумма мощностей, отдаваемых источниками; Σ РН – арифметическая сумма мощностей, потребляемых в сопротивлениях цепи.

РИ = U×I = 120 × 1,5 = 180 Вт ; Р1 = U1× I = 90 × 1,5 = 135 Вт ;

Р23 = U23 × I = 18 × 1,5 = 27 Вт ; Р4 = U4 × I = 12 × 1,5 = 18 Вт

180 Вт = 135 + 27 + 18 = 180 Вт

Задание для Задачи 1.

определить эквивалентное сопротивление цепи, токи в неразветвлённых участках и в ветвях цепи, напряжения на резисторах цепи. Составить баланс мощностей

2. Расчёт сложных цепей методом узловых и контурных уравнений

Пример расчёта методом узловых и контурных уравнений (по правилам Кирхгофа).

Задача. Рассчитать токи в цепи, представленной на рисунке, если Е1 = 48 В, Е2 = 36 В,

1. Определяем количество ветвей цепи : три ветви.

2. Произвольно задаемся положительными направлениями токов в ветвях (указываем на схеме стрелками) и направлениями обходов в контурах ( по часовой стрелке).

3. Определяем количество уравнений, составленных по 1 и 2 правилам Кирхгофа (число уравнений равно числу неизвестных токов в цепи): m = 3 (три уравнения )

4. Определяем число независимых уравнений, составляемых по первому правилу Кирхгофа: (n −1) уравнений, где n − количество узлов в цепи (два); n −1 = 2 − 1 = 1.

5. Определяем число уравнений, составленных по второму правилу Кирхгофа : m − (n − 1) = 3 − (2 − 1) = 3 − 2 + 1 = 2 .

6. Составляем систему уравнений : 7. Подставляем числовые значения:

8. Приведем уравнения к нормальному виду : 9. Вторую и третью строку сократим :

10. Решаем данную систему способом подстановки ( можно решать различными способами) :

откуда 70 I1 = 31,5 I1 = 31,5 / 70 = 0,45 A; I1 = 0,45 A

11. Подставим значение тока I1 в уравнение 10 I1 − 10 I2 = 3 и определим ток второй ветви :

I2 = (10 ∙ 0,45 −3) / 10 = 0,15 A ; I2 = 0,15 A

12. Подставим значения токов I1 и I2 в уравнение I1 + I2 = I3 , определим ток третьей ветви :

13. Поскольку все токи получились положительными, направления всех действительных токов совпадают с

направлениями токов предполагаемых.

Задание для Задачи 2.

Определить токи в ветвях сложной цепи.

Вариант 1

3. РАСЧЁТ потенциалов точек ЭЛЕКТРИЧЕСКой ЦЕПи ПОСТОЯННОГО ТОКА

Расчет потенциалов точек электрической цепи. Потенциальная диаграмма.

Задача.Рассчитать потенциалы точек и построить потенциальную диаграмму для цепи, показанной на рисунке, если Е1 = 36 В, R01 = 6 Ом, Е2 = 12 В, R02 = 3 Ом, R1 = 20 Ом, R2 = 14 Ом, R3 = 5 Ом.

1. Определяем величину тока в цепи :

Ток будет направлен по направлению Е1, т.к. Е1> Е2, т.е. по часовой стрелке.

2. Примем потенциал точки Аза нулевой φА = 0 ( принять за начальный потенциал можно потенциал

любой точки, разность потенциалов от этого не изменится.)

3. Поскольку действительный ток в цепи течет по часовой стрелке, т.е. от точки А к точке В потенциал

точки А больше потенциала точки В на величину падения напряжения на сопротивлении R1:

4. Определяем потенциал точки С цепи:

5. Определяем потенциал точки D цепи :

у источника потенциал зажима D больше потенциала зажима С ( + > − ) :

6. Определяем потенциал точки E :

φD− φE=UDE= I R2; откуда φE = φD − I R2 = 23 − 0,5∙ 14 = 23 − 7 = 16 В

7. Определяем потенциал точки F :

φE − φF = E2 ; откуда φF = φE − E2 = 16 − 12 = 4 В

8. Определяем потенциал точки Q :

φF − φQ=UFQ = I R02; откуда φQ = φF − I R02 = 4 − 0,5∙ 3 = 4 − 1,5 = 2,5 В

7. Определяем потенциал точки M :

φQ− φM = UQM = I R3; откуда φM = φQ − I R3 = 2,5 − 0,5∙ 5 = 2,5 − 2,5 = 0 В

Разумеется, потенциалы точек А и М равны 0, поскольку обе точки являются однопотенциальными

8. Построение потенциальной диаграммы.

По горизонтальной оси откладываются сопротивления цепи с указанием точек, причем сопротивления откладываются не от начала координат, а складываются, т.к. сопротивления в цепи соединены последовательно. Например, для точки В, еще через 6 Ом − точка С ( R01 = 6 Ом ). Поскольку между точками С и D включен идеальный источник( внутреннее сопротивление его вынесено между точками В и С) , сопротивление между ними равно нулю, следовательно по сопротивлениям С и D − одна точка , а по потенциалам − это совершенно различные точки, поскольку между ними находится Е1.

Аналогичным образом откладываются остальные точки цепи. По вертикали откладываются потенциалы точек. Цепь состоит из линейных элементов, поэтому точки соединяются прямыми линиями С помощью потенциальной диаграммы можно определить ток, протекающий в любом сопротивлении цепи :

I = ΔU / R. Чем круче идут линии графика, тем больший ток протекает по данному сопротивлению.

Задача 05

Определить токи во всех ветвях и напряжения Uab

Задача 06

Определить токи во всех ветвях и напряжения в точках a, b, c, при условии, что вывод «–» источника ЭДС заземлён

Задача 07

Определить токи I1, I2, I3 в ветвях пользуясь законами Кирхгофа, если

U=20 B, E2=100 B, R1=R3=10 Om, R2=20 Om

Задача 08

Определить величину и направление напряжения U , при котором ток i2 будет равен нулю, если E2=100 B, R1=R3=10 Oм, R2=20 Oм. Чему, при этом, будут равны значения токов i1 и i3?

Задача 09

Как изменится значение токов i1, i2, i3 в этой схеме (задача 08, E2=100 B, R1=R3=10 Oм, i2=0, R2=20 Oм.), если R2 уменьшится в 10 раз?

Задача 10

Как изменится значение токов i1, i2, i3 в этой схеме (задача 08, E2=100 B, R1=R3=10 Oм, i2=0, R2=20 Oм.), если один вывод R2 оторвётся от схемы?

Задача 11а(вар. 1-36)

Для данной схемы определить потенциалы всех точек (a, b, c, d, e, f, g, h, i) при разомкнутом ключе. Напряжение Е и внутренние сопротивления r

источников ЭДС , а также спротивления
R
в цепи взять из варианта задания. Обратить внимание на знаки ЭДС – при положительном знаке ЭДС они соответствуют приведенным на рисунке.

Задача 11б(вар. 1-36)

Для этой же схемы определить потенциалы всех точек (a, b, c, d, e, f, g, h, i) при замкнутом ключе. Напряжение Е и внутренние сопротивления r

источников ЭДС , а также спротивления
R
в цепи взять из того же варианта задания.

Ответы в обоих задачах приводить в виде таблицы, приведенной ниже.

Преподавателю сообщить (по каждой задаче) только одно число – Сумму (алгебраическую) всех потенциалов с точностью до 1 десятичного знака после запятой.

Задача 11с(вар. 1-36)

Определить, при замкнутом ключе, потенциал какой точки (номер позиции) следует приравнять нулю, чтобы потенциалы всех остальных указанных точек были положительными.

Варианты задачи 11

Источник