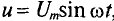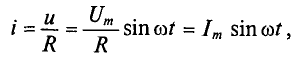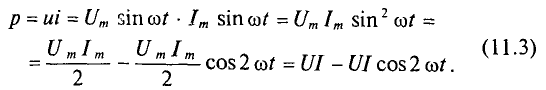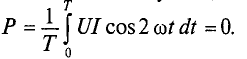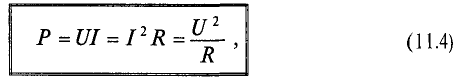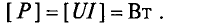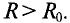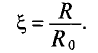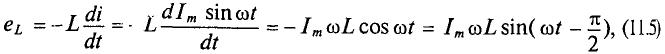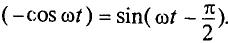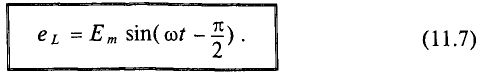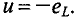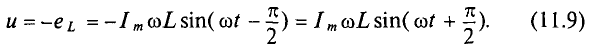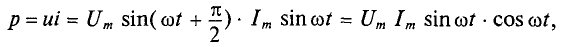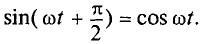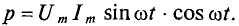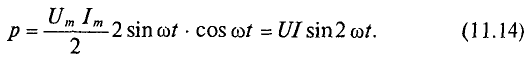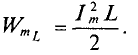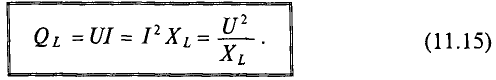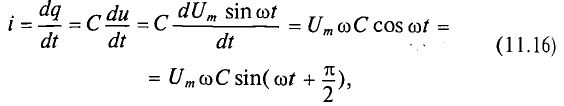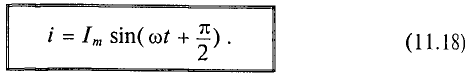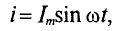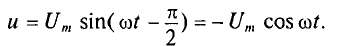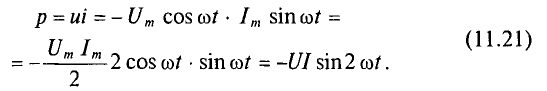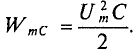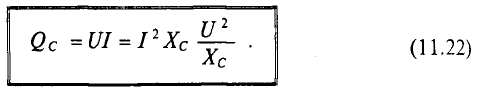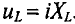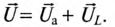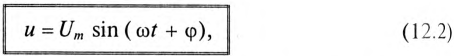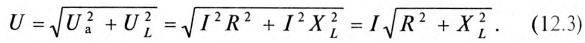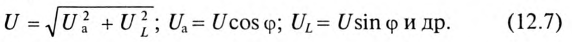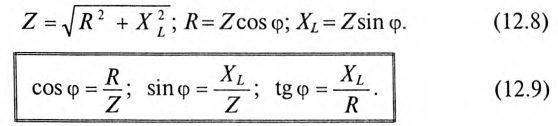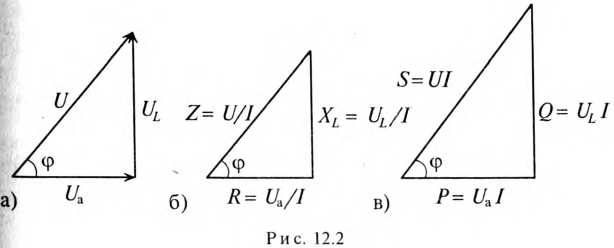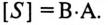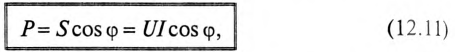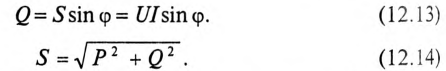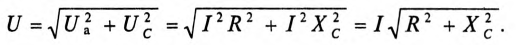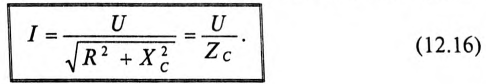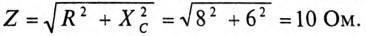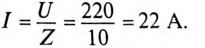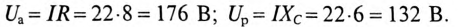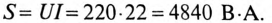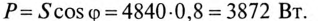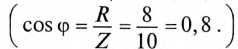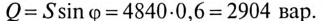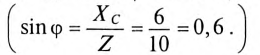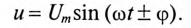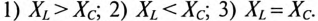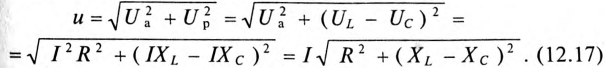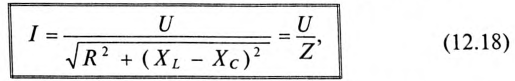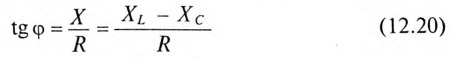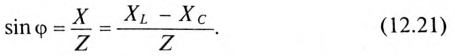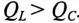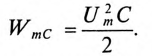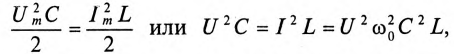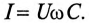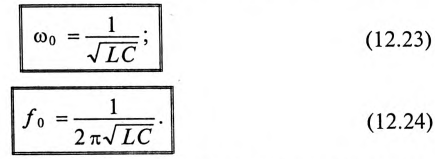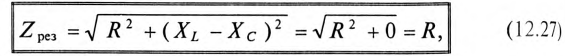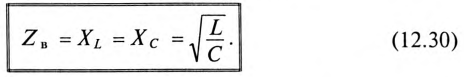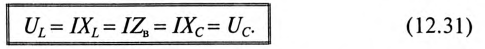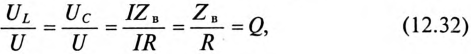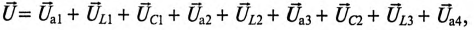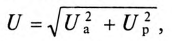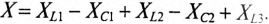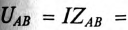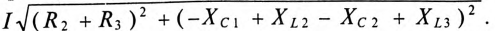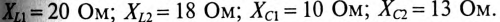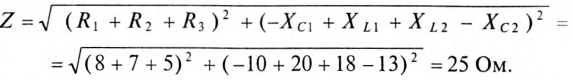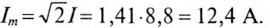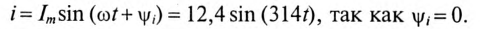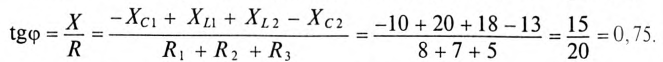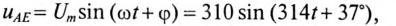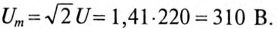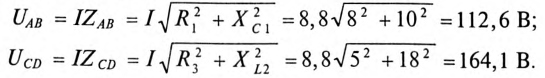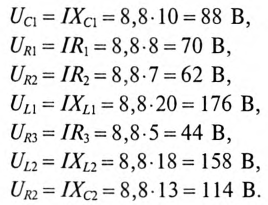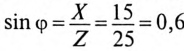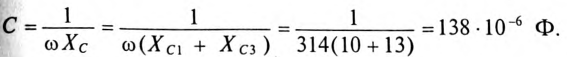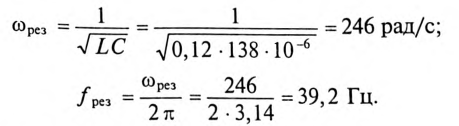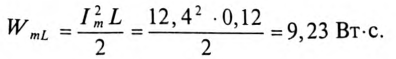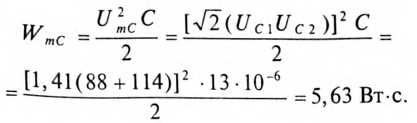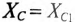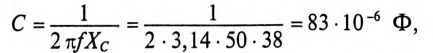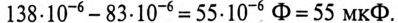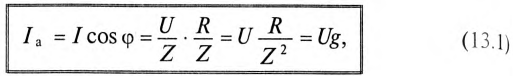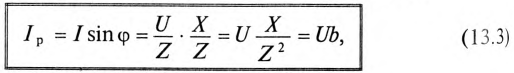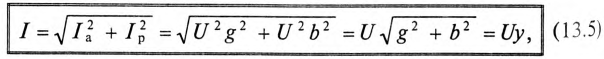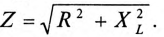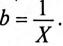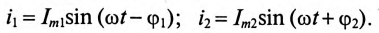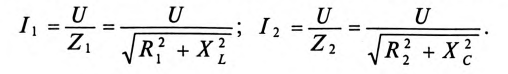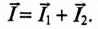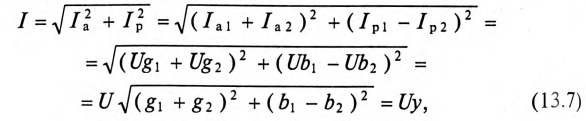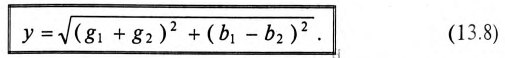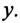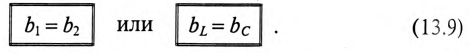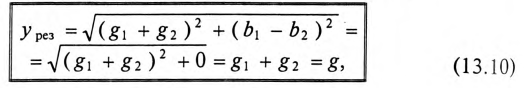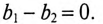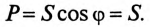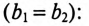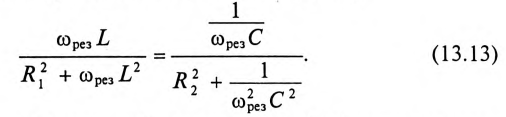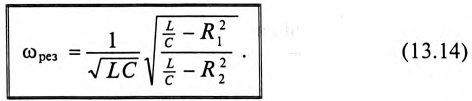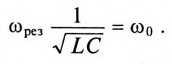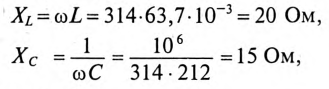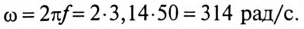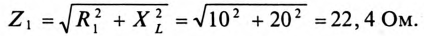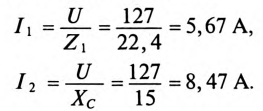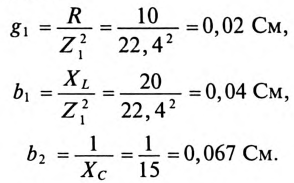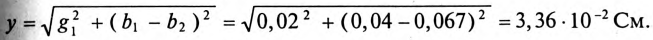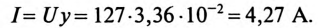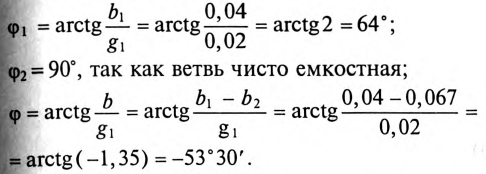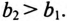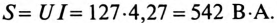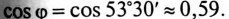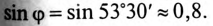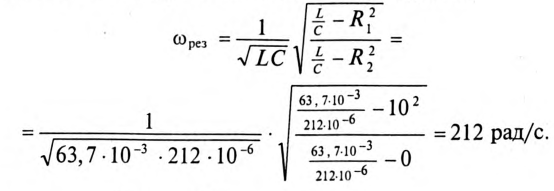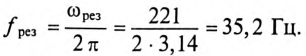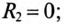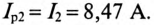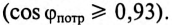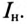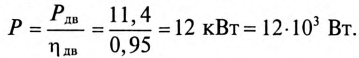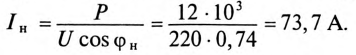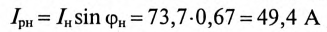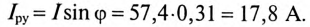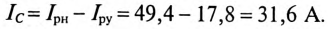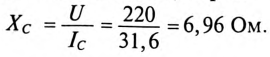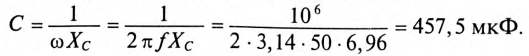Что такое действующее значение напряжения
Содержание
- 1 Как измеряется
- 1.1 Практический пример
- 2 Импульсный электрический заряд
- 2.1 Расчёт кривой
- 2.2 Вычисления
- 3 Сила переменного тока
- 4 Вывод
- 5 Видео по теме
Всем нам известно о 220 вольт в бытовой розетке. Но если подключить к ней вольтметр, напряжение каждый раз будет разным. При этом зачастую напряжение может быть даже больше данной величины. Постараемся в данном материале разобраться — почему это происходит, что такое действующее значение переменного тока, и как его можно рассчитать с помощью различных вариантов.
Как измеряется
Электродинамические параметры в сети постоянно изменяются. Это связано с тем, что они представлены синусоидальным однополярным импульсом разной амплитуды. При измерении напряжения в цепи переменного тока, каждый раз будет получен разный результат. А при вычислении усреднённого параметра, он всегда будет составлять 0.
Получается, что математически вычислить данный параметр невозможно. Есть возможность получить только усреднённый параметр, который зависит от полупериода синусоидальной волны. Однако использовать его на практике или для каких-то вычислений нельзя.
Для решения этой проблемы и стали применять такое понятие, как действующее значение для расчёта силы тока и напряжения. Параметр определяется по характеристикам постоянного тока в цепи, генерирующей тепловую энергию такого же объёма, как и при подаче в цепь переменного тока.
Практический пример
Определение выше будет непонятным для человека, который не имеет особых познаний в области электротехники и электродинамики. Чтобы понять его смысл, предлагается рассмотреть следующий пример:
- Доступны две идентичные электроцепи (длина, элементы цепи и сечение проводников у них совпадают).
- В каждую включён одинаковый резистор — электронный компонент, который изменяет свое сопротивление в зависимости от подаваемого тока.
- Обе цепи подключаются к источникам электроэнергии, имеющим одинаковое напряжение.
Но между цепями есть одна разница. На первую электроцепь подаётся постоянный, а на вторую — переменный ток. По одной из них пойдёт стабильный электроток, а по другой потечет импульсный электрозаряд, который постоянно изменяется и имеет синусоидальной график.
Чтобы найти количества тепла в цепи с сопротивлением, используется такая формула:
После произведения ряда замеров и вычислений можно увидеть, что выделяемое тепло в этих двух электроцепях имеет одинаковую величину. Например, в цепи с постоянным током при подаче напряжения 30 вольт выделяется тепло 200 Джоуль (или Дж). Если вторая цепь имеет идентичные характеристики, то выделение тепла в ней также составит 200 Дж. Получается, что напряжение 30В в этих электроцепях — это и есть эффективное напряжение.
Импульсный электрический заряд
Вышеприведенный пример позволяет только определить действующее и среднее значение напряжения переменного тока. Но на практике такой метод также не применяется, из–за того, что получить доступ к источнику переменного напряжения не всегда представляется возможным. Поэтому параметры цепи рассчитываются с помощью формул, которые основаны на синусоидальных кривых.
Стоит отметить, что действующее напряжение не всегда формируется путём плавного изменения определённого импульсного электрозаряда. Кривая зачастую имеет форму, отличную от привычной нам синусоиды:
- Прямоугольную (меандр);
- треугольную;
- трапециевидную
- и другие.
То есть график электротока может иметь отличную, но при этом стабильную форму. Наглядным примером такого варианта является кривая осциллографа, регистрирующая ритмы сердцебиения человека.
Но независимо от действующего в сети импульсного заряда, во время расчётов используется именно синусоида. Это объясняется тем, что погрешности в расчетах будут крайне малыми. Поэтому ими можно пренебречь, ведь они не скажутся на конечном результате:
- Частота импульса в жилых домах составляет 50 Гц. За 1 сек электрический импульс проходит через фазу 100 раз. Это означает, что работающая от сети лампочка за секунду 100 раз загорается и тухнет, а электрический заряд при этом изменяется довольно плавно. Но человек этого не замечает из-за невосприимчивости человеческого зрения к сверхбыстрым колебаниям.
- Одинаковая площадь фигур. Независимо от формы кривой периода, описывающей переменный электроток идентичных параметров, площадь их фигур всегда будет одинаковой. Следовательно, при любых расчетах получится одно и то же эффективное значение переменного синусоидального тока. Поэтому эффективные значения не зависят от формы кривой. На них оказывает влияние именно величина амплитуды.
Форма кривой импульса важна только для сверхточных расчётов в лабораторных условиях. Также она учитывается для работы суперкомпьютеров. В остальных случаях синусоида позволит вычислить действующее значение переменного синусоидального тока.
Расчёт кривой
Синусоида — это периодическая функция, которую можно всегда описать с помощью уравнения. Если взять её за основу, то на входе имеются следующие исходные данные:
- Т — амплитуда;
- φ — начальная фаза;
- ωt — угловая скорость.
По этим входным характеристикам находим другие переменные параметры:
- Uт — амплитудное напряжение;
- Uм — действующие в момент измерения значения напряжения;
- ωt + φ — фактическая фаза в точке измерения.
Т.к. начальная фаза равняется нулю, на выходе формула кривой будет иметь следующий вид:
Uм = Uт·sin(ωt + φ) = Uт·sin(ωt)
Теперь необходимо обратиться к закону выделения тепла, который еще называется законом Джоуля-Ленца. Согласно него квадрат напряжения — это произведение выделяемого тепла на сопротивление проводника.
| Формулы для расчета тепловой энергии в электроцепях: | |
| с постоянным током | с переменным током |
| Q = U2/R | Q = Uм2/R |
- Uм — величина постоянного напряжения;
- Uм — величина действующего напряжения;
- R — сопротивление проводника.
Мы видим, что при расчетах количества тепла в цепи переменного тока, пользуется именно действующим значением переменного тока.
Из данных формул вытекают два важных нюанса, на которые стоит обратить внимание:
- В расчетах используется среднеквадратичное значение напряжения (СКЗ). Это связано с тем, что величина напряжения постоянно изменяется и можно получить только какую-то усредненную величину.
- Амплитуда постоянного тока довольно условная величина. Ее используют в расчетах, чтобы только описать период синусоиды переменного электрозаряда.
Вычисления
Волны синусоид будут одинаковыми. Однако в пределах периода в каждой точке измерения напряжения будут отличаться. Поэтому, чтобы уравнять между собой среднеквадратичное напряжение постоянного и переменного электротока по тепловыделению, требуется рассчитать объём выделенного тепла в течение времени, равного 1 периоду:
В уравнение теперь можно подставить выражение расчёта мгновенного напряжения
Uм = Uт·sin(ωt + ф) = Uт·sin(ωt)
После математического преобразования можно рассчитать действующее значение электрического напряжения:
U = Uт / √2 = 0,707·Uм
Теперь найдем амплитудное напряжение по формуле:
Uт = U·√2
Амплитудное напряжение так же имеет и другое название – максимально возможное эффективное мгновенное значение напряжения.
Сила переменного тока
С помощью амперметра находим амплитудную силу тока в цепи. Используя её вместе с периодом, который равен 1/50 секунд, можно применить описанную выше формулу, чтобы рассчитать среднеквадратичное значение напряжения. В результате этого будет получена действующие значения силы тока.
Действующее значение тока можно рассчитать, когда других исходных параметров нет, но нам известно эффективное значение величины напряжения в цепи. Следовательно, можно воспользоваться всем нам известным законом Ома вычисления значения силы тока:
U = I·R и I = U/R
где:
- U — будет действующим напряжением переменного синусоидального тока;
- R — сопротивление проводника, которое всегда можно узнать в любом справочнике, зная состав материала проводника.
Ранее электропроводку делали из алюминия и меди, которые отличались довольно высоким сопротивлением. Эффективное значение реальной силы тока этих металлов было меньше 6.5А. По этой причине в старых домах зачастую срабатывает автоматический выключатель, если одновременно подключить в сеть несколько приборов. Сегодня открыты сложные сплавы с низким сопротивлением. Они позволяют достичь с действующее значение силы переменного тока около 16А даже в обычных современных многоквартирных домах.
С уменьшением сопротивления проводника, прямопропорционально возрастает мощность и тепловыделение. При том надо помнить о том, что у каждого сплава есть свой определенный температурный предел. Поэтому в жилых сетях сила тока часто не превышает 20 ампер, а при резком ее скачке, например, при неполадках на подстанции, электронная часть устройств просто сгорает. Для предотвращения таких случаев и подключаются автоматы, которые при регистрации высоких действующих значений размыкают цепь на данном участке. Более мощные источники электроэнергии встречаются только в промышленных трехфазных сетях с напряжением 380В.
Вывод
Мы рассмотрели в данной статье — что называют действующим значением силы тока и напряжения, а так же как определяют эти значения переменного тока в электроцепи. Это эффективные значения переменного тока, под действием которого выделяется точно такое же количества тепла, как и в цепи постоянного тока, имеющей аналогичные характеристики.
Видео по теме
«Не
стыдно не знать, стыдно не учиться».
Задача
1.
В колебательном контуре напряжение на зажимах изменяется по закону .
Найдите действующие значения силы тока и напряжения, если активное
сопротивление цепи равно 50 Ом.
|
ДАНО: |
РЕШЕНИЕ Запишем общее уравнение Исходя из заданного по можно определить, что Из закона Ома для участка Тогда действующие значения |
|
|
Ответ:
Uд = 70,7 В;
Iд = 1,4 А.
Задача
2.
В цепь параллельно включены катушка с индуктивностью 30 мГн и конденсатор с
ёмкостью 50 мкФ. Действующее значение силы тока равно 10 А. Запишете уравнения,
описывающие колебания тока и напряжения, а также найдите активное сопротивление
цепи.
|
ДАНО: |
СИ |
РЕШЕНИЕ Уравнения гармонических колебаний для напряжения и силы Циклическая частота колебательного контура определяется по Действующие значения напряжения и силы тока рассчитываются Тогда амплитудное значение силы тока равно Амплитудное значение напряжения можно рассчитать по формуле С учетом рассчитанных значений уравнения гармонических Активное сопротивление цепи определяется по формуле |
|
|
Задача
3.
Действующее значение напряжения в цепи с колебательным контуром составляет 50 В.
Известно, что в некоторый момент времени t = 2 мс
ток в цепи равен 2 А. Найдите индуктивность катушки, если ёмкость
конденсатора равна 80 нФ,а активное сопротивление цепи равно 20 Ом.
Сдвиг фаз равен нулю.
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем уравнения, Из закона Ома для участка цепи Действующие значения напряжения и силы тока рассчитываются Тогда амплитудные значения напряжения и силы тока равны Циклическая частота колебательного контура определяется по С учётом рассчитанного значения амплитудной силы тока и Т.к. по истечении 2 мс сила тока равна 2А, то |
|
|
Ответ:
53 Гн.
Задача
4.
Активное сопротивление колебательного контура равно 35 Ом, а частота колебаний
равна 25 кГц. Найдите ёмкость конденсатора и индуктивность катушки.
|
ДАНО: |
СИ |
РЕШЕНИЕ Максимальная электрическая энергия колебательного контура Максимальная магнитная энергия колебательного контура Когда электрическая энергия Частота колебательного контура определяется по формуле Преобразуем данное выражение Активное сопротивление определяется по формуле Из равенства максимальной электрической энергии и Получаем систему состоящую из двух уравнений Из первого уравнения получаем Из второго уравнения |
|
|
Ответ:
L = 2,2×10–4 Гн;
C = 1,7×10–7 Ф.
Среднеквадратичное значение
В зарубежной терминологии применяется аббревиатура RMS (rms) — root mean square.
В математике для набора чисел x1, x2, …, xn количеством n среднеквадратичное значение (rms) определяется выражением:
Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04
Среднеквадратичным значением двух или нескольких чисел
является квадратный корень из среднеарифметического значения квадратов этих чисел.
Для любой непрерывной функции в интервале T1 — T2 среднеквадратичное значение можно рассчитать по формуле:
Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.
Действующее значение напряжения и тока
В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.
P = I²R; A = I²Rt; P = U²/R; A = U²t/R
Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока,
действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.
Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности Pavg
или работы Aavg,
пропорциональное квадрату значения тока.
Так же среднеквадратичное значение переменного напряжения за период равносильно
по своему воздействию на активную нагрузку такому же значению постоянного напряжения.
P = UI = Pavg = UrmsIrms
Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.
Величину переменного напряжения или тока, в большинстве случаев,
выражают его среднеквадратичным значением и измеряют приборами электромагнитного типа или специальными среднеквадратичными измерителями — True RMS.
Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках.
Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.
Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.
Расчёт действующего значения
В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.

Запишем выражение Urms с применением интеграла функции
U = Uampsin(t) для одного периода 2π :
Показать расчёт
Скрыть расчёт

Вынесем Uamp из под знака радикала.
Воспользуемся табличным интегралом 
перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:

Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:

В результате решения в итоге получим:
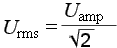
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T
для функции 
Выразим Urms искомой функции с помощью определённого интеграла:
Показать расчёт
Скрыть расчёт
Используя табличный интеграл
и формулу Ньютона-Лейбница, получаем:
В итоге преобразований получим:
Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода.
Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.
Например, для множества функций F1(t) , F2(t) , … , Fn(t)
в соответствующих им интервалах времени (0 — T1), (T1 — T2), …, (Tn — T),
составляющих период T, действующее напряжение (RMS) определится выражением:
Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже,
T и U amp имеют те же расчётные величины,
что и в рассмотренном случае c функцией 
а интегралы, определённые в интервалах, равных T, для квадратов используемых функций 
будут иметь одно и то же значение
Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь
среднеквадратичное значение 
В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью Ti .
Выразим Urms одного периода T, как квадратный корень из среднеарифметического значения интегралов,
определённых в интервалах 0 — Ti и Ti — T для квадратов всех значений периода.
В результате получаем значение RMS, равное произведению амплитуды импульсов Uamp на квадратный корень из
коэффициента заполнения (Ti / T).
В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.
Замечания и предложения принимаются и приветствуются!
Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
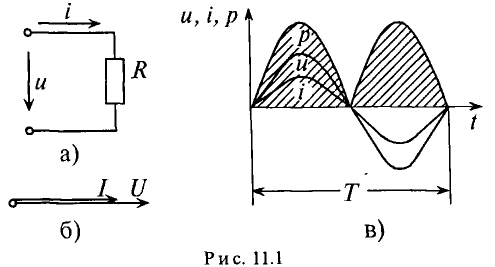
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение
где
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (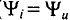
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:
Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 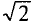
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 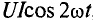
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 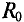
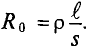
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е.
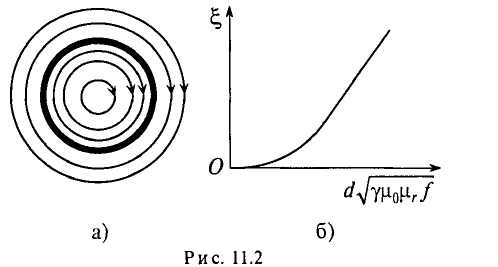
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 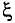
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости 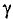
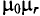

При токах большой частоты 
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
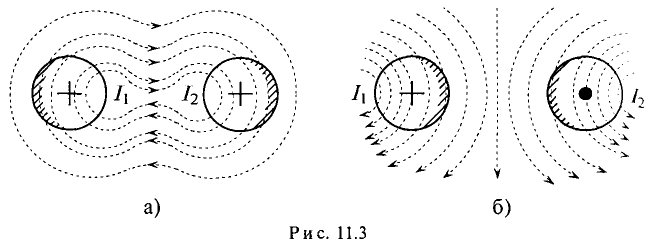
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
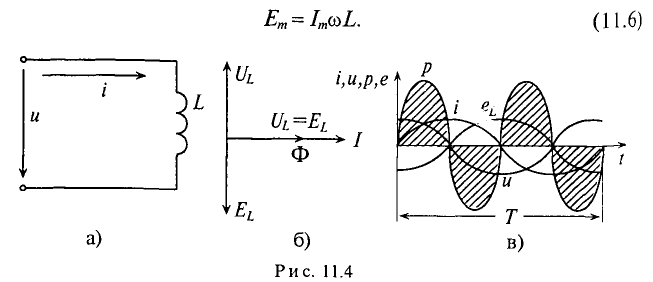
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 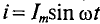
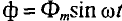
так как
Очевидно, эта ЭДС достигает своего амплитудного значения 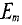
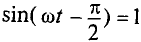
Тогда
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 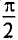
По второму закону Кирхгофа для мгновенных значений можно записать
Откуда
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 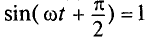
Следовательно,
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 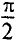
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 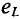
Если уравнение (11.10) разделить на 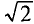
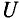
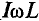
Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Таким образом,
Закон Ома для этой цепи можно записать иначе:
Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
где
Следовательно,
Полученное уравнение умножают и делят на 2:
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (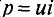
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
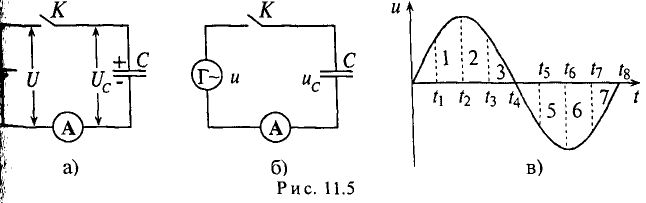
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 — конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 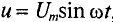
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 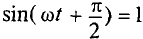
Тогда
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° = 
Если уравнение (11.17) разделить на 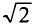
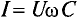
Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:
Когда закон Ома для цепи с конденсатором можно записать:
Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
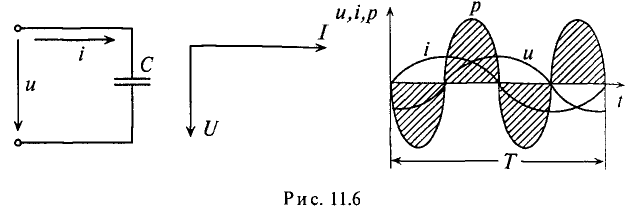
Если в цепи конденсатора емкостью 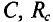
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
Мгновенная мощность в цепи с конденсатором
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) — аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
Цепь с активным сопротивлением и индуктивностью
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 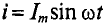
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать
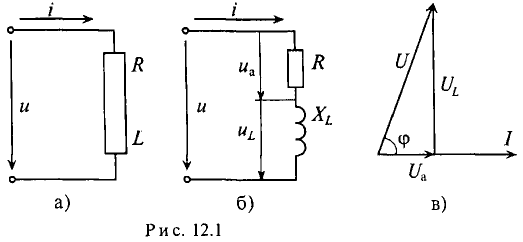
Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 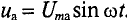
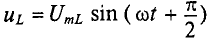
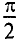
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 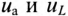
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 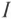
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
Откуда
Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:
где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать
где Z — кажущееся сопротивление этой цепи.
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи
которая измеряется в вольт-амперах, т.е.
Однако потребляется в цепи только часть полной мощности — активная мощность
где cos ф показывает, какая часть полной мощности 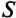
Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 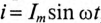
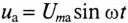
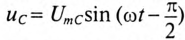
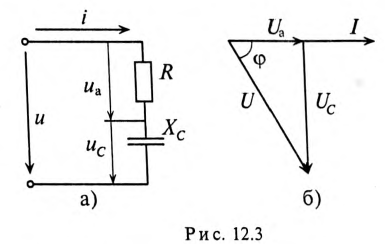
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф < 90°, т. е.
Действующее значение напряжения U, приложенного к этой цепи, определяется по векторной диаграмме (рис. 12.3):
Откуда математическое выражение закона Ома для этой цепи:
Пример 12.1
К цепи с последовательно включенными сопротивлениями R= 8 Ом и Хс= 6 Ом (рис. 12.3а) приложено напряжение U= 220 В. Определить ток цепи I, напряжение на активном 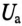
Решение
Для определения тока вычислим полное сопротивление цепи
Тогда ток будет равен
Напряжения на участках:
Полная мощность
Активная мощность
Реактивная мощность
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
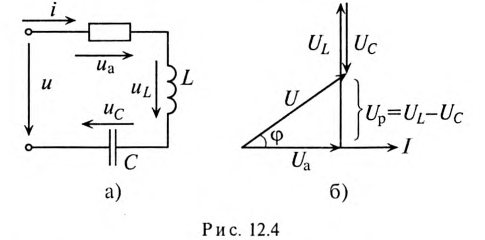
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток 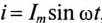
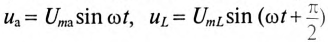
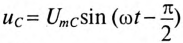
Мгновенное значение напряжения цепи определяется по формуле
Так как в рассматриваемой цепи включены два реактивных сопротивления XL и Хс, то возможны три режима работы цепи:
Векторная диаграмма цепи для режима 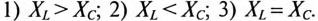
Знак перед углом сдвига фаз ф зависит от режима работы цепи Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е. 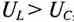
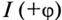
Если в цепи преобладает емкостное напряжение (сопротивление), т.е. 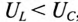
Из векторной диаграммы (рис. 12.46) следует:
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
где Z — полное (или кажущееся) сопротивление неразветвленной цепи с R, L и С, т. е.
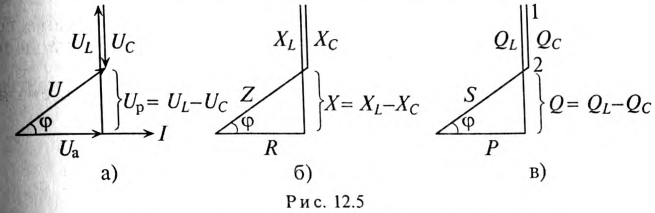
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла ф можно определить из треугольника сопротивлений (рис. 12.56):
или
Из выражений (12.20) и (12.21) видно, что если 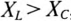
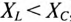
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности 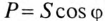
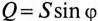
Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= QL— Qc. Эта реактивная мощность (энергия) колеблется между источником и магнитным полем катушки индуктивности, так как
Полная мощность цепи определяется по формуле
Колебательный контур
Электрические цепи, в которых происходят периодические изменения токов, напряжений, энергии называются колебательными.
Для того чтобы исследовать резонансные явления, необходимо иметь представления о процессах в колебательном контуре, состоящем из идеальной катушки и конденсатора без потерь.
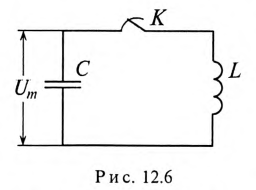
Если конденсатор емкостью С зарядить до напряжения Um, то в электрическом поле этого конденсатора накопится энергия, максимальное значение которой согласно выражению (6.21):
Если к заряженному конденсатору подключить индуктивность L замыканием ключа К (рис. 12.6), то конденсатор будет
разряжаться через индуктивность переменным током i. При этом в индуктивности L создается ЭДС самоиндукции eL, и в магнитном поле ее накапливается энергия, максимальное значение которой (9.12):
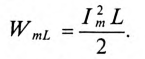
Источником энергии в этом контуре является конденсатор. Ток в контуре, состоящем из индуктивности L и конденсатора С, не прекращается даже когда конденсатор полностью разрядится. За счет ЭДС самоиндукции и энергии, накопившейся в магнитном поле индуктивности, конденсатор будет заряжаться, и энергия магнитного поля индуктивности переходит в электрическое поле конденсатора. При этом источником энергии в этом контуре является индуктивность. Дальше процесс повторяется.
Таким образом, в замкнутом контуре, состоящем из индуктивности и емкости, происходит колебание энергии между электрическим полем конденсатора С и магнитным полем индуктивности L. Поэтому такой замкнутый контур называется колебательным контуром.
Колебание энергии в колебательном контуре происходит с определенной частотой 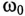
так как из (11.19) в цепи переменного тока с емкостью
Откуда
Таким образом, частота собственных колебаний колебательного контура определяется параметрами этого контура L и С.
Если в колебательном контуре отсутствуют потери (идеальный контур), то колебания в нем будут незатухающими с неизменной амплитудой. Если в колебательном контуре имеется активное сопротивление, т.е. возникают потери, то колебания энергии в нем будут затухающие, с уменьшающейся амплитудой, если эти потери не компенсируются.
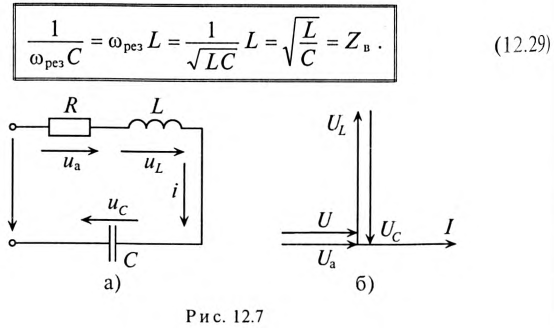
Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R И индуктивностью L (рис. 12.7а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.
Из (12.25) следует 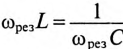
Из (12.26) следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 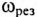
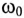
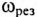
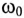
Полное (кажущееся) сопротивление цепи (рис. 12.7а) при резонансе напряжений определяется по формуле
так как XL-Xc=0.
То есть полное сопротивление неразветвленной цепи при резонансе напряжений 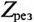
Следовательно, ток в неразветвленной цепи при резонансе напряжений максимальный:
Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
(12.29)
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 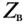
Напряжения на индуктивности UL и на емкости Uc при резонансе напряжений равны между собой, так как равны сопротивления, см. (12.25).
Равенство (12.31) определяет название «резонанс напряжений».
Так как UL и Uc изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 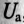
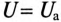
При резонансе напряжений каждое из реактивных напряжений UL и Uc может оказаться большим, чем напряжение цепи U.
где Q — добротность резонансного контура.
Добротность контура Q показывает, во сколько раз напряжение на индуктивности UL и емкости Uc (каждое) больше напряжения цепи U.
Высокая добротность резонансного контура (при малом активном сопротивлении контура) нашла широкое применение в радиотехнике, в частности в антенном контуре.
Из векторной диаграммы (рис. 12.76) видно, что при резонансе напряжение цепи U совпадает по фазе с током 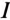
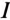
Колеблющаяся между магнитным полем индуктивности и электрическим полем емкости мощность (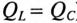
Из выражения (12.33) следует, что при отсутствии активной Мощности Р (активного сопротивления R) резонансный контур становится при резонансе идеальным колебательным контуром. Следовательно, при наличии активного сопротивления R источник расходует свою мощность на компенсацию потерь в контуре, за счет чего колебания в цепи будут незатухающими.
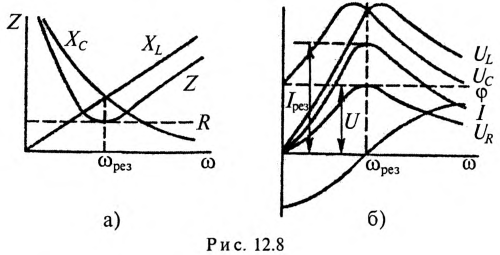
Кроме активного сопротивления R резонансной цепи и напряжения, приложенного к ней, все параметры резонансной цепи (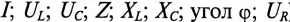
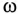
Эти изменения параметров резонансной цепи наглядно иллюстрируются резонансными кривыми, изображенными на рис. 12.8.
На резонансных кривых четко просматриваются значения этих параметров при частоте резонанса 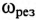
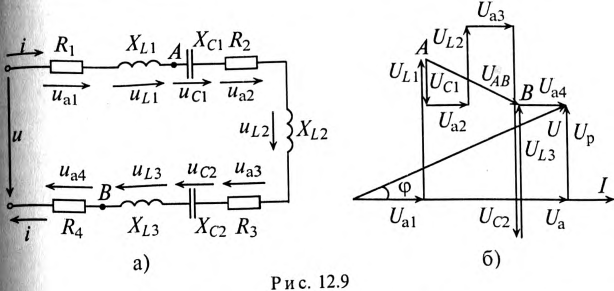
Общий случай неразветвленной цепи
Для неразветвленной цепи, содержащей несколько активных и реактивных сопротивлений различного характера (рис. 12.9а), справедливо геометрическое равенство напряжений (баланс напряжений)
которое лежит в основе построения векторной диаграммы (рис. 12.96).
Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи.
Из векторной диаграммы следует (рис. 12.96)
где 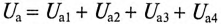
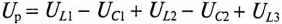
Те же рассуждения можно отнести и к сопротивлениям:
— полное сопротивление цепи 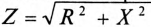
— активное сопротивление цепи 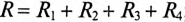
— реактивное сопротивление цепи
Напряжение на каком-либо участке неразветвленной цепи (рис. 12.9а), например на участке АВ, определяется так:_
Вектор напряжения UAB показан на векторной диаграмме (рис. 12.96).
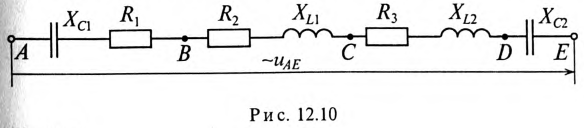
Пример 12.2
Напряжение, приложенное к неразветвленной цепи (рис. 12.10) U=220 В, частота тока сети f = 50 Гц. Начальная фаза тока 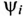
Сопротивление участков цепи: 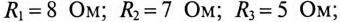
Требуется:
1. Вычислить ток цепи I и записать его мгновенное значение.
2. Записать мгновенное значение напряжения цепи иАЕ, определив предварительно угол ср и характер цепи.
3. Определить напряжение между точками АВ и CD.
4. Построить в масштабе векторную диаграмму цепи, определив едварительно напряжение на каждом сопротивлении.
5. Определить мощности S, Р и Q цепи.
6. Определить частоту, при которой в цепи наступит резонанс напряжений, и ток при резонансе.
7. Определить максимальную энергию, запасенную в магнитном поле катушек WmL и электрическом поле конденсаторов WmC. Как нужно изменить емкость конденсаторов, чтобы в цепи пил резонанс напряжений при частоте f = 50 Гц?
Решение
1. Для определения тока цепи I необходимо вычислить полное сопротивление цепи:
Действующее значение тока 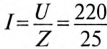
Угловая частота 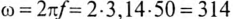
Мгновенное значение тока цепи:
2. Угол сдвига фаз ф и характер цепи определяется через tg ф:
Таким образом, угол ф = 37° (из таблицы), характер цепи индуктивный (+ф).
Тогда мгновенное значение напряжения цепи
где
3. Напряжение на участках:
4. Для построения векторной диаграммы определяются напряжения:
Векторная диаграмма цепи (отображает только характер участков, но не величины напряжений на них) изображена на рис. 12.11.
5. Полная мощность цепи 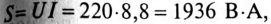
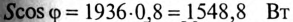
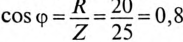
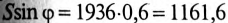
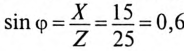
6. Для определения частоты резонанса вычисляется индуктивность L и емкость С цепи:
Тогда
Ток цепи при резонансе 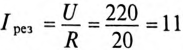
7. Максимальная энергия, запасенная в магнитном поле катушек:
Максимальная энергия, запасенная в электрическом поле конденсаторов:
8. Условие резонанса XL = XC.
По условию задачи 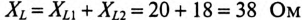
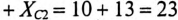
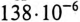
т. е. емкость конденсаторов нужно уменьшить на
Разветвленная цепь синусоидального тока
Активный и реактивный токи:
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
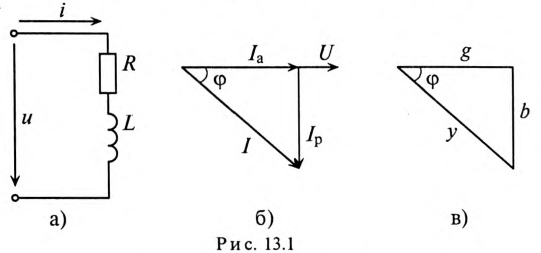
Если к цепи, содержащей активное сопротивление R и индуктивное XL (рис. 13.1а), приложено синусоидальное напряжение 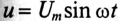
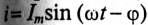
Векторная диаграмма в этом случае изображена на рис. 13.16.
Ток цепи I (рис. 13.16) раскладывается на две составляющие, одна из которых 



Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи (рис. 13.1а) ток на всех участках имеет одинаковое значение. Однако понятия активный 

13.2. Проводимости
Из треугольника токов для рассматриваемой цепи (рис. 13.16) следует: 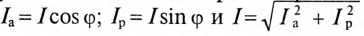
С другой стороны, известно, что 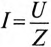
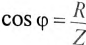
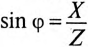
Тогда
где g — активная проводимость цепи, равная
Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.
А так как g определяет активный ток 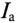
Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.
Величина реактивного тока определяется выражением
где b — реактивная проводимость цепи, равная
Величина полного тока цепи равна
где 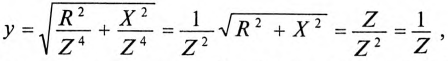
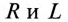
Таким образом, у — полная, или кажущаяся, проводимость цепи:
Полная (кажущаяся) проводимость цепи «у» является обратной величиной полного (кажущегося) сопротивления цепи.
Активная 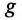
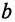
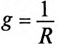
Если же в неразветвленной цепи (или ветви) включены сопротивления 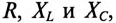
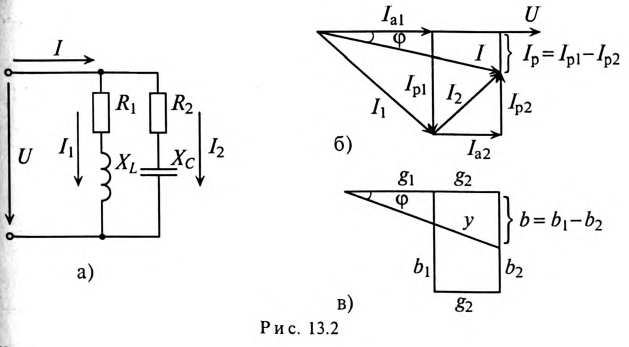
Параллельное соединение катушки и конденсатора
Если к источнику синусоидального напряжения 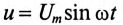
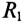
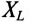
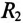
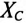
Действующие значения этих токов будут соответственно равны
Ток в неразветвленной цепи 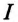
Для определения этого тока строится векторная диаграмма цепи (рис. 13.26), из которой следует:
где
Таким образом, ток в неразветвленной части цепи 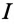
Реактивные проводимости в ветвях имеют различные знаки, так как сопротивления в ветвях различного характера (индуктивное и емкостное).
Треугольник проводимостей рассматриваемой цепи изображен на рис. 13.2в.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток цепи 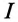
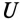
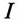
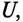
Резонанс токов
Резонанс токов в цепи (рис. 13.2а) с параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях:
Выражение (13.9) является условием резонанса токов в разветвленных цепях синусоидального тока. Полная (кажущаяся) проводимость при этом условии
так как
Таким образом, полная проводимость цепи при резонансе токов 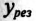
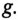
Реактивные токи в ветвях при резонансе токов равны между собой
Это равенство и определяет название «резонанс токов».
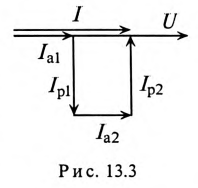
На основании равенства (13.12) строится векторная диаграмма при резонансе токов (рис. 13.3). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 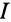
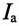
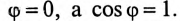
Эта активная мощность компенсирует потери на активном сопротивлении в параллельном резонансном контуре. Мощность (энергия), которая колеблется между электрическим полем конденсатора и магнитным полем индуктивности при резонансе, не является реактивной, так как не загружает источник и провода.
Частота резонанса токов в параллельном резонансном контуре может быть определена из условия резонанса токов, т. е. равенства реактивных проводимостей в ветвях
После ряда преобразований равенства (13.13) определяется частота резонанса токов
Резонансная частота зависит не только от параметров колебательного контура 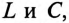
Если в резонансном контуре отсутствуют активные сопротивления в ветвях, то частота резонанса токов 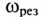
Если в резонансном контуре 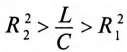
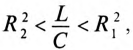
Резонанс токов нашел широкое применение в радиотехнике и выпрямительной технике (в резонансных фильтрах) и др.
Пример 13.1
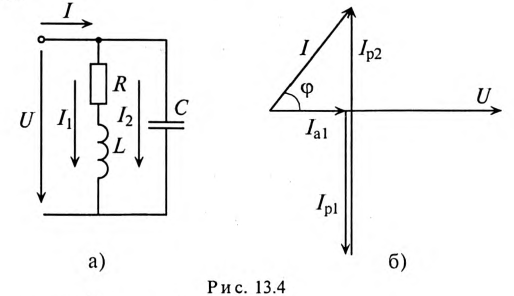
Напряжение, приложенное к параллельно включенным катушке и конденсатору (рис. 13.4а), 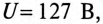
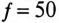
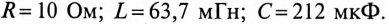
1) токи всех участков цепи:
2) углы сдвига фаз этих токов относительно напряжения:
3) полную S, активную Р и реактивную Q мощности цепи;
4) частоту, при которой наступит резонанс токов в этой цепи. Построить векторную диаграмму.
Решение
1. Сопротивление участков цепи:
где
Сопротивление 1-й ветви:
Токи в ветвях соответственно равны
Для определения тока 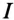
Тогда полная проводимость цепи будет равна
Ток в неразветвленной части цепи
2. Углы сдвига фаз:
.
Знак «минус» перед значением угла 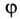
3. Полная мощность цепи
Активная мощность цепи 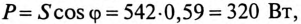
Реактивная мощность цепи 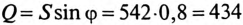
4. Угловая частота резонанса токов в цепи равна
Откуда
Для построения векторной диаграммы определяют активные и реактивные токи в ветвях:
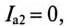
Векторная диаграмма для рассматриваемой цепи изображена на рис. 13.46.
На векторной диаграмме видно, что ток I опережает напряжение U на угол 53°30′ (цепь емкостного характера).
Коэффициент мощности
Номинальные параметры, т.е. мощность источника 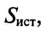
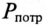
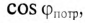
Из (13.15) следует, что чем меньше 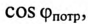
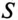
Ток в цепи потребителя с определенным 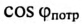
Из (13.16) видно, что чем меньше 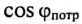
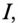
Таким образом, низкий коэффициент мощности потребителя 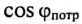

Однако 

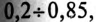
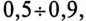
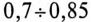
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения 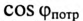
Из векторной диаграммы (рис. 13.56) видно, что с подключением конденсатора С (ключ К замкнут) появляется 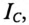
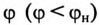
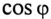
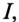
Для повышения коэффициента мощности 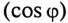
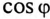
Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки).
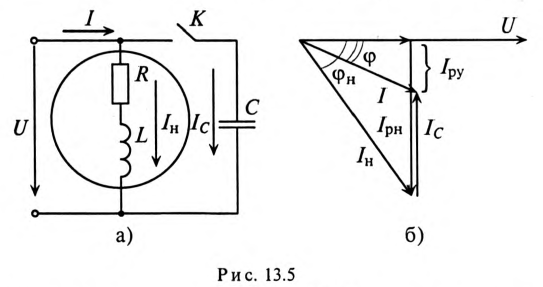
Пример 13.2
Асинхронный двигатель, включенный в сеть с напряжением 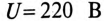
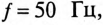
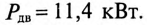
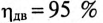
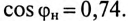
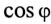
Решение
Мощность, потребляемая двигателем из сети:
Ток нагрузки 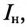
Реактивная составляющая тока двигателя 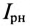
(по таблице 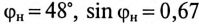
Ток установки 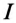
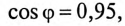
При 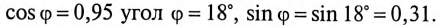
Ток конденсатора 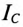
Емкостное сопротивление конденсаторов
Емкость конденсаторов, которые нужно подключить параллельно двигателю для улучшения 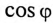
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле