Знак подстановки
Говорят, что в
данной строке элементы i
и j
составляют инверсию, если i
> j,
но i
стоит в этой строке раньше.
(5
3 4 1 2) – число 5 образует 4 инверсии. Общее
число инверсий в строке равно 8.
Знак
подстановки
равен
(-1)a,
где а – число инверсий в строке (α1,
α2,
…, αn)
Пример
3.
Определить
знак подстановки
Решение.
Число
инверсий в строке (3 4 5 2 1 8 7 6) равно
2+2+2+1+0+2+1=10
так
как (-1)10=1,
то данная подстановка является четной.
Знак подстановки
можно определить и другим способом. Для
этого надо разложить подстановку в
произведение независимых циклов.
b
= (k1-1)+(k2-1)+…+(kl-1)=k1+k2+…+kl-S,
(5)
где
k1
, k2
, …, kl
– длины циклов.
Тогда
знак равен (-1)b
Пусть дана
подстановка n-й
степени и пусть s
есть число независимых циклов в её
разложении плюс число символом,
оставляемых ею на месте. Разность n
– s
называется декрементом этой подстановки.
Декремент равен числу действительно
перемещаемых символов, уменьшенному
на число независимых циклов, входящих
в разложение подстановки и равносилен
b
в формуле (5).
Замечание.
Четность подстановки совпадает с
четностью декремента этой подстановки.
Пример
4.
Определите
знак подстановки
с
помощью разложения подстановки в
произведение независимых циклов.
Решение.
Данная
подстановка раскладывается следующим
образом в произведение независимых
циклов.
b
= 3+2+2+1–4 = 4
(-1)4
= 1
Это
четная подстановка.
Умножение подстановок
Определение.
Произведением первой подстановки на
вторую называют последовательное
выполнение двух подстановок n-й
степени, приводящее к некоторой вполне
определенной третьей подстановке n-й
степени.
так,
если даны подстановки четвертой степени
то
Действительно,
при подстановке А символ 1 переходит в
3, но при В символ 3 переходит в 4, поэтому
при АВ символ 1 переходит в 4, и т. д.
Можно перемножить
лишь подстановки одинаковой степени.
Умножение подстановки n-й
степени при n
≥ 3некоммутативно. Действительно, для
рассмотренных выше подстановок А и В
произведение ВА имеет вид
т.
е. подстановка ВА отлична от подстановки
АВ. Такие примеры можно подобрать для
всех n
при n
≥ 3, хотя для некоторых пар подстановок
закон коммутативности случайно может
выполняться.
Умножение подстановок
ассоциативно, т. е. можно говорить о
произведении любого конечного числа
подстановок n-й
степени, взятых (ввиду некоммутативности)
в определенном порядке. В самом деле,
пусть даны подстановки А, В и С и пусть
символ i1,
1 ≤ i1
≤ n,
переходит при подстановке А в символ
i2,
i2
при
подстановке В переходит в символ i3,
а последний при подстановке С – в символ
i4.
Тогда при подстановке АВ символ i1
переходит в i3,
при подстановке ВС символ i2
переходит в i4,
а поэтому как при (АВ)С, так и при А(ВС)
символ i1
,будет переходить в символ i4.
Очевидно, что
произведение любой подстановки А на
тождественную подстановку Е, а также
произведение Е на А, равно А:
АЕ=ЕА=А
Назовем,
наконец, обратной для подстановки А
такую подстановку А-1
той же степени, что
АА-1
= А-1А
= Е
Легко
видеть, что обратной подстановкой для
подстановки
служит
подстановка
получающаяся
из А переменой мест верхней и нижней
строк.
Пример 5.
Найти
подстановку, обратную данной
Решение.
Подстановка
А-1,
обратная подстановке А будет иметь вид
приведем
её к каноническому виду.
Пример
6.
Найти
порядок указанного элемента в группе
Sn,
n=5
Решение:
Наконец,
получили тождественную подстановку Е
Ответ:
6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
Подстановки
проверено
Подстановка
Транспозиции и циклы
Определение 3. Циклической подстановкой2), или циклом3) называется такая подстановка 


Пример 3. В подстановке

действительно перемещаемыми символами являются 1, 3, 4, 5, 6. Выберем любой из них, например, 3. 


Определение 4. Циклы называются независимыми5), если они не имеют общих действительно перемещаемых символов.
Предложение 1. Любая подстановка 

Пример 4. 
Определение 5. Цикл длины 2 называется транспозицией6).
Предложение 2. Каждая подстановка может быть представлена в виде произведения транспозиций.
В отличие от представления в произведение попарно независимых циклов, представление в виде произведения транспозиций может не быть единственным.
Пример 5. Подстановка 


Четность подстановки
См. также
Литература
Наверх
Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
2.1. Группа и связанные с ней понятия
Циклическая форма подстановок
Подстановки удобно записывать в циклической форме. При такой записи индексы, остающиеся на месте, обычно не пишутся. Так, подстановка a имеет следующие переходы индексов: 0 → 0, 1 → 4 → 2 → 1, 3
→ 3, 5 → 6 → 5. Следовательно, в циклической форме она запишется следующим образом:а =
= (0)(142)(3)(56) =
= (0)(142)(3)(56)(7)(8)… = (142)(56).
Считается, что индексы 7, 8 и т.д. так же, как 0 и 3, неявно присутствуют в подстановке
а, но тождественно переходят сами в себя. В связи с этим тождественную подстановку обозначают через единичный цикл: e = (0). Регулярные подстановки группы G имеют следующий циклический вид:0 = (0), 1 = (01)(23)(45)(67),
2 = (02)(13)(46)(57), 3 = (03)(12)(47)(56),
4 = (0426)(1537), 5 = (0527)(1436),
6 = (0624)(1735), 7 = (0725)(1634).
Безразлично, с какой позиции записывать цикл:
(ij) = (ji), (ijk) =
(jki) = (kij), (ijkl) = (jkli) = … ,поэтому
i1 = (0123) = (1230) = (2301) = (3012),
a = (421)(56) = (421)(65) = (214)(56) = (214)(65),
6 = (6240)(1735) = (2406)(3517) = (4062)(3517).
Циклы одной и той же подстановки можно переставлять, т.е. они коммутируют внутри этой подстановки:
(ijk)(l)(mn) = (l)(ijk)(mn) = (mn)(jki)(l) =(nm)(kij)(l),
i2 = (02)(13) = (13)(02), a = (142)(56) = (56)(142),
6 = (1735)(0624), 4 = (3715)(4260).
Разложению подстановки на систему независимых циклов отвечает разложение этой подстановки на систему коммутирующих множителей:
i2 =
=
=
,
a =
=
=
,
=
.
Элементарная циклическая подстановка, переставляющая два любых индекса i и j, называется транспозицией. Транспозиция обладает важным свойством: она обратна сама себе, т.е. (ij) = (ij)–1, так как (ij)(ij)= e. Любую транспозицию (ij) можно представлять произведением смежных транспозиций по формуле:
(ij) = (j,j – 1)(j – 1, j – 2) … (2.25)
… (i + 2, i + 1)(i, i + 1)(i + 1, i + 2) … (j – 2, j – 1)(j – 1, j);
например
(48) = (87)(76)(65)(54)(56)(67)(78).
А любой цикл может быть разложен на транспозиции, причем несколькими способами:
(ijk) = (ij)(ik) = (jk)(ji) = (ki)(kj), (2.26)
(ijkl) = (ij)(ik)(il) = (jk)(jl)(ji) =
(jk)(jli) = (ik)(lij) = (ik)(li)(lj) = …;например:
a = (142)(56) = (14)(12)(56) = (42)(41)(56) =
= (21)(24)(56) = (56)(14)(12),
6 = (0624)(1735) = (06)(02)(04)(17)(13)(15) =
= (26)(46)(06)(35)(37)(13) = …
Справедливость формул (2.25) и (2.26) проверяется путем непосредственного перемножения смежных транспозиций.
Если дана подстановка, представленная в циклическом виде, то обратная ей ищется путем обратной записи последовательности всех ее индексов:
a = (ghijk)(lmn), a–1 = (gkjih)(lnm);
например,
6 = (0624)(1735), 6–1 = (0426)(1537) = 4.
Транспозиции, фигурирующие в формулах (2.25) и (2.26), связанные, так как имеют какой-либо общий индекс. Все связанные транспозиции не коммутируют и не могут быть переставлены местами. Если
a, b и c зависимые транспозиции, циклы или даже целые подстановки, то имеет место равенство:abc = c–1b–1a–1.
В частности, для связанных транспозиций имеем:
(ijkl)–1 = ((ij)(ik)(il))–1 =
((il)(ij)(ik))–1 = (il)(ik)(ij) =
(lkji).Более общий случай проиллюстрируем примером. Пусть дано следующее произведение подстановок:
x = c–1af 3b–2.
Чтобы найти x–1, нужно исходное выражение записать в обратном порядке с противоположными показателями степеней:
x–1 = b2f
–3a–1c.Правильность нахождения обратного выражения проверяется так:
x · x–1 = (c–1a f 3 b–2) · (b 2 f–3 a–1c) =
= (c–1(a (f 3(b–2b2)
f –3) a–1)
c) = e.Используя указанные свойства подстановок, записанных в циклическом виде, можно составить несколько полезных правил, которые сделают процедуру их перемножения почти механической. Вот некоторые из таких правил.
При умножении (слева или справа) смежной транспозиции на n-цикл длина последнего уменьшается на единицу и становится равной n – 1:
(abcdef…) · (cd) = (abdef…)(c),
(cd) · (abcdef…) = (abcef…)(d);
в частности,
(325614) · (56) = (32614)(5), (123) · (12) = (23)(1).
Более общее правило звучит так: произвольная транспозиция делит цикл на два несвязанных подцикла:
(abcdefgh…) · (cf) = (abfgh…)(cde),
(cf) · (abcdefgh…) = (abcgh…)(fde);
в частности,
(1234) · (13) = (12)(34), (13) · (1234) = (14)(23).
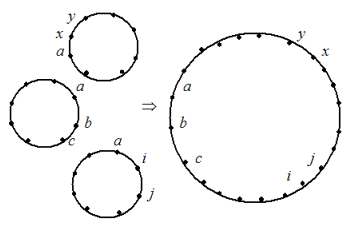
Обратное правило, которое можно было бы назвать правилом склейки двух циклов, проиллюстрированы рис. 2.1.
Рис. 2.1
(vwxyz)(abcdefgh) · (yc) = (vwxcdefghabyz).
Склеивание циклов произойдет и в том случае, если в них имеются одинаковые индексы, которые удобно записать первыми (рис. 2.2):
(abc…) · (aij…) · (axy…) = (abc…ij…xy…).

Рис. 2.2
При совпадении первых двух индексов склейки уже не получится:
(abcd…) · (abij…) = (aij…) · (bcd…).
Когда эти индексы в циклах переставлены местами, склейка снова возможна, но уже с выпадением одного из индексов:
(abcd…) · (baij…) = (a)(bcd…ij…).
В некоторых случаях полезными понятиями являются четность, декремент и число инверсий подстановки а. Декрементом (D) подстановки а называется разность между числом всех индексов (n) и количеством циклов (m), включая циклы единичной длины.
Число инверсий (I) подсчитывается следующим образом: для каждого индекса нижней строки подстановки а определяется количество стоящих правее его меньших индексов, затем полученные результаты складываются. Четность подстановки a определяется четностью числа транспозиций (T), на которые можно разложить подстановку. Если декремент и число инверсий являются нечетными, то и число транспозиций также будет нечетным. Пусть задана подстановка:a =
=
= (1)(253)(4)(67) = (1)(25)(23)(4)(67).
В соответствии с определениями имеем:
T = 3, D = n – m = 7 – 4 = 3,
I = 0 + 3 + 0 + 1 + 0 + 1 + 0 = 5.
К сказанному добавим: тождественная подстановка e четна, любая транспозиция — нечетна. Произведение четных подстановок и двух нечетных всегда даст четную подстановку, а умножение четной и нечетной — нечетную. С подстановками можно встретиться и при решении задач прикладной математики, в частности, при вычислении определителей. Вспомним, как ищется определитель третьего порядка:
det A =
=
= a11a22a33 +
a13a21a32 + a12a23a31 –
a13a22a31 – a12a21a33 –
a11a23a32.Здесь индексы представляют собой шесть подстановок третьего порядка, причем перед четными подстановками стоит плюс, а перед нечетными – минус. Аналогично будут вычисляться определители 4-го, 5-го порядков, только число слагаемых будет равно 24, 120.

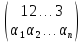
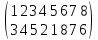
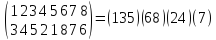
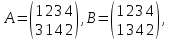

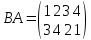


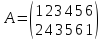
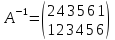
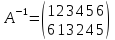
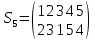
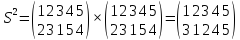
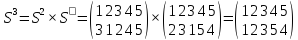
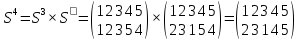
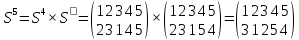
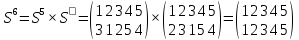
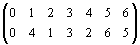 = (0)(142)(3)(56) =
= (0)(142)(3)(56) = 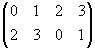 =
= 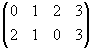
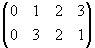 ,
,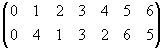 =
= 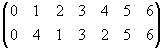
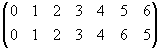 ,
,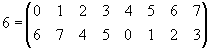
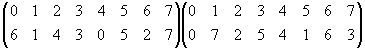 .
.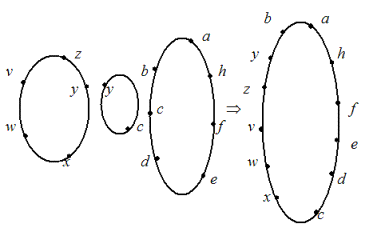
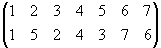 =
=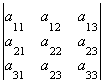 =
=