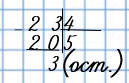- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Деление с остатком
Начнём рассмотрение новой темы с решения задачи.
Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?
8 : 2 = 4 (к.)
Каждый ребёнок получил по 4 конфеты.
На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?
Каждый получил по 2 конфеты и 2 конфеты остались лишними.
Как это записать?
8 : 3 = 2 (ост. 2)
Как сделать проверку?
2 • 3 + 2 = 8
Правило 1
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
16 : 7 = 2 (ост. 2)
23 : 8 = 2 (ост. 7)
Правило 2
При делении с остатком остаток всегда должен быть меньше делителя.
43 : 8 = 5 (ост. 3)
остаток 3 < делимого 5
34 : 4 = 8 (ост. 2)
остаток 2 < делимого 4
Правило 3
Если делимое меньше делителя, в частном получается ноль, а остаток равен делимому.
7 : 10 = 0 (ост. 7)
6 : 9 = 0 (ост. 6)
Порядок решения
14 : 5 = 2 (ост. 4)
1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.
10 : 5 = 2
2. Вычитаю из делимого найденное число: 14 − 10 = 4
3. Сравниваю остаток с делителем
4 < 5
Решение верно.
Проверка деления с остатком
1. Умножаю неполное частное на делитель.
2. Прибавляю остаток к полученному результату.
3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.
Деление в столбик
В 23 содержится 5 раз по 4, и ещё остаётся 3.
Решение записывают так:
23 : 4 = 5 (ост. 3) или так:
, где 23 — делимое, 4 — делитель, 5 — неполное частное, а 3 — остаток.
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
2 класс
Страница 76. Урок 29,
Петерсон, Учебник, часть 3
Страница 77. Урок 29,
Петерсон, Учебник, часть 3
Страница 79. Урок 30,
Петерсон, Учебник, часть 3
Страница 80. Урок 30,
Петерсон, Учебник, часть 3
Страница 81. Урок 31,
Петерсон, Учебник, часть 3
Страница 82. Урок 31,
Петерсон, Учебник, часть 3
Страница 84. Урок 32,
Петерсон, Учебник, часть 3
Страница 87. Урок 33,
Петерсон, Учебник, часть 3
Страница 108. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 61. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 40,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 83. Урок 30,
Петерсон, Учебник, часть 1
Страница 16. Урок 7,
Петерсон, Учебник, часть 2
Страница 91. Урок 40,
Петерсон, Учебник, часть 2
Страница 5. Урок 2,
Петерсон, Учебник, часть 3
Страница 17. Урок 7,
Петерсон, Учебник, часть 3
4 класс
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 12,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 536,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 766,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1091,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1722,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1792,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1820,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 533,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 613,
Мерзляк, Полонский, Якир, Учебник
Номер 769,
Мерзляк, Полонский, Якир, Учебник
Номер 1139,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 357,
Мерзляк, Полонский, Якир, Учебник
Номер 359,
Мерзляк, Полонский, Якир, Учебник
Номер 367,
Мерзляк, Полонский, Якир, Учебник
Номер 435,
Мерзляк, Полонский, Якир, Учебник
Номер 676,
Мерзляк, Полонский, Якир, Учебник
Задание 510,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 586,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 591,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 703,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1539,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 32,
Мерзляк, Полонский, Якир, Учебник
Номер 385,
Мерзляк, Полонский, Якир, Учебник
Номер 431,
Мерзляк, Полонский, Якир, Учебник
Номер 556,
Мерзляк, Полонский, Якир, Учебник
Номер 580,
Мерзляк, Полонский, Якир, Учебник
Номер 583,
Мерзляк, Полонский, Якир, Учебник
Номер 603,
Мерзляк, Полонский, Якир, Учебник
Номер 607,
Мерзляк, Полонский, Якир, Учебник
Номер 773,
Мерзляк, Полонский, Якир, Учебник
Номер 797,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 138,
Мерзляк, Полонский, Якир, Учебник
Номер 141,
Мерзляк, Полонский, Якир, Учебник
Номер 212,
Мерзляк, Полонский, Якир, Учебник
Номер 241,
Мерзляк, Полонский, Якир, Учебник
Номер 254,
Мерзляк, Полонский, Якир, Учебник
Номер 306,
Мерзляк, Полонский, Якир, Учебник
Номер 307,
Мерзляк, Полонский, Якир, Учебник
Математика, 3 класс
Урок № 46. Деление с остатком
Перечень вопросов, рассматриваемых в теме:
1. Может ли при делении число не разделиться полностью?
2. В каких случаях выполняется деление с остатком?
3. Какое правило поможет научиться делить с остатком?
Глоссарий по теме:
Деление – это обратное действие умножению.
Делимое – компонент деления, число которое делят.
Делитель – компонент деления, число на которое делят.
Частное – результат деления.
Неполное частное – результат деления с остатком.
Обязательная литература и дополнительная литература:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для
общеобразовательных организаций М.; Просвещение, 2017. – с. 26.
2. Математика. 3 класс. Часть 2. / Л. Г. Петерсон – М.: Ювента, 2013 – с. 96.
Теоретический материал для самостоятельного изучения
Как узнать, сколько раз по три содержится в семнадцати? Разделим семнадцать на три. В семнадцати пять раз содержится по три и ещё останется два.
Два – это остаток. Число не разделилось полностью, поэтому частное называют неполное.
При делении с остатком можно пользоваться рисунком.
Рисунок может быть не всегда удобным. Записывать деление с остатком можно в столбик или как ещё называют уголком.
Рассмотрим пример. Семнадцать надо разделить на три.
При записи уголком неполное делимое пятнадцать пишем под числом семнадцать, а неполное частное под делителем. Это число пять. Из семнадцати вычитаем пятнадцать останется два. Это остаток.
При делении с остатком результат записывают двумя числами: неполное частное и остаток.
Выполним тренировочные задания.
№ 1. Вставьте пропущенные числа:
59 : 8 = ___ (ост.___)
Ответ: 59 : 8 = 7 (ост.3)
№ 2. Соотнесите деление и результат.
24 : 5 4 (ост. 1)
13 : 3 3 (ост. 2)
17 : 5 4 (ост. 4)
Ответ: 24 : 5 = 4 (ост. 4)
13 : 3 = 4 (ост. 1)
17 : 5 = 3 (ост. 2)
№ 3. Решите задачу:
«Троим детям раздали 7 пирожных. Сколько получилось у каждого и сколько осталось?».
7 : 3 = 2 (ост. 1)
№ 4. Выделите цветом, какой остаток может быть при делении на 4:
Правильный ответ:
№ 5. Заполните таблицу:
Правильный вариант:
Рассмотрим пример.
В танцевальной студии было (14) человек. Для танца их разделили на группы по (2) человека.
Сколько групп получилось?
. Получилось (7) групп.
Действительно, если в одной группе два человека, то для семи групп потребовалось (14) человек, так как
2⋅7=14
.
Для следующего танца танцоров разделили на группы по (3) человека. Сколько получилось таких групп?
Получилось (4) группы, и (2) человека не танцевали.
Это можно записать так:
Действительно, если в каждые из (4) групп поставили по (3) танцора, и ещё два человека остались, то в танцевальной студии было (14) человек:
3⋅4+2=14
.
Деление с остатком — это деление одного натурального числа на другое, при котором остаток не равен нулю.
Пример:
1. Находим наибольшее число до (17), которое делится на (3) без остатка. Это (15).
2. Вычитаем из делимого найденное число из предыдущего пункта:
17−15=2
.
3. Сравниваем остаток с делителем:
При делении с остатком остаток всегда должен быть меньше делителя.
Обрати внимание!
Как проверить деление с остатком?
1. Умножить неполное частное на делитель.
2. Прибавить к полученному результату остаток.
3. Сравнить полученный результат с делимым.
1)5⋅3=15,2)15+2=17,3)17=17.
В случае, когда делимое меньше делителя, в частном получается ноль, а остаток равен делимому.
Например,
4:7=0(ост.4)
, так как
4⋅0+4=4и4<7
.
Источники:
Рисунки: схемы примеров. © Якласс.
В Ы У Ч И! З А П О М Н И!
Н А У Ч И С Ь В Ы П О Л Н Я Т Ь!
Алгоритм выполнения деления с остатком и его проверка.
- Определи в числовом выражении компоненты деления (делимое, делитель).
- В делимом определи, какое самое большое число можно разделить без остатка на делитель.
- Выполни деление. Раздели самое большое полученное число на делитель. Результат деления запиши в частном.
- Вычисли остаток. Для этого из делимого вычти то, число которое, разделили без остатка на делитель. Запиши, чему равен остаток.
Помни: Остаток всегда должен быть меньше делителя.
Выполнение проверки деления с остатком.
Выучи правило и научись его применять:
Чтобы выполнить проверку деления с остатком, нужно частное умножить на делитель и прибавить остаток.
- Выполни проверку письменно или устно, применяя правило. Сделай вывод: если, при проверке получилось делимое, то деление выполнено правильно.
Н А П Р И М Е Р:
Выполним деление: 39 : 5
- Определяем в выражении компоненты деления:
39 – это делимое, 5 – это делитель.
- Определяем, какое самое большое число до 39 делится на 5 без остатка ( Для этого вспомним таблицу умножения и деления). До 39 делится без остатка на 5 –число 35.
- Делим 35 на 5 – получается 7. В частном запишем 7.
- Вычислим остаток. Для этого из делимого 39 вычтем то число, которое делили без остатка на делитель – это число 35.
39 – 35 = 4 (4 – это остаток).
- Выполняем проверку. Применяем правило.
Частное – 7 умножим на делитель 5 и прибавим остаток 4, получается – 39 – это делимое. Значит деление с остатком выполнено верно.
Образец записи в тетради:
Проверка:
39: 5 = 7 (ост. 4) 7 ∙ 5 + 4 = 39
Тема
«Деление с остатком. Проверка деления с остатком»,
3
класс, УМК «Перспектива» — объяснение материала
Учитель
начальных классов МБОУ СШ № 7 г. Павлово Нижегородской обл. Зуева Елена
Витальевна
ДЕЛЕНИЕ
С ОСТАТКОМ
Вначале
вспомним, как называются компоненты деления
Не все числа можно
разделить с помощью таблицы умножения. В таком случае выполняется деление с
остатком.
►
Чтобы выполнить деление с остатком, нужно вспомнить, какое число в таблице
умножения ближе всех к делимому, но меньше его.
1) Например: 28 :
3 – вспоминаю таблицу на 3. Самое близкое число к 28 – это 27. Значит, буду
делить 27 на 3, получается 9 – это частное.
Теперь находим
остаток. Для этого от 28 отнимаю 27, получается 1 – это и есть остаток.
Записывают так
28 : 3 = 9 (ост. 1)
2) Примеры
рассуждения:
|
14 : 3 = ? 12 : 3 = 4 14 – 12 = 2 14 : 3 = 4 (ост. 2) |
52 : 6 = ? 48 : 6 = 8 52 – 48 = 4 52 : 6 = 8 (ост. 4) |
37 : 8 = ? 32 : 8 = 4 37 – 32 = 5 37 : 8 = 4 (ост. 5) |
►
Остаток всегда должен быть меньше делителя! Иначе
этот остаток можно будет ещё раз разделить на делитель.
16 : 5 = 2 (ост.
6) – неверно, так как 6 > 5 и его ещё раз можно разделить на 5.
16 : 5 = 3 (ост.
1) – верно, так как 1 < 5
► Бывает, что делимое
меньше делителя. Например: 3 ручки раздали 5 детям. Сколько ручек получит
каждый ребёнок? (ни одной, то есть — 0). Если делимое меньше делителя, частное
будет – 0, делимое будет остатком.
3 : 5 = 0 (ост. 3)
7 : 9 = 0 (ост. 7)
► Для того, чтобы
изучить и отработать тему «Деление с остатком», выполни задания на платформе
Учи.ру для 3 класса
1 – математика
2 – раздел
«Умножение и деление»
3 – тема
«Внетабличное умножение и деление»
4 – «Деление с
остатком», 3 карточки
ПРОВЕРКА
ДЕЛЕНИЯ С ОСТАТКОМ
►
Как выполнить проверку деления с остатком?
Для этого частное
нужно умножить на делитель (или наоборот) и к результату прибавить остаток. В
итоге должно получиться делимое.
Например:
45 : 7 = 6 (ост.
3)
Проверка:
6 ٠ 7 + 3 = 45
или 7 ٠ 6 + 3 = 45
►
Найдём верно и неверно решённые выражения
1) 21 : 4 = 5
(ост. 1) – верно, так как 4 ٠
5 + 1 = 21 и остаток 1 < делителя 4
2) 27 : 5 = 4
(ост. 7) – неверно. Даже если выполнив проверку 4 ٠
5 + 7 = 27 вы получаете заданное делимое, выражение решено неверно, так как
остаток 7 > делителя 5.
► Для того, чтобы
изучить и отработать тему «Проверка деления с остатком», выполни задания на
платформе Учи.ру для 3 класса
1 – математика
2 – раздел
«Умножение и деление»
3 – тема
«Внетабличное умножение и деление»
4 – «Проверка
деления с остатком», 3 карточки
► Для закрепления
изучаемого материала, вы можете посмотреть видео – урок, пройдя по
ссылке
https://infourok.ru/videouroki/1511