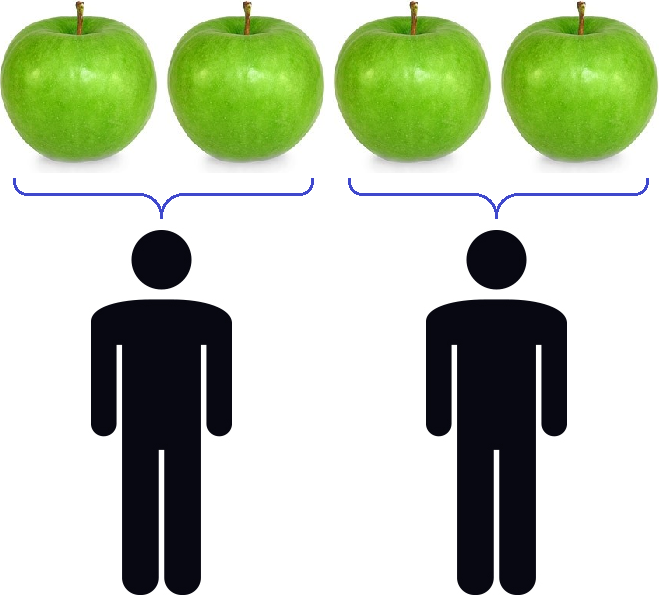
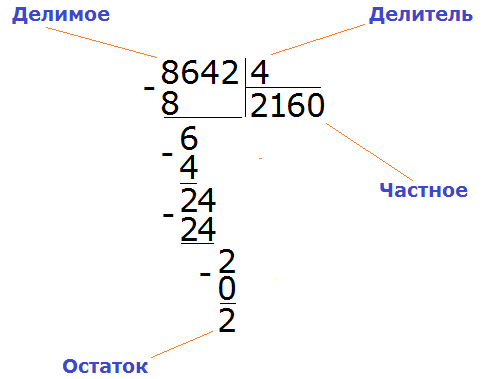
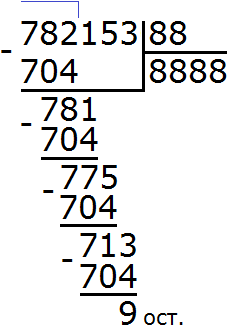
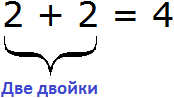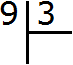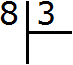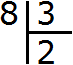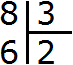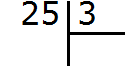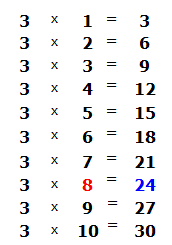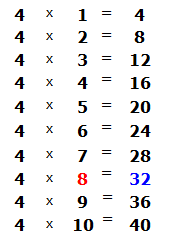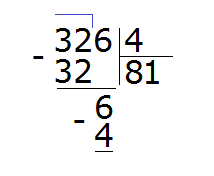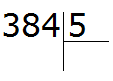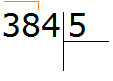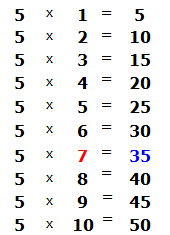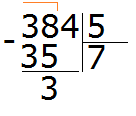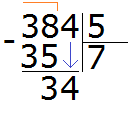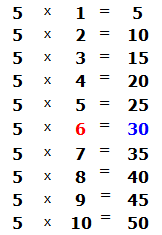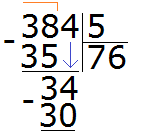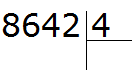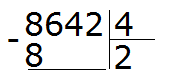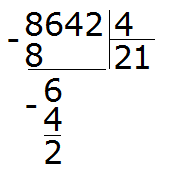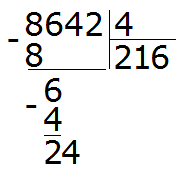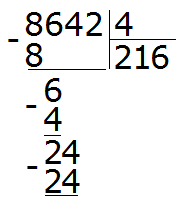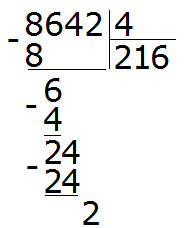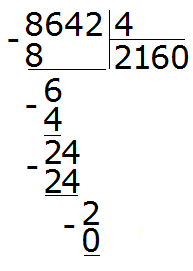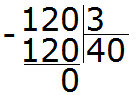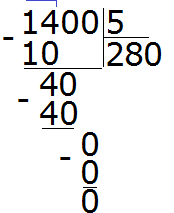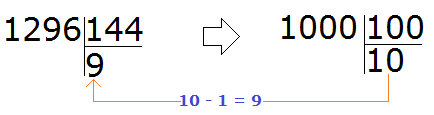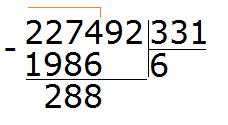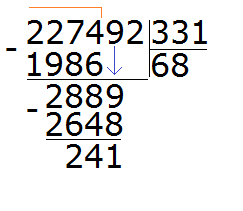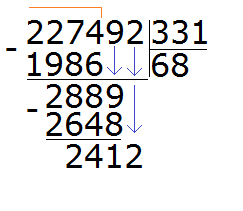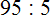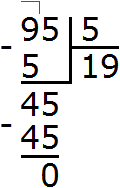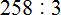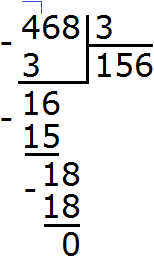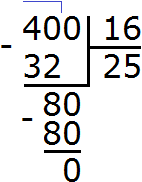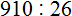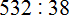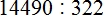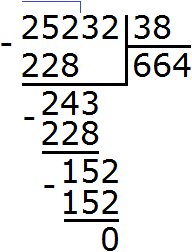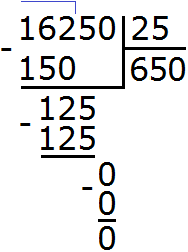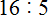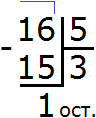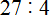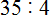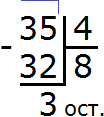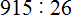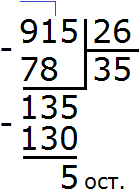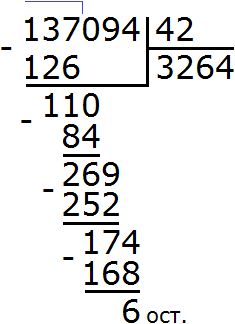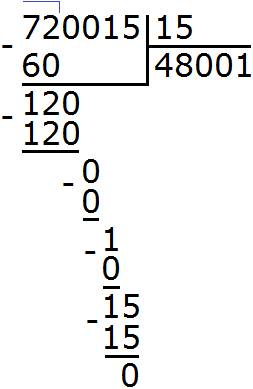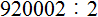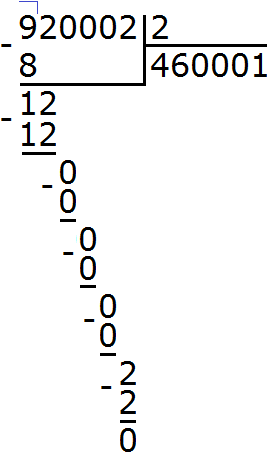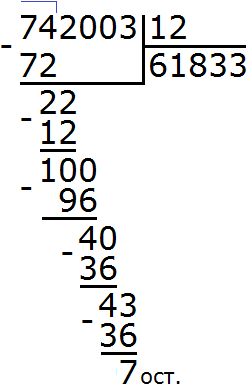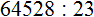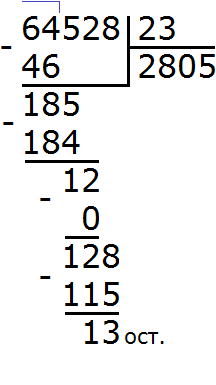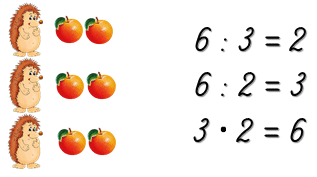Подобно тому, как вычитание является обратным действием для сложения, так и для умножения существует свое обратное арифметическое действие.
Рассмотрим задачу. В школьной столовой раздали 90 яблок по 3 яблока каждому ученику класса. Сколько учеников учатся в этом классе?
Если бы нам было известно количество учеников в классе и количество яблок, которое получил каждый из них, то общее число яблок мы узнали бы, умножив число учеников на число яблок, доставшееся каждому. То есть, количество учеников – это первый сомножитель, количество яблок – второй сомножитель, а сколько яблок раздали – это произведение.
Таким образом, в нашей задаче даны произведение и множитель (один из сомножителей), а неизвестный второй сомножитель необходимо отыскать. То есть, нам нужно найти число, умножив которое на 3, мы получим 90. Это число 30, потому что (textcolor{red} {30 cdot 3 = 90})
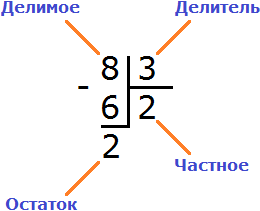
Деление – это арифметическое действие, которое состоит в нахождении одного из
сомножителей при помощи данного произведения и второго сомножителя.
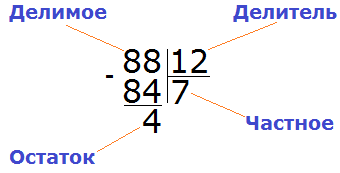
Делимое – это число, которое мы делим на другое. Это то самое произведение,
которое нам дано.
Делитель – это число, на которое мы делим делимое. Это данный нам один из
множителей.
Частное – это результат действия деление, то есть, искомый нами второй
сомножитель.
На записи действие деление обозначается: двоеточием ( (textcolor{red} {:}) ), знаком обелюс ( (textcolor{red} {div}) ), горизонтальной чертой или косой чертой ( (textcolor{red} {/}) ).
Так, решение нашей задачи
можно записать следующими способами:
- (textcolor{red} {90:3=30})
- (textcolor{red} {90div 3=30})
- (textcolor{red} {90/3=30})
- (textcolor{red} {Large frac{90}{3} normalsize =30})
При записи от руки действие деление принято записывать в виде двоеточия, обелюс применяется в печатной литературе, косая черта, которая по-другому называется слеш, – при записи на компьютере, а горизонтальная черта используется при записи деления в виде обыкновенной дроби.
Итак, разделить число a на число b – это значит найти такое число c, которое при умножении его на число b дает в результате числа a.
То есть: (textcolor{red} {adiv b=c}) , если (textcolor{red} {bcdot c=a}) .
И еще одно пояснение для понимания: разделить число a на число b означает разделить число a на b одинаковых частей, каждая из которых равна c. Иными словами, мы одно число a делим на равные части. Количество этих частей равно числу b. А величина каждой из этих частей – это результат действия деления, и эта величина равна c.
Например, нам нужно разделить 15 роз между пятью девочками так, чтобы каждая получила одинаковое количество цветов. Чтобы узнать, какое количество роз получит каждая девочка, нужно общее количество (15) цветов разделить на количество девочек (5), то есть, на 5 одинаковых частей. Нетрудно понять, что каждая из девочек получит 3 розы, потому что (textcolor{red} {5cdot 3=15}) .
Компоненты действия
деление:
Деление с остатком и неполное частное
Но не всегда можно одно число разделить на другое. Вернее сказать, что не всегда можно сделать это полностью. Например, 37 нельзя разделить на 5, потому что нет такого натурального числа, умножив которое на 5, мы получили бы 37. В этом случае говорят, что 37 не делится нацело на 5.
К примеру, если мы захотим раздать все 37 яблок поровну между пятью детьми, то у нас это сделать не получится. Мы сможем раздать (использовать из всего количества яблок) только по 7 яблок каждому ( (textcolor{red} {7cdot 5=35}) ), и у нас останется 2 яблока ( (textcolor{red} {37-35=2}) ).
В таком случае действие деление также состоит из делимого (в нашем случае 37) и делителя (5). Полученное число 7 называется неполное частное, потому что не все делимое число мы смогли разделить на необходимое число частей. А разница между полным делимым (37) и использованными из него единицами (35), то есть число 2, называется остаток.
Итак, деление с остатком – это нахождение
такого наибольшего целого числа, умножив которое на делитель, мы получим число,
максимально близкое к делимому, но не превосходящее его. Это искомое число
называется неполное частное. Разница
между делимым и неполным частным называется остаток.
Остаток всегда меньше делителя!
Отсюда следует общий вид действия деления натуральных чисел для случаев деления без остатка и с остатком.
Разделить целое число a (делимое) на целое число b (делитель) означает найти такие числа c и d, при которых справедливы следующие соотношения:
(textcolor{red} {a=bcdot c+d}) ;
(textcolor{red} {d<b}) .
Если (textcolor{red} {d=0}) , тогда говорят, что a делится на b без остатка.
Компоненты действия
деление с остатком:
Задачи, которые решаются при помощи
действия деления
В курсе математики
средней школы наиболее часто используется деление при решении таких задач,
когда нужно:
- Узнать, во сколько раз одно число меньше и больше другого? Этот вопрос может звучать по-другому: сколько раз меньшее число содержится (помещается) в большем? Или: сколько раз поместится в большем числе меньшее?
Например: сколько пятиграммовых стиков сахара находится в килограммовой упаковке? (1000 г : 5 г = 200 шт.). - Число разделить на заданное количество равных частей.
Например: сколько получится грамм сахара в каждом пакете, если пересыпать килограмм сахара в 5 одинаковых пакетов поровну? (1000 г : 5 шт. = 200 г). - Уменьшить число в заданное количество раз.
Например: для приготовления блюда на 5 человек использовали 1 кг сахара, а сколько сахара потребуется для приготовления этого же блюда для одного человека? (1000 г : 5 чел. = 200 г).
Связь деления с умножением, сложением и
вычитанием
Когда мы выполняем находим
произведение двух чисел, эти числа нам известны, а от нас требуется найти
результат действия умножение. При делении (без остатка) нам известно
произведение двух чисел, а найти нужно такое число, которое при умножении на
известное данное число дает это самое произведение.
Следовательно, действие
деление является обратным действию умножения.
Справедливо также и
обратное, что действие умножение обратно действию деления. Таким образом:
Умножение и деление – это
взаимно обратные действия.
Связь деления с
умножением, а также со сложением и вычитанием прекрасно видна, если
рассмотреть, как с помощью этих действий можно выполнить действие деление.
Рассмотрим их на примере: 345 разделить на 69.
Деление двух чисел при помощи сложения
Чтобы узнать при помощи сложения, сколько раз число 69 содержится в 345, нужно складывать последовательно 69 до тех пор, пока не получим нужного нам числа:
(textcolor{red} {69+69=138}) ; (textcolor{red} {138+69=207}); (textcolor{red} {207+69=276}); (textcolor{red} {276+69=345}).
Число 69 было слагаемым всего 5 раз, значит, (textcolor{red} {345div 69=5}) .
Деление двух чисел при помощи вычитания
Аналогично предыдущему способу, мы можем узнать, сколько раз в числе 345 содержится число 69, вычитанием. Для этого мы будем последовательно вычитать из 345 число 69 до тех пор, пока не получим нуль, и считать количество действий:
(textcolor{red} {345-69=276}); (textcolor{red} {276-69=207}); (textcolor{red} {207-69=138});
(textcolor{red} {138-69=69}); (textcolor{red} {69-69=0}).
То есть, 69 от 345 можно отнять 5 раз, поэтому (textcolor{red} {349div 69=5}).
Деление двух чисел при помощи умножения
При помощи умножения узнать ответ на наш вопрос можно перебирая множитель числа 69 до тех пор, пока не получим заданное нам 345:
(textcolor{red} {69cdot 2=138}); (textcolor{red} {69cdot 3=207}); (textcolor{red} {69cdot 4=276}); (textcolor{red} {69cdot 5=345}).
Искомое частное равно полученному множителю числа 69, то есть, 5.
Но эти три способа очень
громоздки, особенно если частное представляет собой очень большое число. Их
нужно знать только для того, чтобы понимать суть действия деления, суть тех
задач, которые решаются посредством него.
Общий принцип деления в столбик
Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.
Решим пример (textcolor{red} {295383div 34}).
Прежде всего, нужно узнать количество цифр в частном и первое неполное делимое; как их находить, я подробно расписал в этой статье. В нашем случае первое неполное делимое равно 295 тысяч, а в частном будет 4 цифры.
Далее записываем известные
компоненты деления следующим образом:
и начинаем вычисление:
1. Берем первое неполное делимое
и пытаемся его разделить на делитель.
Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.
Записываем в частное первую найденную цифру
разряда тысяч, а под неполным делимым пишем результат произведения неполного
частного и делителя. И сразу же находим остаток от этого действия, т.е.
вычитаем из неполного частного результат этого произведения.
В результате умножения первой найденной цифры частного на делитель у нас получилось (textcolor{red} {8cdot 37=272}). Записываем его под 295 и находим разницу: (textcolor{red} {295-272=23}). Значит, 23 тысячи у нас остаются неразделенными.
В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.
2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.
Находим результат деления второго неполного делимого на делитель. 233 сотни разделить на 34 будет 6 сотен. Значит, в разряде сотен частного будет цифра 6. Умножаем ее на делитель 34, получаем 204 и еще 29 сотен неразделенных.
3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.
При делении второго неполного делимого 298 десятков на делитель 34 получается 8 десятков, и еще 26 десятков неразделенных (как и в предыдущих действиях, я умножил 8 на 34 и результат отнял от 298). Поэтому, в частном, в разряде десятков записываем цифру 8.
4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.
Разделив 263 единицы на 34, получаем 7 полных единиц и 25 неразделенных. Записав в частном последнюю цифру разряда единиц, получаем окончательный ответ действия (textcolor{red} {295383div 34=8687}) и 25 в остатке.
Рассмотрим еще один пример. (textcolor{red} {25326div 63}).
Первое неполное делимое будет 253 сотни, количество цифр в частном – 3.
Делим 253 сотни на 63, получается 4 полных сотни и неразделенная 1 сотня в остатке.
1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.
Но 12 не делится нацело на 63 части, то есть, нет ни одного целого десятка в каждой части. Значит, мы в частном в разряде десятков должны записать 0, поскольку все 12 десятков оказались неразделенными. А к этим 12 десяткам (т.е. 120 сотням) добавить (снести) 6 единиц делимого.
Итак, запомните, что
каждое неполное делимое образует в частном одну цифру соответствующего разряда
и что даже если неполное делимое меньше делителя, то в частном все равно нужно
записать нулевой результат этого действия.
126 единиц делим на 63, получается 2 единицы без остатка. Теперь мы можем записать окончательный ответ деления (textcolor{red} {25326div 63=402}).
Итак, в общем виде алгоритм деления в столбик выглядит так:
1. Находим первое неполное делимое и количество цифр в частном.
2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.
3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.
4. Ставим между ними знак минус и выполняем действие.
5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.
6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.
7. Если неполное делимое невозможно разделить на делитель, то в частном ставится 0 и к этому неполному делимому сносится следующая цифра.
Деление на числа, заканчивающиеся нулями
Как и в случае с
умножением, деление чисел облегчается, если делитель заканчивается одним или
несколькими нулями. Рассмотрим два возможных случая:
- частный – когда делитель является единицей с нулями
- общий – когда делитель любое число, оканчивающееся нулями.
Рассмотрим первый случай.
Деление на единицу с любым количеством
нулей
Единица с любым количеством нулей – это не что иное как единица соответствующего разряда. Например, 10 – это 1 единица разряда десятков, 1000 – это одна единица разряда тысяч, 10000000 – 1 единица разряда десятков миллионов и т.д.
Следовательно, разделить число, к примеру, на 10, 1000, 10000000 и т.д. – это значит определить, сколько в нем содержится десятков, тысяч, десятков миллионов. А как узнать, сколько в каком-либо числе содержится единиц любого разряда я уже рассказывал в уроке разряды и классы. Для завершения действия деления нужно лишь записать в остаток число, которое получается из отбрасываемых нами цифр.
Например:
(textcolor{red} {75427916div 10=7542791}) (остаток 6);
(textcolor{red} {75427916div 1000=75427}) (остаток 916);
(textcolor{red} {75427916div 10000000=7}) (остаток 5427916).
Запишите:
Чтобы разделить какое-нибудь число на единицу с любым количеством нулей, нужно отсчитать в делимом справа столько цифр, сколько нулей содержится в делителе; тогда все цифры, находящиеся слева от разделения, составят частное, а те, что справа – будут остатком.
Деление на число, оканчивающееся нулями
Рассмотрим на примере (textcolor{red} {284556div 2800}).
Делитель здесь не что иное как 28 сотен. Логично предположить, что эти 28 сотен могут хотя бы один раз содержаться только в сотнях делимого. Значит, нам нужно определить, сколько в делимом всего единиц разряда сотен, и разделить их на 28 единиц разряда сотен делимого. А отброшенные цифры десятков и простых единиц добавятся к остатку.
В числе 284556 всего 2845 сотен да еще 56 единиц. Разделим 2845 сотен на 28 сотен, получим частное 101 и 17 сотен неразделенными. Прибавив к неразделенным 17 сотням 56 единиц из делимого, получим 1756. В этом числе делитель 2800 не помещается ни один раз, значит, 1756 – это остаток: (textcolor{red} {284556div 2800=101}) (остаток 1756).
Запишите:
Чтобы разделить какое-нибудь число на число, заканчивающееся нулями, нужно отбросить мысленно нули в делителе, в делимом тоже отбросить мысленно такое же количество цифр, как и нулей в делителе. Получившееся число в делимом разделить на получившееся число в делителе, а к остатку прибавить (снести) те цифры делимого, которые отбросили ранее.
Проверка деления
Так как делимое – это
делитель, умноженный на частное и плюс остаток, что следует из определения
деления, то результат выполнения деления можно проверить умножением.
Например:
После того, как мы умножили частное 241 на делитель 33, а к полученному произведению прибавили остаток 9, мы получили число 7962, что равно делимому. Значит, можно с большой уверенностью сказать, что действие деление выполнено верно.
Если в результате
действия деления не получилось остатка, то деление можно проверить и делением.
Действительно, если делимое – это произведение делителя и частного, то разделив
делимое на частное (один из сомножителей), мы должны получить второй
сомножитель, то есть, делитель.
Например:
Свойства деления
Свойства деления я
представлю двумя группами:
- действия с
единицей и нулем; - распределительные
свойства деления.
Давайте рассмотрим каждую
группу подробнее.
Действия деления с единицей и нулем
При делении числа на единицу получается то же самое число.
Действительно, разделить
число на единицу означает узнать, сколько единиц содержится в данном числе. А
количество единиц в числе – это не что иное, как само это число.
И ли вот, например, если 10 яблок нужно раздать одному человеку (10 поделить на 1), то ему все эти 10 яблок и достанутся, правда?
При деление одинаковых чисел (числа на равное число) в результате будет 1 (единица).
В самом деле, если все единицы какого-то числа разделить на количество частей, равное количеству единиц этого числа, то в каждая часть получит по 1 единице.
Например, если 20 яблок раздать 20 школьникам, то каждому достанется по 1 яблоку.
При делении нуля на любое число, отличное от нуля, в результате будет нуль.
Разделить нуль на число
означает найти такое число, умножив которое на данный делитель, мы получим в
результате нуль. А такое число только одно – это нуль.
На нуль делить нельзя, то есть, нуль не может выступать в роли делителя.
При делении каких угодно
чисел делителем может быть любое число, кроме нуля.
Рассмотрим два случая:
когда нулём является только делитель, и когда делимое и делитель оба нули.
Пусть делимое равно какому угодно числу, отличному от нуля, например, 12. Разделить число 12 на нуль – это значит найти такое число, которое при умножении на 0 дало бы в результате число 12. Но как известно, если любое число умножить на 0, то и получим тоже нуль. Следовательно, такого числа, какое нам нужно, не существует.
Допустим, что делимое и делитель оба являются нулями. В этом случае нам нужно отыскать такое число, которое при умножении на 0 дало бы в результате 0. А поскольку какое бы мы ни взяли число, при умножении его на 0, получим тоже нуль, то частным может выступать любое число из бесконечного множества чисел, следовательно, какого-то определенного результата от такого деления быть не может.
Распределительные свойства деления
Чтобы найти частное от деления суммы на число, нужно поделить каждое слагаемое на это число, и найти сумму полученных частных.
(textcolor{red} {(a+b+c)div d=adiv d+bdiv d+cdiv d}).
При этом подразумевается, что все действия деления получаются без остатка.
Например, чтобы найти результат деления суммы (textcolor{red} {24+16+48}) на 8, то есть, определить, какое количество восьмерок находится в сумме этих чисел, мы узнаем, сколько раз восьмерка содержится отдельно в каждом из чисел, а потом складываем полученные результаты.
Так, в 24 находится 3 восьмерки, в 16 – две, в 48 – шесть, итого (textcolor{red} {3+2+6=11}). А если мы сперва найдем значение всей суммы (textcolor{red} {24+16+48=88}), и поделим ее на 8, то ответ будет также (textcolor{red} {88div 8=11}).
Чтобы найти частное от деления разности на число, нужно поделить на это число отдельно сперва уменьшаемое, а потом вычитаемое, после чего найти разность первого частного и второго.
(textcolor{red} {(a-b)div c=adiv c-bdiv c})
При этом также предполагается, что при делениях уменьшаемого и вычитаемого на число не получается остатков.
Например: [textcolor{red} {(36-24)div 6=36div 6-24div 6=6-4=2}] Число 36 состоит из 6 шестерок, а 24 – из 4 шестерок, а забрав у 6 шестерок 4 шестерки, получим 2 шестерки. Такой же итог будет и если мы сперва у 36 отнимем 24 единицы (останется 12), а потом найдем, сколько в этой разнице содержится шестерок: (textcolor{red} {12div 6=2}).
Чтобы найти частное от деления произведения на число, нужно поделить на него только один из сомножителей, а результат умножить на неизмененные остальные.
(textcolor{red} {(acdot bcdot c)div d=adiv dcdot bcdot c=bdiv dcdot acdot c=cdiv dcdot acdot b}).
В самом деле, разделить, к примеру, (textcolor{red} {20cdot 25cdot 35}) на 5 означает уменьшить произведение в 5 раз. А так как если уменьшить один из сомножителей в определенное количество раз, то и произведение уменьшится в это же количество раз, тогда нам достаточно разделить любое из чисел 20, 25 или 35 на 5, чтобы получить ответ:
(textcolor{red} {(20cdot 25cdot 35)div 5=20div 5cdot 25cdot 35=3500}).
Чтобы найти частное от деления числа на произведение, нужно это число поделить на первый сомножитель, результат деления поделить на второй сомножитель, полученное частное – на третий и так далее.
(textcolor{red} {adiv (bcdot ccdot dcdot e)=adiv bdiv cdiv e}).
При этом предполагается, что при всех этих делениях не получается остатков.
Допустим, нужно поделить 30 на произведение (textcolor{red} {2cdot 3}). Мы знаем, что деление – это разложение числа на равные части. Значит, разделив 30 единиц на 2, мы находим, что в каждой из 2 равных частей содержится по 15 единиц. После этого мы эти 15 единиц делим на 3 равные части, и узнаем, что каждая из них содержит по 5 единиц.
На рисунке наглядно видно, что в итоге после применения этого правила, число 30 получилось разделенным на 6 равных частей.
Изменение частного при изменении
делимого и делителя
При рассмотрении
изменений частного в результате изменений делимого и делителя предполагается,
что действие деление происходит без остатка. В противном случае изменения могут
быть не такими, о которых идет речь ниже.
При увеличении делимого в определенное количество раз, частное увеличится в это же количество раз, а при уменьшении – уменьшится.
Если мы в примере (textcolor{red} {24div 4=6}) делимое увеличим, к примеру, в 3 раза, то мы можем переписать это выражение в виде (textcolor{red} {(24+24+24)div 4}). Используя свойство деления суммы на число, мы увидим, что теперь нам нужно сложить три слагаемых, каждое из которых равно начальному выражению: (textcolor{red} {24div 4+24div 4+24div4}). Отсюда очевидно, что результат будет больше начального в 3 раза.
Если мы в этом же примере (textcolor{red} {24div 6}) уменьшим делимое в 3 раза, то есть, разделим его на три равные части, то очевидно, что результат деления одной части на 6 будет в 3 раза меньше, чем результат деления трех таких же частей. Посмотрите сами. Начальное выражение (textcolor{red} {24div 6}) можно записать в виде: (textcolor{red} {(8+8+8)div 6=8div 6+8div 6+8div 6}), а уменьшенное в 3 раза делимое даст нам только одно из трех таких слагаемых: (textcolor{red} {8div 6}).
При увеличении делителя в определенное количество раз, частное уменьшится в это же количество раз, а при уменьшении – увеличится.
Действительно, изменение
делителя означает, что делимое необходимо разделить на большее или меньшее
количество равных частей. Соответственно, если нужно разделить на большее число
частей, то каждая часть будет меньше, чем изначально, а если делить на меньшее
число частей, то каждая часть будет крупнее.
В случае одновременного изменения делимого и делителя, частное может вести себя по-разному, или же вообще оставаться без изменений. Если нужно узнать, станет оно больше или меньше, нужно сперва посмотреть, как частное изменится после изменения делимого, а потом – как изменится после изменения делителя.
При увеличении или уменьшении делимого и делителя в одинаковое количество раз, частное не меняется.
Попробуйте самостоятельно
доказать справедливость этого утверждения. Пишите в комментариях, получилось
это, или нет.
Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.
Что такое деление?
Деление это действие, позволяющее что-либо разделить.
Деление состоит из трёх параметров: делимого, делителя и частного.
Делимое это то что делят;
Делитель это число, показывающее на сколько частей нужно разделить делимое.
Частное это собственно результат.
Пусть у нас имеются 4 яблока:
Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:
Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:
В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.
Говоря о делении, можно рассуждать и по-другому. Вернёмся к предыдущему выражению 4 : 2 = 2. Можно посмотреть на делитель 2 и задать вопрос «сколько двоек в четвёрке?» и ответить: «две двойки». Действительно, если сложить две двойки, то получится число 4
В ситуации с четырьмя яблоками можно задать вопрос «сколько раз два яблока содержатся в четырёх яблоках» и ответить: «два раза».
Чтобы научиться делить, нужно хорошо знать таблицу умножения. Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если у нас имеются два яблока и мы захотим увеличить их в пять раз, то запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то запишем 10 : 5 = 2
Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷
На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.
Деление с остатком
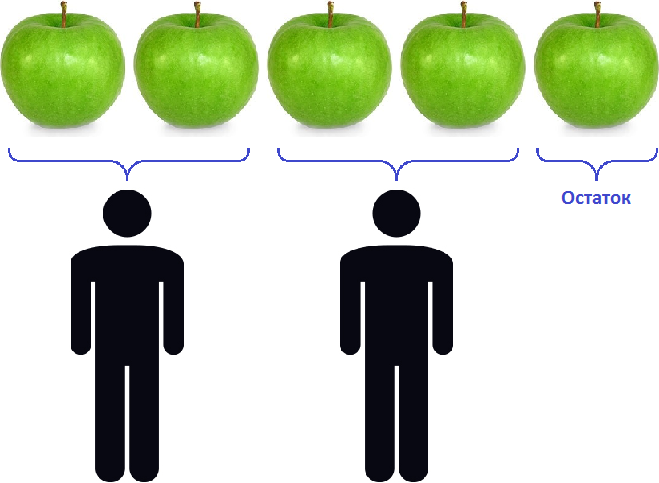
Остаток — это то что осталось от действия деления неразделённым.
Например, пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Можно проверить это умножением:
(2 × 2) + 1 = 5
Допустим, имеются пять яблок:
Разделим их поровну на двоих друзей. Но разделить поровну пять целых яблок не полýчится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:
Деление уголком
Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.
Прежде чем делить уголком, человек должен знать:
- обычное деление маленьких чисел;
- деление с остатком;
- умножение в столбик;
- вычитание в столбик.
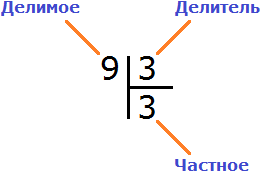
Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9 : 3. Уголком это выражение записывается следующим образом:
Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:
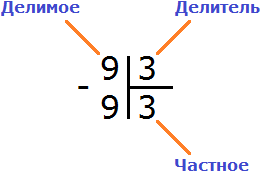
Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа: 3 × 3 = 9. Получили 9. Записываем эту девятку под делимым:
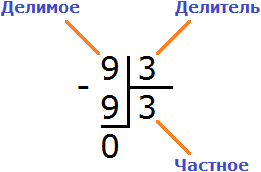
Теперь от делимого вычитаем девятку, которую мы под ним написали: 9 − 9 = 0. Остаток равен нулю. Проще говоря, остатка нет. На этом деление успешно завершено:
Пример 2. Найти значение выражения 8 : 3
Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.
Сначала запишем данное выражение уголком:
Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:
В школе частное подбирается методом подбора. Все мы слышали такие фразы как «берём по одному» , «берём по два» или «берём по три». У нас сейчас как раз такой случай. Мы взяли по два, ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:
Теперь вынимаем остаток. Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:
Далее из 8 вычитаем 6. Полученное число и будет остатком:
8 : 3 = 2 (2 в остатке)
Проверка:
(2 × 3) + 2 = 6 + 2 = 8
Деление многозначного числа на однозначное
Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.
В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.
Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.
Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя. Если больше, то её надо разделить на делитель, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то надо разделить их на делитель, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.
Сложно? Ни чуть, если мы разберём несколько примеров.
Пример 1. Найти значение выражения 25 : 3
25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше чем три? Да. Поэтому выполняем деление числа 25 на 3. Записываем уголком данное выражение и начинаем делить:
Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему. Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:
Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.
Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:
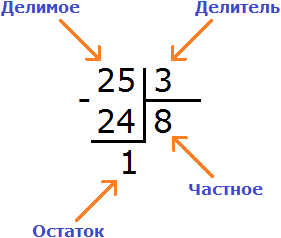
Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:
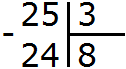
25 : 3 = 8 (1 в остатке)
Проверка:
(8 × 3) + 1 = 24 + 1 = 25
Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.
В приведённом примере последним остатком было число 1, а делителем число 3. Единица меньше чем три, поэтому деление завершено. Последний остаток мéньший делителя говорит о том, что он не содержит чисел равных делителю.
В нашем примере, если задать вопрос «сколько троек в единице?», то ответом будет «нисколько», потому что единица не содержит троек.
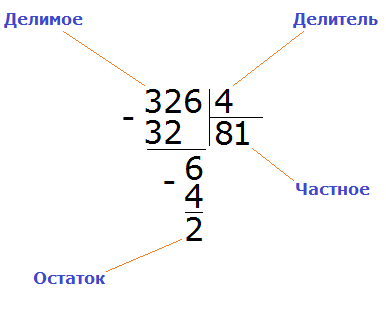
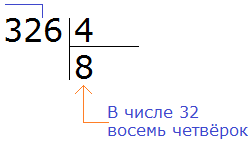
Пример 2. Разделить 326 на 4.
Смóтрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да. Значит можно выполнять деление.
Записываем уголком данное выражение:
Теперь задаём вопрос: «сколько четвёрок в числе 32?». В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:
Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:
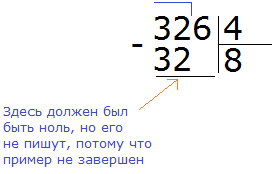
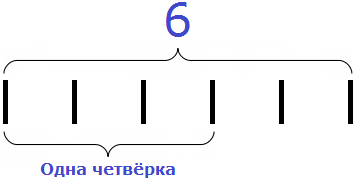
Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:
Записываем единицу в правом уголке нашего ответа:
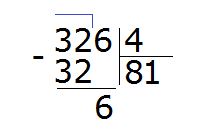
Затем из 6 вычитаем 4, получаем число 2, которое является остатком:
Получили 326 : 4 = 81 (2 в остатке)
Проверка: (81 × 4) + 2 = 324 + 2 = 326
Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.
Вернёмся к предыдущему примеру 326 : 4. Первое неполное делимое в данном выражении было число 32, поскольку его мы разделили в первую очередь.
А в примере 25 : 3 первое неполное делимое было 25.
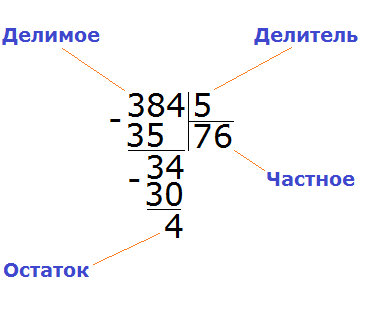
Пример 3. Найти значение выражения 384 : 5
Записываем данное выражение в уголком:
Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:
Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:
Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение. Это множитель 7, который выделен красным.
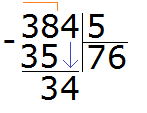
Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:
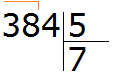
Теперь из 38 вычитаем 35, получим 3:
Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:
Видно, что после того, как мы снесли четвёрку, она вместе с тройкой образовала число 34. Это число 34 мы будем делить на 5. Для этого опять задаем вопрос: «сколько пятёрок в числе 34?». Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему или равно ему:
Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:
Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:
Теперь из 34 вычитаем 30, получаем 4. Эта четвёрка будет остатком от деления 384 на 5
384 : 5 = 76 (и 4 в остатке)
Проверка:
(76 × 5) + 4 = 380 + 4 = 384
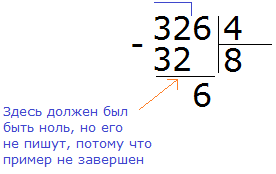
Пример 4. Найти значение выражения 8642 : 4
Этот пример немного посложнее. Записываем уголком данное выражение:
Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2
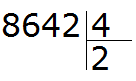
Вытаскиваем остаток: 8 − 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не записываем, поскольку решение примера не завершено.
Далее сносим цифру 6 и делим её на делитель, получаем 1
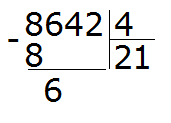
Получили остаток 2. Это остаток, который остался от деления 6 на 4.
Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6
Умножаем 6 на 4, получаем 24. Записываем это число под 24
Вытаскиваем остаток: 24 − 24 = 0. Ноль это остаток от деления 24 на 4. Ноль, как мы уже договорились, не записываем. Далее сносим последнюю цифру 2
Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Если мы зададим вопрос «сколько четвёрок в двойке?«, то ответом будет ноль, поскольку двойка меньше четвёрки и не может содержать в себе число, бóльшее себя самогó.
Поэтому два разделить на четыре это ноль:
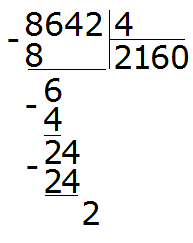
Теперь находим остаток: 2 − 0 = 2. Двойка это остаток от деления 8642 на 4. Таким образом, пример завершён:
8642 : 4 = 2160 (2 в остатке)
Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642
Деление чисел, у которых на конце 0
Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.
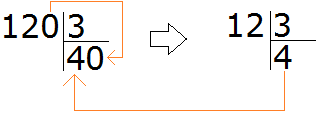
Например, разделим 120 : 3
Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:
Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее находим остаток: 120 − 120 = 0. Остаток равен нулю. Пример завершён.
120 : 3 = 40
Проверка 40 × 3 = 120.
Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:
12 : 3 = 4 (делимое без нулей на конце)
120 : 3 = 40 (здесь у делимого один ноль)
1200 : 3 = 400 (здесь у делимого два нуля)
12000 : 3 = 4000 (здесь у делимого три нуля)
В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.
Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5
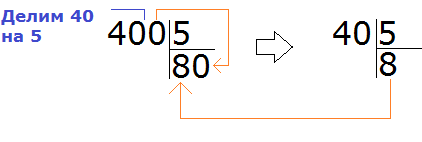
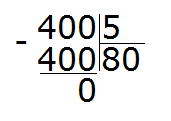
Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.
Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:
1000 + 400 = 1400
Можно по-отдельности разделить 1000 на 5 и 400 на 5:
1000 : 5 = 200
400 : 5 = 80
и сложить полученные результаты:
200 + 80 = 280
Итого: 1400 : 5 = 280
Решим этот же пример уголком:
Деление многозначного числа на многозначное
Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так-то просто.
Принцип деления остаётся тем же что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.
Для начала введём новое понятие — круглое число. Круглым будем называть число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 500, 600, 1000, 13000
Любое число можно превратить в круглое. Для этого первую цифру, образующую самый старший разряд, оставляют без изменений, а остальные цифры заменяют нулями.
Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10
Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.
Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.
Превратим число 13735 в круглое число. Первая цифра 1 образуют старший разряд (разряд десятков тысяч) — эту цифру оставляем без изменений, а остальные цифры заменяем нулями. В итоге получаем 10000.
Внимание! В дальнейшем понятия круглого числа и перевод любого числа в круглое будут рассмотрены более подробно.
Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное надо находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.
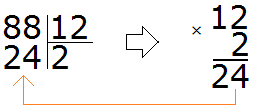
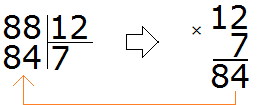
Пример 1. Найти значение выражения 88 : 12
Записываем данное выражение уголком:
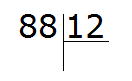
Со школы мы помним, что частное подбиралось методом угадывания, говоря «берем по два» или «берем по три».
Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число которое меньше делимого, но очень близко к нему или равно ему.
Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12
Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит.
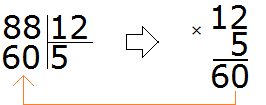
Пробуем следующее число. Допустим частное равно 5
Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит.
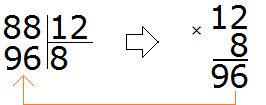
Попробуем сразу взять по 8
На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7
Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.
88 : 12 = 7 (4 в остатке)
Проверка: (12 × 7) + 4 = 84 + 4 = 88
Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.
Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.
Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.
Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.
В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.
Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:
800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)
800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)
900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)
400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 
320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)
Заметно, что всё в конечном итоге свóдится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.
Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания.
Для начала превращаем делимое и делитель в круглые числа.
Круглым числом для 88 будет число 80.
А круглым числом для 12 будет число 10.
Теперь делим полученные круглые числа:
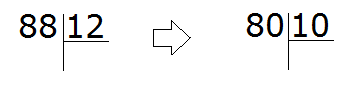
Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.
Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.
Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:
Как видно, этим способом мы решили этот пример намного быстрее.
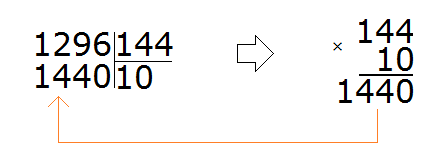
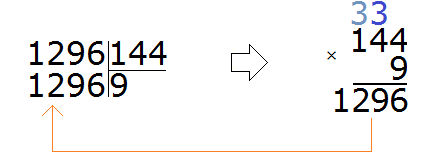
Пример 2. Найти значение выражения 1296 : 144
Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:
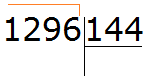
Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.
Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144
Десятка не подходит, поскольку при умножении получается число, которое больше делимого.
Попробуем взять по 9, уменьшив десятку на единицу.
Проверяем девятку. Для этого умножаем её на делитель:
Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296
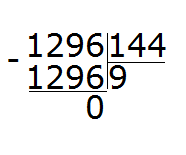
Проверка: 144 × 9 = 1296
Пример 3. Попробуем решить большой и сложный пример 227 492 : 331
Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.
Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300

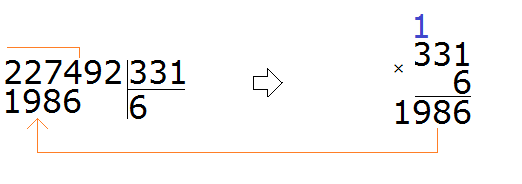
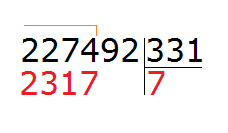
Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:
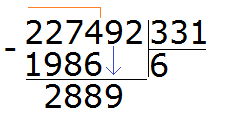
288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:
Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:
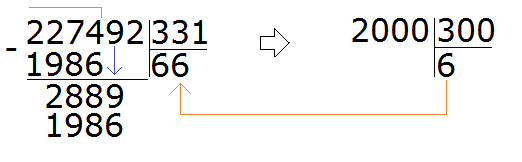

Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.
Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241
241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:
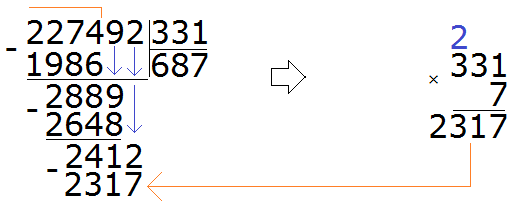
Теперь делим 2412 на 331. Возьмём по 7
Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:
227 492 : 331 = 687 (95 в остатке)
Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492
На этом данный урок можно завершить. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.
Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.
Задания для самостоятельного решения
Задание 1. Выполните деление:
Решение:
Задание 2. Выполните деление:
Решение:
Задание 3. Выполните деление:
Решение:
Задание 4. Выполните деление:
Решение:
Задание 5. Выполните деление:
Решение:
Задание 6. Выполните деление:
Решение:
Задание 7. Выполните деление:
Решение:
Задание 8. Выполните деление:
Решение:
Задание 9. Выполните деление:
Решение:
Задание 10. Выполните деление:
Решение:
Задание 11. Выполните деление:
Решение:
Задание 12. Выполните деление:
Решение:
Задание 13. Выполните деление:
Решение:
Задание 14. Выполните деление:
Решение:
Задание 15. Выполните деление:
Решение:
Задание 16. Выполните деление:
Решение:
Задание 17. Выполните деление:
Решение:
Задание 18. Выполните деление:
Решение:
Задание 19. Выполните деление:
Решение:
Задание 20. Выполните деление:
Решение:
Задание 21. Выполните деление:
Решение:
Задание 22. Выполните деление:
Решение:
Задание 23. Выполните деление:
Решение:
Задание 24. Выполните деление:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Определение
Деление столбиком — это стандартный математический метод для деления простых или сложных многозначных чисел изучаемый в 4 классе начальной школы. При делении столбиком, как и при обычном делении, первое число — это делимое, второе — делитель, а результат — частное.
В столбик можно выполнять как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи чисел при делении столбиком
Сначала делимое и делитель записываются в одну строку слева направо, после чего следует символ вида:
Например, если делимое равно 7439, а делитель 43, то правильная запись в столбце будет следующей:
Рассмотрим следующую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
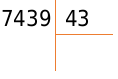
Рассмотрим общую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
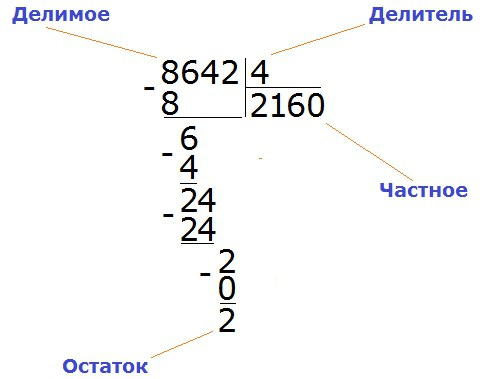
Из схемы выше видно, что частное будет написано под делителем, т.е. ниже горизонтальной линии, а промежуточные расчеты пишутся под делимым.
Деление столбиком на однозначное число
Практические навыки лучше всего отрабатываются на простых примерах. Поэтому делим числа 9 и 3 в столбик. Конечно, эту операцию легко проделать в уме или по таблице умножения, однако подробный разбор для наглядности будет полезен, хотя мы уже знаем, что 9 ÷ 3= 3. Итак, сначала запишем делимое и делитель по методу деления в столбик:
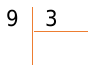
Далее определяем число делителей, имеющихся в делимом. Как определить? Поэтапно умножать делитель на 0, 1, 2, 3…, до тех пор, пока в итоге не получится число, равное или большее, чем делимое. Если в итоге сразу окажется число, равное делимому, под делителем запишем число, на которое делитель умножался.
Иными словами, когда получается число, большее делимого, под делителем записываем число, высчитанное на предпоследнем этапе. Вместо неполного частного записываем число, на которое делитель умножался на предпоследнем этапе.
[3 times 0=0 ; 3 times 1=3 ; 3 times 2=6 ; 3 times 3=9]
Итак, мы имеем число, равное делимому. Запишем его под делимыми, а вместо частного стоит число 3, на которое мы умножили делитель:
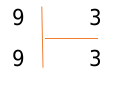
Теперь осталось вычесть числа под делителем (тоже методом столбца). В нашем случае 9 — 9 = 0.
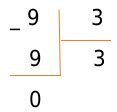
Этот пример деления числа без остатка. Число после вычитания имеетс остаток от деления. Если он равен нулю, числа полностью делятся. Теперь рассмотрим пример деления числа с остатком.
Разделим натуральное число 7 на натуральное число 5.
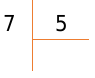
При этом 5 последовательно умножается на 0, 1, 2, 3. ..получаем в результате:
[5 times 0=0<9 ; 5 times 1=5<9 ; 5 times 2=10>9]
Под делимым запишем число, полученное на предпоследнем этапе. Под делителем пишем число 1 — неполное частное, полученное на предпоследнем этапе. Именно на 1 мы помножили делитель, когда получили 5.
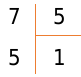
В завершение операции вычитаем 5 из 7 и получаем:
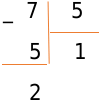
Это пример деления числа с остатком. Неполное частное равно 1, а остаток равен 2. Теперь, после изучения простейших примеров, поделим многозначные натуральные числа на однозначные значения.
Изучим механизм деления столбиком на примере деления числа 140288 на число 4.
Понять суть принципа намного легче на практических примерах, и этот пример был избран неслучайно, так как описывает все вероятные аспекты деления натуральных чисел столбиком.
Алгоритм деления столбиком
Рассмотрим подробне алгоритм деления натуральных чисел в столбик. Для этого запишем числа совместно со знаком деления столбиком. Далее смотрим на первую цифру слева в записи делимого. Вероятны два случая: число, вычисляемое этой цифрой, больше делителя и наоборот. В первом моменте работаем с этим числом, во втором добавочно берем последующую цифру в записи делимого и работаем с подобающим двузначным числом. В соответствии с этим пунктом выберем в примере число, с которым будем работать первоначально. Это число 14, так как первая цифра делимого 1 меньше делителя 4.
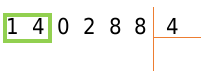
Определите, сколько раз числитель входит в полученное число. Обозначим это число как x = 14 Последовательно умножаем делитель 4 на каждый элемент ряда натуральных чисел N, включая ноль: 0, 1, 2, 3 0, 1, 2, 3 и так далее. Мы делаем это до тех пор, пока результат не будет х или число больше, чем х. Когда результат умножения равен 14, мы записываем его под выбранным числом в соответствии с правилами вычитания столбца. Под делителем пишут множитель, на который умножался делитель. Если результатом умножения является число больше х, то под выбранным числом вписываем число, полученное на предпоследнем шаге, а вместо неполного частного (под делителем) вписываем множитель, на который производилось умножение на предпоследний шаг.
В соответствии с алгоритмом имеем:
[4 times 0=0<14;\4 times 1=4<14;\4 times 2=8<14;\4 times 3=12<14;\14 times 4=16>14.]
Под отмеченным числом пишем полученное на предпоследнем шаге число 12. Вместо частного пишем множитель 3.
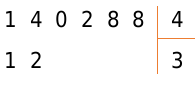
Вычтите 12 из 14 и запишите результат под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
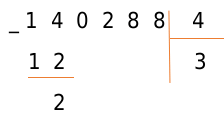
Число 2 меньше числа 4, поэтому запишем под горизонтальной чертой после двойки число, находящееся в следующем числе делимого. Если в делимом больше нет цифр, то деление окончено. В нашем примере после числа 2, полученного в предыдущем пункте, пишем следующую цифру делимого — 0. Соответственно, помечаем новое рабочее число — 20.
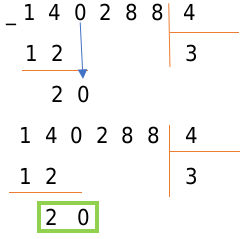
Важно
Пункты 2 − 4 циклически повторяются до окончания деления натуральных чисел.
Снова вычисляем, сколько содержится делителей в числе 20. Умножая 4 на 0, 1, 2, 3. . получаем: [4 times 5=20]. Так как в результате мы получили число равное 20 , пишем под отмеченным числом, а вместо частного в следующем бите пишем 5 — множитель, на который производилось умножение.
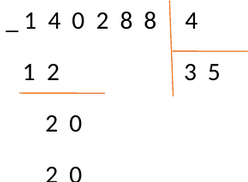
Проведем вычитание: 20 − 20 = 0
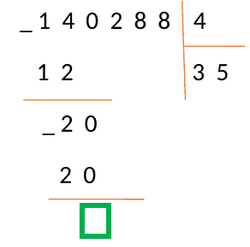
Цифру ноль писать не будем, потому что этот шаг не является концом деления. Давайте просто запомним место, где мы могли его написать и рядом напишем число из следующего разряда делимого — в нашем случае это число 2.
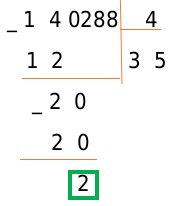
Умножьте делитель на 0, 1, 2, 3.. и сравните результат с отмеченным числом:
[4 times 0=0<2;\4 times 1=4>2]
Следовательно, под отмеченным числом пишем число 0, а под делителем в следующем разряде частного тоже пишем 0.
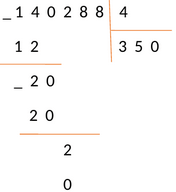
Выполняем операцию вычитания и записываем результат под чертой.
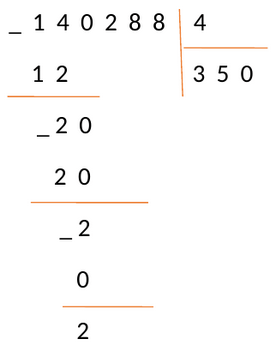
Справа, под чертой, прибавьте число 8, так как это следующая цифра делимого числа.
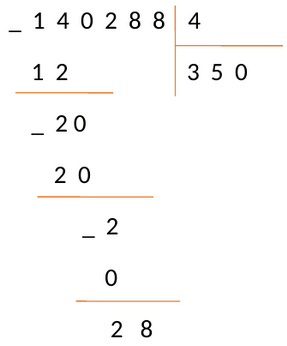
Следовательно, получаем новое рабочее число – 28, и снова повторяем пункты алгоритма.
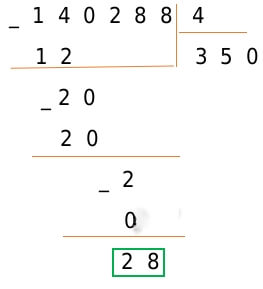
Вычислив все по правилам, получаем результат:
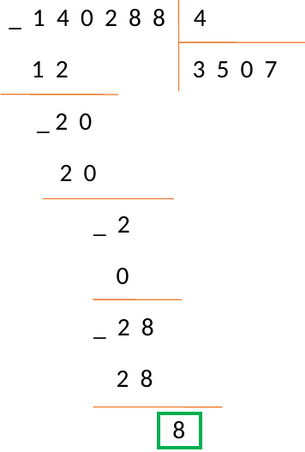
Переносим последнюю цифру делимого 8 под черту. В последний раз повторяем шаги алгоритма 2 − 4 и получаем:
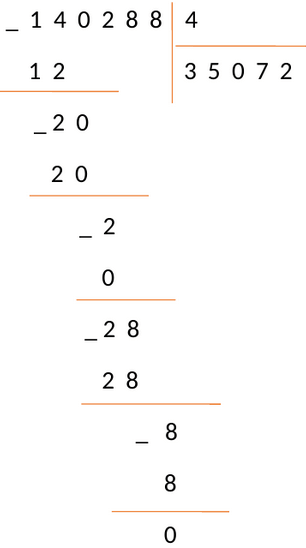
В нижней строке пишем число 0. Это число пишется только в последней фазе деления, когда операция завершена.
Рассмотрев алгоритм деления можно выделить общее правило деления натуральных чисел в столбиком:
- Делим тысячи;
- Делим сотни:
- Делим десятки;
- Делим единицы.
Рассмотрим другие примеры:
Пример №1
Выполним деление 7485 на 3:
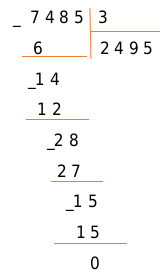
Следовательно, 7485 : 3 = 2495
Проверка:
2495*3=7485
Пример № 2:
Разделим 318624 на 6:
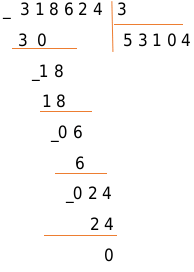
Проверка: [54104 times 6=318624]
Нет времени решать самому?
Наши эксперты помогут!
Деление на многозначные натуральные числа столбиком
Алгоритм деления на многозначные числа столбиком весьма схож с ранее изученным механизмом деления многозначного числа на единичное число. Точнее, преобразования касаются только первого абзаца, а пункты 2-4 остаются без изменений. Если при делении на однозначное число мы смотрели только на первую цифру делимого, то сейчас будем смотреть на столько цифр, сколько их в делителе.Когда число, вычисляемое этими цифрами, больше делителя, мы берём это как рабочую цифру, иначе прибавляем лишнюю цифру из следующей цифры делимого. Далее следуем пунктам, изложенным в прошлом алгоритме. Изучим применение алгоритма многозначного деления на примере.
Пример №3
Разделим 5562 на 206.
В делителе три числа, поэтому в делимом сразу выбираем 556. Умножьте 206 на 0, 1, 2, 3.. и получаем:
[206 times 0=0<556;\206 times 1=206<556\206 times 2=412<556; text { деление}\206 times 3=618>556]
Следовательно, под делителем записываем результат предпоследнего действия, а под делимым — множитель 2.
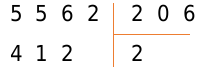
Продолжаем вычисления:
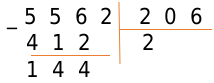
В результате получаем число 144. Справа от результата под чертой пишем число из соответствующей цифры делимого и получаем новое рабочее число – 1442.
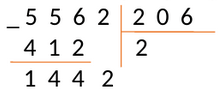
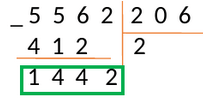
Повторяем пункты 2 − 4. Получаем:
[begin{gathered} 206 times 5=1030<1442; \ 206 times 6=1236<1442; \ 206 times 7=1442,1442=1442 end{gathered}]
Под выделенным числом записываем 1442, а в следующий разряд частного записываем цифру 7- множитель.
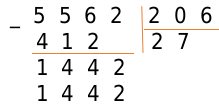
Выполним вычитание в столбик, и поймем, что операция деления окончена: в делителе больше нет цифр, чтобы писать их справа от результата вычитания.
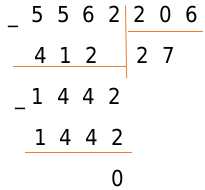
Ответ: 27
Пример № 4
Разделим 36261 на 153
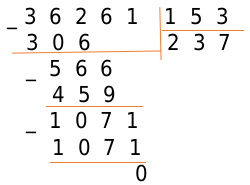
Проверка: [237 times 153=36261].
Ответ: 237
Пример № 5
Разделим 25725000 на 70
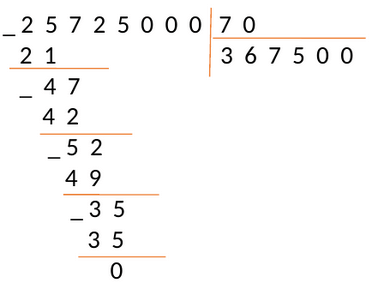
Проверка: [367500 times 70=25725000].
Ответ: 367500
Примеры деления на многозначное число с остатком
Пример №6:
Разделим 14507 на 186
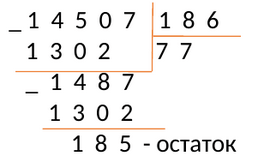
Проверка: [186 times 77=14507].
Пример №7:
Разделим 300428 на 505
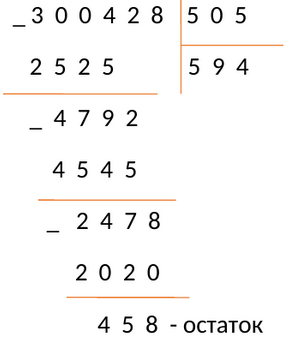
Проверка: [505 times 594=300428].
Деление десятичной дроби на натуральное число
Деление десятичной дроби в столбик производится по правилам деления натуральных чисел.
Рассмотрим детальней на примере: [1505,86 div 43=35,02].

Пример №8:
Разделим 5612,8 на 350,8
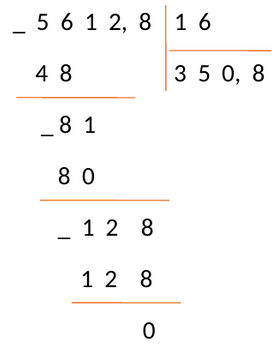
Проверка: [350,8 times 16=5612,8]
Деление столбиком используют, когда нужно разделить простые или сложные многозначные числа. Оно помогает найти ответ за счёт разбивания решения на ряд более простых шагов. В статье объясним на примерах, как делить в столбик и дадим пошаговый алгоритм.
Какие арифметические действия используют при делении в столбик
При знакомстве с делением в столбик у школьника могут возникнуть трудности и недопонимания. Отчасти потому, что при сложении в столбик мы только складываем, а при вычитании только вычитаем. Когда же мы делим в столбик, то по очереди выполняем: деление, умножение и вычитание. Кроме того, нужно знать таблицу умножения, уметь делить с остатком и аккуратно писать цифры, каждую в своей клетке, чтобы не ошибиться в расчётах.
Термины «делимое», «делитель», «частное», «неполное делимое»
Деление двузначного числа на однозначное
Разделим 86 на 2
1. Для начала определим первое неполное делимое и узнаем, сколько будет цифр в частном. 8 можем разделить на 2, значит, 8 — первое неполное делимое, в частном будет первая цифра. После 8 есть ещё одна цифра, значит, и в частном будет ещё одна цифра — всего две цифры.
2. Разделим первое неполное делимое 8 на делитель 2, получим первую цифру частного — 4.
3. Умножим делитель 2 на цифру частного 4, получим ответ — 8. Этот результат записываем под первым неполным делимым.
4. Находим остаток 8 — 8 = 0. Остаток 0 меньше делителя 2, значит, продолжаем вычисления. Остаток 0 можно не писать.
5. Сносим (переписываем) цифру 6 — это новое неполное делимое.
6. Делим неполное делимое 6 на делитель 2, получаем — 3. Результат записываем в частное.
7. Умножаем делитель 2 на новую цифру частного 3, получаем 6. Результат записываем под вторым неполным делимым.
8. Записываем последний остаток 0. Больше мы не можем снести ни одной цифры, значит, неполных делимых не осталось. Деление в столбик закончено.
Деление трёхзначного числа на однозначное
Разделим 486 на 3
1. Сначала определим, сколько цифр в частном: первая цифра делимого — 4, мы можем разделить 4 на 3, значит, в частном будет первая цифра. После первого неполного делимого ещё две цифры, значит, и в частном будет ещё две цифры — всего три.
2. Затем разделим первое неполное делимое 4 на делитель 3. В результате получим 1.
3. Далее умножим делитель на полученную цифру частного: 3 · 1 = 3. Запишем 3 под первым неполным делителем.
4. Теперь нужно найти остаток при помощи вычитания.
5. Остаток 1 меньше делителя 3, значит, продолжаем вычисления. Рядом с цифрой остатка 1 пишем следующую цифру делимого — 8. Следующее неполное делимое — 18.
6. Разделим 18 на 3 и получим вторую цифру частного — 6.
7. Теперь умножим делитель на полученную цифру частного: 3 · 6 = 18 и найдём остаток — 0. Его можно не писать.
8. Сносим цифру 6 — это последнее неполное делимое. Делим 6 на 3 и получаем — 2. В частное пишем 2.
9. Далее умножим делитель на полученную цифру частного: 3 · 2 = 6 и найдём остаток — 0. Вычисления закончены.
Пример деления с нулём в частном, или сколько раз можно сносить цифру делимого, чтобы получить одно новое неполное делимое
Разделим 816 на 8
1. Первое неполное делимое 8, а за ним ещё две цифры. Значит, в частном будет 3 цифры.
2. Разделим первое неполное делимое 8 на делитель 4 и запишем в частное ответ — 2.
3. Умножим делитель 4 на цифру частного 2, получим 8. Запишем число под первым неполным делимым.
4. Сносим цифру 1 — это новое неполное делимое. Остаток 0 не пишем.
5. Вспомним деление с остатком и разделим 1 на 4. В результате получим 0, остаток — 1. Цифру 0 записываем в частное.
6. Умножим делитель 4 на цифру частного 0, результат 0 запишем под вторым неполным делимым. Остаток 1.
7. Сносим 6 и получаем новое неполное делимое 16. Делим 16 на 4, получаем цифру частного 4.
8. Умножаем делитель 4 на цифру частного 4 и пишем результат под неполным делимым.
9. Записываем последний остаток 0 — деление выполнено.
Как можно сократить запись деления
Когда мы получили неполное делимое 1, которое меньше делителя 4, сносим вторую цифру делимого, чтобы новое неполное делимое было больше делителя. А в частное ставим 0. И далее выполняем деление в установленном порядке.
В этом примере мы дважды сносили цифру делимого, чтобы получить неполное делимое, которое больше делителя.
Надеемся, что теперь у вашего ребёнка не возникнет трудностей с делением в столбик. А если вдруг они есть, наши репетиторы с удовольствием готовы вам помочь!
Влюбляем в обучение на уроках в онлайн-школе Тетрика
Оставьте заявку и получите бесплатный вводный урок
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.
Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.
В математике существует знак для умножения — это точка ( • ) посередине строки между числами, которые нужно перемножить, а для деления существует особый знак — это две точки ( : ) между числами, которые нужно поделить между собой.
Как ёжикам поделить между собой яблоки поровну?
Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.
1) 6 : 3 = 2 (яб.) — мы узнали, сколько яблок получит каждый ёжик.
2) 6 : 2 = 3 (ёж.) — мы узнали, сколько ёжиков получат по 2 яблока.
3) 2 • 3 = 6 (яб.) — мы узнали, сколько яблок нужно, чтобы у каждого из трёх ёжиков было по 2 яблока.
Любой пример на умножение можно представить двумя примерами на деление.
Например, для выражения 6 • 4 = 24 есть два обратных выражения:
24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.
24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.
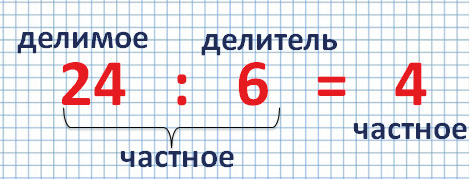
Числа при делении
При делении, как и при другом математическом действии, каждое число имеет свое название.
Число, которое делят, называется делимое.
Число, на которое делят, называется делитель.
Результат деления называется частное.
Чтение числовых выражений
24 : 6 = 4
Этот пример можно прочитать по-разному.
- 24 разделить на 6 равняется 4.
- 24 уменьшить в 6 раз – получится 4.
- Делимое – 24, делитель – 6, частное – 4.
- Частное от деления числа 24 на 6 равно 4.
Деление на 1
4 : 1 = 4
23 : 1 = 23
Деление на 0
Деление числа само на себя
Связь деления и умножения
Чётные и нечётные числа
Числа, которые делятся на 2 без остатка, называются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.
Чётные: 6, 22 44, 60, 74, 82, 96
Нечётные: 7, 13, 21, 37, 45, 97
В несколько раз меньше
Для примера решим задачу:
В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?
составим схему:
Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)
Вывод: Если в задаче есть слова «в … раз меньше», то задача решается делением.
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление с остатком
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Правило встречается в следующих упражнениях:
2 класс
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 59,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 65,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 73. Урок 29,
Петерсон, Учебник, часть 2
Страница 84. Урок 35,
Петерсон, Учебник, часть 2
Страница 18. Урок 6,
Петерсон, Учебник, часть 3
3 класс
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 36,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 13,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 19,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 40. ПР 6. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 26,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 12. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 90. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 441,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 673,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 36,
Мерзляк, Полонский, Якир, Учебник
Номер 520,
Мерзляк, Полонский, Якир, Учебник
Номер 656,
Мерзляк, Полонский, Якир, Учебник
Номер 657,
Мерзляк, Полонский, Якир, Учебник
Номер 673,
Мерзляк, Полонский, Якир, Учебник
Номер 1050,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 1211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1222,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1262,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1266,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1473,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник