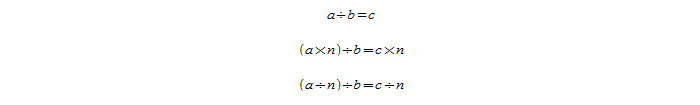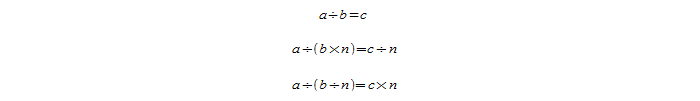Деление целых чисел отличается от деления натуральных чисел, только тем что у целых чисел нужно у частного посчитать знак. Как посчитать знак частного целых чисел? Рассмотрим подробно в теме.
Термины и понятия частного целых чисел.
Чтобы выполнить деление целых чисел нужно вспомнить термины и понятия. В делении есть: делимое, делитель и частное целых чисел.
Делимое – это то целое число, которое делят. Делитель – это целое число, на которое делят. Частное – это результат деления целых чисел.
Можно сказать “Деление целых чисел” или “Частное целых чисел” смысл этих фраз один и тот же, то есть нужно поделить одно целое число на другое и получить ответ.
Деление берет свое начало из умножения. Рассмотрим пример:
3∙4=12
У нас есть два множителя 3 и 4. Но допустим нам известно, что есть один множитель 3 и результат умножения множителей их произведение 12. Как найти второй множитель? На помощь приходит деление.
12:3=4
Правило деления целых чисел.
Определение:
Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.
Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:
Плюс на плюс дает плюс.
“+ : + = +”
Минус на минус дает плюс.
“– : – =+”
Минус на плюс дает минус.
“– : + = –”
Плюс на минус дает минус.
“+ : – = –”
А теперь рассмотрим подробно каждый пункт правила деления целых чисел.
Деление целых положительных чисел.
Вспомним, что целые положительные числа это тоже самое, что натуральные числа. Мы пользуемся теми же правила, что и при делении натуральных чисел. Знак частного от деления целых положительных чисел всегда плюс. Иными словами, при делении двух целых чисел “плюс на плюс дает плюс”.
Пример:
Выполните деление 306 на 3.
Решение:
Оба числа имеют знак “+”, поэтому ответ будет со знаком “+”.
306:3=102
Ответ: 102.
Пример:
Разделите делимое 220286 на делитель 589.
Решение:
Делимое 220286 и делитель 589 имеет знак плюс, поэтому частное тоже будет иметь знак плюс.
220286:589=374
Ответ: 374
Деление целых отрицательных чисел.
Правило деления двух отрицательных чисел.
Пусть у нас будут два отрицательных целых числа a и b. Нам нужно найти их модули и выполнить деление.
a:b=|a|:|b|
Результат деления или частное двух отрицательных целых чисел будет со знаком “+” или “минус на минус дает плюс”.
Рассмотрим пример:
Найдите частное -900:(-12).
Решение:
-900:(-12)=|-900|:|-12|=900:12=75
Ответ: -900:(-12)=75
Пример:
Выполните деление одного целого отрицательного числа -504 на второе отрицательное число -14.
Решение:
-504:(-14)=|-504|:|-14|=504:14=34
Записать выражение можно короче:
-504:(-14)=34
Деление целых чисел с разными знаками. Правило и примеры.
Правило:
При выполнении деления целых чисел с разными знаками, частное будет равно отрицательному числу.
Не важно положительное целое число делим на отрицательное целое число или отрицательное целое число делим на положительное целое число, результат деления всегда будет равен отрицательному числу.
Минус на плюс дает минус.
Плюс на минус дает минус.
Пример:
Найдите частное двух целых чисел с разными знаками -2436:42.
Решение:
-2436:42=-58
Пример:
Вычислите деление 4716:(-524).
Решение:
4716:(-524)=-9
Нуль деленный на целое число. Правило.
Правило:
При деление нуля на целое число ответ будет равен нулю.
Пример:
Выполните деление 0:558.
Решение:
0:558=0
Пример:
Разделите нуль на целое отрицательное число -4009.
Решение:
0:(-4009)=0
Правило:
На нуль делить нельзя.
Нельзя 0 разделить на 0.
Проверка частного деления целых чисел.
Как говорилось ранее деление и умножение тесно связаны. Поэтому чтобы проверить результат деления двух целых чисел, нужно выполнить умножение делителя и частного в результате должно получиться делимое.
Проверка результата деления краткая формула:
Делитель ∙ Частное = Делимое
Рассмотрим пример:
Выполните деление и сделайте проверку 1888:(-32).
Решение:
Обращаем внимание на знаки целых чисел. Число 1888 положительное и имеет знак “+”. Число (-32) отрицательное и имеет знак “–”. Поэтому при делении двух целых чисел с разными знаками ответ будет отрицательное число.
1888:(-32)=-59
А теперь выполним проверку найденного ответа:
1888 – делимое,
-32 – делитель,
-59 – частное,
Делитель умножаем на частное.
-32∙(-59)=1888
Вопросы по теме:
Что такое частное чисел?
Ответ: частное чисел – это результат деления деления двух чисел.
Как найти частное?
Ответ: нужно одно число поделить на другое, то есть делимое поделить на делитель и получим частное.
Чему равно частное от деления целых чисел?
Ответ: если целые числа делятся без остатка, то их частное равно целому числу. Иначе будет дробное число.
Что такое делимое и делитель?
Ответ: число которое делят называют делимым, а число на которое делят называют делителем.
Пример:
Найдите частное суммы и разности чисел 48 и 16.
Решение:
Находим сумму чисел 48 и 16.
48+16=64
Находим разность чисел 48 и 16.
48-16=32
Находим частное.
64:32=2
Ответ: 2.
|
Как называются «а» и «в» в каждом из математических действий: а + в = сумма; а – в = разность; а * в = произведение; а : в = частное? Все приведенные формулы и понятия сложение, вычитание, умножение, деление не что иное как арифметические действия, которыми мы пользуемся в своей повседневной жизни весьма и весьма часто. Понятие сложение практически не нуждается в определении, поскольку вытекает из простых фактов, и не может быть определено формально. В результате сложения чисел получается сумма, а сами складываемые числа называются слагаемыми. Вычитание может быть определено как нахождение одного из слагаемых по сумме и другому слагаемому. Искомое слагаемое — это разность, сама сумма называется уменьшаемым, данное слагаемое — это вычитаемое. В записи а – в = с имеем: а — уменьшаемое, в — вычитаемое, с — разность. Сложение разности с с вычитаемым в даст уменьшаемое а, то есть такое сложение с + в = а будет являться проверкой вычитания. Умножение, в результате которого получается произведение, позволяет повторить некоторое число а (это множимое) слагаемым столько раз, сколько указывает другое число в (множитель). Если множимое и множитель поменять местами, то произведение от этой перестановки не изменится. Поэтому множитель и множимое и называют сомножителями. Деление, в результате которого получается частное, по сути состоит в нахождении одного из сомножителей по произведению и другому сомножителю. Данное произведение а называется делимым, сомножитель в — делителем, искомый сомножитель с — частным. Проверкой деления будет произведение делителя и частного, равное делимому. автор вопроса выбрал этот ответ лучшим Бульбозавр 5 лет назад Компонентами мы тут называет те числа с которыми осуществляется математические действия и они собственно в этих разных действиях, как сложение, вычитание, деление и умножение имеют разные обозначения. Стоит наверно идти от более простого к сложному. Все таки сначала в математике учат складывать и вычитать. При сложении чисел:Все числа называются слагаемыми, единственное, что необходимо, это указать каким по счету идет это Слагаемое — первым, вторым т. д. При вычитании.Тоже не сложно: первое число, из которого вычитают (уменьшают) называется — Уменьшаемое, а то число, которое вычитается, т. е. На это количество первое число уменьшится, называют — Вычитаемое. Ну и в умножении и делении, числа, с которыми производится математические действия, будут звучать так: В делении.Первое число, это то, которое необходимо разделить, называется — Делимое, а второе число, обозначающее, на сколько частей необходимо поделить, называется — Делитель. В умножении.как и при сложении все числа имеют одно название — Множитель. Единственное отличие, это то, что порядковый номер множителя не называется. Урания более года назад Рассмотрим последовательно числа «а» и «в», участвующие в разных арифметических действиях, и дадим им название. 1. а + в = сумма. Это арифметическое действие — сложение. Числа «а» и «в» называются одинаково — слагаемыми. При сложении мы имеем компоненты с одинаковым названием. Спросите — почему? Ответ прост: от перестановки мест слагаемых сумма не меняется. В результате сложения получаем сумму. 2. а – в = разность. Это арифметическое действие — вычитание. Число «а» — это уменьшаемое, «в» — это вычитаемое. В результате мы получаем разность. 3. а * в = произведение. Это арифметическое действие — умножение. Числа «а» и «в» называются тоже одинаково, как при сложении, — множителями. В результате получаем произведение. 4. а : в = частное. Это арифметическое действие — деление. Число «а» — делимое, число «в» — это делитель. В результате получаем частное. Nonsense 5 лет назад Уж простите меня непутёвого, но те «а» и «б», и все им подобные в формулах называются по-простому-научному «операндами», поскольку ещё не определена их сущность; либо они константы, либо переменные. Куда тут ещё из пальца высасывать определения? «Компоненты» деления-умножения-схождения-расхождения-разведения-спился не понять мне эту чушь формуляристики, воспитанному на классическом сопромате, увы! Не надо называть то, что очевидно для многих, тем, что ты выдумал один, играясь в свои игрушки, даже если ты уже и пенсионер. Я даю Вам ответ конкретный на конкретный вопрос «Как называются «а» и «в» в каждом из математических действий» предложенных для созерцания в пояснении к вопросу. Ответ банален и прост, во всех предложенных Вами вариантах отнюдь не компоненты, НО операнды. Прошу это учесть!Спасибо за внимание! SVFE48 4 месяца назад В математике компоненты суммы, разности, произведения и частного называются терминами. Сумма – это результат сложения двух или более чисел или величин. Условия суммы — это числа или количества, которые складываются. Например, в сумме 2 + 3 + 4 члены равны 2, 3 и 4. Разница – это результат вычитания одного числа или количества из другого. Условия разности — это числа или количества, которые вычитаются. Например, в разности 10 — 5 слагаемые равны 10 и 5. Произведение – это результат умножения двух или более чисел или количеств. Термины продукта — это числа или количества, которые умножаются. Например, в произведении 2*3*4 слагаемые равны 2, 3 и 4. Частное – это результат деления одного числа или величины на другое. Члены частного — это числа или количества, которые делятся. Например, в частном 10/2 члены равны 10 и 2. Стоит отметить, что терминами в этих основных операциях являются числа или математические выражения, и что операции могут применяться и к другим типам математических объектов, таким как векторы, матрицы, многочлены и т. д. Rnd 2 месяца назад Вы уже правильно назвали названия математических операций:
Относительно компонентов каждой операции:
Знаете ответ? |
Деление чисел с остатком: формулы, примеры и правила
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Теорема
a = b · q + r, где a — делимое, b — делитель, q — неполное частное, r — остаток. 0 ⩽ r < |b|.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
- 7 * 2 + 1 = 15;
- 2 * 7 + 1 = 15.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Самый удобный способ деления — это столбик.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Как решаем:
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении
|a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя
- получить неполное частное и остаток;
- записать число противоположное полученному.
Пример
Разделить 17 на −5 с остатком.
Как решаем:
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Проверка : a = b * q + r, 17 = −5 * (−3) + 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное q при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1.
r = a − b * q
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
- найти модули делимого и делителя;
- разделить по модулю;
- записать противоположное данному число и вычесть 1;
- использовать формулу для остатка r = a − b * q.
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Как решаем:
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, q = −4, тогда:
r = a − b * q = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Проверка: a = b * q + r, −17 = 5 * (−4) + 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
r = a − b * q
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя;
- получить неполное частное и остаток;
- прибавить 1 к неполному частному;
- вычислить остаток, исходя из формулы r = a − b * q.
Пример
Найти неполное частное и остаток при делении −17 на −5.
Как решаем:
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим r = a − b * q = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Проверка: a = b * q + r, −17 = −5 * 4 + 3.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Как найти неизвестный делитель с остатком правило. Правило деления с остатком целого положительного числа на целое отрицательное, примеры
Осталось доказать возможность представления a=b·q+r
для отрицательных b
.
Так как модуль числа b
в этом случае является положительным числом, то для имеет место представление , где q 1
– некоторое целое число, а r
– целое число, удовлетворяющее условиям .
, получаем нужное нам представление a=b·q+r
для отрицательных b
.
Переходим к доказательству единственности.
Предположим, что помимо представления a=b·q+r
, q
и r
– целые числа и , существует еще одно представление a=b·q 1 +r 1
, где q 1
и r 1
– некоторые целые числа, причем q 1 ≠q
и .
После вычитания из левой и правой части первого равенства соответственно левой и правой части второго равенства, получаем 0=b·(q−q 1)+r−r 1
, которое равносильно равенству r−r 1 =b·(q 1 −q)
. Тогда должно быть справедливо и равенство вида , а в силу свойств модуля числа — и равенство .
Из условий и можно сделать вывод, что . Так как q
и q 1
– целые и q≠q 1
, то , откуда заключаем, что . Из полученных неравенств и следует, что равенство вида невозможно при нашем предположении. Поэтому, не существует другого представления числа a
, кроме a=b·q+r
.
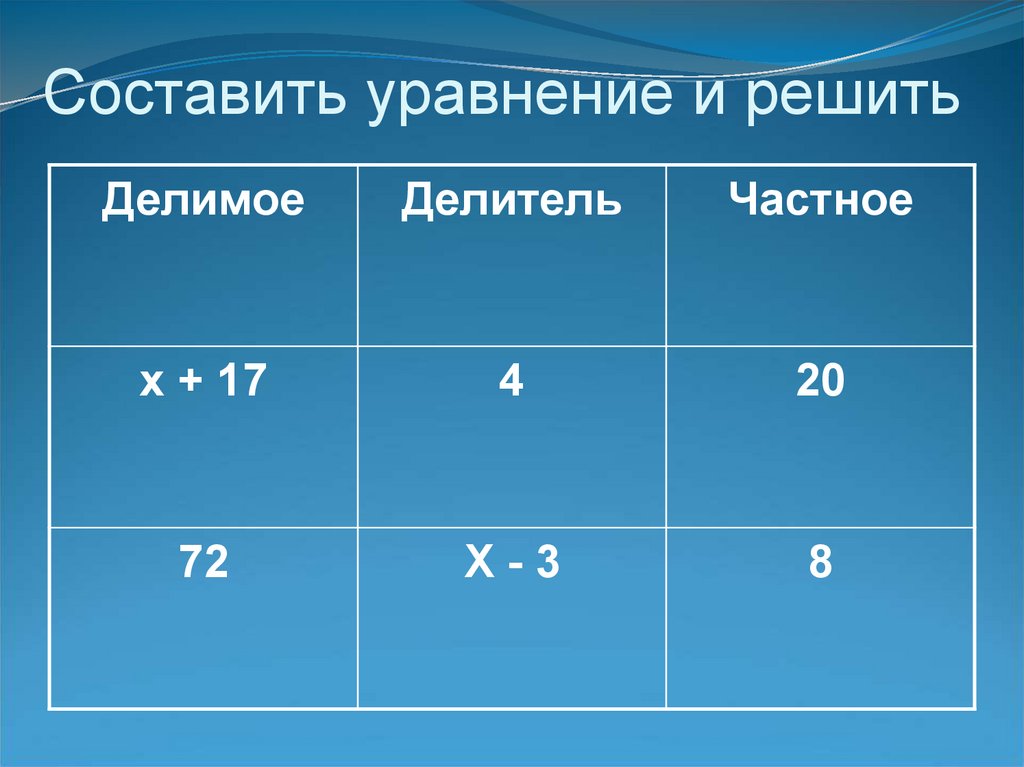
Связи между делимым, делителем, неполным частным и остатком
Равенство a=b·c+d
позволяет находить неизвестное делимое a
, если известны делитель b
, неполное частное c
и остаток d
.
Пример.
Чему равно делимое, если при его делении на целое число −21
получилось неполное частное 5
и остаток 12
?
Решение.
Нам требуется вычислить делимое a
, когда известен делитель b=−21
, неполное частное c=5
и остаток d=12
. Обратившись к равенству a=b·c+d
, получаем a=(−21)·5+12
. Соблюдая , сначала проводим умножение целых чисел −21
и 5
по правилу умножения целых чисел с разными знаками , после чего выполняем сложение целых чисел с разными знаками : (−21)·5+12=−105+12=−93
.
Ответ:
−93
.
Связи между делимым, делителем, неполным частным и остатком также выражаются равенствами вида b=(a−d):c
, c=(a−d):b
и d=a−b·c
. Эти равенства позволяют вычислять делитель, неполное частное и остаток соответственно. Нам часто придется находить остаток от деления целого числа a
на целое число b
, когда известны делимое, делитель и неполное частное, используя формулу d=a−b·c
. Чтобы в дальнейшем не возникало вопросов, разберем пример вычисления остатка.
Пример.
Найдите остаток от деления целого числа −19
на целое число 3
, если известно, что неполное частное равно −7
.
Решение.
Для вычисления остатка от деления воспользуемся формулой вида d=a−b·c
. Из условия имеем все необходимые данные a=−19
, b=3
, c=−7
. Получаем d=a−b·c=−19−3·(−7)=
−19−(−21)=−19+21=2
(разность −19−(−21)
мы вычисляли по правилу вычитания целого отрицательного числа).
Ответ:
Деление с остатком целых положительных чисел, примеры
Как мы уже не раз отмечали, целые положительные числа представляют собой натуральные числа. Поэтому деление с остатком целых положительных чисел проводится по всем правилам деления с остатком натуральных чисел. Очень важно уметь с легкостью выполнять деление с остатком натуральных чисел , так как именно оно лежит в основе деления не только целых положительных чисел, но и в основе всех правил деления с остатком произвольных целых чисел.
С нашей точки зрения наиболее удобно выполнять деление столбиком , этот способ позволяет получить и неполное частное (или просто частное) и остаток.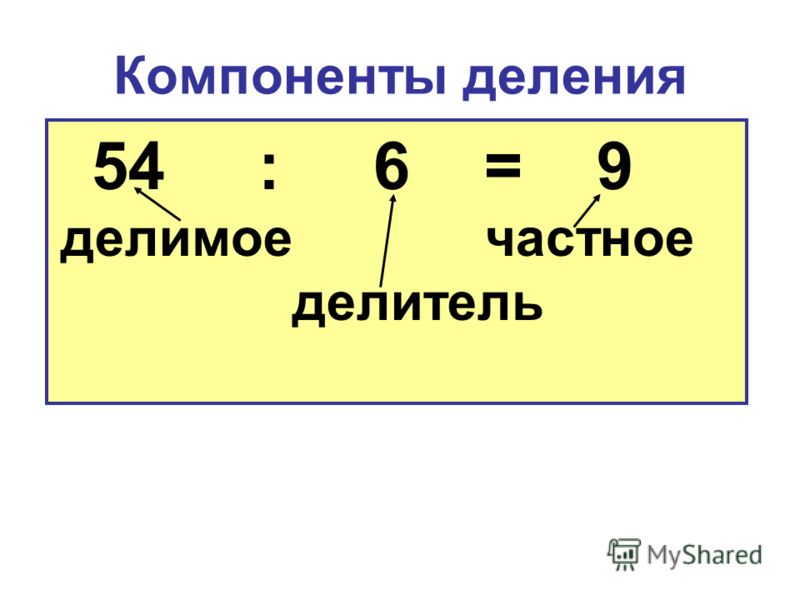
Пример.
Выполните деление с остатком числа 14 671
на 54
.
Решение.
Выполним деление данных целых положительных чисел столбиком:
Неполное частное получилось равным 271
, а остаток равен 37
.
Ответ:
14 671:54=271 (ост. 37)
.
Правило деления с остатком целого положительного числа на целое отрицательное, примеры
Сформулируем правило, позволяющее выполнять деление с остатком целого положительного числа на целое отрицательное число.
Неполное частное от деления целого положительного числа a
на целое отрицательное число b
представляет собой число, противоположное неполному частному от деления a
на модуль числа b
, а остаток от деления a
на b
равен остатку от деления на .
Из этого правила следует, что неполное частное от деления целого положительного числа на целое отрицательное число является целым неположительным числом .
Переделаем озвученное правило в алгоритм деления с остатком целого положительного числа на целое отрицательное:
- Делим модуль делимого на модуль делителя, получаем неполное частное и остаток.
(Если при этом остаток получился равным нулю, то исходные числа делятся без остатка, и по правилу деления целых чисел с противоположными знаками искомое частное равно числу, противоположному частному от деления модулей.)
- Записываем число, противоположное полученному неполному частному, и остаток. Эти числа являются соответственно искомым частным и остатком от деления исходного целого положительного числа на целое отрицательное.
Приведем пример использования алгоритма деления целого положительного числа на целое отрицательное.
Пример.
Выполните деление с остатком целого положительного числа 17
на целое отрицательное число −5
.
Решение.
Воспользуемся алгоритмом деления с остатком целого положительного числа на целое отрицательное.
Разделив
Число, противоположное числу 3
, — это −3
. Таким образом, искомое неполное частное от деления 17
на −5
равно −3
, а остаток равен 2
.
Ответ:
17
:(−5)=−3 (ост.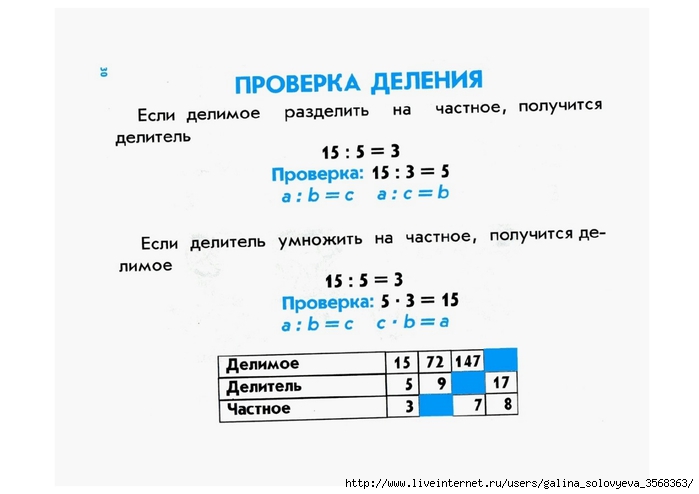
.
Пример.
Разделите 45
на −15
.
Решение.
Модули делимого и делителя равны 45
и 15
соответственно. Число 45
делится на 15
без остатка, частное при этом равно 3
. Следовательно, целое положительное число 45
делится на целое отрицательное число −15
без остатка, частное при этом равно числу, противоположному 3
, то есть, −3
. Действительно, по правилу деления целых чисел с разными знаками имеем .
Ответ:
45:(−15)=−3
.
Деление с остатком целого отрицательного числа на целое положительное, примеры
Дадим формулировку правила деления с остатком целого отрицательного числа на целое положительное.
Чтобы получить неполное частное c
от деления целого отрицательного числа a
на целое положительное число b
нужно взять число, противоположное неполному частному от деления модулей исходных чисел и вычесть из него единицу, после чего остаток d
вычислить по формуле d=a−b·c
.
Из данного правила деления с остатком следует, что неполное частное от деления целого отрицательного на целое положительное число является целым отрицательным числом.
Из озвученного правила вытекает алгоритм деления с остатком целого отрицательного числа a
на целое положительное b
:
- Находим модули делимого и делителя.
- Делим модуль делимого на модуль делителя, получаем неполное частное и остаток. (Если остаток равен нулю, то исходные целые числа делятся без остатка, и искомое частное равно числу, противоположному частному от деления модулей.)
- Записываем число, противоположное полученному неполному частному и вычитаем из него число 1
. Вычисленное число является искомым неполным частным c
от деления исходного целого отрицательного числа на целое положительное.
Разберем решение примера, в котором воспользуемся записанным алгоритмом деления с остатком.
Пример.
Найдите неполное частное и остаток от деления целого отрицательного числа −17
на целое положительное число 5
.
Решение.
Модуль делимого −17
равен 17
, а модуль делителя 5
равен 5
.
Разделив 17
на 5
, получаем неполное частное 3
и остаток 2
.
Число, противоположное 3
, есть −3
. Вычитаем из −3
единицу: −3−1=−4
. Итак, искомое неполное частное равно −4
.
Осталось вычислить остаток. В нашем примере a=−17
, b=5
, c=−4
, тогда d=a−b·c=−17−5·(−4)=
−17−(−20)=−17+20=3
.
Таким образом, неполное частное от деления целого отрицательного числа −17
на целое положительное число 5
равно −4
, а остаток равен 3
.
Ответ:
(−17):5=−4 (ост. 3)
.
Пример.
Разделите целое отрицательное число −1 404
на целое положительное число 26
.
Решение.
Модуль делимого равен 1 404
, модуль делителя равен 26
.
Разделим 1 404
на 26
столбиком:
Так как модуль делимого разделился на модуль делителя без остатка, то исходные целые числа делятся без остатка, причем искомое частное равно числу, противоположному 54
, то есть, −54
.
Ответ:
(−1 404):26=−54
.
Правило деления с остатком целых отрицательных чисел, примеры
Сформулируем правило деления с остатком целых отрицательных чисел.
Чтобы получить неполное частное c
от деления целого отрицательного числа a
на целое отрицательное число b
, нужно вычислить неполное частное от деления модулей исходных чисел и прибавить к нему единицу, после этого остаток d
вычислить по формуле d=a−b·c
.
Из этого правила следует, что неполное частное от деления целых отрицательных чисел является целым положительным числом.
Перепишем озвученное правило в виде алгоритма деления целых отрицательных чисел:
- Находим модули делимого и делителя.
- Делим модуль делимого на модуль делителя, получаем неполное частное и остаток. (Если остаток равен нулю, то исходные целые числа делятся без остатка, и искомое частное равно частному от деления модуля делимого на модуль делителя.)
- К полученному неполному частному прибавляем единицу, это число есть искомое неполное частное от деления исходных целых отрицательных чисел.
- Вычисляем остаток по формуле d=a−b·c
.
Рассмотрим применение алгоритма деления целых отрицательных чисел при решении примера.
Пример.
Найдите неполное частное и остаток от деления целого отрицательного числа −17
на целое отрицательное число −5
.
Решение.
Воспользуемся соответствующим алгоритмом деления с остатком.
Модуль делимого равен 17
, модуль делителя равен 5
.
Деление 17
на 5
дает неполное частное 3
и остаток 2
.
К неполному частному 3
прибавляем единицу: 3+1=4
. Следовательно, искомое неполное частное от деления −17
на −5
равно 4
.
Осталось вычислить остаток. В этом примере a=−17
, b=−5
, c=4
, тогда d=a−b·c=−17−(−5)·4=
−17−(−20)=−17+20=3
.
Итак, неполное частное от деления целого отрицательного числа −17
на целое отрицательное число −5
равно 4
, а остаток равен 3
.
Ответ:
(−17):(−5)=4 (ост. 3)
.
Проверка результата деления целых чисел с остатком
После того, как выполнено деление целых чисел с остатком, полезно выполнить проверку полученного результата. Проверка проводится в два этапа.
неотрицательным числом, а также проверяется выполнение условия . Если все условия первого этапа проверки выполнены, то можно приступать ко второму этапу проверки, в противном случае можно утверждать, что при делении с остатком где-то была допущена ошибка. На втором этапе проверяется справедливость равенства a=b·c+d
. Если это равенство справедливо, то деление с остатком было проведено верно, в противном случае – где-то была допущена ошибка.
Рассмотрим решения примеров, в которых выполняется проверка результата деления целых чисел с остатком.
Пример.
При делении числа −521
на −12
было получено неполное частное 44
и остаток 7
, выполните проверку результата.
Решение.
−2
при b=−3
, c=7
, d=1
. Имеем b·c+d=−3·7+1=−21+1=−20
. Таким образом, равенство a=b·c+d
– неверное (в нашем примере a=−19
).
Следовательно, деление с остатком было проведено неверно.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело
на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу
деления с остатком,
по которой можно сделать проверку решения
.
a
=
b
⋅
c
+
d
a
– делимое,
b
– делитель,
c
– неполное частное,
d
– остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело
или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
Например 40:6=6 (4)
В данном примере
делимое -40, число, стоящее перед знаком деления,
6-делитель, число, стоящее после знака деления или на которое делим делимое.
6-частное, то, что получается в результате деления
4-остаток, число, остающееся при делении
В примере:
20 — это делимое (то, что делится),
10 — это делитель (то, что делит),
2 — это частное (то, что при умножении на делитель образует делимое).
Возьмем другой пример:
17: 3 = 5 (2), где
17 — делимое,
3 — делитель,
5 — неполное частное,
2 — остаток.
При этом интересно, что остаток всегда меньше, чем неполное частное.
Для того чтобы не путаться в определении величин с которыми приходится иметь дело в процессе деления, люди давным давно придумали для них подходящие названия. Прежде всего само число. которое делят стали называть Делимым, ведь это число делится на части, оно буквально делимое. Например урожай плодов.
Число, которое показывает на сколько частей мы поделим Делимое стали называть Делитель. Его задача разделить число на несколько групп, чтобы всем хватило поровну.
Результат деления назвали Частным — это число показывает сколько единиц оказывается в каждой группе, кучке плодов, после того как разделили весь урожай.
Наконец остаток — это то целое число плодов, которое невозможно поделить между всеми поровну.
Собрали 51 яблоко. Это делимое.
Решили поделить между папой, мамой, дочкой и сыном поровну, то есть на четырех. Это делитель.
Поделили и получили что каждому причитается 12 яблок — это частное.
А три яблока нельзя поделить на четырех и это Остаток.
51:4=12 (остаток 3).
Делимое — это число, которое будем делить.
Делитель — это число, на
которое будем делить
Частное — это число, которое образуется при делении
Остаток — это число, которое остается при делении (при этом частное будет неполным)
Например
Здесь 30 — делимое, 4 — делитель, 7 — частное, 2 — остаток
Объяснить, что такое делимое, делитель, частное и остаток — реально легче на различных примерах.
Вот самый простенький вариант, тут все делится без остатка.
Или вот такой еще пример.
Ничего сложного как видим нет, все это дети изучают еще в начальных классах на уроках математики.
Сразу же приведем пример (можно даже несколько примеров):
2). 21: 5 = 4,2 или же 4 и 1 в остатке.
Делимое — это то число, которое мы делим (в наших примерах делимыми являются 18 и 21).
Делитель — это то число, на которое мы делим делимое (делителями в наших примерах являются 9 и 5).
Частное — это результат деления (частное в первом примере 2, а во втором примере 4,2).
В первом случае делимое делится без остатка, а во втором у нас есть остаток — 1.
С понятия делимое, делитель, частное и остаток, начинают изучать деление в средней школе. Так что это просто необходимо при изучении математики. И так делимое это число, которое подвергают делению. Делитель, это то число на которое делят, а соответственно частное это и есть результат деления. Но так уж бывает когда делимое число не делится нацело. Вот и образуемое в процессе деления число которое меньше делителя и которое нельзя разделить нацело и называется остаток.
А пример можно привести следующий.
например.
34: 5 = 6 (остаток 4)
В данном случае 34 — делимое
5 — делитель.
6 — частное отделения
4 — остаток.
делимое делитель частное остаток
Все это части математического действия — деления
.
Попробую простым языкам, как объясняли мне.. лет тридцать назад.
quot;Делимоеquot;
— это число стоящее слева от знака деления, которое делим (дробим)
quot;Делительquot;
— это число стоящее справа от знака деления, число на которое делим Делимое (какими частями делим, дробим)
quot;Частноеquot;
— это число стоящее после знака равно, результат деления (числовое выражение количества целых частей — делителей в делимом)
quot;Неполное частноеquot;
— это число стоящее после знака равно, результат деления при котором оставил quot;лишнееquot; число которое меньше Делителя. Неполное частное это количество только целых частей. Всегда пишется с числом Остатка.
quot;Остатокquot;
— это число оставшееся не делимым, которое меньше Делителя.
А теперь на примерах —
10: 5 = 2
В этом примере quot;10quot; — Делимое, quot;5quot; — Делитель, quot;2quot; — Частное.
13: 5 = 2 (3)
В этом примере quot;13quot; — Делимое, quot;5quot; — Делитель, quot;2quot; — неполное Частное, quot;3quot; — Остаток (как правило пишется в скобках рядом с quot;неполным частнымquot;).
Данные понятия арифметики легче всего рассмотреть на примере.
Пример: 17: 8 = 2 (остаток — 1).
В этом примере 17 — делимое (число, которое делят), 8 — делитель (то, на что мы делим), 2 — остаток (то, что получаем при делении), 1 — остаток.
Все приведнные в вопросе понятия напрямую относятся к делению в математике.
Итак, начнм с quot;делимогоquot; — под ним подразумевается то число, которое будет делиться;
quot;Делительquot; уже подразумевает под собой то число, на которое будет делиться имеющееся quot;делимоеquot;.
quot;Частноеquot; представляет собой результат, полученный от деления.
quot;Остатокquot; представляет собой число остающееся при делении в результате у нас будет неполное частное.
Вот пример:
Цель:
Формирование умений и навыков при
делении с остатком, нахождение делимого по
неполному частному и остатку от деления,
применение знаний при решении задач.
Задачи:
- Научить выполнять деление с остатком;
- Научить находить делимое по неполному частному
и остатку от деления; - Научить применять полученные знания и умения к
решению задач; - Продолжить формировать грамотную
математическую речь; - Пробудить интерес и активность к самоанализу и
контролю.
Тип урока: Урок закрепления полученных
знаний с применением ИКТ.
Метод обучения: Метод усвоения знаний,
основанный на познавательной активности
репродуктивного характера.
Структура урока:
- Организационный момент (2 мин.)
- Ввод в урок. Сообщение о теме, форме проведения
данного урока и его задачах (3 мин.) - Устная работа (Приложение 1) (5-7 мин.)
- Мотивация и актуализация опорного материала с
помощью решения устной задачи (5 мин.) - Первичное закрепление, решение задач. (10-14 мин.)
- Проверка усвоения материала (5-7 мин.)
- Задание на дом (2 мин.)
- Подведение итогов урока с помощью наводящих
вопросов и решения устных задач (5 мин.)
Ход урока
1. Собрать тетради с домашней работой.
Собрать готовые проекты “Старинные способы
умножения и деления”.
2. Показ презентации.
Сообщение о теме,
цели урока, о задачах урока, девизе урока.
урока: “Деление нам служит на деле;
- Оно нам поможет всегда.
- Кто поровну трудности делит,
- Разделит успехи труда”
3. Устная работа.
Устный счет – формирование вычислительных
навыков у учащихся (Приложение 1)
.
Презентация взята с сайта “Карман для
математика”
2*17+33 5+5*12 3500:100+400 48-12:3 200-20*5 13*8-34:2 6*15-15*5 6*4-4:2 68:17+17*2
Собранна картинка – ключ успеха в вычислениях.
Устная работа по повторению теоретических
аспектов темы “Деление с остатком”
Назовите, какие возможны остатки при делении с
остатком на 8?
Что означает, если остаток больше делителя?
Что означает, если остаток от деления ноль?
4.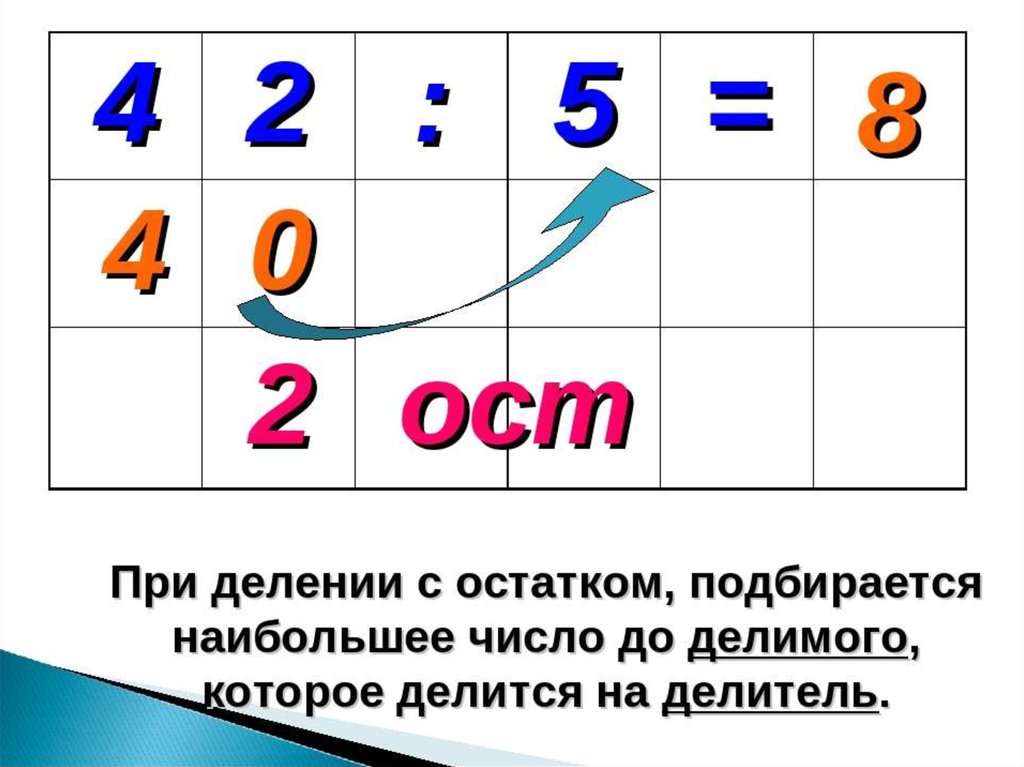
материала.
Задача. В гости к бабушке пришли 4 внука.
Бабушка решила угостить внуков конфетами. В
вазочке 23 конфеты. Сколько конфет достанется
каждому внуку, если бабушка предложит поделить
конфеты поровну?
Решение: 23:4=5 (3 ост.)
Вопросы к учащимся:
- Сколько конфет осталось?
- Можно ли придумать обратную задачу, в которой
главный вопрос “Сколь конфет в вазе?”? - Назвать все компоненты в данном выражении. Что
означает данное выражение?
Делимое -> неполное частное -> делитель ->
остаток
- Записать правило нахождения делимого по
неполному частному и остатку от деления.
5. Первичное закрепление и решение задач.
Выполнить деление с остатком сделать проверку:
882:40
- 1586:15
- 1332:64
- 9763:30
Работа с учебником: № 536 устно; № 537 устно; № 538
устно; № 518
6.
перфокарта.
Деление | Математика
Определить, сколько раз нужно взять слагаемым меньшее число 2, чтобы получить большее число 6, значит определить, сколько раз число 2 содержится в 6, или сколько раз число 6 содержит 2.
Число 2 содержится в 6 три раза, ибо, чтобы получить 6, нужно взять сумму трех равных слагаемых:
6 = 2 + 2 + 2
Найти, сколько раз число 2 содержится в 6, значит разделить 6 на 2.
Определение. Деление есть такое действие, в котором по двум данным числам определяют, сколько раз одно число содержится в другом.
Данные числа в делении называются делимым и делителем, искомое называется частным.
Делимое есть то число, которое содержит другое.
Делитель есть то число, которое содержится в другом.
Частное показывает, сколько раз делитель содержится в делимом.
В данном примере делимое есть 6, делитель 2, частное 3.
Разделить 6 на 2 значит также разбить 6 на 2 равных слагаемых и отыскать их величину. Число 6 представится при помощи двух равных слагаемых в виде:
6 = 3 + 3
Каждое из равных слагаемых называется частью делимого.
Посредством деления целых чисел также узнается, как велико каждое слагаемое, если делимое разобьется на столько равных слагаемых, сколько в делителе единиц.
В этом случае делимое есть то число, которое делится или разбивается на равные части. Делитель показывает, на сколько равных частей делится делимое. Частное показывает, сколько приходится на каждую часть.
Способы деления
Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.
-
С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:
4 + 4 + 4 = 12,
следовательно, 4 содержится в 12 три раза.
-
С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:
12 — 4 = 8
8 — 4 = 4
4 — 4 = 0Отсюда находим, что можно вычесть 4 из 12 ровно три раза.
Деление есть сокращенное вычитание равных вычитаемых.
-
Наконец, посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.
Различные случаи при делении
При делении целых чисел бывают два случая:
-
Разделяя 12 на 4, мы находим в частном 3. Делитель 4 содержится ровно 3 раза в делимом 12. Вычитая последовательно из 12 по 4, мы могли вычесть число 4 ровно три раза и не получили никакого остатка. В этом случае говорят, что деление совершилось нацело или без остатка.
Умножив частное 3 на делитель 4, получаем делимое 12.
-
Разделяя 26 на 8, мы при последовательном вычитании получаем:
26 — 8 = 18
18 — 8 = 10
10 — 8 = 2
Далее нельзя продолжать вычитания, потому что из 2 нельзя вычесть делитель 8. Число 2 называют остатком.
Остаток всегда меньше делителя. В этом случае говорят, что деление не совершается нацело или деление совершается с остатком.
Разделяя 26 на 8, мы могли вычесть делитель 8 три раза, и у нас получился остаток 2. Число 3 мы будем называть целым частным. Целое частное есть не полное частное, ибо оно не выражает вполне, сколько раз меньшее число содержится в большем. Число 8 не содержится в 26 ровно 3 раза. В этом случае говорят: число 8 содержится в 26 три раза и еще получается остаток. Умножив делитель 8 на целое частное 3, мы не получим делимого 26, а число 24 — меньшее делимого. Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.
Целое частное иногда называют просто частным.
Итак, при делении мы имеем два случая:
-
Деление нацело или без остатка. Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом. Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.
Если дается произведение и множимое, отыскивают множитель, то есть число равных слагаемых; если дается произведение и множитель, отыскивают множимое, то есть величину равных слагаемых.
-
Деление с остатком. Когда делитель не содержится в делимом ровное число раз, тогда деление не совершается нацело, или деление совершается с остатком. Остаток всегда меньше делителя и делимое равно произведению делителя на целое частное, сложенное с остатком.
При делении целых чисел делимое всегда уменьшается во столько раз, сколько в делителе единиц, поэтому деление есть действие, обратное умножению.
Знак деления
-
Действие деления изображается знаком двоеточия ÷, который ставится между делимым и делителем.
Деление числа 6 на 2 изображают письменно:
6 ÷ 2 = 3 частное.
-
Действие деления обозначается также начертанием |–, где вертикальная черта отделяет делимое, а горизонтальная делитель от частного.
В данном примере имеем:
В нашем примере деление изображается письменно:
Знак деления прешел к нам от древних математиков.
Основные приемы при делении
Делить значит последовательно вычитать делитель из делимого, пока это возможно. Этот способ деления можно считать общим. Прием этот, однако, приводит к длинным вычислениям, если делимое очень велико, поэтому существуют различные сокращенные приемы деления.
Чтобы определить частное в том случае, когда оно выражается одной цифрой, прибегают к таблице умножения.
Чтобы разделить 27 на 3 мы пишем
Для частного выбираем такое число, чтобы, умножив делитель на частное, получить делимое.
Разделяя 27 на 3 и перебирая в уме все произведения 3 на разные числа, содержащиеся в таблице умножения, находим, что произведение 3 × 9 составляет 27 и потому пишем в частном 9. Вычитая произведение делителя на частное из делимого, получаем в остатке нуль.
Само вычисление выражают письменно:
Деление совершилось нацело.
Иногда делитель не содержится в делимом ровное число раз; так, разделяя 27 на 4, мы не находим в таблице целого числа, которое, будучи помножено на 4, дало бы 27; тогда деление не совершается нацело.
Отыскивая целое частно, мы имеем при этом три случая:
-
Или мы задаемся очень малым числом; так, для данного примера, задавшись в частном 5 и умножив 4 на 5, имеем 20. Подписав произведение 20 под делимым и вычитая из 27, имеем:
в остатке число 7 больше делителя 4.
Это показывает, что частное 5 мало и его нужно увеличить.
-
Или, взяв для частного 7 и умножив его на делителя 4, получаем произведение 28 больше делимого, что показывает, что мы задались в частно очень большим числом. В таком случае нужно уменьшить цифру частного 7.
-
Взяв для частного 6, мы ход вычисления выражаем письменно:
словесно: 4 в 27 содержится 6 раз, 4 * 6 = 24, подписываем 24 под делимым, вычитаем и получаем остаток 3. Остаток 3 меньше делителя, следовательно, цифра частного верна. Отсюда выводим следующее:
Правило определения частного:
-
Если при делении остаток более или равен делителю, цифра частного мала и ее нужно увеличить.
-
Если произведение делителя на частное больше делимого, цифра частно велика и ее нужно уменьшить.
-
Если остаток меньше делителя, цифра частного верна.
Это правило показывает, что при делении нужно для частного выбирать такое число, чтобы остаток был меньше делителя.
В данном примере 27 не делится нацело на 4, а получается остаток 3; число 6 есть целое частное и
27 = 4 × 6 + 3 = 24 + 3
Делимое 27 равно произведению делителя 4 на целое частное 6, сложенному с остатком 3.
Деление многозначного числа на однозначное
Частное от деления многозначного числа на однозначное иногда выражается числом, состоящим также из нескольких цифр. В этом случае деление распадается на несколько отдельных действий.
Разделим 702 на 3. Частное содержит три цифры. Оно больше 100 и меньше 1000, ибо делимое больше 300 (3 × 100) и меньше 3000 (3 × 1000). Включая три цифры, частное содержит сотни, десятки и единицы. В данном случае разбиваем деление на три отдельных действия, то есть отыскиваем последовательно сотни, потом десятки и, наконец, единицы частного. Самое действие начинаем с сотен.
-
Отыскиваем сотни частного. Цифра сотен частного может происходить от деления сотен делимого на делитель 3.
Десятки и единицы делимого не имеют никакого влияния на сотни частного, поэтому на них пока не обращаем внимания. Наибольшее число сотен в частном есть 2, ибо 3 содержится в 7 сотнях 2 сотни раз; пишем в частном 200. Умножая 200 на 3 и вычитая произведение 600 из делимого, получаем первый остаток 132.
-
Отыскиваем десятки частного. В остатке 132 находится 12 десятков. Единицы делимого не имеют влияния на десятки частного. Разделив 13 на 3, находим, что в частном могут быть только 4 десятка, — пишем 40 в частном. Умножая 40 на 3 и вычитая произведение 120, получаем в остатке 12.
-
Отыскиваем единицы частного. Разделив 12 на 3, находим для единиц частного 4. Умножая 4 на 3 и вычитая произведение 12, получаем в остатке 0.
Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, деление изобразится письменно:
словесно:
-
Отделяем 7 — одну цифру делимого; 3 в 7 содержится 2 раза, — пишем в частном 2; умножая на нее делителя 3 и вычитая произведение 6 из 7, получаем первый остаток 1.
-
Сносим 3 — следующую цифру делимого; 3 в 13 содержится 4 раза, 3-жды 4 составляет 12; вычитая 12 из 13, получаем в остатке 1.
-
Сносим 2 следующую цифру делимого; 3 в 12 содержится 4 раза, пишем в частном 4; 3-жды 4 составляет 12. Вычитая 12, получаем в остатке нуль и в частном 244.
Пример. Разделить 2417 на 3. Ход вычисления выразится письменно:
словесно:
-
Отделив одну цифру 2, мы видим, что 3 в 2 не содержится целое число раз, поэтому нужно отделить две цифры; 3 в 24 содержится 8 раз, — пишем 8 в частном. Умножив 8 на делителя 3 и вычитая произведение 24, получаем в остатке нуль.
-
Сносим следующую цифру 1; 3 в 1 не содержится, — пишем в частном нуль.
-
Сносим следующую цифру 7; 3 в 17 содержится 5 раз, — пишем в частном 5; 3-жды 5 составляет 15; вычитая 15 из 17, получим в остатке 2 и целое частное 805.
Деление многозначного числа на многозначное
При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.
Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:
-
Определяем сотни частного:
Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.
Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.
-
Определяем десятки частного:
Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.
Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.
-
Определяем единицы частного:
47 содержится в 77 один раз.
Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.
Итак, после деления имеем в целом частном 791 и в остатке 30.
Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:
словесно:
-
Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.
-
К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.
-
Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.
Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.
Пример. Разделить 671064 на 335. Деление изобразится письменно:
словесно:
-
Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.
-
Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.
-
Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.
-
Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.
Из предложенных примеров выводим следующее правило:
-
Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше.
Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.
-
К остатку сносят следующую цифру делимого и снова задаются.
-
Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.
-
Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.
-
Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.
Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя. Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр.
Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.
Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:
словесно:
-
8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.
-
Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.
-
Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.
Деление на 10, 100, 1000 и т. д.
Разделяя число на 10, мы десятки делимого обращаем в единицы, сотни в десятки, тысячи в сотни, вообще понижаем на единицу все порядки делимого.
Разделяя на 100, мы понижаем все порядки делимого на две единицы, для чего отделяем запятою от правой руки к левой две цифры и т. д. Отсюда правило:
Чтобы разделить какое-нибудь число на единицу с нулями, нужно от правой руки к левой отделить столько цифр, сколько нулей в делителе; тогда число до запятой выражает целое частное, а после запятой — остаток.
Пример. Разделяя 30207 на 100. Отделяя справа 2 цифры, находим 302,07. Целое частное будет 302, а остаток 7.
Деление на число, оканчивающееся нулями
Разделяя число 27057 на 400 и поступая при этом по общему правилу
мы замечаем, что две последние цифры делимого не оказывают никакого влияния на частное. Они являются в остатке без всякой перемены. Откуда правило:
Если делитель оканчивается нулями, отделяют в делимом запятою от правой руки к левой столько цифр, сколько зачеркнуто нулей в делителе, и делят часть делимого до запятой на значащие цифры делителя.
В данном примере деление представится в виде
f
Если делимое и делитель оканчиваются нулями, их зачеркивают поровну в делимом, делителе и производят деление; зачеркнутые нули делимого приписывают к остатку.
Чтобы разделить 27300 на 4100, делим 273 на 41:
Частное будет 6, а остаток 2700.
Число цифр частного. При делении отделяют в делимом от левой руки к правой столько цифр, сколько их находится во делителе, или одною больше. Каждой оставшейся цифре делимого соответствует особая цифра частного, следовательно, число цифр частного будет равно или разности числа цифр делимого и делителя или на единицу больше этой разности.
Зависимость между данными и искомыми деления
При делении целых чисел мы имеем два случая: а) деление нацело, или без остатка, и б) деление с остатком.
Каждому из этих случаев соответствует особая зависимость между данными и искомыми деления.
Деление нацело или без остатка
При делении нацело
-
Частное равно делимому, разделенному на делитель.
Разделяя 42 на 7, имеем в частном 6; следовательно,
42 ÷ 7 = 6, или 6 = 42 ÷ 7
-
Делимое равно делителю, умноженному на частное.
42 = 6 × 7
-
Так как делитель и частное — два множителя, произведение которых равно делимому, то делитель равен делимому, разделенному на частное.
7 = 42 ÷ 6
Деление с остатком
При делении с остатком
-
Делимое равно произведению делителя на целое частное, сложенное с остатком.
При делении 47 на 6, имеем в целом частном 7, в остатке 5.
Делимое 47 = 6 × 7 + 5.
-
Делимое без остатка делится нацело на делитель и на целое частное.
Разность делимого без остатка равна произведению делителя на целое частное, то есть эта разность при делении на делитель дает целое частное, при делении на целое частное дает делитель.
Общее представление о делении натуральных чисел с остатком, частное и остаток, что такое остаток от деления
В данном материале мы разберем, как разделить одно натуральное число на другое с остатком. Для начала сформируем общее представление о таком действии, определимся с терминами и обозначениями, а потом посмотрим, какие задачи можно решить с его помощью. В последнем пункте попробуем объяснить, какие связи существуют между понятиями делимого, делителя, неполного частного и остатка от деления.
Общее представление о делении с остатком
Ранее мы указывали, что сам процесс деления сводится к разъединению одного множества на два или несколько. Чаще всего мы встречаемся с делением на равные части, то есть множества, получившиеся в результате, будут одинаковыми. Но так разделить возможно далеко не всегда. К примеру, 8 конфет разделить поровну на троих детей не выйдет: у каждого будет по 2 конфеты, а две останутся лишними. В данном случае мы имеем остаток 2, то есть остались две конфеты.
Определение 1
Разделить с остатком – значит представить исходное множество в виде некоторого числа равных множеств и еще одного дополнительного, элементов которого недостаточно для создания требуемого множества.
В чем состоит смысл деления с остатком?
В случае натуральных чисел деление с остатком имеет следующий смысл. Мы уже знаем, что понятие натурального числа тесно связано с количеством чего-либо. Допустим, у нас есть некое число предметов (обозначим его a), а после его деления образуется остаток, условно d. У нас остались числа b и c. Есть два основных подхода к их обозначению:
1) если b –количество элементов в каждом равном множестве, полученном после деления, то c – это количество множеств, которое у нас получилось.
2) если b – это количество множеств, то c – это число предметов в каждом из них.
Поясним нашу мысль на конкретных числах. Допустим, натуральное число 13 было разделено на 4.
1) тринадцать предметов были сгруппированы по 4. У нас получилось 3 группы, а в исходном множестве остался всего 1 предмет;
2) тринадцать предметов разложили по 4 группам. У нас получилось, что в каждой группе по 3 предмета, а остаток равен 1.
Если натуральное число a всегда можно разделить с остатком на любое натуральное b, то можно выделить следующие ситуации:
1. A можно разделить на b без остатка, то есть все предметы можно разделить на равные множества. При этом «лишних» у нас не останется, тогда d будет равно 0. Получается, что деление без остатка – это частный случай деления с остатком.
2. A может быть меньше b. Тогда ни одного требуемого множества мы из него составить не можем, и число c будет равно нулю, а остаток равен a (то есть числу предметов в исходном множестве).
3. A может делиться на b с остатком. Тогдазначения a, b, c и d будут натуральными числами.
Подводим итог:
Определение 2
Результат деления натуральных чисел a и b с остатком – это два числа c и d, которые либо оба являются натуральными, либо одно из них равно нулю.
Основные понятия, используемые при делении с остатком
Здесь мы определимся с основными терминами, которые будем использовать, если речь идет о делении с остатком.
То натуральное число, которое делят на части, принято называть делимым, а то, на которое делят – делителем. Получившиеся в результате два числа мы называем соответственно остатком и неполным частным. К примеру, если мы разделим 8 на 3, то в итоге неполным частным будет 2, и остатком тоже 2.
Знак деления, используемый при решении примеров с остатком, аналогичен тому же знаку «разделить» (две точки, расположенные вертикально), что и при делении нацело. В некоторых источниках можно встретить обозначение «÷», смысл которого тот же самый. Так, числовое выражение 16:3 означает деление одного натурального числа на другое с остатком.
Обозначим неполное частное буквой с, остаток – d, исходное число – a, а делитель – b. Тогда суть процесса деления в буквенном виде мы можем выразить как a:b=c (ост. d).
Также можно записать это в виде схемы: делимое: делитель = неполное частное (ост. остаток).
Из самого понятия о делении с остатком следует, что в любом случае остаток будет меньше делителя. Если бы он был равен ему или был нулевым, то это уже было бы деление нацело, поскольку у нас в итоге вышло бы несколько равных множеств.
Задачи, в которых используется деление с остатком
В результате процесса деления, описываемого в этой статье, всегда получаются два числа, одно из которых является остатком, а другое – неполным частным. Поэтому оно будет полезно для решения двух разных типов задач:
1. Нахождение количества необходимых равных множеств, которые можно составить из заданного количества предметов, или же количества предметов в равных множествах, полученных в результате деления.
Например:
Пример 1
У нас есть 67 шаров, которыми мы будем наряжать елки.
Другой пример:
Пример 2
У нас есть 162 книги, которые нужно упаковать в 40 ящиков. Число книг, которое мы будем класть в каждую коробку, можно определить в результате деления 162 на 40.
Вычислять мы можем не только количество предметов, но и изменения величин (массы, времени, длины и др.)
Например, на заводе произведено 6 113 л молока. Его нужно разлить в бутылки по 2 л. Мы можем вычислить неполное частное и понять, сколько бутылок будет в итоге. Или же если на производство какого-то изделия тратится 3 часа, то мы можем найти, сколько можно их выпустить за один восьмичасовой рабочий день.
2. Задачи второго типа направлены на вычисление количества предметов в исходном множестве, которые остались после деления. Это могут быть не только предметы, но и величины.
Например:
Пример 3
У нас есть 197 конфет, которые раскладываются по коробкам.
Пример 4
Чтобы изготовить бетонную плиту, надо израсходовать 750 кг цемента. Если мы закупили 12 900 кг, на сколько плит нам хватит? Результат мы вычислим в результате деления с остатком.
Основные связи между понятиями делимого, делителя, неполного частного и остатка от деления
Для установления этих связей сразу разберем конкретный пример.
У нас есть некоторое множество предметов, обозначим его буквой a. Распределим его по кучкам, количество которых равно b. Всего в каждой кучке у нас будет c предметов. Остаток обозначим d. В буквенном виде это выражение можно записать как a:b=c (ост. d). Теперь проанализируем связи, которые есть в этом равенстве.
Если у нас есть значения делителя, неполного частного и остатка, мы можем найти делимое. Если мы объединим все имеющиеся кучки и добавим к ним остаток, то получим множество из исходного количества предметов.
Учитывая смысл умножения и сложения натуральных чисел, мы можем записать это в виде равенства c·b+d=a. А наличие у умножения и сложения переместительных свойств позволяет нам переформулировать его как a=b·c+d. Получается следующее правило:
Определение 3
Чтобы найти делимое, нужно сложить остаток с произведением делителя на неполное частное.
Верное равенство, полученное в итоге, будет полезно для решения задач с неизвестным делимым, то есть таких, где нужно найти исходное число предметов. Приведем пример:
Пример 5
Вычислите делимое, если неполное частное равно одиннадцати, остаток двум, а делитель семи.
Решение
Имеем b=7, c=11 и d=2. Это все данные, которые нам нужны для вычислений. Подставим нужные значения: b·c+d=7·11+2. Следуя правильному порядку выполнения математических действий, получим в итоге 7·11+2=77+2=79 (если нужно, повторите основы умножения и сложения натуральных чисел).
Ответ: делимое будет равно 79.
Если нужно проверить верность результата действия деления с остатком, то для этого мы также проверяем справедливость равенства a=b·c+d.
Если нам известны значения делимого, делителя и неполного частного, то мы можем найти остаток.
Вспомним, что остаток от деления, который мы выше договорились обозначить буквой d, представляет собой число элементов, оставшееся в исходном множестве после его разделения на равные части. Значит, d=a−b·c. Записать это равенство мы можем благодаря свойствам умножения и вычитания натуральных чисел. Сформулируем определение:
Определение 4
Чтобы найти остаток от деления одного натурального числа на другое, нужно вычесть из делимого произведение делителя на неполное частное.
У нас получилось буквенное выражение d=a−b·c, которое будет нам полезно при нахождении остатка от деления. Разберем такую задачу.
Пример 6
Мы разделили 67 на 15 и получили неполное частное 4. Вычислите остаток от деления.
Решение
Имеем a=67, b=15, c=4.
Ответ: остаток от деления равен 7.
Мы также можем найти неполное частное, если знаем значение делимого, делителя и остатка. Исключим из исходного множества те элементы, которые образуют остаток. Благодаря свойствам вычитания натуральных чисел количество элементов в множестве мы теперь можем записать как a−d. После этого уже можно произвести деление без остатка, в результате которого получится b множеств по c элементов в каждом. Мы получили равенство (a−d):b=c. Его также можно записать в виде c=(a−d):b.
Определение 5
Если нужно найти неполное частное, нужно из делимого вычесть остаток и результат разделить на делитель.
Пример 7
Мы разделили 221 на 52 и получили остаток 13. Вычислите неполное частное.
Решение
Отнимем остаток от делимого и результат разделим на делитель. Считаем: (221−13):52=208:52=4 (для подсчета мы использовали метод подбора частного).
Ответ: неполное частное равно 4.
Осталось разобрать последний случай: как быть, если нужно найти делитель при известных значениях делимого, остатка и неполного частного? Начнем опять же с исключения остатка из делимого, то есть запишем a-d. Вспомнив смысл деления одного натурального числа на другое, запишем следующее равенство: (a−d):c=b. Также будет верно b=(a−d):c. Сформулируем правило:
Определение 6
Найти делитель можно, если вычесть из делимого остаток и получившуюся разность разделить на неполное частное.
Возьмем пример решения такой задачи.
Пример 8
Было выполнено деление 877 на некоторое число с остатком 2, неполное частное при этом составило 35. Найдите значение делителя.
Решение
Вычтем остаток из делимого и получим 875. Результат нужно разделить на известное нам неполное частное 35. В итоге получится нужное нам значение делителя. Вычислим столбиком:
Ответ: делитель равен 25.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Как найти делитель. Делитель частное найти делитель. Частное чисел делимое делитель.
- Альфашкола
- Статьи
- Как найти делитель?
Существует определенное правило для нахождения делителя. Вспомним, что такое делимое, делитель и частное.
В примере выше делитель у нас 4, поэтому мы разделим делимое 12 на частное 3 , чтобы найти делитель. Легко не так ли ? Теперь попробуем найти делитель в более сложных примерах.
Пример 1. Найдите делитель: (1080 : 24x = 15)
Решение:
(1080 : 24x = 15)
Алгоритм решения тот же: делимое делим на частное:
(1080:15 =72)
(24x=72)
(72:24=3)
Данное правило мы можем применять везде, где есть деление чисел.
Ответ: делитель равен (72) ((x=3)).
Если вы сомневаетесь, что на что надо делить, то придумайте такой же пример, только с простыми числами. Рассмотрим это на примере ниже.
Пример 2. Найтите делитель: (784:x=14)
Решение:
(784:x=14)
аналогичный пример с простыми числами:
(6:x=2) — здесь понятно, чтобы найти (x) надо (6) разделить на (2), то есть делитель равен (3)
(784:14 = 56) — искомый делитель
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Сергеевна Соколюк
Репетитор по математике
Стаж (лет)
Образование:
Южный федеральный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-9 классов.
Елена Ивановна Качанова
Репетитор по математике
Стаж (лет)
Образование:
Витебский государственный педагогический институт им. С.М. Кирова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов.
С радостью жду Вас на своих занятиях!
Татьяна Валентиновна Дмитриева
Репетитор по математике
Стаж (лет)
Образование:
Ивановский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов по математике и 7-11 классов по физике.
В математике и физике всё подчиняется определенным законам, которые легко понять, и которые одинаковы абсолютно для всех. Я люблю математику за её универсальность. Как говорил известный российский физик-теоретик Ландау: «Математика царица наук и служанка физики», замечательный «тренажер для ума». Люблю работать с детьми независимо от их начальной подготовки и буду рада, если они увидят сами свой рост, приобретут уверенность в себе и научатся не пасовать при любой трудности. Не имея базовой подготовки по математике, трудно достичь хороших результатов при сдаче ОГЭ и ЕГЭ по физике. Ежегодно все, кто работает со мной на 100%, успешно сдают ОГЭ и ЕГЭ по физике. Буду рада помочь успешно усвоить материал школьной программы как по математике, так и по физике. Стану добрым наставником для вашего ребёнка!
Похожие статьи
- Сфера
- Смежные углы
- Основные формулы: треугольник, параллелограмм и четырехугольник
- Площадь произвольного четырехугольника
- Обратные тригонометрические функции
- Финансовый Университет при Правительстве Российской Федерации | Баллы на бюджет (2017 / 2018), вступительные испытания, факультеты
- Определение чисел по их сумме и разности
- Умные по-разному: 8 видов интеллекта, о которых должен знать каждый родитель
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Математика Письменное деление на трехзначное число с остатком
Расшифровка видео
Которое делится на 40 чтобы найти частное и остаток также, проверить деление по формуле Давида равно делителю в частном плюс остаток. Итак, давайте посмотрим на это.
Хорошо. Итак, что мне нравится, так это то, что в нем есть? Вот что даст наш ответ как 240 вольт. Так что я напишу это здесь или я просто хорошо, я напишу это. Итак, нам нравится слышать 44 после вычитания теоремы 4446, мы получаем остаток вот так. У нас есть все наши ценности, которые у нас есть деньги, другой вопрос.
Итак, однажды я сделал, что если он даст нам 593 полное право, и, наконец, 4 плюс 2 даст нам до свидания 936. Следовательно, наш ответ правильный, и он правильный. Большое спасибо, ребята, за просмотр видео. Если у вас есть какие-либо сомнения, дайте мне знать комментарий ниже, и я вернусь как можно скорее. Так же ставьте лайк под видео подписывайтесь на канал. Большое спасибо.
Связанные вопросы
Q1) Найдите разницу между наибольшим четырехзначным числом и наименьшим шестизначным числом…
Q2) Найдите разницу между наименьшим числом из восьми цифр и наибольшим числом из пяти.
Q3) Произведение двух чисел равно 528. Если произведение цифр их единиц равно 8, а произведение…
Q4) Существует ли число a такое, что a ÷ a = a?
Фейсбук
WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 5(А)
Упражнение 5(B)
Упражнение 5(C)
Упражнение 5(D)
Упражнение 5(E)
Упражнение 5(F)
Главы
Система счисления (Закрепление чувства числа3)
Оценка
Числа в Индии и международной системе (со сравнением)
Разрядное значение
Натуральные числа и целые числа (включая шаблоны)
Отрицательные числа и целые числа
Числовая строка
HCF0 и LCM
Игра с номерами
Наборы
Соотношение
Доля (включая проблемы с словами)
Unitary Method
Фракции
Десятичные фракции
процент (процент)
Идея скорости, расстояние и время
Фундаментальные концепции (Алгебра.
Основные операции (связанные с алгебраическими выражениями)
Подстановка (включая использование скобок в качестве группирующих символов)
Обрамление алгебраических выражений (включая вычисление)
Простые (линейные) уравнения (включая текстовые задачи)
Основные понятия (геометрия)
Углы (с их типами)
Свойства углов и линий (включая параллельные линии)
Треугольники (включая типы, свойства и построение)
Четырехугольник
Многоугольники
Окружность
Повторное упражнение по симметрии (включая построения по симметрии)
Распознавание твердых тел
Периметр и площадь плоских фигур
Обработка данных (включая пиктограмму и гистограмму)
Среднее и медиана
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены основа математики. Этими четырьмя основными операциями являются сложение, вычитание, умножение и деление.
Значение деления
Деление — это элементарная арифметическая операция, широко используемая во всех областях математики. Его цель состоит в том, чтобы разбить число на равные части.
Например, когда мы делим число 20 на число 4, мы получаем ответ как 5. Мы разделили число 20 на 4 равные части, значение каждой части равно 5.
Символ деления
Для обозначения операции деления используется множество символов. Однако два наиболее часто используемых символа для представления деления — это «÷» и обратная косая черта дроби «/».
Например, выражение 10 разделить на 5 можно записать так:
- 10÷5
- 10/5
Общая форма деления
Деление также можно рассматривать как процесс вычитания повторений. . Одним из популярных методов выполнения операции деления является метод длинного деления, при котором мы продолжаем делить делимое на делитель до тех пор, пока не получим нулевой остаток. На каждом шаге мы вычитаем из делимого наибольшее кратное делителя, равное или меньшее делимого.
Ниже приведена общая формула деления:
Делимое = (Делитель × Частное) + Остаток
Деление, по существу, является обратным процессом умножения. Этот факт помогает нам проверить наш результат, подставив соответствующие значения в общую формулу деления.
Что такое делитель?
В процессе деления делитель является одним из важных членов помимо делимого, частного и остатка.
Давайте более подробно ответим на вопрос, что такое делитель, взглянув на определение делителя.
Определение делителя
Делитель — это число, на которое при вычислении делится другое число. Определение делителя гласит, что это член, выполняющий операцию деления делимого.
Например, когда мы делим число 28 на число 7, 7 называется делителем, а число 28 называется делимым.
Теперь, когда мы ответили, что такое делитель, давайте рассмотрим еще несколько важных понятий.
Формула делителя
Переставив члены в общей формуле деления, мы можем получить следующую формулу.
Делитель = (Дивиденд – Остаток) / Частное
Делитель и его примеры
Рассмотрим утверждение 33÷11=3. Здесь число 33 — это делимое, число 11 — делитель, а число 3 — частное.
Рассмотрим утверждение 50÷10=5. Здесь число 50 — это делимое, число 10 — делитель, а число 5 — частное.
Интересные свойства делителя
Делитель — это число, которое делит делимое на равные части. Однако он может оставить или не оставить остаток. Ниже приведены некоторые интересные свойства делителя.
- Остаток всегда меньше делителя для любого процесса деления.
- 1 является делителем всех чисел.
- Если частное равно делимому, то делитель всегда будет равен 1.
- Если делимое равно делителю, то частное всегда будет равно 1.
- Если остаток равен нулю, это означает, что число является полным делителем делимого и может быть полностью разделено.
- Если делитель больше делимого, то частное всегда будет равно десятичному числу.
Делители и множители
Делитель делит делимое. Если делитель полностью делит делимое, не оставляя остатка, то делитель называется коэффициентом дивиденда.
Пример 1: Рассмотрим число 8. 1, 2, 4 и 8 — это числа, которые полностью делят число 8, не оставляя остатка. Эти числа являются множителями, а также делителем.
Пример 2. Рассмотрим деление 12 на 5. После операции деления мы получаем 2 как частное и остаток. Поскольку остаток отличен от нуля, делитель не может полностью разделить делимое в этом случае. Здесь 5 — делитель 12, но не его множитель.
Дивиденд против делителя
Делитель и делимое — два основных компонента процесса деления. Используя эти два члена, мы получаем остальные компоненты операции деления — частное и остаток. Давайте разберемся в отличии делимого от делителя от их определения.
Делитель — это число, которое выполняет операцию деления над делимым. Делимое — это число, над которым делитель выполняет операцию деления.
Для еще большей ясности отношения делимого и делителя рассмотрим следующий пример.
Когда мы делим число 60 на число 15, мы получаем 4 в частном и 0 в остатке. Число 15, которое выполняет операцию деления, называется делителем. Делимое — это число 60, над которым выполняется операция деления.
Остаток
Остаток — еще один важный термин операции деления. Это оставшаяся часть делимого после его деления на делитель. Когда делитель не способен разделить делимое на равные части, в результате мы получаем ненулевой остаток. Некоторые важные свойства остатка приведены ниже.
Делитель всегда больше полученного остатка для каждой операции деления. Если полученный остаток больше или равен делителю, то это означает, что мы неправильно выполнили деление.
Что касается частного, то остаток может быть больше, меньше или даже равен частному.
Если на делитель можно точно разделить делимое, то остаток всегда равен нулю.
Пример метода длинного деления № 1
Рассмотрим деление 25 на 12.
Здесь 25 — делимое, а 12 — делитель. Решив операцию деления, мы получим 2 в частном и 1 в остатке.
Метод длинного деления Пример № 2
Рассмотрим деление 235 на 15.
Здесь 235 — делимое, а 15 — делитель. Решив операцию деления, мы получим 15 в частном и 10 в остатке.
Увлекательные факты о подразделении
- Де Морган в 1845 году ввел косую черту, используемую как знак этого процесса в делении.
- Символ косой черты, используемый для деления, был введен Де Морганом в 1845 году.
- Согласно правилам арифметики, деление числа на ноль не определено.
- Раздел также представлен термином двоеточие в некоторых неанглоязычных странах. Готфрид Вильгельм Лейбниц ввел этот термин в свой Acta eruditorum 1684 года.
- Швейцарский математик Иоганн Ран ввел символ обела «÷» в 1659 году..
Часто задаваемые вопросы
- Что такое делитель?
Делитель — это число, которое делится на другое число, называемое делимым, для получения результата.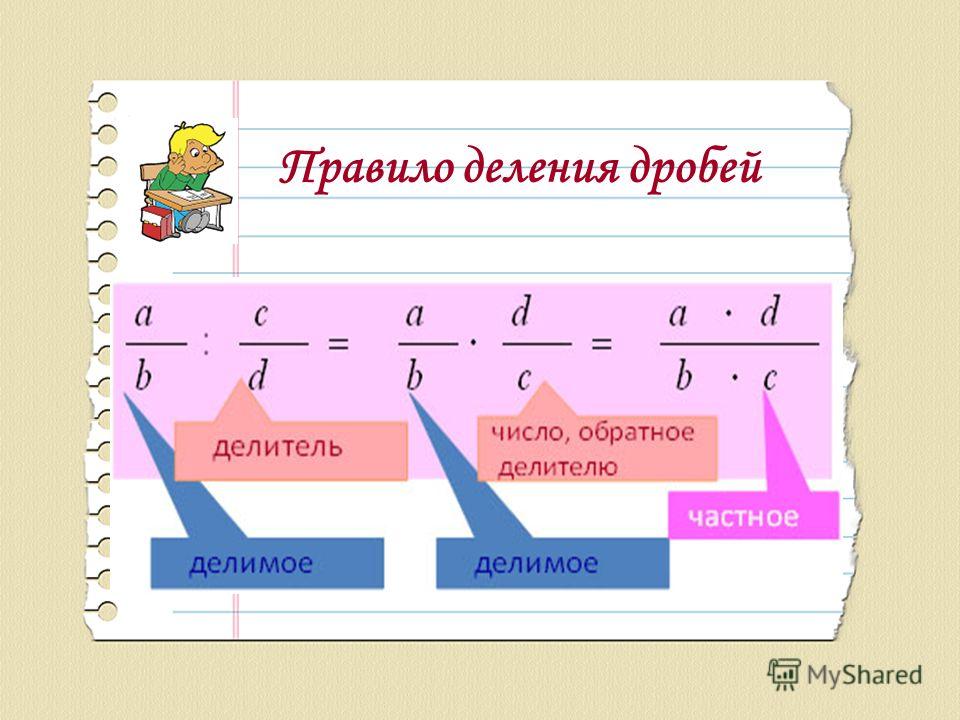
- Можно ли назвать число делителем самого себя?
Каждое число действует как делитель самого себя. При делении числа на себя оно дает в частном 1 и остаток равен нулю.
- Возможны ли отрицательные делители?
Да, делители могут быть как положительными, так и отрицательными. Обычно мы рассматриваем только положительные числа как делители. Например, у числа 6 всего восемь делителей: -6, -3, -2, -1 и 1, 2, 3, 6. Однако здесь мы рассматриваем только положительные члены.
- Как узнать делитель и делимое в дробях?
Дроби или рациональные числа представлены в форме p/q. Здесь p называется числителем, который также является делимым. Член q обозначает знаменатель, который также является делителем.
- Что такое простые делители?
Делители, которые также удовлетворяют условию быть простым числом, называются простыми делителями.
Синтетическое деление — Темы предварительного исчисления
Темы в
ПРЕДВАРИТЕЛЬНАЯ РАБОТА
Содержание | Дом
12
Теорема об остатках
Факторная теорема
В АРИФМЕТИКЕ пишем, например,
или
Эквивалентно
47 = 9 · 5 + 2
5 называется делителем, 47 — делимым, 9 — частным, а 2 — остатком.
| Дивиденд Делитель |
= Частное + | Остаток Делитель |
или
Дивиденд = Частное · Делитель + Остаток.
В алгебре, если мы разделим многочлен P ( x ) на многочлен D ( x ) (где степень D меньше степени P ), мы найдем
P ( x ) = Q ( x ) · D ( x ) + R (90).
P ( x ) — делимое, Q ( x ) — частное, R ( x ) — остаток.
Например, если делением в большую сторону мы разделили
x 3 — 5 x 2 + 3 x — 7 на x — 2,
мы найдем
| x − 2 | = | x 2 − 3 x − 3 − | 13 x − 2 |
или
= ( x 2 − 3 x − 3)( x − 2) − 13,
x 3 — 5 x 2 + 3 x — 7 — дивиденд, x 2 — 3 x 2 — 3 x .
Вот как решить эту задачу синтетическим делением.
Во-первых, чтобы использовать синтетическое деление, делитель должен быть первой степени и иметь вид x − a . В этом примере делитель равен 90 822 x 90 823 − 2, где 90 822 равно 90 823 = 2,
.
Вот опять проблема:
Выполните следующие действия:
1. Запишите коэффициенты делимого:
1 − 5 + 3 − 7
2. Поместите и , в данном случае 2, в поле справа, оставьте пробел и нарисуйте
2. строка:
3. Уменьшите старший коэффициент (1), умножьте его на на (2) и
3. напишите этот продукт (1 · 2) во второй колонке:
4. Добавить:
5. Повторите процесс. −3 · 2 = −6. И так далее, пока все коэффициенты
5. исчерпаны.
Первые три числа, 1 − 3 − 3, являются коэффициентами частного, а последнее число, −13, является остатком .
У нас есть
х 3 − 5 х 2 + 3 х − 7 = ( х 2 − 3 х )0822 х — 2) — 13,
Пример 1. Используйте синтетическое деление, чтобы разделить
.
2 x 5 + 3 x 4 + 25 x 2 − 1 на x + 3.
Решение . Здесь есть пара моментов. Во-первых, мы должны учесть все шести коэффициентов общего вида.
2 + 3 + 0 + 25 + 0 — 1
Коэффициент x 3 равен 0, как и коэффициент x .
Затем делитель равен x + 3. Но делитель должен иметь вид x − a .
х + 3 = х — (-3).
Следовательно, a = −3.
Вот синтетическое деление:
Это говорит нам
| x + 3 | = | 2 x 4 − 3 x 3 + 9 x 2 − 2 x + 6 − | 19 x + 3 |
или
| 2 x 5 + 3 x 4 + 25 x 2 − 1 | = | (2 х 4 − 3 х 3 + 9 х 2 − 2 х + 6)( 909 2 + 908) |
| Дивиденд | = | Частное · Делитель + Остаток. |
Примечание. Степень частного на единицу меньше, чем степень делимого на . И степень остатка меньше степени делителя, x + 3, что в данном случае равно 1. Таким образом, остаток имеет степень 0, то есть число.
В общем случае, если мы разделим многочлен степени n на многочлен степени 1, то степень частного будет n − 1. А остаток будет числом.
Задача 1. Используйте синтетическое деление, чтобы разделить
x 3 − 8 x 2 + x + 2 на x − 7,
Напишите свой ответ в форме
P ( x ) = Q ( x ) · D ( x ) + R .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
х 3 − 8 х 2 + х + 2 = ( х 2 — х — 6)( х — 7) — 40
Теорема об остатках
Значение многочлена P ( x ) при x = a ,
Р ( а ),
равно остатку от деления P( x )
на x − a .
То есть когда
P ( x ) = Q ( x ) ( x − a ) + R ,
, где Q ( x ) — частное, а R — остаток, тогда
Р ( a ) = Р .
Для,
| П ( а ) | = | Вопрос ( а )( а − а ) + Р |
| = | Q ( a ) · 0 + R | |
| = | 0 + Р | |
| = | Р . |
Пример 2. Пусть f ( x ) = x 3 — 3 x 2 — 13 x + 15,
Мы будем использовать синтетическое деление, чтобы разделить f ( x ) на x + 4.
Теперь, что говорит нам теорема об остатках?
Значение f ( x ) при x = −4 равно остатку:
ж (-4) = -45.
Теперь давайте разделим f ( x ) на x − 5:
.
Что здесь говорит нам теорема об остатках?
ф (5) = 0,
Но это означает, что 5 является корнем f ( x )
Более того, так как остаток равен 0 — остатка нет — то ( x — 5) — это коэффициент из f ( x ). Синтетическое подразделение показывает:
x 3 — 3 x 2 — 13 x + 15 = ( x 2 + 2 x – 3) (232323 ( ( (. 2 + 2 2 x .
Это иллюстрирует теорему о факторах:
Факторная теорема. x − r является делителем многочлена P ( x ) тогда и только тогда, когда r является корнем P ( x ).
Задача 2. Let F ( x ) = x 3 — 5 x 2 — 4 x + 7. Используйте деление синтетического дел. х — 7,
Следовательно, по теореме об остатках
ф (7) = 77.
Поскольку остаток не равен 0 — f (7) 0 — при делении f ( x ) на x − 7, то ( x − 7) не является множителем f ( х ). И согласно факторной теореме 7 не является корнем из ( x ).
Задача 3. Пусть г ( х ) = 3 х 4 + 17 х 3 + 16 x 2 − 10 x + 4. Используйте синтетическое деление, чтобы разделить г ( x ) на x + 2.
Согласно теореме об остатках,
г (−2) = 0,
Итак, что вы можете сказать об −2?
−2 — это корень из g ( x ).
Что вы можете сказать о ( x + 2)?
( x + 2) является коэффициентом g ( x ).
Задача 4. Используйте синтетическое деление, чтобы разделить
x 3 + 125 на x + 5.
х 3 + 125 = ( х 2 − 5 х + 25)( х + 5)
Следующая тема: Корни многочленов
Содержание | Главная
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Чему равен остаток, если дивиденд меньше делителя?
Мы начнем с обновления следующих условий, которые соблюдаются.
В задачах на остаток, когда целое число n делится на ненулевое целое число d :
- n должно быть целым числом,
- d должно быть ненулевым целым числом, d ? 0
- частное должно быть целым числом,
- остаток должен быть неотрицательным целым числом, т.
е. остаток ? 0
Когда вы делите 19 ( n ) на 5 ( d ), вы получаете частное 3 и остаток 4. .
Остаток также определяется как расстояние от n до ближайшего кратного d , которое меньше n .
Давайте рассмотрим пример, чтобы понять это определение остатка.
19 нельзя разделить точно на 5.
В этом случае n равно 19, а d равно 5. : Список кратных d (5), которые меньше n (19). Это …, -15, -10, -5, 0, 5, 10, 15, ….
19 – 15 = 4. Это ваш остаток.
Это показано на рисунке ниже.
Вы также можете найти остаток, используя деление в большую сторону. Это сэкономит вам время на вопрос.
Какой остаток при делении 5 на 8?
В этом случае n равно 5, а d равно 8.
Давайте снова повторим описанный выше трехэтапный процесс.
- Шаг 1: Перечислите кратные d (8), которые меньше, чем n (5). Это …, -24, -16, -8, 0, ….
- Шаг 2: Выберите кратное, ближайшее к n . В данном случае это 0,
- Шаг 3: Найдите расстояние от n (5) до кратного, выбранного на шаге 2 (0).
.
5 – 0 = 5. Это ваш остаток.
Опять же, вы также можете использовать деление в большую сторону, чтобы найти остаток.
Пара замечаний.
Если n меньше d , то
- частное = 0
- остаток = n
Деление в длинное можно выполнить следующим образом:
Хотя это и правильный способ деления в длинное, в результате получается десятичное значение частного. Поскольку частное всегда должно быть целым числом, это неправильный способ нахождения остатка.
Чтобы найти остаток, частное должно быть целым числом. В этом случае единственно возможное целочисленное значение частного равно нулю.
Если вам нравятся аналогии, рассмотрите ту же проблему в контексте реальной жизни;
«У вас есть 5 апельсинов, есть 8 человек, и каждый человек должен получить одинаковое количество апельсинов (Это то же самое, что сказать 5 ÷ 8, т.е. разделить 5 апельсинов на 8 человек). Сколько апельсинов получит каждый (частное) и сколько апельсинов останется нераспределенным (остаток)?».
Очевидный ответ: никто не получит апельсин, т. е. частное = 0
Если никто не получит ни одного апельсина, то у вас останутся все 5 апельсинов, т. е. остаток = 5,
Подытожим:
Если n < d , то
- частное = 0
- остаток = n
- Любите аналогии 🙂
Как и у большинства людей, сдающих GRE, ваши знания по математике могут быть немного заржаветыми.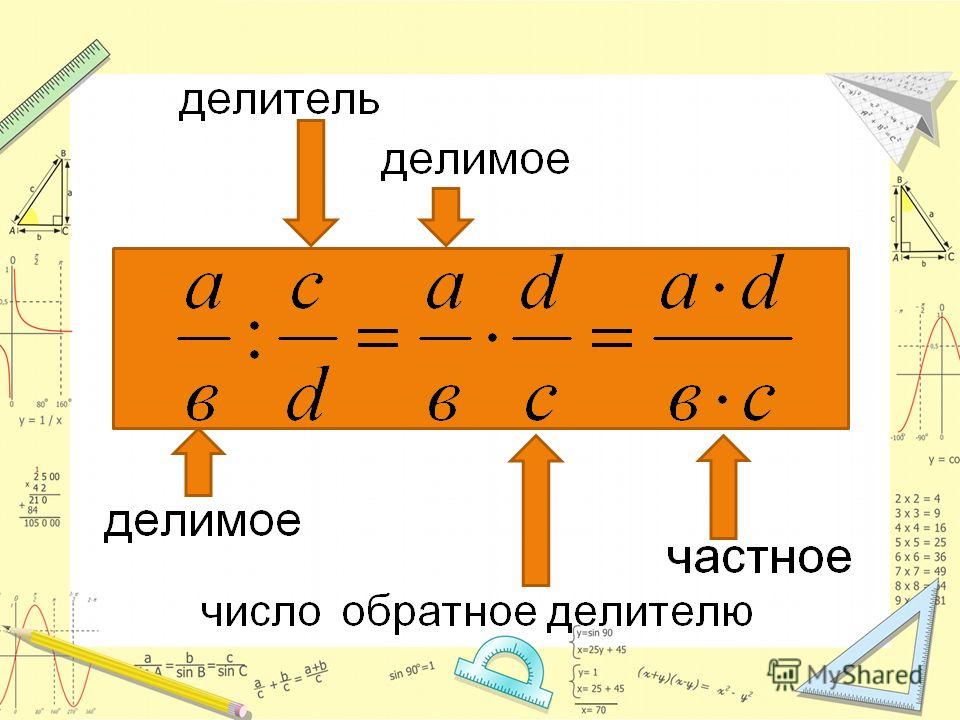
подробнее
Стандартное отклонение – важный статистический термин, проверенный на GRE. Это дает вам представление об отклонении или разбросе набора чисел от его среднего значения; следовательно, низкое стандартное отклонение означает, что числа очень близки к среднему, и наоборот….
читать дальше
Каждое целое число больше 1 является либо простым, либо составным числом. Все составные числа можно представить в виде произведения простых чисел. Например, 6 можно выразить как 2 × 3. Простые делители числа 6 — это 2 и 3. Тогда как выражение 2 × 3 называется…
подробнее
Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет 100? Настройте диаграмму: 100 Левая колонка Правая колонка 1 100 2 50 4 25 5 20 10 10 Помните правило: как только факторы повторяются (например, 10 и 10), остановитесь.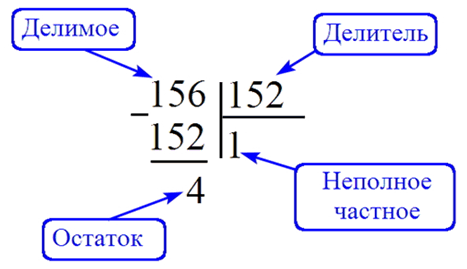
читать далее
Вы уже видели прекрасную таблицу множителей — простой способ найти все множители целого числа. Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет число 140? Вопрос касается факторов, поэтому таблица факторов…
подробнее
Некоторые целочисленные вопросы могут потребовать от вас найти множители целого числа. Таблица множителей — это основной метод нахождения всех множителей любого целого числа. Этот метод также может быть полезен для вопросов о том, сколько множителей имеет конкретное целое число. Техника…
подробнее
Простые числа играют центральную роль в целочисленных вопросах. Излишняя самоуверенность здесь опасна: в то время как почти каждый может без труда назвать определение простого числа, поле на самом деле изобилует неправильными представлениями.
Памятка по нахождению неизвестных компонентов действий.
Скачать:
Предварительный просмотр:
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
По теме: методические разработки, презентации и конспекты
- Мне нравится
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
10 : 2 = 5.
Частное чисел – это итог процесса деления одного значения на второе. Пример:
28 : 7 = 4,
где 28 — делимое;
7 — делитель;
4 — частное.
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
Приведём пример:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.




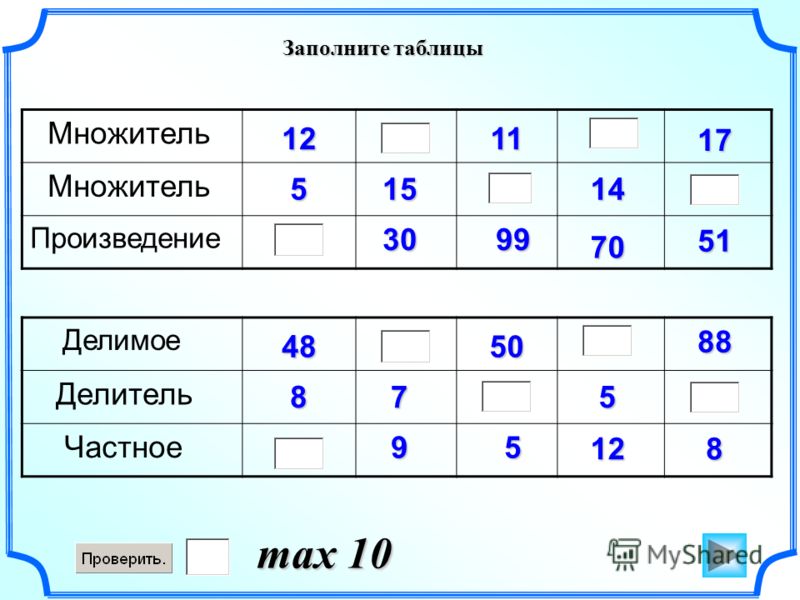
 (Если при этом остаток получился равным нулю, то исходные числа делятся без остатка, и по правилу деления целых чисел с противоположными знаками искомое частное равно числу, противоположному частному от деления модулей.)
(Если при этом остаток получился равным нулю, то исходные числа делятся без остатка, и по правилу деления целых чисел с противоположными знаками искомое частное равно числу, противоположному частному от деления модулей.)

 Умножив частное 3 на делитель 4, получаем делимое 12.
Умножив частное 3 на делитель 4, получаем делимое 12. Это показывает, что частное 5 мало и его нужно увеличить.
Это показывает, что частное 5 мало и его нужно увеличить.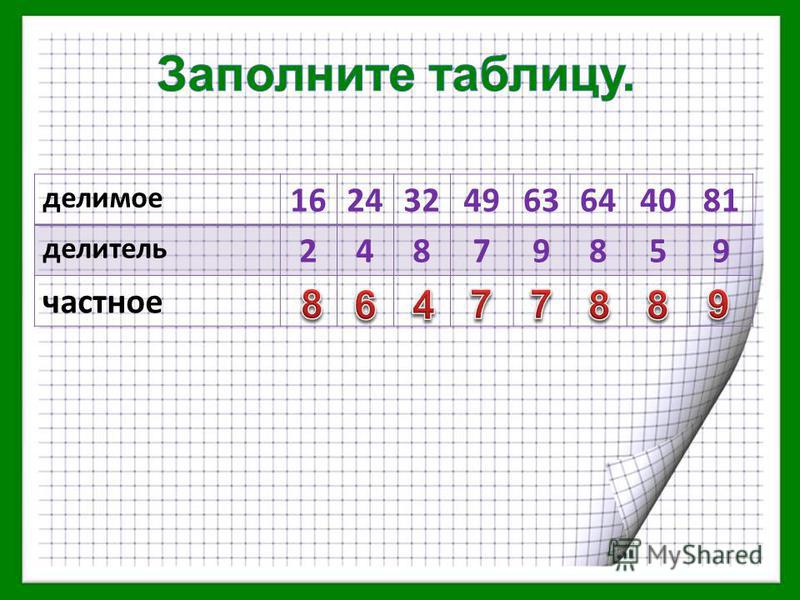 Десятки и единицы делимого не имеют никакого влияния на сотни частного, поэтому на них пока не обращаем внимания. Наибольшее число сотен в частном есть 2, ибо 3 содержится в 7 сотнях 2 сотни раз; пишем в частном 200. Умножая 200 на 3 и вычитая произведение 600 из делимого, получаем первый остаток 132.
Десятки и единицы делимого не имеют никакого влияния на сотни частного, поэтому на них пока не обращаем внимания. Наибольшее число сотен в частном есть 2, ибо 3 содержится в 7 сотнях 2 сотни раз; пишем в частном 200. Умножая 200 на 3 и вычитая произведение 600 из делимого, получаем первый остаток 132.
 Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.
Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.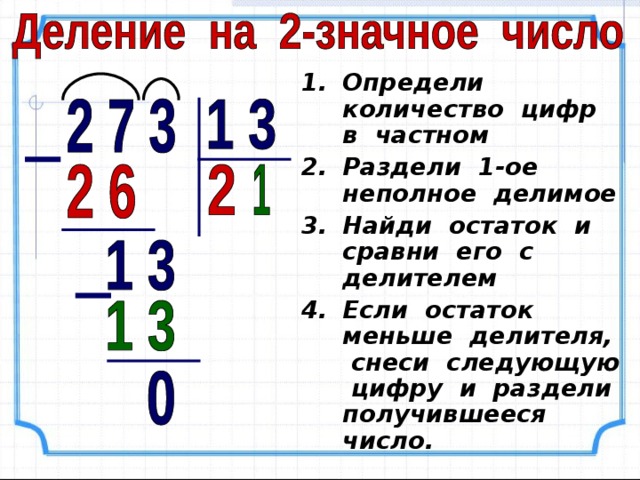 Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.
Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.
 е. остаток ? 0
е. остаток ? 0