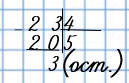- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Деление с остатком
Начнём рассмотрение новой темы с решения задачи.
Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?
8 : 2 = 4 (к.)
Каждый ребёнок получил по 4 конфеты.
На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?
Каждый получил по 2 конфеты и 2 конфеты остались лишними.
Как это записать?
8 : 3 = 2 (ост. 2)
Как сделать проверку?
2 • 3 + 2 = 8
Правило 1
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
16 : 7 = 2 (ост. 2)
23 : 8 = 2 (ост. 7)
Правило 2
При делении с остатком остаток всегда должен быть меньше делителя.
43 : 8 = 5 (ост. 3)
остаток 3 < делимого 5
34 : 4 = 8 (ост. 2)
остаток 2 < делимого 4
Правило 3
Если делимое меньше делителя, в частном получается ноль, а остаток равен делимому.
7 : 10 = 0 (ост. 7)
6 : 9 = 0 (ост. 6)
Порядок решения
14 : 5 = 2 (ост. 4)
1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.
10 : 5 = 2
2. Вычитаю из делимого найденное число: 14 − 10 = 4
3. Сравниваю остаток с делителем
4 < 5
Решение верно.
Проверка деления с остатком
1. Умножаю неполное частное на делитель.
2. Прибавляю остаток к полученному результату.
3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.
Деление в столбик
В 23 содержится 5 раз по 4, и ещё остаётся 3.
Решение записывают так:
23 : 4 = 5 (ост. 3) или так:
, где 23 — делимое, 4 — делитель, 5 — неполное частное, а 3 — остаток.
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
2 класс
Страница 76. Урок 29,
Петерсон, Учебник, часть 3
Страница 77. Урок 29,
Петерсон, Учебник, часть 3
Страница 79. Урок 30,
Петерсон, Учебник, часть 3
Страница 80. Урок 30,
Петерсон, Учебник, часть 3
Страница 81. Урок 31,
Петерсон, Учебник, часть 3
Страница 82. Урок 31,
Петерсон, Учебник, часть 3
Страница 84. Урок 32,
Петерсон, Учебник, часть 3
Страница 87. Урок 33,
Петерсон, Учебник, часть 3
Страница 108. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 58. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 30,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 60,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 44. Урок 17,
Петерсон, Учебник, часть 2
Страница 10. Урок 4,
Петерсон, Учебник, часть 3
Страница 49. Урок 22,
Петерсон, Учебник, часть 3
4 класс
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 44,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 51. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 28,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 55,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 553,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 600,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 766,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1091,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1109,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1721,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1724,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 801,
Мерзляк, Полонский, Якир, Учебник
Номер 860,
Мерзляк, Полонский, Якир, Учебник
Номер 1139,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 128,
Мерзляк, Полонский, Якир, Учебник
Номер 363,
Мерзляк, Полонский, Якир, Учебник
Номер 370,
Мерзляк, Полонский, Якир, Учебник
Номер 373,
Мерзляк, Полонский, Якир, Учебник
Номер 764,
Мерзляк, Полонский, Якир, Учебник
Номер 1005,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Задание 591,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 999,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1145,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 421,
Мерзляк, Полонский, Якир, Учебник
Номер 431,
Мерзляк, Полонский, Якир, Учебник
Номер 573,
Мерзляк, Полонский, Якир, Учебник
Номер 574,
Мерзляк, Полонский, Якир, Учебник
Номер 602,
Мерзляк, Полонский, Якир, Учебник
Номер 606,
Мерзляк, Полонский, Якир, Учебник
Номер 607,
Мерзляк, Полонский, Якир, Учебник
Номер 797,
Мерзляк, Полонский, Якир, Учебник
Номер 873,
Мерзляк, Полонский, Якир, Учебник
Номер 1031,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 138,
Мерзляк, Полонский, Якир, Учебник
Номер 139,
Мерзляк, Полонский, Якир, Учебник
Номер 141,
Мерзляк, Полонский, Якир, Учебник
Номер 193,
Мерзляк, Полонский, Якир, Учебник
Номер 212,
Мерзляк, Полонский, Якир, Учебник
Номер 241,
Мерзляк, Полонский, Якир, Учебник
Номер 304,
Мерзляк, Полонский, Якир, Учебник
Номер 306,
Мерзляк, Полонский, Якир, Учебник
Номер 307,
Мерзляк, Полонский, Якир, Учебник
Деление с остатком.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
16=5⋅3+1
a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.
Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
Итак, мы уже познакомились с делением. Но есть еще один важный и нужный вид деления — это деление с остатком.
Откуда берется остаток
Остаток получается, если делимое нельзя разделить на делитель нацело (то есть до получения целого числа).
Представим, что мы купили $textcolor{orange}{10}$ яблок. К нам пришли друзья, и мы захотели поделиться с ними яблоками, и при этом дать каждому равное количество.
Если друга всего $textcolor{coral}{2}$, то каждому дадим по $textcolor{green}{5}$ яблок.
Но что делать, если друзей будет $textcolor{coral}{3}$, $textcolor{coral}{7}$ или $textcolor{coral}{9}?$ У нас не получится разделить $textcolor{orange}{10}$ яблок поровну на такое количество человек.
Предположим, что в итоге у нас $textcolor{coral}{7}$ друзей и $textcolor{orange}{10}$ яблок. Чтобы никого не обидеть, мы можем дать каждому по $textcolor{green}{1}$ яблоку и у нас останется $textcolor{blue}{3}$ яблока. Теперь давайте рассмотрим пример:$$textcolor{orange}{10}:textcolor{coral}{7}=textcolor{green}{1}space (ост.spacetextcolor{blue}{3})$$В данном случае, $textcolor{orange}{10}$ яблок — это делимое, $textcolor{coral}{7}$ друзей — делитель, а $textcolor{green}{1}$ — неполное частное. Что же означает цифра $textcolor{blue}{3}$ и откуда она взялась?
То число, которое осталось при делении, называют остатком.
В нашем случае $textcolor{blue}{3}$ яблока и будут остатком.
Как найти остаток
Рассмотрим другой пример$$textcolor{orange}{42}:textcolor{coral}{9}=textcolor{green}{x}space(ост.space textcolor{blue}{y})$$Давайте попробуем найти $textcolor{green}{x}$ и $textcolor{blue}{y}$:
- Сначала нужно проверить, есть остаток или нет. В нашем случае $textcolor{orange}{42}$ не делится нацело на $textcolor{coral}{9}$, значит, остаток есть.
- Теперь подберем самое большое число, которое можно разделить нацело на делитель. При этом данное число должно быть меньше самого делимого. $textcolor{purple}{36}$ — самое большое число, которое делится нацело на $textcolor{coral}{9}$.
- Чтобы получить $textcolor{purple}{36}$, нужно $textcolor{coral}{9}$ умножить на $textcolor{green}{4}$, значит, $textcolor{green}{4}$ и будет неполным частным $textcolor{green}{x}$.
- Из $textcolor{orange}{42}$ вычтем произведение делителя и неполного частного $(textcolor{orange}{42} — textcolor{purple}{36})$. В ответе получаем $textcolor{blue}{6}$ — это как раз и будет остаток $textcolor{blue}{y}$. Пример решен!
Запомним еще два правила, которые необходимы при работе с остатком:
Остаток всегда меньше делителя.
Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка, то есть нацело.
Как найти делимое
Нужно уметь находить не только частное и остаток, но и делимое. На самом деле здесь также все просто.
Чтобы найти $textcolor{orange}{делимое}$ при делении с остатком, нужно умножить $textcolor{green}{неполноеspaceчастное}$ на $textcolor{coral}{делитель}$ и к полученному произведению прибавить $textcolor{blue}{остаток}$.
Рассмотрим пример$$textcolor{orange}{x}:textcolor{coral}{11}=textcolor{green}{3} space(ост. spacetextcolor{blue}{9})$$Умножаем $11$ на $3$, получаем $33$. К этому значению прибавляем $9$, и в ответе получается $42.$ Это и есть искомый $x$!$$textcolor{coral}{11}cdottextcolor{green}{3}=33newline33+textcolor{blue}{9}=textcolor{orange}{42}$$
Часто задаваемые вопросы
Что означает, если остаток получается больше делителя?
Это означает, что деление произведено неправильно или не полностью.
Можно ли разделить остаток на делитель?
Можно, данную операцию мы будем проходить в разделе дроби.
Онлайн калькулятор поможет вам быстро вычислить остаток от деления двух чисел. Этот инструмент очень полезен для проверки решений в задачах по математике и арифметике. Это очень важная арифметическая операция, которую нужно знать для решения многих задач.
Онлайн калькулятор деление с остатком
Деление с остатком
Деление с остатком — это когда вы делите одно натуральное число на другое, и получаете остаток, который не равен нулю.
Деление с остатком целых положительных чисел
Это операция, при которой одно целое положительное число (делимое) делится на другое целое положительное число (делитель), и остается некоторое число, которое нельзя разделить на делитель без остатка.
Формула
a=b⋅q+ra = b cdot q + r
Деление с остатком может быть полезно при решении математических задач, например, для определения четности или нечетности числа. Если остаток от деления на 2 равен 0, то число четное, иначе — нечетное.
Пример
При делении 1010 на 33 с остатком получится результат 33 и остаток 11, так как 3⋅3=93 cdot3=9, и оставшаяся единица не может быть разделена на 33.
Деление с остатком целых отрицательных чисел
Деление с остатком для целых отрицательных чисел работает по тем же правилам, что и для целых положительных чисел.
Формула
r=a−b⋅qr = a − b cdot q
Вот простой алгоритм деления с остатком целых отрицательных чисел:
- Найдите модуль делимого и делителя, то есть возьмите их положительные значения;
- Разделите модуль делимого на модуль делителя, так же как при обычном делении с остатком;
- Получите неполное частное и остаток;
- Если делимое и делитель имеют разные знаки, то прибавьте 1 к неполному частному;
- Вычислите остаток, используя формулу r=a−b⋅qr = a — b cdot q.
Пример
Если мы делим −7-7 на 33, мы получим неполное частное −2-2 и остаток −1-1. А если мы делим −7-7 на −3-3, то неполное частное будет равно 22, а остаток будет 11.
Деление с остатком положительного числа на целое отрицательное
Деление с остатком положительного числа на целое отрицательное выполняется так же, как и деление с остатком двух положительных чисел, но с некоторыми отличиями.
Первым шагом необходимо найти модули делимого и делителя, то есть их значения без учета знака. Затем выполнить обычное деление модуля делимого на модуль делителя и получить неполное частное и остаток. Далее, если знаки делимого и делителя различны, необходимо к неполному частному прибавить 1. Если же знаки одинаковы, то ничего добавлять не нужно. Наконец, вычислить окончательный остаток, используя формулу r=a−b⋅qr = a — b cdot q, где rr — остаток, aa — делимое, bb — делитель, qq — неполное частное.
Пример
Если нужно выполнить деление 2727 на −5-5, то сначала найдем модули: ∣27∣=27|27| = 27 и ∣−5∣=5|-5| = 5. Затем выполним обычное деление: 275=5frac{27}{5} = 5 (остаток 22). Так как знаки чисел различны, добавляем 11 к неполному частному и получаем 66. Наконец, вычисляем окончательный остаток: 27−(−5)⋅6=727 — (-5) cdot 6 = 7. Итак, 27:−5=−627:-5 = -6 (остаток 77).
Деление с остатком отрицательного числа на положительное
Деление с остатком отрицательного числа на положительное выполняется аналогично делению с остатком положительного числа на положительное. Нужно выполнить деление столбиком, а затем проверить правильность ответа, умножив неполное частное на делитель и добавив к произведению остаток. Если результат равен делимому, то деление с остатком выполнено верно.
Пример
Рассмотрим выражение: (−15):4=(−3)(-15) : 4 = (-3) (остаток −3-3). В этом выражении −15-15 — это делимое, 44 — делитель, −3-3 — остаток, а −3-3 — неполное частное. Чтобы проверить правильность ответа, нужно умножить неполное частное (−3)(-3) на делитель (4)(4) и добавить к произведению остаток (−3)(-3). Получим: (−3)⋅4+(−3)=−15(-3) cdot 4 + (-3) = -15. Результат равен делимому, значит, деление с остатком выполнено верно.
Как проверить деление с остатком
Чтобы проверить деление с остатком, необходимо выполнить два шага:
Выполнить деление с остатком, как это делается обычно.
Проверить правильность результата, используя формулу: делимое == делитель ⋅cdot частное ++ остаток.
Формула
a=b⋅c+da = b cdot c + d, где aa — делимое, bb — делитель, cc — неполное частное, dd — остаток.
Если формула выполняется, то результат деления с остатком верный. Если нет, значит, была допущена ошибка при делении.
Пример
Задача: 274=6frac{27}{4} = 6 и остаток 33:
- Делимое равно 2727.
- Делитель равен 44.
- Частное равно 66.
- Остаток равен 33.
Проверяем формулу: 27=4⋅6+327 = 4 cdot 6 + 3. Формула выполняется, поэтому результат верный.