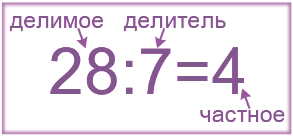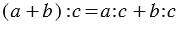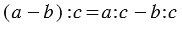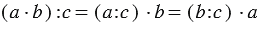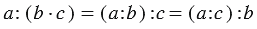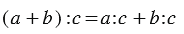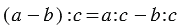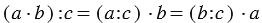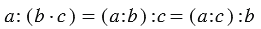Математика, 2 класс
Урок № 55. Название чисел при делении
Перечень вопросов, рассматриваемых в теме:
1. Как называются числа при делении?
2. Как называется числовое выражение со знаком деление?
Глоссарий по теме:
Деление — это арифметическое действие, обратное умножению. С помощью деления по произведению и одному из множителей определяется второй множитель.
Делимое — это число стоящее слева от знака деления, которое делим.
Делитель — это число стоящее справа от знака деления, число на которое делим делимое. (какими частями делим, дробим)
Частное — это число стоящее после знака равно, результат деления, числовое выражение со знаком деление.
Обязательная литература и дополнительная литература:
- Моро М. И., Бантова М. А. и др. Математика 2 класс. Учебник для общеобразовательных организаций. М.; Просвещение, 2017. – с. 62.
- С. И. Волкова. Математика 2 класс. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 44-47.
Теоретический материал для самостоятельного изучения
Запишем равенство, используя необходимое арифметическое действие:
10 яблок разложили на две тарелки поровну.
10 : 2 = 5
9 конфет раздали трём детям поровну.
9 : 3 = 3
8 тетрадей раздали четырём ученикам поровну.
8 : 4 = 2
Для того, чтобы выполнит задание, нам понадобилось действие деление.
Вы уже знаете, как называются числа при сложении и вычитании, недавно вы познакомились с названиями чисел при умножении.
Вы умеете называть выражения со знаками «плюс», «минус», со знаком умножения. Сегодня вы узнаете, как называются числа при делении. Выражение со знаком деления тоже имеет своё название. Хотите узнать? Вперёд!
Числа при делении имеют свои названия.
Рассмотрим рисунок.
8 листьев раздали детям, по 2 листа каждому.
8 : 2 = 4
4 человека получили листья.
Число, которое делят, называется делимым. 8 – это делимое. Число, на которое делят делимое, называется делитель. 2 – это делитель Результат действия деления называется частным. 4 – это частное. Выражение 8 разделить на 2 тоже называется частным.
Компоненты деления: делимое, делитель, частное.
Найдите частное, если делимое – 6, делитель – 3.
Проверьте: 6 : 3 = 2
Найдите частное чисел 12 и 6. Проверьте: 12 : 6 = 2
Решим задачу: 12 клубничек раздали 4 детям поровну. По сколько клубничек получил каждый ребёнок?
Для решения задачи выберем действие деление, так как надо узнать, сколько раз по 4 содержится в числе 12.
12 : 4 = 3 (кл.)
Ответ: по 3 клубнички получил каждый ребёнок.
Вспомним название чисел при делении. 12 – делимое, 4 – делитель. 3 – частное. 12 : 4 – это частное.
Вывод: компоненты действия деление – делимое, делитель, результат деления – частное.
Ответим на вопросы, поставленные в начале урока.
Число, которое делят, называется делимое.
Число, на которое делят делимое, называется делитель.
Результат деления – частное.
Числа, которые соединены знаком деления, тоже называются частное.
Выполним несколько тренировочных заданий.
1. По рисунку составьте задачи на деление. Запишите решение. Назовите компоненты действия деление.
а) 15 яблок разложили в 3 вазы, в каждую вазу поровну. Сколько яблок положили в одну вазу?
Проверьте: 15 : 3 = 5 (яб.).
Ответ: 5 яблок.
15 – делимое. 3 – делитель. 5 – частное. Выражение 15:3 – частное.
б) 15 яблок разложили в вазы, по 5 штук в каждую. Сколько ваз заняты яблоками?
15 : 5 = 3 (в.)
Ответ: 3 вазы.
15 – делимое. 5 – делитель. 3 – частное. Выражение 15:5 – частное.
2. Запишите выражение и найдите их значения:
Частное чисел 12 и 2.
Делитель 4, делимое 20.
Делимое 8, делитель 4.
Произведение 5 и 3.
Сумма чисел 6 и 4.
Проверьте.
12 : 2 = 6
20 : 4 = 5
8 : 4 = 2
5 ∙ 3 = 15
6 + 4 = 10
Деление
Деление в математике соответствует в жизни делению поровну. Только в математике все участвующие в делении величины имеют определённые названия, что позволяет формулировать правила и соблюдать точность при решении задач.
Как называются числа при делении?
При делении число, которое делят, называют делимое. Число, на которое делят, называют делитель. Результат называют частное. Выражение, составленное из делимого и делителя, называется частное.
30 : 2 = 15
30 — это делимое
2 — это делитель
15 — это частное
30 : 2 — это частное
Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
? : 2 = 15
? = 15 × 2
Как найти неизвестный делитель?
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
30 : ? = 15
? = 30 : 15
Изменение частного с изменением делимого
При увеличении делимого в x раз частное увеличивается в x раз. При уменьшении делимого в x раз частное уменьшается в x раз.
90 : 2 = 45
30 : 2 = 15
10 : 2 = 5
Изменение частного с изменением делителя
При увеличении делителя в x раз частное уменьшается в x раз. При уменьшении делителя в x раз частное увеличивается в x раз.
90 : 18 = 5
90 : 6 = 15
90 : 2 = 45
Изменение частного с изменением делимого и делителя одновременно
При увеличении делимого в x раз и уменьшении делителя в x раз частное не изменяется. При уменьшении делимого в x раз и увеличении делителя в x раз частное не изменяется.
90 : 18 = 5
30 : 6 = 5
10 : 2 = 5
Деление нуля и деление на ноль
Ноль можно делить на любое число — получается ноль. Никакое число нельзя разделить на ноль. Можно вычислить 0 : 5 = 0 И можно написать 5 : 0 , но невозможно вычислить значение этого выражения.
|
Все это части математического действия — деления. Попробую простым языкам, как объясняли мне.. лет тридцать назад..) «Делимое» — это число стоящее слева от знака деления, которое делим (дробим) «Делитель» — это число стоящее справа от знака деления, число на которое делим Делимое (какими частями делим, дробим) «Частное» — это число стоящее после знака равно, результат деления (числовое выражение количества целых частей — делителей в делимом) «Неполное частное» — это число стоящее после знака равно, результат деления при котором оставил «лишнее» число которое меньше Делителя. Неполное частное это количество только целых частей. Всегда пишется с числом Остатка. «Остаток» — это число оставшееся не делимым, которое меньше Делителя. А теперь на примерах — 10 : 5 = 2 В этом примере «10» — Делимое, «5» — Делитель, «2» — Частное. 13 : 5 = 2 (3) В этом примере «13» — Делимое, «5» — Делитель, «2» — неполное Частное, «3» — Остаток (как правило пишется в скобках рядом с «неполным частным»). система выбрала этот ответ лучшим
Для того чтобы не путаться в определении величин с которыми приходится иметь дело в процессе деления, люди давным давно придумали для них подходящие названия. Прежде всего само число. которое делят стали называть Делимым, ведь это число делится на части, оно буквально делимое. Например урожай плодов. Число, которое показывает на сколько частей мы поделим Делимое стали называть Делитель. Его задача разделить число на несколько групп, чтобы всем хватило поровну. Результат деления назвали Частным — это число показывает сколько единиц оказывается в каждой группе, кучке плодов, после того как разделили весь урожай. Наконец остаток — это то целое число плодов, которое невозможно поделить между всеми поровну. Пример: Собрали 51 яблоко. Это делимое. Решили поделить между папой, мамой, дочкой и сыном поровну, то есть на четырех. Это делитель. Поделили и получили что каждому причитается 12 яблок — это частное. А три яблока нельзя поделить на четырех и это Остаток. 51:4=12 (остаток 3).
Ладлен 6 лет назад С понятия делимое, делитель, частное и остаток, начинают изучать деление в средней школе. Так что это просто необходимо при изучении математики. И так делимое это число , которое подвергают делению. Делитель, это то число на которое делят, а соответственно частное это и есть результат деления. Но так уж бывает когда делимое число не делится нацело. Вот и образуемое в процессе деления число которое меньше делителя и которое нельзя разделить нацело и называется остаток. А пример можно привести следующий. например. Возьмем. 34: 5 = 6 (остаток 4) В данном случае 34 — делимое 5 — делитель. 6 — частное отделения 4 — остаток.
moreljuba 6 лет назад Все приведённые в вопросе понятия напрямую относятся к делению в математике. Итак, начнём с «делимого» — под ним подразумевается то число, которое будет делиться; «Делитель» уже подразумевает под собой то число, на которое будет делиться имеющееся «делимое». «Частное» представляет собой результат, полученный от деления. «Остаток» представляет собой число остающееся при делении в результате у нас будет неполное частное. Вот пример:
Бархатные лапки 6 лет назад Объяснить, что такое делимое, делитель, частное и остаток — реально легче на различных примерах.
Вот самый простенький вариант, тут все делится без остатка. Далее, рассматриваем немного сложней вариант, когда число делится не полностью и остается у нас остаток, который обычно обозначается в скобочках.
Или вот такой еще пример.
Ничего сложного как видим нет, все это дети изучают еще в начальных классах на уроках математики.
Nelli4ka 6 лет назад В примере: 20 : 10 = 2; 20 — это делимое (то, что делится), 10 — это делитель (то, что делит), 2 — это частное (то, что при умножении на делитель образует делимое). Возьмем другой пример: 17 : 3 = 5 (2), где 17 — делимое, 3 — делитель, 5 — неполное частное, 2 — остаток. При этом интересно, что остаток всегда меньше, чем неполное частное.
OlyaSh 8 лет назад Делимое — это число, которое будем делить. Делитель — это число, на которое будем делить Частное — это число, которое образуется при делении Остаток — это число, которое остается при делении (при этом частное будет неполным) Например 30/4=7(2) Здесь 30 — делимое, 4 — делитель, 7 — частное, 2 — остаток
Тори Торичка 6 лет назад Данные понятия арифметики легче всего рассмотреть на примере. Пример: 17 : 8 = 2 (остаток — 1). В этом примере 17 — делимое (число, которое делят), 8 — делитель (то, на что мы делим), 2 — остаток (то, что получаем при делении), 1 — остаток.
Azamatik 6 лет назад Сразу же приведем пример (можно даже несколько примеров): 1). 18 : 9 = 2; 2). 21 : 5 = 4,2 или же 4 и 1 в остатке. Делимое — это то число, которое мы делим (в наших примерах делимыми являются 18 и 21). Делитель — это то число, на которое мы делим делимое (делителями в наших примерах являются 9 и 5). Частное — это результат деления (частное в первом примере 2, а во втором примере 4,2). В первом случае делимое делится без остатка, а во втором у нас есть остаток — 1.
Бекки Шарп 6 лет назад Например 40:6=6 (4) В данном примере делимое -40, число, стоящее перед знаком деления, 6-делитель, число, стоящее после знака деления или на которое делим делимое. 6-частное , то, что получается в результате деления 4-остаток , число, остающееся при делении
25 : 4 = 6 (1) делимое делитель частное остаток Знаете ответ? |
Перед тем как найти делитель, нужно понимать, что такое делитель, что такое делимое и частное.
Делитель — это число, на которое можно разделить другое число без остатка.
Давайте рассмотрим пример: число 12. Если мы разделим 12 на 2, то получим 6, а если разделим на 3, то получим 4 без остатка. Это значит, что 2 и 3 являются делителями числа 12. Чтобы найти все делители числа, нужно просто проверять все числа, начиная с 1 и заканчивая самим числом.
Если число делится на какое-то из этих чисел без остатка, то это число является делителем. Например, чтобы найти все делители числа 12, мы можем проверить, делится ли 12 на 1, 2, 3, 4, 6 и 12 без остатка.
Также можно заметить, что делители всегда идут парами: например, 2 и 6, 3 и 4 являются парами делителей числа 12, так как 2 * 6 = 12 и 3 * 4 = 12.
Существует определенное правило для нахождения делителя. Вспомним, что такое делимое, делитель и частное.
Чтобы найти делитель, нужно делимое разделить на частное. В примере выше делитель у нас 4, поэтому мы разделим делимое 12 на частное 3. Легко, не так ли ? Теперь попробуем найти делитель в более сложных примерах.
Пример 1. Найдите делитель: (1080 : 24x = 15)
Решение:
(1080 : 24x = 15)
Алгоритм решения тот же: делимое делим на частное:
(1080:15 =72)
(24x=72)
(72:24=3)
Данное правило мы можем применять везде, где есть деление чисел.
Ответ: делитель равен (72) ((x=3)).
Если вы сомневаетесь, что на что надо делить, то придумайте такой же пример, только с простыми числами. Рассмотрим это на примере ниже.
Пример 2. Найдите делитель: (784:x=14)
Решение:
(784:x=14)
Аналогичный пример с простыми числами:
(6:x=2) — здесь понятно, чтобы найти (x) надо (6) разделить на (2), то есть делитель равен (3)
(784:14 = 56) — искомый делитель
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Деление натуральных чисел
Вы уже знакомы с общими понятиями о делении и о том как делить в столбик, рассмотрим более подробно деление натуральных чисел и его свойства.
Рассмотрим задачу:
У Вани 7 кроликов, он собрал для них 28 яблок. Сколько яблок досталось каждому кролику?
Пусть x яблок досталось каждому кролику, тогда мы можем сказать, что общее количество яблок равно: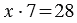 
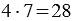
. Чтобы решить данное уравнение, мы должны найти число, которое при умножении на 7 даст результат 28, мы знаем, что такое число только одно — это 4: 
— верно. Следовательно, если известно произведение и один из множителей, можно найти второй множитель.
Действие, с помощью которого по произведению и одному из множителей находят другой множитель, называют делением.
Данное действие записывают так: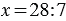 
, 
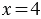
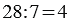
или 
, где:
Запомните:
Делимое — это то число, которое делят. Делитель — это то число, на которое делят. Частное — это результат деления.
Частное показывает во сколько раз делимое больше делителя, то есть в нашем примере: 28 больше 7 в 4 раза. Поэтому, если в задаче звучит вопрос «во сколько?», для её решения мы используем деление. При этом не всегда возможно одно число поделить на другое, тогда возникает необходимость деления с остатком.
Из вышесказанного мы можем сделать вывод:
1. Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель.
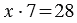
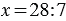
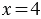
Пример: , следовательно, , то есть .
2. Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Пример: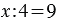 
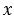
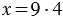
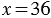
, по смыслу деления 
— это произведение 4 и 9, следовательно, 
, то есть 
.
3. Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Пример: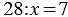 
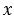
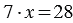
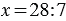
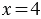
, по смыслу деления число 28 — это произведение множителей и 7, то есть мы можем записать: 
, теперь, применяя пункт 1, получаем: , то есть .
Свойства деления
Распределительные свойства:
1. Деление суммы на число: 
2. Деление разности на число: 
3. Деление произведения на число: 
4. Деление числа на произведение: 
Действия с единицей и нулем
1. Деление числа на единицу: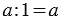 
то есть,при делении числа на единицу получается само число
2. Деление числа на себя: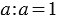 
, то есть при делении числа, не равного нулю, на само себя получается единица.
3. Деление нуля на число: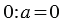 
, то есть при делении нуля на любое число, не равное нулю, получаем ноль.
НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Свойства деления
Распределительные свойства:
1. Деление суммы на число:
У Вани и Маши 3 кролика. Маша нашла 9 яблок, а Ваня — 15. Сколько яблок досталось каждому кролику?
Решение:
а) Мы можем сложить яблоки, которые нашли Маша и Ваня, а потом разделить полученное число на количество кроликов, то есть:
1) 9 + 15 = 24 (я) — собрали Маша и Ваня вместе.
2) 24 : 3 = 8 (я) — досталось каждому кролику.
б) Мы можем разделить яблоки, которые собрала Маша, затем разделить яблоки, которые собрал Ваня, а результат сложить:
1) 9 : 3 = 3 (я) — принесла Маша каждому кролику.
2) 15 : 3 = 5 (я) — принес Ваня каждому кролику.
3) 3 + 5 = 8 (я) — досталось каждому кролику.
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (9+15):3=9:3+15:3.
Вывод: Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.
2. Деление разности на число:
Всего трем братьям папа дал 150 рублей. На 72 рубля они купили сестре цветы на день рождения. Сколько рублей осталось у каждого брата?
а) Мы можем из общей суммы вычесть то, что братья потратили, а затем поделить сдачу:
1) 150 — 72 = 78 (руб.) — осталось после покупки цветов.
2) 78 : 3 = 26 (руб.) — осталось у каждого брата.
б) Мы можем найти, сколько получил каждый брат, затем посчитать, сколько потрачено каждым из них, а затем вычесть из полученной суммы денег потраченную:
1) 150 : 3 = 50 (руб.) — получил каждый брат.
2) 72 : 3 = 24 (руб.) — потратил каждый брат.
3) 50 — 24 = 26 (руб.) — осталось у каждого брата.
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (150 — 72) : 3 = 150 : 3 — 72 : 3.
Вывод: Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.
3. Деление произведения на число:
В зооуголке в саду 3 кролика. 12 детей принесли по 6 яблок для кормления питомцев. Сколько яблок досталось каждому кролику?
а) Сначала можем найти общее количество яблок, которые принесли дети, а затем поделить на число кроликов:
1) 12 · 6 = 72 (я) — принесли всего дети.
2) 72 : 3 = 24 (я) — досталось каждому кролику.
б) Мы можем найти сколько детей принесли яблоки одному кролику, а затем умножить на количество принесенных яблок:
1) 12 : 3 = 4 (чел.) — принесли яблоки 1 кролику.
2) 4 · 6 =24 (я) — досталось каждому кролику.
б) Мы можем найти по сколько яблок принес 1 ребенок для 1 кролика, а затем умножить на количество детей:
1) 6 : 3 = 2 (я) — принес каждый ребенок для одного кролика.
2) 2 · 12 = 24 (я) — досталось каждому кролику.
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: (12 · 6) : 3 = (12 : 3) · 6 = (6 : 3) ·12.
Вывод: Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.
4. Деление числа на произведение:
В 4 клетках сидят по 3 кролика. Ваня принес 48 яблок. Сколько яблок досталось каждому кролику?
а) Мы можем найти сколько кроликов всего, а потом поделить яблоки на полученное число:
1) 4 · 3 = 12 (к) — всего в клетках.
2) 48 : 12 = 4 (я) — досталось каждому кролику.
б) Мы можем найти сколько яблок положат в каждую клетку, а затем, сколько получит яблок каждый кролик:
1) 48 : 4 = 12 (я) — положат в каждую клетку.
2) 12 : 3 = 4 (я) — досталось каждому кролику.
Если мы рассадим наших кроликов по 4 в три клетки, решая задачу аналогично получим:
а) 1) 4 · 3 = 12 (к) — всего в клетках.
2) 48 : 12 = 4 (я) — досталось каждому кролику.
б) 1) 48 : 3 = 16 (я) — положат в каждую клетку.
2) 16 : 4 = 4 (я) — досталось каждому кролику.
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: 48 : (4 · 3) = (48 : 4) : 3 = (48 : 3) : 4
Вывод: Чтобы разделить число на произведение двух множителей, можно разделить это число сначала на один из множителей, а затем на второй.
Действия с единицей и нулем
1. Деление числа на единицу:
У Вани один кролик. Он принёс 3 яблока. Сколько яблок достанется кролику?
Будем рассуждать, у Вани всего один кролик, значит все яблоки достанутся ему:
3 : 1 = 3 (я) — достанется кролику, следовательно, мы можем сделать вывод: При делении числа на единицу получается само число:
2. Деление числа на себя:
Из свойств умножения мы знаем, что: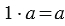 
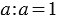
, а мы знаем, что по смыслу деления можно записать, что: , то есть при делении числа, не равного нулю, на само себя получается единица.
3. Деление нуля на число:
Рассуждая аналогично пункту 2 получаем: 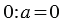, то есть при делении ноля на любое число, не равное нулю, получаем ноль.
Обратите внимание, что НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Это легко объяснить следующими рассуждениями: пусть мы взяли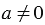 
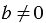
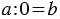
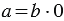
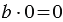
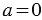
карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по 
карандашей в каждой коробке: 
, из смысла деления 
, в то же время мы знаем из свойств умножения, что: 
, то есть получаем, что 
, а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 527,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 810,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 843,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 911,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1207,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1441,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1800,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 585,
Мерзляк, Полонский, Якир, Учебник
Номер 999,
Мерзляк, Полонский, Якир, Учебник
Номер 7,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 68,
Мерзляк, Полонский, Якир, Учебник
Номер 205,
Мерзляк, Полонский, Якир, Учебник
Номер 664,
Мерзляк, Полонский, Якир, Учебник
Номер 947,
Мерзляк, Полонский, Якир, Учебник
Номер 1138,
Мерзляк, Полонский, Якир, Учебник
Номер 1188,
Мерзляк, Полонский, Якир, Учебник
Номер 1196,
Мерзляк, Полонский, Якир, Учебник
Задание 28,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 66,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 412,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 7,
Мерзляк, Полонский, Якир, Учебник
Номер 12,
Мерзляк, Полонский, Якир, Учебник
Номер 63,
Мерзляк, Полонский, Якир, Учебник
Номер 328,
Мерзляк, Полонский, Якир, Учебник
Номер 549,
Мерзляк, Полонский, Якир, Учебник
Номер 820,
Мерзляк, Полонский, Якир, Учебник
Номер 849,
Мерзляк, Полонский, Якир, Учебник
Номер 1069,
Мерзляк, Полонский, Якир, Учебник
Номер 1070,
Мерзляк, Полонский, Якир, Учебник
Номер 1232,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 265,
Мерзляк, Полонский, Якир, Учебник