Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Теория чисел
- Простые числа
- Разложение на простые множители
- Решето Эратосфена
- Линейное решето Эратосфена*
- НОД и НОК
- Алгоритм Евклида
- Расширенный алгоритм Евклида*
- Операции по модулю
- Быстрое возведение в степень
- Деление по простому модулю*
Простые числа
Простым называется натуральное число, которое делится только на единицу и на себя. Единица при этом простым числом не считается. Составным числом называют непростое число, которое еще и не единица.
Примеры простых чисел: (2), (3), (5), (179), (10^9+7), (10^9+9).
Примеры составных чисел: (4), (15), (2^{30}).
Еще одно определение простого числа: (N) — простое, если у (N) ровно два делителя. Эти делители при этом равны (1) и (N).
Проверка на простоту за линию
С точки зрения программирования интересно научиться проверять, является ли число (N) простым. Это очень легко сделать за (O(N)) — нужно просто проверить, делится ли оно хотя бы на одно из чисел (2, 3, 4, ldots, N-1) . (N > 1) является простым только в случае, если оно не делится на на одно из этих чисел.
def is_prime(n):
if n == 1:
return False
for i in range(2, n): # начинаем с 2, так как на 1 все делится; n не включается
if n % i == 0:
return False
return True
for i in range(1, 10):
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(4, False)
(5, True)
(6, False)
(7, True)
(8, False)
(9, False)Проверка на простоту за корень
Алгоритм можно ускорить с (O(N)) до (O(sqrt{N})).
Пусть (N = a times b), причем (a leq b). Тогда заметим, что (a leq sqrt N leq b).
Почему? Потому что если (a leq b < sqrt{N}), то (ab leq b^2 < N), но (ab = N). А если (sqrt{N} < a leq b), то (N < a^2 leq ab), но (ab = N).
Иными словами, если число (N) равно произведению двух других, то одно из них не больше корня из (N), а другое не меньше корня из (N).
Из этого следует, что если число (N) не делится ни на одно из чисел (2, 3, 4, ldots, lfloorsqrt{N}rfloor), то оно не делится и ни на одно из чисел (lceilsqrt{N}rceil + 1, ldots, N-2, N-1), так как если есть делитель больше корня (не равный (N)), то есть делитель и меньше корня (не равный 1). Поэтому в цикле for достаточно проверять числа не до (N), а до корня.
def is_prime(n):
if n == 1:
return False
# Удобно вместо for i in range(2, n ** 0.5) писать так:
i = 2
while i * i <= n:
if n % i == 0:
return False
i += 1
return True
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(10, False)
(11, True)
(12, False)
(1000000006, False)
(1000000007, True)Разложение на простые множители
Любое натуральное число можно разложить на произведение простых, и с такой записью очень легко работать при решении задач. Разложение на простые множители еще называют факторизацией.
[11 = 11 = 11^1] [100 = 2 times 2 times 5 times 5 = 2^2 times 5^2] [126 = 2 times 3 times 3 times 7 = 2^1 times 3^2 times 7^1]
Рассмотрим, например, такую задачу:
Условие: Нужно разбить (N) людей на группы равного размера. Нам интересно, какие размеры это могут быть.
Решение: По сути нас просят найти число делителей (N). Нужно посмотреть на разложение числа (N) на простые множители, в общем виде оно выглядит так:
[N= p_1^{a_1} times p_2^{a_2} times ldots times p_k^{a_k}]
Теперь подумаем над этим выражением с точки зрения комбинаторики. Чтобы «сгенерировать» какой-нибудь делитель, нужно подставить в степень (i)-го простого число от 0 до (a_i) (то есть (a_i+1) различное значение), и так для каждого. То есть делитель (N) выглядит ровно так: [M= p_1^{b_1} times p_2^{b_2} times ldots times p_k^{b_k}, 0 leq b_i leq a_i] Значит, ответом будет произведение ((a_1+1) times (a_2+1) times ldots times (a_k + 1)).
Алгоритм разложения на простые множители
Применяя алгоритм проверки числа на простоту, мы умеем легко находить минимальный простой делитель числа N. Ясно, что как только мы нашли простой делитель числа (N), мы можем число (N) на него поделить и продолжить искать новый минимальный простой делитель.
Будем перебирать простой делитель от (2) до корня из (N) (как и раньше), но в случае, если (N) делится на этот делитель, будем просто на него делить. Причем, возможно, нам понадобится делить несколько раз ((N) может делиться на большую степень этого простого делителя). Так мы будем набирать простые делители и остановимся в тот момент, когда (N) стало либо (1), либо простым (и мы остановились, так как дошли до корня из него). Во втором случае надо еще само (N) добавить в ответ.
Напишем алгоритм факторизации:
def factorize(n):
factors = []
i = 2
while i * i <= n: # перебираем простой делитель
while n % i == 0: # пока N на него делится
n //= i # делим N на этот делитель
factors.append(i)
i += 1
# возможно, в конце N стало большим простым числом,
# у которого мы дошли до корня и поняли, что оно простое
# его тоже нужно добавить в разложение
if n > 1:
factors.append(n)
return factors
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, '=', ' x '.join(str(x) for x in factorize(i)))1 =
2 = 2
3 = 3
10 = 2 x 5
11 = 11
12 = 2 x 2 x 3
1000000006 = 2 x 500000003
1000000007 = 1000000007Задание
За сколько работает этот алгоритм?
.
.
.
.
Решение
За те же самые (O(sqrt{N})). Итераций цикла while с перебором делителя будет не больше, чем (sqrt{N}). Причем ровно (sqrt{N}) операций будет только в том случае, если (N) — простое.
А итераций деления (N) на делители будет столько, сколько всего простых чисел в факторизации числа (N). Понятно, что это не больше, чем (O(log{N})).
Задание
Докажите, что число (N) имеет не больше, чем (O(log{N})) простых множителей в факторизации.
Разные свойства простых чисел*
Вообще, про простые числа известно много свойств, но почти все из них очень трудно доказать. Вот еще некоторые из них:
- Простых чисел, меньших (N), примерно (frac{N}{ln N}).
- N-ое простое число равно примерно (Nln N).
- Простые числа распределены более-менее равномерно. Например, если вам нужно найти какое-то простое число в промежутке, то можно их просто перебрать и проверить — через несколько сотен какое-нибудь найдется.
- Для любого (N ge 2) на интервале ((N, 2N)) всегда найдется простое число (Постулат Бертрана)
- Впрочем, существуют сколь угодно длинные отрезки, на которых простых чисел нет. Самый простой способ такой построить — это начать с (N! + 2).
- Есть алгоритмы, проверяющие число на простоту намного быстрее, чем за корень.
- Максимальное число делителей равно примерно (O(sqrt[3]{n})). Это не математический результат, а чисто эмпирический — не пишите его в асимптотиках.
- Максимальное число делителей у числа на отрезке ([1, 10^5]) — 128
- Максимальное число делителей у числа на отрекзке ([1, 10^9]) — 1344
- Максимальное число делителей у числа на отрезке ([1, 10^{18}]) — 103680
- Наука умеет факторизовать числа за (O(sqrt[4]{n})), но об этом как-нибудь в другой раз.
- Любое число больше трёх можно представить в виде суммы двух простых (гипотеза Гольдбаха), но это не доказано.
Решето Эратосфена
Часто нужно не проверять на простоту одно число, а найти все простые числа до (N). В этом случае наивный алгоритм будет работать за (O(Nsqrt N)), так как нужно проверить на простоту каждое число от 1 до (N).
Но древний грек Эратосфен предложил делать так:
Запишем ряд чисел от 1 до (N) и будем вычеркивать числа: * делящиеся на 2, кроме самого числа 2 * затем деляющиеся на 3, кроме самого числа 3 * затем на 5, затем на 7, и так далее и все остальные простые до n. Таким образом, все незачеркнутые числа будут простыми — «решето» оставит только их.
Красивая визуализация
Задание
Найдите этим способом на бумажке все простые числа до 50, потом проверьте с программой:
N = 50
prime = [1] * (N + 1)
prime[0], prime[1] = 0, 0
for i in range(2, N + 1): # можно и до sqrt(N)
if prime[i]:
for j in range(2 * i, N + 1, i): # идем с шагом i, можно начиная с i * i
prime[j] = 0
for i in range(1, N + 1):
if prime[i]:
print(i)2
3
5
7
11
13
17
19
23
29
31
37
41
43
47У этого алгоритма можно сразу заметить несколько ускорений.
Во-первых, число (i) имеет смысл перебирать только до корня из (N), потому что при зачеркивании составных чисел, делящихся на простое (i > sqrt N), мы ничего не зачеркнем. Почему? Пусть существует составное (M leq N), которое делится на %i%, и мы его не зачеркнули. Но тогда (i > sqrt N geq sqrt M), а значит по ранее нами доказанному утверждению (M) должно делиться и на простое число, которое меньше корня. Но это значит, что мы его уже вычеркнули.
Во-вторых, по этой же самое причине (j) имеет смысл перебирать только начиная с (i^2). Зачем вычеркивать (2i), (3i), (4i), …, ((i-1)i), если они все уже вычеркнуты, так как мы уже вычеркивали всё, что делится на (2), (3), (4), …, ((i-1)).
Асимптотика
Такой код будет работать за (O(N log log N)) по причинам, которые мы пока не хотим объяснять формально.
Гармонический ряд
Научимся оценивать асимптотику величины (1 + frac{1}{2} + ldots + frac{1}{N}), которая нередко встречается в задачах, где фигурирует делимость.
Возьмем (N) равное (2^i — 1) и запишем нашу сумму следующим образом: [left(frac{1}{1}right) + left(frac{1}{2} + frac{1}{3}right) + left(frac{1}{4} + ldots + frac{1}{7}right) + ldots + left(frac{1}{2^{i — 1}} + ldots + frac{1}{2^i — 1}right)]
Каждое из этих слагаемых имеет вид [frac{1}{2^j} + ldots + frac{1}{2^{j + 1} — 1} le frac{1}{2^j} + ldots + frac{1}{2^j} = 2^j frac{1}{2^j} = 1]
Таким образом, наша сумма не превосходит (1 + 1 + ldots + 1 = i le 2log_2(2^i — 1)). Тем самым, взяв любое (N) и дополнив до степени двойки, мы получили асимптотику (O(log N)).
Оценку снизу можно получить аналогичным образом, оценив каждое такое слагаемое снизу значением (frac{1}{2}).
Попытка объяснения асимптотики** (для старших классов)
Мы знаем, что гармонический ряд (1 + frac{1}{2} + frac{1}{3} + ldots + frac{1}{N}) это примерно (log N), а значит [N + frac{N}{2} + frac{N}{3} + ldots + frac{N}{N} sim N log N]
А что такое асимптотика решета Эратосфена? Мы как раз ровно (frac{N}{p}) раз зачеркиваем числа делящиеся на простое число (p). Если бы все числа были простыми, то мы бы как раз получили (N log N) из формули выше. Но у нас будут не все слагаемые оттуда, только с простым (p), поэтому посмотрим чуть более точно.
Известно, что простых чисел до (N) примерно (frac{N}{log N}), а значит допустим, что k-ое простое число примерно равно (k ln k). Тогда
[sum_{substack{2 leq p leq N \ text{p is prime}}} frac{N}{p} sim frac{1}{2} + sum_{k = 2}^{frac{N}{ln N}} frac{N}{k ln k} sim int_{2}^{frac{N}{ln N}} frac{N}{k ln k} dk =N(lnlnfrac{N}{ln N} — lnln 2) sim N(lnln N — lnlnln N) sim N lnln N]
Но вообще-то решето можно сделать и линейным.
Задание
Решите 5 первых задач из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Линейное решето Эратосфена*
Наша цель — для каждого числа до (N) посчитать его минимальный простой делитель. Будем хранить его в массиве min_d. Параллельно будем хранить и список всех найденных простых чисел primes — это ровно те числа (x), у которых (min_d[x] = x).
Основное утверждение такое:
Пусть у числа (M) минимальный делитель равен (a). Тогда, если (M) составное, мы хотим вычеркнуть его ровно один раз при обработке числа (frac{M}{a}).
Мы также перебираем число (i) от (2) до (N). Если (min_d[i]) равно 0 (то есть мы не нашли ни один делитель у этого числа еще), значит оно простое — добавим в primes и сделаем (min_d[i] = i).
Далее мы хотим вычеркнуть все числа (i times k) такие, что (k) — это минимальный простой делитель этого числа. Из этого следует, что необходимо и достаточно перебрать (k) в массиве primes, и только до тех пор, пока (k < min_d[i]). Ну и перестать перебирать, если (i times k > N).
Алгоритм пометит все числа по одному разу, поэтому он корректен и работает за (O(N)).
N = 30
primes = []
min_d = [0] * (N + 1)
for i in range(2, N + 1):
if min_d[i] == 0:
min_d[i] = i
primes.append(i)
for p in primes:
if p > min_d[i] or i * p > N:
break
min_d[i * p] = p
print(i, min_d)
print(min_d)
print(primes)2 [0, 0, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3 [0, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4 [0, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
5 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
6 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
7 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
8 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
9 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
10 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
11 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 5, 0, 3, 0, 0, 0]
12 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 0, 3, 0, 0, 0]
13 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 0, 0, 0]
14 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 0]
15 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
16 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
17 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
18 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
19 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
20 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
21 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
22 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
23 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
24 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
25 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
26 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
27 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
28 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
29 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
30 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]Этот алгоритм работает асимптотически быстрее, чем обычное решето. Но на практике, если писать обычное решето Эратсфена с оптимизациями, то оно оказывается быстрее линейнего. Также линейное решето занимает гораздо больше памяти — ведь в обычном решете можно хранить просто (N) бит, а здесь нам нужно (N) чисел и еще массив primes.
Зато один из «побочных эффектов» алгоритма — он неявно вычисляет факторизацию всех чисел от (1) до (N). Ведь зная минимальный простой делитель любого числа от (1) до (N) можно легко поделить на это число, посмотреть на новый минимальный простой делитель и так далее.
НОД и НОК
Введем два определения.
Наибольший общий делитель (НОД) чисел (a_1, a_2, ldots, a_n) — это максимальное такое число (x), что все (a_i) делятся на (x).
Наименьшее общее кратное (НОК) чисел (a_1, a_2, ldots, a_n) — это минимальное такое число (x), что (x) делится на все (a_i).
Например, * НОД(18, 30) = 6 * НОД(60, 180, 315) = 15 * НОД(1, N) = 1 * НОК(12, 30) = 6 * НОК(1, 2, 3, 4) = 12 * НОК(1, (N)) = (N)
Зачем они нужны? Например, они часто возникают в задачах.
Условие: Есть (N) шестеренок, каждая (i)-ая зацеплена с ((i-1))-ой. (i)-ая шестеренка имеет (a_i) зубчиков. Сколько раз нужно повернуть полносьтю первую шестеренку, чтобы все остальные шестеренки тоже вернулись на изначальное место?
Решение: Когда одна шестеренка крутится на 1 зубчик, все остальные тоже крутятся на один зубчик. Нужно найти минимальное такое число зубчиков (x), что при повороте на него все шестеренки вернутся в изначальное положение, то есть (x) делится на все (a_i), то есть это НОК((a_1, a_2, ldots, a_N)). Ответом будет (frac{x}{a_1}).
Еще пример задачи на применение НОД и НОК:
Условие: Город — это прямоугольник (n) на (m), разделенный на квадраты единичного размера. Вертолет летит из нижнего левого угла в верхний правый по прямой. Вертолет будит людей в квартале, когда он пролетает строго над его внутренностью (границы не считаются). Сколько кварталов разбудит вертолёт?
Решение: Вертолет пересечет по вертикали ((m-1)) границу. С этим ничего не поделать — каждое считается как новое посещение какого-то квартала. По горизонтали то же самое — ((n-1)) переход в новую ячейку будет сделан.
Однако еще есть случай, когда он пересекает одновременно обе границы (то есть пролетает над каким-нибудь углом) — ровно тот случай, когда нового посещения квартала не происходит. Сколько таких будет? Ровно столько, сколько есть целых решений уравнения (frac{n}{m} = frac{x}{y}). Мы как бы составили уравнение движения вертолёта и ищем, в скольки целых точках оно выполняется.
Пусть (t = НОД(n, m)), тогда (n = at, m = bt).
Тогда (frac{n}{m} = frac{a}{b} = frac{x}{y}). Любая дробь с натуральными числителем и знаменателем имеет ровно одно представление в виде несократимой дроби, так что (x) должно делиться на (a), а (y) должно делиться на (b). А значит, как ответ подходят ((a, b), (2a, 2b), (3a, 3b), cdots, ((t-1)a, (t-1)b)). Таких ответов ровно (t = НОД(n, m))
Значит, итоговый ответ: ((n-1) + (m-1) — (t-1)).
Кстати, когда (НОД(a, b) = 1), говорят, что (a) и (b) взаимно просты.
Алгоритм Евклида
Осталось придумать, как искать НОД и НОК. Понятно, что их можно искать перебором, но мы хотим хороший быстрый способ.
Давайте для начала научимся искать (НОД(a, b)).
Мы можем воспользоваться следующим равенством: [НОД(a, b) = НОД(a, b — a), b > a]
Оно доказывается очень просто: надо заметить, что множества общих делителей у пар ((a, b)) и ((a, b — a)) совпадают. Почему? Потому что если (a) и (b) делятся на (x), то и (b-a) делится на (x). И наоборот, если (a) и (b-a) делятся на (x), то и (b) делится на (x). Раз множства общих делитей совпадают, то и максимальный делитель совпадает.
Из этого равенства сразу следует следующее равенство: [НОД(a, b) = НОД(a, b operatorname{%} a), b > a]
(так как (НОД(a, b) = НОД(a, b — a) = НОД(a, b — 2a) = НОД(a, b — 3a) = ldots = НОД(a, b operatorname{%} a)))
Это равенство дает идею следующего рекурсивного алгоритма:
[НОД(a, b) = НОД(b operatorname{%} a, a) = НОД(a operatorname{%} , (b operatorname{%} a), b operatorname{%} a) = ldots]
Например: [НОД(93, 36) = ] [= НОД(36, 93spaceoperatorname{%}36) = НОД(36, 21) = ] [= НОД(21, 15) = ] [= НОД(15, 6) = ] [= НОД(6, 3) = ] [= НОД(3, 0) = 3]
Задание:
Примените алгоритм Евклида и найдите НОД чисел: * 1 и 500000 * 10, 20 * 18, 60 * 55, 34 * 100, 250
По-английски наибольший общий делитель — greatest common divisor. Поэтому вместо НОД будем в коде писать gcd.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
print(gcd(1, 500000))
print(gcd(10, 20))
print(gcd(18, 60))
print(gcd(55, 34))
print(gcd(100, 250))
print(gcd(2465473782, 12542367456))1
10
6
1
50
6Вообще, в C++ такая функция уже есть в компиляторе g++ — называется __gcd. Если у вас не Visual Studio, то, скорее всего, у вас g++. Вообще, там много всего интересного.
А за сколько оно вообще работает?
Задание
Докажите, что алгоритм Евклида для чисел (N), (M) работает за (O(log(N+M))).
Кстати, интересный факт: самыми плохими входными данными для алгоритма Евклида являются числа Фибоначчи. Именно там и достигается логарифм.
Как выразить НОК через НОД
(НОК(a, b) = frac{ab}{НОД(a, b)})
По этой формуле можно легко найти НОК двух чисел через их произведение и НОД. Почему она верна?
Посмотрим на разложения на простые множители чисел a, b, НОК(a, b), НОД(a, b).
[ a = p_1^{a_1}times p_2^{a_2}timesldotstimes p_n^{a_n} ] [ b = p_1^{b_1}times p_2^{b_2}timesldotstimes p_n^{b_n} ] [ ab = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} ]
Из определений НОД и НОК следует, что их факторизации выглядят так: [ НОД(a, b) = p_1^{min(a_1, b_1)}times p_2^{min(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)} ] [ НОК(a, b) = p_1^{max(a_1, b_1)}times p_2^{max(a_2, b_2)}timesldotstimes p_n^{max(a_n, b_n)} ]
Тогда посчитаем (НОД(a, b) times НОК(a, b)): [ НОД(a, b)НОК(a, b) = p_1^{min(a_1, b_1)+max(a_1, b_1)}times p_2^{min(a_2, b_2)+max(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)+max(a_n, b_n)} =] [ = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} = ab]
Формула доказана.
Как посчитать НОД/НОК от более чем 2 чисел
Для того, чтобы искать НОД или НОК у более чем двух чисел, достаточно считать их по цепочке:
(НОД(a, b, c, d, ldots) = НОД(НОД(a, b), c, d, ldots))
(НОК(a, b, c, d, ldots) = НОК(НОК(a, b), c, d, ldots))
Почему это верно?
Ну просто множество общих делителей (a) и (b) совпадает с множеством делителей (НОД(a, b)). Из этого следует, что и множество общих делителей (a), (b) и еще каких-то чисел совпадает с множеством общих делителей (НОД(a, b)) и этих же чисел. И раз совпадают множества общих делителей, то и наибольший из них совпадает.
С НОК то же самое, только фразу “множество общих делителей” надо заменить на “множество общих кратных”.
Задание
Решите задачи F, G, H, I из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Расширенный алгоритм Евклида*
Очень важным для математики свойством наибольшего общего делителя является следующий факт:
Для любых целых (a, b) найдутся такие целые (x, y), что (ax + by = d), где (d = gcd(a, b)).
Из этого следует, что существует решение в целых числах, например, у таких уравнений: * (8x + 6y = 2) * (4x — 5y = 1) * (116x + 44y = 4) * (3x + 11y = -1)
Мы сейчас не только докажем, что решения у таких уравнений существуют, но и приведем быстрый алгоритм нахождения этих решений. Здесь нам вновь пригодится алгоритм Евклида.
Рассмотрим один шаг алгоритма Евклида, преобразующий пару ((a, b)) в пару ((b, a operatorname{%} b)). Обозначим (r = a operatorname{%} b), то есть запишем деление с остатком в виде (a = bq + r).
Предположим, что у нас есть решение данного уравнения для чисел (b) и (r) (их наибольший общий делитель, как известно, тоже равен (d)): [bx_0 + ry_0 = d]
Теперь сделаем в этом выражении замену (r = a — bq):
[bx_0 + ry_0 = bx_0 + (a — bq)y_0 = ay_0 + b(x_0 — qy_0)]
Tаким образом, можно взять (x = y_0), а (y = (x_0 — qy_0) = (x_0 — (a operatorname{/} b)y_0)) (здесь (/) обозначает целочисленное деление).
В конце алгоритма Евклида мы всегда получаем пару ((d, 0)). Для нее решение требуемого уравнения легко подбирается — (d * 1 + 0 * 0 = d). Теперь, используя вышесказанное, мы можем идти обратно, при вычислении заменяя пару ((x, y)) (решение для чисел (b) и (a operatorname{%} b)) на пару ((y, x — (a / b)y)) (решение для чисел (a) и (b)).
Это удобно реализовывать рекурсивно:
def extended_gcd(a, b):
if b == 0:
return a, 1, 0
d, x, y = extended_gcd(b, a % b)
return d, y, x - (a // b) * y
a, b = 3, 5
res = extended_gcd(a, b)
print("{3} * {1} + {4} * {2} = {0}".format(res[0], res[1], res[2], a, b))3 * 2 + 5 * -1 = 1Но также полезно и посмотреть, как будет работать расширенный алгоритм Евклида и на каком-нибудь конкретном примере. Пусть мы, например, хотим найти целочисленное решение такого уравнения: [116x + 44y = 4] [(2times44+28)x + 44y = 4] [44(2x+y) + 28x = 4] [44x_0 + 28y_0 = 4] Следовательно, [x = y_0, y = x_0 — 2y_0] Будем повторять такой шаг несколько раз, получим такие уравнения: [116x + 44y = 4] [44x_0 + 28y_0 = 4, x = y_0, y = x_0 — 2y_0] [28x_1 + 16y_1 = 4, x_0 = y_1, y_0 = x_1 — y_1] [16x_2 + 12y_2 = 4, x_1 = y_2, y_1 = x_2 — y_2] [12x_3 + 4y_3 = 4, x_2 = y_3, y_2 = x_3 — y_3] [4x_4 + 0y_4 = 4, x_3 = y_4, y_3 = x_4 — 3 y_4] А теперь свернем обратно: [x_4 = 1, y_4 = 0] [x_3 = 0, y_3 =1] [x_2 = 1, y_2 =-1] [x_1 = -1, y_1 =2] [x_0 = 2, y_0 =-3] [x = -3, y =8]
Действительно, (116times(-3) + 44times8 = 4)
Задание
Решите задачу J из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Операции по модулю
Выражение (a equiv b pmod m) означает, что остатки от деления (a) на (m) и (b) на (m) равны. Это выражение читается как «(a) сравнимо (b) по модулю (m)».
Еще это можно опрделить так: (a) сравнимо c (b) по модулю (m), если ((a — b)) делится на (m).
Все целые числа можно разделить на классы эквивалентности — два числа лежат в одном классе, если они сравнимы по модулю (m). Говорят, что мы работаем в «кольце остатков по модулю (m)», и в нем ровно (m) элементов: (0, 1, 2, cdots, m-1).
Сложение, вычитение и умножение по модулю определяются довольно интуитивно — нужно выполнить соответствующую операцию и взять остаток от деления.
С делением намного сложнее — поделить и взять по модулю не работает. Об этом подробнее поговорим чуть дальше.
a = 30
b = 50
mod = 71
print('{} + {} = {} (mod {})'.format(a, b, (a + b) % mod, mod))
print('{} - {} = {} (mod {})'.format(a, b, (a - b) % mod, mod)) # на C++ это может не работать, так как модуль от отрицательного числа берется странно
print('{} - {} = {} (mod {})'.format(a, b, (a - b + mod) % mod, mod)) # на C++ надо писать так, чтобы брать модулю от гарантированно неотрицательного числа
print('{} * {} = {} (mod {})'.format(a, b, (a * b) % mod, mod))
# print((a / b) % mod) # а как писать это, пока неясно30 + 50 = 9 (mod 71)
30 - 50 = 51 (mod 71)
30 - 50 = 51 (mod 71)
30 * 50 = 9 (mod 71)Задание
Посчитайте: * (2 + 3 pmod 5) * (2 * 3 pmod 5) * (2 ^ 3 pmod 5) * (2 — 4 pmod 5) * (5 + 5 pmod 6) * (2 * 3 pmod 6) * (3 * 3 pmod 6)
Для умножения (в C++) нужно ещё учитывать следующий факт: при переполнении типа всё ломается (разве что если вы используете в качестве модуля степень двойки).
intвмещает до (2^{31} — 1 approx 2 cdot 10^9).long longвмещает до (2^{63} — 1 approx 8 cdot 10^{18}).long long longв плюсах нет, при попытке заиспользовать выдает ошибкуlong long long is too long.- Под некоторыми компиляторами и архитектурами доступен
int128, но не везде и не все функции его поддерживают (например, его нельзя вывести обычными методами).
Зачем нужно считать ответ по модулю
Очень часто в задаче нужно научиться считать число, которое в худшем случае гораздо больше, чем (10^{18}). Тогда, чтобы не заставлять вас писать длинную арифметику, автор задачи часто просит найти ответ по модулю большого числа, обычно (10^9 + 7)
Кстати, вместо того, чтобы писать (1000000007) удобно просто написать (1e9 + 7). (1e9) означает (1 times 10^9)
int mod = 1e9 + 7; # В C++
cout << mod;1000000007N = 1e9 + 7 # В питоне такое число становится float
print(N)
print(int(N))1000000007.0
1000000007Быстрое возведение в степень
Задача: > Даны натуральные числа (a, b, c < 10^9). Найдите (a^b) (mod (c)).
Мы хотим научиться возводить число в большую степень быстро, не просто умножая (a) на себя (b) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.
Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):
- (3^2)
- (3^4)
- (3^8)
- (3^{16})
- (3^{32})
- (3^{33})
- (3^{66})
- (3^{132})
- (3^{133})
- (3^{266})
- (3^{532})
- (3^{533})
- (3^{1066})
Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на (a=3), либо возвести в квадрат. Так и получается рекурсивный алгоритм:
- (a^0 = 1)
- (a^{2k}=(a^{k})^2)
- (a^{2k+1}=a^{2k}times a)
Нужно только после каждой операции делать mod: * (a^0 pmod c = 1) * (a^{2k} pmod c = (a^{k} pmod c)^2 pmod c) * (a^{2k+1} pmod c = ((a^{2k}pmod c) times a) pmod c)
Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)
Асимптотика этого алгоритма, очевидно, (O(log c)) — за каждые две итерации число уменьшается хотя бы в 2 раза.
Задание
Решите задачу K из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Задание
Решите как можно больше задач из практического контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Деление по модулю*
Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?
(a / b) = (a times b^{-1}), где (b^{-1}) — это обратный элемент к (b).
Определение: (b^{-1}) — это такое число, что (bb^{-1} = 1)
Утверждение: в кольце остатков по простому модулю (p) у каждого остатка (кроме 0) существует ровно один обратный элемент.
Например, обратный к (2) по модулю (5) это (3) ((2 times 3 = 1 pmod 5)))
Задание
Найдите обратный элемент к: * числу (3) по модулю (5) * числу (3) по модулю (7) * числу (1) по модулю (7) * числу (2) по модулю (3) * числу (9) по модулю (31)
Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток (1, 2, ldots, (p-1)) умножить на ненулевой остаток (a), то получатся числа (a, 2a, ldots, (p-1)a) — и они все разные! Они разные, потому что если (xa = ya), то ((x-y)a = 0), а значит ((x — y) a) делится на (p), (a) — ненулевой остаток, а значит (x = y), и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!
Из этого следует, что среди этих чисел есть (1), причем ровно один раз. А значит существует ровно один обратный элемент (a^{-1}). Доказательство закончено.
Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за (O(p)).
Есть несколько способов это сделать.
Через малую теорему Ферма
Малая теорема Ферма: > (a^{p-1} = 1 pmod p), если (p) — простое, (a neq 0 pmod p)).
Доказательство: В предыдущем пункте мы выяснили, что множества чисел (1, 2, ldots, (p-1)) и (a, 2a, ldots, (p-1)a) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: ((p-1)! = a^{p-1} (p-1)! pmod p).
((p-1)!neq 0 pmod p) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число — значит умножить на обратный к нему, который существует).
А значит, (a^{p — 1} = 1 pmod p).
Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что (a^{p-2}) — это обратный элемент к (a), а значит мы свели задачу к возведению (a) в степень (p-2), что благодаря быстрому возведению в степень мы умеем делать за (O(log p)).
Обобщение У малой теоремы Ферма есть обобщение для составных (p):
Теорема Эйлера: > (a^{varphi(p)} = 1 pmod p), (a) — взаимно просто с (p), а (varphi(p)) — это функция Эйлера (количество чисел, меньших (p) и взаимно простых с (p)).
Доказывается теорема очень похоже, только вместо ненулевых остатков (1, 2, ldots, p-1) нужно брать остатки, взаимно простые с (p). Их как раз не (p-1), а (varphi(p)).
Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера (varphi(p)) и найти (a^{-1} = a^{varphi(p) — 1}).
Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.
Через расширенный алгоритм Евклида
Этим способом легко получится делить по любому модулю! Рекомендую.
Пусть мы хотим найти (a^{-1} pmod p), (a) и (p) взаимно простые (а иначе обратного и не будет существовать).
Давайте найдем корни уравнения
[ax + py = 1]
Они есть и находятся расширенным алгоритмом Евклида за (O(log p)), так как (НОД(a, p) = 1), ведь они взаимно простые.
Тогда если взять остаток по модулю (p):
[ax = 1 pmod p]
А значит, найденный (x) и будет обратным элементом к (a).
То есть надо просто найти (x) из решения того уравнения по модулю (p). Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.
Тема 25.
Программирование — Обработка целочисленной информации
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
программирование — обработка целочисленной информации
Решаем задачи
Показать ответ и решение
Если число имеет разложение вида …
, то количество чётных делителей такого числа равно
…
(выбрали степень двойки от
до
, степень каждого простого от
до
). По
условию это равно — простое число, как произведение натуральных чисел его можно представить как
или
.
Случай :
, все
число равно
, не подходит.
Случай :
, какое-то
, все остальные
— приходим к разложению вида
.
На частном случае решение будет выглядеть так:
С помощью стандартной программы найдем подходящие нам числа до
для того, чтобы рассмотреть
их:
def dividers(n): k = 0 for i in range(1, int(n ** 0.5) + 1): if n % i == 0: if i % 2 == 0: k += 1 if (n // i) % 2 == 0 and n // i != i: k += 1 return k for i in range(1, 100000): if dividers(i) == 7: print(i)
Подходящие нам числа в диапазоне до
— это
,
и
. Хочется разложить эти
числа:
Заметим, что все числа раскладываются на , где
— простое число.
Воспользуемся выведенной формулой для решения:
def prime(x): for i in range(2, int(x**0.5)+1): if x % i == 0: return False return True ans = 0 for i in range(int((33333333 // 2)**(1/6)), int((333333333 // 2)**(1/6)) + 1): if prime(i): if 33333333 <= 2*(i**6) <= 333333333: ans += 1 print(ans)
Найдите все натуральные числа, принадлежащие отрезку [22 333 888; 88 999 888], у которых ровно различных
нечётных делителя (количество чётных делителей может быть любым). В ответе укажите количество данных
чисел.
Показать ответ и решение
def is_prime(n): if n <= 1: return False for j in range(2, int(n ** 0.5) + 1): if n % j == 0: return False return True ans = 0 for j in range(3, 10000): if is_prime(j): for i in range(26): if 22333888 <= 2**i*j**2 <= 88999888: ans += 1 print(ans)
Найдите все натуральные числа, принадлежащие отрезку [11 111 111; 77 777 777], у которых ровно различных
делителей. В ответе укажите количество данных чисел.
Показать ответ и решение
def prime(x): for i in range(2, int(x**0.5)+1): if x % i == 0: return False return True ans = 0 for i in range(int(11111111**0.25), int((77777777+1)**0.25)+1): if prime(i): ans += 1 print(ans)
Напишите программу, которая получает на вход число и возвращает количество его делителей. В ответе укажите
количество делителей для числа .
Показать ответ и решение
Решение 1
count = 0 x = int(input()) for i in range(1, int(x ** 0.5) + 1): if x % i == 0: count += 1 if x // i != i: count += 1 print(count)
Решение 2
a = set() x = int(input()) for i in range(1, int(x ** 0.5) + 1): if x % i == 0: a.add(i) a.add(x // i) print(len(a))
Показать ответ и решение
a = [1, 2, 98, 43, 89, 739] x = 1052336 summa = 0 for i in a: if x % i == 0: summa += x // i print(summa)
Показать ответ и решение
Обратим внимание, что если — делитель числа
, то и
— делитель числа
. Очевидно, эти два числа находятся
по разную сторону от (иначе, предположим, что они оба меньше, тогда
чего явно не
может быть, случай, когда оба больше — аналогичен). Таким образом, мы видим, что все делители разбиваются на пары, в
которых один делитель меньше корня, а другой — больше. Отсюда понимаем, что делителей, меньших корня столько же,
сколько и больших.
print(0)
А теперь представим, что мы не знаем математику, и попробуем решить это другим способом:
x = 3052336 sq = x ** 0.5 more = 0 less = 0 for i in range(1, x + 1): if x % i == 0: if i > sq: more += 1 if i < sq: less += 1 print(more - less)
Утверждается, что количество делителей числа четно. Найдите количество пар делителей числа
,
произведение которых равно исходному числу. При этом пары делителей выбираются следующим образом минимальный
делитель * максимальный делитель, предминимальный делитель * предмаксимальный делитель и т.д. В ответе укажите
два числа через пробел: сначала количество рассматриваемых пар, затем количеством пар, произведение которых равно
исходному числу.
Показать ответ и решение
a = [] x = 2052336 for i in range(1, x + 1): if x % i == 0: a.append(i) count = 0 n = len(a) for i in range(n // 2): if a[i] * a[n - i - 1] == x: count += 1 print(n // 2, count)
Назовём числа и
числами-близнецами, если
.
Найдите наименьшее натуральное число, имеющее ровно 512 делителей, простые делители которого образуют не менее
трёх пар чисел-близнецов. В ответе укажите число, а также все его простые делители.
Показать ответ и решение
from itertools import combinations_with_replacement
def prime(x):
for i in range(2, int(x ** 0.5) + 1):
if x % i == 0:
return False
return True
def count_del(x):
ans = []
for i in range(2, int(x ** 0.5) + 1):
if x % i == 0:
ans += [i]
ans += [x // i]
return sorted(list(set(ans)))
def check(a):
ans = 1
for i in range(len(a)):
ans *= a[i]
if ans > 512:
return False
return ans == 512
dels = count_del(512)
primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
# Если скобок 9 штук и каждое альфа равно 1
minim = 2 ** 511
# Если скобок 9 штук и каждое альфа равно 1
t = 1
degrees = [2] * 9
for k in range(len(degrees)):
t *= (primes[k] ** (degrees[k] - 1))
minim = min(minim, t)
# Все остальные случаи
for j in range(2, 9):
for i in combinations_with_replacement(dels, j):
if check(i):
t = 1
degrees = i[::-1]
for k in range(len(degrees)):
t = t * (primes[k] ** (degrees[k] - 1))
minim = min(minim, t)
print(minim, *[i for i in count_del(minim) if prime(i)])
Ответ:
17297280 2 3 5 7 11 13
Найдите максимальное число на отрезке [1010101; 101010101], имеющее ровно 128 делителей, которое будет кратно
16. Выведите на экран в первой строке найденное число, а во второй все его нечетные делители в порядке
возрастания.
Показать ответ и решение
def count_del(x): ans = [1, x] for i in range(2, int(x**0.5)+1): if x % i == 0: ans += [i] if i != x // i: ans += [x//i] if len(ans) > 128: return ans return ans for i in range(101010101, 1010101-1, -1): if len(count_del(i)) == 128 and i % 16 == 0: print(i, *sorted([i for i in count_del(i) if i % 2 != 0])) break
Ответ:
101008512 1 3 9 11 27 33 99 297 2657 7971 23913 29227 71739 87681 263043 789129
Найдите пять последних натуральных чисел на отрезке , которые имеет ровно
делителя. В ответе
укажите подходящие числа в порядке возрастания.
Показать ответ и решение
def count_del(x): count = 2 for i in range(2, int(x**0.5)+1): if x % i == 0: count += 1 if i != x // i: count += 1 if count > 64: return False return count == 64 ans = [] for i in range(101010101, 1010101-1, -1): if count_del(i): ans += [i] if len(ans) == 5: print(*sorted(ans)) break
Ответ:
101009928
101009937
101009958
101010024
101010090
Найдите наибольшее натуральное число на отрезке , которое имеет ровно
делителей. В ответе укажите
число.
Показать ответ и решение
def divs(n): count = 0 for i in range(1,int(n**0.5)+1): if n%i==0: count += 1 if i!=n//i: count += 1 return count for x in range(5000000, 10000 - 1, -1): if divs(x) == 10: print(x) break
Найдите наименьшее натуральное число, которое имеет ровно делителей. В ответе укажите число.
Показать ответ и решение
from itertools import combinations_with_replacement
def prime(x):
for i in range(2, int(x**0.5)+1):
if x % i == 0:
return False
return True
def count_del(x):
ans = []
for i in range(2, int(x**0.5)+1):
if x % i == 0:
ans += [i]
ans += [x//i]
return sorted(list(set(ans)))
def check(a):
ans = 1
for i in range(len(a)):
ans *= a[i]
if ans > 20:
return False
return ans == 20
dels = count_del(20)
primes = [i for i in range(2, 100) if prime(i)]
#Если одна скобка
minim = 2**19
#Все остальные случаи
for j in range(2, 4):
for i in combinations_with_replacement(dels, j):
if check(i):
t = 1
degrees = i[::-1]
for k in range(len(degrees)):
t = t * (primes[k] ** (degrees[k]-1))
minim = min(minim, t)
print(minim)
Показать ответ и решение
Если число имеет разложение вида …
, то количество чётных делителей такого числа равно
…
(выбрали степень двойки от
до
, степень каждого простого от
до
). По
условию это равно — простое число, как произведение натуральных чисел его можно представить как
или
.
Случай :
, все
число равно
, не подходит.
Случай :
, какое-то
, все остальные
— приходим к разложению вида
.
На частном случае решение будет выглядеть так:
С помощью стандартной программы найдем подходящие нам числа до
для того, чтобы рассмотреть
их:
def dividers(n): k = 0 for i in range(1, int(n ** 0.5) + 1): if n % i == 0: if i % 2 == 0: k += 1 if (n // i) % 2 == 0 and n // i != i: k += 1 return k for i in range(1, 100000): if dividers(i) == 7: print(i)
Подходящие нам числа в диапазоне до
— это
,
и
. Хочется разложить эти
числа:
Заметим, что все числа раскладываются на , где
— простое число.
Воспользуемся выведенной формулой для решения:
def prime(x): for i in range(2, int(x**0.5)+1): if x % i == 0: return False return True ans = 0 for i in range(int((33333333 // 2)**(1/6)), int((99999999 // 2)**(1/6)) + 1): if prime(i): if 33333333 <= 2*(i**6) <= 99999999: ans += 1 print(ans)
Показать ответ и решение
def is_prime(n): if n <= 1: return False for j in range(2, int(n ** 0.5) + 1): if n % j == 0: return False return True ans = 0 for j in range(3, 10000): if is_prime(j): for i in range(26): if 33222555 <= 2**i*j**2 <= 99888999: ans += 1 print(ans)
Найдите все натуральные числа, принадлежащие отрезку [22 222 222; 88 888 888], у которых ровно различных
делителей. В ответе укажите количество данных чисел.
Показать ответ и решение
def prime(x):
for i in range(2, int(x**0.5)+1):
if x % i == 0:
return False
return True
ans = 0
for i in range(int(22222222**0.25), int((88888888+1)**0.25)+1):
if prime(i):
ans += 1
print(ans)
Рассматривается множество целых чисел, принадлежащих числовому отрезку [854321; 1087654]. Найдите числа,
нетривиальные делители которых образуют арифметическую прогрессию с разностью d = 10 (чисел > 1). В ответе для
каждого такого числа (в порядке возрастания) запишите сначала само число, а потом – его минимальный нетривиальный
делитель.
Показать ответ и решение
def divs(n):
a = []
for i in range(2, int(n**0.5)+1):
if n % i == 0:
a.append(i)
if i != n//i:
a.append(n//i)
a.sort()
if len(a)>1:
for i in range(len(a)-1):
if a[i]+10 != a[i+1]:
return False
return a
for i in range(854321, 1087654+1):
x = divs(i)
if x != False and len(x) > 1:
print(i, x[0])
Ответ:
887339 937
944759 967
1028171 1009
1052651 1021
Показать ответ и решение
def count_del(x): ans = [] for i in range(2, int(x ** 0.5) + 1): if x % i == 0: if len(str(i)) == 2: ans += [i] if i != x // i: if len(str(x // i)) == 2: ans += [x // i] return sorted(ans) ans = 0 for i in range(333555, 777999 + 1): if len(count_del(i)) == 38: print(i, count_del(i)[0], count_del(i)[-1])
Ответ:
360360 10 99 776160 10 99
Среди целых чисел, принадлежащих числовому отрезку [398790; 863777], найдите числа, сумма натуральных делителей
которых больше 2700000. Для каждого найденного числа запишите количество делителей и их сумму. В качестве делителей
не рассматривать числа 1 и исследуемое число. Так, например, для числа 8 учитываются только делители 2 и 4. Поиск
ведется от меньших чисел к большим.
Показать ответ и решение
def count_del(x):
ans = []
for i in range(2, int(x**0.5)+1):
if x % i == 0:
ans += [i]
if i != x//i:
ans += [x//i]
return ans
ans = 0
for i in range(398790, 863777+1):
if sum(count_del(i)) > 2700000:
print(len(count_del(i)), sum(count_del(i)))
Ответ:
238 2858639
214 2799215
190 2734919
198 2739119
Число называется избыточным, если оно строго меньше суммы своих собственных делителей (то есть всех
положительных делителей, отличных от самого числа). Определите количество избыточных чисел из диапазона [5;
50000].
Показать ответ и решение
def count_del(x):
ans = [1]
for i in range(2, int(x**0.5)+1):
if x % i == 0:
ans += [i]
if i != x//i:
ans += [x//i]
return sum(ans) > x
ans = 0
for i in range(5, 50000+1):
if count_del(i):
ans += 1
print(ans)
Определите количество составных натуральных чисел из диапазона , у которых количество нетривиальных
делителей не менее трех.
Примечание. Нетривиальный делитель — делитель, не равный единице и самому числу.
Показать ответ и решение
def count_del(x): ans = 0 for i in range(2, int(x ** 0.5) + 1): if x % i == 0: ans += 1 if i != x // i: ans += 1 if ans >= 3: return True return False ans = 0 for i in range(3, 30000 + 1): if count_del(i): ans += 1 print(ans)
Общие соображения
Заметим, что:
-
Величины
С = lg (X * p1 * p2 * … * pk) и П = cnt(X) * lg p1 * lg p2 * … * lg pk
— это сумма и произведение величин (a1+1) lg p1, (a2+1) lg p2,…, (ak+1) lg pk.
Не будь задача дискретной, в соответствии с теоремами о средних оптимум достигался бы при равенстве этих величин, (а с учётом потенцирования — и величин вида piai+1). -
Наш случай — дискретное приближение к оптимуму, так что эти величины должны хотя бы стремиться к равенству. А поскольку основания растут, то показатели не должны возрастать (a1>=a2>=…>=ak).
-
Сумма и произведение величин идут «в одном флаконе», и алгоритмы линейного динамического программирования здесь неприменимы.
-
Так как показатели степеней канонического разложения не возрастают, то требуемое оптимальное число X можно представить в виде произведения X=Pk…P2P1, где Pk=p1p2…pk— это произведения последовательных простых чисел (праймориалы), которые могут повторяться и которые можно протабулировать.
И поскольку праймориал при возрастании k растёт быстрее факториала, то их произведение для числа X подбирается очень быстро.
_Известно, что
Every highly composite number is a product of primorials_
Алгоритм и анализ результатов
Алгоритм по п.4 рекурсивный, параметром является частное от деления числа на уже готовую часть цепочки.
Для поиска текущего оптимального праймориала (звена цепочки) ведётся перебор по убыванию в границах от «жадного» звена для текущего частного до «жадного» звена для квадратного корня из этого частного.
Перебор обрывается, когда целевая функция (количество множителей) начинает падать.
Такая схема обеспечивает решение задачи.
Дополнительный контроль невозрастания звеньев в цепочке избавляет от повторения пройденного.
Для случая N=1018 оптимальное решение нашлось за 118 шагов и совпало с предыдущим ответом:
X = P12P4P2P2P1P1P1P1 = 28 * 34 * 52 * 72 * 11 * 13 … 37 = 897612484786617600,
cnt(X) = (8+1) (4+1) (2+1)2 (1+1)8 = 103680.
При этом порядок величин 29=512, 35=243, 53=125, 73=343, 112=121, …, 372=1369 примерно одинаков, что подтверждает теорию оптимума.
Для случая N=1036 (cnt(X)=127401984 множителей) понадобилось всего 168 шагов. Т.е. сложность алгоритма возрастает не быстрее логарифма. Хотя разрядность данных меняется.
Исходный код на PHP использует библиотеку BCMath. границу возможностей не тестировал (скорее всего, первым подведёт int для cnt(X)):
function prods(&$prod){
$p = array( "2", "3", "5", "7", "11", "13", "17", "19", "23", "29",
"31", "37", "41", "43", "47", "53", "59", "61", "67", "71",
"73", "79", "83", "89", "97",);
$str="1";
foreach($p as $val){
$str = bcmul($str,$val);
array_push($prod,$str);
}
return 1;
}
function greedy_prod($n){
global $p_prod;
foreach($p_prod as $key=>$val){
if(bccomp($val,$n)>0) break;
$i_m=$key+1;
}
if (!isset($i_m)) $i_m=0;
return $i_m;
}
function show_chain($chain){
$s = "[";
foreach($chain as $len) $s = $s . sprintf("%d.",$len);
$s = $s."]";
return $s;
}
function multi_prod($chain){
global $p_prod;
$m_prod = "1";
foreach($chain as $val) $m_prod= bcmul($m_prod, $p_prod[$val-1]);
return $m_prod;
}
function multi_count($chain){
$cnt = array();
for ($i=0; $i<$chain[0]; $i++) array_push($cnt, 0);
foreach($chain as $key=>$val){
for ($i=0; $i<$val; $i++) $cnt[$i]++;
}
$count=1;
foreach($cnt as $val) $count *= $val+1;
return $count;
}
function maxi_count($n, &$main_chain, &$latch_chain){
global $maxi_counter, $p_prod;
$maxi_counter++;
$m_prod = multi_prod($main_chain);
$nn = bcdiv($n,$m_prod);
$long_chain = greedy_prod($nn);
if(count($main_chain)>0){
$last = array_pop($main_chain); array_push($main_chain,$last);
$long_chain = min($long_chain, $last);
}
$short_chain = greedy_prod(bcsqrt($nn));
$short_chain = max($short_chain,1);
if ($long_chain==0) {
$max_count = multi_count($main_chain);
if($max_count> multi_count($latch_chain)) $latch_chain=$main_chain;
}
else {
$max_count = 0;
for ($cur_chain=$long_chain; $cur_chain>$short_chain-1; $cur_chain--){
array_push($main_chain,$cur_chain);
$counter = maxi_count($n, $main_chain, $latch_chain);
array_pop($main_chain);
if($counter>$max_count) $max_count = $counter;
else break;
}
}
$s1 = show_chain($main_chain); $s2=show_chain($latch_chain);
print("<tr><td align="right"> $m_prod</td><td align="right">$max_count</td><td>$s2</td><td>$s1</td></tr>");
return $max_count;
}
//$N="1000000000000000000";
$N="1000000000000000000000000000000000000";
$p_prod = array();
if (prods($p_prod)>0){
print("<br>p_prod:<br>");
foreach($p_prod as $key=>$val) printf(" %d=>%s", $key, $val);
}
$maxi_counter = 0; $chain=array(); $optimal_chain=array();
print("<br><br>maxi_count:<br>N=$N");
print('<table border="2">');
print('<tr><th>current number</th><th>multi_prod</th><th>optimal chain</th><th>current chain</th></tr>');
$max_count=maxi_count($N, $chain, $optimal_chain);
print('</table>');
printf("<br>Количество последовательностей = %d<br>Цепочка произведений = %s,<br>Kоличество множителей = %d<br>Минимальное число = %s", $maxi_counter, show_chain($optimal_chain), $max_count, multi_prod($optimal_chain));
Результаты для N = 1036:
<pre>
p_prod:
0=>2 1=>6 2=>30 3=>210 4=>2310 5=>30030 6=>510510 7=>9699690 8=>223092870
9=>6469693230 10=>200560490130 11=>7420738134810 12=>304250263527210
13=>13082761331670030 14=>614889782588491410 15=>32589158477190044730
16=>1922760350154212639070 17=>117288381359406970983270
18=>7858321551080267055879090 19=>557940830126698960967415390
20=>40729680599249024150621323470 21=>3217644767340672907899084554130
22=>267064515689275851355624017992790 23=>23768741896345550770650537601358310
24=>2305567963945518424753102147331756070
maxi_count:
N=1000000000000000000000000000000000000
current number multi_prod optimal chain current chain
713062256890366523119516128040749300 56623104 [24.3.] [24.3.]
855674708268439827743419353648899160 67108864 [24.2.2.] [24.2.2.]
570449805512293218495612902432599440 62914560 [24.2.2.] [24.2.1.1.]
285224902756146609247806451216299720 62914560 [24.2.2.] [24.2.1.]
142612451378073304623903225608149860 67108864 [24.2.2.] [24.2.]
23768741896345550770650537601358310 67108864 [24.2.2.] [24.]
616919031242227216631491481563344900 63700992 [24.2.2.] [23.5.]
673002579536975145416172525341830800 94371840 [23.4.2.1.] [23.4.2.1.]
336501289768487572708086262670915400 94371840 [23.4.2.1.] [23.4.2.]
897336772715966860554896700455774400 99090432 [23.4.1.1.1.1.] [23.4.1.1.1.1.]
448668386357983430277448350227887200 99090432 [23.4.1.1.1.1.] [23.4.1.1.1.]
224334193178991715138724175113943600 99090432 [23.4.1.1.1.1.] [23.4.1.1.]
112167096589495857569362087556971800 99090432 [23.4.1.1.1.1.] [23.4.1.]
56083548294747928784681043778485900 99090432 [23.4.1.1.1.1.] [23.4.]
961432256481393064880246464774044000 100663296 [23.3.3.1.1.] [23.3.3.1.1.]
480716128240696532440123232387022000 100663296 [23.3.3.1.1.] [23.3.3.1.]
240358064120348266220061616193511000 100663296 [23.3.3.1.1.] [23.3.3.]
576859353888835838928147878864426400 94371840 [23.3.3.1.1.] [23.3.2.2.1.]
288429676944417919464073939432213200 94371840 [23.3.3.1.1.] [23.3.2.2.]
769145805185114451904197171819235200 100663296 [23.3.3.1.1.] [23.3.2.1.1.1.1.]
384572902592557225952098585909617600 100663296 [23.3.3.1.1.] [23.3.2.1.1.1.]
192286451296278612976049292954808800 100663296 [23.3.3.1.1.] [23.3.2.1.1.]
96143225648139306488024646477404400 100663296 [23.3.3.1.1.] [23.3.2.1.]
48071612824069653244012323238702200 100663296 [23.3.3.1.1.] [23.3.2.]
8011935470678275540668720539783700 100663296 [23.3.3.1.1.] [23.3.]
267064515689275851355624017992790 100663296 [23.3.3.1.1.] [23.]
579755234179442444545257054963143400 84934656 [23.3.3.1.1.] [22.6.2.]
773006978905923259393676073284191200 95551488 [23.3.3.1.1.] [22.6.1.1.1.]
386503489452961629696838036642095600 95551488 [23.3.3.1.1.] [22.6.1.1.]
193251744726480814848419018321047800 95551488 [23.3.3.1.1.] [22.6.1.]
96625872363240407424209509160523900 95551488 [23.3.3.1.1.] [22.6.]
891931129506834530069626238404836000 113246208 [22.5.3.1.1.] [22.5.3.1.1.]
445965564753417265034813119202418000 113246208 [22.5.3.1.1.] [22.5.3.1.]
222982782376708632517406559601209000 113246208 [22.5.3.1.1.] [22.5.3.]
535158677704100718041775743042901600 106168320 [22.5.3.1.1.] [22.5.2.2.1.]
267579338852050359020887871521450800 106168320 [22.5.3.1.1.] [22.5.2.2.]
713544903605467624055700990723868800 113246208 [22.5.3.1.1.] [22.5.2.1.1.1.1.]
356772451802733812027850495361934400 113246208 [22.5.3.1.1.] [22.5.2.1.1.1.]
178386225901366906013925247680967200 113246208 [22.5.3.1.1.] [22.5.2.1.1.]
89193112950683453006962623840483600 113246208 [22.5.3.1.1.] [22.5.2.1.]
44596556475341726503481311920241800 113246208 [22.5.3.1.1.] [22.5.2.]
7432759412556954417246885320040300 113246208 [22.5.3.1.1.] [22.5.]
851388805438342051430097773022798000 104857600 [22.5.3.1.1.] [22.4.4.2.]
567592536958894700953398515348532000 100663296 [22.5.3.1.1.] [22.4.4.1.1.]
283796268479447350476699257674266000 100663296 [22.5.3.1.1.] [22.4.4.1.]
141898134239723675238349628837133000 104857600 [22.5.3.1.1.] [22.4.4.]
608134861027387179592926980730570000 98304000 [22.5.3.1.1.] [22.4.3.3.]
729761833232864615511512376876684000 113246208 [22.5.3.1.1.] [22.4.3.2.2.]
973015777643819487348683169168912000 125829120 [22.4.3.2.1.1.1.] [22.4.3.2.1.1.1.]
486507888821909743674341584584456000 125829120 [22.4.3.2.1.1.1.] [22.4.3.2.1.1.]
243253944410954871837170792292228000 125829120 [22.4.3.2.1.1.1.] [22.4.3.2.1.]
121626972205477435918585396146114000 125829120 [22.4.3.2.1.1.1.] [22.4.3.2.]
20271162034246239319764232691019000 125829120 [22.4.3.2.1.1.1.] [22.4.3.]
675705401141541310658807756367300 125829120 [22.4.3.2.1.1.1.] [22.4.]
3217644767340672907899084554130 125829120 [22.4.3.2.1.1.1.] [22.]
790130551223459534127080290097448600 71663616 [22.4.3.2.1.1.1.] [21.8.1.]
395065275611729767063540145048724300 71663616 [22.4.3.2.1.1.1.] [21.8.]
623787277281678579574010755340091000 84934656 [22.4.3.2.1.1.1.] [21.7.3.]
748544732738014295488812906408109200 99532800 [22.4.3.2.1.1.1.] [21.7.2.2.]
998059643650685727318417208544145600 111476736 [22.4.3.2.1.1.1.] [21.7.2.1.1.1.]
499029821825342863659208604272072800 111476736 [22.4.3.2.1.1.1.] [21.7.2.1.1.]
249514910912671431829604302136036400 111476736 [22.4.3.2.1.1.1.] [21.7.2.1.]
124757455456335715914802151068018200 111476736 [22.4.3.2.1.1.1.] [21.7.2.]
20792909242722619319133691844669700 111476736 [22.4.3.2.1.1.1.] [21.7.]
513707169526088242002126504397722000 94371840 [22.4.3.2.1.1.1.] [21.6.4.1.]
256853584763044121001063252198861000 94371840 [22.4.3.2.1.1.1.] [21.6.4.]
880640862044722700575074007538952000 123863040 [22.4.3.2.1.1.1.] [21.6.3.2.1.1.]
440320431022361350287537003769476000 123863040 [22.4.3.2.1.1.1.] [21.6.3.2.1.]
220160215511180675143768501884738000 123863040 [22.4.3.2.1.1.1.] [21.6.3.2.]
587093908029815133716716005025968000 113246208 [22.4.3.2.1.1.1.] [21.6.3.1.1.1.1.]
293546954014907566858358002512984000 113246208 [22.4.3.2.1.1.1.] [21.6.3.1.1.1.]
146773477007453783429179001256492000 113246208 [22.4.3.2.1.1.1.] [21.6.3.1.1.]
73386738503726891714589500628246000 113246208 [22.4.3.2.1.1.1.] [21.6.3.1.]
36693369251863445857294750314123000 123863040 [22.4.3.2.1.1.1.] [21.6.3.]
528384517226833620345044404523371200 111476736 [22.4.3.2.1.1.1.] [21.6.2.2.2.1.]
264192258613416810172522202261685600 111476736 [22.4.3.2.1.1.1.] [21.6.2.2.2.]
704512689635778160460059206031161600 119439360 [22.4.3.2.1.1.1.] [21.6.2.2.1.1.1.1.]
352256344817889080230029603015580800 119439360 [22.4.3.2.1.1.1.] [21.6.2.2.1.1.1.]
176128172408944540115014801507790400 119439360 [22.4.3.2.1.1.1.] [21.6.2.2.1.1.]
88064086204472270057507400753895200 119439360 [22.4.3.2.1.1.1.] [21.6.2.2.1.]
44032043102236135028753700376947600 119439360 [22.4.3.2.1.1.1.] [21.6.2.2.]
7338673850372689171458950062824600 119439360 [22.4.3.2.1.1.1.] [21.6.2.]
1223112308395448195243158343804100 123863040 [22.4.3.2.1.1.1.] [21.6.]
869350594582610871080521776673068000 100663296 [22.4.3.2.1.1.1.] [21.5.5.1.1.]
434675297291305435540260888336534000 100663296 [22.4.3.2.1.1.1.] [21.5.5.1.]
217337648645652717770130444168267000 100663296 [22.4.3.2.1.1.1.] [21.5.5.]
592739041760871048463992120458910000 98304000 [22.4.3.2.1.1.1.] [21.5.4.3.]
711286850113045258156790544550692000 113246208 [22.4.3.2.1.1.1.] [21.5.4.2.2.]
948382466817393677542387392734256000 125829120 [22.4.3.2.1.1.1.] [21.5.4.2.1.1.1.]
474191233408696838771193696367128000 125829120 [22.4.3.2.1.1.1.] [21.5.4.2.1.1.]
237095616704348419385596848183564000 125829120 [22.4.3.2.1.1.1.] [21.5.4.2.1.]
118547808352174209692798424091782000 125829120 [22.4.3.2.1.1.1.] [21.5.4.2.]
19757968058695701615466404015297000 125829120 [22.4.3.2.1.1.1.] [21.5.4.]
508062035795032327254850388964780000 106168320 [22.4.3.2.1.1.1.] [21.5.3.3.2.]
677416047726709769673133851953040000 117964800 [22.4.3.2.1.1.1.] [21.5.3.3.1.1.1.]
338708023863354884836566925976520000 117964800 [22.4.3.2.1.1.1.] [21.5.3.3.1.1.]
169354011931677442418283462988260000 117964800 [22.4.3.2.1.1.1.] [21.5.3.3.1.]
84677005965838721209141731494130000 117964800 [22.4.3.2.1.1.1.] [21.5.3.3.]
609674442954038792705820466757736000 115605504 [22.4.3.2.1.1.1.] [21.5.3.2.2.2.]
812899257272051723607760622343648000 127401984 [21.5.3.2.2.1.1.1.] [21.5.3.2.2.1.1.1.]
406449628636025861803880311171824000 127401984 [21.5.3.2.2.1.1.1.] [21.5.3.2.2.1.1.]
203224814318012930901940155585912000 127401984 [21.5.3.2.2.1.1.1.] [21.5.3.2.2.1.]
101612407159006465450970077792956000 127401984 [21.5.3.2.2.1.1.1.] [21.5.3.2.2.]
16935401193167744241828346298826000 127401984 [21.5.3.2.2.1.1.1.] [21.5.3.2.]
2822566865527957373638057716471000 127401984 [21.5.3.2.2.1.1.1.] [21.5.3.]
94085562184265245787935257215700 127401984 [21.5.3.2.2.1.1.1.] [21.5.]
40729680599249024150621323470 127401984 [21.5.3.2.2.1.1.1.] [21.]
746835726498886408969432055023615800 71663616 [21.5.3.2.2.1.1.1.] [20.9.2.]
995780968665181878625909406698154400 80621568 [21.5.3.2.2.1.1.1.] [20.9.1.1.1.]
497890484332590939312954703349077200 80621568 [21.5.3.2.2.1.1.1.] [20.9.1.1.]
248945242166295469656477351674538600 80621568 [21.5.3.2.2.1.1.1.] [20.9.1.]
124472621083147734828238675837269300 80621568 [21.5.3.2.2.1.1.1.] [20.9.]
974133556302895316047085289161238000 99532800 [21.5.3.2.2.1.1.1.] [20.8.3.2.]
649422370868596877364723526107492000 95551488 [21.5.3.2.2.1.1.1.] [20.8.3.1.1.]
324711185434298438682361763053746000 95551488 [21.5.3.2.2.1.1.1.] [20.8.3.1.]
162355592717149219341180881526873000 99532800 [21.5.3.2.2.1.1.1.] [20.8.3.]
779306845042316252837668231328990400 104509440 [21.5.3.2.2.1.1.1.] [20.8.2.2.1.1.]
389653422521158126418834115664495200 104509440 [21.5.3.2.2.1.1.1.] [20.8.2.2.1.]
194826711260579063209417057832247600 104509440 [21.5.3.2.2.1.1.1.] [20.8.2.2.]
519537896694877501891778820885993600 95551488 [21.5.3.2.2.1.1.1.] [20.8.2.1.1.1.1.]
259768948347438750945889410442996800 95551488 [21.5.3.2.2.1.1.1.] [20.8.2.1.1.1.]
129884474173719375472944705221498400 95551488 [21.5.3.2.2.1.1.1.] [20.8.2.1.1.]
64942237086859687736472352610749200 95551488 [21.5.3.2.2.1.1.1.] [20.8.2.1.]
32471118543429843868236176305374600 104509440 [21.5.3.2.2.1.1.1.] [20.8.2.]
5411853090571640644706029384229100 104509440 [21.5.3.2.2.1.1.1.] [20.8.]
657967402064236309961627783029959000 75497472 [21.5.3.2.2.1.1.1.] [20.7.5.]
717782620433712338139957581487228000 106168320 [21.5.3.2.2.1.1.1.] [20.7.4.2.1.]
358891310216856169069978790743614000 106168320 [21.5.3.2.2.1.1.1.] [20.7.4.2.]
957043493911616450853276775316304000 113246208 [21.5.3.2.2.1.1.1.] [20.7.4.1.1.1.1.]
478521746955808225426638387658152000 113246208 [21.5.3.2.2.1.1.1.] [20.7.4.1.1.1.]
239260873477904112713319193829076000 113246208 [21.5.3.2.2.1.1.1.] [20.7.4.1.1.]
119630436738952056356659596914538000 113246208 [21.5.3.2.2.1.1.1.] [20.7.4.1.]
59815218369476028178329798457269000 113246208 [21.5.3.2.2.1.1.1.] [20.7.4.]
512701871738365955814255415348020000 99532800 [21.5.3.2.2.1.1.1.] [20.7.3.3.1.]
256350935869182977907127707674010000 99532800 [21.5.3.2.2.1.1.1.] [20.7.3.3.]
615242246086039146977106498417624000 111476736 [21.5.3.2.2.1.1.1.] [20.7.3.2.2.1.]
307621123043019573488553249208812000 111476736 [21.5.3.2.2.1.1.1.] [20.7.3.2.2.]
820322994781385529302808664556832000 119439360 [21.5.3.2.2.1.1.1.] [20.7.3.2.1.1.1.1.]
410161497390692764651404332278416000 119439360 [21.5.3.2.2.1.1.1.] [20.7.3.2.1.1.1.]
205080748695346382325702166139208000 119439360 [21.5.3.2.2.1.1.1.] [20.7.3.2.1.1.]
102540374347673191162851083069604000 119439360 [21.5.3.2.2.1.1.1.] [20.7.3.2.1.]
51270187173836595581425541534802000 119439360 [21.5.3.2.2.1.1.1.] [20.7.3.2.]
8545031195639432596904256922467000 119439360 [21.5.3.2.2.1.1.1.] [20.7.3.]
284834373187981086563475230748900 119439360 [21.5.3.2.2.1.1.1.] [20.7.]
503151542755004237029480069375851000 67108864 [21.5.3.2.2.1.1.1.] [20.6.6.]
928895155855392437592886281924648000 110100480 [21.5.3.2.2.1.1.1.] [20.6.5.2.1.1.]
464447577927696218796443140962324000 110100480 [21.5.3.2.2.1.1.1.] [20.6.5.2.1.]
232223788963848109398221570481162000 110100480 [21.5.3.2.2.1.1.1.] [20.6.5.2.]
619263437236928291728590854616432000 100663296 [21.5.3.2.2.1.1.1.] [20.6.5.1.1.1.1.]
309631718618464145864295427308216000 100663296 [21.5.3.2.2.1.1.1.] [20.6.5.1.1.1.]
154815859309232072932147713654108000 100663296 [21.5.3.2.2.1.1.1.] [20.6.5.1.1.]
77407929654616036466073856827054000 100663296 [21.5.3.2.2.1.1.1.] [20.6.5.1.]
38703964827308018233036928413527000 110100480 [21.5.3.2.2.1.1.1.] [20.6.5.]
738893873975880348085250451530970000 92160000 [21.5.3.2.2.1.1.1.] [20.6.4.4.]
633337606265040298358786101312260000 106168320 [21.5.3.2.2.1.1.1.] [20.6.4.3.2.]
844450141686720397811714801749680000 117964800 [21.5.3.2.2.1.1.1.] [20.6.4.3.1.1.1.]
422225070843360198905857400874840000 117964800 [21.5.3.2.2.1.1.1.] [20.6.4.3.1.1.]
211112535421680099452928700437420000 117964800 [21.5.3.2.2.1.1.1.] [20.6.4.3.1.]
105556267710840049726464350218710000 117964800 [21.5.3.2.2.1.1.1.] [20.6.4.3.]
760005127518048358030543321574712000 115605504 [21.5.3.2.2.1.1.1.] [20.6.4.2.2.2.]
506670085012032238687028881049808000 113246208 [21.5.3.2.2.1.1.1.] [20.6.4.2.2.1.1.]
253335042506016119343514440524904000 113246208 [21.5.3.2.2.1.1.1.] [20.6.4.2.2.1.]
126667521253008059671757220262452000 115605504 [21.5.3.2.2.1.1.1.] [20.6.4.2.2.]
21111253542168009945292870043742000 115605504 [21.5.3.2.2.1.1.1.] [20.6.4.2.]
3518542257028001657548811673957000 117964800 [21.5.3.2.2.1.1.1.] [20.6.4.]
16754963128704769797851484161700 117964800 [21.5.3.2.2.1.1.1.] [20.6.]
557940830126698960967415390 119439360 [21.5.3.2.2.1.1.1.] [20.]
1 127401984 [21.5.3.2.2.1.1.1.] []
Количество последовательностей = 168
Цепочка произведений = [21.5.3.2.2.1.1.1.],
Kоличество множителей = 127401984
Минимальное число = 812899257272051723607760622343648000
</pre>Расширенная постановка задачи
Итак, мы нашли оптимальное решение задачи, которому соответствует минимальное среди n<N. В приведённом примере отношение N/n=1.23. Но если бы потребовалось найти все возможные числа до N с полученным количеством делителей, то возникла бы комбинаторная задача на тему возможных обменов простых множителей.
На этой странице вы узнаете
- Как быстро работает программа?
- Есть ли смысл перебирать делители после корня?
- Что количество делителей может сказать о самом числе?
Гадание на кофейной гуще или на картах Таро? Может, на ромашке? Хотя лучше не доверять свои отношения цветку. Наша судьба — только в наших руках. А судьба чисел предопределена заранее. Сегодня мы будем предсказывать их жизнь и судьбу по делителям. Но главная проблема — найти эти делители.

Постановка проблемы. Переборное решение
Встречали ли вы странных персонажей в задачах, которым резко понадобилось купить 50 арбузов? А что подумаете, если ваш учитель математики задаст найти число, у которого 50 делителей?
Поиск делителей в математике не самый сложный процесс. Есть разные способы: разложение на простые множители, обычный перебор и так далее. Сложность задания будет зависеть от самого числа. Довольно быстро получится найти делители числа 24 — число небольшое, красивое, удобное. Нахождение делителей числа 1234567 займет гораздо больше времени.
Я предлагаю включить компьютер, открыть среду разработки и заставить код сделать за нас всю работу.
Идея в следующем:
- Создадим список, в который мы сохраним все делители числа.
- С помощью цикла for переберем все числа из диапазона от 1 до самого числа.
- Если в переборе мы нашли такое число, которое является делителем исходного — остаток от деления будет равен 0 — сохраним это число в список.
В итоге мы получим список всех делителей исходного числа.
number = 1234567
dels = []
for i in range(1, number + 1):
if number % i == 0:
dels.append(i)
print(dels)
_____________________________________________________________________
Вывод: [1, 127, 9721, 1234567]У этого метода есть очень большая проблема — время его работы.
Программа выполняет команды очень быстро, но не бесконечно быстро.
Время работы программы можно измерить. Например, Sublime Text 3 занимается этим автоматически. И он помог посчитать, что программа выше выполнилась за 0.2 секунды. Давайте постепенно повышать ставки и смотреть, сколько времени понадобится этой же программе для поиска делителей других чисел:
— число 1234567 — 0.2 секунды;
— число 12345670 — 0.9 секунды;
— число 123456700 — 8.0 секунд;
— число 1234567000 — 115.7 секунд.
С числом 1234567 программа сделала 1234567 шагов цикла for, и справилась неимоверно быстро. Но чем больше ей придется выполнять команд, тем дольше придется работать.
Замеры времени зависят от многих факторов, например, мощности компьютера. Но мы можем повысить эффективность работы программы.
Ускоренный перебор делителей
Идея ускоренного перебора делителей заключается в том, что, найдя один делитель, мы сразу можем подобрать второй — его пару.
Возьмем число 24. Найдя его делитель 2, мы сразу можем сказать, что у 24 есть еще один делитель — 12, потому что 12 = 24 / 2. Интересная мысль? Давайте ее развивать.
Найдем по такой логике все делители числа 16.
- Самый простой делитель числа — 1. И по этой логике сразу найдем второй делитель — само число 16, так как 16 / 1 = 16.

- Проверим число 2. Это делитель, так что сразу найдем его пару: 16 / 2 = 8.

- Проверяем число 3 — это не делитель, его просто пропускаем.

- При проверке числа 4 мы столкнемся с интересной ситуацией. Его парой будет 16 / 4 = 4 — то же самое число, а мы ищем различные пары. Значит, у корня числа пары не будет: найдя корень, мы найдем только один делитель.

Если мы продолжим перебор, числа 5, 6 и 7 — не будут делителями. А за ними — 8, делитель, который мы уже нашли.
Нет. Найдя “маленький” делитель, при ускоренном переборе мы можем найти его пару, которая будет “большим” делителем. Перебирая делители, рано или поздно мы дойдем до корня числа, у которого нет пары. Перебирая числа после корня, мы будем находить только “большие” делители, которые уже нашли в паре с “маленькими”.
Если у числа целого корня нет, перебираем до его округленного вниз значения.
Нам нет смысла перебирать числа после корня, так что будем перебирать до предельно близкого к нему значения, но не больше.
Логика программы будет такой:
- Перебираем числа от 1 до корня исходного числа.
- Если мы нашли корень числа, добавляем в список делителей только его.
- Если мы нашли не корень, а обычный делитель — добавляем в список сразу пару делителей.
Пример реализации ускоренного перебора делителей для числа 1234567000:
number = 1234567000
dels = []
for i in range(1, int(number ** 0.5) + 1):
if i * i == number:
dels.append(i)
elif number % i == 0:
dels.append(i)
dels.append(number // i)
print(len(dels))
_____________________________________________________________________
Вывод: 64Эта программа нашла все делители числа и выдала их количество — 64. А на ее работу ушло меньше секунды.
Но и это не панацея. Что, если нам придется проверить делители сразу нескольких чисел? Например, мы хотим найти все числа, у которых ровно 7 делителей, в диапазоне от 1 до 10000.
Программу надо немного модифицировать:
- заведем переменную-счетчик, которая будет считать подходящие числа;
- number сделаем перебираемой переменной по нужному диапазону с помощью цикла for;
- ускоренный перебор будет внутри перебора number;
- в конце каждого шага цикла проверяем — если делителей у числа ровно 7, то увеличиваем наш счетчик на 1.
Теперь программа будет выглядеть следующим образом:
count = 0
for number in range(1, 10000):
dels = []
for i in range(1, int(number ** 0.5) + 1):
if i * i == number:
dels.append(i)
elif number % i == 0:
dels.append(i)
dels.append(number // i)
if len(dels) == 7:
count += 1
print(count)
_____________________________________________________________________
Вывод: 2Эта программа работала всего 0.2 секунды. Звучит неплохо, но давайте снова поднимать ставки:
- диапазон 1 — 10000 — 0.2 секунды;
- диапазон 1 — 100000 — 2.6 секунды;
- диапазон 1 — 1000000 — 80.2 секунды.
Время снова увеличивается очень быстро. Что можно с этим сделать?
Еще более ускоренный перебор делителей
Не считаем, что не нужно
Обратите внимание — программа выше нашла среди чисел 1–10000 всего 2 числа, имеющих ровно 7 делителей. А сколько же у остальных? Может быть и больше, может быть и меньше. Например, у числа 9864 делителей аж 24 штуки. Стоило ли тратить время на поиск их всех, если количество делителей больше 7?
Конечно, нет. Как только мы нашли 8 штук, мы уже можем понять, что анализировать число далее нам неинтересно. Значит, нужно остановить работу цикла.
Команда break полностью останавливает работу цикла.
Мы можем модернизировать нашу последнюю программу: если в переборе делителей мы увидим, что их больше семи, завершаем цикл командой break.
count = 0
for number in range(1, 10000):
dels = []
for i in range(1, int(number ** 0.5) + 1):
if i * i == number:
dels.append(i)
elif number % i == 0:
dels.append(i)
dels.append(number // i)
if len(dels) > 7:
break
if len(dels) == 7:
count += 1
print(count)При этом завершится именно цикл перебора делителей i, так как break находится именно в нем, а цикл перебора number продолжит свою работу.
Давайте произведем замеры еще раз:
- диапазон 1-10000 — 0.2 секунды;
- диапазон 1-100000 — 2.1 секунды;
- диапазон 1-1000000 — 53.5 секунды.
В последнем случае мы сэкономили около трети от времени работы программы. Но и это не предел.
Не считаем, что не нужно 2.0
Вернемся на несколько абзацев выше, когда мы искали делители числа 16. Мы нашли 5 делителей — 2 пары и 1 корень, который не даст пару. Это справедливо для любого числа: целый корень не будет давать пару ни с каким другим числом, а все остальные делители — будут.
Если у числа есть целый корень, количество делителей числа будет нечетным, так как корень не даст пару ни с кем.
Если же у числа целого корня нет — количество его делителей будет четным, так как все делители будут иметь пару.
Нам нужны числа, у которых ровно 7 делителей. Следовательно, нам нужны числа, у которых есть целый корень. Это можно проверить, вычислив точный корень числа и его округленное значение. Если они совпадут, значит, округлять корень было некуда и он целый.
Но как пропускать числа, которые нам не нужны?
Команда continue останавливает работу текущего шага цикла и сразу переходит к следующему.
Если мы найдем число number, у которого нет целого корня, мы можем применить команду continue: данный шаг цикла перебора number завершается, и мы сразу перейдем к следующему.
Включить эту проверку в программу можно следующим образом:
count = 0
for number in range(1, 10000):
if number ** 0.5 != int(number ** 0.5):
continue
dels = []
for i in range(1, int(number ** 0.5) + 1):
if i * i == number:
dels.append(i)
elif number % i == 0:
dels.append(i)
dels.append(number // i)
if len(dels) > 7:
break
if len(dels) == 7:
count += 1
print(count)
Снова посмотрим на время работы программы при разных диапазонах:
- диапазон 1-100000 — 0.1 секунды;
- диапазон 1-1000000 — 0.5 секунды;
- диапазон 1-10000000 — 4.5 секунды;
- диапазон 1-100000000 — 44.4 секунды.
А делители — это вообще для чего? А таблицы со временем — это точно важно? Может, подождать проще, чем учить все это?
Нахождению делителей чисел посвящена задача 25 ЕГЭ, и без этих теоретических знаний решить ее крайне сложно. Что же касается времени работы, то за ним приходится следить внимательнейшим образом, ведь в задачах могут встречаться ситуации, когда надо найти делители для сотен миллионов чисел за раз!
Зная все особенности ускорения перебора делителей и поиска чисел с конкретными делителями, за считанные секунды можно решать задачи огромных диапазонов.
Фактчек
- Ускоренный перебор делителей подразумевает нахождение делителей попарно, при этом перебирать делители достаточно только до корня числа.
- Команда break полностью останавливает работу цикла, а команда continue завершает работу лишь текущего шага цикла, перенося нас сразу на следующий.
- Если у числа есть целый корень, количество делителей числа будет нечетным, так как корень не даст пару ни с кем. Если же у числа целого корня нет — количество его делителей будет четным, так как все делители будут иметь пару.
Проверь себя
Задание 1.
Для чего нужен ускоренный перебор делителей?
- Обычный перебор слишком скучный
- Для большей точности вычислений
- Для ускорения работы программы
Задание 2.
Найдите количество делителей числа 2568568668.
- 5
- 6
- 7
- 8
Задание 3.
Найдите, сколько чисел из диапазона от 2000 до 1002000 имеют ровно 5 делителей.
- Ни одного
- 1
- 10
- 8
Ответы: 1. — 3; 2. — 3; 3. — 4.

В задание №25
Тема: Обработка целых чисел. Проверка делимости
Проверяется умение создавать собственные программы (10–20 строк) для обработки целочисленной информации.
Немного теории:
Что нужно знать:
- в данных задачах нет ограничения на время выполнения, но отметим, что простой перебор иногда может выполняться в Phyton достаточно долго, поэтому необходимо написать эффективный алгоритм.
- задачи этого типа можно решать с помощью электронных таблиц или собственной программы;
k = 0
for n in range(a, b+1):
if условие выполнено:
k += 1
print( count )
⇐ Пусть необходимо перебрать все целые числа на отрезке [a; b] и подсчитать, для скольких из них выполняется некоторое условие; общая структура цикла перебора записывается так (Python)
if i % j == 0:
print("Делится")
else: print("Не делится")
- проверку условия удобно оформить в виде функции, возвращающей логическое значение (True/False), но можно этого и не делать
- проверить делимость числа i на число j можно с помощью операции взятия остатка от деления i на j — если остаток == 0, число i делится на j нацело.
- ⇐ проверка делимости на языке Python выглядит так:
k = 0
for d in range(1, n+1):
if i % j == 0:
k += 1
print(k) # вывести количество делителей
- для определения количества делителей натурального числа n можно использовать цикл, в котором перебираются все возможные делители d от 1 до n, при обнаружении делителя увеличивается счётчик делителей:
d = []
# перебор всех возможных делителей
for i in range(1,n+1):
if n % i == 0: # если нашли делитель d
d.append(i) # добавили его в массив
- если требуется определить не только количество делителей, но и сами делители, нужно сохранять их в массиве
- в языке Python удобно использовать динамический массив: сначала он пуст, а при обнаружении очередного делителя этот делитель добавляется в массив:
- перебор делителей можно оптимизировать, учитывая, что наименьший из пары делителей, таких что a × b = n, не превышает квадратного корня из n; нужно только аккуратно обработать случай, когда число n представляет собой квадрат другого целого числа;
- отметим, что для чисел, которые предлагаются в вариантах заданий, такая оптимизация не обязательна; более того, усложнение программы может привести к дополнительным ошибкам…
nDel = 0 # количество делителей числа
for d in range(1, n+1): # все делители
if n % d == 0:
nDel += 1 # нашли ещё делитель
if nDel == 2:
print( "Число простое" )
else:
print( "Число составное" )
- простое число n делится только на 1 и само на себя, причём единица не считается простым числом; таким образом, любое простое число имеет только два делителя
- для определения простоты числа можно считать общее количество его делителей; если их ровно два, то число простое, если не два – не простое:
nDel = 0 # количество делителей числа
for i in range(1, n+1): # все делители
if n % i == 0:
nDel += 1 # нашли ещё делитель
if nDel > 2: # уже не простое число
break # досрочный выход из цикла
if nDel == 2:
print( "Число простое" )
else:
print( "Число составное" )
- работу программы можно ускорить: если уже найдено больше двух делителей, то число не простое и можно досрочно закончит работу цикла с помощью оператора break:
nDel = 0
for i in range(2, n):
if n % i == 0:
nDel += 1 # нашли делитель
break # досрочный выход из цикла
if nDel == 0:
print( "Число простое" )
else:
print( "Число составное" )
- другой вариант – считать количество делителей числа на отрезке [2; n–1]; как только хотя бы один такой делитель будет найден, можно завершить цикл, потому что число явно не простое:
prime = True # сначала считаем число простым
for d in range(2, n):
if n % d == 0:
prime = False # уже не простое
break # досрочный выход из цикла
if prime:
print( "Число простое" )
else:
print( "Число составное" )
- можно сделать то же самое с помощью логической переменной:
- в этом задании обычно предлагаются большие числа, поэтому проверка делимости на все числа от 2 до n-1 выполняется очень долго, и на устаревших компьютерах время работы приведённого выше алгоритма может быть слишком велико
- программу можно оптимизировать, если вспомнить, что наименьший из пары делителей, таких что a × b = n, не превышает квадратного корня из n; поэтому можно закончить перебор значением , округлив его до ближайшего целого числа ; если на отрезке [2;] не найден ни один делитель, их нет и на отрезке [+ 1, n – 1]
- следовательно, можно существенно ускорить перебор, изменив конечное значение переменной цикла:
С подключением библиотеки from math import sqrt
for d in range(2, round(sqrt(n))+1):
или без библиотеки
for d in range(2, round(n**0.5)+1):
Особенности языка Python
- (В. Ялдыгин) при записи больших чисел в Python можно использовать знаки подчеркивания; например, 7_777_777 обозначает то же самое, что и 7777777.
Пример задания:
Задание 1. Пять различных нечётных делителей
Найдите все натуральные числа, принадлежащие отрезку [35 000 000; 40 000 000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
Тренировочный вариант №4 от 17 марта 2021 года СтатГрад Вариант ИН2010401
Решение:

- простой перебор будет в Phyton выполняться долго!!! поэтому обратимся к математике.
- любое число единственным образом (с точностью до порядка сомножителей) представимо в виде произведения простых чисел:
Вот более быстрый метод: если есть простое число, 4-я степень которого равна самому числу, то это число имеет ровно 5 нечетных делителей.
Разложим искомое число на простые. Так как в дальнейшем нас будут интересовать нечётные делители, степень двойки выписана отдельно:
n = 2^k0 * p1^k1 * p2^k2 * ... * pi*ki,
где k0 — целое неотрицательное, k1, ..., ki — натуральные, p1, ..., pi — различные нечётные простые.
Любой делитель n конструируется как произведение простых из разложения выше. Сколько нечётных делителей мы можем сконструировать? (k1 + 1)(k2 + 1) ... (ki + 1). Это прозведение может быть равно пяти только если у числа ровно один нечётный простой делитель, который возводится в четвёртую степень.
Искомое число должно иметь вид:
n = 2k * p4
, где k — целое неотрицательное, p — нечетное простое. Сами нечётные делители тогда имеют вид 1, p, pp, ppp, pppp.
Источник: ИНФОРМАТИКА ЭКСПЕРТ >>
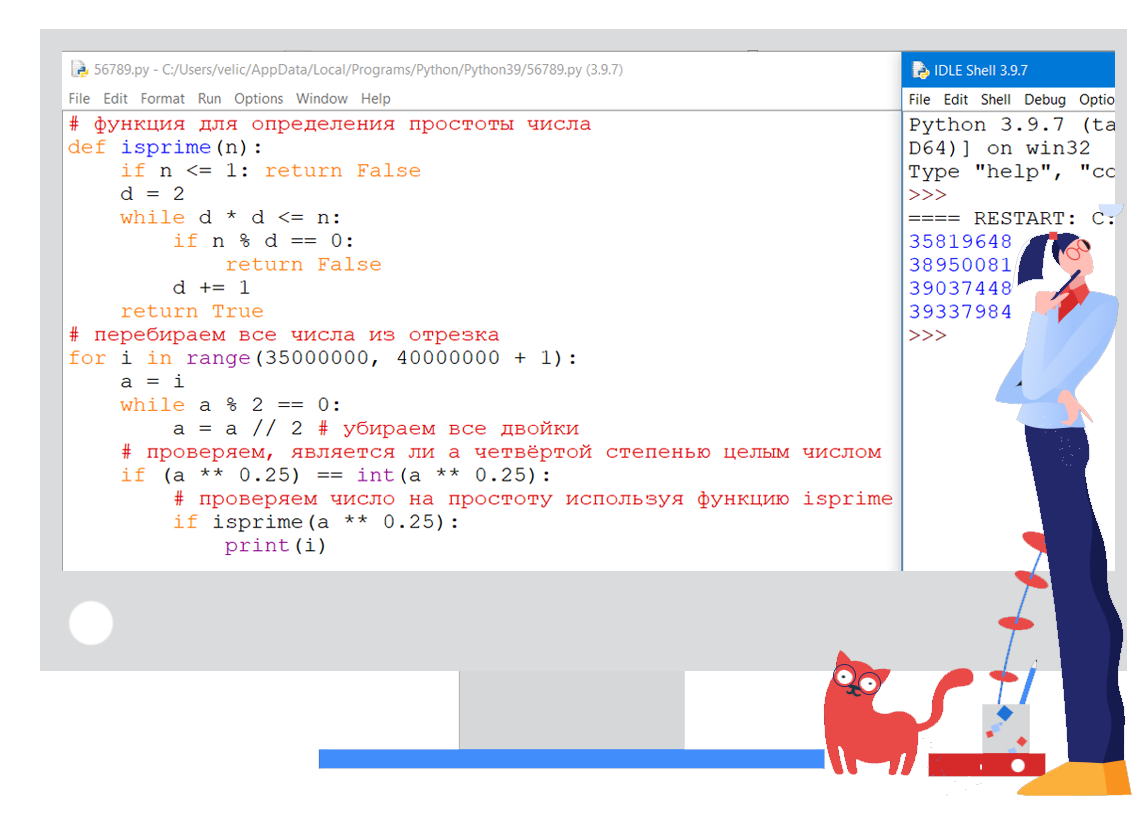
def isprime(n):
if n <= 1: return False
d = 2
while d * d <= n:
if n % d == 0:
return False
d += 1
return True
for i in range(35000000, 40000000 + 1):
a = i
while a % 2 == 0:
a = a // 2
if (a ** 0.25) == int(a ** 0.25):
if isprime(a ** 0.25):
print(i)
☆ Для тех, кто не любит набирать код 🙂

start, end = 35000000, 40000000
primes = [2]
for i in range(3, int(end**0.25) + 1, 2):
for d in range(2, int(i**0.5) + 1):
if i % d == 0:
break
else:
primes.append(i)
ans = []
for el in primes[1:]:
num = el**4
while num <= end:
if num >= start:
ans.append([num])
num *= 2
print(*sorted(ans), sep='n')
Решение (программа перебирает только простые числа, В.Н. Шубинкин)
1) Основная идея решения та же, но теперь будем перебирать не числа из отрезка, а простые числа. Если при возведении нечётного простого числа в четвёртую степень и умножении его на какую-либо степень двойки (в т.ч. нулевую), получится число, входящее в отрезок из условия, то оно пойдёт в ответ.
Ответ:
35819648
38950081
39037448
39337984
38950081
39037448
39337984
Задание 2. Ровно два делителя
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [174457; 174505], числа, имеющие ровно два различных натуральных делителя, не считая единицы и самого числа. Для каждого найденного числа запишите эти два делителя в два соседних столбца на экране с новой строки в порядке возрастания произведения этих двух делителей. Делители в строке также должны следовать в порядке возрастания.
Например, в диапазоне [5; 9] ровно два различных натуральных делителя имеют числа 6 и 8, поэтому для этого диапазона вывод на экране должна содержать следующие значения:
2 3
2 4
Решение (программа):
for i in range (174457, 174505+1):
k = 0
for j in range (2, i):
if i % j == 0:
k +=1
if k == 1: d1 = j
if k == 2: d2 = j
if k == 2:
print( d1, d2 )
Если число имеет ровно два делителя, отличных от единицы и самого числа, то произведение этих делителей и есть само число; таким образом, строки в таблице должны быть записаны в порядке возрастания чисел, которые они образуют.
Решение (программа без массива, И.В. Степанов)
ОЧЕНЬ БЫСТРО!!!
учитывая, что в этой задаче нас интересуют только два делителя, можно вместо массива использовать две дополнительных переменные, d1, если количество == 1, d2, если k == 2 🙂
ОТВЕТ:
3 58153
7 24923
59 2957
13 13421
149 1171
5 34897
211 827
2 87251
7 24923
59 2957
13 13421
149 1171
5 34897
211 827
2 87251
Решение (Ecxel):
Решение (электронные таблицы, И.В. Степанов):
Перебор можно организовать и с помощью электронных таблиц, используя функцию ОСТАТ (MOD) ;
- найдем квадратный корень самого большого числа нашего отрезка, функция =КОРЕНЬ(174505)
- в первый столбец занесём все делители от 2 до квадратного корня из наибольшего числа 417
- в первую строку – все натуральные числа заданного отрезка
★ в Excel для этого можно использовать команду Заполнить — Прогрессия
Начиная с B2, заполняем остатками от деления чисел из первой строки на делители из первого столбца;
Ниже 417-й строки считаем для каждого числа количество делителей; нас интересуют числа, у которых один делитель на отрезке [2; 417]; используем функцию СЧЁТЕСЛИ, с помощью которой считаем нули в каждом столбце (ноль говорит о том, что число из первой строки разделилось нацело на делитель в первом столбце)
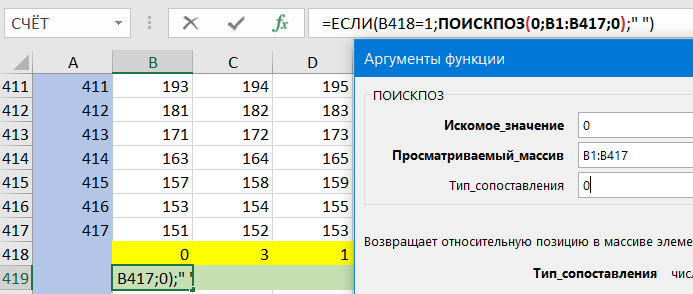
Для тех чисел, у которых всего один делитель, меньший или равный 417, находим его с помощью функции ПОИСКПОЗ; она находит в столбце 0 и определяет его позицию (третий аргумент функции ПОИСКПОЗ означает точное совпадение)
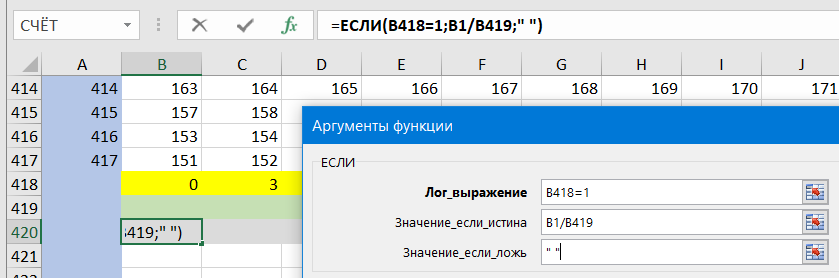
Теперь вычисляем второй делитель: делим число в первой строке на первый делитель, всё это только для подходящих чисел:
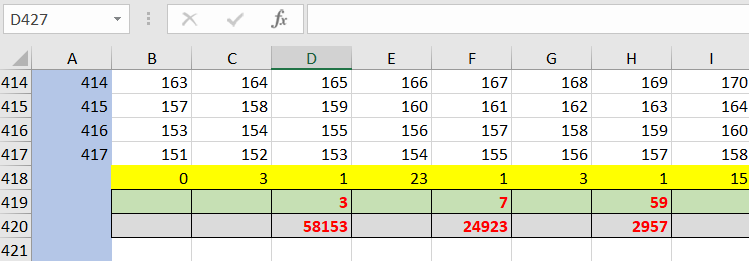
- Остаётся выписать найденные пары делителей
ОТВЕТ:
3 58153
7 24923
59 2957
13 13421
149 1171
5 34897
211 827
2 87251
7 24923
59 2957
13 13421
149 1171
5 34897
211 827
2 87251
Задание 3. Поиск простых чисел
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [3532000; 3532160], простые числа. Выведите все найденные простые числа в порядке возрастания, слева от каждого числа выведите его номер по порядку.
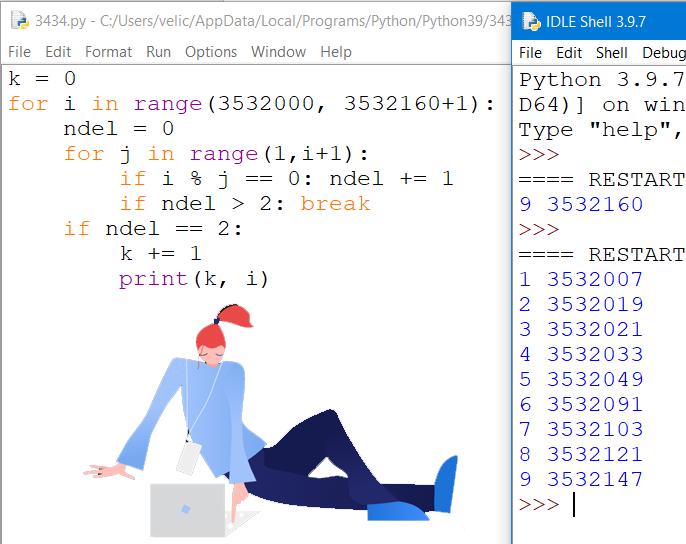
- поскольку нужно вывести не только сами числа, но и их порядковые номера, нужно использовать счётчик:
- простой перебор, может работать очень долго
- для определения простоты числа ищем полное количество делителей, если оно равно 2, то число простое:
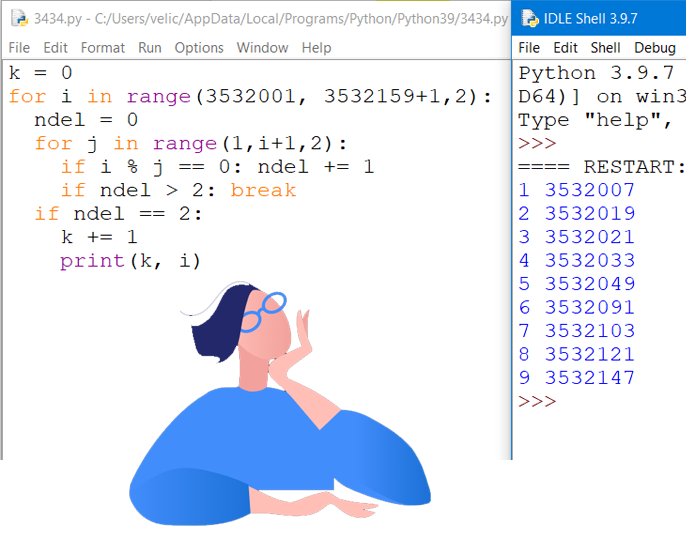
- идея ускорения времени выполнения программы состоит в том, что все простые числа, кроме 2 являются нечетными числами;
- тогда внешний цикл надо начинать не с числа 3532000, а с числа 3532001, при этом шаг цикла составит +2. Окончанием цикла также можно сделать не число 3532160, а 3532159;
- внутренний цикл также должен иметь шаг +2
k = 0
for i in range(3532000, 3532160+1):
ndel = 0
for j in range(1,i+1):
if i % j == 0: ndel += 1
if ndel > 2: break
if ndel == 2:
k += 1
print(k, i)
k = 0
for i in range(3532001, 3532159+1,2):
ndel = 0
for j in range(1,i+1,2):
if i % j == 0: ndel += 1
if ndel > 2: break
if ndel == 2:
k += 1
print(k, i)
Задание 4. Ровно четыре делителя
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [185 311; 185 330], числа, имеющие ровно четыре различных натуральных делителя. Для каждого найденного числа запишите эти четыре делителя в четыре соседних столбца на экране с новой строки. Делители в строке должны следовать в порядке возрастания.
Например, в диапазоне [12; 14] ровно четыре различных натуральных делителя имеет число 14, поэтому для этого диапазона вывод на экране должна содержать следующие значения:
1 2 7 14
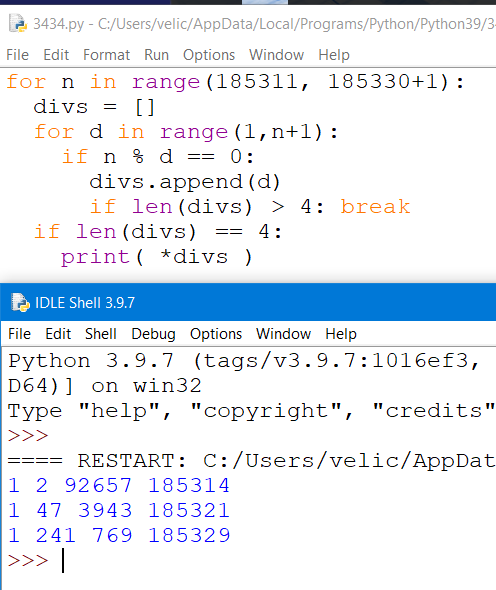
- заданный отрезок [194455; 194500] содержит не много чисел, будем решать перебором
- в качестве оптимизации можно прерывать работу внутреннего цикла, когда найден пятый делитель (число n уже точно не подходит), но это не критично
