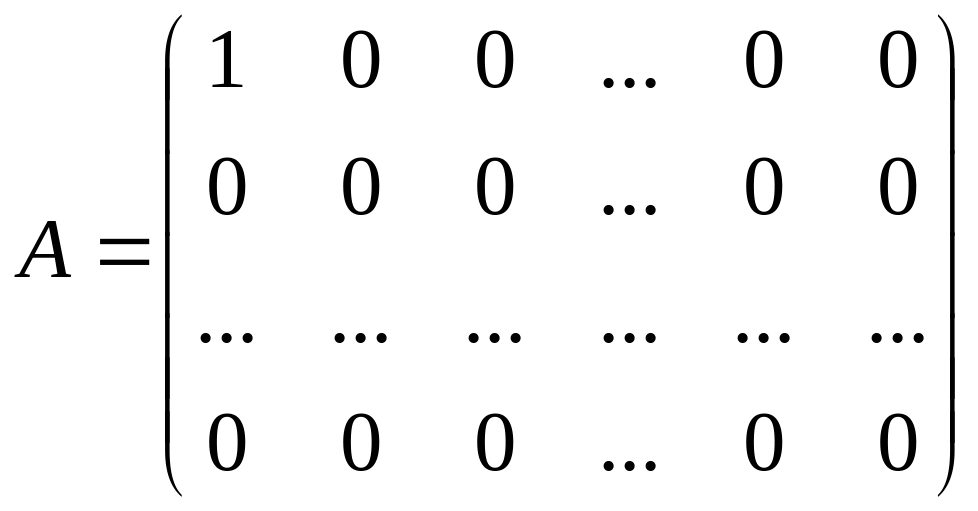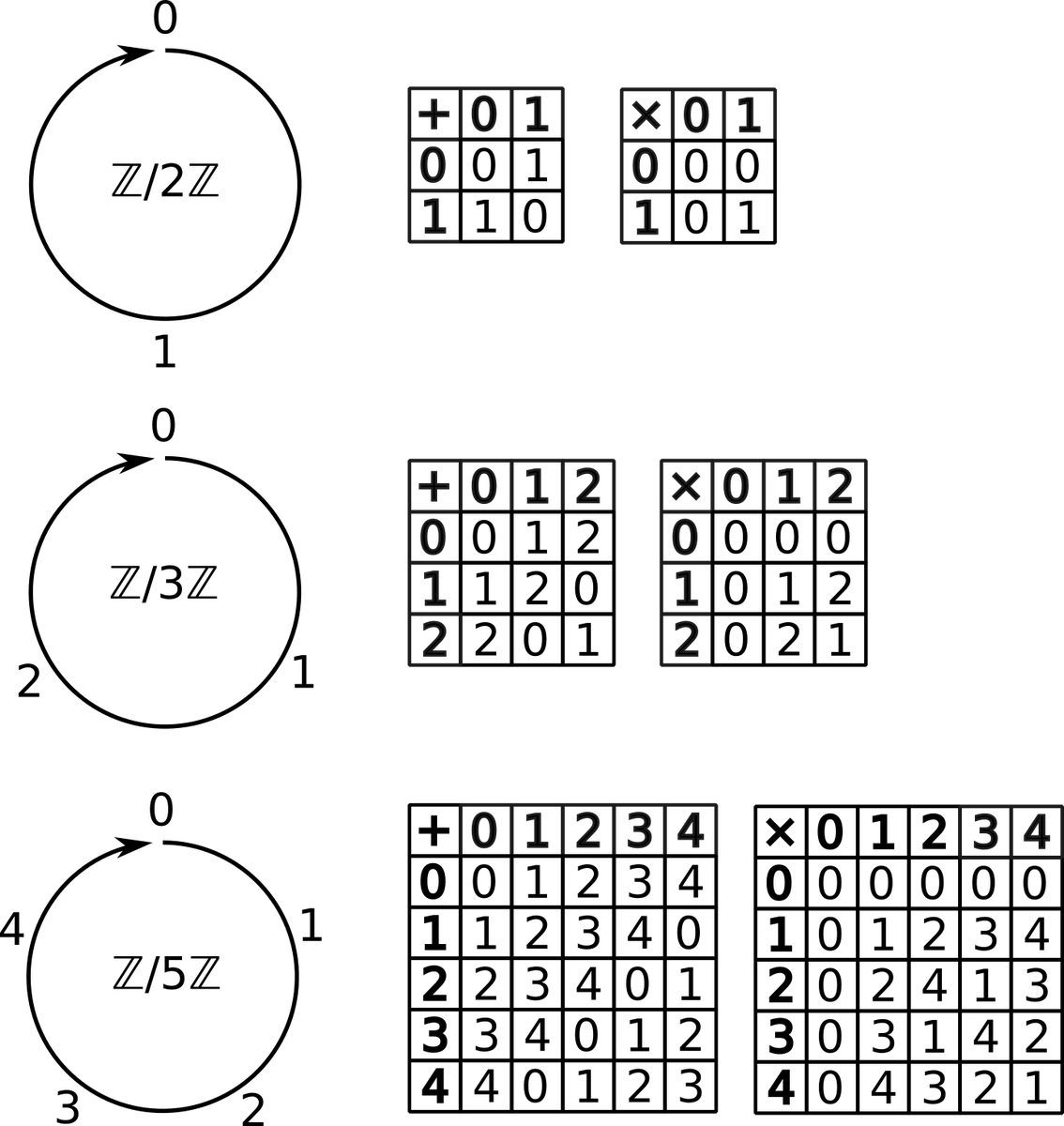Как найти делители нуля кольца

Кольца, тела, поля

Определение 2.5. Кольцом называют алгебру сигнатура которой состоит из двух бинарных и двух нульарных операций, причем для любых выполняются равенства:

1) ;
2) ;
3) ;
4) для каждого существует элемент , такой, что ;
5) ;
6) ;
7) .

Операцию называют сложением кольца, операцию умножением кольца, элемент — нулем кольца, элемент — единицей кольца.

Равенства 1–7, указанные в определении, называют аксиомами кольца. Рассмотрим эти равенства с точки зрения понятия группы и моноида.

Аксиомы кольца 1-4 означают, что алгебра , сигнатура которой состоит только из операций сложения кольца и нуля кольца , является абелевой группой. Эту группу называют аддитивной группой кольца и говорят также, что по сложению кольцо есть коммутативная (абелева) группа.

Аксиомы кольца 5 и 6 показывают, что алгебра , сигнатура которой включает только умножение кольца и единицу кольца , есть моноид. Этот моноид называют мультипликативным моноидом кольца и говорят, что по умножению кольцо есть моноид.

Связь между сложением кольца и умножением кольца устанавливает аксиома 7, согласно которой операция умножения дистрибутивна относительно операции сложения.

Учитывая сказанное выше, отметим, что кольцо — это алгебра с двумя бинарными и двумя нульарными операциями , такая, что:

1) алгебра — коммутативная группа;
2) алгебра — моноид;
3) операция (умножения кольца) дистрибутивна относительно операции (сложения кольца).

Замечание 2.2. В литературе встречается иной состав аксиом кольца, относящихся к умножению. Так, могут отсутствовать аксиома 6 (в кольце нет 1) и аксиома 5 (умножение не ассоциативно). В этом случае выделяют ассоциативные кольца (к аксиомам кольца добавляют требование ассоциативности умножения) и кольца с единицей. В последнем случае добавляются требования ассоциативности умножения и существования единицы.

Определение 2.6. Кольцо называют коммутативным, если его операция умножения коммутативна.

Пример 2.12. а. Алгебра есть коммутативное кольцо. Отметим, что алгебра кольцом не будет, поскольку — коммутативный моноид, но не группа.

б. Рассмотрим алгебру с операцией сложения по модулю и (умножения по модулю ). Последняя аналогична операции сложения по модулю равно остатку от деления на числа . Эта алгебра есть коммутативное кольцо, которое называют кольцом вычетов по модулю .

в. Алгебра — коммутативное кольцо, что следует из свойств пересечения и симметрической разности множеств.

г. Пример некоммутативного кольца дает множество всех квадратных матриц фиксированного порядка с операциями сложения и умножения матриц. Единицей этого кольца является единичная матрица, а нулем — нулевая.

д. Пусть — линейное пространство. Рассмотрим множество всех линейных операторов, действующих в этом пространстве.

Напомним, что суммой двух линейных операторов и называют оператор , такой, что

Произведением линейных операторов и называют линейный оператор , такой, что для любого .

Используя свойства указанных операций над линейными операторами, можно показать, что множество всех линейных операторов, действующих в пространстве , вместе с операциями сложения и умножения операторов образует кольцо. Нулем этого кольца служит нулевой оператор, а единицей — тождественный оператор.

Это кольцо называют кольцом линейных операторов в линейном пространстве .

---

Основные аксиомы и тождества кольца

Аксиомы кольца называют также основными тождествами кольца. Тождество кольца — это равенство, справедливость которого сохраняется при подстановке вместо фигурирующих в нем переменных любых элементов кольца. Основные тождества постулируются, и из них затем могут быть выведены как следствия другие тождества. Рассмотрим некоторые из них.

Напомним, что аддитивная группа кольца коммутативна и в ней определена операция вычитания.

Теорема 2.8. В любом кольце выполняются следующие тождества:

1) ;
2) ;
3) .

Докажем тождество . Запишем для произвольного а:

Итак, . Последнее равенство можно рассматривать как уравнение в аддитивной группе кольца относительно неизвестного элемента . Так как в аддитивной группе любое уравнение вида имеет единственное решение , то . Тождество доказывается аналогично.

Докажем теперь тождество . Имеем

откуда . Точно так же можно доказать, что .

Докажем третью пару тождеств. Рассмотрим первое из них. С учетом доказанного выше имеем

т.е. тождество справедливо. Второе тождество этой пары доказывается аналогично.

Следствие 2.1. В любом кольце справедливо тождество .

Указанное следствие вытекает из второго тождества теоремы 2.8 при и .

Первые два тождества из доказанных в теореме 2.8 выражают свойство, называемое аннулирующим свойством нуля в кольце. Третья же пара тождеств указанной теоремы выражает свойство дистрибутивности операции умножения кольца относительно операции вычитания. Таким образом, производя вычисления в любом кольце, можно раскрывать скобки и менять знаки так же, как и при сложении, вычитании и умножении действительных чисел.

---

Кольца и делители нуля

Ненулевые элементы и кольца называют делителями нуля, если или . Пример кольца с делителем нуля дает любое кольцо вычетов по модулю , если — составное число. В этом случае произведение по модулю любых и , дающих при обычном перемножении число, кратное , будет равно нулю. Например, в кольце вычетов по модулю 6 элементы 2 и 3 являются делителями нуля, поскольку . Другой пример дает кольцо квадратных матриц фиксированного порядка (не меньшего двух). Например, для матриц второго порядка имеем

При отличных от нуля и приведенные матрицы являются делителями нуля.

По умножению кольцо является только моноидом. Поставим вопрос: в каких случаях кольцо по умножению будет группой? Прежде всего заметим, что множество всех элементов кольца, в котором , не может образовывать группы по умножению, так как нуль не может иметь обратного. Действительно, если предположить, что такой элемент существует, то, с одной стороны, , а с другой — , откуда . Это противоречит условию . Таким образом, поставленный выше вопрос можно уточнить так: в каких случаях множество всех ненулевых элементов кольца образует группу по умножению?

Если в кольце имеются делители нуля, то подмножество всех ненулевых элементов кольца не образует группы по умножению уже хотя бы потому, что это подмножество не замкнуто относительно операции умножения, т.е. существуют ненулевые элементы, произведение которых равно нулю.

Кольцо, в котором множество всех ненулевых элементов по умножению образует группу, называют телом, коммутативное тело — полем, а группу ненулевых элементов тела (поля) по умножению — мультипликативной группой этого тела (поля). Согласно определению, поле есть частный случай кольца, в котором операции обладают дополнительными свойствами. Выпишем все свойства, выполнение которых требуется для операций поля. Их еще называют аксиомами поля.

Поле есть алгебра , сигнатура которой состоит из двух бинарных и двух нульарных операций, причем справедливы тождества:

1) ;
2) ;
3) ;
4) для каждого существует элемент , такой, что ;
5) ;
6) ;
7) ;
для каждого , отличного от , существует элемент , такой, что ;
9) .

Пример 2.13. а. Алгебра есть поле, называемое полем рациональных чисел.

б. Алгебры и есть поля, называемые полями действительных и комплексных чисел соответственно.

в. Примером тела, не являющегося полем, может служить алгебра кватернион.

Итак, мы видим, что известным законам сложения и умножения чисел соответствуют аксиомы поля. Занимаясь числовыми расчетами, мы «работаем в полях», а именно имеем дело преимущественно с полями рациональных и вещественных чисел, иногда «переселяемся» в поле комплексных чисел.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

1. Кольцо с единицей

Из определения
кольца не вытекает существование или
отсутствие в нем единицы е. Но, как
было доказано в алгебре на I
курсе, если в кольце К единичный
элемент существует, то только один. В
нулевом кольце

,
состоящем только из одного нуля, элемент
0 одновременно является и единицей,
т.к.

.

Определение.
Нулевое кольцо К, в котором есть
единичный элемент е, называется
кольцом с единицей.

Примерами колец
с единицей являются: кольцо целых чисел
Z; кольцо рациональных
чисел Q; кольцо
действительных чисел R;
кольцо комплексных чисел С; кольцо
матриц n-го порядка над
полями R, Q,
C, единицей этих
колец является матрица

Примерами кольца,
в котором нет единицы, служит кольцо
целых чисел, кратных произвольно
выбранному натуральному числу m>1;
в частности, нет единицы в кольце четных
целых чисел.

Пусть К –
произвольное кольцо с единицей е.
Для всякого отличного от нуля элемента
а
К
справедливы равенства

Отсюда следует,
что

.

Если для элемента
а
К
в кольце К существует обратный
элемент а^-1, то только один.
Элемент е является обратным для
самого себя. Из равенства

следует, что элемент – е также
является обратным для самого себя.
Элемент 0 не имеет обратного элемента,
т.к.

для любого а
К.
Если для а
К
в кольце К существует обратный
элемент а^-1, то а , по
определению делителей элемента кольца,
является делителем e,
т.к.

.

Поэтому можно
принять такое определение.

Определение
2. Элемент а, для которого в
кольце К существует обратный элемент
а^-1, называется обратимым
или делителем единицы.

Пример.
Кольцо Z является
самым простым примером коммутативного
кольца, в котором только 1 и -1 являются
делителями единицы.

Теорема 3. Множество
К^* всех делителей единицы
кольца К является группой по
умножению.

□ Пусть элементы

,
т.е. являются делителями единицы е.
Значит

и

,
а это значит, что а^-1 и ab
тоже являются делителями е, а, значит,
содержатся в К^*, е также
содержится в К^*. Поэтому
К^* является мультипликативной
группой.

Группа К^*
называется группой делителей единичного
элемента, или группой обратимых
элементов кольца К.■

1. Делители нуля. Область целостности

Пусть К –
произвольное кольцо. Для

выполняется равенство

.
Следовательно, каждый элемент кольца
является делителем нуля. Но в теории
колец принимают следующее определение
делителей нуля.

Определение
3. Элементы а
и b
кольца К
называются делителями
нуля, если

и

,
но ab=0,
при этом а
называется левым,
а b
– правым
делителем нуля.

В коммутативных
кольцах очевидно, что понятия левого и
правого делителей нуля совпадают.

Пример 1.
В качестве кольца К рассмотрим
кольцо классов вычетов Z_m,
где m – некоторое составное
целое число, например,

.
Тогда классы вычетов

и

отличные от нулевого класса

,
а их произведение равно нулевому классу:

.
Следовательно, классы

и

являются делителями нуля

в кольце Z_m.

Пример 2.
В кольце R_n
матриц n-го порядка
(
)
с действительными элементами матрицы

и

являются делителями
в кольце R_n.

Определение
4. Коммутативное кольцо с единицей,
в котором нет делителей нуля, называется
областью целостности.

Пример 1.
Очевидно, что всякое числовое кольцо
является областью целостности.

Пример 2.
Областью целостности является всякое
поле Р, т.к.

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пусть — произвольное кольцо.

Определение 1. Элемент называется левым делителем нуля¹⁾, если существует такой , что . Элемент называется правым делителем нуля²⁾, если существует такой , что . Элемент называется делителем нуля³⁾, если он является одновременно левым и правым делителем нуля.

Замечание 1. Если — коммутативное кольцо, то левый делитель нуля является правым делителем нуля и наоборот.

Пример 1. Пусть — кольцо матриц порядка 2. Матрица является делителем нуля, так как

.

Определение 2. Кольцо называется целостным⁴⁾, или областью целостности⁵⁾, если это коммутативное ассоциативное кольцо с единицей отличной от нуля и в нем нет ненулевых делителей нуля.

Пример 2. Кольцо целых чисел — целостное.

Пример 3. Кольцо классов вычетов целостное тогда и только тогда, когда — простое число.

В теории некоммутативных колец в определении области целостности не требуют коммутативности. Кроме того, иногда убирают требование , которое исключает случай . Поэтому определение принимает следующую форму:

Определение 2′. Кольцо называется целостным, или областью целостности, если оно ассоциативное с единицей и в нем нет ненулевых левых или правых делителей нуля.

Предложение 1. Пусть — целостное кольцо, тогда кольцо многочленов от одной переменной — целостное.

В общей алгебре элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0.

Аналогично, элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0.

Элемент, который одновременно является и правым, и левым делителем нуля, называется делителем нуля. Если умножение в кольце коммутативно, то понятия правого и левого делителя совпадают. Элемент кольца, который не является ни правым, ни левым делителем нуля, называется обычным элементом.

0 называется собственным (тривиальным) делителем нуля. Соответственно, элементы, отличные от нуля и являющиеся делителями нуля, называются несобственными (нетривиальными) делителями нуля.

Пример: в кольце элементы 2, 3, 4 — делители нуля.

Ассоциативное коммутативное кольцо с единицей без нетривиальных делителей нуля называется областью целостности.

Ссылки

• А. В. Михалев, А. А. Михалев Введение в алгебру

Источники

• Делитель нуля — Википедия (список авторов)

Представляю вашему вниманию собранные в одну статью заметки к циклу занятий математического кружка, посвящённых элементам теории чисел. Кружковая математика не только про олимпиады, про успеваемость в школе и про хитровыдуманные задачки на смекалку. Это и расширение эрудиции, и небольшие самостоятельные исследования и своеобразные «экскурсии к предгорьям» большой математики.

Статья посвящена модулярным арифметикам, простым для понимания и доступным для экспериментов алгебраическим структурам, которые, тем не менее, способны показать «внутреннее устройство» числовой системы и познакомить с элементами теории чисел и теории колец. Это ни в коем случае не учебник по алгебре, не учебное пособие и не туториал в духе «теория колец за 10 минут». Это неформальное приглашение к исследованию тех, кому любопытно, что же мы имеем в виду, когда говорим слово «число».

Пусть вас не смущает сочетание довольно вольного изложения с серьёзными терминами и уравнениями. Это вполне обычно для математического кружка, в котором, с одной стороны, публика уже достаточно искушена и готова к трудностям, а с другой стороны состоит из неофитов, причём, достаточно молодых. Думаю, и для первокурсника, приступившего к изучению аглебры, эти заметки могут быть небесполезны.

Когда маленькие круче больших

Все мы знаем и любим целые числа. У них есть куча достоинств! С них начинается арифметика и знакомство с нетривиальной математикой. Целые числа можно складывать и вычитать, а также перемножать и решать разнообразные уравнения, которые называются диофантовыми. Правда, математики их, мягко говоря, недолюбливают, потому что общих методов их решения немного и задачи, которые выглядят простыми, на деле оказываются сверхсложными или почти неразрешимыми.

А если использовать не все целые числа сразу, а только их конечное подмножество? Действуя аккуратно, из них можно сооружать небольшие полноценные арифметики. Самые простые из них — модулярные арифметики. Они получаются когда мы от числовой прямой переходим к «числовой окружности», разбивая её на равные части, как на циферблате. Если арифметику целых чисел обозначают ℤ, то для арифметик на циферблате с делениями используется обозначение ℤ/nℤ.

Когда дело касается исчисления времени, мы пользуемся именно такими арифметиками, считая минуты (ℤ/60ℤ), часы (ℤ/24ℤ), месяцы (ℤ/12ℤ) и дни недели (ℤ/7ℤ), градусы для измерения углов (ℤ/360ℤ). Цифры, которые мы используем в позиционной системе счисления тоже образуют конечную арифметику ℤ/10ℤ. А компьютеры, логики и грамотные IT-шники используют двоичное счисление, основанное на самой маленькой нетривиальной арифметике с двумя элементами ℤ/2ℤ.

Разумно предположить, что маленькие конечные арифметики окажутся слабее «большой» ℤ с бесконечным числом элементов. Например, в ℤ/10ℤ нет моего любимого числа 13. Однако, кое в чём они могут быть и сильнее.

Во-первых, таких арифметик много — столько же, сколько натуральных чисел, и каждая из них имеет свои особенности, делающие её непохожей на остальные. Во-вторых, конечные арифметики содержат конечное число элементов, а значит, задачи в них можно решать простым перебором. В-третьих, некоторые диофантовы уравнения, которые сложно или невозможно решить в ℤ, могут иметь решения в конечных арифметиках.

Вот несколько примеров для разогрева.

Отрицательные числа и формальные дроби

В арифметике ℤ/5ℤ из пяти элементов у каждого элемента есть противоположный, то есть такой, что в сумме они дают ноль. То есть, в этом смысле оно включает в себя и «отрицательные числа»:

Более того, в этой системе у любого корректного линейного уравнения , есть решение, которое записывается формальной дробью . Таким образом, оно содержит в себе все возможные корректные формальные дроби, не существующие в целых числах:

Большая теорема Ферма

Большая теорема Ферма, гласит, что в ℤ уравнение не имеет нетривиальных решений при. В то же самое время, в модулярных арифметиках, это уравнение решается. Например, для ℤ/2ℤ, простым перебором легко проверить, что решения есть при Наконец, доказана теорема Шу́ра, утверждающая, что для любого натуральногонайдется натуральное число , такое, что для простого  уравнение Ферма решается в ℤ/mℤ.

Корень из минус единицы

Число , решающее уравнение , не существует не только в ℤ, но и в вещественных числах. Однако, это уравнение решается, например, в ℤ/5ℤ, потому что . И вообще, это уравнение имеет решения в арифметиках ℤ/mℤ, где m кратно 2, 5, 13, 17, 29 и т. д. Только не надо думать что 2 это некая мнимая единица в ℤ/5ℤ, это рядовое число.

Автоморфные числа

А вот ещё один пример числа, не существующего ни в ℤ, ни в ℝ. Это решение уравнения , отличное от 0 и 1. Такие числа, например, существуют в арифметиках ℤ/10ℤ, ℤ/100ℤ, ℤ/1000ℤ и т.д. Смотрите сами:

Золотое сечение

Уравнение имеет два иррациональных решения, которые связаны с числами Фибоначчи. Одно из них, положительное, называется золотым сечением и обозначается . В ℤ таких чисел нет, а в ℝ, как известно, . Это уравнение решается во всех модулярных арифметиках, содержащих (арифметиках ℤ/mℤ, в которых ). Самая простая из них — ℤ/11ℤ, в которой . Во всех этих арифметиках можно напрямую использовать знаменитую формулу Бине, которая позволяет в конечной форме вычислить k-ое число Фибоначчи. Впрочем, о том, почему использовать формулу Бине можно там, где это уравнение не решается (как в ℤ, например), стоит поговорить отдельно, но для этого нужно хоть немного познакомиться с тем, что такое алгебраическая структура под названием кольцо

Может возникнуть вопрос: а почему я называю конечные арифметики арифметиками? Достаточно ли возможности складывать и умножать для того, чтобы носить это гордое имя? Как в них обстоят дела с делимостью, с решением уравнений, с простыми числами, с основной теоремой арифметики, наконец? Сразу скажу, тут всё непросто. Но ведь тем и интереснее! К тому же, как известно, распределение простых чисел и в привычной нам арифметике целых чисел представляет многовековую загадку.

Звёздочки и колечки

У большинства из нас с вами на руках по пять пальцев. Так что для экспериментов и препарирования мы будем использовать ℤ/5ℤ и ℤ/10ℤ, которые образуют одна и две наши руки. Благо, они у нас всегда есть перед глазами.

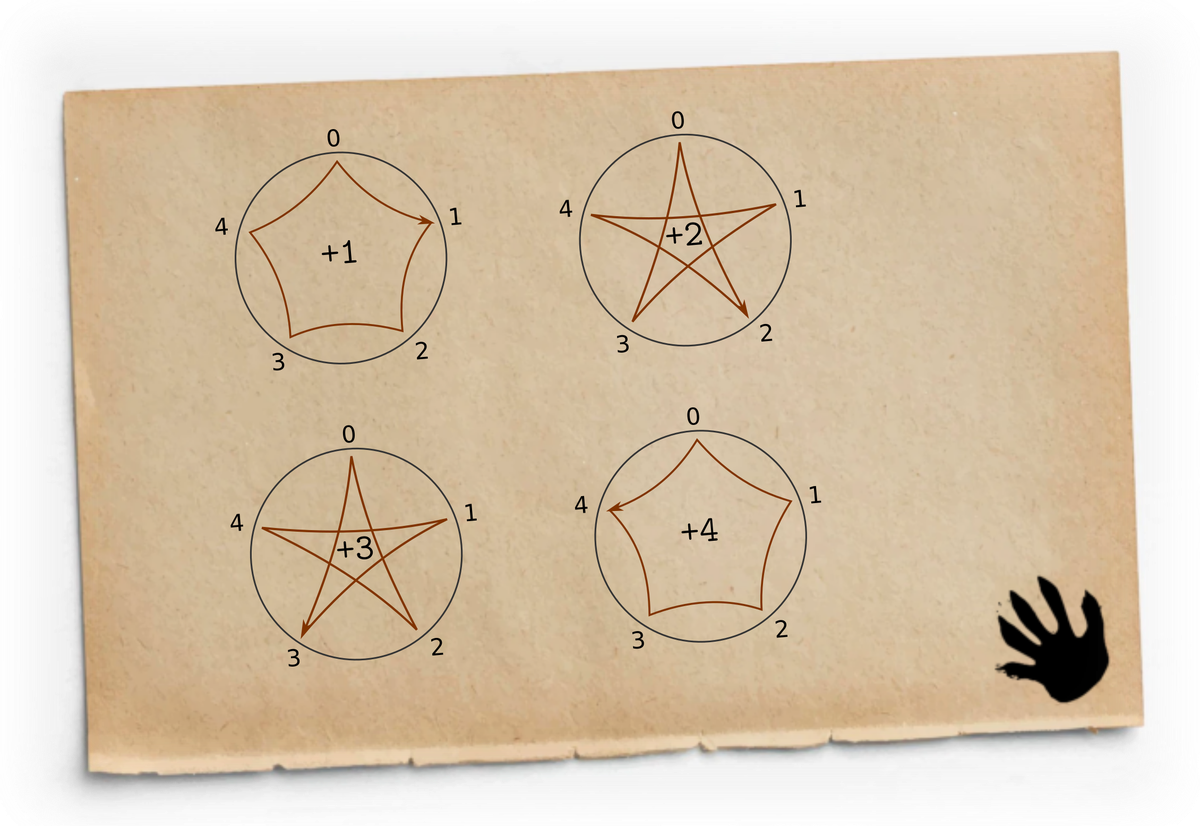
Начнём мы свой анализ с того, что станем сосредоточенно возить пальцем по кругу. Нарисуем циферблат с пятью делениями и пройдёмся по нему, делая шаги по одному, два, три и четыре деления:

Мы получили симпатичные «звёздочки», которые демонстрируют построение таблицы умножения в ℤ/5ℤ. Каждая из этих «звёздочек» соответствует своему ряду в таблице умножения.

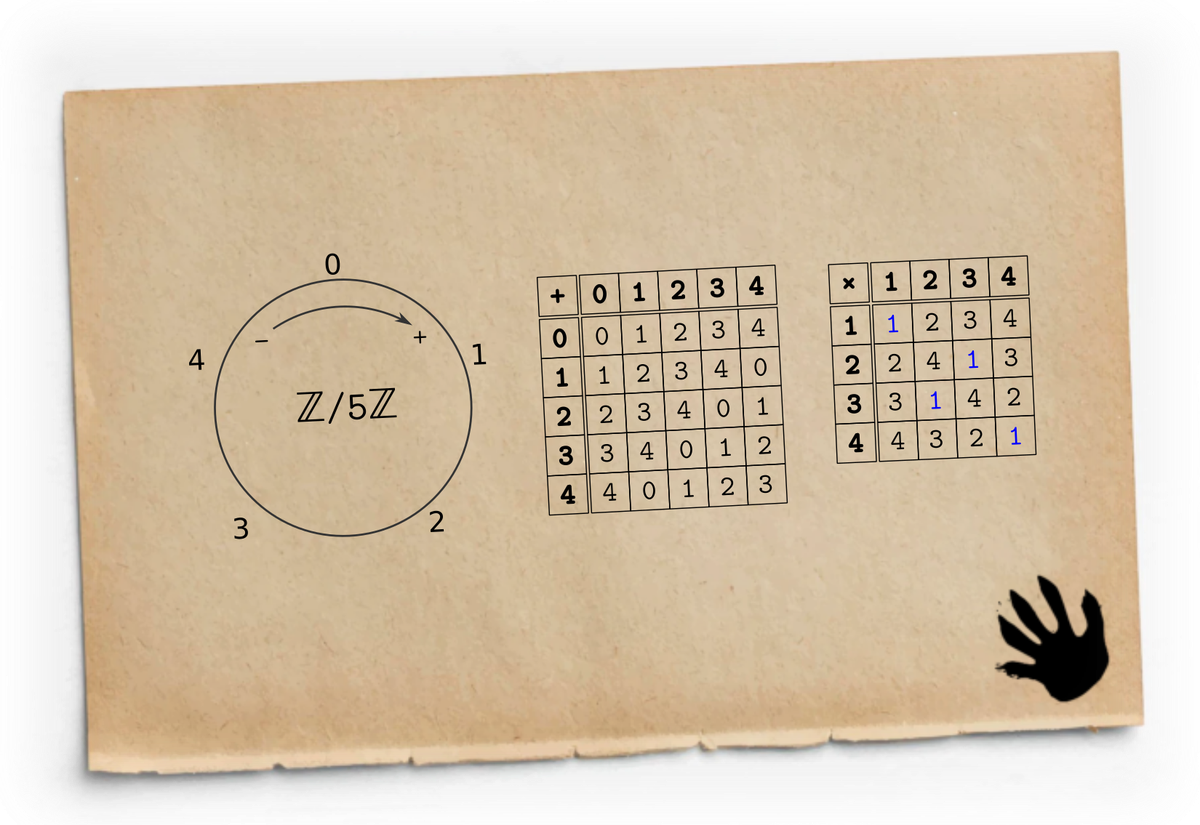
Таблица сложения в этой арифметике устроена очень просто: каждая строка получается циклическим сдвигом предыдущей. Это соответствует идее сложения, как сдвига числовой оси, но поскольку ось у нас зациклена, то роль сложения с числом на циферблате выполняет поворот всего циферблата на соответствующее числу количество делений.

В ℤ/5ℤ верно, что 1 + 4 = 2 + 3 = 0, а значит пары чисел (1, 4) и (2, 3), это пары противоположных друг другу чисел. Это же показывают и «звёздочки»: умножение на 1 и умножение на 4 выглядят одинаково, но производятся в противоположную сторону. То же верно и для умножения на 2 и на 3.

Противоположными положительным числам в целых числах являются отрицательные. Но в нашей конечной арифметике отрицательных чисел нет, а их роль берут на себя обыкновенные числа. Поэтому мы не будем использовать термин «отрицательные числа» применительно к конечным арифметикам, поскольку каждое число одновременно является и положительным и отрицательным. Например, раз 3 + 2 = 0, то −3 = 2, и в тоже время −2 = 3. Лучше говорить, что 2 и 3 противоположны друг другу.

Из симметрии, которую образуют противоположные числа, следует симметрия таблицы умножения относительно диагонали, идущей из левого нижнего угла в правый верхний. А то что эта таблица симметрична относительно другой диагонали, идущей от левого верхнего угла до правого нижнего, значит, что для умножения выполняется перестановочный закон. Алгебраисты говорят, что в таком случае «умножение коммутативно». Кроме того, для умножения выполняется и сочетательный закон: . Это свойство у алгебраистов называется ассоциативностью, оно позволяет не писать лишних скобок. Кроме того, для умножения в ℤ/5ℤ выполняется распределительный закон, который алгебраисты зовут дистрибутивностью.

В отличие от привычной нам арифметики, геометрически продемонстрировать эти два закона для конечной арифметики не так просто. Но поскольку она конечна, то можно просто перебрать все сочетания из трёх элементов и убедиться в их справедливости. Сейчас поверьте мне, или проверьте сами, но все эти законы выполняются.

А ещё обратите внимание на то, что все «звёздочки» в ℤ/5ℤ честно проходят через все числа. Это интересно: многократным вычитанием любого числа из любого можно попасть в ноль, а это значит, что в нашем кольце любое число делится на любое число. Но об этом мы подробнее поговорим позже.

Перед тем, как продолжать, надо поговорить про правильные имена и названия. У нас тут не учебник, а занимательные заметки, однако термины — вещь нужная и точность в них небесполезна. С этого момента я буду избегать слова «арифметика», а вместо этого стану использовать более точный математический термин кольцо, который придумал Рихард Дедекинд, а в широкий обиход ввел великий Давид Гильберт.

Кольцом в математике называются числовые системы, в которых определена операция сложения с перестановочным и сочетательным законами, а также операция умножения с сочетательным и распределительным законами.

Все эти законы те же самые, что мы проходили в школе. Кроме того, все элементы кольца можно разбить на пары противоположных друг другу так, что числа в этих парах в сумме дают ноль.

Легко убедиться, что числовое кольцо образуют целые числа. А любимые нами натуральные — не образуют, поскольку среди них нет противоположных (отрицательных) чисел. Рациональные и вещественные числа тоже образуют кольца. Исследованием свойств этих и куда более сложных объектов занимается весьма содержательный раздел алгебры: теория колец.

Так что мы теперь можем сказать, что числа на круглом циферблате с пятью делениями образуют кольцо ℤ/5ℤ с циклическим сдвигом в качестве операции сложения и многократным повторением сдвига в качестве умножения. И вообще, циферблаты с любым числом одинаковых делений и описанными выше операциями, образуют кольца. Такие арифметики называются кольцами вычетов или модулярными арифметиками. Кроме них можно строить и другие конечные кольца, но этим мы пока заниматься не будем. Хватит с нас пока и алгебры «на пальцах».

Сейчас мы не просто балуемся с отвлечёнными математическими конструкциями, мы следуем путём Леонарда Эйлера, заложившего основы теории делимости, Фридриха Гаусса, детально исследовавшего модулярные арифметики, а также Рихарда Дедекинда, Давида Гильберта, Эмми Нёттер и других замечательных математиков. Результаты теории вычетов и теории колец сейчас лежат в основе алгебраической геометрии и используются для решения ряда прикладных задач геометрии, комбинаторики, криптографии и т.д.

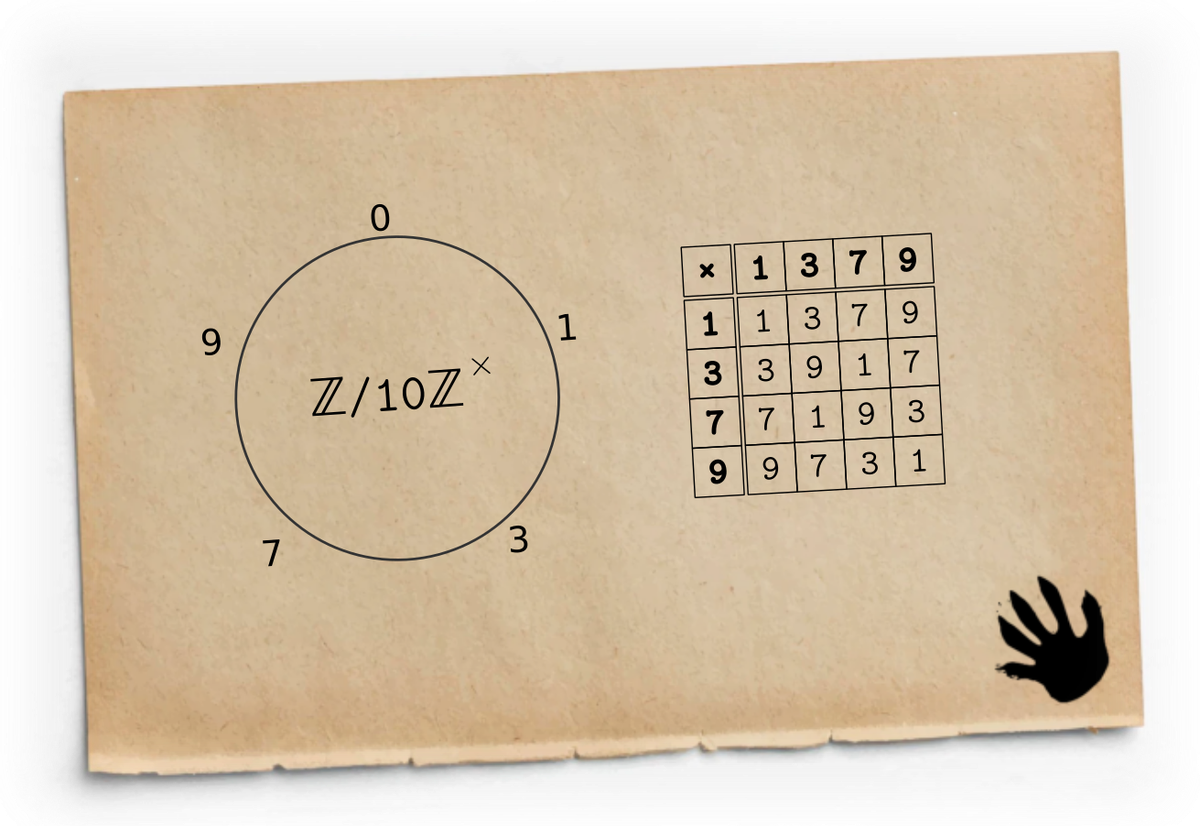
Ну что, посмотрим что у нас делается в кольце ℤ/10ℤ? Опять сначала нарисуем звёздочки:

Тут у нас получился целый цветник разнообразных звёздочек! Симметрия между противоположными числами тут тоже очевидна: все числа делятся на пары противоположных, в сумме дающих 0: (1, 9), (2, 8), (3, 7), (4, 6), (5, 5). Число 5 особенное — оно противоположно самому себе, как число ноль. Ни в ℤ, ни в ℤ/5ℤ таких чисел, кроме нуля, нет.

Таблица сложения в этой арифметике устроена также как и в ℤ/5ℤ: каждая строка получается циклическим сдвигом предыдущей, так что рисовать мы её не будем, а сразу перейдём к таблице умножения:

Эта таблица нам уже знакома, она заполнена младшими разрядами привычной таблицы Пифагора. Есть в ней несколько по-настоящему занятных особенностей. Во-первых, в ней появились нули, как результат перемножения чётных чисел с пятёркой. Во-вторых, есть строчки, в которых присутствуют все числа, а есть те, в которых наблюдаются только чётные. В отличие от ℤ/5ℤ, некоторые «звёздочки» проходят не по всем числам, а проскакивают часть из них. Это значит, что в этом кольце некоторые числа могут не делиться на другие, а это значит, что в кольце ℤ/10ℤ имеет смысл рассуждать о простых и составных числах, тогда как в ℤ/5ℤ такого разделения чисел нет.

Заучивать полученные таблицы сложения и умножения не нужно, потому что выбранные нами кольца очень удобны для пятипалых математиков. Чтобы вычислить сумму или произведение двух чисел в ℤ/10ℤ достаточно вычислить его в целых числах и оставить только последнюю цифру. Например, 6×8 + 4 = 52 в ℤ и 6×8 + 4 = 2 в ℤ/10ℤ. В кольце ℤ/5ℤ всë то же самое, как и в ℤ/10ℤ, только если ответ вышел больше пяти, нужно вычесть из него пятерку. Таким образом 6 = 1, 7 = 2, 8 = 3 и 9 = 4.

Задания для дальнейших исследований:

• Постройте звёздочки и таблицу умножения для циферблата обычных часов, то есть, для кольца ℤ/12ℤ.

• Поищите в кольце ℤ/12ℤ интересные элементы, например, квадратные корни чисел.

• Чему равны сумма и произведение всех элементов конечного кольца?

Делители нуля

Главная особенность, которая бросается в глаза: в таблице умножения для ℤ/10ℤ есть нули. Это интересно! Раз 2×5 = 0, то это значит, что произведение двух ненулевых чисел смогло стать нулевым. Получается, что в ℤ/10ℤ все чётные числа и пятёрки являются делителями нуля. Формально значит, можно записать что 2 = 0/5.

Целых чисел очень и очень много, но среди них нет ни одного делителя нуля, то есть такого числа x, которое могло бы быть решением уравнения: Школьникам, заучивающим таблицу умножения, делители нуля только на руку: чем больше круглых чисел в ней окажется, тем проще учить. Но с точки зрения алгебры, это, прямо скажем, неприятность. Она означает, что решать уравнения типа не так просто, как в целых числах, поскольку никаких гарантий, что какое-то из множителей равно нулю нет. Вместо этого, мы имеем целых 2×4 + 2 = 10 вариантов, которые нужно проанализировать, чтобы получить верное равенство.

А вот в кольце ℤ/5ℤ такого безобразия нет, так что в этом смысле ℤ/5ℤ ближе к целым числам, чем ℤ/10ℤ. Кольца, без делителей нуля называются областями целостности. Самый привычный для нас пример области целостности — целые числа (отсюда и название).

Кто прячется в кольце?

Что ещё интересного можно сказать про делители нуля в ℤ/10ℤ? Давайте выпишем их все: это числа 2, 4, 6, 8 и 5. Вот как выглядят «звездочки» на циферблате для этих чисел:

А теперь сравним их с устройством кольца ℤ/5ℤ:

Смотрите-ка делители нуля образуют внутри ℤ/10ℤ полноценное кольцо идентичное ℤ/5ℤ. А «звездочка» для числа 5 в ℤ/10ℤ соответствует кольцу всего с двумя делениями ℤ/2ℤ.

Подкольца и идеалы

Кольцо ℤ/10ℤ, действительно, содержит внутри себя два полноценных кольца с элементами и . Мы обозначим их, соответственно, 2ℤ/10ℤ и 5ℤ/10ℤ. Причём, если , опять же, формально, «сократить» числа в обозначении колец, то 2ℤ/10ℤ ≃ ℤ/5ℤ, а 5ℤ/10ℤ ≃ ℤ/2ℤ. Это подобие мы и наблюдали на звёздочках. Обозначение колец имеет такой смысл, чтобы подобное сокращение стало возможным. О смысле знака мы поговорим позже.

Давайте обратим внимание вот на что. Если оперировать только чётными числами и нулём, то любая их сумма будет чётной, так же как и любое их произведение. Это же относится и к числам, кратным пяти: сложение и перемножение этих чисел в результате опять производят числа, кратные пяти. Это свойство множеств называется замкнутостью относительно той или иной операции.

Тут важно заметить, что под операциями сложения и умножения в этих кольцах понимаются операции из ℤ/10ℤ. Это тонкий момент. Сумма чисел 2 и 6 будет разной в разных кольцах: например, в кольце ℤ/5ℤ, где 6 = 5 + 1 = 1, их сумма равна 3, то есть, перестаёт быть чётной. А в ℤ/10ℤ или в ℤ чётность при сложении чётных чисел сохраняется.

Итак, в кольце ℤ/10ℤ обнаружились два подкольца, то есть, две числовые системы, замкнутые относительно сложения и умножения, принятых в кольце. Более того, можно заметить, что если умножить любое число из ℤ/10ℤ на любой элемент из подкольца 2ℤ/10ℤ, то результат обязательно окажется в этом подкольце. Действительно, любое нечётное число, умноженное на чётное даст чётный результат, и оказавшись таким образом внутри подкольца, из него ему уже не выбраться ни сложением, ни умножением с элементами подкольца. То же самое верно и для подкольца 5ℤ/10ℤ: какое бы число мы не умножили на 5, результат будет либо пятёркой, либо нулём.

Подкольца, обладающие такими поглощающими свойствами, называются идеалами и играют очень важную роль в теории колец. Первым понятие идеальных чисел ввел в середине XIX века немецкий алгебраист Эрнст Куммер. Он обнаружил их и описал их замечательные свойства, борясь с Великой теоремой Ферма. За работы над идеальными числами он получил Большой приз Парижской Академии наук. Позже, ученик Гаусса, Дедекинд, которому мы обязаны появлению теории колец, обобщил идеальные числа до идеалов в произвольных кольцах и с тех пор они стали одним из важнейших понятий в алгебре.

А есть ли идеалы в ℤ/5ℤ? Есть, но они не интересные. Один из них состоит из одного только нуля: действительно, сумма и произведение нулей дает только нули, так же как и произведение нуля и любого элемента кольца. А второй идеал — это всё кольцо целиком. Такие идеалы обязаны быть в любом кольце, и никакой информации о кольцах они не несут.

Можно показать, что количество элементов в нетривиальном подкольце обязательно должно быть делителем количества элементов в кольце. Поскольку 10 = 2×5, то кольцо с десятью элементами способно иметь два подкольца: с пятью и двумя элементами. Они же оказались идеалами, что, в общем, не обязательно. В тоже время, число 5 — простое. Поэтому ℤ/5ℤ тоже будет простым кольцом, оно не может иметь нетривиальных подколец, а значит, и идеалов.

Нетривиальные идеалы выявляют структуру колец, наподобие того, как делители числа дают информацию о числе. У них даже есть своя классификация, но мы туда пока не полезем.

В привычном нам кольце целых чисел ℤ тоже есть идеалы. Это все подмножества чисел, кратных какому-то одному. Так, все чётные числа образуют идеал, равно как и все числа, кратные трём или десяти и т.д. Для них принято обозначение nℤ, показывающее, что это множество можно получить умножением каждого целого числа на n. Например, множество чисел, кратных семи {…, −35, −28, −14, −7, 0, 7, 14, 28, 35, …} является идеалом 7ℤ в ℤ.

Вы можете сами проверить, что такие подмножества образуют подкольца, и более того, эти множества обладают свойствами идеалов и способны «поглощать» любые другие числа посредством умножения на любой свой элемент.

Кстати, в обозначении кольца вычетов ℤ/5ℤ, выражение «5ℤ» − это обозначение идеала из кольца ℤ.

Для тех, кому стало любопытно, есть задание:

• Поищите делители нуля на циферблате часов, то есть в кольце ℤ/12ℤ, и выпишите его идеалы.

• На примере ℤ/12ℤ, убедитесь в ещё одном «идеальном» свойстве идеалов: пересечение идеалов тоже является идеалом.

Делители единицы

Что бы ещё такого поделить! Ноль мы уже делили и получилось интересно. Пора выяснить на что может делиться единица! Для этого обратим наше внимание на единицы в таблицах умножения. Они выделены синим цветом.

Среди целых чисел есть только два числа, которые в произведении дают единицу, это 1 и −1. В ℤ/10ℤ единицу представить в виде произведения, можно тремя разными способами (с точностью до коммутативности):

Эти числа: 1, 3, 7, 9 в ℤ/10ℤ так и называются делители единицы и они же являются обратимыми элементами кольца. Обратимые элементы способны быть решениями уравнения . В нашем случае, уравнение решается только если если или равны 1, 3, 7 или 9. При этом числа 3 и 7 являются взаимно обратными, а 9 — обратно самому себе:

Тут полезно вспомнить, что у всякого элемента в кольце имеется противоположный элемент, такой, что в сумме они дают 0. Причём 1 противоположно 9, а 3 противоположно 7. Это значит, что мы можем формально написать, что 9 = −1 и 7 = −3. Таким образом, делителями единицы в ℤ/10ℤ будут ±1 и ±3. А единицу можно получить такими тремя способами:

Первый и последний способы имеются и в кольце целых чисел, а вот −3×3 — это уже особенность ℤ/10ℤ. Теперь, кстати, становится понятно, что значит, что число 9 обратно самому себе. Если записать его как −1 то выражение 1/9 = 9 запишется как 1/(−1) = −1. Это равенство верно для всех колец.

Ещё вот на что следует обратить внимание: строки и столбцы для делителей единицы содержат все ненулевые элементы кольца. Помните, «звездочки» для 1,3,7 и 9 честно проходили по всем делениям циферблата без пропусков. Это фундаментальное свойство делителей единицы. Оно означает, что любое число в кольце можно представить как произведение какого-либо элемента и делителя единицы, а значит, линейные уравнения вида  решаются для любого из ℤ/10ℤ.

А что в ℤ/5ℤ? Тут единицы встречаются в каждом ряду, так что в ℤ/5ℤ все без иключения ненулевые элементы являются делителями единицы и обратимыми элементами. Это, в свою очередь, означает, что в ℤ/5ℤ можно решить любое линейное уравнение. И если в ℤ/10ℤ. уравнение  ожидаемо решается только для чётной правой части, в ℤ/5ℤ нет проблем решить уравнение , потому что — это обратимый элемент, а значит, формально, .

Области целостности, в которых все элементы обратимы (а, значит все линейные уравнения имеют решения), называются полями. Как видим, ℤ/5ℤ хоть и маленькая арифметика, но является полем. Самое маленькое поле это кольцо из двух элементов ℤ/2ℤ.

В 1905 году Джозеф Веддербёрн доказал что, все конечные области целостности являются полями. То есть, если в таблице умножения для конечного кольца нет нетривиальных нулей, то все его элементы обратимы и все линейные уравнения разрешимы.

Арифметика на бесконечном множестве целых чисел, хоть и является областью целостности, но поле не образует. Наименьшее поле с бесконечным числом элементов формируют рациональные числа. В рациональных числах можно решить любое корректное линейное уравнение (если не делить на ноль) и не стоит вопрос о делимости чисел: все делятся на всех.

Среди модулярных арифметик те, которые образованы простыми модулями, такие как ℤ/2ℤ, ℤ/3ℤ, ℤ/5ℤ и т.д. являются полями. В то время, как кольца вычетов по составных модулям: ℤ/6ℤ, ℤ/8ℤ, ℤ/10ℤ и т.д. являются просто коммутативными кольцами.

На что ещё похожи делители едницы?

Давайте ещё раз обратим наше внимание на множество делителей единицы в ℤ/10ℤ — Не образуют ли и оно идеал? Не похоже. Это даже не подкольцо, потому что сумма любых двух элементов из него выходит за пределы множества. Но зато произведение любых этих чисел замкнуто внутри множества. Посмотрите на таблицу умножения для них (напомню, что умножаются все эти числа в ℤ/10ℤ, то есть 3×7 = 1, как в большой таблице):

Эта подсистема, образованная делителями единицы, называется мультипликативной группой обратимых элементов кольца ℤ/10ℤ. И вот что замечательно: с точностью до замены её таблица умножения эквивалентна таблице умножения из ℤ/5ℤ!

В поле ℤ/5ℤ все элементы делят единицу, значит мультипликативная группа обратимых элементов совпадает с группой умножения в этом кольце, вернее, в поле. Чтобы лучше понять, как она устроена, построим несложный граф, в котором узлы будут соответствовать элементам группы, а стрелки разного цвета — умножению на неединичные элементы:

Если вы построете такой же граф для таблицы умножения в ℤ/5ℤ, то убедитесь, что эти две алгебраические системы одинаковы.

Ну, и, как обчно, для тех, кому стало интересно, есть задание:

• Выпишите для циферблате часов, то есть для кольца ℤ/12ℤ, делители единицы и таблицу умножения для мультипликативной группы обратимых элементов.

• Постройте граф Кэйли для мультипликативной группы обратимых элементов ℤ/12ℤ.

Приступаем к делёжке

Как известно, если попытаться разделить пять яблок на двоих енотов, появится остаток из одного яблока из-за которого может случиться драка. Пятый класс, вторая четверть. А как обстоят дела с делимостью в других кольцах?

Разговор о делимости надо сразу начать с того, что появившееся понятие поля проводит черту между алгебраическими системами, в которых вопрос делимости актуален, и теми, где он теряет смысл.

Мы привыкли к тому, что натуральные и целые числа бывают чётными и нечётными, круглыми (кратными 10) и нет, составными и простыми. В этих числах мы решаем задачи на поиск наибольшего общего делителя и наименьшего общего кратного, используем алгоритм Евклида и так к этому привыкли, что уже подчас не замечаем, что в рациональных числах всего этого нет. При том, что в целых числителях и натуральных знаменателях дробей вопросы делимости актуальны, сами дроби делятся друг на друга в любых сочетаниях и без всяких проблем. И связано это с тем, что любое ненулевое рациональное число обратимо и входит в мультипликативную группу обратимых элементов, а значит, с точки зрения алгебры, рациональные числа образуют уже не кольцо, а поле.

На школьном пути постижения алгебраических структур мы приучаемся к мысли о том, что расширение наших возможностей связано с пополнением привычной числовой системы чем-то новым. От натуральных чисел мы переходим к целым, добавляя отрицательные (противоположные) числа и это даёт нам возможность вычитать любые числа друг из друга. Далее от целых переходим к рациональным, добавляя пары чисел, называемые дробями, которые позволяют формально делить любые числа на любые ненулевые. От рациональных переходим к вещественным, пополняя их корнями неразрешимых рациональных уравнений и трансцендентными величинами, а на самом деле, просто разрешая существовать пределам всех мыслимых сходящихся последовательностей. И, наконец, добавляя мнимую единицу, то есть корень ещё одного неразрешимого вещественного уравнения, переходим к комплексным числам, алгебраически замыкая числовую систему, и позволяя возводить любые числа в любые степени.

Однако, в самом начале этого пути, можно было получить полноценное поле не пополняя систему натуральных чисел, а напротив, сокращая её, и переходя в конечную арифметику вычетов. Так, полем может быть любое конечное кольцо без делителей нуля, а значит, все кольца вычетов ℤ/pℤ с простым p, позволяют не только складывать, вычитать и перемножать любые входящие в них числа, но и находить их отношения (решать любые корректные линейные уравнения) а так же возводить любые числа в любые доступные степени. И хотя сами эти системы не являются алгебраически замкнутыми (в них нельзя выразить решение произвольного алгебраического уравнения), в начале XIX века французский математик Эварист Галуа показал, каким образом их можно пополнять, оставляя полями. А почти век спустя, немецкий математик Курт Гензель показал способ перейти от них к комплексным числам минуя вещественные, через p-адические числа.

Так что наши игрушечные поля вовсе не игрушки, а способны стать мощным инструментом в теории чисел и алгебре. Но, повторю, в полях любые вопросы делимости «уже всё». Тривиальны. Таким образом, мы заключаем, что в ℤ/5ℤ нет не только простых чисел, но даже разделение чисел на чётные и нечётные не имеет смысла. Выходит, теорию делимости на пяти пальцах толком не объяснить. А на десяти?

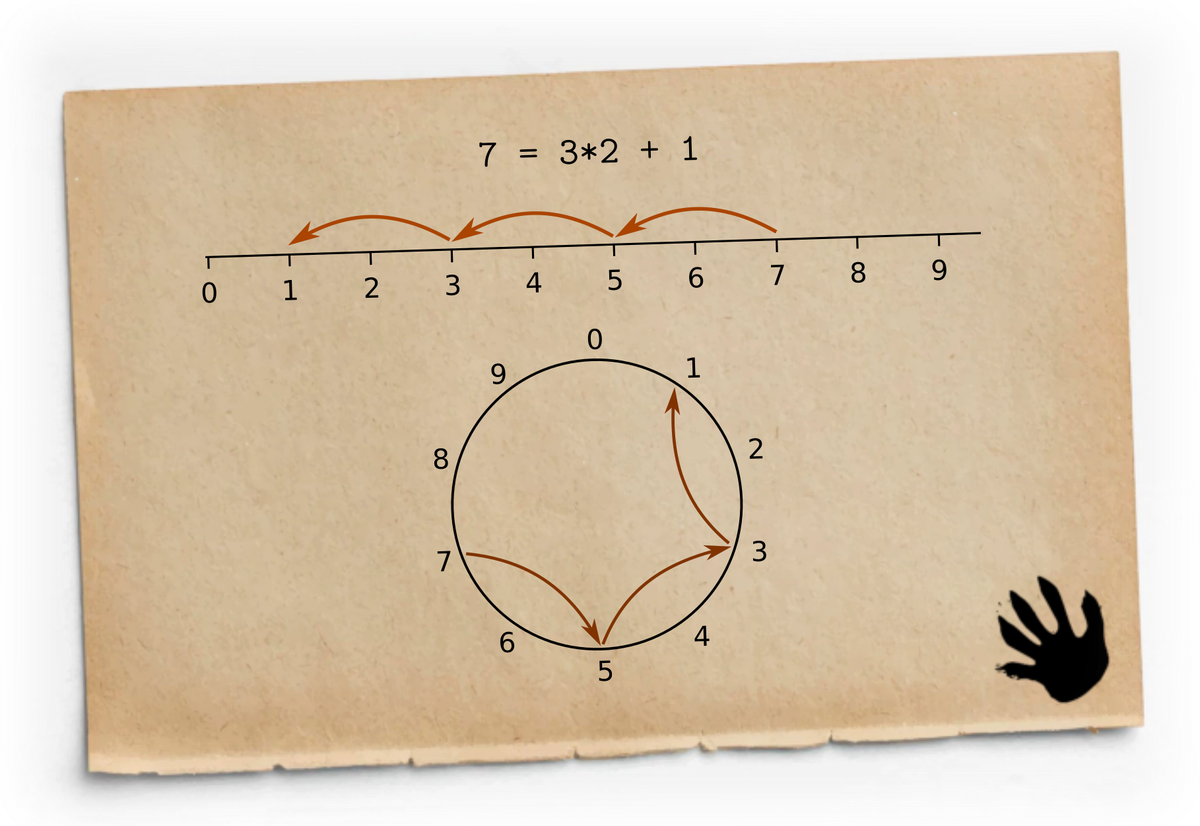
В кольце ℤ/10ℤ есть шанс. Давайте начнём наши соображения со знаменитого алгоритма Евклида, который мы используем в школе для того, чтобы выявлять общие делители и взаимно простые числа.

В целых и натуральных числах, желая выяснить остаток от деления одного числа на другое, мы можем вычитать из большего числа меньшее, до тех пор, пока не получим число, не превышающее делитель.

Давайте выясним с помощью вычитания, как делится, например, 7 на 2 в целых числах и в кольце ℤ/10ℤ:

Можем сказать, что у нас всё получилось 7 = 3×2 + 1 в обеих арифметиках. Вроде бы, всё в порядке. И вообще, если начиная с единицы построить в ℤ/10ℤ звёздочку с шагом 2, то мы получим все числа, дающие в остатке от деления на 2 единицу, то есть, нечётные числа: , а если начнём с нуля, — то все чётные:. Полученные нами подмножества не пересекаются, а их объединение равно всему множеству чисел. В таких случаях говорят, что всё множество удалось разбить на смежные классы.

Хорошо, а что с делимостью на 3? Точно таким же способом, с помощью многократного вычитания, мы можем выяснить, что остаток от деления 7 на 3 тоже равен 1. И вообще:

Получается, что и тут никаких проблем нет?

Но, всё-таки, они есть. Вычитание это операция обратная сложению, значит с помощью сложения мы тоже должны получить множества чисел, имеющих одинаковый остаток. Однако, как мы знаем, тройка обратимый элемент в ℤ/10ℤ, и её «звёздочка» проходит все числа без исключения, с какого бы числа мы ни начали обход. Значит ли это, что все числа в ℤ/10ℤ делятся на 3 без остатка? А как же наши вычисления с помощью вычитания и нормы? Дело в том, что они, в присутствии делителей единицы, могут дать некорректный результат. Смотрите, мы получили, например, вычитанием что 4 = 1×3 + 1. Но мы знаем, что 1 = 3×7, а значит 4 = 1×3 +3×7 = 3×8, то есть 4 можно поделить на 3 без остатка, получив 8. Это противоречие говорит не только о том, что выбранный нами метод вычисления остатка от деления некорректен, но и что разложение числа в форме , где в каком-то смысле меньше , единственно. Или, иными словами, разбить на смежные классы по остаткам от деления 3 множество чисел в ℤ/10ℤ не получится.

Попытка с помощью звёздочки выделить числа, кратные четырём тоже обречена на провал: ими окажутся не только все чётные числа, включая 6 и 2, но при этом любое число будет одновременно иметь два разложения: либо

В то же время, с делимостью на 5 у нас снова не будет никаких проблем! Все числа будут иметь единственное разложение и внятный корректный остаток. Убедитесь в этом сами с помощью «звёздочек».

Что на что делится, а что на что нет?

Подводим итог. В кольце ℤ/10ℤ можно корректно определить делимость только на 2 и на 5. Все остальные числа либо ведут себя, как единица, то есть, делят нацело всех без разбора, либо делят числа с остатком не единственным образом.

Легко понять, что подобно единице ведут себя обратимые элементы, а 2 и 5 — это числа, которые порождают идеалы нашего кольца. Любой идеал, который можно получить просто многократным прибавлением одного и того же элемента, называется главным идеалом, а число, его порождающее — генератором. Получается, что в ℤ/10ℤ деление с остатком корректно определяется только для генераторов главных идеалов.

Раз деление с остатком некорректно в общем случае, то и алгоритм Евклида для нахождения наименьшего общего делителя нам не применить. Да и сам этот общий делитель может быть неоднозначным.

Ух, как всё непросто! Но давайте теперь взглянем с позиции теории колец на привычные целые числа. В ℤ только два обратимых элемента: ±1, которые делят все числа без остатка. Все идеалы в ℤ главные, и имеют вид nℤ, то есть генерируются произвольным от нуля числом . А это значит, что понятие остатка от деления корректно для всех чисел из ℤ. Вот почему в целых числах работают и деление с остатком, и алгоритм Евклида, и китайская теорема об остатках и другие плюшки. Такие кольца называются евклидовыми.

При этом все целые числа можно разбить с помощью числа на смежные классы с одинаковыми остатками от деления на число . Один из них, содержащий ноль, будет идеалом nℤ, все другие могут быть получены из этого идеала прибавлением остатка ко всем его элементам. Такое разбиение и обозначается знаком и называется факторизацией.

А если вспомнить, что сумма, разность и произведение любых элементов идеала остаётся внутри него, то это означает, что при сложении двух элементов разных классов, например, и , идеальная часть останется идеальной, а все операции будут проводиться только с остатками. Так что попадёт в класс . Это же верно и для вычитания с умножением. Получается, что классы образуют самостоятельное кольцо (не являющееся подкольцом ℤ), которое получается факторизацией кольца целых чисел по идеалу nℤ, то есть ℤ/nℤ. Вот откуда взялись термин «идеальные числа» и принятое обозначение колец вычетов. Получается, делить можно не только числа, но и кольца!

Итак. В кольцах вычетов корректно делить с остатком можно только на числа, которые генерируют главные идеалы. Все делители единицы ведут себя как единица и делят любое число без остатка. В евклидовых полях все идеалы главные и в них имеется содержательная теория делимости. В полях же все числа обратимы, а значит, они все ведут себя, как единицы и вопрос делимости становится тривиальным.

Задание-вопросы:

• А интересно, на какие числа можно делить с остатком на циферблате часов, то есть в кольце ℤ/12ℤ?

• Что мы получим, если факторизуем ℤ/10ℤ по идеалам 2ℤ/10ℤ и 5ℤ/10ℤ?

Основная теорема арифметики

Как известно математикам и любителям математики, простые числа не так уж и просты. С ними связаны многие сложные и даже не решённые за сотни лет задачи теории чисел. В конечных арифметиках с ними разобраться должно быть проще, поскольку, все числа в них можно перечислить и выяснить всё про все числа.

Мы уже знаем, что в полях, числовых системах, в которых все числа делятся на все ненулевые числа, понятие простоты не имеет смысла. Значит кольцо ℤ/5ℤ, являющееся полем, мы в этом разделе рассматривать не будем.

Простые числа играют важную роль в основной теореме арифметики (ОТА), а она, в свою очередь, лежит в основе большинства методов целочисленного анализа. Так что, если мы хотим по-настоящему понять устройство конечных арифметик, надо выяснить как для них будет выглядеть и как будет работать ОТА.

Знакомая нам со школы, а человечеству — со времён Евклида, основная теорема арифметики гласит:

Любое натуральное число может быть единственным способом представлено в виде произведения простых чисел.

Простыми же мы называем числа, которые делятся только на себя и на единицу.

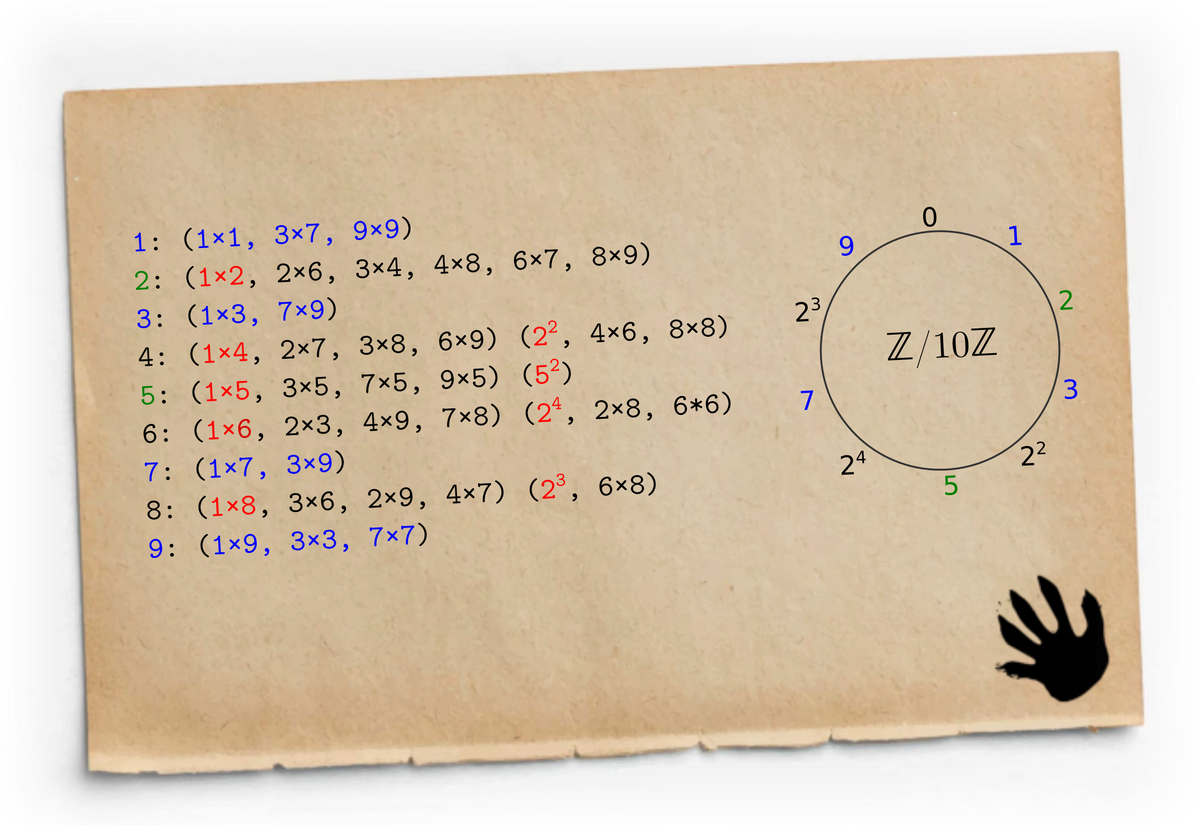
Давайте с помощью таблицы умножения выпишем, как раскладываются на множители положительные числа в ℤ/10ℤ.

Кошмар и путаница! Не похоже, чтобы числа раскладывались на простые множители единственным способом, как предписывает основная теорема арифметики. Давайте разбираться. И начнём с того, что от натуральных чисел, которые не образуют даже кольца, перейдём к целым. А в них ОТА выглядит немного по другому, потому что среди целых чисел есть два делителя единицы (обратимых элемента): 1 и −1. Так что, например, простое число 7 и составное 12 можно представить в виде произведения не одним, а несколькими разными способами:

Это наводит на мысль, что если в кольце существует несколько делителей единицы, то они могут сбивать с толку, создавая видимость нескольких различных представлений числа в виде произведения.

Почему я назвал это видимостью? Смотрите, умножение на единицу ничего не меняет, верно? Давайте умножим произведение (−1)×(−7) на 1, но представим эту единицу нетривиальным образом, и пользуясь коммутативностью и ассоциативностью, перегруппируем множители:

Получается, что «с точностью до множителей единицы», это одно и тоже разложение. Также можно показать, что три разных представления числа 12 эквивалентны.

Получается, что делители единицы, или обратимые элементы кольца — это особые числа, не учитывать которые нельзя.

По ассоциациям рразойдись!

Делители единицы образуют мультипликативную группу, то есть, некоторое подмножество чисел, замкнутое относительно умножения и имеющее обратные элементы. А что мы получим, если умножим все элементы мультипликативной группы, на число, в него не входящее? Давайте продолжим оставаться в привычных целых числах, в которых эта группа состоит из двух элементов , и умножим её, скажем, на 2. Получим множество , чем оно примечательно? С точки зрения делимости, тем, что оба этих числа делят друг друга нацело: 2 делится на −2, и наоборот, −2 делится на 2. И никакие другие пары чисел, кроме пар не обладают такой взаимной делимостью.

Числа, которые взаимно делятся друг на друга называются ассоциированными и получаются друг из друга умножением на делитель единицы. Действительно, пусть  это делитель единицы, с обратным ему элементом w. Для любых a и b, если a = bu, то b = aw. Значит, если a делится на b, то и b делится на .

В кольце ℤ/10ℤ делителей единиц четыре: 1, 3, 7 и 9, а это значит, что для каждого числа в этом кольце можно построить множество ассоциированных с ним чисел. Например, с числом 2 ассоциированы числа 6, 4 и 8; число 5 ассоциировано само с собой, а с любым делителем единицы, ассоциированы все делители единицы.

Умножение на делители единицы позволяет разбить множество элементов кольца на смежные классы ассоциированных друг с другом чисел, в каждом из которых все числа делятся нацело друг на друга. В нашем случае эти классы будут такими:

То есть, в ℤ/10ℤ не только число 4 делится на 2, но и 2 делится на 4, что легко проверить, заглянув в таблицу разложений на множители, и увидев, что 2 = 3×4 = 8×4.

Как же понимать такую симметрию? Обратите внимание на то, что все элементы класса можно представить степенями двойки:

Более того, не выходя за пределы таблицы умножения, эти же числа можно представить ещё большими степенями:

В этом смысле 2 = 2⁵ вполне может делиться на 4 = 2² или на 6 = 2⁴ и никакого противоречия не возникает!

В классе число 5 является автоморфным, то есть равно самому себе при возведении в любую степень. И, наконец, элементы мультипликативной группы делителей единиц тоже можно представить как степени: или

Получается, что все числа в ℤ/10ℤ можно представить, как степень себя или какого-то другого числа:

Какой кошмар! И в каком же смысле прикажете понимать разложение числа на простые множители, да ещё и единственным образом, если перед нами такое разнообразие и чисел и разложений, да к тому же, и отношение делимости может оказаться симметричным? И вообще, какое из этих чисел простое, а какое составное?

Усложняем простоту

Определение простого числа, как числа, которое делится только на себя и на единицу, необходимо как-то расширить. Для колец существует несколько эквивалентных определений простого элемента. Мы воспользуемся таким:

элемент кольца  называется простым, если он является генератором простого идеала.

В свою очередь,

нетривиальный идеал  в кольце  называется простым, если и если для любых двух элементов из , таких что их произведение  входит в следует, что или  входят в .

Последнее определение соответствует лемме Евклида:

Число p является простым, если произведение ab делится на p тогда и только тогда, когда a или b делятся на p.

И вот что мы можем заключить из этих определений:

Во-первых, в нашем кольце всего два идеала 2ℤ/10ℤ и 5ℤ/10ℤ. И оба подходят под определение простых. Глядя на таблицу разложений чисел на множители, легко убедиться в том, что все элементы этих идеалов получаются только из произведений, содержащих числа, ассоциированные с генераторами этих идеалов. А в таком случае, эти генераторы — числа 2 и 5, и будут являться простыми элементами кольца ℤ/10ℤ.

Во-вторых, делитель единицы не может быть простым элементом, потому что он не может является генератором какого-либо идеала, отличного от всего кольца. Поэтому числа 1, 3, 7 и 9 не могут быть простыми. По этой же причине не являются простыми числа 1 и −1 в целых числах.

Однако, согласно ОТА, разложение на простые множители должно не только существовать, но и быть единственным. Что нужно подправить в этой теореме для колец? Надо лишь добавить, что единственность разложения требуется с точностью до умножения на делители единицы.

Например, мы видим в таблице умножения, что 2 = 1×2 = 3×4. Давайте умножим произведение 3×4 справа и слева на нетривиальные делители единицы (в произведении они дают единицу, так что это не изменит результата) и, переставив скобки, заменим множители на ассоциированные числа:

Получилось, что два эти разложения можно получить друг из друга умножив на единицу, собранную из её делителей. Точно таким же образом можно показать, что все разложения чисел на множители разбиваются на смежные классы по этому признаку эквивалентности:

Здесь в скобках сгруппированы разложения чисел на множители, эквивалентные с точностью до умножения на делители единицы. И вот теперь мы видим подтверждение тому, что в нашей арифметике лишь два простых числа: вполне нормальное 2 и автоморфное 5. Кроме этого, отчётливо выделились составные числа, которые имеют более одного разложения на эти простые.

Ура! Значит, ОТА в общей формулировке действует, и все наши числа, действительно раскладываются на произведения простых чисел.

Эта наиболее общая формулировка ОТА и расширенное понятия простоты оказываются ключевыми в прикладной теории колец. Именно простота идеалов и элементов, а также связанное с ними понятие неразложимости элементов колец, лежат в основе анализа разрешимости алгебраических уравнений и сводимых к ним задач из самых разных областей математики.

Задание:

• Исследуйте классы ассоциированных чисел, выделите простые и разложите составные числа на циферблате часов, то есть, в кольце ℤ/12ℤ.

• Примените определение простого идеала к идеалам в ℤ и покажите, что идеалы, генерируемые составными числами, не являются простыми.

Зачем нам всё это знать?

Вы задумывались, почему можно использовать для записи чисел строчки из цифр?

Понятно, что много веков назад индусы придумали отличную систему счисления, потом арабы принесли её в Европу и теперь мы все учим её в школе. Понятно также, почему система именно десятичная. Вопрос не в этом: почему эта система работает?

Я не буду сейчас рассказывать вам, что число это абстракция количества, или уверять, что число это просто. Нет, числа — это хитрая вещь. Важно, что числа, это не только множество. Для его элементов должны быть корректно определены арифметические операции и отношения, а для них, в свою очередь, должны выполняться всякие законы и связи между этими законами.

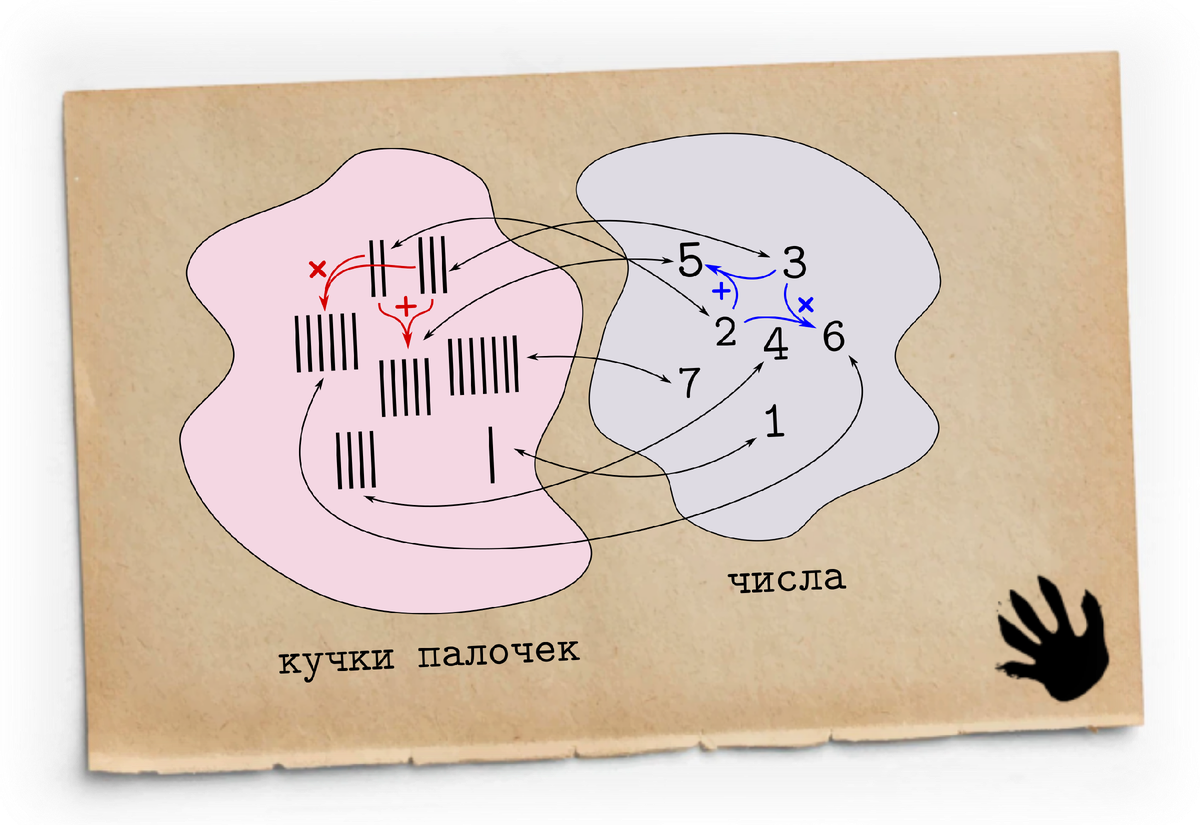
Возьмем, например, палочки, и станем с их помощью записывать числа: |, ||, |||, ||||, … Далее, определим ряд операций с рядами палочек: сложение — это пририсовывание палочек, умножение — замена одной палочки несколькими. Их можно даже вычитать, пока палочек хватает, а также раскладывать кучки палочек на кучки одинаковых кучек, то есть, делить с остатком. С описанными операциями они уже образуют некоторую алгебраическую структуру, но всё же, палочки — это палочки, а никакие не числа.

В свою очередь, натуральные числа — это вовсе не кучки палочек. В современной математике они определяются через набор аксиом Пеано, ничего общего с палочками не имеющих, и тоже образуют некоторую алебраическую структуру.

И вот, что замечательно. Каждое число можно соединить стрелочкой с уникальной кучкой палочек и наоборот каждую кучку — с уникальным числом. Кроме того, сумма любых двух чисел соединится стрелочкой с суммой соответствующих этим числам кучек палочек. И наоборот. То же относится и к произведениям.

Такие стрелочки легко нарисовать, но что они будут работать правильно, нужно доказывать, что и было сделано алгебраистами в конце XIX века. Такая «похожесть» между алгебраическими системами называется изоморфизмом, она играет роль равенства между ними. Система кучек из палочек изоморфна системе натуральных чисел. Это отношение записывают так: кучки палочек ≃ ℕ.

Это значит, что одну из них можно использовать вместо другой и наоборот. Вот поэтому мы можем в младших классах объяснять арифметику натуральных чисел и все её законы на палочках, яблоках или енотах.

Целые числа уже не изоморфны кучкам палочек, поэтому так непросто бывает человеку, воспитанному палочками, принять отрицательные числа. Но можно отыскать иную модель, изоморфную системе целых чисел, например, перемещение по бесконечному ряду одинаковых клеток, где сложение это добавление шагов, а умножение — прыжки через несколько клеток разом.

Для рациональных и вещественных чисел удобной изоморфной системой может быть система преобразования непрерывной прямой с операциями сдвига, отражения и масштабирования. Так мы получаем декартову числовую прямую и систему координат. А, например, логарифмическая линейка предлагает изоморфизм между вещественными числами с операцией умножения и сдвигом числовой прямой, к которой применили нелинейное логарифмическое масштабирование.

Повторюсь, изоморфизм не означает, что точки на прямой, шаги по клеткам или кучки палочек и числа это одно и тоже. Они кое в чëм ведут себя как точные модели друг друга, но это совершенно разные системы.

Если стрелочки, согласующиеся с операциями можно нарисовать только в одну сторону, а в другую — нет, то такое отношение называется гомоморфизмом.

Это тоже очень важное отношение. Например, гомоморфизмом будет отображение всех целых чисел на множество из двух элементов: {чётное, нечётное}. И вообще, остаток от деления на , задаёт гомоморфизм из целых чисел на кольцо вычетов ℤ/nℤ. А из житейских примеров гомоморфизмов можно привести всякую проекцию или тень трёхмерного объекта на плоскость.

Цифры, как мы увидели, вовсе не изоморфны числам ни натуральным, ни целым. Они образуют принципиально иную алгебраическую систему — конечное кольцо ℤ/10ℤ, изоморфное циферблату с десятью делениями, которым мы и пользовались для наглядности.

В этом кольце есть делители нуля, идеалы, своя система делимости… Почему же строки из цифр, каждая из которых складывается и умножается по законам кольца ℤ/10ℤ, ведут себя, как система, изоморфная натуральным или целым числам, а так же всем изоморфным им системам? Почему работают вычисления «в столбик», в которых мы явно пользуемся именно арифметикой вычетов, а не арифметикой целых чисел?

Вспомним, что такое 123 в позиционной записи:

Вспомнили? А теперь забудем про то, что, что наша система счисления десятичная и заменим число 10 на произвольную величину . Таким образом, мы получим многочлен:

в котором все коэффициенты принадлежат кольцу ℤ/10ℤ, а величина — уже нет. Если подставить в него , то есть, значение, котрого нет в ℤ/10ℤ, то получим число 123.

Множество всех многочленов с коэффициентами из кольца , обозначается так и, в свою очередь, образует кольцо, на сей раз, с бесконечным числом элементов. При этом ещё раз стоит заметить, что величина x не обязана принадлежать кольцу .

Теория колец многочленов составляет бóльшую содержательную часть теории колец и именно для их исследования, применительно к решению диофантовых уравнений и других задач теории чисел, вся теория колец и была разработана. Для колец многочленов тоже вычисляются идеалы, находятся простые элементы (неприводимые многочлены) и другие характеристики. Сотни лет люди возятся с ними, потому что вопрос разрешимости многих задач из разных областей математики можно свести к вопросу приводимости какого-либо многочлена в том или ином кольце или поле. Именно так доказывается невозможность с помощью одних только циркуля и линейки совершить трисекцию угла, удвоение куба или построение произвольного правильного многоугольника.

Я не стану здесь углубляться в теорию колец многочленов. Нам важно знать, что существует общая теорема о том, что вычисляя многочлен для фиксированного значения из иной алгебраической системы, можно построить гомоморфизм из кольца многочленов в эту систему.

Именно таким гомоморфизмом , мы и пользуемся, производя вычисления над многозначными числами «в столбик». Двоичная, троичная, шестнадцатиричная и прочие системы счисления строятся благодаря существованию гомоморфизмов для любого .

Наконец, можно построить изоморфизм для большого то есть, между многочленами над конечным кольцом в конечное кольцо с бóльшим числом элементов. Этот изоморфизм демонстрируют системы зубчатых колёс в шаговом счётчике, механическом одометре в автомобиле, в старом кассовом аппарате, или в арифмометре. Такие системы не могут считать до бесконечности. Когда во всех допустимых разрядах оказываются одни девятки, прибавление единицы возвращает систему в состояние соотвествующее нулю.

Торчат ли уши кольца?

А можно ли распознать какие-либо свойства кольца ℤ/10ℤ в десятичной системе счисления? Я приведу пару примеров, которые мы с вами теперь вполне можем понять.

Признаки делимости на 2 и 5

Мы выяснили, что в ℤ/10ℤ есть два простых идеала, содержащих числа и , которые генерируются простыми элементами 2 и 5. Отсюда следуют хорошо нам всем известные признаки делимости на 2 и на 5, опирающиеся на то, принадлежит ли последняя цифра соответствующему идеалу. Нам, по привычке, эти признаки кажутся очевидными, но они работают только в системах счисления, основанных на кольцах вычетов, имеющих именно эти идеалы. Например, поскольку в ℤ/15ℤ число 2 не является простым элементом (это делитель единицы), то в системе счисления по основанию 15 признак делимости на 2 будет достаточно сложным, а признак делимости на 5 останется таким же, как в десятичной системе. А поскольку в простом кольце ℤ/5ℤ простых идеалов вообще нет, то в пятиричной системе счисления ни один признак делимости (кроме делимости, собственно, на 5) не будет опираться на последнюю цифру числа.

В тоже время, удобные признаки делимости на 3 и на 9 в десятичной системе связаны не с каким-то особым положением этих чисел в ℤ/10ℤ, а с тем, что число 10 отображается в единицу гомоморфизмами и

Конечные десятичные дроби

Простые элементы в кольце цифр подсказывают нам, какие дроби будут конечными, а какие периодичными в выбранной системе счисления. Опять же, только дроби со степенями простых элементов в знаменателе будут давать конечные позиционные представления. Например, в ℤ/10ℤ простые элементы это 2 и 5, значит только десятичные дроби вида , для   будут конечными. А в системах счисления, основанных на цифрах из ℤ/pℤ при любом простом  конечные дроби возможны только со степенями  в знаменателе.

Кстати, конечные десятичные дроби, образуют своё собственное подкольцо внутри поля рациональных чисел. А это значит, что компьютеры и калькуляторы в которых принципиально конечное число разрядов в записи дробей, работают в некотором подкольце кольца конечных десятичных дробей.

Внешний признак простоты

Делители единицы в ℤ/10ℤ тоже способны дать кое-какую информацию. Кроме 2 и 5, все остальные простые числа в десятичной записи должны заканчиваться на делитель единицы, то есть, на 1, 3, 7 или 9. Кроме того, и любые произведения простых чисел, кроме 2 и 5, будут заканчиваться на одну из этих цифр, поскольку они образуют мультипликативную группу и замкнуты относительно умножения.

Опять же, нам, воспитанным на десятичной системе счисления, это свойство может показаться очевидным. Но стоит перейти в иную систему, очевидность «внешнего вида» простых чисел и их произведений потеряется.

Так, например, мы уже сразу можем заключить, что раз в ℤ/5ℤ все ненулевые элементы обратимы, то простые числа, кроме 5, вольны оканчиваться в пятиричной записи на любую цифру, кроме нуля (исключеним будет простое число 5). Вот как выглядит начало последовательности простых чисел из ℤ, записанных в пятиричной системе счисления:

Заключение

Вынужден признать, что кольца вычетов, выбранные нами для первого знакомства с кольцами, просты для понимания, но достаточно скудны на интересные особенности и большая часть их свойств и следствий сводится к простым соотношениям делимости целых чисел.

В кольце вычетов ℤ/nℤ, по составному модулю 

• все делители нуля это числа, кратные простым множителям числа 

• все идеалы в кольцах вычетов главные и генерируются делителями нуля;

• делителями единицы будут числа, взаимно простые с 

• простыми элементами кольца будут делители нуля, которые являются простыми в ℤ.

Кроме простых, в кольцах можно отыскать и другие особые элементы — неразложимые числа. От простых неразложимые элементы отличаются тем, что для них не выполняется лемма Евклида: для простого и только для простого верно, что если произведение делится на , то либо  делится на , либо  делится на .

Например, в ℤ/12ℤ число 10 является неразложимым. Число 8 делится на 10, потому что 8 = 2×10, однако, с другой стороны, 8 = 4×5, а на 4, ни 5 не делятся на 10 и не являются ассоциированными с числом 10. Число 10 невозможно разложить в кольце ℤ/12ℤ на простые множители. Конечно, 10 = 2×5, однако 5 не является простым, это делитель единицы в этом кольце. В кольце ℤ/10ℤ таких чисел не было, и мы о них и не упоминали. А в областях целостности (таких, как целые числа) все неразложимые числа просты. Поэтому в школе мы с ними и не сталкивались.

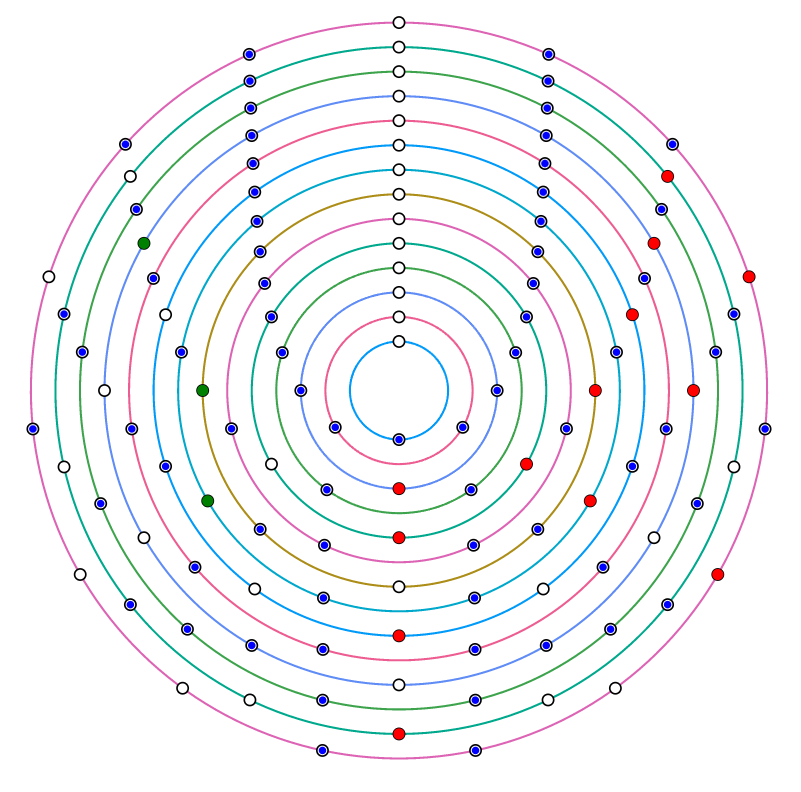
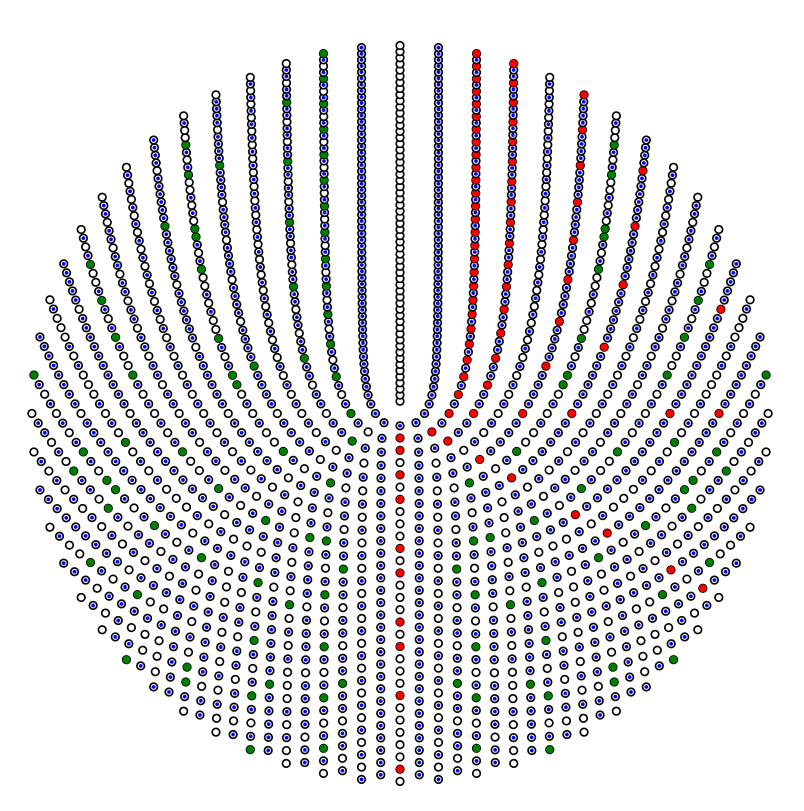
А вот, полюбуйтесь на устройство колец вычетов, в виде изоморфных им колечек с разноцветными кружочками.

Не смотря на свою относительную простоту, познакомиться с кольцами вычетов небесполезно, они позволяют изучить себя в деталях при первом знакомстве и приоткрывают дверь в большую математику. Неожиданные свойства колец и полей, как конечных, так и бесконечных, начинаются, когда мы начинаем их расширять и превращать в большие системы, такие как кольца многочленов, гауссовы числа или числа Эйзенштейна.