Глава 8. зацепления зубчатые
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса:
где z – число зубьев;
Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
где t – шаг зацепления.
где h a – высота головки зуба, h a = m ; h f – высота ножки зуба, h f = 1,25 m .
Диаметр окружности выступов зубьев :
Диаметр окружности впадин :
Служит для передачи вращения при параллельных осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2 .
Служит для преобразования вращательного движения в возвратно-поступательное.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращательного движения между валами со скрещивающимися осями.
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращения при пересекающихся осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Расчет делительного диаметра зубчатого колеса
Зубчатое колесо — это основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса.
Формула расчета делительного диаметра зубчатого колеса:
d — диаметр делительной окружности в мм;
z — количество зубьев шестерни в мм;
m — модуль шестерни.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета делительного диаметра зубчатого колеса по простой математической формуле в зависимости от модуля шестерни и числа зубьев. С помощью этого калькулятора вы в один клик сможете выполнить расчет делительного диаметра зубчатого колеса.
Модуль шестерни: виды, определение, стандартные показатели
Что представляет собой шестерня
Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.
Шестеренчатые передачи также имеют свою классификацию:
- Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
- Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
- Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
- Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.
Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.
При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.
Почему шестеренку называют так?
Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».
Характеристики и применение
Зубья шестеренки находятся в радиальных плоскостях. Линия контакта прямозубых цилиндрических шестерней параллельна оси вращения.
В зависимости от необходимых нагрузочных характеристик и точности передаваемого вращения, подбирается модуль (расстояние между центрами зубов) от 1 до 6.
Используется в подвижных частях механизмов соместно с зубчатой рейкой.
Цилиндрическая зубчатая передача применяется во всех типах автоматических ворот, конвейерных линиях с повышенной нагрузкой, 3D принтерах, станках ЧПУ и многом другом.
Параметры модуля шестерни
Рассматриваемая характеристика обозначается литерой m, указывает на прочность зубчатых передач. Единица измеряется в миллиметрах (чем выше нагрузка на передачу, тем больше модульное значение). В расчете параметра используются следующие показатели:
- диаметр делительной окружности;
- шаг и число зубьев;
- эвольвент (диаметр основной окружности);
- аналогичная характеристика впадин темной шестеренки;
- высота зуба темного и светлого колеса.
В машиностроительной отрасли расчеты ведутся по стандартным значениям для удобства изготовления и замены шестерен с числами от 1-го до 50-ти.
Что такое модуль на чертеже?
Модуль — это унифицированный элемент любых систем, состоящий из взаимозаменяемого комплекса деталей массового производства. Чертеж модуля выполняется на основании ГОСТ 2.109-73 — единая система конструкторской документации (ЕСКД).
Как найти модуль шестерни?
Как определить модуль косозубой шестерни.
- Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
Как узнать высоту зуба шестерни?
h = ha + hf, где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как обозначается делительный диаметр?
Окружность, являющаяся начальной при зацеплении с рейкой – делительная; её диаметр обозначается d (рис. 2). Для колес без смещения делительные окружности совпадают с начальными. Толщина зуба по делительной окружности S равна ширине впадины между двумя зубьями е.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Что такое модуль зубчатого колеса?
m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб.
Чему равен модуль нормального зубчатого колеса?
Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.
Какие бывают зубчатые колеса?
Виды зубчатых колес, шестерен
- Поперечный профиль зуба Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. …
- Продольная линия зуба Прямозубые шестерни …
- Шестерни с внутренним зацеплением …
- Винтовые шестерни …
- Секторные шестерни …
- Шестерни с круговыми зубьями
Прямозубые и косозубые колесики
Модуль и диаметр шестерни прямозубого типа — один из самых востребованных видов. Зубцы размещаются в радиальных плоскостях, а площадь контакта пары колес параллельна оси вращения. Аналогичным образом располагаются оси обеих шестерен.
Косозубые колесики представляют собой усовершенствованную вариацию вышеуказанной модификации. Зубцы находятся под определенным углом к вращательной оси. Зацепление осуществляется плавней и тише, что позволяет эксплуатировать элементы в малошумных приспособлениях, гарантируя передачу большего крутящего момента на высокой скорости. К минусам относят увеличенную площадь контакта зубцов, провоцирующую повышенное трение и нагрев деталей. Это чревато ослаблением мощности и повышенным расходом смазки. Кроме того, механическое воздействие вдоль оси шестерни требует использования упорных подшипников для монтажа вала.
Шевронные модификации и аналоги с внутренним зацеплением
Шевронные шестерни позволяют справиться с проблемами механической осевой силы. В отличие от прямых и косозубых версий, зубья выполнены в виде литеры V. Осевое воздействие двух половин приспособления компенсируется взаимодействием, что дает возможность избежать применения упорных подшипников на валу. Указанная модель самостоятельно устанавливается по оси, один из рабочих редукторов монтируется на цилиндрических укороченных подшипниках (плавающие опоры).
Модуль шестерни с внутренним зацеплением оснащается зубцами, имеющими нарезку внутри. Эксплуатация детали предполагает односторонние обороты ведущего и ведомого колеса. В такой конструкции меньше затрат уходит на трение, что способствует повышению КПД. Подобные приспособления применяются в механизмах, ограниченных по габаритным размерам, а также планетарных передачах, специальных насосах и танковых башенках.
Винтовые, круговые, секторные версии
Модуль шестерни винтового типа представляет собой цилиндр с зубцами, которые размещены по винтовому направлению. Подобные элементы устанавливаются на непересекающиеся валы, расположенные перпендикулярно по отношению друг к другу. Угол совмещения составляет 90 градусов.
Секторное зубчатое колесо — часть любой шестерни, применяемая в передачах, где не нужно вращение основного элемента на полный оборот. Такая деталь дает возможность сэкономить ценное пространство в размерах полноценного аналога.
Шестерни по модулю и количеству зубьев с круговым расположением отличаются контактным соприкосновением в одной точке зацепления, расположенной параллельно основным осям. Второе название механизма — передача Новикова. Она обеспечивает хорошие ходовые характеристики, плавную и бесшумную работу, повышенную зацепляющую способность. При этом коэффициент полезного действия таких деталей немного ниже аналогов, а процесс изготовления существенно сложнее. Указанные детали имеют значительно ограниченную отрасль эксплуатации ввиду своих особенностей.
Конические шестерни
Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.
Зубчатая рейка
Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Звездочка
Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.
Коронная шестерня
Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.
В чем заключаются сходства между шестерней и зубчатым колесом
Между шестерней и зубчатым колесом можно отметить несколько схожих моментов:
- Как и шестерня, зубчатое колесо может быть как ведомым, так и ведущим элементом в общей системе.
- У шестерни и у зубчатого колеса форма может быть как цилиндрической, так и конической, все зависит от той функции, которую конкретная деталь выполняет.
- При помощи шестеренки и зубчатого колеса можно маневрировать на почве скорости вращательного элемента, либо уменьшая ее, либо увеличивая.
- Шестеренки и зубчатые колеса одинаково эффективно можно использовать на электрических и бензоинструментах, однако больше всего используют именно шестеренки, так как они обеспечивают устойчивость механизма.
- Шестеренка и зубчатое колесо могут использоваться для запуска вращательных осей.
Внешние сходства между шестеренкой и зубчатым колесом обоснованы также еще тем, что зачастую эти два элемента могут выполнять схожие функции и быть взаимозаменяемыми в определенных системах и механизмах.
Когда применяют цилиндрические зубчатые передачи?
Цилиндрической зубчатой передачей называется передача с параллельными осями. Косозубые передачи применяют при окружных скоростях м/с; шевронные передачи – преимущественно в тяжело нагруженных передачах. … Кинематика и геометрия цилиндрические зубчатых колес.
Подытожим
Расчетные чертежи и схемы для шестеренок различных конфигураций преимущественно совпадают для косых и прямозубчатых версий. Основные различия возникают при расчетах на прочность. В графических отображениях применяются характеристики, ориентированные на типовые габаритные размеры шестеренок. Среди представленного ассортимента на рынке вполне реально подобрать зубчатое колесо с необходимыми характеристиками и прочностными показателями.
http://www.center-pss.ru/math/raschet-delitelnogo-diametra.htm
На чтение 10 мин Просмотров 21к. Опубликовано 27.07.2021
Содержание
- Что представляет собой шестерня
- Почему шестеренку называют так?
- Характеристики и применение
- Что такое модуль на чертеже?
- Как найти модуль шестерни?
- Как узнать высоту зуба шестерни?
- Как найти делительный диаметр шестерни?
- Как обозначается делительный диаметр?
- Формула расчета параметров прямозубой передачи
- Что такое модуль зубчатого колеса?
- Чему равен модуль нормального зубчатого колеса?
- Какие бывают зубчатые колеса?
- Прямозубые и косозубые колесики
- Шевронные модификации и аналоги с внутренним зацеплением
- Винтовые, круговые, секторные версии
- Конические шестерни
- Зубчатая рейка
- Звездочка
- Коронная шестерня
- В чем заключаются сходства между шестерней и зубчатым колесом
- Когда применяют цилиндрические зубчатые передачи?
- Подытожим
Что представляет собой шестерня
Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.
Шестеренчатые передачи также имеют свою классификацию:
- Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
- Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
- Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
- Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.
Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.
При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.
Почему шестеренку называют так?
Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».
Характеристики и применение
Зубья шестеренки находятся в радиальных плоскостях. Линия контакта прямозубых цилиндрических шестерней параллельна оси вращения.
В зависимости от необходимых нагрузочных характеристик и точности передаваемого вращения, подбирается модуль (расстояние между центрами зубов) от 1 до 6.
Используется в подвижных частях механизмов соместно с зубчатой рейкой.
Цилиндрическая зубчатая передача применяется во всех типах автоматических ворот, конвейерных линиях с повышенной нагрузкой, 3D принтерах, станках ЧПУ и многом другом.
Параметры модуля шестерни
Рассматриваемая характеристика обозначается литерой m, указывает на прочность зубчатых передач. Единица измеряется в миллиметрах (чем выше нагрузка на передачу, тем больше модульное значение). В расчете параметра используются следующие показатели:
- диаметр делительной окружности;
- шаг и число зубьев;
- эвольвент (диаметр основной окружности);
- аналогичная характеристика впадин темной шестеренки;
- высота зуба темного и светлого колеса.
В машиностроительной отрасли расчеты ведутся по стандартным значениям для удобства изготовления и замены шестерен с числами от 1-го до 50-ти.
Что такое модуль на чертеже?
Модуль — это унифицированный элемент любых систем, состоящий из взаимозаменяемого комплекса деталей массового производства. Чертеж модуля выполняется на основании ГОСТ 2.109-73 — единая система конструкторской документации (ЕСКД).
Как найти модуль шестерни?
Как определить модуль косозубой шестерни.
- Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
Как узнать высоту зуба шестерни?
Высота зуба:
h = ha + hf, где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как обозначается делительный диаметр?
Окружность, являющаяся начальной при зацеплении с рейкой – делительная; её диаметр обозначается d (рис. 2). Для колес без смещения делительные окружности совпадают с начальными. Толщина зуба по делительной окружности S равна ширине впадины между двумя зубьями е.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Что такое модуль зубчатого колеса?
m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб.
Чему равен модуль нормального зубчатого колеса?
Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.
Какие бывают зубчатые колеса?
Виды зубчатых колес, шестерен
- Поперечный профиль зуба Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. …
- Продольная линия зуба Прямозубые шестерни …
- Шестерни с внутренним зацеплением …
- Винтовые шестерни …
- Секторные шестерни …
- Шестерни с круговыми зубьями
Прямозубые и косозубые колесики
Модуль и диаметр шестерни прямозубого типа — один из самых востребованных видов. Зубцы размещаются в радиальных плоскостях, а площадь контакта пары колес параллельна оси вращения. Аналогичным образом располагаются оси обеих шестерен.
Косозубые колесики представляют собой усовершенствованную вариацию вышеуказанной модификации. Зубцы находятся под определенным углом к вращательной оси. Зацепление осуществляется плавней и тише, что позволяет эксплуатировать элементы в малошумных приспособлениях, гарантируя передачу большего крутящего момента на высокой скорости. К минусам относят увеличенную площадь контакта зубцов, провоцирующую повышенное трение и нагрев деталей. Это чревато ослаблением мощности и повышенным расходом смазки. Кроме того, механическое воздействие вдоль оси шестерни требует использования упорных подшипников для монтажа вала.
Шевронные модификации и аналоги с внутренним зацеплением
Шевронные шестерни позволяют справиться с проблемами механической осевой силы. В отличие от прямых и косозубых версий, зубья выполнены в виде литеры V. Осевое воздействие двух половин приспособления компенсируется взаимодействием, что дает возможность избежать применения упорных подшипников на валу. Указанная модель самостоятельно устанавливается по оси, один из рабочих редукторов монтируется на цилиндрических укороченных подшипниках (плавающие опоры).
Модуль шестерни с внутренним зацеплением оснащается зубцами, имеющими нарезку внутри. Эксплуатация детали предполагает односторонние обороты ведущего и ведомого колеса. В такой конструкции меньше затрат уходит на трение, что способствует повышению КПД. Подобные приспособления применяются в механизмах, ограниченных по габаритным размерам, а также планетарных передачах, специальных насосах и танковых башенках.
Винтовые, круговые, секторные версии
Модуль шестерни винтового типа представляет собой цилиндр с зубцами, которые размещены по винтовому направлению. Подобные элементы устанавливаются на непересекающиеся валы, расположенные перпендикулярно по отношению друг к другу. Угол совмещения составляет 90 градусов.
Секторное зубчатое колесо — часть любой шестерни, применяемая в передачах, где не нужно вращение основного элемента на полный оборот. Такая деталь дает возможность сэкономить ценное пространство в размерах полноценного аналога.
Шестерни по модулю и количеству зубьев с круговым расположением отличаются контактным соприкосновением в одной точке зацепления, расположенной параллельно основным осям. Второе название механизма — передача Новикова. Она обеспечивает хорошие ходовые характеристики, плавную и бесшумную работу, повышенную зацепляющую способность. При этом коэффициент полезного действия таких деталей немного ниже аналогов, а процесс изготовления существенно сложнее. Указанные детали имеют значительно ограниченную отрасль эксплуатации ввиду своих особенностей.
Конические шестерни
Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.
Зубчатая рейка
Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Звездочка
Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.
Коронная шестерня
Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.
В чем заключаются сходства между шестерней и зубчатым колесом
Между шестерней и зубчатым колесом можно отметить несколько схожих моментов:
- Как и шестерня, зубчатое колесо может быть как ведомым, так и ведущим элементом в общей системе.
- У шестерни и у зубчатого колеса форма может быть как цилиндрической, так и конической, все зависит от той функции, которую конкретная деталь выполняет.
- При помощи шестеренки и зубчатого колеса можно маневрировать на почве скорости вращательного элемента, либо уменьшая ее, либо увеличивая.
- Шестеренки и зубчатые колеса одинаково эффективно можно использовать на электрических и бензоинструментах, однако больше всего используют именно шестеренки, так как они обеспечивают устойчивость механизма.
- Шестеренка и зубчатое колесо могут использоваться для запуска вращательных осей.
Внешние сходства между шестеренкой и зубчатым колесом обоснованы также еще тем, что зачастую эти два элемента могут выполнять схожие функции и быть взаимозаменяемыми в определенных системах и механизмах.
Когда применяют цилиндрические зубчатые передачи?
Цилиндрической зубчатой передачей называется передача с параллельными осями. Косозубые передачи применяют при окружных скоростях м/с; шевронные передачи – преимущественно в тяжело нагруженных передачах. … Кинематика и геометрия цилиндрические зубчатых колес.
Подытожим
Расчетные чертежи и схемы для шестеренок различных конфигураций преимущественно совпадают для косых и прямозубчатых версий. Основные различия возникают при расчетах на прочность. В графических отображениях применяются характеристики, ориентированные на типовые габаритные размеры шестеренок. Среди представленного ассортимента на рынке вполне реально подобрать зубчатое колесо с необходимыми характеристиками и прочностными показателями.
Не редко на конвейерных линиях из строя выходят узлы и агрегаты. Ремонт конвейерных лент от специалистов быстро вернет ваше оборудование в строй.
Рисунок 3. Параметры эвольвентного зубчатого колеса.
К основным геометрическим параметрам эвольвентного зубчатого колеса относятся: модуль m, шаг p, угол профиля α, число зубьев z и коэффициент относительного смещения x.
Виды модулей: делительный, основной, начальный.
Для косозубых колес дополнительно различают: нормальный, торцевой и осевой.
Для ограничения числа модулей ГОСТом установлен стандартный ряд его значений, которые определяются по делительной окружности.
Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб.
m =p /π
Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения
d = Z · m
Делительная окружность делит зуб на головку и ножку.
Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности.
Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин.
Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин.
Сумма высот головки ha и ножки hf соответствует высоте зубьев h:
h = ha + hf
Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев.
da=d+2(h*a + x — Δy)m
Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины.
df = d — 2(h*a — C* — x) · m
Согласно ГОСТ 13755-81 α = 20°, С* = 0,25.
Коэффициент уравнительного смещения Δу:
Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев.
p = m·π
Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу
Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев
pb = p · cos α
Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба
S = 0,5 · ρ + 2 · х · m · tg α
Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев
е = p — S
Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба.
Толщина зуба Sa по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба.
Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра
1.1. Пример расчета прямозубого внешнего эвольвентного зубчатого зацепления.
1.2. Вычерчивание элементов зубчатого зацепления
1
1. Выполнение чертежей цилиндрических зубчатых колес
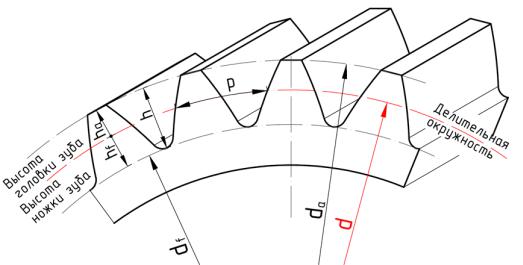
Основным параметром цилиндрического зубчатого колеса является делительная окружностью. Диаметр делительной окружности обозначается буквой d и называется делительным. (Термины, определения и обозначения цилиндрических зубчатых колес устанавливает ГОСТ 16531-83). По делительной окружности откладывается окружной шаг зубьев, обозначаемый p и представляющий собой расстояние по дуге делительной окружности между соседними зубьями зубчатого колеса (рис. 1). Отрезки делят делительную окружность на столько частей, сколько зубьев имеет зубчатое колесо. Число зубьев обозначается буквой z. Делительный диаметр для зубчатого колеса всегда один. По делительной окружности измеряют окружную толщину зуба и окружную ширину впадин.
Делительная окружность делит высоту зуба h на две неравные части – головку зуба высотой ha и ножку высотой hf.
Зубчатый венец ограничивается окружностью вершин зубьев диметром da и окружностью впадин диаметром df.
Рис. 1
Основным расчетным параметром зубчатых колёс является модуль. Через него выражаются все остальные параметры. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности d к числу зубьев z или отношение окружного шага к числу .
m = d / z = p /
Иными словами, модуль – это длина дуги делительной окружности, приходящаяся на один зуб колеса. Для унификации зубчатых колес в промышленных масштабах для изготовления зубчатых колес применяют
2
стандартные значения модулей, которые установлены ГОСТ 9563-60. Некоторые значения стандартного модуля приведены в таблице . Значения из первого ряда предпочитаются второму, второй ряд значений модуля приводится для расширения ассортимента изготавливаемых зубчатых колес и применяется в тех случаях, когда по техническим, конструктивным или иным причинам невозможно изготовить зубчатое колесо со значением модуля из первого ряда.
|
Таблица |
|||||||||||||
|
Модуль зацепления — m, (мм) |
|||||||||||||
|
1-й |
1 |
1,25 |
1,5 |
2 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
|
|
ряд |
|||||||||||||
|
2-й |
1,125 |
1,375 |
1,75 |
2,25 |
2,75 |
3,5 |
4,5 |
5,5 |
7 |
8 |
11 |
14 |
|
|
ряд |
Прежде чем выполнить чертеж зубчатого колеса или его твердотельную модель, необходимо выполнить расчеты геометрических параметров и определить размеры всех частей зубчатого колеса. Обычно сначала рассчитывают делительный диаметр и межосевое значение передачи, число зубьев, а затем назначают размеры всех остальных частей, которые уточняются при выполнении проверочных расчетов.
ГОСТ 2.403-75 устанавливает правила выполнения рабочих чертежей зубчатых колес. Как правило, учебные чертежи выполняются с допустимыми упрощениями, относительно рабочих чертежей, разрабатываемых в промышленности. На учебных чертежах не наносятся допуски размеров, требования к прочности и точности и детали и т. д. При выполнении чертежей зубчатых колес также следует руководствоваться требованиями ГОСТ 2. 402
На рис. 2 представлен пример выполнения учебного чертежа зубчатого колеса, выполняемого студентами в процессе изучения дисциплины «Инженерная графика».
В соответствии с этими правилами в правом верхнем углу формата должна выполняться таблица параметров, размеры которой показаны на рисунке. Таблица параметров состоит из трех частей, которые должны быть отделены друг от друга сплошными основными линиями. Первая часть таблицы содержит основные параметры необходимые для изготовления зубчатого венца колеса, вторая – данные для контроля размеров зуба и третья
– справочные данные.
На учебных чертежах обычно размещают некоторые данные из первой и третьей части таблицы.

3
ВАРИАНТЫ ЗАДАНИЯ по теме «Зубчатые передачи»
|
№ |
Модуль |
Число |
Толщина |
Длина |
Диаметр |
Диаметр |
||||||||
|
варианта |
— т |
зубьев — z |
обода — В |
ступицы — l |
ступицы-D |
отв. — d |
||||||||
|
1 |
2,5 |
40 |
20 |
30 |
50 |
30 |
||||||||
|
2 |
3 |
30 |
25 |
36 |
60 |
40 |
||||||||
|
3 |
4 |
20 |
15 |
30 |
52 |
35 |
||||||||
|
4 |
4 |
15 |
15 |
25 |
36 |
22 |
||||||||
|
5 |
2 |
45 |
25 |
30 |
70 |
50 |
||||||||
|
6 |
3 |
25 |
20 |
25 |
50 |
35 |
||||||||
|
№ |
Моду |
Число |
Толщин |
Длина |
Диаметр |
Диаметр |
Толщи |
Диаметр |
||||||
|
вариа |
ль — т |
зубьев |
а обода — |
ступицы |
ступицы |
отв. — d |
на |
углубле |
||||||
|
нта |
— z |
В |
— l |
— D |
диска-с |
ния-D1 |
||||||||
|
7 |
2 |
50 |
20 |
28 |
45 |
28 |
7 |
80 |
||||||
|
8 |
3 |
40 |
20 |
25 |
46 |
30 |
8 |
100 |
||||||
|
9 |
2,5 |
36 |
18 |
30 |
70 |
24 |
6 |
70 |
||||||
|
10 |
4 |
25 |
40 |
33 |
30 |
25 |
10 |
80 |
||||||
|
11 |
5 |
24 |
45 |
36 |
40 |
30 |
12 |
100 |
||||||
|
12 |
5 |
22 |
15 |
32 |
42 |
24 |
7 |
95 |
||||||

4
|
№ |
Модуль — |
Число |
Толщина |
Длина |
Диаметр |
Диаметр |
||||||
|
варианта |
т |
зубьев — z |
обода — В |
ступицы — l |
углубления-D |
отв. — d |
||||||
|
13 |
2,5 |
40 |
25 |
18 |
80 |
40 |
||||||
|
14 |
3 |
30 |
25 |
20 |
66 |
40 |
||||||
|
15 |
4 |
20 |
30 |
26 |
52 |
34 |
||||||
|
16 |
4 |
15 |
15 |
12 |
36 |
24 |
||||||
|
17 |
3 |
40 |
35 |
30 |
90 |
45 |
||||||
|
18 |
4 |
25 |
40 |
30 |
70 |
35 |
||||||
|
19 |
3 |
30 |
50 |
40 |
65 |
50 |
||||||
|
№ |
Модуль — |
Число |
Толщина |
Длина |
Диаметр |
Диаметр |
||||||
|
варианта |
т |
зубьев — z |
обода — В |
ступицы — l |
ступицы-D |
отв — d |
||||||
|
20 |
2,5 |
34 |
20 |
28 |
35 |
20 |
||||||
|
21 |
2 |
20 |
12 |
22 |
30 |
16 |
||||||
|
22 |
4 |
23 |
20 |
40 |
50 |
30 |
||||||
|
23 |
2,5 |
28 |
15 |
30 |
50 |
24 |
||||||
|
24 |
2 |
45 |
35 |
45 |
50 |
35 |
||||||
|
25 |
3 |
35 |
20 |
36 |
56 |
35 |
||||||
Примечание. Обод зубчатого колеса расположен относительно ступицы симметрично

5
Рис. 2 Пример выполнения чертежа

6
Справочные данные
Элементы конструкции зубчатых, червячных колес, звездочек,
шкивов, маховиков. Детали, насаживаемые на вал и предназначенные для передачи вращательного движения от одного вала к другому, имеют общие конструктивные элементы, к которым относятся ступицы, диски, спицы, обод и т. д. (рис. 3).
1 – обод
2 – зуб
3 – венец (верхняя часть обода с зубьями)
4 – посадочное отверстие 5 — диск 6 – ступица
7 – отверстия в диске 8 – шпоночный паз
Рис. 3
Обод – наружная рабочая часть шкива, зубчатого колеса, звездочки. Может иметь различные конструктивные исполнения. На деталях зубчатых передач на наружной поверхности обода нарезают зубья, наружную поверхность шкивов плоскоременной передачи выполняют выпуклой, на наружной поверхности шкива для клиноременной передачи выполняют радиальные канавки для клиновых ремней и т. д.
Венец – часть обода зубчатых колес и звездочек, на котором нарезаны зубья.
Диск – часть зубчатого колеса, шкива, звездочки, при помощи которого обод соединяется со ступицей. Диск в деталях простой конструкции и малых размеров выполняется как единое целое вместе с ободом и ступицей. Для облегчения веса тяжелых деталей в диске могут выполняться отверстия (отв. 7 на рис.3), сам диск может быть выполнен в виде спиц, как например, на велосипедном колесе, в сварных зубчатых колесах больших размеров к дискам привариваются ребра для увеличения жесткости колеса.
7
Посадочное отверстие – центральное отверстие в ступице вращающейся детали, которым деталь надевается на вал. Выполняется по точным размерам и может иметь различные формы. Это зависит от вида соединения колеса с валом. В посадочном отверстии могут выполняться различные отверстия и пазы, для предотвращения проворота насаживаемой детали относительно вала. Чаще всего для этой цели выполняют шпоночный паз.
Ступица – центральная часть вращающейся детали вместе с посадочным отверстием. Размеры ступицы выбирают в зависимости от размеров посадочного отверстия. В общем случае наружный диаметр ступицы должен больше диаметра посадочного отверстия в 1,5 раза, длина ступицы приблизительно должна быть равна диаметру отверстия. В отдельных случаях для тяжелонагруженных и ответственных деталей выбранные размеры ступиц проверяются расчетами.
Шпоночный паз – углубление в отверстии или на валу для закладывания в это углубление детали, называемой шпонкой.
Шпонка — крепежная деталь призматической или цилиндрической формы, вставляемая в пазы двух деталей и предотвращающая их относительный поворот или сдвиг. Шпоночное соединение – один из видов соединений вала с втулкой с использованием дополнительного конструктивного элемента (шпонки), предназначенной для предотвращения их взаимного поворота.
Последовательность выполнения чертежа зубчатого колеса
1. По указанным в таблицах данным посчитать три диаметра зубчатого колеса:
диаметр делительной окружности d равен:
d = m Z; .
z — число зубьев колеса m — модуль
Диаметр выступов
dвыст = m (Z + 2);
Диаметр впадин
dвп = m (Z – 2,5).
2.Все остальные размеры даны в таблицах
3.Чертеж выполнять в масштабах 1:1, 1:2 или 2:1 в зависимости от величины изображения зубчатого колеса
4.На ф. А4 выполнить чертеж колеса по примеру на рис. 2: на месте главного вида выполнить разрез, справа на продолжении оси вращения
8
выполнить вынесенное сечение, показывающее контур отв. вместе с размерами шпоночного паза
5.Размеры шпоночного паза выбрать из справочных таблиц призматических шпонок, в зависимости от диаметра отв. колеса из любого учебника по инженерной графике. В качестве справочного пособия можно взять методичку «Конструктивные элементы деталей», стр. 44, табл. П1. (Автор методички Кициева В.Д. Библиотечный шифр 74/М85. Данные по шпонкам есть также в «Техническом черчении» Новичихиной и т. д.)
6.В основной надписи записать условное обозначение материала. Примеры условного обозначения материала есть в вышеуказанном учебнике, также можно взять методичку «Инженерная графика. Чертежи деталей, сборочные чертежи» (Автор методички Кициева В.Д. Библиотечный шифр И622. стр. 49-50.)
7.На чертеже зубчатого колеса в обязательном порядке в правом верхнем углу любого формата помещается таблица со справочными данными. Таблицу заполнить, размеры таблицы на чертеже не наносить.
8.Строчки в табл. «исходный контур, степень точности и справ. данные» оставить свободными.
9.Обозначение шероховатости рабочих боковых поверхностей зубьев проставляют на продолжении штрих-пунктирной линии, показывающей делительный диаметр зубчатого колеса. Обозначение шероховатости впадин
ивершин зубьев наносят на линиях, соответствующих окружностям впадин и окружности вершин зубьев.
10.На изображении зубчатого колеса должны быть нанесены размеры: диаметра окружности вершин зубьев, ширины зубчатого венца, фасок на торцевых кромках цилиндра вершин зубьев. Остальные размеры наносят в зависимости от конструкции зубчатого колеса. Значение делительного диаметра указано в таблице, размер диаметра впадин на чертеже не указывают. Расположение делительного диаметра указывают штрих-пунктирной линией. Высоту зуба на разрезе показывают незаштрихованной.
11.Размеры фасок выполнить шириной от 1 до 2 мм, радиусы скруглений от 3 до 5 мм. Фаски выполнить под углом 45 градусов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основу конструкции любого механизма составляют элементы, призванные передать механическое усилие от двигателя на рабочий орган. В зависимости от принципа действия принято различать несколько видов таких передач: клиноременные, фрикционные или червячные. Но самое широкое распространение в технике получили зубчатые передачи.
Такие механизмы в простейшем случае использующие сопрягаемую пару, включающую ведущую шестерню и колесо зубчатое. Благодаря зубчатой форме поверхности эти элементы входят в зацепление между собой и за счет этого передают вращение с одного вала на другой. Кроме возможности передать механическую мощность, такая передача способна обеспечить изменение скорости вращения выходного вала, относительно входного. Благодаря таким свойствам, практически в каждом промышленном механическом устройстве встречается редуктор, понижающий скорость вращения или мультипликатор, наоборот увеличивающий ее. В более сложных механизмах, так называемых коробках передач, группа зубчатых колес способна выполнить ступенчатое изменение скорости.
Широкое распространениезубчатые передачи получили благодаря высокой надежности и способности передавать момент в большом диапазоне нагрузок и скоростей вращения. При этом конструкция таких механизмов отличается относительной простотой и компактностью. Зубчатые передачи не предъявляют высоких требований к обслуживанию и характеризуются длительным сроком службы.
Наряду с очевидными достоинствами, этим механизмам присущ и ряд недостатков. В отличие от других типов передач, они более сложны в изготовлении, требуют более высокой точности обработки и применения специализированного обрабатывающего оборудования. Выбор материалов для зубчатых колес должен обеспечить сопротивляемость значительным механическим усилиям. Высокая жесткость, реализуемая зубчатой передачей, способствует минимизации потерь при передаче механической энергии. КПД таких механизмов приближаются к абсолютным значениям. Но при этом конструкция не позволяет преодолевать большие значения динамической нагрузки, что часто приводит к разрушению механизма. Еще одним негативным явлением, возникающим в процессе работы зубчатой пары, становится шум. Его уровень напрямую связан частотой вращения механизма и зависит от качества изготовления колес.
Виды зубчатых колес
Само название зубчатой передачи отражает ее конструкцию. В простейшем случае в состав такого механизма входят два вращающихся диска, на боковой поверхности, которых выполнены зубья. В процессе работы эти зубья зацепляются между собой. Колесо, связанное с источником вращающего момента, увлекает за собой второе. В итоге ведомый вал начинает вращаться.
В зависимости от направления передачи энергии используются разные обозначения зубчатых колес. Элемент, к которому присоединен вал двигателя, называется ведущим зубчатым колесом. В понижающих передачах оно характеризуется небольшим диаметром и малым числом зубьев. В технической литературе этот элемент часто называют шестерней. Сопрягаемое с ней колесо большого диаметра с большим числом зубьев называется ведомым. Вал этого колеса используется для передачи мощности на рабочий орган исполнительного механизма. Более сложные виды передач используют большее количество зубчатых колес. Например, такие устройства используются для реализации возможности отбора мощности от одного вала на несколько устройств или переключения скоростей вращения.
Высокие технические характеристики передачи и различные направления применения привели к созданию большого числа вариантов зубчатых колес. Наиболее простыми и распространенными из них являются цилиндрические прямозубые колеса. Зуб такой детали расположен на боковой поверхности колеса, параллельно оси. Второе колесо механической передачи имеет аналогичную геометрию. Оси обеих колес должны располагаться параллельно, на строго заданном расстоянии. Высокая технологичность изготовления этого типа деталей способствует массовому применению прямозубых передач в различных отраслях промышленности.
Из недостатков следует отметить только невысокий предельный момент. В сложных условиях работы используют другие виды зубчатых колес. Благодаря изменению геометрии зацепления, такие передачи обладают улучшенными свойствами. Например, для передач повышенной мощности проектируют косозубые колеса. В них ось зуба расположена под углом к оси вращения, за счет чего достигается большая зона контакта сопрягаемых деталей. В механизмах, характеризующихся сверхтяжелыми нагрузками, применяют шевронные модели. Зацепление в такой передаче выполняется на основе V-образных зубьев, чем обеспечивается оптимальное распределение нагрузки. Еще один вид зуба, называемый, круговым или криволинейным, выполняется в виде дуги. Он обеспечивает улучшенные механические характеристики, но достаточно трудоемок в изготовлении, поэтому большого распространения не получил.
Профиль или поперечное сечение зуба в механических передачах может быть практически любым. Встречаются варианты с треугольным, трапециевидным, прямоугольным или круглым профилем. Всем им, несмотря на простоту изготовления, свойственны недостатки, связанные с неравномерностью зацепления. Поэтому, в современных механических передачах, профиль чаще всего выполняется эвольвентным. Он представляет собой сложную кривую, обеспечивающую постоянное качество зацепления, вне зависимости от углового положения отдельных деталей и как следствие постоянство передаточного отношения. Такой профиль показывает оптимальные характеристики и относительно прост в изготовлении.
Кроме вида и профиля зуба, принято выделять и место его расположения. В зависимости от назначения, элементы зацепления могут быть расположены на внешней или внутренней части колеса. Также встречаются колеса с расположением зацепляющихся элементов со стороны торцевой части. Подобные шестерни называют корончатыми. Область их применения достаточно узка, поэтому встречаются они сравнительно редко. Гораздо более широкое применение получили передачи конического типа. Элементы зацепления в таких механизмах выполнены на поверхности усеченного конуса. Результирующее расположение конических шестерен подразумевает разное положение их осей в пространстве.
Еще один вид зубчатой передачи применяется в механизмах, преобразующих вращательное движение в возвратно-поступательное. Общее название таких устройств — рейка-шестерня.
Ведущий элемент такой передачи выполнен в виде обычного зубчатого колеса. Ведомая деталь представляет собой рейку, с нанесенными на одной из граней, зубьями. Вращение шестерни приводит к продольному перемещению рейки. Подобные передачи широко распространены в станочном оборудовании.
С зубчатыми колесами часто сравнивают звездочки цепных передач. Схожая форма деталей приводит к путанице. На самом деле цепная передача имеет иной принцип действия, а конструкция звездочки рассчитывается по собственным формулам.
Редкие модели
В общем случае считается, что зубчатое колесо должно иметь цилиндрическую форму. Но встречаются модели и некруглого типа. Главной их особенностью является переменное передаточное отношение, зависящее от угла поворота детали. Сегодня разработаны модели треугольной и квадратной формы, а также эллиптические шестерни. При постоянном вращении ведущего вала эти модели обеспечивают неравномерную скорость выходного. Высокая сложность изготовления и ограниченная область применения не дали подобным конструкциям широкого распространения. Тем не менее, сегодня встречаются отдельные устройства, в составе которых можно встретить некруглые шестерни. Примером могут служить редукторы некоторых насосов или специфические измерительные приборы.
Конструкция зубчатого колеса
Несмотря на кажущуюся простоту, в технике принято выделять несколько отдельных частей зубчатого колеса. Как и любое другое колесо, зубчатый вариант в своей основе имеет диск необходимого диаметра. Основной частью является обод, на боковой или торцевой поверхности которого выполнены зубья. Все вместе они образуют так называемый венец зубчатого колеса. Геометрия зубьев различна у разных типов зубчатой передачи. Сам зуб условно разбивается на несколько частей. Наружная часть называется вершиной. Прилегающие к ней боковые поверхности носят название головки зуба. Внутренняя часть именуется ножкой зуба. Две соседние ножки образуют впадину зубчатого колеса.
Для крепления на валу механизма в центре диска изготавливается ступица со сквозным отверстием. Форма отверстия зависит от геометрии сечения вала и может быть цилиндрической, квадратной или многоугольной. При использовании цилиндрических валов, в ступице обычно выполняют шпоночный паз.
С целью уменьшения веса толщина диска колеса выполняется обычно меньше, чем толщина ступицы или обода. Также для этого в теле диска могут присутствовать окна разнообразной формы.
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Диаметры окружностей
Рассмотрение геометрии зубчатых пар невозможно без определения диаметров. На каждой детали их выделяется несколько. Широкое распространение имеет диаметр окружности по выступам, иногда называемый диаметром вершин. Он определяет максимальные габариты диска колеса. Его противоположностью считается диаметр окружности впадин. Разность этих величин, поделенная пополам, дает полную длину зуба. Но этот параметр в чистом виде не используется. При расчетах принято выделять высоту головки и ножки зуба. Граница, отделяющая два этих понятия, называется делительной окружностью зубчатого колеса. Диаметр данной окружности выполняет функцию опорного параметра при выполнении расчетов геометрии, так как именно по ней определяется окружной шаг и модуль зацепления. Еще один диаметральный параметр, называемый основной окружностью, описывает теоретическую кривую, которая является базой при построении эвольвенты. Диаметр основной окружности используется для построения конкретного профиля зуба.
Модуль зубчатого колеса
Универсальным понятием, позволяющим определить геометрические параметры деталей, выступает модуль зубчатой передачи. Его значение равно длине дуги в миллиметрах, приходящейся на один зуб колеса. Конкретное значение определяется по делительной окружности. Ее численно подбирают таким образом, что бы значение модуля совпадало с одним из общепринятых значений, найти которые можно в специальной литературе. В отечественной практике стандартные модули зубчатых колес нормированы в ГОСТ 9563-60. При проектировании шестерен обычно задаются значением этого параметра, а от него легко рассчитают все множество других. Исходными данными для определения требуемого модуля зубчатого колеса выступают расчеты прочности, призванные обеспечить требуемую мощность механической передачи.
Скачать ГОСТ 9563-60
Модуль зубчатого колеса связан с целым набором производных параметров. Используя несложные формулы расчета и значение необходимого числа зубьев, можно получить окружной шаг, диаметры верши и впадин, толщину зуба и ширину впадины по делительной окружности.
В зарубежной литературе аналогом отечественного модуля выступает питч. По своей сути это обратная к модулю зацепления величина, приведенная к дюймовой системе измерений. Аналогично для питчей разработаны специальные таблицы, содержащие нормированные значения параметра.
Расчет параметров
Расчет параметров зубчатых колес выполняют комплексно, для всей передачи. Необходимость расчета отдельного колеса возникает только в процессе ремонта оборудования с неизвестными данными. Расчет начинают с определения требуемого числа зубьев и модуля зацепления. Для того чтобы узнать значение модуля, предварительно проводят расчеты на прочность, исходя из срока службы и выбранного материала будущего механизма. Также на этом этапе рассчитывают межосевое расстояние между колесами. На основе полученных данных выносливости зубьев вычисляется минимально допустимая величина модуля зацепления. Конкретное его значение выбирается на основе таблиц, приведенных в справочной литературе. Далее, используя требуемое передаточное отношение, производится вычисление числа зубьев на сопрягаемых колесах.
При известном модуле зацепления и количестве зубьев шестерни и колеса, доступно произвести вычисление геометрических размеров отдельных деталей. Основные диаметры и профиль зуба передачи рассчитываются с использованием несложных арифметических действий. Сложные операции потребуются только для ограниченного числа параметров. Для цилиндрического прямозубого колеса тригонометрические функции содержат только формулы расчета делительного диаметра. При проектировании других типов зубчатых колес, используют тот же математический аппарат, что и для прямозубых, но с добавлением расчетов, учитывающих иную геометрию деталей. Результаты расчетов используют для построения чертежей будущих шестерен, а также при вычислении параметров редукторов.
Заключительным этапом расчета зубчатой передачи становится окончательная проверка механизма на прочность. Если результаты этих вычислений укладываются в принятые нормативы, то полученные значения величин можно использовать для изготовления готового механизма. В противном случае может потребоваться выполнить новый расчет, изменив исходные данные, например, увеличить геометрические размеры, либо поменять тип зубчатой передачи или количество ступеней редуктора.
Применение
Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.
С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Зубчатые передачи позволяют реализовать и функцию регулирования скорости. Для этого применяются сменные комплекты колес, имеющих одинаковое межосевое расстояние и разное передаточное отношение.
Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.
Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма. Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.
Зубчатые колеса используются также для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.
Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой массой и стоимостью.
Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач, отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.




















