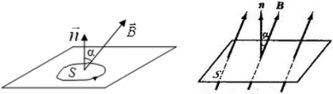
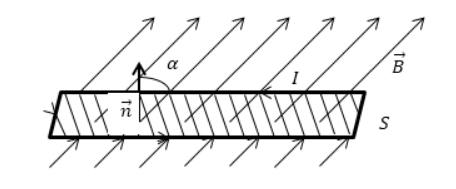
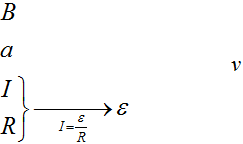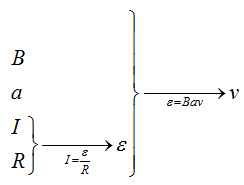Как найти дельта ф магнитный поток - Исправление недочетов и поиск решений вместе с Examum.ru

Магнитный поток, проходящий через площадь S равен:

Ф = BScosα;

где:

Ф ― величина магнитного потока [Вб],

S ― площадь контура [м2],

B ― индукция магнитного поля [Тл],

α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.

Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:

Ф = BScos90° = BS;

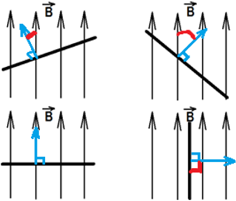
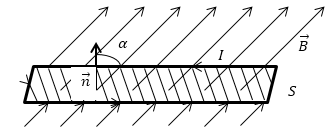
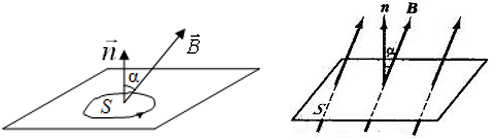
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

где:

$varepsilon_i $ ― ЭДС электромагнитной индукции [B],

$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],

∆Ф ― изменение магнитного потока [Вб],

∆t ― время, за которое происходит это изменение [c].

Кроме того, ЭДС индукции равна производной магнитного потока по времени:

$varepsilon_i = -text{Ф}_t’$

где:

― ЭДС электромагнитной индукции [B],
― производная магнитного потока по времени [Вб/с].

Задача 1

Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?

Решение:

Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.

Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.

По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$

И это очень важный момент, без которого мы не сможем решить такого рода задачу.

Теперь посчитаем ЭДС индукции.

Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса

$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.

Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$

Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).

Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.

По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.

Мы получили зависимость силы тока от времени.

Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.

В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.

Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.

Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$

Ответ: 0,002

Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:

увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
изменением направления вектора магнитного поля (т. е. изменением угла α);
деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
изменением нескольких из этих величин одновременно.

Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.

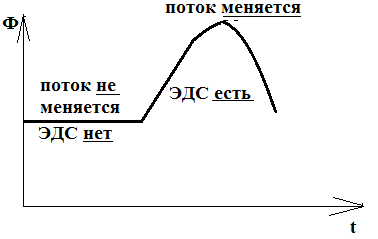
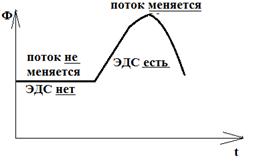
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:

Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Задача 2

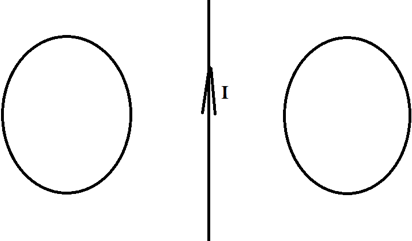
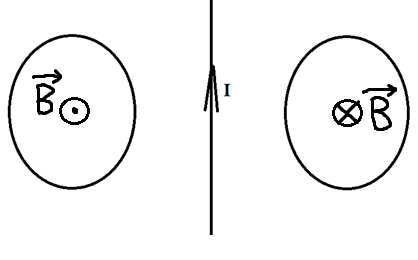
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?

Решение:

Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?

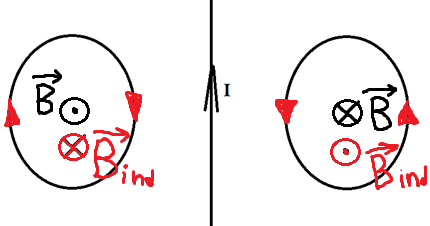
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.

Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?

Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.

Движение проводников

Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).

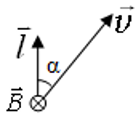
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;

где:

$varepsilon_i$― ЭДС электромагнитной индукции [B],

B ― индукция магнитного поля [Тл],

l ― длина проводника [м],

v ― скорость движения проводника [м/с],

α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$

Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.

В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.

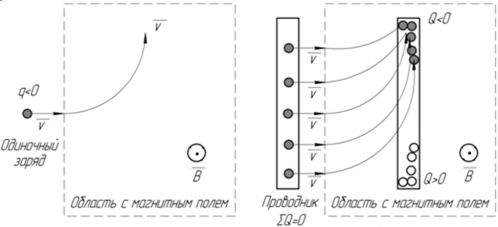
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.

В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;

где:

U — разность потенциалов [В],

l — длина проводника [м],

v — скорость движения проводника $big[ frac{text{м}}{c} big]$

B — индукция магнитного поля [Тл],

α — угол между направлением скорости и длиной проводника.

В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.

В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = — frac{Delta text{Ф}}{Delta t}$

В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.

Задача 3

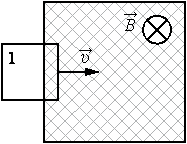
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

Решение:

Составим цепочку.

Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.

Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.

А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.

Пройдёмся вдоль этой цепочки.

Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$

Ответ: 1

Источник

Поток вектора магнитной индукции (магнитный поток)

Роман Алексеевич Лалетин

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Определение

Потоком вектора магнитной индукции (магнитным потоком) (Ф) через площадку S называют скалярную величину равную:

[Ф=BScosalpha ={ B}_nS=overrightarrow{B}overrightarrow{S}left(1right),]

где $alpha $ угол между $overrightarrow{n}$ и $overrightarrow{B}$, $overrightarrow{n}$ — нормаль к площадке S.

Ф равен количеству линий магнитной индукции, которые пересекают площадку S (рис.1). Поток магнитной индукции может быть положительным и отрицательным. Знак потока зависит от выбора положительного направлении нормали к площадке S. Обычно, положительное направление нормали связывают с направлением обхода контура током. За положительное направление нормали принимают поступательное перемещение правого винта, при вращении его по току.

Рис. 1

В том случае, если магнитное поле неоднородно, S не является плоской, то поверхность можно разбить на элементарные площадки dS, которые рассматриваются как плоские, а поле на этой площадке можно считать однородным. В таком случае магнитный поток (dФ) можно через такую поверхность определить как:

[dФ=BdScosalpha =overrightarrow{B}doverrightarrow{S}left(2right).]

Тогда полный поток через поверхность S находится как:

[Ф=intlimits_S{BdScosalpha =intlimits_S{overrightarrow{B}doverrightarrow{S}}left(3right).}]

Основная единица измерения магнитного потока в системе СИ — вебер (Вб). $1 Вб=frac{1Тл}{1м^2}$.

Связь магнитного потока и работы сил магнитного поля

Элементарную работу ($delta A$), которую совершают силы магнитного поля можно выразить через элементарное изменение потока вектора магнитной индукции (dФ):

[delta A=IdФ left(4right).]

В том случае, когда проводник с током совершил конечное перемещение, а сила тока постоянна, то работа сил поля равна:

[A=Ileft(Ф_2-Ф_1right)left(5right),]

где $Ф_1$ — поток через контур в начале перемещения, $Ф_2$ — поток через контур в конце перемещения.

Теорема Гаусса для магнитного поля

Суммарный магнитный поток через замкнутую поверхность S равен нулю:

[oint{overrightarrow{B}doverrightarrow{S}}=0 (6) .]

Уравнение (6) справедливо для любых магнитных полей. Это уравнение аналог теоремы Остроградского — Гаусса в электростатике (в вакууме):

[oint{overrightarrow{E}doverrightarrow{S}}=frac{q}{{varepsilon }_0}left(7right).]

Уравнение (6) означает, что источником магнитного поля являются не магнитные заряды (их в природе не существует), а электрические токи. Данную теорему мы подробно рассматривали в разделе «Отсутствие в природе магнитных зарядов».

Пример 1

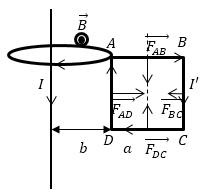
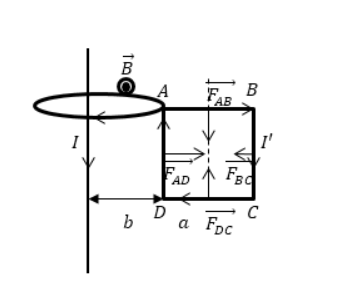
Задание: Недалеко от бесконечно длинного прямого проводника с током I находится квадратная рамка, по которой течет ток с силой $I’$. Сторона рамки равна $а$. Рамка лежит в плоскости с проводом (рис.2). Расстояние от ближайшей стороны рамки до проводника равно b. Найдите работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

Рис. 2

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направлена на нас.

Решение:

При решении этой задачи необходимо помнить, что рамка с током находится в неоднородном поле, магнитная индукция убывает при удалении от провода.

В качестве основы для решения задачи используем формулу связи потока и работы:

[A=I’left(Ф_2-Ф_1right)left(1.1right),]

$I’$- сила тока в рамке, $Ф_1$- поток через квадратную рамку, когда расстояние от ее стороны, ближайшей к проводу равна $b$. $Ф_2=0$, так как в конечном положении рамка вне магнитного поля по условию. Следовательно, формула (1.1) запишется как:

[A=-I’Ф_1left(1.2right).]

Выберем направление нормали ($overrightarrow{n}$) к квадратному контуру от нас (по правилу правого винта). Тогда для всех элементов поверхности, которая ограничена контуром квадратной рамки угол между нормалью $overrightarrow{n}$ и вектором $overrightarrow{B}$ равен $pi $. Тогда формула для потока через поверхность рамки на расстоянии x от провода имеет вид:

[dФ=-BdS=-Bcdot acdot dх=-frac{{mu }_0}{2pi }Ilfrac{dх}{х} left(1.3right),]

где индукция магнитного поля бесконечно длинного проводника с током силы I равна:

[B=frac{mu_0}{2pi х}Illeft(1.4right).]

Следовательно, весь поток из (1.3) найдем как:

[Ф_1=intlimits_S{-frac{{mu }_0}{2pi }Ilfrac{dх}{х}}=-frac{{mu }_0}{2pi }Ilintlimits^{b+a}_b{frac{dх}{х}}=-frac{{mu }_0}{2pi }Ilcdot lnfrac{b+a}{b}left(1.5right).]

Подставим формулу (1.5) в выражение (1.2) найдем искомую работу:

[A=I’frac{{mu }_0}{2pi }Ilcdot lnfrac{b+a}{b}.]

Ответ: $A=frac{{mu }_0}{2pi }II’lcdot lnfrac{b+a}{b}.$

«Поток вектора магнитной индукции (магнитный поток)» 👇

Пример 2

Задание: Найдите силу, которая действует на рамку в предыдущем примере.

Решение:

Для того чтобы найти силу, которая действует на квадратную рамку с током в поле длинного провода положим, что под действием магнитной силы рамка сместилась на малое расстояние dx. В таком случае сила совершает работу равную:

[delta A=Fdx (2.1)]

Элементарную работу $delta A$ с другой стороны выразим как:

[delta A=I’dФ left(2.2right).]

Выразим силу, используя (2.1) и (2.2), получим:

[Fdx=I’dФ to F=I’frac{dФ}{dx}left(2.3right).]

Используя формулу, полученную в примере 1:

[dФ=-frac{{mu }_0}{2pi }Ilfrac{dх}{х} to frac{dФ}{dx}=-frac{{mu }_0}{2pi }frac{Il}{х} left(2.4right).]

Подставим $frac{dФ}{dx}$ в выражении для модуля силы (2.3), получим:

[F=I’frac{{mu }_0}{2pi }frac{Il}{х}left(2.5right).]

На каждый элемент контура квадратной рамки действует сила (сила Ампера), всего на рамку действует четыре составляющих силы, однако, очевидно, что силы, которые действуют на стороны AB и DC равны по модулю и противоположны по направлению:

[overrightarrow{F_{AB}}+overrightarrow{F_{DC}}=0 (2.6)]

их сумма равна нулю, в таком случае, результирующая сила, приложенная к контуру будет:

[overrightarrow{F}=overrightarrow{F_{AD}}+overrightarrow{F_{BC}}left(2.6right).]

Эти силы, в соответствии с правилом левой руки, направлены вдоль одной прямой в противоположные стороны, то есть:

[F=F_{AD}-F_{BC} left(2.7right).]

Найдем силу $F_{AD,}$ используя формулу (2.5), где $x=b$, получим:

[F_{AD}=I’frac{м_0}{2pi}frac{Il}{b}left(2.8right).]

Тогда $F_{BC}$ равна:

[F_{BC}=I’frac{{mu }_0}{2pi }frac{Il}{b+a}left(2.9right).]

Искомая сила получается равной:

[F=I’frac{{mu }_0}{2pi }frac{Il}{b}-I’frac{{mu }_0}{2pi }frac{Il}{b+a}={II}’frac{{mu }_0l}{2pi }left(frac{1}{b}-frac{1}{b+a}right).]

Ответ: $F={II}’frac{{mu }_0l}{2pi }left(frac{1}{b}-frac{1}{b+a}right). $Магнитные силы выталкивают рамку стоком, пока она сохраняет первоначальную ориентацию относительно поля провода.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 10.02.2023

Источник

Индукция

Магнитный поток, проходящий через площадь S равен Ф = BS cosα, где:

Ф ― величина магнитного потока, [Вб];

S ― площадь контура, [м²];

B ― индукция магнитного поля, [Тл];

α ― угол между нормалью (overrightarrow{n}) к площади контура и вектором индукции магнитного поля (overrightarrow{B}).

Если вектор индукции магнитного поля (overrightarrow{B}) перпендикулярен площади контура, то магнитный поток равен Ф = BS cos 90° = BS.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока: (varepsilon_{i} = — frac{mathrm{Delta}Ф}{mathrm{Delta}t}), где:

ε_i ― ЭДС электромагнитной индукции, [B];

(frac{mathrm{Delta}Ф}{mathrm{Delta}t}) ― скорость изменения магнитного потока, [Вб/с];

∆Ф ― изменение магнитного потока, [Вб];

∆t ― время, за которое происходит это изменение, [c].

В пределе, при ∆t → 0 ЭДС индукции равна производной магнитного потока по времени:

(varepsilon_{i} = — frac{mathrm{Delta}Ф}{mathrm{Delta}t} = — Ф'(t)), где:

ε_i ― ЭДС электромагнитной индукции, [B];

Ф^’_t ― производная магнитного потока по времени, [Вб/с].

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобочках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

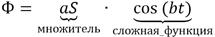
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что (varepsilon_{i} = — Ф'(t)).

Подставив сюда значение производной, получим (varepsilon_{i})= abS · sin (bt).

Либо так, тогда будет меняться поток и возникать ЭДС:

Как видно из формулы магнитного потока Ф = BS cosα, изменение магнитного потока может быть вызвано разными факторами:

Увеличением или уменьшением модуля индукции магнитного поля (соответственно, величины (frac{mathrm{Delta}B}{mathrm{Delta}t}));
Изменением направления вектора магнитного поля (т. е. изменением угла α);
Деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины (frac{mathrm{Delta}S}{mathrm{Delta}t}));
Изменением нескольких из этих величин одновременно.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Самоиндукция

При изменении тока через катушку в ней возникает ЭДС самоиндукции, которое будет мешать протеканию тока : (varepsilon_{i} = — Lfrac{mathrm{Delta}I}{mathrm{Delta}t}), где:

(varepsilon) — ЭДС [В];

(L) — индуктивность [Гн];

(mathrm{Delta}I) — изменение тока [А];

(mathrm{Delta}t) — время изменения тока [с];

ЭДС самоиндукции, так же как и обычное ЭДС — это производная(text{ ε}_{i} = — LI’), где

(varepsilon) — ЭДС самоиндукции [В];

(L) — индуктивность [Гн];

(I) — производная тока [А/с].

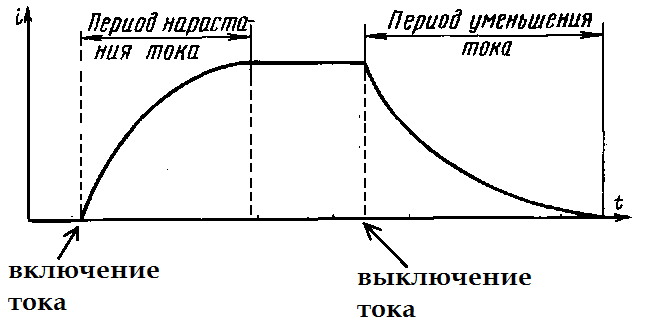
ЭДС самоиндукции приводит к тому, что при подключении цепи с катушкой к источнику тока, сила тока в цепи нарастает постепенно, а не сразу принимает постоянное значение – из-за того, что в момент включения в цепи возникают индукционные токи, стремящиеся уменьшить общий ток в цепи.

При отключении цепи с катушкой от источника тока, ЭДС самоиндукции наоборот приводит к тому, что ток в цепи медленно затухает, а не исчезает сразу – из-за наличия индукционных токов.

Источник

Закон электромагнитной индукции

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Магнитный поток

Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.

Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.

Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции B, площади поверхности S, пронизываемой данным потоком, и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Магнитный поток

Ф — магнитный поток [Вб]

B — магнитная индукция [Тл]

S — площадь пронизываемой поверхности [м^2]

n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла α магнитный поток может быть положительным (α 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.

Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки

Вот, что показали эти опыты:

Индукционный ток возникает только при изменении линий магнитной индукции.
Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Закон Фарадея

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Закон Фарадея для контура из N витков

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

N — количество витков [-]

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:

Закон Ома для проводящего контура

Ɛi — ЭДС индукции [В]

I — сила индукционного тока [А]

R — сопротивление контура [Ом]

Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:

ЭДС индукции для движущегося проводника

Ɛi — ЭДС индукции [В]

B — магнитная индукция [Тл]

v — скорость проводника [м/с]

l — длина проводника [м]

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.

Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.

Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.

Поток вектора магнитной индукции

Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:

Φ = B S cos α = B n S = B → S → с углом между n → и B → , обозначаемым α , n → является нормалью к площадке S .

Формула магнитного потока

Φ равняется количеству линий магнитной индукции, пересекающих площадку S , как показано на рисунке 1 . Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S . Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.

В чем измеряется магнитный поток

В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки d S , рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока d Φ производится через эту поверхность. Запись примет вид:

d Φ = B d S cos α = B → d S → .

Нахождение полного потока через поверхность S :

Φ = ∫ S B d S cos α = ∫ S B → d S → .

Основной единицей измерения магнитного потока в системе СИ считаются веберы ( В б ) . 1 В б = 1 Т л 1 м 2 .

Связь магнитного потока и работы сил магнитного поля

Элементарная работа δ A , совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции d Φ :

Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:

A = I Φ 2 — Φ 1 с Φ 1 , обозначаемым потоком через контур в начале перемещения, Φ 2 является потоком через контур в конце перемещения.

Теорема Гаусса для магнитного поля

Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:

Выражение ∮ B → d S → = 0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:

Запись ∮ B → d S → = 0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.

Дан бесконечно длинный прямой проводник с током I , недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I ‘ . Сторона рамки равна a . Она располагается в одной плоскости с проводом, как показано на рисунке 2 . Значение расстояния от ближайшей стороны рамки до проводника равняется b . Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.

Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.

За основу возьмем формулу магнитного потока и работы, которая их связывает:

A = I ‘ Φ 2 — Φ 1 ( 1 . 1 ) , где I ‘ принимают за силу тока в рамке, Φ 1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b . Φ 2 = 0 . Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы ( 1 . 1 ) изменится:

A = — I ‘ Φ 1 ( 1 . 2 ) .

Перейдем к нормали n → и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n → и вектором B → равняется π . Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:

d Φ = — B d S = — B · a · d x = — μ 0 2 π I l d x x ( 1 . 3 ) , значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:

B = μ 0 2 π x I l ( 1 . 4 ) .

Отсюда следует, что для нахождения всего потока из ( 1 . 3 ) потребуется:

Φ 1 = ∫ S — μ 0 2 π I l d x x = — μ 0 2 π I l ∫ b b + a d x x = — μ 0 2 π I l · ln b + a b ( 1 . 5 ) .

Произведем подстановку формулы ( 1 . 5 ) в ( 1 . 2 ) . Искомая работа равняется:

A = I ‘ μ 0 2 π I l · ln b + a b .

Ответ: A = μ 0 2 π I I ‘ l · ln b + a b .

Найти силу, действующую на рамку, из предыдущего примера.

Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние d x . Это говорит о совершении силой работы, равной:

δ A = F d x ( 2 . 1 ) .

Элементарная работа δ A может быть выражена как:

δ A = I ‘ d Φ ( 2 . 2 ) .

Произведем то же с силой, применяя формулы ( 2 . 1 ) , ( 2 . 2 ) . Получаем:

F d x = I ‘ d Φ → F = I ‘ d Φ d x ( 2 . 3 ) .

Используем выражение, которое было получено в примере 1 :

d Φ = — μ 0 2 π I l d x x → d Φ d x = — μ 0 2 π I l x ( 2 . 4 ) .

Произведем подстановку d Φ d x в ( 2 . 3 ) . Имеем:

F = I ‘ μ 0 2 π I l x ( 2 . 5 ) .

Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны A B и D C равные по модулю и противоположные по направлению. Выражение принимает вид:

F A B → + F D C → = 0 ( 2 . 6 ) , то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:

F → = F A D → + F B C → ( 2 . 6 ) .

Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:

F = F A D — F B C ( 2 . 7 ) .

Произведем поиск силы F A D , действующей на сторону A D , применив формулу ( 2 . 5 ) , где x = b :

F A D = I ‘ м 0 2 π I l b ( 2 . 8 ) .

Значение F B C будет:

F B C = I ‘ μ 0 2 π I l b + a ( 2 . 9 ) .

Для нахождения искомой силы:

F = I ‘ μ 0 2 π I l b — I ‘ μ 0 2 π I l b + a = I I ‘ μ 0 l 2 π 1 b — 1 b + a .

Ответ: F = I I ‘ μ 0 l 2 π 1 b — 1 b + a . Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.

Поток вектора магнитной индукции (магнитный поток)

Вы будете перенаправлены на Автор24

Определение

где $alpha $ угол между $overrightarrow$ и $overrightarrow$, $overrightarrow$ — нормаль к площадке S.

Тогда полный поток через поверхность S находится как:

Основная единица измерения магнитного потока в системе СИ — вебер (Вб). $1 Вб=frac<1Тл><1м^2>$.

Связь магнитного потока и работы сил магнитного поля

[delta A=IdФ left(4right).]

где $Ф_1$ — поток через контур в начале перемещения, $Ф_2$ — поток через контур в конце перемещения.

Теорема Гаусса для магнитного поля

Суммарный магнитный поток через замкнутую поверхность S равен нулю:

В качестве основы для решения задачи используем формулу связи потока и работы:

Выберем направление нормали ($overrightarrow$) к квадратному контуру от нас (по правилу правого винта). Тогда для всех элементов поверхности, которая ограничена контуром квадратной рамки угол между нормалью $overrightarrow$ и вектором $overrightarrow$ равен $pi $. Тогда формула для потока через поверхность рамки на расстоянии x от провода имеет вид:

где индукция магнитного поля бесконечно длинного проводника с током силы I равна:

Следовательно, весь поток из (1.3) найдем как:

Подставим формулу (1.5) в выражение (1.2) найдем искомую работу:

источники:

http://zaochnik.com/spravochnik/fizika/magnitnoe-pole/potok-vektora-magnitnoj-induktsii/

http://spravochnick.ru/fizika/postoyannoe_magnitnoe_pole/potok_vektora_magnitnoy_indukcii_magnitnyy_potok_/

Источник

Магнитный поток

Скалярное произведение вектора площади (Deltavec{S}) на вектор магнитной индукции (vec{B}) называют потоком вектора магнитной индукции (магнитным потоком) через площадь (Delta vec{S}):

(boxed{Phi=vec{B}cdotvec{S}}). ((1))
Полный поток через некоторую поверхность может быть записан в виде:
(Phi=sum limits_{i} B_i S_i cos{alpha_i}). ((2))
В том случае, если контур является плоским, а магнитное поле — однородным, то магнитный поток может быть определён по формуле:
(boxed{Phi=B S cos{alpha}}), ((3))
где (alpha) — угол между векторами (vec{B}) и (vec{S}).
Размерность магнитного потока: ([Phi]=1, Вб=1, В cdot c).
Линии магнитного поля замкнуты, поэтому количество линий, которые входят в замкнутую поверхность, такое же, как количество линий, выходящих из неё, следовательно, поток вектора магнитной индукции через такую поверхность равен нулю.

Явление электромагнитной индукции

В (1831) году Фарадей, ставя опыты, обнаружил интересный эффект. На железном сердечнике намотаны две катушки. Первая из них подключается к источнику тока, а вторая — к гальванометру (рис. (1)). При включении тока в первой катушке стрелка гальванометра отклоняется.

Рис. (1). Опыт Фарадея

Явление электромагнитной индукции объясняется следующим образом. Когда в первой катушке включается электрический ток, в сердечнике начинает появляться магнитное поле. Магнитное поле, увеличивающееся со временем, создаёт во второй катушке ток. Из-за этого тока появляется магнитное поле, которое препятствует нарастанию поля во второй катушке. Ток, создаваемый магнитным полем, называется индукционным током.
Важно отметить, что направление этого тока не противоречит закону сохранения энергии. Поскольку если бы индукционный ток шёл в другую сторону, то небольшое увеличение магнитного поля в катушке приводило бы к бесконечному увеличению поля, которое снова создавало бы ток, который бы ещё увеличивал магнитное поле… И так могло бы повторяться до бесконечности.

Правило Ленца

При увеличении (уменьшении) магнитного потока, пронизывающего катушку, в ней начинает течь индукционный ток, направленный так, что магнитное поле, созданное им, препятствует любому изменению магнитного потока через катушку.

Закон электромагнитной индукции

Количественно из эксперимента было получено, что сила индукционного тока пропорциональна скорости изменения магнитного потока:
(Isim frac{Delta Phi}{Delta t}). ((4))

В замкнутом контуре ЭДС электромагнитной индукции по величине равна скорости изменения магнитного потока и направлена таким образом, чтобы препятствовать этому изменению:
(boxed{E_i=-frac{Delta Phi}{Delta t}=-Phi’}). ((5))

Источники:

Источник