Как рассчитать дельту
Четвертой буквой греческого алфавита, «дельтой», в науке принято называть изменение какой-либо величины, погрешность, приращение. Записывается этот знак различными способами: чаще всего в виде небольшого треугольника Δ перед буквенным обозначением величины. Но иногда можно встретить и такое написание δ, либо латинской строчной буквой d, реже латинской прописной — D.

Инструкция
Для нахождения изменения какой-либо величины вычислите или измерьте ее начальное значение (x1).
Вычислите или измерьте конечное значение этой же величины (x2).
Найдите изменение данной величины по формуле: Δx=x2-x1. Например: начальное значение напряжения электрической сети U1=220В, конечное значение — U2=120В. Изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В-120В=100В
Для нахождения абсолютной погрешности измерения определите точное или, как его иногда называют, истинное значение какой-либо величины (x0).
Возьмите приближенное (при измерении – измеренное) значение этой же величины (x).
Найдите абсолютную погрешность измерения по формуле: Δx=|x-x0|. Например: точное число жителей города — 8253 жителя (х0=8253), при округлении этого числа до 8300 (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет равна Δx=|8300-8253|=47, а при округлении до 8200 (х=8200), абсолютная погрешность — Δx=|8200-8253|=53. Таким образом, округление до числа 8300 будет более точным.
Для сравнения значений функции F(х) в строго фиксированной точке х0 со значениями этой же функции в любой другой точке х, лежащей в окрестностях х0, используются понятия «приращение функции» (ΔF) и «приращение аргумента функции» (Δx). Иногда Δx называют «приращением независимой переменной». Найдите приращение аргумента по формуле Δx=x-x0.
Определите значения функции в точках х0 и х и обозначьте их соответственно F(х0) и F(х).
Вычислите приращение функции: ΔF= F(х)- F(х0). Например: необходимо найти приращение аргумента и приращение функции F(х)=х˄2+1 при изменении аргумента от 2 до 3. В этом случае х0 равно 2, а х=3.
Приращение аргумента (или дельта икс) будет Δx=3-2=1.
F(х0)= х0˄2+1= 2˄2+1=5.
F(х)= х˄2+1= 3˄2+1=10.
Приращение функции (или дельта эф) ΔF= F(х)- F(х0)=10-5=5
Обратите внимание
Вычитать нужно не из большего числа меньшее, а из конечного значения (не важно: больше оно или меньше) начальное!
Полезный совет
При нахождении Δ все значения используйте только в одинаковых единицах измерения.
Источники:
- Справочник по математике для средних учебных заведений, А.Г. Цыпкин, 1983
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Математики любят греческие буквы и используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы символизировать изменение. Когда дело доходит до пары чисел, дельта обозначает разницу между ними. Вы получаете эту разницу, используя основную арифметику и вычитая меньшее число из большего. В некоторых случаях числа располагаются в хронологическом порядке или в некоторой другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.
Абсолютная Дельта
Если у вас есть случайная пара чисел, и вы хотите узнать дельту — или разницу — между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 составляет (6 — 3) = 3.
Если одно из чисел отрицательно, сложите два числа вместе. Операция выглядит следующим образом: (6 — {-3}) = (6 + 3) = 9. Легко понять, почему в этом случае дельта больше, если вы визуализируете два числа на оси x графика. Число 6 равно 6 единицам справа от оси, но отрицательное значение 3 равно 3 единицам слева. Другими словами, он дальше от 6, чем от положительного 3, который находится справа от оси.
Вам нужно запомнить некоторую арифметику вашей начальной школы, чтобы найти дельту между парой дробей. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель в каждой дроби на знаменатель другой дроби. В этом случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая составляет 1/6.
Относительная дельта
Относительная дельта сравнивает разницу между двумя числами, A и B, в процентах от одного из чисел. Базовая формула A — B / A x100. Например, если вы зарабатываете 10 000 долларов в год и жертвуете 500 долларов на благотворительность, относительная дельта вашей зарплаты составляет 10 000 — 500/10 000 x 100 = 95%. Это означает, что вы пожертвовали 5 процентов своей зарплаты, а у вас осталось 95 процентов. Если вы зарабатываете 100 000 долларов в год и делаете то же самое пожертвование, вы сохранили 99, 5% своей зарплаты и пожертвовали только 0, 5% на благотворительность, что не очень впечатляет в момент налогообложения.
От дельты к дифференциалу
Вы можете представить любую точку на двумерном графике парой чисел, которые обозначают расстояние от точки до пересечения осей в направлениях x (горизонтальное) и y (вертикальное). Предположим, у вас есть две точки на графике, называемые точкой 1 и точкой 2, и эта точка 2 находится дальше от пересечения, чем точка 1. Дельта между значениями x этих точек — ∆ x — определяется как (x 2 — x 1), и y для этой пары точек равно (y 2 — y 1). Когда вы делите ∆y на ∆x, вы получаете наклон графика между точками, который говорит вам, как быстро x и y изменяются относительно друг друга.
Склон предоставляет полезную информацию. Например, если вы наносите время вдоль оси x и измеряете положение объекта при его перемещении в пространстве по оси Y, наклон графика показывает среднюю скорость объекта между этими двумя измерениями.
Скорость может быть не постоянной, и вы можете узнать скорость в определенный момент времени. Дифференциальное исчисление обеспечивает концептуальный трюк, который позволяет вам сделать это. Хитрость заключается в том, чтобы представить две точки на оси х и позволить им бесконечно сближаться. Отношение ∆y к ∆x — ∆y / ∆x — при приближении ∆x к 0 называется производной. Обычно это выражается как dy / dx или как df / dx, где f — алгебраическая функция, которая описывает граф. На графике, на котором время (t) отображается на горизонтальной оси, «dx» становится «dt», а производная dy / dt (или df / dt) является мерой мгновенной скорости.
Путь и перемещение, теория и онлайн калькуляторы
Путь и перемещение
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь — длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь — это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
[Delta s=left|x_2-x_1right|left(1right),]
где $x_1$ — координата начального положения тела; $x_2$ — конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
[Delta s=vt left(2right),]
где $t$ — время движения тела.
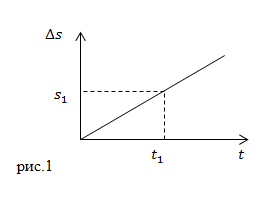
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку ${Delta s}_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
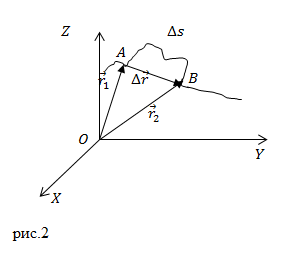
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
[Delta overline{r}=overline{r }left(t+Delta tright)-overline{r }left(tright)left(3right).]
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки — это перемещение ($Delta overline{r}$).
В декартовой системе координат радиус-вектор точки представляют в виде:
[overline{r }left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(4right),]
где $overline{i}$, $overline{j}$,$ overline{k}$ — единичные орты осей X,Y,Z. Тогда $Delta overline{r}$ равен:
[Delta overline{r}=left[xleft(t+Delta tright)-xleft(tright)right]overline{i}+left[yleft(t+?tright)-yleft(tright)right]overline{j}+left[zleft(t+?tright)-zleft(tright)right]overline{k}left(5right).]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overline{r}right|=Delta s left(6right).]
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overline{r}right|$ или просто $Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
[Delta overline{r}=Delta {overline{r}}_1+Delta {overline{r}}_2+dots left(7right).]
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
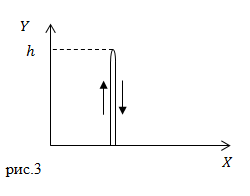
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь — длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
[Delta s=2h.]
Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
[Delta r=0.]
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Пример 2
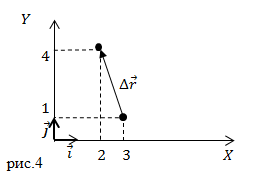
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
Радиус — вектор начальной точки запишем как:
[{overline{r }}_0left(tright)=x_0left(tright)overline{i}+y_0left(tright)overline{j}=3overline{i}+1overline{j}left(2.1right).]
Радиус — вектор конечной точки имеет вид:
[overline{r}left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}=2overline{i}+4overline{j}left(2.2right).]
Вектор перемещения представим как:
[Delta overline{r}=left[xleft(tright)-x_0left(tright)right]overline{i}+left[уleft(tright)-у_0left(tright)right]overline{j}=left[2-3right]+left[1-4right]overline{j}=-1overline{i}+3overline{j}(2.3).]
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Читать дальше: равнодействующая всех сил.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Mathematicians are fond of Greek letters, and they use the capital letter delta, which looks like a triangle (∆), to symbolize change. When it comes to a pair of numbers, delta signifies the difference between them. You arrive at this difference by using basic arithmetic and subtracting the smaller number from the larger one. In some cases, the numbers are in chronological order or some other ordered sequence, and you may have to subtract the larger one from the smaller one to preserve the order. This might result in a negative number.
Absolute Delta
If you have a random pair of numbers and you want to know the delta – or difference – between them, just subtract the smaller one from the larger one. For example, the delta between 3 and 6 is (6 — 3) = 3.
If one of the numbers is negative, add the two numbers together. The operation looks like this: (6 — {-3}) = (6 + 3) = 9. It’s easy to understand why delta is bigger in this case if you visualize the two numbers on the x-axis of a graph. The number 6 is 6 units to the right of the axis, but negative 3 is 3 units to the left. In other words, it’s farther from the 6 than positive 3, which is to the right of the axis.
You need to remember some of your grade school arithmetic to find the delta between a pair of fractions. For example, to find the delta between 1/3 and 1/2, you must first find a common denominator. To do this, multiply the denominators together, then multiply the numerator in each fraction by the denominator of the other fraction. In this case, it looks like this: 1/3 x 2/2 = 2/6 and 1/2 x 3/3 = 3/6. Subtract 2/6 from 3/6 to arrive at the delta, which is 1/6.
Relative Delta
A relative delta compares the difference between two numbers, A and B, as a percentage of one of the numbers. The basic formula is A — B/A x100. For example, if you make $10,000 a year and donate $500 to charity, the relative delta in your salary is 10,000 — 500/10,000 x 100 = 95%. This means you donated 5 percent of your salary, and you still have 95 percent of it left. If you earn $100,000 a year and make the same donation, you’ve kept 99.5 percent of your salary and donated only 0.5 percent of it to charity, which doesn’t sound quite as impressive at tax time.
From Delta to Differential
You can represent any point on a two-dimensional graph by a pair of numbers that denote the distance of the point from the intersection of the axes in the x (horizontal) and y (vertical) directions. Suppose you have two points on the graph called point 1 and point 2, and that point 2 is farther from the intersection than point 1. The delta between the x values of these points – ∆ x – is given by (x2 — x1), and ∆ y for this pair of points is (y2 — y1). When you divide ∆y by ∆x, you get the slope of the graph between the points, which tells you how fast x and y are changing wth respect to each other.
The slope provides useful information. For example, if you plot time along the x-axis and measure the position of an object as it travels through space on the y-axis, the slope of the graph tells you the average speed of the object between those two measurements.
Speed may not be constant, though, and you may want to know the speed at a particular point in time. Differential calculus provides a conceptual trick that allows you to do this. The trick is to imagine two points on the x-axis and allow them to get infinitely close together. The ratio of ∆y to ∆x – ∆y/∆x – as ∆x approaches 0 is called the derivative. It’s usually expressed as dy/dx or as df/dx, where f is the algebraic function that describes the graph. On a graph on which time (t) is mapped on the horizontal axis, «dx» becomes «dt,» and the derivative, dy/dt (or df/dt), is a measure of instantaneous speed.
Как рассчитать дельту между двумя числами
Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу между ними. Вы получаете эту разницу, используя простую арифметику и вычитая меньшее число из большего. В некоторых случаях числа расположены в хронологическом порядке или в другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.
Абсолютная дельта
Если у вас есть случайная пара чисел и вы хотите узнать дельту — или разницу — между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 составляет (6 — 3) = 3.
Если одно из чисел отрицательное, сложите два числа. Операция выглядит так: (6 — <-3>) = (6 + 3) = 9. Легко понять, почему дельта больше в этом случае, если вы визуализируете два числа на оси x графика. Число 6 находится на 6 единиц справа от оси, а отрицательное 3 — на 3 единицы слева.Другими словами, она дальше от 6, чем положительная 3, которая находится справа от оси.
Чтобы найти дельту между парой дробей, вам нужно запомнить некоторые из школьных арифметических действий. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель каждой дроби на знаменатель другой дроби. В данном случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая равна 1/6.
Относительная дельта
Относительная дельта сравнивает разницу между двумя числами, A и B, в процентах от одного из чисел. Основная формула — A — B / A x100. Например, если вы зарабатываете 10 000 долларов в год и жертвуете 500 долларов на благотворительность, относительная разница в вашей зарплате составляет 10 000–500 / 10 000 x 100 = 95%. Это означает, что вы пожертвовали 5 процентов своей зарплаты, и у вас все еще осталось 95 процентов. Если вы зарабатываете 100000 долларов в год и делаете такое же пожертвование, вы оставляете 99,5 процента своей зарплаты и жертвуете только 0,5 процента на благотворительность, что не столь впечатляюще с точки зрения налоговой отчетности.
От дельты к дифференциалу
Вы можете представить любую точку на двумерном графике парой чисел, которые обозначают расстояние от точки до пересечения осей в направлениях x (по горизонтали) и y (по вертикали). Предположим, у вас есть две точки на графике, называемые точкой 1 и точкой 2, и эта точка 2 находится дальше от пересечения, чем точка 1. Дельта между значениями x этих точек — ∆ x — задается выражением (x2 — Икс1), а ∆ y для этой пары точек есть (y2 — у1). Когда вы делите ∆y на ∆x, вы получаете наклон графика между точками, который показывает, насколько быстро x и y изменяются относительно друг друга.
Наклон дает полезную информацию. Например, если вы наносите время на ось x и измеряете положение объекта во время его перемещения в пространстве по оси y, наклон графика показывает вам среднюю скорость объекта между этими двумя измерениями.
Однако скорость может быть непостоянной, и вы можете узнать скорость в определенный момент времени. Дифференциальное исчисление предоставляет концептуальный трюк, который позволяет вам это делать. Уловка состоит в том, чтобы представить две точки на оси x и позволить им приблизиться друг к другу бесконечно близко. Отношение ∆y к ∆x — ∆y / ∆x — когда ∆x приближается к 0, называется производной. Обычно это выражается как dy / dx или как df / dx, где f — алгебраическая функция, описывающая график. На графике, на котором время (t) отложено по горизонтальной оси, «dx» становится «dt», а производная dy / dt (или df / dt) является мерой мгновенной скорости.
Как найти разницу между двумя числами?
Чтобы найти разницу между двумя числами, вычесть число с наименьшим значением из числа с наибольшим значением. Произведение этой суммы и есть разница между двумя числами. Следовательно, разница между 45 и 100 составляет 55.
Кроме того, как рассчитать процент?
Как рассчитать процент
- Определите общую или целую сумму.
- Разделите число, которое будет выражено в процентах, на общую сумму. В большинстве случаев вы разделите меньшее число на большее.
- Полученное значение умножьте на 100.
При этом, какова абсолютная разница между двумя числами?
Абсолютная разница — это, по сути, расстояние между двумя числами в строке, рассчитываемое по формуле х — у. Абсолютная разница — это значение между двумя числами, это всегда абсолютное значение, которое является неотрицательным числом.
Также знать, как найти разницу между двумя числами в Excel? Вычислите разницу между двумя числами, введя формулу в новую пустую ячейку. Если A1 и B1 являются числовыми значениями, вы можете использовать Формула «= A1-B1». Ваши ячейки не обязательно должны быть в том же порядке, что и ваша формула. Например, вы также можете использовать формулу «= B1-A1» для вычисления другого значения.
Как проще всего рассчитать проценты?
Вы делите свой процент на 100. Итак, 40 процентов будет 40 разделено на 100. Как только у вас будет десятичная версия вашего процента, просто умножьте его на заданное число (в данном случае на сумму вашей зарплаты).
Как найти дельту между двумя числами?
Если у вас есть случайная пара чисел и вы хотите узнать дельту — или разницу — между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 равна (6 — 3) = 3.
Как найти разницу между двумя отрицательными числами?
Рассчитайте разницу между двумя отрицательными значениями
После того, как вы узнаете сравниваемые отрицательные значения, вы сможете рассчитать разницу. Сделайте это вычитание одного отрицательного значения из другого. Например, вы вычтете -7 из -5, чтобы получить -2.
Всегда ли разница между двумя числами положительна?
Если вы хотите наблюдать только разницу между двумя числами, вы должны получить положительное значение и определить разницу между двумя числами как абсолютное значение их разницы, всегда получая положительное значение. В примере -5 и 2 разница будет | −5−2 | = | 2 — (- 5) | = 7.
Как найти разницу между двумя числами в процентах в Excel?
Пожалуйста, сделайте следующее.
- Выберите пустую ячейку для определения рассчитанного процентного изменения, затем введите формулу = (A3-A2) / A2 в панель формул и нажмите клавишу Enter. …
- Продолжайте выбирать ячейку результата, затем нажмите кнопку «Стиль процентов» в группе «Число» на вкладке «Главная», чтобы отформатировать ячейку в процентах.
Что такое дельта в расчете?
Формула дельты — это тип коэффициента, который сравнивает изменения цены актива с соответствующими изменениями цены его базового актива. … Формула Дельты: Дельта = изменение цены актива / изменение цены базового актива.
Как найти процентную разницу между двумя числами в Excel?
формула = (новое_значение-старое_значение) / старое_значение может помочь вам быстро рассчитать процентное изменение между двумя числами. Пожалуйста, сделайте следующее. 1. Выберите пустую ячейку для определения рассчитанного процентного изменения, затем введите формулу = (A3-A2) / A2 в строку формул и нажмите клавишу Enter.
Какое правило отрицательных чисел?
Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число. Правило работает так же, когда вам нужно умножить или разделить более двух чисел. Четное число отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.
Может ли разница двух отрицательных чисел быть положительной?
Разница двух отрицательных чисел может быть отрицательной, а может и не быть. Это зависит от взятых чисел, а также от последовательности, в которой они взяты. Тогда ab = ba = 0 (что не является ни отрицательным, ни положительным .. . ) Итак, разница двух отрицательных чисел может быть положительным, отрицательным или даже нулевым.
Сумма двух отрицательных чисел отрицательна?
Пояснение: Сумма два отрицательных числа всегда отрицательны, следовательно, это правильный выбор. Что касается других вариантов: произведение или частное двух отрицательных чисел всегда положительно.
Как найти разницу между положительными и отрицательными числами?
Если вы сложите положительное число с другим положительным числом, сумма всегда будет положительным числом.
Как вычитать положительные и отрицательные числа
- Измените знак минус (на операторе) на знак плюс. …
- Измените число после знака минус на противоположное.
Может ли разница между двумя отрицательными числами быть положительной?
Разница двух отрицательных чисел может или не может быть отрицательным. Это зависит от взятых чисел, а также от последовательности, в которой они взяты. Тогда ab = ba = 0 (что не является ни отрицательным, ни положительным .. . ) Таким образом, разница двух отрицательных чисел может быть положительной, отрицательной или даже нулевой.
В чем разница между положительными числами и отрицательными числами?
Положительное число — это число больше нуля. Он может быть написан со знаком + перед ним или без него. Прирост в чем-либо записывается положительным числом. Отрицательное число — это число меньше нуля.
Как рассчитать дельту между двумя числами в Excel?
Как найти процент разницы между значениями в Excel
- Вы можете использовать Excel, чтобы быстро вычислить процент изменения между двумя значениями. …
- Начните с выбора первой ячейки в столбце «Процент изменения».
- Введите следующую формулу и нажмите Enter: = (F3-E3) / E3.
- Результат появится в ячейке.
Почему Дельта — треугольник?
Назван по четвертой букве греческого алфавита. (в форме треугольника) дельта — это треугольная область, где большая река разделяется на несколько меньших частей, которые обычно впадают в более крупный водоем. Первой так называемой дельтой была дельта Нила, названная греческим историком Геродотом.
Что такое дельта-символ в математике?
Дельта в верхнем регистре (Δ) в большинстве случаев означает «изменение» или «изменение» в математике. Рассмотрим пример, в котором переменная x обозначает движение объекта. Итак, «Δx» означает «изменение движения». Ученые используют это математическое значение дельты в различных областях науки.
Какое правило вычитания отрицательных чисел?
Вычитание отрицательного числа — это нравится добавлять позитив; вы двигаетесь вправо по числовой строке. Пример 4: Вычтем −4 — (- 7). Начните с −4 и переместитесь на 7 единиц вправо.
Какое правило умножения отрицательных чисел?
Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила: когда вы умножаете отрицательное число на положительное, тогда продукт всегда отрицательный. Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.
Каковы правила отрицательных и положительных чисел?
Правила умножения и деления просты: Если оба числа положительны, результат положительный. Если оба числа отрицательны, результат положительный.. (По сути, два отрицательных значения компенсируют друг друга).
0 положительное или отрицательное целое число?
Так как ноль не является ни положительным, ни отрицательным, термин неотрицательный иногда используется для обозначения положительного или нулевого числа, в то время как неположительный используется для обозначения отрицательного или нулевого числа. Ноль — нейтральное число.
Какова сумма двух отрицательных чисел?
Сумма двух отрицательных целых чисел равна всегда отрицательное целое число. Например -2 + -3 = -5.
Можете ли вы вычесть два отрицательных числа?
Правило 3: вычитание отрицательного числа из отрицательного числа — знак минус, за которым следует отрицательный знак, превращает два знака в знак плюс. Итак, вместо того, чтобы вычитать отрицательное, вы добавляете положительный. Обычно — (-4) становится +4, а затем вы складываете числа. … Это будет выглядеть как «два отрицательных минус 4 отрицательных».
ДЕЛЬТА
Эта функция сравнивает два значения и проверяет, являются ли они абсолютно одинаковыми.
Если числа совпадают, результатом будет 1, в противном случае — 0.
Работает только с числами, текстовые значения на входе отдают результат #ЗНАЧ!
Форматирование числа не имеет существенного значения, поэтому числа, которые выглядят округленными из-за удаления десятичных разрядов, будут по-прежнему корректно соответствовать не округленным значениям.
Синтаксис
Пример
Следующая таблица используется для определения того, сколько одинаковых пар чисел в списке.
Функция ДЕЛЬТА проверяет каждую пару, а затем функция СУММ суммирует их.
Как посчитать дельту (разницу в процентах) в Excel
По иронии судьбы, функция ДЕЛЬТА не поможет посчитать дельту в Excel. Сравнивая данные в ячейках, функция лишь отвечает на вопрос, равна ли их дельта нулю или нет (иными словами, есть ли дельта).
А посчитать дельту между A и B можно без применения каких-либо функций вовсе, лишь зная две простые формулы ее подсчета:
формула подсчета дельты между числами A и B
Второй вариант в Excel использовать удобнее, т.к. первый требует использования скобок.
Не дайте буквам в формуле вас запутать — B обозначает первый замер (результат «до»), а A — второй (результат «после»). Иными словами, A случилось после B, их алфавитный порядок здесь не при чем.
Чтобы полученный результат выражался в процентах, нужно изменить формат ячеек на процентный: