Как найти дельта нулевое то

Как рассчитать дельту между двумя числами

Математики любят греческие буквы, и они используют дельту заглавной буквы, которая выглядит как треугольник (∆), чтобы обозначить изменение. Когда дело доходит до пары чисел, дельта означает разницу между ними. Вы получаете эту разницу, используя простую арифметику и вычитая меньшее число из большего. В некоторых случаях числа расположены в хронологическом порядке или в другой упорядоченной последовательности, и вам, возможно, придется вычесть большее из меньшего, чтобы сохранить порядок. Это может привести к отрицательному числу.

Абсолютная дельта

Если у вас есть случайная пара чисел и вы хотите узнать дельту — или разницу — между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 составляет (6 — 3) = 3.

Если одно из чисел отрицательное, сложите два числа. Операция выглядит так: (6 — <-3>) = (6 + 3) = 9. Легко понять, почему дельта больше в этом случае, если вы визуализируете два числа на оси x графика. Число 6 находится на 6 единиц справа от оси, а отрицательное 3 — на 3 единицы слева.Другими словами, она дальше от 6, чем положительная 3, которая находится справа от оси.

Чтобы найти дельту между парой дробей, вам нужно запомнить некоторые из школьных арифметических действий. Например, чтобы найти дельту между 1/3 и 1/2, вы должны сначала найти общий знаменатель. Для этого умножьте знаменатели вместе, а затем умножьте числитель каждой дроби на знаменатель другой дроби. В данном случае это выглядит так: 1/3 x 2/2 = 2/6 и 1/2 x 3/3 = 3/6. Вычтите 2/6 из 3/6, чтобы получить дельту, которая равна 1/6.

Относительная дельта

Относительная дельта сравнивает разницу между двумя числами, A и B, в процентах от одного из чисел. Основная формула — A — B / A x100. Например, если вы зарабатываете 10 000 долларов в год и жертвуете 500 долларов на благотворительность, относительная разница в вашей зарплате составляет 10 000–500 / 10 000 x 100 = 95%. Это означает, что вы пожертвовали 5 процентов своей зарплаты, и у вас все еще осталось 95 процентов. Если вы зарабатываете 100000 долларов в год и делаете такое же пожертвование, вы оставляете 99,5 процента своей зарплаты и жертвуете только 0,5 процента на благотворительность, что не столь впечатляюще с точки зрения налоговой отчетности.

От дельты к дифференциалу

Вы можете представить любую точку на двумерном графике парой чисел, которые обозначают расстояние от точки до пересечения осей в направлениях x (по горизонтали) и y (по вертикали). Предположим, у вас есть две точки на графике, называемые точкой 1 и точкой 2, и эта точка 2 находится дальше от пересечения, чем точка 1. Дельта между значениями x этих точек — ∆ x — задается выражением (x₂ — Икс₁), а ∆ y для этой пары точек есть (y₂ — у₁). Когда вы делите ∆y на ∆x, вы получаете наклон графика между точками, который показывает, насколько быстро x и y изменяются относительно друг друга.

Наклон дает полезную информацию. Например, если вы наносите время на ось x и измеряете положение объекта во время его перемещения в пространстве по оси y, наклон графика показывает вам среднюю скорость объекта между этими двумя измерениями.

Однако скорость может быть непостоянной, и вы можете узнать скорость в определенный момент времени. Дифференциальное исчисление предоставляет концептуальный трюк, который позволяет вам это делать. Уловка состоит в том, чтобы представить две точки на оси x и позволить им приблизиться друг к другу бесконечно близко. Отношение ∆y к ∆x — ∆y / ∆x — когда ∆x приближается к 0, называется производной. Обычно это выражается как dy / dx или как df / dx, где f — алгебраическая функция, описывающая график. На графике, на котором время (t) отложено по горизонтальной оси, «dx» становится «dt», а производная dy / dt (или df / dt) является мерой мгновенной скорости.

Как найти разницу между двумя числами?

Чтобы найти разницу между двумя числами, вычесть число с наименьшим значением из числа с наибольшим значением. Произведение этой суммы и есть разница между двумя числами. Следовательно, разница между 45 и 100 составляет 55.

Кроме того, как рассчитать процент?

Как рассчитать процент

1. Определите общую или целую сумму.
2. Разделите число, которое будет выражено в процентах, на общую сумму. В большинстве случаев вы разделите меньшее число на большее.
3. Полученное значение умножьте на 100.

При этом, какова абсолютная разница между двумя числами?

Абсолютная разница — это, по сути, расстояние между двумя числами в строке, рассчитываемое по формуле х — у. Абсолютная разница — это значение между двумя числами, это всегда абсолютное значение, которое является неотрицательным числом.

Также знать, как найти разницу между двумя числами в Excel? Вычислите разницу между двумя числами, введя формулу в новую пустую ячейку. Если A1 и B1 являются числовыми значениями, вы можете использовать Формула «= A1-B1». Ваши ячейки не обязательно должны быть в том же порядке, что и ваша формула. Например, вы также можете использовать формулу «= B1-A1» для вычисления другого значения.

Как проще всего рассчитать проценты?

Вы делите свой процент на 100. Итак, 40 процентов будет 40 разделено на 100. Как только у вас будет десятичная версия вашего процента, просто умножьте его на заданное число (в данном случае на сумму вашей зарплаты).

Как найти дельту между двумя числами?

Если у вас есть случайная пара чисел и вы хотите узнать дельту — или разницу — между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 равна (6 — 3) = 3.

Как найти разницу между двумя отрицательными числами?

Рассчитайте разницу между двумя отрицательными значениями

После того, как вы узнаете сравниваемые отрицательные значения, вы сможете рассчитать разницу. Сделайте это вычитание одного отрицательного значения из другого. Например, вы вычтете -7 из -5, чтобы получить -2.

Всегда ли разница между двумя числами положительна?

Если вы хотите наблюдать только разницу между двумя числами, вы должны получить положительное значение и определить разницу между двумя числами как абсолютное значение их разницы, всегда получая положительное значение. В примере -5 и 2 разница будет | −5−2 | = | 2 — (- 5) | = 7.

Как найти разницу между двумя числами в процентах в Excel?

Пожалуйста, сделайте следующее.

1. Выберите пустую ячейку для определения рассчитанного процентного изменения, затем введите формулу = (A3-A2) / A2 в панель формул и нажмите клавишу Enter. …
2. Продолжайте выбирать ячейку результата, затем нажмите кнопку «Стиль процентов» в группе «Число» на вкладке «Главная», чтобы отформатировать ячейку в процентах.

Что такое дельта в расчете?

Формула дельты — это тип коэффициента, который сравнивает изменения цены актива с соответствующими изменениями цены его базового актива. … Формула Дельты: Дельта = изменение цены актива / изменение цены базового актива.

Как найти процентную разницу между двумя числами в Excel?

формула = (новое_значение-старое_значение) / старое_значение может помочь вам быстро рассчитать процентное изменение между двумя числами. Пожалуйста, сделайте следующее. 1. Выберите пустую ячейку для определения рассчитанного процентного изменения, затем введите формулу = (A3-A2) / A2 в строку формул и нажмите клавишу Enter.

Какое правило отрицательных чисел?

Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число. Правило работает так же, когда вам нужно умножить или разделить более двух чисел. Четное число отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.

Может ли разница двух отрицательных чисел быть положительной?

Разница двух отрицательных чисел может быть отрицательной, а может и не быть. Это зависит от взятых чисел, а также от последовательности, в которой они взяты. Тогда ab = ba = 0 (что не является ни отрицательным, ни положительным .. . ) Итак, разница двух отрицательных чисел может быть положительным, отрицательным или даже нулевым.

Сумма двух отрицательных чисел отрицательна?

Пояснение: Сумма два отрицательных числа всегда отрицательны, следовательно, это правильный выбор. Что касается других вариантов: произведение или частное двух отрицательных чисел всегда положительно.

Как найти разницу между положительными и отрицательными числами?

Если вы сложите положительное число с другим положительным числом, сумма всегда будет положительным числом.

Как вычитать положительные и отрицательные числа

1. Измените знак минус (на операторе) на знак плюс. …
2. Измените число после знака минус на противоположное.

Может ли разница между двумя отрицательными числами быть положительной?

Разница двух отрицательных чисел может или не может быть отрицательным. Это зависит от взятых чисел, а также от последовательности, в которой они взяты. Тогда ab = ba = 0 (что не является ни отрицательным, ни положительным .. . ) Таким образом, разница двух отрицательных чисел может быть положительной, отрицательной или даже нулевой.

В чем разница между положительными числами и отрицательными числами?

Положительное число — это число больше нуля. Он может быть написан со знаком + перед ним или без него. Прирост в чем-либо записывается положительным числом. Отрицательное число — это число меньше нуля.

Как рассчитать дельту между двумя числами в Excel?

Как найти процент разницы между значениями в Excel

1. Вы можете использовать Excel, чтобы быстро вычислить процент изменения между двумя значениями. …
2. Начните с выбора первой ячейки в столбце «Процент изменения».
3. Введите следующую формулу и нажмите Enter: = (F3-E3) / E3.
4. Результат появится в ячейке.

Почему Дельта — треугольник?

Назван по четвертой букве греческого алфавита. (в форме треугольника) дельта — это треугольная область, где большая река разделяется на несколько меньших частей, которые обычно впадают в более крупный водоем. Первой так называемой дельтой была дельта Нила, названная греческим историком Геродотом.

Что такое дельта-символ в математике?

Дельта в верхнем регистре (Δ) в большинстве случаев означает «изменение» или «изменение» в математике. Рассмотрим пример, в котором переменная x обозначает движение объекта. Итак, «Δx» означает «изменение движения». Ученые используют это математическое значение дельты в различных областях науки.

Какое правило вычитания отрицательных чисел?

Вычитание отрицательного числа — это нравится добавлять позитив; вы двигаетесь вправо по числовой строке. Пример 4: Вычтем −4 — (- 7). Начните с −4 и переместитесь на 7 единиц вправо.

Какое правило умножения отрицательных чисел?

Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила: когда вы умножаете отрицательное число на положительное, тогда продукт всегда отрицательный. Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.

Каковы правила отрицательных и положительных чисел?

Правила умножения и деления просты: Если оба числа положительны, результат положительный. Если оба числа отрицательны, результат положительный.. (По сути, два отрицательных значения компенсируют друг друга).

0 положительное или отрицательное целое число?

Так как ноль не является ни положительным, ни отрицательным, термин неотрицательный иногда используется для обозначения положительного или нулевого числа, в то время как неположительный используется для обозначения отрицательного или нулевого числа. Ноль — нейтральное число.

Какова сумма двух отрицательных чисел?

Сумма двух отрицательных целых чисел равна всегда отрицательное целое число. Например -2 + -3 = -5.

Можете ли вы вычесть два отрицательных числа?

Правило 3: вычитание отрицательного числа из отрицательного числа — знак минус, за которым следует отрицательный знак, превращает два знака в знак плюс. Итак, вместо того, чтобы вычитать отрицательное, вы добавляете положительный. Обычно — (-4) становится +4, а затем вы складываете числа. … Это будет выглядеть как «два отрицательных минус 4 отрицательных».

ДЕЛЬТА

Эта функция сравнивает два значения и проверяет, являются ли они абсолютно одинаковыми.

Если числа совпадают, результатом будет 1, в противном случае — 0.

Работает только с числами, текстовые значения на входе отдают результат #ЗНАЧ!

Форматирование числа не имеет существенного значения, поэтому числа, которые выглядят округленными из-за удаления десятичных разрядов, будут по-прежнему корректно соответствовать не округленным значениям.

Синтаксис

Пример

Следующая таблица используется для определения того, сколько одинаковых пар чисел в списке.

Функция ДЕЛЬТА проверяет каждую пару, а затем функция СУММ суммирует их.

Как посчитать дельту (разницу в процентах) в Excel

По иронии судьбы, функция ДЕЛЬТА не поможет посчитать дельту в Excel. Сравнивая данные в ячейках, функция лишь отвечает на вопрос, равна ли их дельта нулю или нет (иными словами, есть ли дельта).

А посчитать дельту между A и B можно без применения каких-либо функций вовсе, лишь зная две простые формулы ее подсчета:

формула подсчета дельты между числами A и B

Второй вариант в Excel использовать удобнее, т.к. первый требует использования скобок.

Не дайте буквам в формуле вас запутать — B обозначает первый замер (результат «до»), а A — второй (результат «после»). Иными словами, A случилось после B, их алфавитный порядок здесь не при чем.

Чтобы полученный результат выражался в процентах, нужно изменить формат ячеек на процентный:

Ответ:

Смотрите процесс ниже

Объяснение:

Пусть будет #t> 0 #

Мы хотим # 100 <1 / (10t) # что это то же самое # 1000t <1 # или же #t <1/1000 #

Выбор # Дельта = 1/1000> 0 # мы достигли нашей цели

Одной рукой #t <delta #с другой стороны #delta> 0 # и наконец выбирая #t <delta # (скажем # Т = 1/10000 #) мы получаем результат

Как рассчитать дельту

Четвертой буквой греческого алфавита, «дельтой», в науке принято называть изменение какой-либо величины, погрешность, приращение. Записывается этот знак различными способами: чаще всего в виде небольшого треугольника Δ перед буквенным обозначением величины. Но иногда можно встретить и такое написание δ, либо латинской строчной буквой d, реже латинской прописной- D.

Для нахождения изменения какой-либо величины вычислите или измерьте ее начальное значение (x1).

Вычислите или измерьте конечное значение этой же величины (x2).

Найдите изменение данной величины по формуле: Δx=x2-x1. Например: начальное значение напряжения электрической сети U1=220В, конечное значение — U2=120В. Изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В-120В=100В

Для нахождения абсолютной погрешности измерения определите точное или, как его иногда называют, истинное значение какой-либо величины (x0).

Возьмите приближенное (при измерении – измеренное) значение этой же величины (x).

Найдите абсолютную погрешность измерения по формуле: Δx=|x-x0|. Например: точное число жителей города — 8253 жителя (х0=8253), при округлении этого числа до 8300 (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет равна Δx=|8300-8253|=47, а при округлении до 8200 (х=8200), абсолютная погрешность — Δx=|8200-8253|=53. Таким образом, округление до числа 8300 будет более точным.

Для сравнения значений функции F(х) в строго фиксированной точке х0 со значениями этой же функции в любой другой точке х, лежащей в окрестностях х0, используются понятия «приращение функции» (ΔF) и «приращение аргумента функции» (Δx). Иногда Δx называют «приращением независимой переменной». Найдите приращение аргумента по формуле Δx=x-x0.

Определите значения функции в точках х0 и х и обозначьте их соответственно F(х0) и F(х).

Вычислите приращение функции:ΔF= F(х)- F(х0). Например: необходимо найти приращение аргумента и приращение функции F(х)=х˄2+1 при изменении аргумента от 2 до 3. В этом случае х0 равно 2, а х=3.
Приращение аргумента (или дельта икс) будет Δx=3-2=1.
F(х0)= х0˄2+1= 2˄2+1=5.
F(х)= х˄2+1= 3˄2+1=10.
Приращение функции (или дельта эф) ΔF= F(х)- F(х0)=10-5=5

Источник

Дельта Формула

Дельта Формула (Содержание)

Что такое Дельта Формула?

В мире опционов или деривативов термин «дельта» относится к изменению стоимости опциона вследствие изменения стоимости его базового запаса. Другими словами, дельта измеряет скорость изменения стоимости опциона по отношению к движению стоимости базовой акции. Поскольку дельта преимущественно используется для стратегий хеджирования, она также известна как коэффициент хеджирования. Формула для дельты может быть получена путем деления изменения стоимости опциона на изменение стоимости его базового запаса. Математически это представляется как

• O _f = конечное значение опции
• O _i = начальное значение опции
• S _f = конечная стоимость базового запаса
• S _i = начальная стоимость базового запаса

Примеры формулы дельты (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять расчет Delta.

Вы можете скачать этот шаблон Delta Formula Excel здесь — шаблон Delta Formula Excel

Формула Дельта — Пример № 1

Давайте возьмем пример товара X, который торговался по 500 долларов на товарном рынке месяц назад, и опцион колл для товара торговался с премией в 45 долларов при цене исполнения в 480 долларов. Сейчас товар продается по цене 600 долларов, а стоимость опциона выросла до 75 долларов. Рассчитать дельту опциона колл на основе предоставленной информации.

Дельта Δ рассчитывается по формуле, приведенной ниже

• Дельта Δ = (75–45 долл. США) / (600–500 долл. США)
• Дельта = 0, 30 $

Таким образом, дельта опциона составляет $ 0, 30, где положительный знак указывает на увеличение стоимости с увеличением базовой цены акции, которая является характеристикой опциона на покупку.

Формула Дельта — Пример № 2

Давайте возьмем другой пример эталонного индекса, который в настоящее время торгуется на уровне 8000 долларов, в то время как опцион пут на индекс торгуется на уровне 150 долларов. Если индекс торговался по 7800 долларов в месяц назад, тогда как опцион пут торговался по 200 долларов, рассчитайте дельту опциона пут.

Дельта Δ рассчитывается по формуле, приведенной ниже

• Дельта Δ = (150–200 долл. США) / (8 000–7 800 долл. США)
• Дельта Δ = — $ 0, 25

Таким образом, дельта опциона «пут» составляет — 0, 25 доллара США, где отрицательный знак указывает на уменьшение стоимости с увеличением базовой цены акции, которая является характеристикой опциона «пут».

объяснение

Формула для дельты может быть рассчитана с помощью следующих шагов:

Шаг 1: во- первых, рассчитайте начальную стоимость опциона, которая является премией, взимаемой за опцион. Обозначается O _i .

Шаг 2: Затем вычислите окончательное значение опции, которое обозначено O _f .

Шаг 3: Затем рассчитайте изменение значения опции, вычтя начальное значение опции (шаг 1) из окончательного значения опции (шаг 2).

Изменение значения опции, Δ _O = O _f — O _i

Шаг 4: Затем вычислите начальную стоимость базовой акции, которая может быть любой акцией компании, товарным индексом или эталонным индексом и т. Д. Он обозначается как S _i .

Шаг 5: Далее рассчитайте окончательную стоимость базового запаса, обозначенную S _f .

Шаг 6: Затем рассчитайте изменение стоимости базового запаса, вычтя его начальное значение (шаг 4) из его окончательного значения (шаг 5).

Изменение стоимости базового запаса, ΔS = S _f — S _i

Шаг 7: Наконец, формула для дельты может быть получена путем деления изменения стоимости опциона (шаг 3) на изменение стоимости базового запаса (шаг 6), как показано ниже.

Актуальность и использование формулы Delta

В мире опционов и деривативов концепция дельты (одного из греков) очень важна, поскольку она помогает оценить цену опциона и направление базовой акции. Дельта может иметь как положительные, так и отрицательные значения в зависимости от типа опции, с которой мы имеем дело, т. Е. Дельта может находиться в диапазоне от 0 до 1 для опций вызова, что означает, что значение опции вызова увеличивается с увеличением базового значения, в то время как оно может быть в диапазоне от -1 до 0 для опционов пут, что означает в точности противоположность опциону колл. Дельта часто используется в качестве стратегии хеджирования, когда управляющий портфелем намерен создать дельта-нейтральную стратегию, чтобы портфель практически не чувствовал к любому движению в основе. Таким образом, дельта является хорошим индикатором сообщества инвесторов.

Калькулятор формулы Delta

Вы можете использовать следующий Delta Calculator

Рекомендуемые статьи

Это руководство к Delta Formula. Здесь мы обсудим, как рассчитать Дельта вместе с практическими примерами. Мы также предоставляем Delta калькулятор с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —

1. Как рассчитать стоимость капитала по формуле?
2. EBITDA Formula
3. Расчет эффективной налоговой ставки
4. Примеры формулы корреляции

Источник

Как найти дельту напряжения

Доброго времени суток.
Требуется помощь уважаемых радиолюбителей. Итак, постараюсь сформулировать вопрос:

Есть 2 синусоиды, скажем, 100мгц и 150мгц. Требуется определить дельту частот.
Порывшись в тех книжках, которые были у меня, найти ничего не удалось. Да и занятия в университете я посещал не слишком здорово, но, тем не менее, есть такая идея:

Из курса тригонометрии мы знаем, что sin(a-b) = sin(a)cos(b) — cos(a)sin(b). Получить косинусоиду из синусоиды, на сколько я могу помнить, не так уж и сложно. Останется перемножить их и вычесть. Таким образом мы получим синусоиду с частотой в разность частот a и b.

Вообще, данная задача ставится для того, чтобы по дельте частот определить скорость движущегося объекта(задача на эффект Допплера). Так что, осмелюсь задать еще один вопрос:

как имея синусоиду с частотой величиной в разницу двух частот(отправленной и полученной) определить саму величину (a-b)?
ведь все рассчеты производятся именно с этой величиной.
из моих догадок — перевести сигнал в цифру, а затем по его длительности уже вычислять нужные данные.
Надеюсь на вашу помощь. Заодно, на всякий случай, извиняюсь, если создал тему не в том разделе.

Поставщик валерьянки для Кота

Ну и закрутили вопрос.
Можно было написать нужен доплеровский измеритель скорости и все.
Что бы получить разность частот эти сигналы нужно подать на нелинейный элемент, например диод, а на выходе поставить ФНЧ с частотой среза чуть больше предполагаемой разницы частот.
Дальше все это на частотометр.
В качестве нелинейного элемента лучше поставить специализированную микросхему смесителя, что бы на выходе «грязи» поменьше было.

Можно также подать на фазовый детектор и на выходе получить напряжение пропорциональное скорости объекта.
Техническую реализацию можно посмотреть в схеме какого либо охранного устройства на этом эффекте.
В интернете они есть..

Последний раз редактировалось VT1 Пн июл 19, 2010 14:25:27, всего редактировалось 1 раз.

JLCPCB, всего $2 за прототип печатной платы! Цвет — любой!

Зарегистрируйтесь и получите два купона по 5$ каждый:https://jlcpcb.com/cwc

спасибо большое. Как раз откопал у отца в пыльном ящике старый учебник по радиолокации и принялся за статью по допплеровским РЛС.

Готовых схем датчиков движения на УЗ и СВЧ(именно так звучало задание) — полно, но они не подходят по ряду причин:
например, дальность локации должна быть порядка 500-1000 метров, да и необходимо, вдобавок, определять расстояние до цели(уверен, что в этой книжке все рассматривается), но, все же, встанет вопрос как объеденить две системы.
Но, это будет несколько после)

Сборка печатных плат от $30 + БЕСПЛАТНАЯ доставка по всему миру + трафарет

Поставщик валерьянки для Кота

Так «гугл» предлагает вот это почитать.
Возможно книжки в интернете можно скачать.

Бартон Д. и Вард Г. Справочник по радиолокационным измерениям. Пер. с англ. под ред. М. М. Вейсбенна — М.: Сов. радио, 1976

Гришин Ю. П., Ипатов В. П., Казаринов Ю. М. Радиотехнические системы — 1990

Построение источников бесперебойного питания с двойным преобразованием, широко используемых в современных хранилищах данных, на базе карбид-кремниевых MOSFETs производства Wolfspeed позволяет уменьшить мощность потерь в них до 40%, а также значительно снизить занимаемый ими объем и стоимость комплектующих.

Кто сейчас на форуме

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 10

Источник

Дельта и кумулятивная дельта: что это такое и чем они помогут внутридневному трейдеру?

Термин Дельта (англ. Delta) вошел в обиход трейдеров в далеком 2002 году, когда был изобретен революционный график Футпринт (англ. Footprint chart). Толчком для этого послужило повсеместное распространение информационных технологий и интернета, затронувшее и сферу трейдинга. Именно тогда доступ к данным о реальных объемах торговли на бирже перестал быть привилегией узкого круга участников рынка, а метод VSA (англ. Volume Spread Analysis — анализ объема и спреда) получил широкое распространение в среде ритейл трейдеров.

Сегодня ритейл трейдер, анализирующий, например, котировки валют Форекс (Forex), благодаря платформе ATAS может подкрепить свои решения торговыми объемами валютных фьючерсов (евро, британского фунта и других). Передовой, интуитивно понятный, а главное ставший доступным каждому, способ визуализации потока ордеров продолжает и по сей день помогать ритейл трейдерам выходить на новый профессиональный уровень.

Начни пользоваться ATAS абсолютно бесплатно! Первые две недели использования платформы дают доступ к полному функционалу с ограничением истории в 7 дней.

Расчет Дельты

Дельта представляет собой разницу между рыночными покупками и рыночными продажами по каждой цене (footprint delta), в каждой свече/баре (bar delta) или за период (cumulative delta — кумулятивная дельта).

Дельта рассчитывается путем вычитания объема контрактов, проторгованных по цене Bid из объема контрактов, проторгованных по цене Ask. В платформе ATAS сделками, совершенными по цене Ask, считаются сделки, инициированные «агрессивными» покупателями. Сделками же, совершенными по цене Bid, считаются сделки, инициированные «агрессивными» продавцами.

Таким образом, положительная Дельта отражает более высокий объем «агрессивных» покупок, прошедших по цене Ask в результате торговли решительно настроенных покупателей. В свою очередь отрицательная Дельта отражает более высокий объем «агрессивных» продаж, прошедших по цене Bid в результате торговли решительно настроенных продавцов.

Объем торговли по цене Ask — Объем торговли по цене Bid = Дельта

Для расчета Дельты вам потребуется знать следующие переменные: цена Bid, цена Ask, последняя цена по которой торговался инструмент, объем последней сделки и время ее заключения.

Например, представьте себе, что в определенный момент времени цена Bid фьючерса на нефть марки WTI = $63.50 за баррель, а цена Ask =$63.51 и по цене Ask совершается сделка на 25 контрактов. В результате этой сделки значение Дельты увеличится на 25. Сразу же после этого на рынке совершается вторая сделка на 10 контрактов, которая на этот раз уже проходит по цене Bid ($63.50). Это приведет к уменьшению Дельты на 10. Общее изменение Дельты за время совершения двух сделок составит +25-10 =+15.

Пожалуйста, помните, что Дельта рассчитывается как разница между объемом рыночных покупок и рыночных продаж. Из этого следует, что приведенный выше пример подразумевает, что первые 25 контрактов были куплены рыночным ордером по цене $63.51, а вторые 10 контрактов были проданы рыночным ордером по цене $63.50.

Расчет Дельты по рыночным, или как еще говорят «агрессивным», ордерам объясняется тем, что именно рыночные ордера двигают цену на рынке. Если немного углубиться в тему, то учитывать объемы лимитных ордеров в расчете Дельты нет необходимости. Ведь для заключения сделки, рыночному ордеру на покупку 25 контрактов потребуется лимитный ордер(а) на продажу 25 контрактов и дублировать эти объемы в показателях Дельты просто не имеет смысла.

Если сейчас вам это кажется немного сложным, не беспокойтесь. В данном вопросе вы сможете разобраться прочитав нашу статью «Механика рынка: Что нужно знать новичку о сведении ордеров», в которой данный аспект трейдинга подробно рассмотрен.

График Футпринт

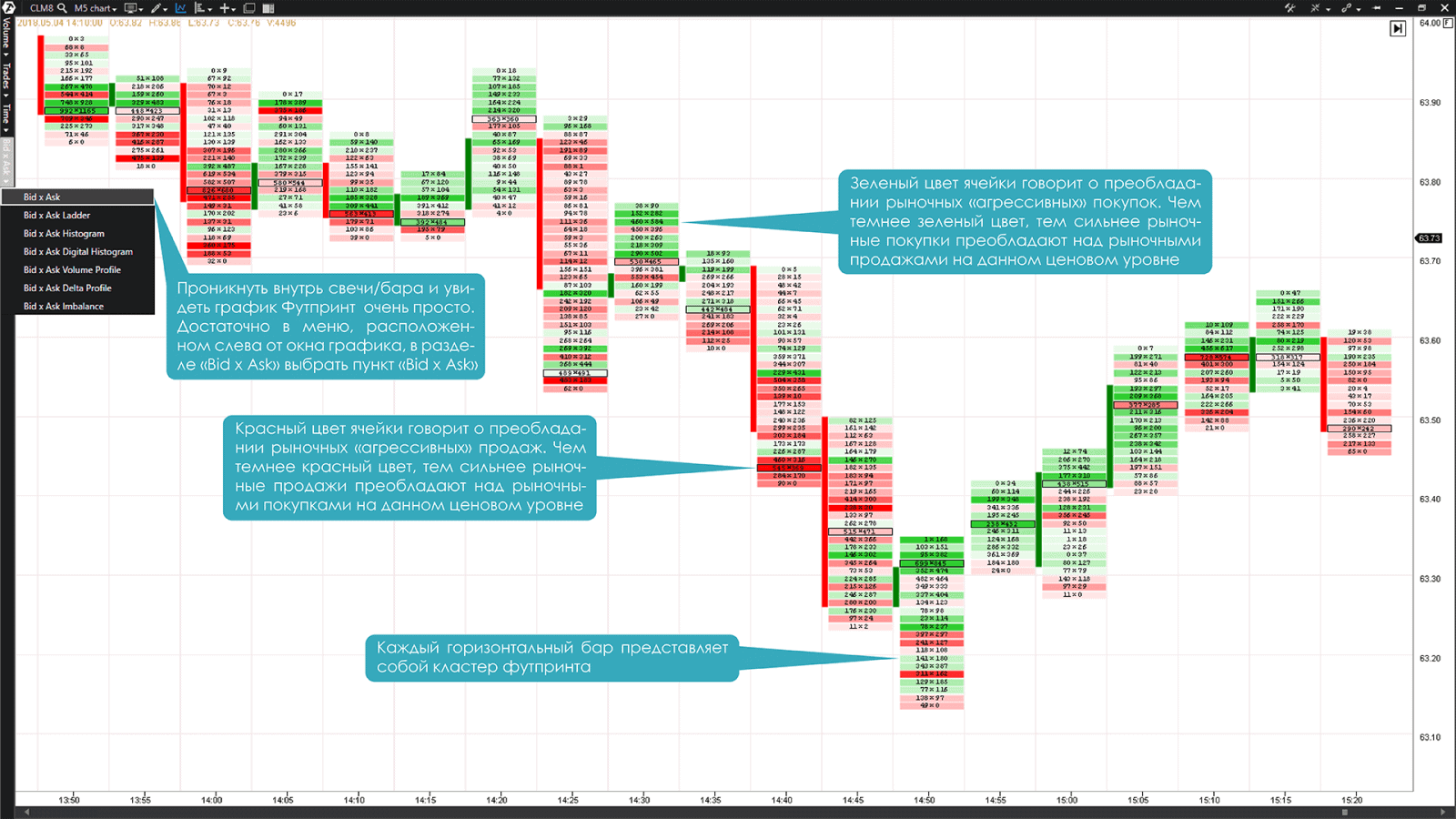
График Футпринт отражает положительное или отрицательное значение Дельты внутри каждой свечи как это видно на Графике №1. Ячейка Футпринта с положительной Дельтой отмечена зеленым цветом и характеризует «положительный» поток ордеров, в результате которого покупатели «агрессивнее» проявили себя на конкретном ценовом уровне. Ячейка Футпринта с отрицательной Дельтой отмечена красным цветом и характеризует «отрицательный» поток ордеров, в результате которого продавцы «агрессивнее» проявили себя на конкретном ценовом уровне.

График №1. 5-минутный таймфрейм фьючерса на нефть Light Sweet Crude Oil (тикер CL). График Футпринт Bid x Ask

На рынке существует высокая степень корреляции между направлением движения цены и потоком ордеров. Именно по этой причине график Футпринт платформы ATAS может стать ценным инструментом анализа текущей рыночной ситуации для проницательных трейдеров.

Индикатор Delta

Данный индикатор показывает суммарное значение Дельты для каждой свечи в виде вертикальной гистограммы в нижней части графика, причем не важно какой тип графика (фрейм) вы используете.

Бары индикатора Delta, могут быть как положительными, так и отрицательными. Положительная Дельта отмечена барами зеленого цвета и характерна для «положительного» потока ордеров, в результате которого покупатели «агрессивнее» проявили себя в конкретной свече. Отрицательная Дельта отмечена барами красного цвета и характерна для «отрицательного» потока ордеров, в результате которого продавцы «агрессивнее» проявили себя в конкретной свече.

Одно из преимуществ баров индикатора Delta платформы ATAS состоит в том, что они позволяют трейдеру переключить внимание с анализа свечей графика Футпринт, внутри которых Дельта распределена по цене, на суммарный поток ордеров этих свечей. Этому можно найти хорошее применение сравнивая цвет бара индикатора Delta с направлением свечи графика Футпринт и находить расхождения. Вероятно, у вас может возникнуть вопрос, а разве может быть у растущей бычьей свечи отрицательная Дельта, и наоборот, у падающей медвежьей свечи положительная Дельта? Да может, и это встречается довольно часто.

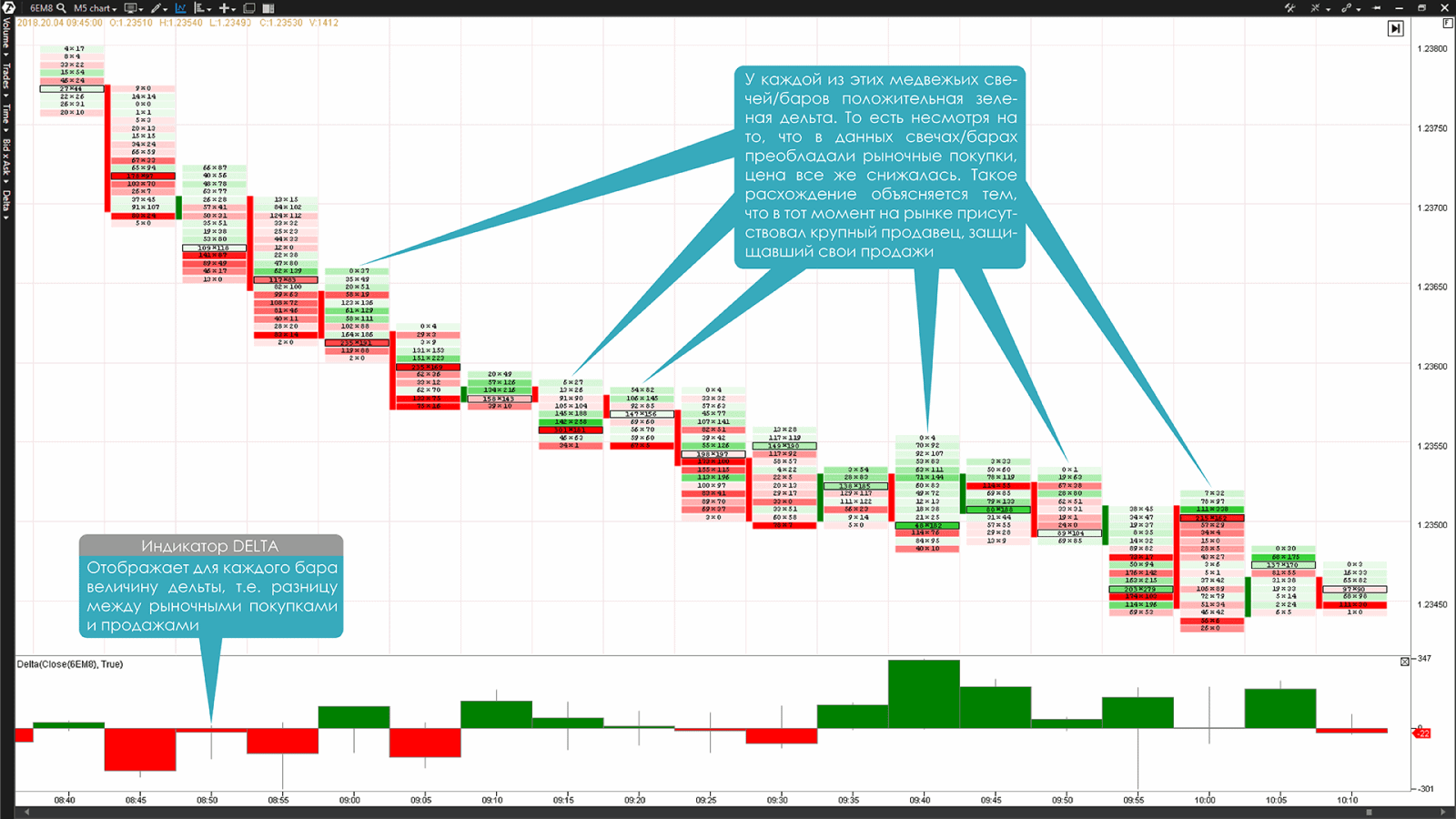
График №2. 5-минутный таймфрейм фьючерса на евро (тикер 6E). График Футпринт Bid x Ask и индикатор Delta в нижней части графика

Обратите внимание, что на Графике №2 у некоторых медвежьих свечей положительная зеленая Дельта. То есть несмотря на то, что в данных свечах преобладали рыночные покупки, цена все же снижалась. Такое расхождение объясняется тем, что на рынке в тот момент времени присутствовал крупный продавец, который открывая свои рыночные продажи, защищал их лимитными ордерами на продажу (англ. sell limit order).

В результате таких действий, все покупки, которые приходили в то время от «агрессивных» покупателей, пытавшихся сопротивляться нисходящему движению цены, исполнялись на защитных лимитных ордерах крупного продавца. Действуя таким образом, крупному продавцу, чтобы толкнуть цену в прибыльном для него направлении, не нужно было открывать крупных рыночных сделок на продажу.

Его продажи в значительной степени открывались на защитных лимитных ордерах, которые полностью поглощали все рыночные покупки. Стоит отметить, что цена продолжала снижаться еще и потому, что покупатели, в свою очередь, не стремились защитить свои рыночные покупки лимитными ордерами на покупку или же ставили их в недостаточном количестве для сдерживания продавцов.

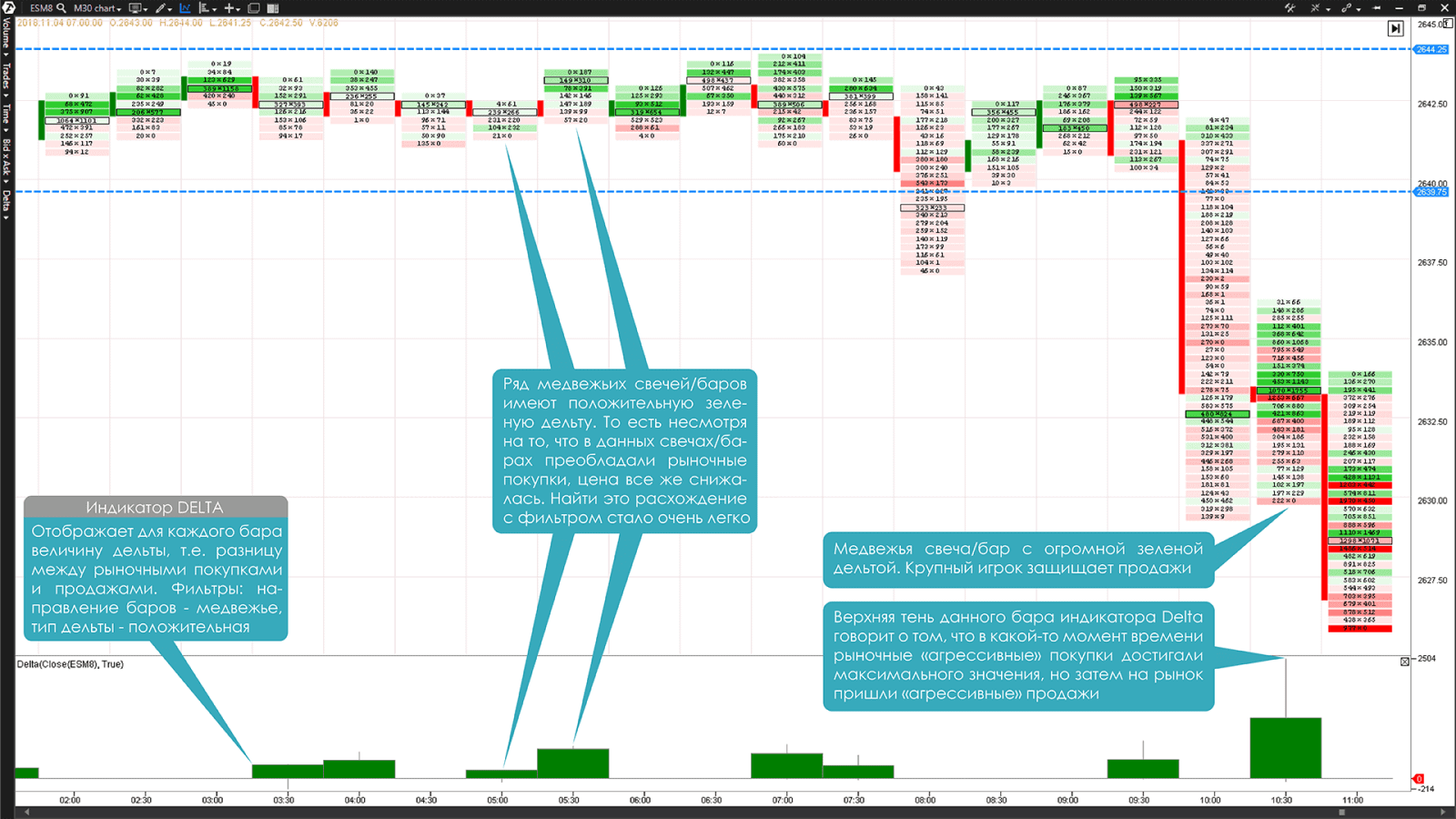
Если вдруг выявление таких расхождений из общего потока рыночной информации кажется вам сложным, то платформа ATAS сможет максимально облегчить эту задачу. На Графике №3 фьючерса E-mini S&P 500, показатели индикатора Delta строятся с использованием двух фильтров: направление баров — медвежье , тип дельты — положительная .

График №3. 30-минутный таймфрейм фьючерса E-mini S&P 500 (тикер ES). График Футпринт Bid x Ask и индикатор Delta в нижней части графика с использованием фильтров

Пример на Графике №3 хорошо демонстрирует работу крупного продавца в период консолидации рынка в диапазоне цен от 2639.75 до 2644.25 а индикатор Delta, благодаря фильтрам, значительно облегчает нахождение расхождений.

В данном примере крупный игрок не пускал «агрессивных» покупателей выше уровня 2644.25 сдерживая их своими лимитными ордерами на продажу. Об этом нам говорит ряд медвежьих свечей с положительной Дельтой. Все рыночные покупки поглощались лимитными ордерами, расположенными у верхней границы консолидации.

Когда вы наблюдаете на рынке подобные ситуации помните, что часто они свидетельствуют о присутствии крупного, или как еще говорят, институционального игрока. Как вы уже наверняка знаете из наших предыдущих статей, только крупный игрок, в отличии от ритейл трейдеров, располагает достаточными финансовыми ресурсами для защиты своих открытых позиций. Уже два этих примера демонстрируют колоссальное преимущество торговли с использованием продвинутых инструментов анализа потока ордеров платформы ATAS.

Кумулятивная Дельта

Кумулятивная Дельта (англ. Cumulative Delta) — это накопительная дельта за определенный промежуток времени. Если обычная Дельта, которую мы рассматривали выше, показывает разницу между рыночными покупками и продажами для каждой свечи/бара, то кумулятивная Дельта отображает полную динамику баланса рыночных покупок и продаж начиная с определенного момента времени (с начала торговой сессии или контракта).

Таким образом кумулятивная Дельта позволяет увидеть более широкую картину Дельты, так как она может охватывать торговую сессию или же целый день. Поэтому не имеет значения какой фрейм или период вы используете для построения графика. Индикатор Cumulative Delta платформы ATAS подсчитывает накопительную Дельту и отображает ее текущий итоговый показатель в нижней части графика.

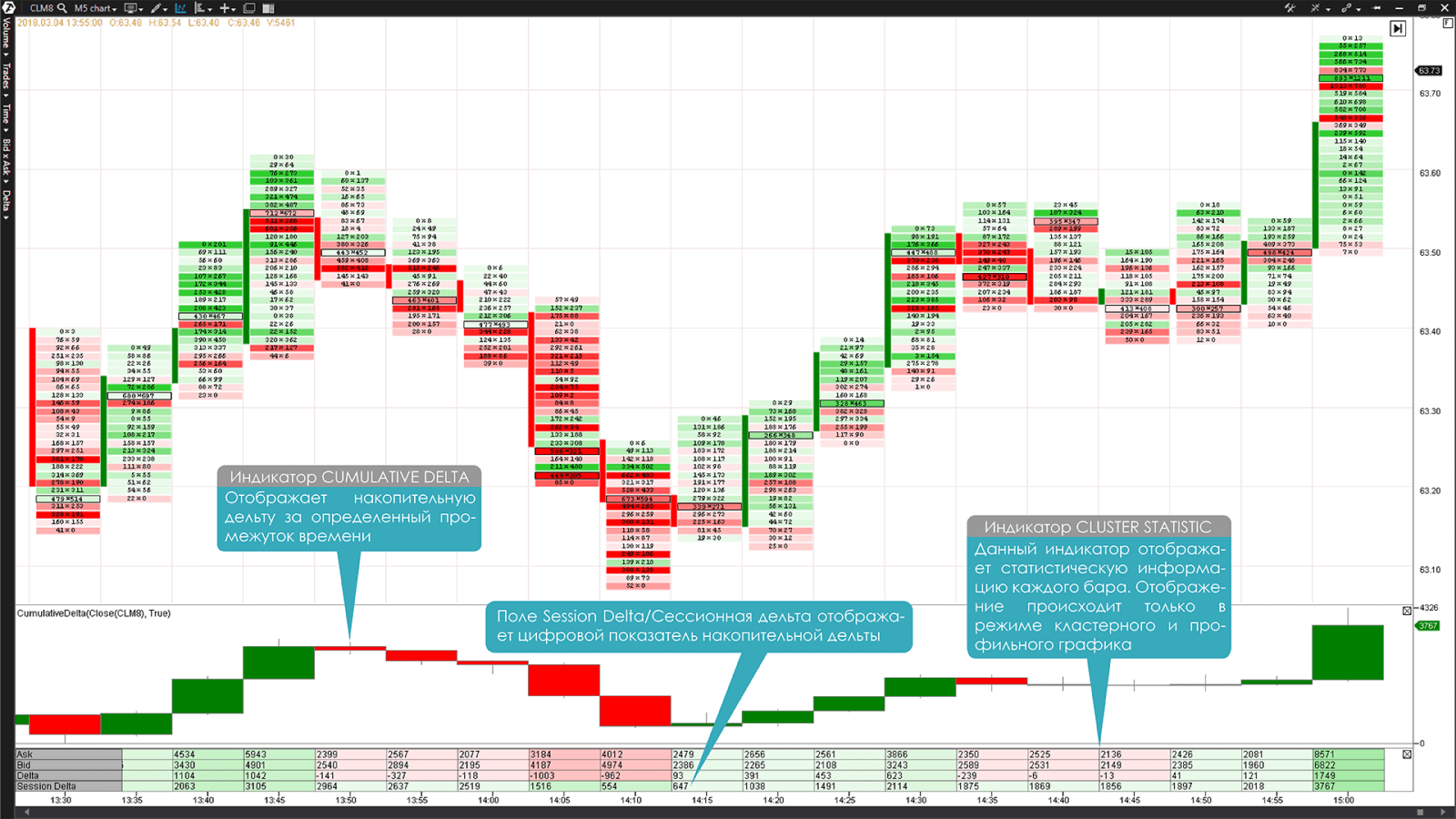
Помимо этого, показатель кумулятивной Дельты, как и другие подробные цифровые показатели Дельты можно вывести на график при помощи индикатора Cluster Statistic. В нем показатели кумулятивной Дельты будут выводиться в строке Session Delta.

Кумулятивная Дельта, может быть как положительной, так и отрицательной. Положительная кумулятивная Дельта окрашивается в зеленый цвет и характеризует «положительный» поток ордеров за торговую сессию, как результат более агрессивного поведения покупателей. Отрицательная кумулятивная Дельта окрашивается в красный цвет и характеризует «отрицательный» поток ордеров за торговую сессию, как результат более «агрессивного» поведения продавцов.

График №4. 5-минутный таймфрейм фьючерса на нефть Light Sweet Crude Oil (тикер CL). График Футпринт Bid x Ask и индикаторы Cumulative Delta и Cluster Statistic в нижней части графика

Одна из стратегий применения кумулятивной Дельты заключается в использовании ее для определения направления заключения сделки. Когда кумулятивная Дельта положительная, это говорит о доминировании «агрессивно» настроенных покупателей в течение торговой сессии. И наоборот, когда кумулятивная Дельта отрицательная, это значит, что в течение торговой сессии доминируют «агрессивно» настроенные продавцы. Это очень полезный аналитический инструмент для подтверждения направления движения цены.

В заключении статьи следует отметить, что Дельту, несмотря на все ее сильные стороны, следует использовать лишь в связке с другими торговыми элементами вашей торговой стратегии.

Внимание! Торговля на бирже сопряжена с финансовыми рисками и подходит не всем инвесторам. Данная публикация носит исключительно информационный характер. Проведение торговых операций на финансовых рынках может привести к получению убытков и потере инвестиционных средств. Перед использованием торговых идей убедитесь, что вы в полной мере осознаете все риски, а также обладаете соответствующими знаниями и опытом для торговли на бирже.

Понравилось? Расскажите друзьям:

Ответить

Добавить комментарий Отменить ответ

Другие статьи блога:

This site uses cookies. By continuing to browse the site, you are agreeing to our use of cookies.

Cookie и настройки приватности

Мы можем запросить сохранение файлов cookies на вашем устройстве. Мы используем их, чтобы знать, когда вы посещаете наш сайт, как вы с ним взаимодействуете, чтобы улучшить и индивидуализировать ваш опыт использования сайта.

Чтобы узнать больше, нажмите на ссылку категории. Вы также можете изменить свои предпочтения. Обратите внимание, что запрет некоторых видов cookies может сказаться на вашем опыте испольхования сайта и услугах, которые мы можем предложить.

These cookies are strictly necessary to provide you with services available through our website and to use some of its features.

Because these cookies are strictly necessary to deliver the website, refuseing them will have impact how our site functions. You always can block or delete cookies by changing your browser settings and force blocking all cookies on this website. But this will always prompt you to accept/refuse cookies when revisiting our site.

We fully respect if you want to refuse cookies but to avoid asking you again and again kindly allow us to store a cookie for that. You are free to opt out any time or opt in for other cookies to get a better experience. If you refuse cookies we will remove all set cookies in our domain.

We provide you with a list of stored cookies on your computer in our domain so you can check what we stored. Due to security reasons we are not able to show or modify cookies from other domains. You can check these in your browser security settings.

These cookies collect information that is used either in aggregate form to help us understand how our website is being used or how effective our marketing campaigns are, or to help us customize our website and application for you in order to enhance your experience.

If you do not want that we track your visit to our site you can disable tracking in your browser here:

We also use different external services like Google Webfonts, Google Maps, and external Video providers. Since these providers may collect personal data like your IP address we allow you to block them here. Please be aware that this might heavily reduce the functionality and appearance of our site. Changes will take effect once you reload the page.

Google reCaptcha Settings:

Vimeo and Youtube video embeds:

The following cookies are also needed — You can choose if you want to allow them:

Подробнее о нашей политике конфиденциальности и файлах cookies вы можете прочесть на странице Политики конфиденциальности.

Источник

➤ Adblock
detector

Как рассчитать дельту

Четвертой буквой греческого алфавита, «дельтой», в науке принято называть изменение какой-либо величины, погрешность, приращение. Записывается этот знак различными способами: чаще всего в виде небольшого треугольника Δ перед буквенным обозначением величины. Но иногда можно встретить и такое написание δ, либо латинской строчной буквой d, реже латинской прописной — D.

Инструкция

Для нахождения изменения какой-либо величины вычислите или измерьте ее начальное значение (x1).

Вычислите или измерьте конечное значение этой же величины (x2).

Найдите изменение данной величины по формуле: Δx=x2-x1. Например: начальное значение напряжения электрической сети U1=220В, конечное значение — U2=120В. Изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В-120В=100В

Для нахождения абсолютной погрешности измерения определите точное или, как его иногда называют, истинное значение какой-либо величины (x0).

Возьмите приближенное (при измерении – измеренное) значение этой же величины (x).

Найдите абсолютную погрешность измерения по формуле: Δx=|x-x0|. Например: точное число жителей города — 8253 жителя (х0=8253), при округлении этого числа до 8300 (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет равна Δx=|8300-8253|=47, а при округлении до 8200 (х=8200), абсолютная погрешность — Δx=|8200-8253|=53. Таким образом, округление до числа 8300 будет более точным.

Для сравнения значений функции F(х) в строго фиксированной точке х0 со значениями этой же функции в любой другой точке х, лежащей в окрестностях х0, используются понятия «приращение функции» (ΔF) и «приращение аргумента функции» (Δx). Иногда Δx называют «приращением независимой переменной». Найдите приращение аргумента по формуле Δx=x-x0.

Определите значения функции в точках х0 и х и обозначьте их соответственно F(х0) и F(х).

Вычислите приращение функции: ΔF= F(х)- F(х0). Например: необходимо найти приращение аргумента и приращение функции F(х)=х˄2+1 при изменении аргумента от 2 до 3. В этом случае х0 равно 2, а х=3.
Приращение аргумента (или дельта икс) будет Δx=3-2=1.
F(х0)= х0˄2+1= 2˄2+1=5.
F(х)= х˄2+1= 3˄2+1=10.
Приращение функции (или дельта эф) ΔF= F(х)- F(х0)=10-5=5

Обратите внимание

Вычитать нужно не из большего числа меньшее, а из конечного значения (не важно: больше оно или меньше) начальное!

Полезный совет

При нахождении Δ все значения используйте только в одинаковых единицах измерения.

Источники:

• Справочник по математике для средних учебных заведений, А.Г. Цыпкин, 1983

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Экстремум функции двух переменных. Примеры исследования функций на экстремум.

Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.

Точки максимума и минимума часто называют общим термином – точки экстремума.

Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.

Алгоритм исследования функции $z=f(x,y)$ на экстремум

1. Найти частные производные $frac{partial z}{partial x}$ и $frac{partial z}{partial y}$. Составить и решить систему уравнений $
   left { begin{aligned}
   & frac{partial z}{partial x}=0;\
   & frac{partial z}{partial y}=0.
   end{aligned} right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными.
2. Найти $frac{partial^2z}{partial x^2}$, $frac{partial^2z}{partial xpartial y}$, $frac{partial^2z}{partial y^2}$ и вычислить значение $Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
   1. Если $Delta > 0$ и $frac{partial^2z}{partial x^2} > 0$ (или $frac{partial^2z}{partial y^2} > 0$), то в исследуемая точка есть точкой минимума.
   2. Если $Delta > 0$ и $frac{partial^2z}{partial x^2} < 0$ (или $frac{partial^2z}{partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
   3. Если $Delta < 0$, то в расматриваемой стационарной точке экстремума нет.
   4. Если $Delta = 0$, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.

Примечание (желательное для более полного понимания текста): показатьскрыть

Пример №1

Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.

Решение

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=8x-6y-34; frac{partial z}{partial y}=-6x+10y+42.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 8x-6y-34=0;\
& -6x+10y+42=0.
end{aligned} right.
$$

Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:

$$
left { begin{aligned}
& 4x-3y=17;\
& -3x+5y=-21.
end{aligned} right.
$$

Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.

$$ begin{aligned}
& Delta=left| begin{array} {cc} 4 & -3\ -3 & 5 end{array}right|=4cdot 5-(-3)cdot (-3)=20-9=11;\
& Delta_x=left| begin{array} {cc} 17 & -3\ -21 & 5 end{array}right|=17cdot 5-(-3)cdot (-21)=85-63=22;\
& Delta_y=left| begin{array} {cc} 4 & 17\ -3 & -21 end{array}right|=4cdot (-21)-17cdot (-3)=-84+51=-33.end{aligned} \
x=frac{Delta_{x}}{Delta}=frac{22}{11}=2; ; y=frac{Delta_{y}}{Delta}=frac{-33}{11}=-3.
$$

Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=8; frac{partial^2 z}{partial y^2}=10; frac{partial^2 z}{partial x partial y}=-6.
$$

Вычислим значение $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
8cdot 10-(-6)^2=80-36=44.
$$

Так как $Delta > 0$ и $frac{partial^2 z}{partial x^2} > 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:

$$
z_{min}=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90.
$$

Ответ: $(2;-3)$ – точка минимума; $z_{min}=-90$.

Пример №2

Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.

Решение

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=3x^2+3y^2-15; frac{partial z}{partial y}=6xy-12.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 3x^2+3y^2-15=0;\
& 6xy-12=0.
end{aligned} right.
$$

Сократим первое уравнение на 3, а второе – на 6.

$$
left { begin{aligned}
& x^2+y^2-5=0;\
& xy-2=0.
end{aligned} right.
$$

Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac{2}{x}$. Подставляя $y=frac{2}{x}$ в первое уравнение, будем иметь:

$$
x^2+left(frac{2}{x} right)^2-5=0;\
x^2+frac{4}{x^2}-5=0;\
x^4-5x^2+4=0.
$$

Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):

$$
t^2-5t+4=0;\
begin{aligned}
& D=(-5)^2-4cdot 1 cdot 4=9;\
& t_1=frac{-(-5)-sqrt{9}}{2}=frac{5-3}{2}=1;\
& t_2=frac{-(-5)+sqrt{9}}{2}=frac{5+3}{2}=4.end{aligned}
$$

Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac{2}{x}$, получим:

begin{aligned}
& y_1=frac{2}{x_1}=frac{2}{1}=2;\
& y_2=frac{2}{x_2}=frac{2}{-1}=-2;\
& y_3=frac{2}{x_3}=frac{2}{2}=1;\
& y_4=frac{2}{x_4}=frac{2}{-2}=-1.
end{aligned}

Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=6x; frac{partial^2 z}{partial y^2}=6x; frac{partial^2 z}{partial x partial y}=6y.
$$

Найдём $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
6xcdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2).
$$

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:

$$Delta(M_1)=36(1^2-2^2)=-108.$$

Так как $Delta(M_1) < 0$, то согласно алгоритму в точке $M_1$ экстремума нет.

Исследуем точку $M_2(-1;-2)$. В этой точке имеем:

$$Delta(M_2)=36((-1)^2-(-2)^2)=-108.$$

Так как $Delta(M_2) < 0$, то согласно алгоритму в точке $M_2$ экстремума нет.

Исследуем точку $M_3(2;1)$. В этой точке получим:

$$
Delta(M_3)=36(2^2-1^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_3}=6cdot 2=12.
$$

Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$
z_{min}=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27.
$$

Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:

$$
Delta(M_4)=36((-2)^2-(-1)^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_4}=6cdot (-2)=-12.
$$

Так как $Delta(M_4) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_4} < 0$, то согласно алгоритму $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:

$$
z_{max}=z(-2;-1)=(-2)^3+3cdot (-2)cdot (-1)^2-15cdot (-2)-12cdot (-1)+1=29.
$$

Исследование на экстремум завершено. Осталось лишь записать ответ.

Ответ:

• $(2;1)$ – точка минимума, $z_{min}=-27$;
• $(-2;-1)$ – точка максимума, $z_{max}=29$.

Примечание

Вычислять значение $Delta$ в общем случае нет необходимости, потому что нас интересует лишь знак, а не конкретное значение данного параметра. Например, для рассмотренного выше примера №2 в точке $M_3(2;1)$ имеем $Delta=36cdot(2^2-1^2)$. Здесь очевидно, что $Delta > 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа

Пример №3

Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.

Решение

Будем следовать алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=4x^3-4x+4y; frac{partial z}{partial y}=4y^3+4x-4y.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 4x^3-4x+4y=0;\
& 4y^3+4x-4y=0.
end{aligned} right.
$$

Сократим оба уравнения на $4$:

$$
left { begin{aligned}
& x^3-x+y=0;\
& y^3+x-y=0.
end{aligned} right.
$$

Добавим к второму уравнению первое и выразим $y$ через $x$:

$$
y^3+x-y+(x^3-x+y)=0;\
y^3+x^3=0; y^3=-x^3; y=-x.
$$

Подставляя $y=-x$ в первое уравнение системы, будем иметь:

$$
x^3-x-x=0;\
x^3-2x=0;\
x(x^2-2)=0.
$$

Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt{2}$ или $x=sqrt{2}$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt{2}$, $x_3=sqrt{2}$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt{2}$, $y_3=-x_3=-sqrt{2}$.

Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt{2},sqrt{2})$, $M_3(sqrt{2},-sqrt{2})$.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=12x^2-4; frac{partial^2 z}{partial y^2}=12y^2-4; frac{partial^2 z}{partial x partial y}=4.
$$

Найдём $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
(12x^2-4)(12y^2-4)-4^2=\
=4(3x^2-1)cdot 4(3y^2-1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1).
$$

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:

$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$

Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.

Исследуем точку $M_2(-sqrt{2},sqrt{2})$. В этой точке получим:

begin{aligned}
& Delta(M_2)=16cdot((3cdot (-sqrt{2})^2-1)(3cdot (sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_2}=12cdot (-sqrt{2})^2-4=24-4=20.
end{aligned}

Так как $Delta(M_2) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_2} > 0$, то согласно алгоритму $M_2(-sqrt{2},sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:

$$
z_{min}=z(-sqrt{2},sqrt{2})=(-sqrt{2})^4+(sqrt{2})^4-2(-sqrt{2})^2+4cdot (-sqrt{2})sqrt{2}-2(sqrt{2})^2+3=-5.
$$

Аналогично предыдущему пункту исследуем точку $M_3(sqrt{2},-sqrt{2})$. В этой точке получим:

begin{aligned}
& Delta(M_3)=16cdot((3cdot (sqrt{2})^2-1)(3cdot (-sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_3}=12cdot (sqrt{2})^2-4=24-4=20.
end{aligned}

Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(sqrt{2},-sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$
z_{min}=z(sqrt{2},-sqrt{2})=(sqrt{2})^4+(-sqrt{2})^4-2(sqrt{2})^2+4cdot sqrt{2}(-sqrt{2})-2(-sqrt{2})^2+3=-5.
$$

Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается «делайте, что хотите» :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) < 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Рассмотрим точки, у которых $y=0$, т.е. точки вида $(x,0)$. В этих точках функция $z$ будет принимать такие значения:

$$
z(x,0)=x^4+0^4-2x^2+4xcdot 0-2cdot 0^2+3=x^4-2x^2+3=x^2(x^2-2)+3.
$$

В всех достаточно малых окрестностях $M_1(0;0)$ имеем $x^2-2 < 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Но, может быть, точка $M_1(0;0)$ – точка максимума? Если это так, то для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) < z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > 3$? Тогда в точке $M_1$ точно не будет максимума.

Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:

$$
z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3.
$$

Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.

Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.

Ответ: $(-sqrt{2},sqrt{2})$, $(sqrt{2},-sqrt{2})$ – точки минимума функции $z$. В обеих точках $z_{min}=-5$.