Как найти дельта угла альфа - Исправление недочетов и поиск решений вместе с Examum.ru

Как вычислить дельту

Греческой буквой Δ в науке принято обозначать разность между конечным и начальным значениями некой величины. Например, Δt – разность температур в начале и конце реакции или время, за которое выполнена работа. В некоторых случаях четвертую букву греческого алфавита заменяют прописной или строчной латинской d. Но латиницей в данном случае необходимо пользоваться осторожно, поскольку этой же буквой обозначаются и другие понятия.

Вам понадобится

— измерительные приборы;
— калькулятор.

Инструкция

Чтобы узнать, на сколько изменилась та или иная величина, нужно в первую очередь узнать начальное и конечное значение. Если речь идет о практической задаче, нужные параметры можно измерить. Нужный вам параметр можно в принципе назвать любой буквой, но лучше использовать принятые в науке обозначения. Допустим, вам нужно найти, насколько изменился объем вещества при нагревании. Результат первого измерения запишите как V1

Проведите второе измерение. Например, после того, как закончите нагревать объект. Определите его объем и обозначьте его как V2. Вычислите дельту по формуле ΔV = V2-V1. Может получиться так, что второй результат будет меньше первого. Посчитайте модуль числа так же, как и в любом другом случае, и поставьте знак «-». Не забудьте, что оба измерения должны быть в одних и тех же единицах. Если нужно, переведите их.

Нередки задачи, когда необходимо вычислить дельту между фактическим и средним значением. Например, вам дана точка, которая поменяла свои координаты по двум осям. Обозначьте координаты как x1,x2, x3 и т. д. Найдите среднее значение. Затем вычислите разницу между полученным результатом и значением каждой координаты.

Если вам нужно вычислить приращение функции f(x), определите ее значение в жестко заданной точке — пусть это будет, например, х0. Чтобы вычислить дельту, вам необходимо сравнить значение функции в этой точке с ее же значением в любой другой точке по заданной оси. Для этого вычтите значение функции в точке х1 из ее же значения в точке х0. Это и будет Δf. Чтобы найти приращение аргумента, определите его значения в заданных точках и вычислите разность.

Буквой Δ обозначают и абсолютную погрешность. Она тоже представляет собой разность. За начальное и конечное значение принимаются истинное и приближенное значения. Величина дельты в данном случае соответствует классу точности прибора.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.

Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).

Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.

Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника

Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co

Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.

Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.

Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.

Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.

Итак,

Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.

Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.

Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.

Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.

Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.

Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.

Как найти углы в прямоугольном треугольнике, если известны стороны?

Дан треугольник АВС, угол С — прямой.

Стороны АВ, АС и ВС известны.

Т.к. угол С — прямой, он равен 90 градусам.

Другие углы можно найти, например, так:

если известен катет и гипотенуза

sinA = BC / AB,

sinB = AC / AB,

если известны два катета

tg A = BC / AC

tg B = AC / BC

Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.

Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.

Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.

sin 15° = 0,259

arcsin0,259 = 15°

Как найти углы в прямоугольном треугольнике, если известен один угол?

Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.

Еединичная окружность (единичный круг)

Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).

Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).

Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.

Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).

Координатные четверти отсчитываются так:

(II четверть) | (I четверть)

________________________ x

(III четверть) | (IV четверть)

Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).

Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).

Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).

Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).

Например:

углы первой четверти: 30 градусов, 85 градусов, пи/4;
углы второй четверти: 120 градусов, 178 градусов;
углы третьей четверти: 205 градусов, 260 градусов;
углы четвертой четверти: 272 градуса, 305 градусов.

Тригонометрические функции

К тригонометрическим функциям относятся функции:

y = sin x;

y = cos x;

y = tg x;

y = ctg x;

y = sec x;

y = cosec x.

Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.

Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.

Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.

Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.

Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.

Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.

Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.

Как найти синус угла, если известен косинус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

sin²a = 1 − cos²a

|sin a| = КОРЕНЬ(1 − cos²a)

sin a = ± КОРЕНЬ(1 − cos²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти косинус угла, если известен синус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

cos²a = 1 − sin²a

|cos a| = КОРЕНЬ(1 − sin²a)

cos a = ± КОРЕНЬ(1 − sin²a)

Как найти синус угла, если известен котангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + ctg² a = 1/sin² a

sin² a = 1 / (1 + ctg² a)

|sin a| = 1/ КОРЕНЬ(1 + ctg² a)

sin a = ±1/ КОРЕНЬ(1 + ctg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)

Как найти косинус угла, если известен тангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + tg² a = 1/cos² a

cos² a = 1 / (1 + tg² a)

|cos a| = 1/ КОРЕНЬ(1 + tg² a)

cos a = ±1/ КОРЕНЬ(1 + tg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)

Тригонометрическое тождество

Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.

Основные тригонометрические тождества:

sin²a + cos²a = 1

tg a = sin a / cos a

ctg a = cos a / sin a

sec a = 1 / cos a

cosec a = 1 / sin a

Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)

arcsin — читается: арксинус;
arcos — читается: арккосинус;
arctg — читается: арктангенс;
arcctg — читается: арккотангенс.

arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.

Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:

y = arcsin x sin y = x

Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:

y = arccos x cos y = x

Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:

y = arctg x tg y = x

Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:

y = arctg x tg y = x

Например,

sin 30° = 0,5

arcsin0,5 = 30°

Синусоида и косинусоида

График функции y = sin x называется синусоидой.

График функции y = cos x называется косинусоидой.

Источники информации:

Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
docme.ru — зачем нужна тригонометрия?
ru.wikipedia.org — Википедия — тригонометрия;
ru.wikihow.com — как изучать тригонометрию?

Источник

Как рассчитать дельту

Четвертой буквой греческого алфавита, «дельтой», в науке принято называть изменение какой-либо величины, погрешность, приращение. Записывается этот знак различными способами: чаще всего в виде небольшого треугольника Δ перед буквенным обозначением величины. Но иногда можно встретить и такое написание δ, либо латинской строчной буквой d, реже латинской прописной- D.

Для нахождения изменения какой-либо величины вычислите или измерьте ее начальное значение (x1).

Вычислите или измерьте конечное значение этой же величины (x2).

Найдите изменение данной величины по формуле: Δx=x2-x1. Например: начальное значение напряжения электрической сети U1=220В, конечное значение — U2=120В. Изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В-120В=100В

Для нахождения абсолютной погрешности измерения определите точное или, как его иногда называют, истинное значение какой-либо величины (x0).

Возьмите приближенное (при измерении – измеренное) значение этой же величины (x).

Найдите абсолютную погрешность измерения по формуле: Δx=|x-x0|. Например: точное число жителей города — 8253 жителя (х0=8253), при округлении этого числа до 8300 (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет равна Δx=|8300-8253|=47, а при округлении до 8200 (х=8200), абсолютная погрешность — Δx=|8200-8253|=53. Таким образом, округление до числа 8300 будет более точным.

Для сравнения значений функции F(х) в строго фиксированной точке х0 со значениями этой же функции в любой другой точке х, лежащей в окрестностях х0, используются понятия «приращение функции» (ΔF) и «приращение аргумента функции» (Δx). Иногда Δx называют «приращением независимой переменной». Найдите приращение аргумента по формуле Δx=x-x0.

Определите значения функции в точках х0 и х и обозначьте их соответственно F(х0) и F(х).

Вычислите приращение функции:ΔF= F(х)- F(х0). Например: необходимо найти приращение аргумента и приращение функции F(х)=х˄2+1 при изменении аргумента от 2 до 3. В этом случае х0 равно 2, а х=3.
Приращение аргумента (или дельта икс) будет Δx=3-2=1.
F(х0)= х0˄2+1= 2˄2+1=5.
F(х)= х˄2+1= 3˄2+1=10.
Приращение функции (или дельта эф) ΔF= F(х)- F(х0)=10-5=5

Источник

Дэльта Т это разница параметров.
Например температуры или времени.
Стандартно вычисляется как Т конечное минус Т начальное.
Или же разница между 2мя разными измерениями.
Например: начальная температура 55 градусов, конечная 20, дельта Т = 20-55 = -35 градусов
Например: один бегун прошел дистанцию за 15 минут, а второй за 7.
Разница во времени, т. е. дельта Т = 15-7 =8 минут

Комментариев (0)

Дельта t = t2-t1-t0=0,5-0,3-0,1=0,1

Комментариев (0)

Ваш ответ

Источник

Альфа бета гамма треугольник

Греческий алфавит

Буквы греческого алфавита в геометрии используются для обозначения плоскостей, величин углов и в некоторых других случаях.

Поскольку греческий алфавит школьникам незнаком, написание и прочтение букв греческого алфавита вызывает у них вопросы.

*Буквы*	*Название*	*Прочтение*
Α α	альфа	а́льфа
Β β	бета	бэ́та
Γ γ	гамма	га́мма
Δ δ	дельта	дэ́льта
Ε ε	эпсилон	э́псилон
Ζ ζ	дзета	дзэ́та
Η η	эта	э́та
Θ θ	тета	тэ́та
Ι ι	йота	йо́та
Κ κ	каппа	ка́ппа
Λ λ	ламбда	ля́мбда
Μ μ	мю	мю
Ν ν	ню	ню
Ξ ξ	кси	кси
Ο ο	омикрон	омикрон
Π π	пи	пи
Ρ ρ	ро	ро
Σ ς	сигма	си́гма
Τ τ	тау	та́у
Υ υ	ипсилон	ипсилон
Φ φ	фи	фи
Χ χ	хи	хи
Ψ ψ	пси	пси
Ω ω	омега	оме́га

Нет нужды в 7 классе изучать весь греческий алфавит.

Для начала достаточно запомнить те буквы, которые встречаются чаще всего — α, β, γ, π.

Другие буквы добавлять по мере необходимости.

Помимо геометрии, буквы греческого алфавита используются в алгебре и физике.

Созвездие Треугольник

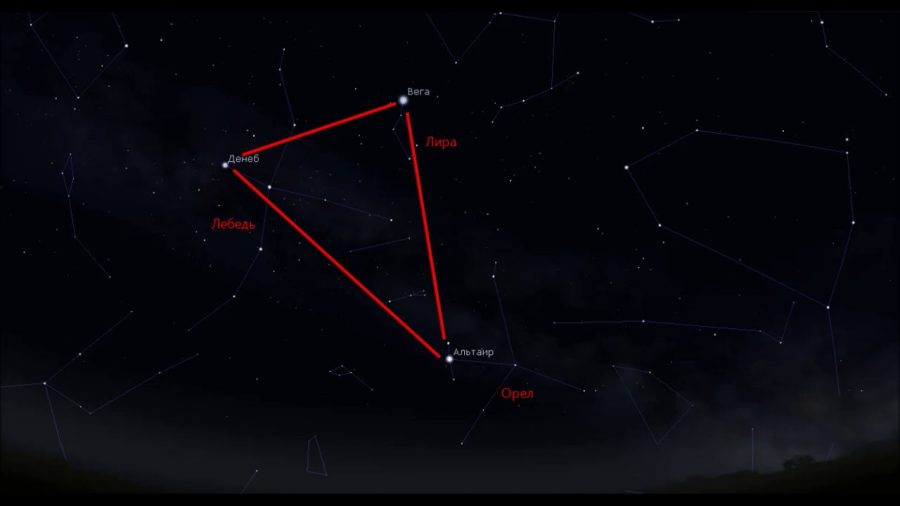
В северном полушарии неба лежит созвездие Треугольник. Это не большая, не имеющая ярких объектов область. Три самые яркие звезды в созвездии образуют треугольник. Отсюда, как вы догадались, и название.

Площадь, которую занимает созвездие Треугольник, составляет 132 квадратных градусов. Таким образом, оно занимает 78 место среди всех созвездий по размеру.

Соседями являются такие северные участки, как Андромеда, Овен, Персей и Рыбы.

Поиск созвездия Треугольник на небе

Созвездие Треугольник не располагает в своем составе яркими звездами. На занимаемом им кусочке неба наблюдателю можно различить примерно полтора десятка светил, и только у трех из них яркость превышает четвертую звездную величину. Именно эта тройка и предопределила название созвездия – эти ярчайшие звезды образуют фигуру Треугольника. Нам, как жителям Северного полушария, повезло наблюдать данный объект с территории России круглый год. Но для детального изучения наиболее подходящими условиями можно охарактеризовать осенний месяц ноябрь.

История созвездия Треугольник

Так как созвездие Треугольник довольно древнее, то его появление на небесной сфере не лишено мифологической истории.

Изначально участок назывался Сицилией. По легенде, богиня Церера обратилась к Юпитеру с просьбой поместить остров Сицилия на небо. В результате, она хотела увековечить его на все времена.

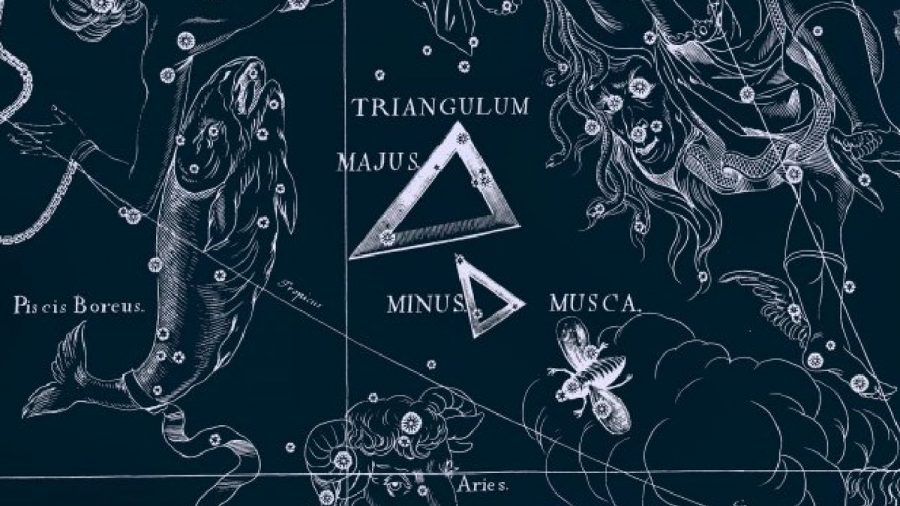
Созвездие Треугольник также известно под другими именами. Например, в Древней Греции его называли Дельтотон. Это имя дали в честь буквы греческого алфавита, на которую область была похожа по форме.

Звёзды, образующие созвездие Треугольник

Бета Треугольника

Самой заметной для наблюдателя является бета Треугольника, поскольку его видимая звездная величина составляет 3,0m. Данную звезду, расположенную в 124 св. годах от нашей планеты, можно встретить под собственным именем Дельтотум. Бета Треугольника является белым гигантом, который принадлежит к спектральному классу A5III.

Альфа Треугольника

Еще одной яркой звездой, но более слабой чем предыдущая, является альфа Треугольника. Это спектрально-двойная система со средней видимой величиной 3,42m, которую часто называют Мотхаллах, что значит «вершина треугольника». С Землей данное светило разделяет расстояние 63 св. лет. Спектральный класс данной звезды не однозначен: Альфа является представителем класса F5III-F6IV.

Гамма Треугольника

Крайней звездой по яркости блеска в тройке считается гамма Треугольника. Звезда является белым карликом спектрального класса A1Vnn. Видимая звездная величина гаммы равняется 4,03m. От Земли до данной звезды лежит расстояние в 128 св. лет.

Треугольник в Треугольнике

Самым любопытным объектом глубокого космоса в Треугольнике является галактика, расположенная примерно в 3 млн. св. лет от нашей планеты. Она имеет одноименное название с созвездием, в котором расположилась, а в астрономических атласах обозначается как Мессье 33 либо NGC 598. Являясь членом Местной группы галактик, она занимает в ней третью позицию по величине, обладая диаметром порядка 50 тыс. св. лет. Видимая звездная величина галактики Треугольник – 5,7m, благодаря чему ее можно наблюдать даже в бинокль.

Интересные объекты, которые входят в созвездие

Галактика «Треугольника» является спиральной и выступает в качестве одного из отдаленных объектов, который может быть без труда найден невооруженным взглядом. Показатель визуальной величины составляет 5,72 единиц, а норма удаленности – до 3070 световых лет. Объект занимает третье по величине место в рамках третьей группы после Млечного Пути, а диаметре способен охватить 5 000 лет и 40 млрд светил.

В рамках галактики присутствует 54 скопления (шаровых). Без труда можно обнаружить и черную дыру, происхождение которой ознаменовалось гравитационным коллапсом. Она была отыскана в 2007 г., и ее масса составляет 15,7 масс Солнца. Уильямом Гершелем в отношении данного объекта было свершено немало открытий, и он отнес его в свой персонально разработанный каталог туманностей.

Наряду с этим созвездие Треугольник содержит в себе еще несколько объектов, получивших буквенно-цифровые обозначения.

NGC 604

Это туманность эмиссионного типа, которая располагается северо-восточнее относительно центрального ядра. Удаленность равняется 1 500 лет, а показатель видимого значения – 14 единиц. Элемент был найден вследствие трудов У. Гершеля.

NGC 595

Это одна из распространенных областей с удаленностью в 3 000 000 световых лет. Она была открыта науке в 1864 г. (1 октября).

NGC 634

Это галактика спирального типа, обладающая видимой величиной, составляющей 14 единиц. Показатель ее удаленности составляет 250 млн лет. Первооткрывателем стал Э. Стефан.

NGC 925

Еще одна группа светил спирального типа, оснащенная перемычкой и визуальной величиной в 10,7 ед.

NGC 672, IC 1727

Объекты взаимодействуют между собой и имеют разделение на 88 000 лет.

NGC 784

Еще одна распространенная категория, относящаяся к спиральному типу, оснащенная перемычкой. Видимый показатель – 12,23 ед., а отдаленность – 16 млн лет.

NGC 953

Эта галактика имеет эллиптическую природу и оснащена параметром видимой величины, равным 14,5 единиц. Она была найдена силами Г. Луи в 1865 г.

Таким образом, рассматриваемая группа светил играет важную роль и может быть рассмотрена невооруженным глазом. В ее составе присутствует множество космических объектов, которые продолжают изучаться силами современных специалистов.

Угол альфа и угол бета. Расшифровка

Положение суставов и головки бедренной кости оценивается не только визуально. Для определения их состояния используется специальное измерение углов по таблице Графа. Есть угол Альфа и угол Бета.

Альфа обозначает развитие костной части ветлужной ямки.
Бета описывает хрящевое пространство внутри ветлужной впадины.

Для здоровых детей считается нормальным, если угол Альфа составляет более 60 градусов, а угол Бета — менее 55 градусов.

Небольшое превышение нормы в 55 градусов допустимо, такой сустав считается нормальным, зрелым. Но если угол Бета составит 77 градусов, врач поставит в заключении подозрение на вывих или подвывих. Также на патологию указывает угол Альфа, который находится в диапазоне от 43 градусов.

Норма углов в таблице выглядит следующим образом.

Более 60 градусов

В пределах 55 градусов

Зрелый здоровый сустав

Менее 55 градусов, плотно облегает головку бедра

Физиологически незрелый сустав

Менее 55 градусов

Круглый, почти плоский

Менее 77 градусов

Более 77 градусов

Уплощенный или плоский

Менее 43 градусов

Не охватывает головку

Децентрация, полная незрелость сустава

В ходе роста ребенка показатели могут меняться, именно это будет учитывать доктор во время проведения УЗИ. Если ребенку уже исполнилось четыре месяца, наиболее правильным и точным методом обследования станет рентгеновский снимок.

В случае обнаружения проблем врачи стараются обследовать одновременно и костное строение малого таза. Довольно часто патология тазобедренного сустава отражается именно на нем.

В заключении доктор может быть немногословен и предпочтет ограничиться буквенно-числовым обозначением типа сустава, обнаруженного у ребенка. Запомните, что здоровый сустав всегда обозначается как 1А или 1В.

Если в заключении указано, что обнаружен сустав 2А или 2В, это означает, что у ребенка есть признаки физиологической незрелости, которая пройдет самостоятельно с огромной вероятностью, но все-таки потребует наблюдения у детского ортопеда.

Сустав 2С — сустав с признаками предвывиха. Обязательно требуется наблюдение у врача и выполнение всех его рекомендаций. 3А и 3В — суставы с подвывихом. Самая тяжелая патология — сустав 4 типа. Именно так обозначается тазобедренный сустав с признаками вывиха (дисплазии).

Угол альфа в физике. Что такое угол альфа?

Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. У г о л , образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол альфа .

Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q + R + S) в I и III стандартных отведениях.

Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (-), поскольку находятся ниже изоэлектрической линии, а зубец R — знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).

Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен минус 70°.

Если угол альфа находится в пределах 50-70° , говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме. При отклонении электрической ось сердца вправо угол альфа будет определяться в пределах 70-90° . В обиходе такое положение электрической оси сердца называют правограммой .

Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса .
Определяя угол альфа в пределах 50-0° говорят об отклонении электрической оси сердца влево, или о левограмме .
Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме .
И наконец, если значение угла альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса .

Определение отклонения электрической оси сердца по углу альфа с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой.
Однако определить отклонение электрической оси сердца можно и без необходимых таблиц.

В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса заменяют понятием «определяющий зубец» комплекса QRS, визуально сопоставляя по абсолютной величине зубцы R и S. Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец R. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.

Если на электрокардиограмме в I стандартном отведении желудочковый комплекс представлен R-типом, а комплекс QRS в III стандартном отведении имеет форму S-типа, то в данном случае электрическая ось сердца отклонена влево (левограмма) . Схематично это условие записывается как RI-SIII.

Напротив, если в I стандартном отведении мы имеем S-тип желудочкового комплекса, а в III отведении R-тип комплекса QRS, то электрическая ось сердца отклонена вправо (правограмма) .
Упрощенно это условие записывается как SI-RIII.

Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так , что его направление совпадает с направлением оси II стандартного отведения.

На рисунке видно, что амплитуда зубца R во II стандартном отведении наибольшая. В свою очередь зубец R в I стандартном отведении превосходит зубец RIII. При таком условии соотношения зубцов R в различных стандартных отведениях мы имеем нормальное положение электрической оси сердца (электрическая ось сердца не отклонена). Краткая запись этого условия — RII>RI>RIII.

Угол альфа символ. Угол атаки

Датчики углов атаки у ракеты «воздух-воздух»

Для самолёта в горизонтальном прямолинейном полёте увеличение скорости и угла атаки приводит к увеличению подъёмной силы , создаваемой крылом. В то же время увеличение угла атаки сопровождается ростом.

Торпедоносец/пикирующий бомбардировщик Supermarine Type 322 , истребитель палубного базирования Воут F-8 «Крусейдер» (Vought F-8 Crusader, 1953 г.) и прототип бомбардировщика Martin XB-51 ( англ. ) (1949 г.) имели изменяемый в полёте угол установки крыла.

Угол альфа в треугольнике. Как найти угол в прямоугольном треугольнике

Здравствуйте!
Как найти угол в прямоугольном треугольнике? Расскажите, пожалуйста, как можно подробнее.
Спасибо!

Прежде, чем разобрать вопрос о том, как найти угол в прямоугольном треугольнике , рассмотрим основные свойства такого вида треугольников. Первое, что нас будет интересовать — это углы данного треугольника. Поскольку треугольник прямоугольный, то один его угол будет прямым, то есть равным 90 градусов. Известно, что если сложить все углы любого из треугольников, то получим 180 градусов. Соответственно, если один из углов в прямоугольном треугольнике равен 90 градусов, то сумма двух других будет равна 180 — 90 = 90 градусов. Следовательно, достаточно найти один из двух острых углов, и тогда легко можно вычислить и величину второго острого угла:
ugol1 = 90 — ugol2.
Зная две любые стороны прямоугольного треугольника и используя определения основных из тригонометрических функций, можно найти величину любого угла прямоугольного треугольника.
Например, если известна длина любого из катетов и длина гипотенузы, то можно вычислить синус или косинус одного из острых углов. А если даны длины обоих катетов. То можно вычислить значение тангенса или котангенса любого из острых углов.

Далее необходимо вычислить с помощью таблицы значений тригонометрических функций величину угла и рассчитать значение второго острого угла по выше упомянутой формуле:
ugol1 = 90 — ugol2.

Угол альфа, как определить. Таблица определения положения электрической оси сердца (по Дьеду)

Таблица определения угла альфа

Если угол альфа находится в пределах 50—70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме.

При отклонении электрической ось сердца вправо угол альфа будет определяться в пределах 70—90°. В обиходе такое положение электрической оси сердца называют правограммой.

Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса.

Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме.

Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме.

И наконец, если значение угла альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.

Пределы отклонения электрической оси сердца

Однако определить отклонение электрической оси сердца можно и без необходимых таблиц.

Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец R. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.

Сопоставление зубцов R и S комплекса QRS

Схематично это условие записывается как RI-SIII.

Визуальное определение электрической оси сердца. Левограмма

Упрощенно это условие записывается как SI-RIII.

Визуальное определение электрической оси сердца. Правограмма

Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так, что его направление совпадает с направлением оси II стандартного отведения.

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение треугольников.

Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.

Эта математическая программа находит сторону ( c ), углы ( alpha ) и ( beta ) по заданным пользователем сторонам ( a, b ) и углу между ними ( gamma )

Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Введите стороны ( a, b ) и угол между ними ( gamma ) Решить треугольник

Созвездие Треугольник

Соседями являются такие северные участки, как Андромеда, Овен, Персей и Рыбы.

Поиск созвездия Треугольник на небе

История созвездия Треугольник