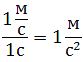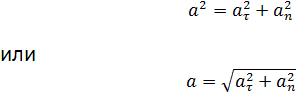Как найти дельта ускорения в физике

Была ли эта статья полезной?

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

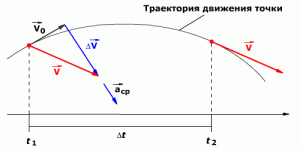
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

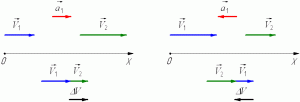
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с², то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

v2 > v1

а направление вектора ускорения совпадает с вектором скорости 

Если скорость тела по модулю уменьшается, то есть

v2 < v1

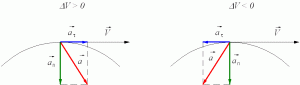
то направление вектора ускорения противоположно направлению вектора скорости  Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения  (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Для описания
движения выбирают тело отсчета – это
произвольны выбор тела относительно
которых определяется положение других
движущихся тел.

Система
координат
– это система связанная с телом отсчета
(в противном случае декартовая система
координата)

Система
отсчета –
это совокупность тел отсчета связанная
с ним системой координат и синхронизированных
между сомой часов.

Положение точки А
характеризуется 3 координатами

При движении
материальной точки координаты будут
изменяться

Уравнение
движения материальной точки

x=x(f)

y=y(f)

z=z(f)

r=r(f)

6.Скорость (средняя. Ее модуль, мгновенная скорость и ее модуль). Путь, траектория, вектор перемещения, длинна пути.

Траектория
– это линия
отсчитываемая движущиеся материальной
точкой то есть выбор системы координат.

Траектория в разл.
системе отсчета может быть разная если
траектория деления

прямая линия
–прямолинейной

Кривая линия –
криволинейной

Если тело находится
в точке А потом перемещается в точку В
то

дельтаr=r0-r

Это приращения
вектора r
за промежуток времени дельта ф

Длинна пути

дельта s(t)
– это пройденный промежуток времени

s
– скалярный вектор

Если все точки
траектории лежат в одной плоскости то
движение называется плоским

Скорость
– векторная
величина определяющая как быстроту
движения так и его направление в данный
момент времени.

Средняя
скорость
– векторная величина определяемая
дельта r
вращения к прошедшему времени вращения.

<v>=дельта
r/дельта
t

Направление вектора
средней
скорости

<v>=|<v>|=дельта
r/дельта
t
= |дельта r/дельта
t|=
дельта s/дельта
t

Мгновенная
скорость
v
– это векторная величина определяемая
первой производной r
вектора движущейся точки ко времени

v=lim
дельта r/дельта
t
(при t
стрем. к 0)= дельта r/дельта
t

Векторные скорости
направлены по касательной к т.А

Модуль
мгновенной скорости
v

v=|v|=|lim
дельта r/дельта
t
(при t
стрем. к 0)|= дельта s/дельта
t

Длинна
пути s
пройденного за промежуток точкой есть

s=интеграл
от t2
до t1
от v(t)dt
(м/с)

7. Ускорение и его составляющее (среднее, мгновенное, нормальное, тангинцеальное, полное ускорение при криволинейном движении)

Ускорение
– есть
характеристика ее равномерного движения
и определяет быстроту

изменения скорости
как по модулю или по направлению.
Существует понятие движение по окружности
с ускорением.

Среднее
ускорение
– это векторная величина равная отношению
изменения скорости к интервалу времени

<a>=
дельта v/дельта
t

Мгновенное
ускорение
а векторная величина определяемое
первой производной скорости ко времени

a=
lim
дельта v/дельта
t
(при t
стрем. к 0)|= дельта v/дельта
t

Составляющее
ускорение может быть

а).Тангенциальным
– характеризует
быстроту изменения скорости по модулю.
Она направлена по касательной к траектории

а тангенциальное
дельта v/дельта
t

б).Нормальное
составляющее
характеризует изменение скорости по
величине и направлению, характеризует
быстроту изменения скорости по
направленности. Она направлена к центру
изменения траектории.

а нормальное дельта
v
в квадрате/дельта r

Тангенциальное
ускорение – постоянная величина .

Нормальное ускорение
=0 появляется при движении по окружности.

Криволинейное
равнопеременное движение

Полное ускорение
при криволинейном геометрическом
движении

нормальное+тангенциальное
движение

а (м/с²)

8.Угловая скорость,
период вращения, углы поворота, частота,
скорость. Вращательное
движение твердого тела – движение при
котором все точки движущейся по окружности
центры которых лежат на одной прямой
называемой осью вращения.

Существует угловая
скорость
векторная величина определяемая
следующим образом.

w=lim
дельта f/дельта
t
(при t
стрем. к 0)|= дельта f/дельта
t

Пер. угла поворота
ко времени

где df
– вектор

Элементы угла
поворота df
рассчитываются как вектора

Модуль вектора df
равен углу
поворота,
а что направление совпадает с направлением
поступательного движения острия винта
головка которого вращается в в направлении
движения точки по окружности что
подчиняется правилу правого винта (если
точка движется по окружности против
часовой стрелки).

Поэтому угловая
скорость будет направлена по оси движения

Еденица w=1
рад/с

Период
вращения
время за которое точка совершает полный
оборот

w=2пи/Т

где Т-период

Линейная
скорость
точка движущейся по окружности

Линейная скорость

v=lim
дельта s/дельта
t
(при t
стрем. к 0)=lim
R*дельта
f/дельта
t
(при d
стрем. к 0)

v=Rw

Частота
вращения
– это число полных оборотов совершаемых
телом в единицу времени

Число полных
оборотов совершаемом за единицу времени
назывеется частотой вращения

n=1/T=w/2пи

w=2пи*n

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Нам уже известно понятие ускорения тела. Так именуют величину, характеризующую изменение его скорости. Также нам известно понятие угловой скорости. Для характеристики этого изменения используют величину, называемую угловым ускорением. Рассмотрим его особенности и использование.

Определения углового ускорения тела. Среднее и мгновенное угловое ускорение

Слово «кинематическая» означает, что движение рассматривается без учёта действия на тело сил, независимо от них. Обозначим промежуток времени как Δt. Изменение угловой скорости за этот промежуток обозначим как Δω. Отношение Δω/Δt называют средним угловым ускорением. Среднее угловое ускорение равно угловой скорости за определённый интервал времени. Однако, как она себя вела, например, в самом его начале, середине или конце ничего не скажешь.

Если мы будем выбранный нами интервал времени постоянно уменьшать, изменение скорости получится описывать всё более и более точно. В идеале, чтобы Δt вообще стремился к нулю:

ε = lim (Δt→0)(Δω/Δt) = dω/dt = d²φ /d²t

Так мы перешли ко второму определению углового ускорения, только оно уже не среднее, а, как говорят, мгновенное.

Угловое ускорение тела равно:

ε = dω/dt = d²φ /d²t

Размерностью величины будет 1/T² (1/время²). Измеряют его обычно в радианах на секунду в квадрате, рад/с² или 1/с² (с^-2).

Обязательно следует отметить, что ε может рассматриваться, в качестве вектора, т. е. ему приписывается направление. Хотя в отличие от направления обычной скорости, воспринимается это несколько сложнее, ведь наглядность отсутствует.

Угловое ускорение через радиус выражается как a = ε*R, где a – ускорение, направленное по касательной траектории.

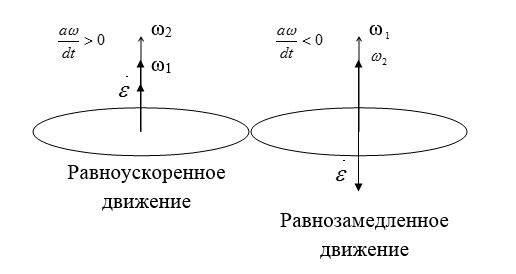
Угловое ускорение и формула закона движения при равнопеременном вращении

Выведем его закон. Пусть в начальный момент времени (t=0) равен φ₀, а его начальная скорость ω_0.

Из определений выше следует

ε = dω/dt следует, что dω = ε dt.

Чтобы найти угловую скорость нам нужно найти первообразную от этого выражения по времени. Получаем

 ω = εt + С1.

С1 – некоторая постоянная. В нашем случае, по начальным условиям, она равна начальной угловой скорости тела, ω₀.

Поэтому

ω = εt + ω₀

Напомним, что мгновенная угловая скорость равна: ω = dφ /dt

Отсюда

dφ /dt = εt + ω₀

φ = (εt + ω₀)dt

Находим первообразную по времени

φ = εt²/2 + ω₀t + С2

С2 – некоторая постоянная. Исходя из начальных условий она равна φ₀. Приходим к выражению

φ = εt²/2 + ω₀t + φ₀

Это и есть закон равнопеременного вращательного движения.

Примеры

Пример. 1

Колесо стало вращаться с постоянным угловым ускорением и, спустя 10 оборотов от начала вращения, получило скорость 20 рад/с. Чему равно угловое ускорение?

Решение:

Применим к вращению колеса формулу равнопеременного движения, исходя из того, что его начальная угловая скорость ω₀ была равна нулю. Формулы, с которыми нам придётся иметь дело:

φ = εt²/2; ω = εt;  φ = 2πN

Из первой формулы выражаем ε

ε = (φ/t²)

Из второй формулы выражаем время

t = ω/ε

Подставляем его в формулу выше.

ε = (2*φ)/(ω/ε)² = ( 2* φ * ε²)/ω²

Проводим необходимые сокращения и приходим к формуле углового ускорения:

ε = ω²/2φ

Вместо угла φ подставляем в выражение третью формулу

ε = ω²/2*2πN = ω²/4πN

После подстановки численных значений получим ε = 3,2 рад/c²

Ответ: Угловое ускорение колеса равно 3,2 рад/c².

Пример. 2

Тело вокруг собственной оси вращается по следующему закону:

φ = 10 + 20*t – 2*t²

Нужно найти угловое и полное ускорение точки, находящейся в 109 см. от оси вращения через 4 секунды после начала движения.

Решение:

Формулы, с которыми нам придётся иметь дело:

[a=sqrt{a_{n}^{2}+a_{T}^{2}}]

A_t = dv/dt = Rε

a_n = v²/R = ω²R

Если известен закон движения, то ω и ε не составляет труда выразить через производные. Сначала находим ω.

ω = d(10 + 20t – 2t²)/dt = 20 – 4t

Ускорение находим, дифференцируя последнее полученное выражение:

ε = d(20 — 4t)/dt = (- 4 )рад/с²

Смотрим на формулу нахождения полного a и выражение ε через радиус, после чего делаем соответствующие подстановки.

[a=sqrt{R^{2} varepsilon^{2}+omega^{4} R^{2}}]

После численных подстановок выясняем, что a точки равно 1,65 м/с².

Ответ: Угловое ускорение точки равно (-4) рад/с², а полное её ускорение – 1,65 м/с².