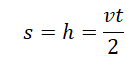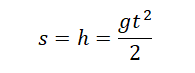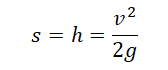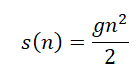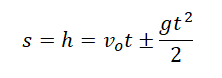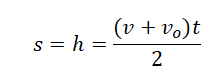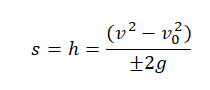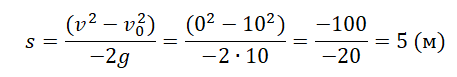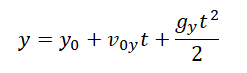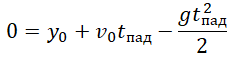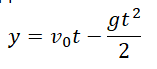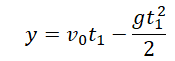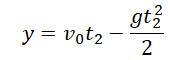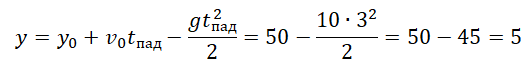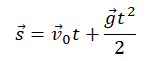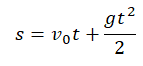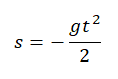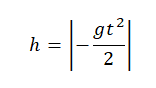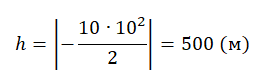Формула ускорения свободного падения в физике
Формула ускорения свободного падения
Гравитационное поле и ускорение свободного падения
Гравитационные взаимодействия тел можно описывать, применяя понятие гравитационного поля. Считают, что передача любых взаимодействий между телами реализуется при помощи полей, которые создают рассматриваемые тела. Одно из тел не оказывает непосредственного действия на другое тело, но оно создает в окружающем его пространстве гравитационное поле, особый вид материи, которая и оказывает воздействие на второе тело. Наглядной картины поля дать нельзя, понятие физического поля относят к основным понятиям, которые невозможно определить, используя другие более простые понятия. Можно только определить свойства поля.
Гравитационное поле может создавать силу. Поле зависит только от тела, которое его создает и не зависит от тела, на которое оно действует. Силовой характеристикой гравитационного поля является его напряжённость, которую обозначают $overline{g}$. Напряженность гравитационного поля измеряется силой, которая действует на материальную точку единичной массы:
[overline{g}=frac{overline{F}}{m}left(1right).]
Если гравитационное поле создается материальной точкой массы $M$, то оно имеет сферическую симметрию. Это значит, что вектор $overline{g}$ в каждой точке поля направлен к точечной массе $M$, которое создает данное поле. Из закона всемирного тяготения следует, что модуль вектора напряженности гравитационного поля:
[gleft(rright)=gamma frac{M}{r^2}left(2right).]
Из формулы (2) следует, что $g$ зависит от расстояния ($r$) от источника поля до точки, в которой поле рассматривается. В таком поле движение происходит по законам Кеплера.
Гравитационные поля удовлетворяют принципу суперпозиции. Напряженность поля, которая создается несколькими телами, равна векторной сумме напряженностей полей, которые порождаются каждым телом отдельно. Принцип суперпозиции выполняется, поскольку гравитационное поле, создаваемое какой-либо массой, не зависит от присутствия других масс. Принцип суперпозиции дает возможность рассчитывать гравитационные поля, которые созданы телами, отличающимися от точечных (размеры которых следует учитывать).
Ускорение при свободном падении
Если тело около поверхности Земли движется только под воздействием силы тяжести ($overline{F}$), говорят, что оно свободно падает. Ускорение свободного падения обозначают буквой $g$. В соответствии со вторым законом Ньютона это ускорение равно:
[overline{g}=frac{overline{F}}{m}left(3right),]
где $m$ — масса свободно падающего тела.
В соответствии с законом гравитации величина силы $overline{F}$ на расстоянии $h$ от поверхности Земли равна:
[left|overline{F}right|=gamma frac{mM}{{(R+h)}^2}left(4right),]
где $gamma $- гравитационная постоянная; $M$ — масса Земли; $R$ — радиус Земли.
Получается, что модуль ускорения свободного падения у поверхности Земли ($hll R$) равен:
[g=gamma frac{M}{R^2}left(5right).]
Направлено ускорение свободного падения к центру Земли.
Правая часть выражения (5) дает величину напряженности гравитационного поля Земли вблизи к ее поверхности.
Получаем, что напряжённость гравитационного поля и ускорение свободного падения в поле гравитации — это одно и то же. Поэтому эти величины были сразу обозначены одной буквой.
Величина ускорения свободного падения на расстоянии $h$ от поверхности Земли вычисляется при помощи формулы:
[g=gamma frac{M}{({R+h)}^2}left(6right).]
В задачах о движении тел около поверхности Земли ускорение свободного падения считают постоянной величиной, которую вычисляют с помощью формулы (5), так как в сравнении с радиусом Земли рассматриваемые расстояния много меньше, чем $R$. Обычно, ускорение свободного падения на Земле считают равным $g=9,8 frac{м}{с^2}$.
Примеры задач с решением
Пример 1
Задание. Каково ускорение свободного падения на Меркурии, если его масса меньше массы Земли в 18,18 раза, отношение радиусов Земли ($R_z$) и радиуса Меркурия ($R_m$) составляет $frac{R_z }{R_m}=2,63$?
Решение. Модуль ускорения свободного падения у поверхности Земли определен формулой:
[g=gamma frac{M}{{R_z}^2}left(1.1right).]
Величина вектора напряженности гравитационного поля любого тела равна:
[gleft(rright)=gamma frac{M}{r^2} left(1.2right),]
если в формулу (1.2) вместо массы $M$ подставить массу Меркурия, а вместо $r$ его радиус, то мы получим ускорение свободного падения около поверхности Меркурия:
[g_m=gamma frac{M_m}{{R_m}^2}left(1.3right).]
Найдем отношение выражений (1.1) и (1.3):
[frac{g}{g_m}=frac{gamma frac{M}{{R_z}^2}}{gamma frac{M_m}{{R_m}^2}}=frac{M}{M_m}frac{{R_m}^2}{{R_z}^2}left(1.4right).]
Считая, что нам известно ускорение свободного падения на Земле ($g=9,8 frac{м}{с^2}$), выразим ускорение свободного падения на Меркурии:
[g_m=gfrac{M_m}{M}cdot frac{{R_z}^2}{{R_m}^2}.]
Вычислим искомое ускорение:
[g_m=9,8cdot frac{1}{18,18}cdot {left(2,63right)}^2=3,73 left(frac{м}{с^2}right).]
Ответ. $g_m=3,73frac{м}{с^2}$
Пример 2
Задание. Ускорение свободного падения на поверхности Земли считают равным $g_0$. Тело опускают в глубокую шахту под Землю. На какой глубине ($h$) от поверхности ускорение свободного падения данного тела будет составлять $g=$0,3 $g_0. $Радиус Земли равен $R. $Землю считайте однородным шаром.
Решение. Если тело находится на некоторой глубине, то считаем, что находящиеся выше слои Земли действуют на тело с силами гравитации, которые взаимно компенсируют друг друга. Поэтому тело притягивается только той массой Земли, которая находится ниже рассматриваемого тела.
В качестве основы для решения задачи используем закон всемирного тяготения в виде:
[F=gamma frac{mM}{r^2}left(2.1right),]
где $m$ — масса тела; $M$ — масса Земли; $r$ — расстояние от центра Земли до рассматриваемого тела, то есть:
[r=R-h left(2.2right),]
где $R$ — радиус Земли. Мы можем использовать закон гравитации в виде (2.1), так как по условию задачи Землю считаем однородным шаром (ее масса распределена сферически симметрично), а тело материальной точкой. С другой стороны на тело действует сила, которая равна:
[F=mg left(2.3right).]
Приравняем правые части выражений (2.1) и (2.3), учтем (2.2):
[mg=gamma frac{mM’}{{(R-h )}^2}to g=gamma frac{M’}{{left(R-h right)}^2}left(2.4right),]
где $M’=frac{4pi }{3}{rho left(R-h right)}^3$ — масса слоев Земли ниже рассматриваемого тела; $rho $ — плотность Земли.
У поверхности Земли мы знаем, что:
[g_0=gamma frac{M}{R^2}=gamma frac{frac{4pi }{3}rho R^3}{R^2}=frac{4pi }{3}gamma rho Rleft(2.5right).]
Выразим из (2.5) плотность Земли:
[rho =frac{3}{4pi }frac{g_0}{gamma R}left(2.6right).]
Подставим результат (2.6) в формулу (2.4) выразим высоту:
[g=gamma frac{frac{4pi }{3}{left(R-h right)}^3}{{left(R-h right)}^2}frac{3}{4pi }frac{g_0}{gamma R}=g_0frac{R-h}{R}to h=Rleft(1-frac{g}{g_0}right)=0,7R.]
Ответ. $h=Rleft(1-frac{g}{g_0}right)=0,7R$
Читать дальше: формула центростремительного ускорения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
Свободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
Внимание!
В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Ускорение свободного падения — векторная физическая величина. Вектор ускорения свободного падения всегда направлен вниз к центру Земли. Обозначается как g.
Единица измерения ускорения свободного падения — 1 м/с2.
Модуль ускорения свободного падения — скалярная величина. Обозначается как g. Численно равна 9,8 м/с2. При решении задач это значение округляется до целых: g = 10 м/с2.
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
Скорость
v = gt
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
v = gt = 10∙3 = 30 (м/с).
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Высота падения
Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
Формула определения перемещения тела в n-ную секунду свободного падения:
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.
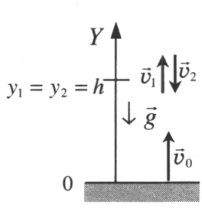
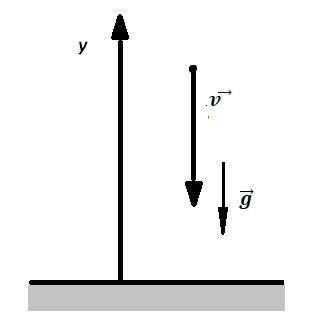
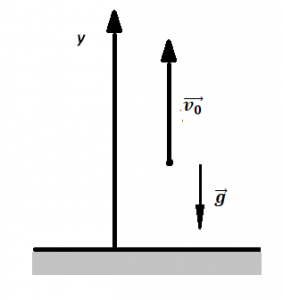
Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
Два этапа движения тела, брошенного вертикально вверхЭтап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях (v↑↓g).
Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону (v↑↑g).
Формулы для расчета параметров движения тела, брошенного вертикально вверхПеремещение тела, брошенного вертикально вверх, определяется по формуле:
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
Если время движения неизвестно, для определения перемещения используется следующая формула:
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
- Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
- Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
Уравнение скорости при свободном падении:
vy = v0y + gyt
Полезные факты
- В момент падения тела на землю y = 0.
- В момент броска тела от земли y0 = 0.
- Когда тело падает без начальной скорости (свободно) v0 = 0.
- Когда тело достигает наибольшей высоты v = 0.
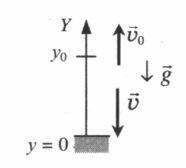
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
План построения чертежа
- Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
- Отмечаются начальная и конечная координаты тела (y и y0).
- Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.
Свободное падение на землю с некоторой высоты
Чертеж:
Уравнение скорости:
–v = v0 – gtпад
Уравнение координаты:
Тело подбросили от земли и поймали на некоторой высоте
Чертеж:
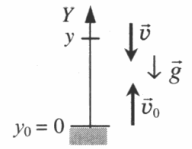
–v = v0 – gt
Уравнение координаты:
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Чертеж:
Интервал времени между моментами прохождения высоты h:
∆t = t2 – t1
Уравнение координаты для первого прохождения h:
Уравнение координаты для второго прохождения h:
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Поэтому:
Через 3 с после падения тело окажется на высоте 5 м.
Задание EF17519
С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17483
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.7k
You should upgrade or use an alternative browser.
-
Forums
-
Other Sciences
-
Chemistry
How do you calculate delta G
-
Thread starter
afcwestwarrior -
Start date
Apr 12, 2007 -
-
Tags -
Delta
-
- Apr 12, 2007
- #1
or could i calculate it like i calculate delta h, products — reactants
Answers and Replies
- Apr 14, 2007
- #2
- Apr 14, 2007
- #3
ΔG = ΔH – T * ΔS
Is a more general way to do it since this will be true for any specified temperature, T.
You could calculate it as,
ΔG = G_products – G_reactants
But this will only be valid for the temperature which your table has its G values calculated in. You might have access to a table of standard G of formation, but this would only be true under standard conditions.
What if you had a non-spontaneous reaction (under standard conditions) and you wanted to find out the temperature you needed to raise it to in order to make it spontaneous? To do this, you would have to calculate it the old fashion way without the Free Energy table.
- Nov 28, 2020
- #4
Suggested for: How do you calculate delta G
- Apr 28, 2023
- Nov 1, 2020
- Nov 17, 2022
- Mar 14, 2021
- Feb 18, 2021
- Sep 30, 2019
- Nov 12, 2019
- May 17, 2022
- Jan 29, 2023
- Oct 31, 2018
-
Forums
-
Other Sciences
-
Chemistry
Выберем тело, например, камень. Расположим его не некотором расстоянии от поверхности земли. Расстояние от центра Земли до камня равно ( R = left( r + h right) ), как представлено на рисунке 1.
Рис. 1. Камень (черная точка), притягивается к планете (центральная окружность).
Пусть на камень действует только сила, с которой Земля притягивает его, а других сил нет (нет, например, силы сопротивления воздуха).
Свободное падение – это движение тела под действием только одной силы — силы притяжения.
Из законов Ньютона известно: если на тело действует сила, то тело получает ускорение.
Ускорение свободного падения – это ускорение, с которым движется тело, когда на него действует только сила тяжести.
Формула для расчета ускорения свободного падения
Ускорение свободного падения можно посчитать по формуле:
[ large boxed { g = G cdot frac{M}{left( r + h right)^{2}} }]
( g left( frac{text{м}}{c^{2}} right) ) (метры, деленные на секунду в квадрате) – ускорение свободного падения
( M left( text{кг} right) ) (килограммы) — масса планеты, которая притягивает
( r left( text{м} right) ) (метры) – радиус планеты
( h left( text{м} right) ) (метры) — расстояние от поверхности планеты до тела
(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная
Интересные факты
У разных планет ускорение свободного падения различается.
- чем больше масса планеты (или звезды), тем больше будет ускорение свободного падения рядом с такой планетой (или звездой);
- чем дальше от планеты, тем меньше ускорение свободного падения;
- на полюсах ускорение свободного падения больше, чем на экваторе планеты;
Важно!
Все тела под действием силы тяжести падают с одинаковым ускорением! Это ускорение не зависит от массы тела.
Из житейского опыта мы знаем: чем больше площадь тела, тем больше времени ему нужно, чтобы упасть с какой-либо высоты. При своем падении тело опирается на воздух, поэтому, к примеру, лист бумаги будет падать дольше, чем шарик из пластилина, или гирька.
В безвоздушном пространстве опираться не на что. Поэтому гирька, лист бумаги, птичье перо и пластилиновый шарик, стартовав с одной и той же высоты одновременно, упадут на поверхность планеты тоже одновременно.
Ускорение свободного падения у поверхности некоторых небесных тел
- у поверхности Земли ( g = 9{,}8 left( frac{text{м}}{c^{2}} right) )
- у поверхности Луны ( g = 1{,}68 left( frac{text{м}}{c^{2}} right) )
- у поверхности Марса ( g = 3{,}86 left( frac{text{м}}{c^{2}} right) )
- у поверхности Солнца ( g = 273{,}1 left( frac{text{м}}{c^{2}} right) )
- у поверхности Юпитера ( g = 23{,}95 left( frac{text{м}}{c^{2}} right) )
Как вывести формулу ускорения свободного падения
Рассмотрим камень, находящийся на некотором расстоянии от Земли.
Земля и камень притягиваются, запишем закон притяжения между планетой и камнем
[ F = G cdot frac{mcdot M}{left( r + h right)^{2}} ]
С другой стороны, у камня есть вес, так как на него действует сила тяжести.
[ F_{text{тяж}} = m cdot g ]
Мы можем записать эти уравнения в виде системы.
[ begin{cases} displaystyle F = G cdot frac{mcdot M}{( r + h)^{2}} \ displaystyle F_{text{тяж}} = m cdot g end{cases} ]
Земля и камень притягиваются, благодаря этому на камень действует сила тяжести. На языке математики это запишется так:
[ F = F_{text{тяж}} ]
А если равны левые части уравнений, то будут равны и правые:
[ G cdot frac{mcdot M}{left( r + h right)^{2}} = m cdot g ]
Масса ( m ) камня встречается в обеих частях уравнения. Поделим обе части уравнения на массу камня.
[ G cdot frac{M}{ left( r + h right)^{2}} = g ]
Все)
Вам будет интересно почитать:
Закон всемирного тяготения
Законы Ньютона
Первая космическая скорость
Вторая космическая скорость