|
|
немогу понять как найти дельта от эпсилон
|
|
30/11/07 |
|
|
|
|
|
ewert |
Re: немогу понять как найти дельта от эпсилон
|
||
11/05/08 |
Решить неравенство. Но сначала, конечно, сократить дробь.
|
||
|
|
|||
|
Eiktyrnir |
Re: немогу понять как найти дельта от эпсилон
|
|
30/11/07 |
Решить неравенство. Но сначала, конечно, сократить дробь. Извините 1000 раз. Я вот понял, что это система неравенств. Т.е. получил вот что
|
|
|
|
|
ewert |
Re: немогу понять как найти дельта от эпсилон
|
||
11/05/08 |
|||
|
|
|||
|
ShMaxG |
Re: немогу понять как найти дельта от эпсилон
|
||
11/04/08 |
|||
|
|
|||
|
ewert |
Re: немогу понять как найти дельта от эпсилон
|
||
11/05/08 |
А не наоборот ли? Да, наоборот. Я, как обычно, не обратил внимания на направление неравенства.
|
||
|
|
|||
|
Eiktyrnir |
Re: немогу понять как найти дельта от эпсилон
|
|
30/11/07 |
To ShMaxG ewert — спасибо огромное. Вывели из умственного «ступора».
|
|
|
|
|
Eiktyrnir |
Re: немогу понять как найти дельта от эпсилон
|
|
30/11/07 |
|
|
|
|
|
Sasha2 |
Re: немогу понять как найти дельта от эпсилон
|
|
21/06/06 |
А какой вообще смысл в этой задаче поиска дельты для епсилон, коли предел уже найден?
|
|
|
|
|
ShMaxG |
Re: немогу понять как найти дельта от эпсилон
|
||
11/04/08 |
|||
|
|
|||
|
maxmatem |
Re: немогу понять как найти дельта от эпсилон
|
|
15/08/09 |
Sasha2 Цитата: А какой вообще смысл в этой задаче поиска дельты для епсилон, коли предел уже найден? Вполне возможно, что тс.,решил проверить верно ли он вычислил предел, вот и воспользовался определение предела, чз епсилон-дельту.Но это мне так показалось
|
|
|
|
|
Eiktyrnir |
Re: немогу понять как найти дельта от эпсилон
|
|
30/11/07 |
Значит, еще раз. Вот теперь я кажется вас начинаю понимать…
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
As commenters in this question and the linked question have stated, it is impossible to solve this problem. Here is a proof of the negation.
You are asked to show that
$$exists delta > 0,forall (x,y)in mathbb{R}^2, 0 < sqrt{x^2+y^2} < delta implies |f(x,y)| < 0.01$$
I will show that
$$ forall delta > 0,exists (x,y)inmathbb{R}^2, 0 < sqrt{x^2+y^2} < delta wedge |f(x,y)| geq 0.01
$$
Let $delta > 0$ be given.
Setting $y=x$ in the function and taking the limit as $xto 0$ gives
$$
lim_{xto 0} f(x,x) = lim_{xto 0} frac{2x^5 — 5 x^4 + x^5}{4x^4} = — frac{5}{4}
$$
This means there exists $delta_1 > 0$ such that for all $xinmathbb{R}$,
$0 < |x| < delta_1 implies f(x,x) < -1$. Set $x = y = minleft{frac{delta}{2},frac{delta_1}{2}right}$. Then $0 < sqrt{x^2+y^2} < delta$ and $|x|< delta_1$ are both satisfied. It follows from the second inequality that $|f(x,y)| geq 1 > 0.01$.
Лекция 2
Предел
функции
Предел
функции
Зададим
некоторую функцию
и рассмотрим поведение этой функции
при изменении
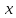
в частности, при
и т.д.
Когда
и
число, то будем предполагать, что функция
определена в окрестности точки
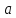
за исключением, быть может, самой точки
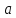
Определение
1.
Число
называется пределом функции
при
,
если
для
любого сколь угодно малого эпсилон
больше нуля найдется дельта, функция
от эпсилон , больше нуля, такое что из
условия,
следует условие для функции
или
запишем определение на языке
или,
используя, определение окрестности
точки, получим:
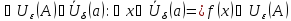
Геометрическая
интерпретация :
Для
любой эпсилон окрестности предела
найдется дельта окрестность предельной
точки
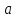
такая что как только
попадает в дельта окрестность предельной
точки
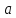
так функция
попадает в эпсилон
окрестность предела
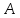
Аналогично
можно дать определение предела при
предположив, что функция
определена при достаточно больших
значениях аргумента
Определение
2.
Число
называется пределом функции
при
,
если
Геометрическая
интерпретация :
Односторонние
пределы функции
Введем
понятие одностороннего предела функции
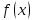
предположив при этом , что функция
определена слева ( или справа) от точки
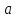
то есть в интервале
( или в интервале
)
Определение
3.
Число
называется левосторонним пределом
функции
при
,
если
Определение
4.
Число
называется правосторонним пределом
функции
при
,
если
Пример1:Найти
левосторонний
и правосторонний
пределы функции
Данная
функция имеет левосторонний
при
и правосторонний
при
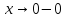
но не имеет предела при
Теорема
: Если
функция
имеет в точке
оба односторонних предела( справа и
слева) и эти пределы равны числу
, то функция
в точке
имеет предел, равный
.
Отметим,
что справедливо и обратное утверждение:
Из
существования у функции
предела в точке
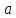
равного числу
, следует существование в этой точке
обоих односторонних пределов , также
равных числу
.
Свойства
функции, имеющих предел
Теорема
1(
об ограниченности функции, имеющей
предел): Если
то
функция
ограничена в окрестности точки
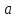
Доказательство:
Обозначим
через
, тогда
то
есть функция
ограничена в окрестности точки
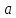
Теорема
2(
о сохранении знака предела): Если
то
в некоторой окрестности предельной
точки
функция
сохраняет знак предела, т.е. знак числа
Доказательство:
Возьмём
, тогда
имеют знак совпадающий со знаком числа
Для
этого
функция
одного знака с числом
в
некоторой окрестности предельной точки
.
Теорема
3(
о единстве предела): Если
у функции
то
этот предел единственный.
Доказательство(
методом от противного):
Предположим, что у функции
существует два предела
при
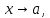
между собой, т.е.
В
силу определения пределов это означает,
что
Обозначим
через
тогда при
будут выполняться оба неравенства:
где
любое число, например возьмем
получили
противоречие, значит наше предположение
было не верно, а
Теорема
4(
о пределе промежуточной функции): Если
в окрестности точки
определены
три функции
, причем выполняется соотношение
и
Доказательство:
из
существования пределов у функций
Обозначим
через
тогда при
будут выполняться оба неравенства:
Замечательные
пределы
Первый
замечательный предел:
Второй
замечательный предел:
Доказательство:
нам
известно
Пусть
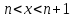
где целое положительное число
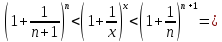
Найдем
пределы последовательностей, стоящих
по краям неравенства.
Тогда
по теореме о пределе промежуточной
функции
Пусть
теперь
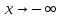
введем переменную
8
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
Did you know that there is a formal, mathematical definition of limits?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In our lessons so far, we have learned how to evaluate a limit of a function graphically and algebraically using limit laws and properties.
And while these laws and definitions enable us to evaluate limits quickly, they have a tiny flaw — they aren’t precise.
Think about it.
Whenever we read a limit, we use the following words: “approach,” “sufficiently close,” “near to,” etc.
So, is there a way to be accurate in our evaluation of the limit of a function?
There sure is! And that’s what this calculus lesson is all about.
Limit Definition
The formal definition of a limit, which is typically called the Epsilon-Delta Definition for Limits or Delta-Epsilon Proof, defines a limit at a finite point that has a finite value.
Epsilon Delta Definition Of A Limit
This probably seems completely abstract, doesn’t it?
How To Find Epsilon Delta Definition Of A Limit
Let’s see if we can shine a light on what is happening.
- First, we create two variables, delta (δ) and epsilon (ε).
- Next we choose an epsilon region around the number L on the y-axis.
- Then, we use this region to help us define a delta region around the number a on the x-axis so that all x-values, excluding a, inside the region correspond to y-values inside the epsilon region.
- Finally, we show (prove) that we can find y-values of the function as close as we want to the value L by using only the points in a small enough interval around a.
And as Milefoot Mathematics quickly points out, we will define our limit in such a way as to allow epsilon to represent any number, while we restrict the value of delta; thus, ensuring that our region is precise.
In fact, it’s this restriction on the delta that holds the key to this unique proof!
Let’s look at a few questions to help us make sense of things.
For each of the following, sketch the open interval (a,b) with point c inside. Then find the value of δ > 0 such that a < x < b whenever 0 < | x – c | < δ.
Hint: delta always represents the shortest distance, so it will be your job to determine the shortest distance from either a to c or b to c!
Example #1
Find Delta Given Epsilon Example 1
Example #2
Find Delta Given Epsilon — Example 2
Example #3
Find Delta Given Epsilon — Example 3
Example #4
Okay, so now that we have a better understanding of what we are looking for in terms of the delta to ensure a precise region, now it’s time to see the formal definition of the limit in action to find epsilon.
Find The Largest Delta That Works For Epsilon
Therefore, the largest value that δ can have is ¼.
Example #5
But what do we do if we aren’t given the value of epsilon?
Then we will leave our answer in terms of epsilon, as seen in the following problem.
Use Epsilon Delta To Prove Limit
Thoughts On The Epsilon Delta Proof
Our video lesson will work through this style of proof in much more detail, and you will see that the proof above is only half complete, as the epsilon-delta proofs are a two-part process.
First, we use the proof to find the value of delta, and then we must “redo” it to prove that our choice of delta is correct. While this may seem tedious, I assure you that it will make sense with a bit of practice.
I will admit that just looking at the proof can seem scary due to all the weird letters and symbols. Still, after seeing it in action and following along with two step-by-step examples of how it is constructed in the video, you will see that this proof is quite straightforward and comes full-circle in the end. Khan Academy even calls it a beautiful proof, and after some practice I think you will see why.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Get My Subscription Now
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.
-
Теоретический минимум
Понятие предела применительно к числовым последовательностям уже вводилось в теме «МА. Предел последовательности. Определение на языке «эпсилон-дельта».
Рекомендуется сначала ознакомиться с содержащимся там материалом.Переходя к предмету этой темы, напомним понятие функции. Функция представляет собой очередной пример отображения. Мы будем рассматривать самый простой случай
вещественной функции одного вещественного аргумента (в чём заключается сложность других случаев — будет сказано позже). Функция в рамках этой темы понимается как
закон, по которому каждому элементумножества
, на котором определена функция, ставится в соответствие один или несколько элементов
множества, называемого множеством значений функции. Если каждому элементу области определения функции ставится в соответствие один элемент
множества значений, то функция называется однозначной, в противном случае функция называется многозначной. Мы здесь будем говорить для простоты только об
однозначных функциях.Сразу хотелось бы подчеркнуть принципиальное отличие функции от последовательности: существенно различны множества, связанные отображением в этих двух случаях.
Чтобы избежать необходимости использовать терминологию общей топологии, поясним различие с помощью неточных рассуждений. При обсуждении предела
последовательности мы говорили только об одном варианте: неограниченный рост номера элемента последовательности. При этом росте номера сами элементы
последовательности вели себя гораздо разнообразнее. Они могли «накапливаться» в малой окрестности некоторого числа; они могли неограниченно расти и т.п.
Грубо говоря, задание последовательности — задание функции на дискретной «области определения». Если же говорить о функции, определение которой дано
в начале темы, то понятие предела следует строить аккуратнее. Имеет смысл говорить о пределе функции при стремлении её аргумента к определённому значению.
Такая постановка вопроса не имела смысла применительно к последовательностям. Возникает необходимость внести некоторые уточнения. Все они связаны с тем,
как именно аргумент стремится к тому значению, о котором идёт речь.
Рассмотрим несколько примеров — пока что вскользь:
Эти функции позволят нам рассмотреть самые разные случаи. Приведём здесь же графики этих функций для большей наглядности изложения.
Функция
в любой точке области определения имеет предел — это понятно интуитивно. Какую бы точку области определения мы ни взяли,
сразу можно сказать, к какому значению стремится функция, при стремлении аргумента к выбранному значению, причём предел будет конечным, если только аргумент
не стремится к бесконечности. График функцииимеет излом. Это сказывается на свойствах функции в точке излома, но с точки зрения предела
эта точка ничем не выделена. Функцияуже интереснее: в точке
непонятно, какое значение предела приписать функции.
Если мы подходим к точкесправа, то функция стремится к одному значению, если слева — функция стремится к другому значению. В предыдущих
примерах такого не было. Функцияпри стремлении к нулю хоть слева, хоть справа ведёт себя одинаково, стремясь к бесконечности —
в отличие от функции, которая при стремлении аргумента к нулю стремится к бесконечности, но знак бесконечности зависит от того, с какой
стороны мы подходим к нулю. Наконец, функцияведёт себя в нуле совершенно непонятно.
Формализуем понятие предела с помощью языка «эпсилон-дельта». Основное отличие от определения предела последовательности будет заключаться в необходимости
прописать стремление аргумента функции к некоторому значению. Для этого требуется вспомогательное в данном контексте понятие предельной точки множества.
Точканазывается предельной точкой множества
, если в любой окрестности
содержится бесчисленное множество точек,
принадлежащихи отличных от
. Чуть позже станет ясно, зачем требуется давать такое определение.
Итак, число
называется пределом функции
в точке
, являющейся предельной точкой множества
, на котором определена
функция, если
Последовательно разберём это определение. Выделим здесь части, связанные со стремлением аргумента к значениюи со стремлением функции
к значению. Следует понимать общий смысл записанного утверждения, который приближённо можно трактовать следующим образом.
Функциястремится к
при
, если взяв число из достаточно малой окрестности точки
, мы будем
получать значение функции из достаточно малой окрестности числа. И чем меньше будет окрестность точки
, из которой берутся значения
аргумента, тем меньше станет окрестность точки, в которую будут попадать соответствующие значения функции.
Снова вернёмся к формальному определению предела и прочитаем его в свете только что сказанного. Положительное число
ограничивает окрестность
точки, из которой будем брать значения аргумента. Причём значения аргумента, конечно, из области определения функции и не совпадающие с самой
точкой: мы ведь стремление пишем, а не совпадение! Так вот если мы возьмём значение аргумента из указанной
-окрестности точки
,
то значение функции попадёт в-окрестности точки
.
Наконец, сводим определение воедино. Какой бы малой мы ни выбрали-окрестность точки
, всегда найдётся такая
-окрестность точки
,
что при выборе значений аргумента из неё мы попадём в окрестность точки. Разумеется, размер
-окрестности точки
при этом
зависит от того, какая была задана окрестность точки. Если окрестность значения функции будет достаточно велика, то и соответствующий разброс значений
аргумента будет большим. С уменьшением окрестности значения функции уменьшится и соответствующий разброс значений аргумента (см. рис. 2).
Осталось уточнить некоторые детали. Во-первых, требование, чтобы точка
была предельной, избавляет от необходимости заботиться, что точка
из-окрестности вообще принадлежит области определения функции. Во-вторых, участие в определении предела условия
означает,
что аргумент может стремиться к значениюкак слева, так и справа.
Для случая, когда аргумент функции стремится к бесконечности, следует отдельно определить понятие предельной точки.
называется предельной
точкой множества, если для любого положительного числа
в интервале
содержится бесчисленное множество
точек из множества.
Вернёмся к примерам. Функция
особого интереса для нас не представляет. Разберёмся подробнее с другими функциями.
Примеры.
Пример 1. График функции имеет излом.
Функциянесмотря на особенность в точке
имеет в этой точке предел. Особенность в нуле — потеря гладкости.
Пример 2. Односторонние пределы.
Функцияв точке
не имеет предела. Как уже отмечалось, для существования предела требуется, чтобы при стремлении
слева и справа функция стремилась к одному и тому же значению. Здесь это, очевидно, не выполняется. Однако можно ввести понятие одностороннего предела.
Если аргумент стремится к данному значению со стороны бòльших значений, то говорят о правостороннем пределе; если со стороны меньших значений —
о левостороннем пределе.
В случае функции
— правосторонний предел
— левосторонний предел
На языке «эпсилон-дельта» формальное определение одностороннего предела
:
Аналогично даётся определение левостороннего предела.Пример 3. Бесконечный предел и предел на бесконечности.
Функцияв точке
имеет бесконечный предел. Формальное определение бесконечного предела
.
А вот функция
в точке
предела не имеет. Зато она имеет там односторонние пределы: правосторонний
и левосторонний
.
Обе эти функции имеют пределы при
, равные нулю. Формальное определение предела на бесконечности:
.
Пример 4. Отсутствие односторонних пределов.
Функцияв точке
не только не имеет предела, она не имеет там даже односторонних пределов. Действительно, при стремлении
аргумента к нулю со стороны положительных или отрицательных значений дробьпо модулю неограниченно растёт. Синус не имеет на бесконечности
определённого значения. Поэтому и односторонние пределы в точкене существуют.
Однако можно привести пример, когда бесконечные колебания синуса не мешают существованию предела (причём двустороннего).
Примером может служить функция. График приведён ниже; по понятным причинам построить его до конца в окрестности
начала координат невозможно. Предел приравен нулю.
Замечания.
1. Существует подход к определению предела функции, использующий предел последовательности — т.н. определение Гейне. Там строится последовательность точек, сходящаяся к требуемому значению
аргумента — тогда соответствующая последовательность значений функции сходится к пределу функции при этом значении аргумента. Эквивалентность определения Гейне и определения на языке
«эпсилон-дельта» доказывается.
2. Случай функций двух и более аргументов усложняется тем, что для существования предела в точке требуется, чтобы значение предела получалось одним и тем же при любом способе стремления аргумента
к требуемому значению. Если аргумент один, то стремиться к требуемому значению можно слева или справа. В случае большего количества переменных число вариантов резко возрастает. Случай функций
комплексной переменной и вовсе требует отдельного разговора.
Поделиться этой страницей






![$[0 < delta left( varepsilon right) le frac{varepsilon }{4}]$ $[0 < delta left( varepsilon right) le frac{varepsilon }{4}]$](https://dxdy-01.korotkov.co.uk/f/c/a/b/cabe4ddf040ef95c314cda7db00a224782.png) , то
, то ![$[0 < left| {x - 3} right| < delta left( varepsilon right) le frac{varepsilon }{4} Rightarrow left| {x - 3} right| < frac{varepsilon }{4}]$ $[0 < left| {x - 3} right| < delta left( varepsilon right) le frac{varepsilon }{4} Rightarrow left| {x - 3} right| < frac{varepsilon }{4}]$](https://dxdy-01.korotkov.co.uk/f/0/5/b/05b74787d2f118075963136397f78c8782.png) , что и нужно.
, что и нужно.
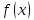
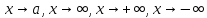
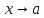
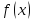
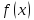
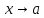
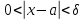
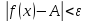
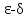
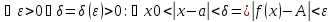
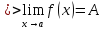
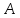
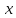
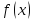
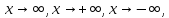

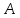
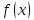
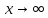
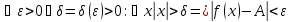
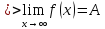
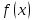
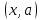
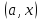
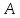
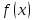
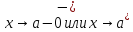
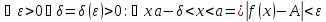
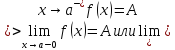
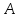
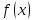
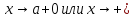
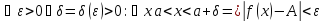
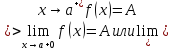
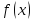
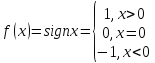
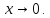
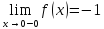
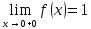
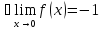
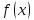
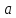
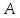
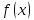
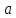
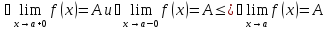
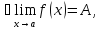
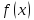
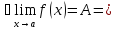
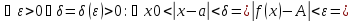
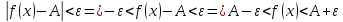
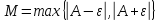
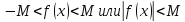
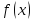
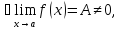
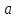
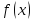
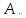

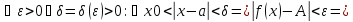
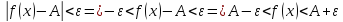
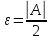
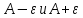
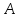
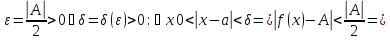
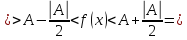
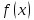
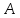
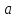
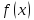
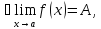
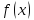

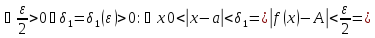
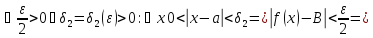
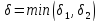
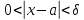
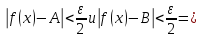
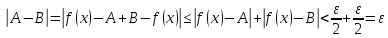
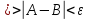
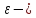
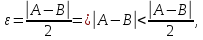
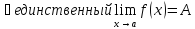
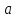
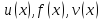
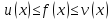
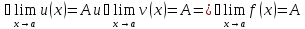
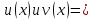
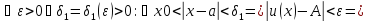
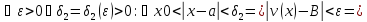
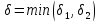
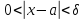
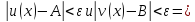
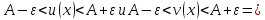
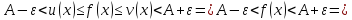
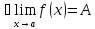
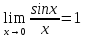
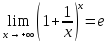
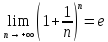
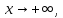
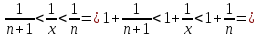
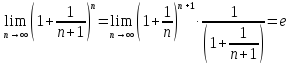
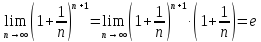
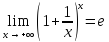
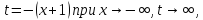
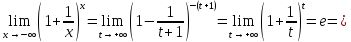
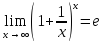


![[IMG]](http://corum.mephist.ru/tex/images/8725029ea89712eed8670bae64d30e47.gif) множества
множества ![[IMG]](http://corum.mephist.ru/tex/images/474e6c59d39ab2b9f9eb79ab75b9da90.gif) , на котором определена функция, ставится в соответствие один или несколько элементов
, на котором определена функция, ставится в соответствие один или несколько элементов ![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif)
![[IMG]](http://corum.mephist.ru/tex/images/39abfebb66c060cd7541c76ff73c12da.gif) , называемого множеством значений функции. Если каждому элементу области определения функции ставится в соответствие один элемент
, называемого множеством значений функции. Если каждому элементу области определения функции ставится в соответствие один элемент![[IMG]](http://corum.mephist.ru/tex/images/b0dc15d502d67805b23c816770a166d1.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/3f2b60c5edf0dd995fef4db6528bec3d.gif)
![[IMG]](http://corum.mephist.ru/tex/images/cb492208b3ff459be7b30e1438d8a769.gif)
![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_71273.jpg)
![[IMG]](http://corum.mephist.ru/tex/images/7aadffa13d8527707b6b92a6bd77f2f2.gif) в любой точке области определения имеет предел — это понятно интуитивно. Какую бы точку области определения мы ни взяли,
в любой точке области определения имеет предел — это понятно интуитивно. Какую бы точку области определения мы ни взяли,![[IMG]](http://corum.mephist.ru/tex/images/ff588e68cba2b6ff2160ded5a2527acd.gif) имеет излом. Это сказывается на свойствах функции в точке излома, но с точки зрения предела
имеет излом. Это сказывается на свойствах функции в точке излома, но с точки зрения предела![[IMG]](http://corum.mephist.ru/tex/images/a835d864a3e675940230b41c6e93dd7c.gif) уже интереснее: в точке
уже интереснее: в точке ![[IMG]](http://corum.mephist.ru/tex/images/1567ccbc3aa038b2ecac14e445922a7d.gif) непонятно, какое значение предела приписать функции.
непонятно, какое значение предела приписать функции.![[IMG]](http://corum.mephist.ru/tex/images/d8911b7f8549f7297e185d1728b307d6.gif) при стремлении к нулю хоть слева, хоть справа ведёт себя одинаково, стремясь к бесконечности —
при стремлении к нулю хоть слева, хоть справа ведёт себя одинаково, стремясь к бесконечности —![[IMG]](http://corum.mephist.ru/tex/images/0d7979271f6ac447e112f33fb098bb3a.gif) , которая при стремлении аргумента к нулю стремится к бесконечности, но знак бесконечности зависит от того, с какой
, которая при стремлении аргумента к нулю стремится к бесконечности, но знак бесконечности зависит от того, с какой![[IMG]](http://corum.mephist.ru/tex/images/49e597db094e4215bf693b0766ffe937.gif) ведёт себя в нуле совершенно непонятно.
ведёт себя в нуле совершенно непонятно.![[IMG]](http://corum.mephist.ru/tex/images/04cd061300cde122009c0c451f53ba13.gif) содержится бесчисленное множество точек,
содержится бесчисленное множество точек, ![[IMG]](http://corum.mephist.ru/tex/images/b8921ca1d75b852da96e95cda4aafeb8.gif) называется пределом функции
называется пределом функции ![[IMG]](http://corum.mephist.ru/tex/images/465a703f084c610f250f9ab50ff3f895.gif) в точке
в точке ![[IMG]](http://corum.mephist.ru/tex/images/13acc050d022c395fb51b0cc28d9890c.gif)
![[IMG]](http://corum.mephist.ru/tex/images/01563991d0a9fb218567f432de589884.gif) , если взяв число из достаточно малой окрестности точки
, если взяв число из достаточно малой окрестности точки ![[IMG]](http://corum.mephist.ru/tex/images/40d35aec6a38678f7cb2741d73435c14.gif) ограничивает окрестность
ограничивает окрестность![[IMG]](http://corum.mephist.ru/tex/images/80143d6aee9baf966ffc50105bdb03ad.gif) -окрестности точки
-окрестности точки ![[IMG]](http://corum.mephist.ru/tex/images/ad53e3d8b0ba6681c67b6278ce3ffcd3.gif) .
. ![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_9987.jpg)
![[IMG]](http://corum.mephist.ru/tex/images/a65ec76fd3c631c7acf613f20acc4d71.gif) означает,
означает,![[IMG]](http://corum.mephist.ru/tex/images/a5f2a912b5fd19da74188840a2201796.gif) называется предельной
называется предельной![[IMG]](http://corum.mephist.ru/tex/images/7d47b66519d27f5821540aa071c3d561.gif) в интервале
в интервале ![[IMG]](http://corum.mephist.ru/tex/images/6a6ceef076bfa2e188032b77abf99c51.gif) содержится бесчисленное множество
содержится бесчисленное множество![[IMG]](http://corum.mephist.ru/tex/images/9aaf33c3b6debc0221375d8d51608dab.gif) несмотря на особенность в точке
несмотря на особенность в точке ![[IMG]](http://corum.mephist.ru/tex/images/db524aa87dd37b5368b4a57bcc91d535.gif)
![[IMG]](http://corum.mephist.ru/tex/images/3c543713867629ad5a243a83631e0ddc.gif) — правосторонний предел
— правосторонний предел![[IMG]](http://corum.mephist.ru/tex/images/0b90d0f16ad268d6780902009d6b816f.gif) — левосторонний предел
— левосторонний предел![[IMG]](http://corum.mephist.ru/tex/images/38e64d8d95756c56206888800178111d.gif) :
:![[IMG]](http://corum.mephist.ru/tex/images/073ff490d5fce1b9c6f700a3c4b230a8.gif)
![[IMG]](http://corum.mephist.ru/tex/images/3549e3c5219ffcb7a2f8d8cf525eb6b0.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/e0bbdc41da4dbaf21bf4ca91c9257520.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/b509dbf2f6cbda299bdc81bb6f6ea4f3.gif) , равные нулю. Формальное определение предела на бесконечности:
, равные нулю. Формальное определение предела на бесконечности: ![[IMG]](http://corum.mephist.ru/tex/images/ea264aa2e2c7e39af0e6fbc6f298a8e2.gif)
![[IMG]](http://corum.mephist.ru/tex/images/cf9e0f1401bc597020db01d7b1acced9.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/bf029a6a49f7a2e3c9bd377328e36ffb.gif) по модулю неограниченно растёт. Синус не имеет на бесконечности
по модулю неограниченно растёт. Синус не имеет на бесконечности![[IMG]](http://corum.mephist.ru/tex/images/3c5a0e7caddd89445c619303138ec0b5.gif) . График приведён ниже; по понятным причинам построить его до конца в окрестности
. График приведён ниже; по понятным причинам построить его до конца в окрестности![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_1262.jpg)